Вернер М. Основы кодирования

Подождите немного. Документ загружается.

5.3.

Коды Рида - Соломона 273,

5.3.

Коды

Рида

Соломона

Прежде,

чем

приступить

изложению теории кодов Рида

Соломо-

на,

введем понятие кода

максимальным расстоянием.

Теорема

5.3.1. Граница Синглтона.

Минимальное расстояние

;

любого

(п,

&)-кода (необязательно

линейного) удовлетворяет неравенству

< п

—

к + 1.

Доказательство.

Пусть символы кода принадлежат полю

GF(q).

В множестве

кодовых слов выделим

зафиксируем

—

разря-

дов.

Эти

разряды

могут

содержать самое большее

различных

g-ичных чисел. Следовательно,

во

всем множестве кодовых слов

выделенных к—1 разрядах имеет место

по

крайней мере

—q

сов-

падений.

Рассмотрим любые

два

кодовых слова, совпадающие

меж-

ду собой

в к

—

разрядах.

Так как эти

слова

могут

иметь различие

только

вп-Н1

компонентах, расстояние

между

ними

не

может

превышать величины

—

к + 1. •

Определение.

Любой

код с

минимальным расстоянием, удовлетво-

ряющим равенству

dmin

= П — к + 1

называется кодом

максимальным расстоянием.

Определение.

Код,

который может быть приведен

системати-

ческому

виду

путем

операций,

не

изменяющих дистанционный

про-

филь

кодовых слов, называется разделимым.

Так

как

линейный

код

может быть приведен

систематическому

ви-

ду элементарными преобразованиями порождающей матрицы,

лю-

бой линейный

код

является разделимым.

Определение.

Разделимый

код с

максимальным расстоянием

на-

зывается

МДР

кодом (разделимым кодом

максимальным расстоя-

нием).

Теперь вернемся

кодам Рида

Соломона.

Определение.

Кодом Рида Соломона называется линейный

цик-

лический

(п,п- d+

1)-код

над GF(q), где q = р

длины

п = q - 1,

порождающий многочлен которого

д(Х)

имеет своими корнями

—

последовательных степеней примитивного элемента

а из

поля

GF(q).

Глава

Дискретные

преобразования

Фурье

коды

В качестве порождающего многочлена кода Рида Соломона можно

выбрать, например

д(Х)

= (Х- а){Х

-а

)---(Х-

а"-

Замечание.

Так как

мы

ограничиваемся

только

полями

характе-

ристики

2, то

будем

дальнейшем

вместо

операций

вычитания

использовать

операцию

сложения.

В теории помехоустойчивого кодирования доказывается, что свой-

ства (п, &)-кода Рида Соломона

символами

из GF(q) и

парамет-

рами

—

I, k = п

—

d + 1 не

зависят

от

метода

его

построения

определяются только выбранными значениями

q и d.

Наиболее

просто

код

Рида

Соломона,

а так же

алгоритм

его

декодирова-

ния

реализуется

на

основе дискретных преобразований Фурье,

рас-

смотренных нами

предыдущем разделе. Процедуры кодирования

декодирования такого кода

могут

быть значительно ускорены

помощью техники быстрых преобразований Фурье

(БПФ).

Выберем

зафиксируем некоторое поле

Галуа

GF(q) с q = 2

примитивный

элемент

а £

GF(q)

параметр

Рассмотрим

инфор-

мационный

вектор

и =

(мо,

ui,...,

Wfc-i)

длины

к = п

—

I = q

—

d с

компонентами

из

GF(q).

Поставим

соответствие вектору

вектор

длины

п = q - 1, у

которого первые

компонент совпадают

компо-

нентами вектора

и, а

остальные компоненты

нулевые. Рассмотрим

прямое преобразование Фурье вектора

v в

вектор

определяемое

(5.1)

удовлетворяющее теореме 5.2.1. Тогда справедлива следую-

щая

теорема:

Теорема

5.3.2. Множество

векторов

V в

частотной области

об-

разует (п, к)-код Рида Соломона.

Доказательство.

Представим векторы

v и V в

виде многочленов

v(X)

+ v

X--- + v

-iX

+ 0

•

+ 0

•

k+1

• • •

+ 0

•

Так

как г-ые

временные компоненты вектора

равны нулю

при

< г < п

—

то, согласно теореме

5.2,

многочлен

V(X)

имеет корни

= a

(fc+1

,...

,а~(

= а.

Таким образом, много-

5.4- Декодирование кодов Рида

Соломона

275J

члены

V(X)

образуют

(п,

к)-код Рида

Соломона

порождающим

многочленом

д(Х)

= {Х + а){Х + а

)

• • •

Спектральный

подход

позволяет легко доказать

следующую

теоре-

му.

Теорема

5.3.3. Любой

код

Рида

Соломона является МДР кодом.

Доказательство.

Так как код

Рида

Соломона является линей-

ным,

равно минимальному

весу

кодового слова. Любое кодовое

слово

V =

(Vo,

Vi,.. .Vj,..

•,

Ki-i)

является прямым преобразовани-

ем Фурье некоторого вектора

n-k

В силу теоремы

5.2.2,

j'-ая

частотная компонента равна нулю

тогда

только

тогда,

когда

а?

является корнем многочлена

v(X) =

v\X + h Vfc-iX*-

Согласно основной теореме алгебры, которая

справедлива

и для

конечных полей

Галуа,

многочлен

v(X)

степени

А;

—1

может иметь

поле

GF(q) не

более

А;

—1 корней. Следовательно,

вес любого слова (п,

к)-код&

Рида

Соломона

не

может быть меньше,

чем п—(к— 1)

п—к+1

и, в

силу границы Синглтона d

п—к+1,

то есть код обладает максимальным расстоянием.

Так

как коды Рида

Соломона линейны, они являются МДР кодами.

•

Спектральный

подход

позволяет также достаточно просто интер-

претировать процедуру декодирования кодов Рида

Соломона.

5.4.

Декодирование

кодов

Рида

Соломона

Не

трудно заметить,

что при

образовании кодов Рида

Соломона

информационные

символы можно размещать

любых

рядом стоя-

щих разрядах вектора

v. Из

методических соображений отведем

под

информацию

старшие компоненты

V. В

этом

случае

многочлен

v(X)

будет

иметь, вид

v(X)

= Vn-iX

•

•+v

X"-

+0-X

•

-+0-Х

а порождающий многочлен соответствующего крда Рида

Соломона

имеет

вид

д{Х)

= (Х +

к+1

)(Х

к+2

)

• • •

(X + а").

Глава 5. Дискретные преобразования

Фурье

и коды PC

Как

уже отмечалось ранее, слова рассматриваемого кода Рида Со-

ломона являются прямым преобразованием Фурье множества век-

торов V, то есть v

т±

V. В канале кодовому слову V добавляется

вектор ошибки Е кратности I < d — \.

Рассмотрим обратное преобразование Фурье принятого из канала

слова

R = V + Е, (5.8)

В силу свойства линейности обратного преобразования Фурье имеем

(«

_i +e

_i,...,w

_fc +

_fc,e

_fc_i,e

_ifc_2,...,eo)

^ V + Е, (5.9)

где v = (v

-k,v

-k-\,

• • •

-\) - информационный вектор, лежащий

во временной области, е = (eo,ei,...

_i)

- обратное преобразова-

ние

вектора ошибок. Так как п

—

к правых компонент вектора обрат-

ного преобразования Фурье от V+E не зависят от кодового слова V,

эти

компоненты образуют синдром ошибок. Запишем этот синдром

виде

Sd-2,Sd-l,--.

,Si,S

(5.10)

где so = eo,Si = ei,... ,Sd-2 =

_fc_i.

Заметим, что Синдром явля-

ется некоторым «окном», через которое можно наблюдать обратное

преоразование Фурье вектора ошибки Е.

Обозначим индексы I ненулевых компонент вектора Е через

JitJ2,

• • •

,ji- Определим вектор во временной области, прямое преоб-

разование Фурье которого содержит нулевые компоненты для всех

частот j, для которых Ej ф 0. Проще всего такой вектор задать в

виде многочлена локаторов ошибок

...

(5.11)

Покомпонентное

произведение прямого преобразования Фурье от

многочлена сг(Х) на вектор ошибки Е в частотной области рав-

но

нулю, следовательно циклическая свертка во временной области

вектора а с векторм е также равна нулю '

<г*е = О.

(5.12)

Из

(5.9) и

(5.10)

следует,

что для определения компонент (Ti,<T2,

• • •

,<ri

5.4-

Декодирование

кодов

Рида

Соломона

(согласно

(5.11)

<т

= 1), используя (5.12), мы можем составить си-

стему d

—

I линейных уравнений с 2 неизвестными

<TiS;_i + ... +

ffiso

= О

(5.13)

-2-l = 0.

Сложность, возникающая при решении системы уравнений

(5.13)

со-

стоит в том, что кратность ошибки I нам заранее не известна. Таким

образом, в процессе решения должна еще осуществляться и миними-

зация

значения /, при котором возможно выполнение всех d

—

уравнений из (5.13). Такой простой и эффективный алгоритм был

найден Берлекэмиом в 1967 г. Без преувеличения молено сказать, что

этот алгоритм произвел настоящую революцию в теории и практике

помехоустойчивого кодирования. Он

будет

рассмотрен в следующем

разделе этой главы.

Предположим, что все коэффициенты многочлена а{Х) опреде-

лены.

В этом

случае

остальные к компонент вектора е, то есть ком-

поненты е

-к, e

_fc+i,..., e

_i во временной области,

могут

быть ре-

курентно определены, исходя из (5.12).

Для определения компоненты e^-i нам достаточно решить урав-

нение

_i_j = 0

относительно e^-i, так как все остальные компоненты уже опреде-

лены.

На'втором шаге мы уже можем составить уравнение для опреде-

ления

efc_2- Это уравнение имеет вид

_fc

О\е

-к

<?2Sd-2

•••

<?iSd-l

= 0.

Рекурентно продолжая описанную процедуру, мы найдем все остав-

шихся компоненты вектора е.

Для определения информационного вектора v нам достаточ-

но

вычесть найденные компоненты

_fc,e

_fc

i,...

_i из полу-

ченных обратным преобразованием Фурье от R значений v

-k +

-k,v

-k+i

_fc+i,...

-i

_i.

Самое замечательное в рассмотренном алгоритме состоит в том,

что при его реализации не приходится находить ни корни многочлена

а(Х) (локаторы ошибок), ни значения ошибок.

Теперь общая картина процедуры декодирования ясна и ее можно

сформулировать в виде пяти шагов.

278

Глава

Дискретные

преобразования

Фурье

коды

Шаг 1. Вычислить обратное преобразование Фурье принятого век-

тора R = V + Е. Выделить

SQ,

..., s^-2 во временной области

зангумлениые компоненты информационного вектора v;

Шаг 2. Найти а(Х) из (5.13);

Шаг 3. С помощью рекурентной процедуры вычислить компонен-

ты

_fc

...,

_i;

Шаг 4. Найти информационный вектор v;

Замечание.

Рассмотренный

алгоритм

всегда

исправляет

\^jr\

менее

ошибок.

следующем

разделе

будет

рассмотрен

также

слу-

чай,

когда

число

канальных

ошибок

превышает

L^pJ

•

Для контроля правильности декодирования часто проводится

следующий шаг.

Шаг 5. Вычислить прямое преобразование Фурье вектора v, полу-

чив при этом кодовай вектор V (не всегда совнадаяющий с V).

5.5.

Итеративный алгоритм для нахождения а(Х)

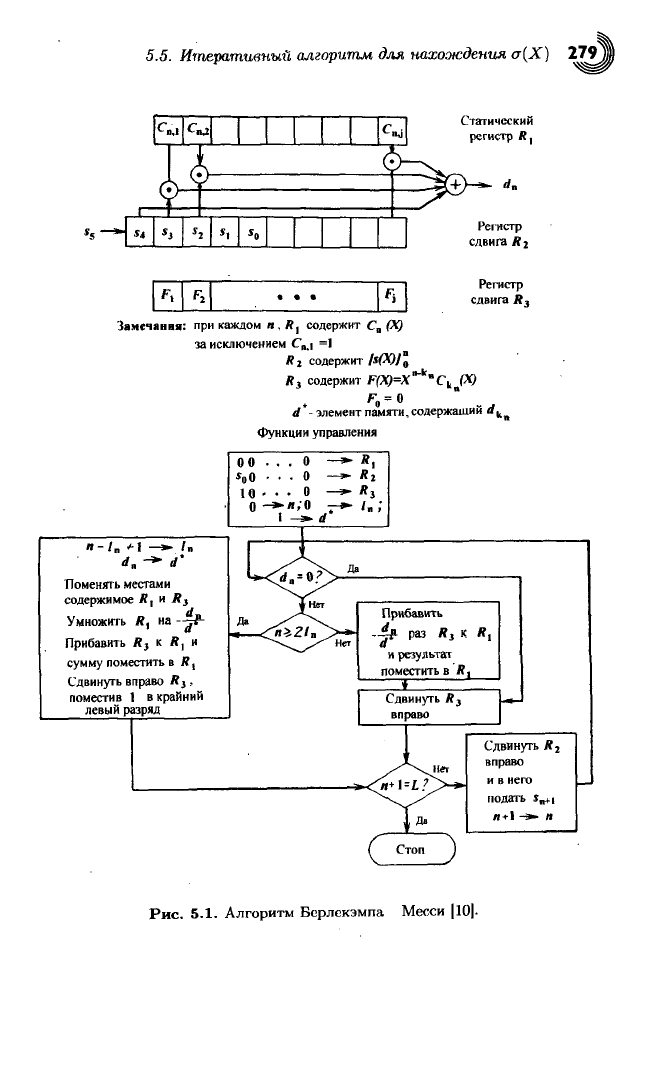
Будем руководствоваться блок-схемой алгоритма, приведенной на

рис.

5.1 ([10] стр. 271). Отметим, что эта блок-схема содержит всю

необходимую информацию для программной или схемной реализа-

ции

алгоритма. Если число ошибок не превышает величины [^pj>

т0

алгоритм находит многочлен о~(Х) минимальной степени I, при ко-

тором выполняется система уравнений (5.13). Доказательству этого

факта в [10] посвящено несколько довольно сложных теорем и заин-

тересованному читателю мы советуем обратится к [10]. Ограничимся

описанием

основных принципов работы алгоритма.

В работе алгоритма используются три регистра. В регистре ди-

намических связей fti на каждом такте декодирования содержит-

ся

очередное итеративное значение а

(Х). Компоненты многочлена

о-

(Х)

на n-ом такте декодирования С

д, С„,2,

• • •,

j, где j - сте-

пень

многочлена.

Рассмотрим процесс вычисления

сг

(Х)

более подробно. В ре-

гистр сдвига Дг последовательно, на каждом такте декодирования

5.5. Итеративный алгоритм

для

нахождения

а{Х)

Статический

регистр

Я,

Регистр

сдвига

Регистр

сдвига

Замечания:

при

каждом

я, Я,

содержит

С„ (X)

за

исключением

j =1

содержит Ы001

содержит

FfX)=X°"

ki|

= О

rf*-

злемент памяти,содержащий

Функции

управления

•

-/„ * I -»- /•

Поменять местами

содержимое

Л, и Jf

Умножить

Л, на

--^J

Прибавить

Я, к Я, и

сумму поместить

в Л

{

Сдвинуть

вправо

поместив

1 в

крайний

левый

разряд

00 ... 0

0 • • • 0

•

• • 0

-*-«;о

я,

«2

/»;

Прибавить

раз

К Я,

и результат

поместить

в I

Сдвинуть

вправо

Сдвинуть

вправо

него

подать

$„+(

я+1

-^- л

Рис.

5.1.

Алгоритм

Берлекэмпа Месси [10].

Глава

Дискретные

преобразования

Фурье

коды

подаются компоненты синдрома .so,

s\,...,

s<j-2- Пусть l

- итератив-

ная

длина регистра R\ на такте п,

тогда

на этом же такте на

выходе

вычисляется

dn =

,i.s

nii

,s-

декодер стремится так скорректировать а

(Х), чтобы реализовать

первое уравнение из системы (5.13). Далее декодер добивается вы-

полнения

второго уравнения из

(5.13)

при сохранении первого и т.д.

Оказывается, что процесс коррекции можно начинать прямо с пер-

вого такта, то есть с

CLQ

SQ.

В результате мы получим а(Х)

мини-

мальной степени, при котором выполняются все уравнения из (5.13).

Контроль правильности всего процесса декодирования происхо-

дит на пятом шаге декодирования. Пусть на этом шаге вычислен

кодовый вектор V. Сравнивая V с R = V + Е можно найти чис-

ло исправлений. Если в канале произошло не более

[^j^-J

ошибок, то

число исправлений должно совпадать со степенью многочлена

<г{Х).

Если число канальных ошибок превышает

L^i^Ji

может про-

изойти одно из

трех

событий. Во-первых, степень многочлена о~(Х)

может оказаться выше

[^y^J.

Тогда процесс декодирования преры-

вается уже на втором этапе декодирования. Во-вторых, число ис-

правлений может не совпадать со степенью а{Х), такая ошибка об-

наруживается в конце декодирования. И, наконец, вполне возможно,

что число исправлений совпадает со степенью о(Х) и не превышает

L~3pJ-

Здесь имеет место необнаружимая ошибка декодирования.

Заметим, что для реализации этого алгоритма требуются незна-

чительные технические затраты и в настоящее время декодеры кодов

Рида - Соломона работают на скоростях до 40 Гбит/сек.

Литература

[1] С. Е. Shenon: A mathematical theory of communication

Bell

Sys.

Tech. J., vol 27, 1948,

S.379-423,

(Имеется перевод: Шеннон К.

Математическая теория связи.-В сб.: Работы по теории инфор-

мации

и кибернетики. -М.: ИЛ, 1963)

[2] С. Berrou, A. Glavieux: "Near Optimum Error-Correcting Coding

and Decoding: Turbo Codes."IEEE Trans. Commun. Vol. 44, 1996,

S.1261-1270

[3) C. Berrou, A. Glavieux, P.Thitimajshima: "Near Shannon Limit

Error-Correcting Coding and Decoding: Turbo Codes."Proc. IEEE

Int.

Conf.

Commun., May 1993, S.

1064-1070

[4) R. E. Blahut: Principles and practice of information theory, Reading,

Mass.:

Addison-Wesley

Publishing Company,1987

[5] R. E. Blahut: Principles and practice of error control coding,

Addison-Wesley

Publishing Company,1984 (Имеется перевод: Блей-

хут. Р. Теория и практика кодов, контролирующих ошибки. -М.:

Мир,

1986)

[6] D. A. Huffman: "A method for the Construction of Minimum

Redunduncy Codes."Proc. IRE, vol.

40,1952,S.1098-1101,

(Имеет-

ся

перевод: Хаффман Д. А. Методы построения кодов с мини-

мальной избыточностью.-Кибернетический сб. вып. З.-М.: ИЛ,

1961)

[7] S. Lin, D. J. Costello: Error control coding: Fundamentals and

Applications,

Englewood

Cliffs,

NJ,: Prentice- Hall Inc., 1983

[8] F. J.

MacWilliams,

N. J. Sloane: The Theory of Error-Correcting j

Codes. Amsterdam: North-Holland, 1977, (Имеется перевод: Мак-

Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов исправляющих

ошибки.

-М.: Связь, 1979)

[9] N.

Wiener:

Cybernetics or Control and Communication in the

Animal and the Mashine. Paris: Hermann, 1948

282

Литература

[10] R. G. Gallager: Information Theory and Reliable Communication.

New

York:

John

Willey

and Sons Inc. 1968, (Имеется перевод: Га-

лагер Р. Теория информации и надежная связь.-М.: Сов. радио,

1974)

[11] W. W. Peterson, E. J. Weldon: Error- Correcting Codes. 2nd ed.

-Cambrige (Mass.): MIT Press, 1971 (Имеется перевод: Питерсен

У., Уэлдон Э. Коды, исправляющие ошибки. -М.: Мир, 1976)

[12] G. Ungerbock: Channel Coding with Multilevel/phase Signals.

IEEE

Trans. Inform. Theory, IT-28,1982,

S.55-67.

[13] J. G.Proakis: Digital Communications. New

York:

McGraw-Hill,

2000.