Venables J. Introduction to Surface and Thin Film Processes
Подождите немного. Документ загружается.

BCF then showed that x
s
5(D
t
a
)
1/2
is a characteristic length, which governs the fate of
the adatom, and defines the role of ledges (steps) in evaporation or condensation. It is
a useful exercise to familiarize oneself with the ideas of local equilibrium, and diffusion
in one dimension. Local equilibrium can be described either in terms of differential
equations or of chemical potentials as set out in problems 1.2 and 1.4; diffusion needs
a differential equation formulation and/or a MC simulation.
The main points that result from the above considerations are as follows.
(1) Crystal growth (or sublimation) is difficult on a perfect terrace, and substantial
supersaturation (undersaturation) is required. When growth does occur, it pro-
ceeds through nucleation and growth stages, with monolayer thick islands (pits)
having to be nucleated before growth (sublimation) can proceed; this is illustrated
by early MC calculations in figure 1.12.
(2) A ledge, or step on the surface captures arriving atoms within a zone of width x
s
either
side of the step, statistically speaking. If there are only individual steps running across
the terrace, then these will eventually grow out, and the resulting terrace will grow
much more slowly (as in point 1). In general, rough surfaces grow faster than smooth
surfaces, so that the final ‘growth form’ consists entirely of slow growing faces;
(3) The presence of a screw dislocation in the crystal provides a step (or multiple step),
which spirals under the flux of adatoms. This provides a mechanism for continu-
ing growth at modest supersaturation, as illustrated by MC calculations in figure
1.13 (Weeks & Gilmer 1979).
Detailed study shows that the growth velocity depends quadratically on the super-
saturation for mechanism 3, and exponentially for mechanism 1, so that dislocations
are dominant at low supersaturation, as shown in figure 1.14. Growth from the liquid
and from solution has been similarly treated, emphasizing the internal energy change
on melting L
m
, and a single parameter
a
proportional to L
m
/kT, where
a
,2 typical for
melt growth of elemental solids corresponds to rough liquid–solid interfaces (Jackson
1.3 Thermodynamics versus kinetics 17
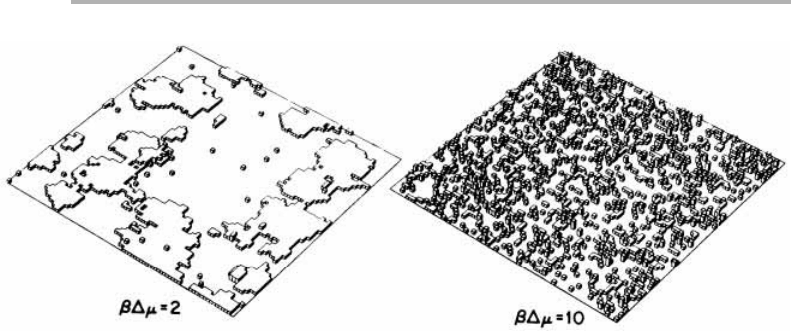
Figure 1.12. MC interface configurations after 0.25 monolayer deposition at the same
temperature on terraces, under two different supersaturations
b
Dm52 and 10; the bond
strength is expressed as
f
54kT (Weeks & Gilmer 1979, reproduced with permission).

Figure 1.13. MC interface configurations during deposition in the pr
esence of a screw dislocation which causes a double step (a) i
n
equilibrium, and (b)–(d) as a function of time under supersatura
tion
b
Dm51.5, for bond strength expressed in terms of temperature as
L/kT5
12, equivalent to
f
54kT (Weeks & Gilmer 1979, reproduced with permission).
L
/
kT
=12
(a) D
m
/
kT
=0
(b) D
m
/
kT
=1.5
(c) D
m
/
kT
=1.5
(d) D
m
/
kT
=1.5

1958, Jackson et al. 1967, Woodruff 1973). Growth from the vapor via smooth inter-
faces are characterized by larger
a
values, either because the sublimation energy L
0
..
L
m
, and/or the growth temperature is much lower than the melting temperature. Such
an outline description is clearly only an introduction to a complex topic, and further
information can be obtained from the books quoted, from several review articles (e.g.
Leamy et al. 1975, Weeks & Gilmer 1979), or from more recent handbook articles
(Hurle 1993, 1994). But the reader should be warned in advance that this is not a simple
exercise; there are considerable notational difficulties, and the literature is widely dis-
persed. We return to some of these topics in chapters 5, 7 and 8.
1.4 Introduction to surface and adsorbate reconstructions
1.4.1 Overview
In this section, the ideas about surface structure which we will need for later chapters
are introduced briefly. However, if you have never come across the idea of surface
1.4 Introduction to surface and adsorbate reconstructions 19
Figure 1.14. MC growth rates (R/k
1
a) during deposition for spiral growth (in the presence of a
screw dislocation) compared with nucleation on a perfect terrace as a function of
supersaturation
b
Dm, for bond strength expressed in terms of temperature as L/kT512,
equivalent to
f
54kT (Weeks & Gilmer 1979, reproduced with permission).

reconstruction, it is advisable to supplement this description with one in another text-
book from those given under further reading at the end of the chapter. This is also a
good point to become familiar with low energy electron diffraction (LEED) and other
widely used structural techniques, either from these books, or from a book especially
devoted to the topic (e.g. Clarke 1985, chapters 1 and 2). A review by Van Hove &
Somorjai (1994) contains details on where to find solved structures, most of which are
available on disc, or in an atlas with pictures (Watson et al. 1996). We will not need this
detail here, but it is useful to know that such material exists (see Appendix D).
The rest of this section consists of general comments on structures (section 1.4.2),
and, in sections 1.4.3–1.4.8, some examples of different reconstructions, their vibra-
tions and phase transitions. There are many structures, and not all will be interesting
to all readers: the structures described all have some connection to the rest of the book.
1.4.2 General comments and notation
Termination of the lattice at the surface leads to the destruction of periodicity, and
a loss of symmetry. It is conventional to use the z-axis for the surface normal, leaving
x and y for directions in the surface plane. Therefore there is no need for the lattice
spacing c(z) to be constant, and in general it is not equal to the bulk value. One can
think of this as c(z) or c(m) where m is the layer number, starting at m51 at the surface.
Then c(m) tends to the bulk value c
0
or c, a few layers below the surface, in a way which
reflects the bonding of the particular crystal and the specific crystal face.
Equally, it is not necessary that the lateral periodicity in (x,y) is the same as the bulk
periodicity (a,b). On the other hand, because the surface layers are in close contact with
the bulk, there is a strong tendency for the periodicity to be, if not the same, a simple
multiple, sub-multiple or rational fraction of a and b, a commensurate structure. This
leads to Wood’s (1964) notation for surface and adsorbate layers. An example related
to chemisorbed oxygen on Cu(001) is shown here in figure 1.15 (Watson et al. 1996).
Note that we are using (001) here rather than the often used (100) notation to empha-
size that the x and y directions are directions in the surface; however, these planes are
equivalent in cubic crystals and can be written in general as {100}; similarly, specific
directions are written [100] and general directions 冓100冔 in accord with standard crys-
tallographic practice (see e.g. Kelly & Groves 1970).
But first let us get the basic notation straight, as this can be somewhat confusing. For
example, here we have used (a,b,c) for the lattice constants; but these are not necessar-
ily the normal lattice constants of the crystal, since they were defined with respect to a
particular (hkl) surface. Also, several books use a
1,2,3
for the real lattice and b
1,2,3
for the
reciprocal lattice, which is undoubtedly more compact. Wood’s notation originates in
a (232) matrix M relating the surface parameters (a,b) or a
s
to the bulk (a
0
,b
0
) or a
b
.
But the full notation, e.g. Ni(110)c(232)O, complete with the matrix M, is rather for-
bidding (Prutton 1994). If you were working on oxygen adsorption on nickel you
would simply refer to this as a c(232), or ‘centered 2 by 2’ structure; that of adsorbed
O on Cu(001)-(2冑23冑2)R45°-2O shown in figure 1.15 would, assuming the context
were not confusing, be termed informally a 2冑2 structure.
20 1 Introduction to surface processes
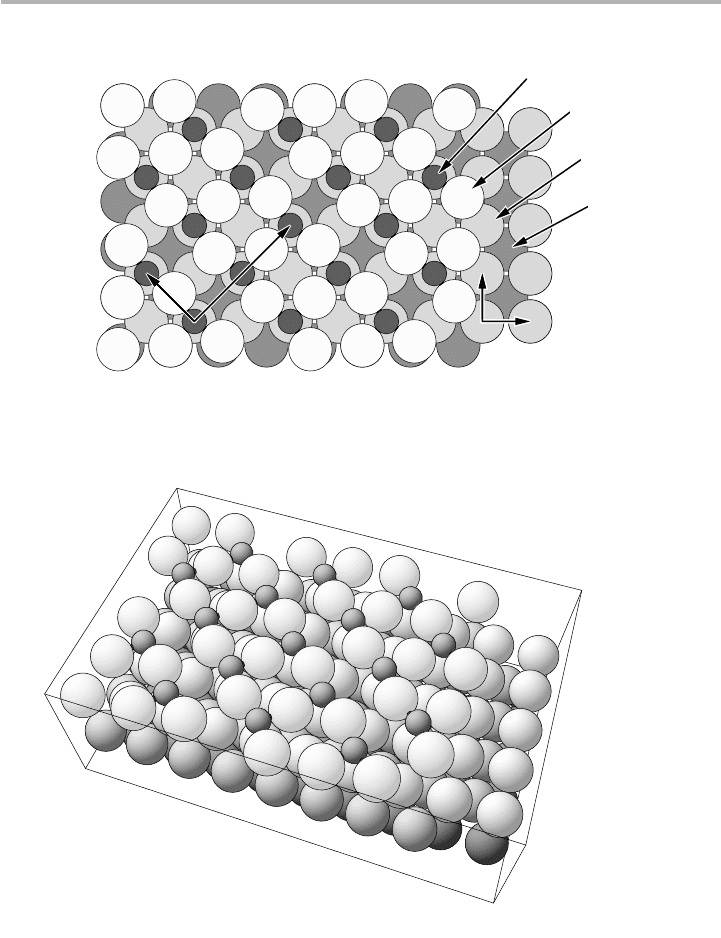
1.4 Introduction to surface and adsorbate reconstructions 21
Figure 1.15. Wood’s notation, as illustrated for the chemisorbed structure Cu(001)-
(2冑23冑2)R45°-2O in (a) top and (b) perspective view. The 2冑2 and the 冑2 represent the ratios
of the lengths of the absorbate unit cell to the substrate Cu(001) surface unit cell. The R45°
represents the angle through which the adsorbate cell is rotated to this substrate surface cell,
and the 2O indicates there are two oxygen atoms per unit cell. The different shading levels
indicate Cu atoms in layers beneath the surface (after Watson et al. 1996, reproduced with
permission).
BALSAC plot
Cu(100)-(2√2x√2)R45°-2O (perspective)
O
Cu(1)
Cu(2)
Cu(3)
BALSAC plot
Cu(100)-(2√2x√2)R45°-2O (top view)
(a)
(b)

From the surface structure sections of the textbooks referred to, we can learn that
there are five Bravais lattices in 2D, as against fourteen in 3D. For example, many struc-
tures on (001) have a centered rectangular structure. If the two sides of the rectangle
were the same length, then the symmetry would be square; but is it a centered square?
The answer is no, because we can reduce the structure to a simple square by rotating
the axes through 45°. This means that the surface axes on commonly discussed sur-
faces, e.g. the f.c.c. noble metals such as the Cu(001) of figure 1.15 or the diamond cubic
{001} surfaces discussed later, are typically at 45° to the underlying bulk structure; the
surface lattice vectors are a/2冓110冔.
Typical structures that one encounters include the following.
*(131): this is a ‘bulk termination’. Note that this does not mean that the surface is
similar to the bulk in all respects, merely that the average lateral periodicity is the
same as the bulk. It may also be referred to as ‘(131)’, implying that ‘we know it isn’t
really’ but that is what the LEED pattern shows. Examples include the high temper-
ature Si and Ge(111) structures, which are thought to contain mobile adatoms that
do not show up in the LEED pattern because they are not ordered.
*(231), (232), (434), (636), c(232), c(234), c(238), etc: these occur frequently
on semiconductor surfaces. We consider Si(001)231 in detail later. Note that the
symmetry of the surface is often less than that of the bulk. Si(001) is four-fold sym-
metric, but the two-fold symmetry of the 231 surface can be constructed in two
ways (231) and (132). These form two domains on the surface as discussed later in
section 1.4.4.
* 冑33冑3R30°: this often occurs on a trigonal or hexagonal symmetry substrate,
including a whole variety of metals adsorbed on Si or Ge(111), and adsorbed gases
on graphite (0001). Anyone who works on these topics calls it the 冑3, or root-three,
structure. This structure can often be incommensurate, as shown in figure 1.16,
drawn to represent xenon adsorbed on graphite, as can be explored later via problem
4.1. If a structure is incommensurate, it doesn’t necessarily have to have the full sym-
metry of the surface. Sometimes we can have structures which are commensurate in
one direction and incommensurate in another: these may be referred to as striped
phases. These will also form domains, typically three, because of the underlying sym-
metry.
1.4.3 Examples of (1x1) structures
These ‘bulk termination’ structures include some f.c.c. metals, such as Ni, Ag, Pt(111),
Cu and Ni(001), and Fe, Mo and W(110) amongst b.c.c. metals. One may expect this
list to get shorter with time, rather than longer, as more sensitive tests may detect depar-
tures from (131). For example, W and Mo(001) are 131 at high temperature, but have
phase transitions to (231) and related incommensurate structures at low temperature
(Debe & King 1977, Felter et al. 1977, Estrup 1994). Lower symmetries are more
common at low temperature than at high temperature in general. This is a feature that
surfaces have in common with bulk solids such as ferroelectrics. The interaction
between the atoms is strongly anharmonic, leading perhaps to double-well interaction
22 1 Introduction to surface processes

potentials. At high temperature, the vibrations of the atoms span both the wells, but at
low temperature the atoms choose one or the other. There is an excellent executive toy
which achieves the same effect with a pendulum and magnets . . . check it out!
The c-spacing of metal (131) surface layers have been extensively studied using
LEED, and are found mostly to relax inwards by several percent. This is a general
feature of metallic binding, where what counts primarily is the electron density around
the atom, rather than the directionality of ‘bonds’. The atoms like to surround them-
selves with a particular electron density: because some of this density is removed in
forming the surface, the surface atoms snuggle up closer to compensate. We return to
this point, which is embodied in embedded atom, effective medium and related theo-
ries of metals in chapter 6.
Rare gas solids (Ar, Kr, Xe, etc.) relax in the opposite sense. These solids can be
modeled fairly well by simple pair potentials, such as the Lennard-Jones 6–12 (LJ)
potential; they are accurately modeled with refined potentials plus small many-body
corrections (Klein & Venables 1976). Such LJ potential calculations have been used to
explore the spacings and lattice vibrations at these (131) surfaces (Allen & deWette
1969, Lagally 1975). The surface expands outwards by a few percent in the first
two–three layers, more for the open surface (110) than the close packed (111), as shown
1.4 Introduction to surface and adsorbate reconstructions 23
Figure 1.16. The incommensurate 冑33冑3R30° structure of adsorbed xenon (lattice parameter
a) on graphite with a lattice parameter a
c
. Note that the Xe adatoms approximately sit in every
third graphite hexagon, close to either A, B or C sites; they would do so exactly in the
commensurate phase. The arrows indicate the displacement, or Burgers, vectors associated
with the domain walls, sometimes called misfit dislocations. On a larger scale these domain
walls form a hexagonal network, spacing d, as in problem 4.1 (after Venables & Schabes-
Retchkiman, 1978, reproduced with permission).
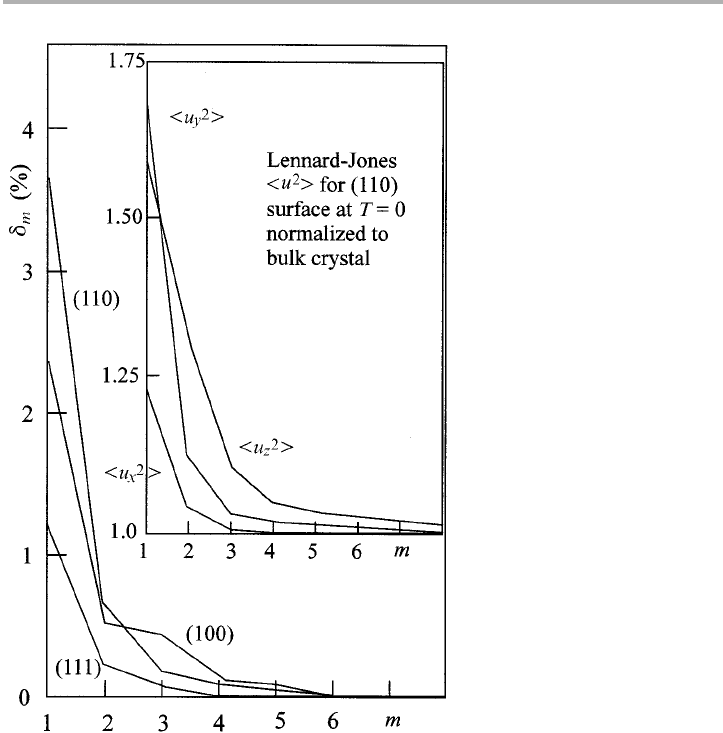
in figure 1.17. The inset in figure 1.17 and table 1.2 explore the vibrations calculated for
the LJ potential, and remind us that the lower symmetry at the surface means that the
mean square displacements are not the same parallel and perpendicular to the surface;
on (110) all three modes are different. Different lattice dynamical models have given
rather different answers. This is because the vibrations are sufficiently large for anhar-
monicity to assume greater importance at the surface.
1.4.4 Si(001) (2
3
1) and related semiconductor structures
Let us start by drawing Si(001) 231 and 132. First, draw the diamond cubic structure
in plan view on (001), labeling the atom heights as 0, 1/4, 1/2 or 3/4 (or equivalently
24 1 Introduction to surface processes
Figure 1.17. Static displacements
d
m
, expressed as a percentage of the lattice spacing m layers
from the surface, for (001), (110) and (111) surfaces of an f.c.c. Lennard-Jones crystal; right-
hand inset). Ratios of mean square displacement amplitudes 冓u
2
冔, expressed as a ratio of the
bulk value, for the (110) surface of an f.c.c. Lennard-Jones crystal approximating solid argon
(after Allen & deWette 1969, Lagally 1975, replotted with permission).

21/4), three to four unit cells being sufficient, after the manner of figure 1.18. The
surface can occur between any of these two adjacent heights. There are two domains
at right angles, aligned along different 冓110冔 directions. The reconstruction arises
because the surface atoms dimerize along these two [110] and [11
¯
0] directions, to reduce
the density of dangling bonds, producing a unit cell which is twice as long as it is broad;
hence the 231 notation. Once you have got the geometry sorted out, you can see that
the two different domains are associated with different heights in the cell, so that one
terrace will have one domain orientation, then there will be a step of height 1/4 lattice
constant, and the next terrace has the other domain orientation. This is already quite
complicated!
Listening to specialists in this area can tax your geometric imagination, because the
dimers form into rows, which are perpendicular to the dimers themselves – dimer and
dimer row directions are both along 冓110冔 directions, but are not along the same direc-
tion, they are at right angles to each other. Moreover, there are two types of ‘single
height steps’, referred to as S
A
and S
B
, which have different energies, and alternate
domains as described above. There are also ‘double height steps’ D
A
and D
B
, which go
with one particular domain type. Then you can worry about whether the step direction
will run parallel, perpendicular or at an arbitrary angle to the dimers (or dimer rows,
if you want to get confused, or vice versa). The dimers can also be symmetric (in height)
or unsymmetric, and these unsymmetric dimers can be arranged in ordered arrays,
232, c(234), c(238), etc.
With all the intrinsic and unavoidable complexity, it is sensible to ask yourself
whether you really need to know all this stuff. Semiconductor surface structures, and
the growth of semiconductor devices, are specialist topics, which we will return to later
1.4 Introduction to surface and adsorbate reconstructions 25
Table 1.2. The ratios of the mean square displacements of surface atoms to those in the
bulk for a Lennard-Jones crystal
Surface Component SFC [1] QH (T
m
/2) [2] MD (T
m
/2) [3]
(001) 冓u
x
2
冔5冓u
y
2
冔 1.46 2.03 2.23 6 0.17
冓u
z
2
冔 1.87 2.77 3.07 6 0.15
(111) 冓u
x
2
冔5冓u
y
2
冔 1.30 1.45 1.27 6 0.07
冓u
z
2
冔 1.86 2.85 3.48 6 0.18
(110) 冓u
x
2
冔 1.50 1.78 1.89 6 0.20
冓u
y
2
冔 2.14 3.21 4.99 6 0.65
冓u
z
2
冔 1.83 3.03 3.57 6 0.25
Notes:
[1] Simple force-constant model, with force constants at the surface equal to those in the bulk.
[2] Quasi-harmonic approximation, changes in the surface force constants determined at T
m
/2
(where T
m
is melting temperature).
[3] Molecular Dynamics (MD) computer experiment at T
m
/2, which includes anharmonicity.
Sources: After Allen & deWette 1969, Lagally 1975.
in chapters 7 and 8. However, I am assuming that several of you really do need to know
about these structures. To my way of thinking, they are remarkably interesting and
important! Why? Because semiconductor technology has arrived at the point of
growing devices with nanometer dimensions on clean surfaces, using MBE, CVD, ALE
or whatever new technique is invented next year; the surface processes which take place
at the monolayer level actually influence performance and reliability. This is an
amazing fact of late twentieth century life, one which is set to be dominant for electri-
cal and chemical engineering in the twenty-first century. As we will explore in chapters
2 and 3, we now have experimental techniques for producing, analyzing and visualiz-
ing these nanometer scale structures, often down to atomic detail. Thus, it is worth
sticking with the topic for awhile.
Meanwhile, on the subject of surface reconstructions, we abstract three salient
points.
(a) The existence of a particular type of structure, e.g. 231, does not determine the
actual atomic arrangement. This typically has been determined by a detailed anal-
ysis of LEED Intensity–Voltage (I–V) curves, and an experiment–theory compar-
ison in the form of a reliability or R-factor (Clarke 1985, chapter 7). For example,
as shown in figure 1.19, three different models of Si(001) 231 were proposed
before the dimer model (figure 1.19(a)) became widely accepted.
(b) The number of possible domains depends on the symmetry. For Si(111) with the
26 1 Introduction to surface processes
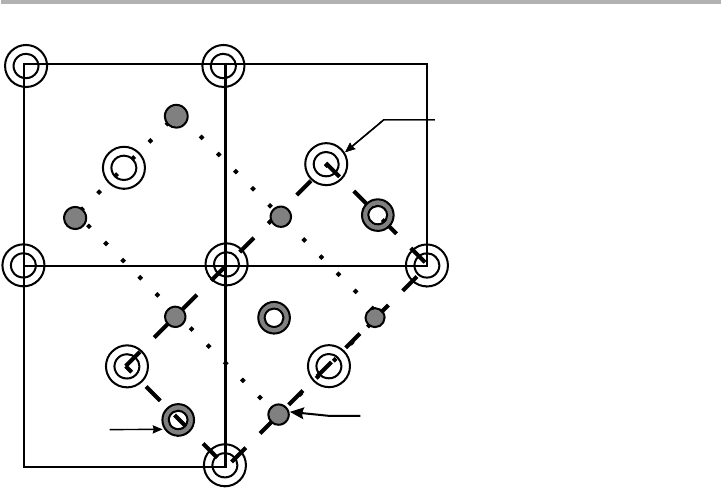
Figure 1.18. Diagram of Si(001) bulk unit cells (full lines), showing how the 231 and 132
domains arise. If the surface atoms are at level 0, atoms A and B move together, i.e. they
dimerize, leading to the 231 cell given by the dotted line; but if the surface atoms are at level
11/4, atoms C and D dimerize, leading to the 132 cell shown by the dashed line.
A
B
Level –1/4
(2x1)
C
D
Level 0
(1x2)
Level 0
(1x2)
Level
+1/4
