Вавиловский В.И., Махалесова О.Е. Теоретические основы инженерного проектирования автоматических систем
Подождите немного. Документ загружается.

21
Аппроксимация объекта, не имеющего чистого запаздывания
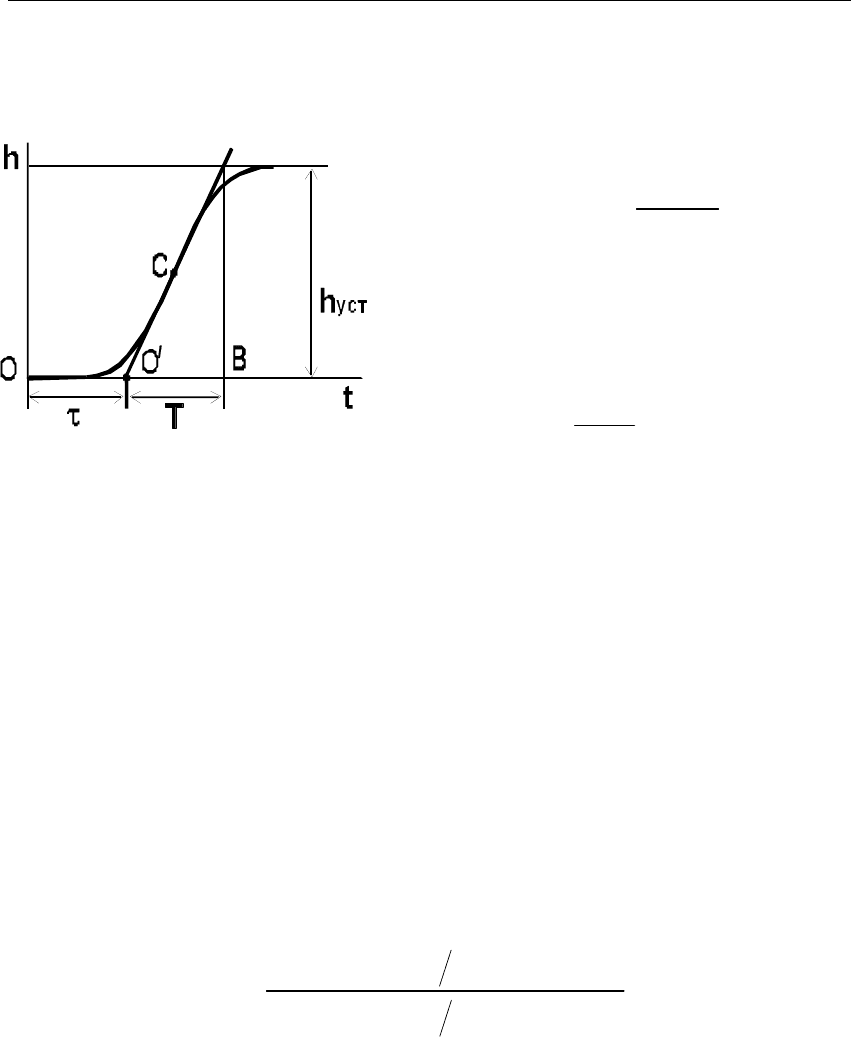
Переходный процесс объекта представлен S-образной кривой
(рисунок 4.22), которую можно аппроксимировать звеном с запазды-
ванием и апериодическим звеном.
Рисунок 4.22 − Переходная характеристика
звена не имеющего чистого запаздывания
;
1
)(
p
е
Tp
k
pW
⋅−
⋅
+
=
τ
;
/
ОО=
τ
;
/
СОТ =
.
А
h
k
УСТ
=
Подход с искусственным введением звена запаздывания при
аппроксимации объекта в общем случае усложняет математическую
модель объекта, для синтеза системы выбор регулятора в соответст-
вии с моделью (с учетом е
-
τ
р
) обеспечит устойчивость системы в це-
лом с запасом. Для подобных случаев существуют специальные ме-
тоды выбора регуляторов по соответствующим графикам с координа-
тами в логарифмическом масштабе для выбора типа регулятора и па-
раметров его настройки в функции относительно времени τ /T.
При синтезе и анализе систем с запаздыванием функцию е
-
τ
р
целесообразно разложить в ряд Пада, и учитывать только два, три
члена ряда
(
)
()
...1215,01
...1215,01
22
22
+++
++−
=
−
рр
рр
е
р
ττ
ττ
τ
.
4.6 Выбор математических моделей и значений
параметров объекта по результатам активного
эксперимента
При различных режимах работы объекта математическая мо-
дель его может быть одинаковой или разной, например при одном
режиме – апериодический процесс, а при другом − колебательный.
22
В каждом режиме работы объекта проводится группа экспери-
ментов при одних и тех же условиях.
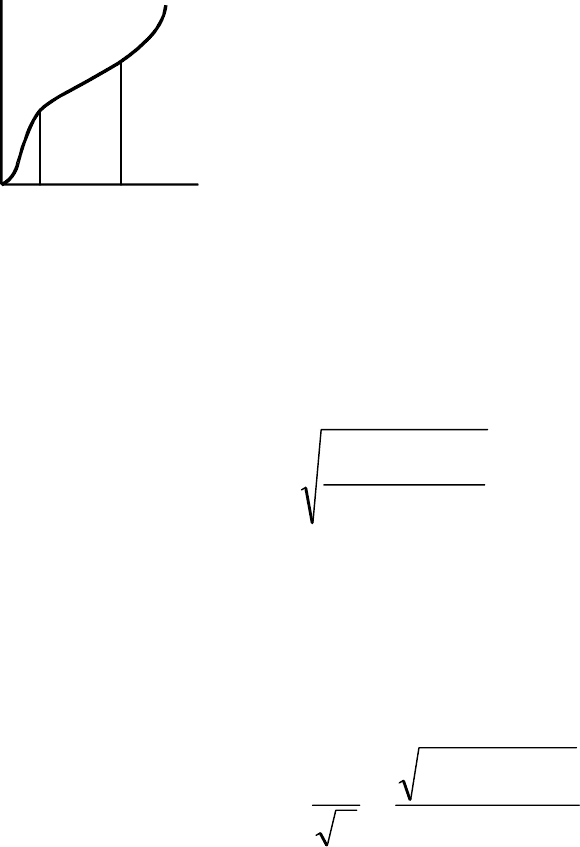
Рисунок 4.23 − нелинейная
модель объекта
Например, в точках А и В (рисунок
4.23) получено по n значений передаточно-
го коэффициента…
По результатам группы опытов при
конкретном режиме работы объекта опре-
деляется среднее арифметическое значение
параметров объекта.
Чтобы оценить точность полученных результатов определяется
средняя квадратичная ошибка полученного значения параметра, на-
пример для передаточного коэффициента k
n
kk
срi
k
2
)( −Σ
=
σ
(4.1)
где k
i
– текущее значение передаточного коэффициента;
k
cp
– среднее арифметическое его значение;
n – количество измерений.
Затем определяется среднеквадратичная ошибка найденного
среднего значения
n
kk
n
срi
k
срk
2
.
)( −Σ
==
σ
σ
. (4.2)
При этом должно соблюдаться условие
срзадсрk
k)15,010,0(
)(.
−
≤
σ
, (4.3)
где
σ
k cp.(зад)
– заданное значение среднеквадратичной ошибки.
Если полученное значение
σ
k.cp
>
σ
k.cp.(зад)
следовательно, необ-
ходимо провести дополнительные измерения при тех же условиях.
Тогда количество требуемых измерений вычисляется из формулы
(4.2), с учетом (4.3).
Для различных групп экспериментов математическая модель и
параметры объекта могут существенно различаться. Целесообразно
попробовать выбрать для разных режимов его работы регулятор с по-
y
A
B
0
x
23
стоянными параметрами настройки и законом регулирования, то есть
типа регулятора.
Если не удастся выбрать регулятор с постоянными параметра-
ми настройки, то следует применить систему адаптивного управления
с регулятором, алгоритм и параметры которого подстраиваются под
математическую модель и параметры объекта, т.е. подстраиваются
под различные режимы.
Для выбора математической модели согласно минимаксному
критерию оценки оптимальности САУ целесообразно применять ми-
нимаксный подход, который заключается в следующем.
Из всех возможных вариантов математических моделей объек-
та выбирается модель и ее параметры, наиболее неблагоприятные с
позиции динамики САУ, исходя из запасов устойчивости по ампли-
туде и по фазе. Тогда структура и сочетание параметров модели объ-
екта для более благоприятного режима его работы с выбранным ре-
гулятором обеспечит с гарантией заданные показатели качества про-
цесса регулирования. Процесс при этом будет более монотонным, хо-
тя несколько может увеличиться время регулирования (рисунок 4.24).
Например, для устойчивых (минимально-фазовых) объектов, а
также для астатических объектов принимается наибольшее значение
передаточного коэффициента k. Если настроить регулятор на макси-
мальное значение k, то при меньшем его значении запас устойчивости
будет больше. При этом постоянные времени объекта также прини-
маются максимальными.
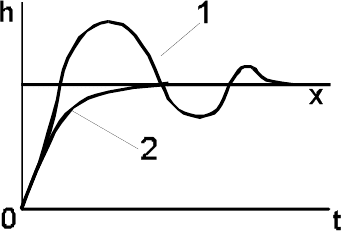
1 − переходный процесс САР
при неблагоприятном режиме рабо-
ты объекта;
2 − переходный процесс САР
при благоприятном режиме работы
объекта.
Рисунок 4.24 − Переходные процессы САР
Для неустойчивых объектов, представленными неминемально-
фазовыми математическими моделями, следуя минимаксному подхо-
ду к оценке их параметров, в большинстве случаев следует прини-
мать минимальные значения параметров модели объекта. Например,
для объекта описываемого неустойчивым апериодическим звеном не-

24
обходимо принимать минимальные значения параметров этого звена
(рисунок 4.25 а и б).
а
б
а − логарифмическая фазовая частотная характеристика;
б − переходная характеристика
Рисунок 4.25 − Характеристики устойчивого (1) и неустойчивого (2)
апериодического звена
Рассмотрим вышеизложенное на примере асинхронного элек-
тродвигателя (рисунок 4.26) с тиристорным преобразователем напря-
жения в цепи статора.
1 – при регулировании напряжения на статоре; 2 –при регулировании
напряжения на статоре с введением отрицательной обратной связи.
Рисунок 4.26 − Механические характеристики асинхронного двигателя
Передаточные функции рассматриваемого двигателя (без
введения обратной связи) как объекта управления при его пуске
будут иметь вид:
ekSSпри
pT
k
W >
−
= ,
1
1
1
1
(4.4)

25
kSSпри
p
k
W == ,
2
2
(4.5)
ekSSпри
pT
k
W <
+
= ,
13
3
3
(4.6)
Приведенные передаточные функции (4.4), (4.5) и (4.6) как ма-
тематические модели объекта, имеют существенно переменные пара-
метры, зависящие от напряжения и скольжения двигателя. В связи с
этим, согласно минимаксному критерию оценки оптимальности
управления при синтезе САР скорости следует в качестве математи-
ческой модели принять электродвигатель. Как объект управления
следует принять математическую модель, представленную неустой-
чивым апериодическим звеном W
1
(р), с минимальными значениями
параметров к и Т.
4.7 Особенности определения математической модели и
параметров объекта с относительно большой
длительностью переходного процесса
При длительном переходном процессе объекта управления тре-
буется определить его математическую модель и параметры для кон-
кретных режимов его работы объекта, исходя из требуемых показате-
лей качества процесса регулирования настраиваемой САУ. Сказанное
определяется возможной изменчивостью математической модели и
параметров объекта, при его работе в конкретных режимах.
В качестве примера рассмотрим тяговую аккумуляторную ба-
тарею шахтового и общепромышленного назначения, функциональ-
ная схема которой представлена на рисунок 4.27. Как объект управ-
ления в системе стабилизации зарядного тока, т.е. САР тока при заря-
де и разряде тяговой аккумуляторной батареи.
Рисунок 4.27 − Функциональная схема силовой части систем зарядно-
разрядного устройства тяговых аккумуляторных батарей.
26
4.8 Экспериментальное определение и выбор параметров
тяговой аккумуляторной батареи как объекта
автоматического регулирования
Эксплуатационно-технические характеристики химических ис-
точников тока и, в частности, тяговых аккумуляторных батарей (ТАБ)
существенно зависят от качества их формировки при вводе в работу,
заряда и тренировочно-востановительных циклов в процессе эксплуа-
тации. Разрабатываемые для этих целей тиристорные зарядные (ЗУ) и
зарядно-разрядные (ЗРУ) устройства базируются на системах автома-
тического регулирования(САР) тока и напряжения, при построении
которых возникает необходимость в исследовании общих динамиче-
ских свойств ТАБ как объекта автоматического регулирования и в
выборе конкретных значений данного объекта.
Необходимый объем и достоверность информации о ТАБ как
объекте автоматического регулирования обеспечиваются примене-
нием при исследованиях экспериментального метода переходного
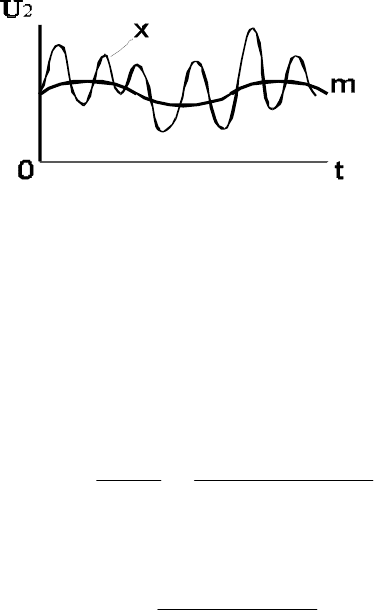
процесса Внешним возмущающим воздействием для зарядно-
разрядных устройств является изменение напряжения питающей се-
ти, которое имеет высокочастотную составляющую х и медленно из-
меняющуюся составляющую m (рисунок 4.28 ).
m – математическое ожидание; x – высокочастотная составляющая
Рисунок 4.28 − Возмущающие воздействия для зарядно-разрядных
устройств
При этом установлено, что на заданном интервале времени ре-
гулирования САР (0,5÷0,7с) тяговая батарея в режимах заряда и раз-
ряда ведет себя как звено общего вида первого порядка с преоблада-
нием дифференцирующего эффекта, передаточная функция которого
,
1
)1(
)(
)(
+
+
=
∆
=
pT
pTk
U
tI
рW
Б
БББ
Б
З
Б
α
(4.7)
или
1
)1(
)(
+
+
=
pT
pTk
рW
Б
ПБ
Б
, (4.8)
27
где I
Б
– ток батареи;
к
Б
– передаточный коэффициент;
Т
П
– постоянная времени поляризации электродов;
Т
Б
– постоянная времени батареи;
∆
U
Б
– падение напряжения на внутреннем сопротивлении
батареи;
α
Б
>1 – коэффициент кратности постоянных времени, харак-
теризующий степень дифференцирования батареей
входного воздействия.
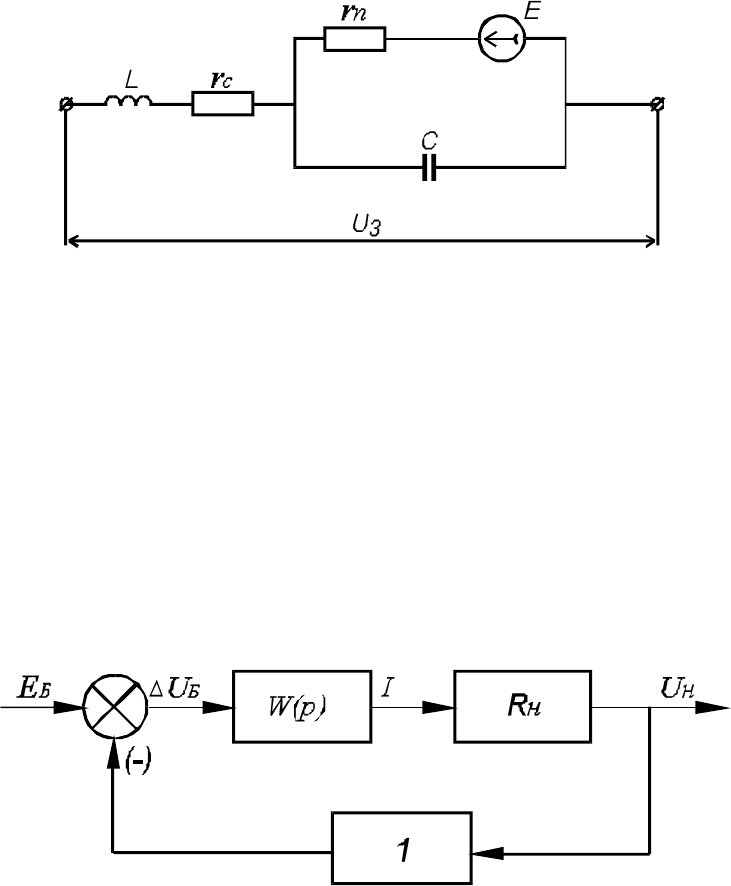
Передаточная функция (4.8) соответствует также и схеме за-
мещения (рисунок 4.29).
Рисунок 4.29 − Электрическая схема замещения ТАБ
Получение экспериментальных кривых переходных процессов
ТАБ в режиме заряда сопряжено с существенными техническими
трудностями, обусловленными большой мощностью источника тока,
обладающими либо значительной инерционностью, либо сложной
формой кривых выпрямленных напряжения и тока, что усложняет
обработку экспериментальных данных. Значительно проще снимают-
ся и обрабатываются переходные процессы в режиме разряда ТАБ
при включении ее на известное нагрузочное сопротивление R
Н
(ри-
сунок 4.30).
Рисунок 4.30 − Функциональная структура ТАБ в режиме заряда при
включении на сопротивление
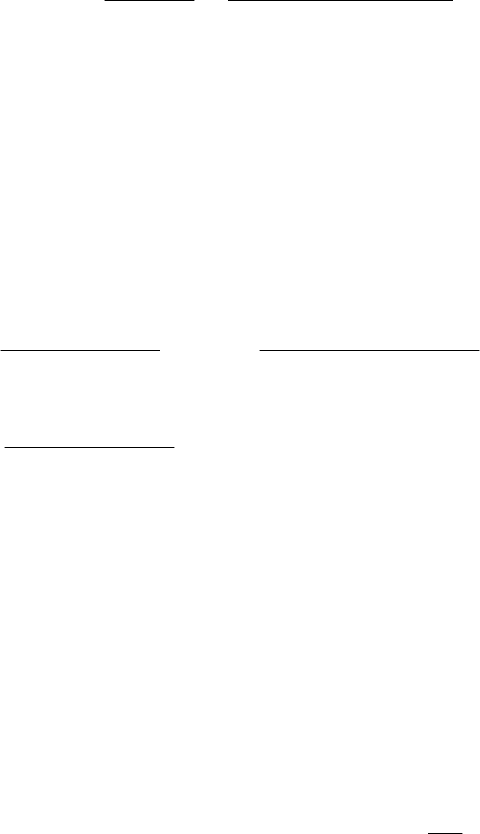
28
Кроме того, такой способ, в сравнении с рассмотренным выше,
обеспечивает более точную количественную оценку параметров ТАБ
и применим как в лабораторных так и в производственных условиях.
Поэтому он положен в основу предлагаемой методики определения
параметров батареи как объекта регулирования для проектирования
САР тока и САР напряжения ЗУ, ЗРУ. Таким образом, предполагает-
ся, что для синтеза САР указанных устройств достаточно знать толь-
ко параметры ТАБ, полученные для режима разряда.
Параметры математических моделей ТАБ (4.7) и (4.8) опреде-
ляются через параметры системы «батарея-нагрузка», которая струк-
турно представляет собой последовательное соединение двух звеньев
(батареи и нагрузки ), охваченных единичной обратной связью. Пере-
даточная функция этой системы
1
)1(
)(
)(
)(
+
+
==
pT
pTk
рЕ
рU
рW
БН
БНБНБН
Б
Н
БН
α
, (4.9)
где Е
Б
– ЭДС батареи;
к
БН
– передаточный коэффициент;
Т
БН
– постоянная времени;
α
БН
– коэффициент кратности для системы (батарея и на-
грузка).
Параметры батареи и рассматриваемой системы связаны между
собой соотношениями:
.;
)1(
)1(
;
)1(
)1(
;
)1(
БНБНББП
БНБН
БНБН
Б
БН
БНБНБН
Б
БНH
БН
Б
ТТТ
к
к
к
кТ
Т
кR
к
к
αα
α
α
α
α
==
−
−
=
−
−
=
−
=
(4.10)
При аппроксимации экспериментальной кривой U
Н.ЭКСП
рас-
четной кривой U
Н.РАСЧ
на интервале времени обусловленной быстро-
действием САР: (0,5 – 0,7) до 1с по точкам О, А, В (рисунок 4.31) со-
ответствующим моментам времени t
0
= 0c, t
1
, t
2
= 2t
1
находим величи-
ны к
БН
,
α
БН,
Т
БН
.
Так как на рассматриваемом интервале времени ЭДС батареи
практически не изменяется, то согласно (4.9) уравнение расчетной
кривой переходного процесса определяется выражением
])1(1[)(
._
БН
T
t
БНББНРАСЧН
еЕкtU
−
−+=
α
(4.11)
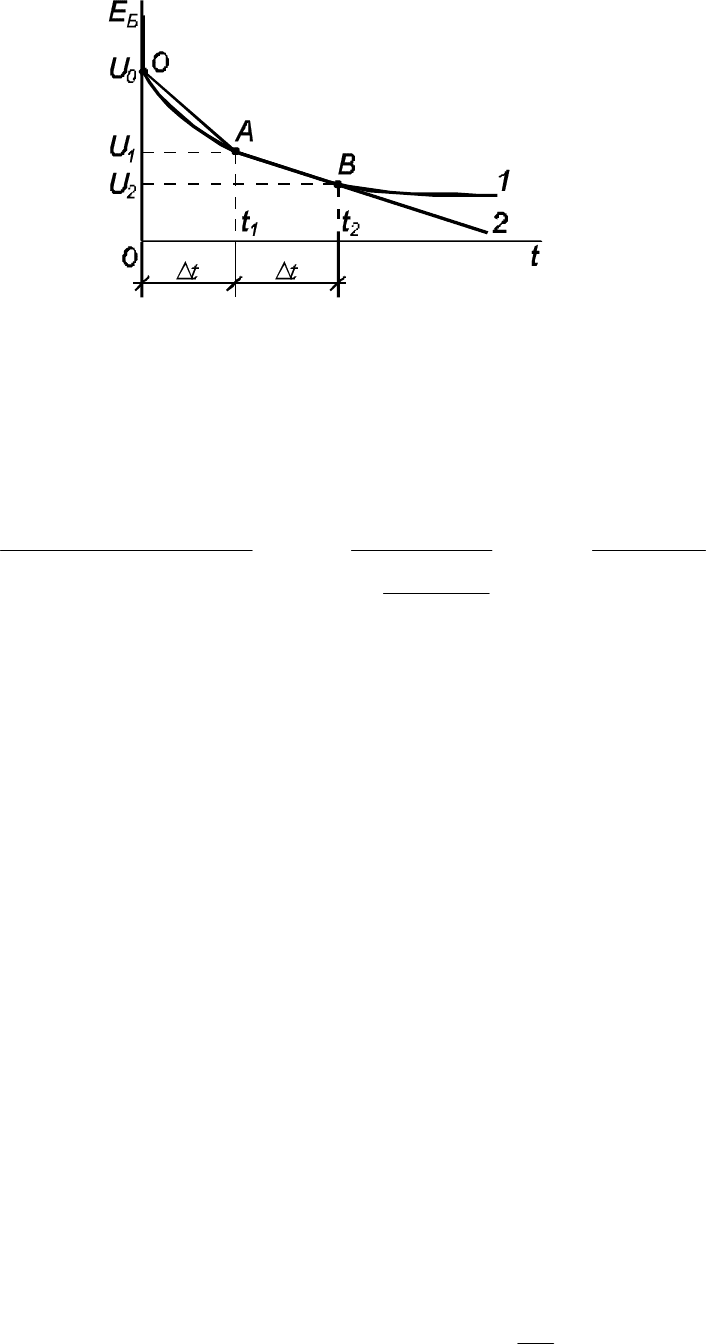
29
1 – расчетная кривая; 2 − экспериментальная кривая
Рисунок 4.31 – Переходный процесс в системе «батарея − нагрузка
»
Записывая (4.11) для заданных точек и разрешая полученную
систему уравнений относительно неизвестных, определяем
Б
БНБН
Б
БН
EK
U
UU
UU
t
Т
UUUE
UUU
к
+
=
−
−
=
−+
−
=
0
0
21
10
1
120
2
2
102
;
ln
;
)2(
α
(4.12)
где U
0
, U
1
, U
2
– ординаты экспериментальных точек О, А и В
(рисунок 4.31).
Численное значение параметров батареи находятся подстанов-
кой величин (4.12) в (4.10).
Количественная оценка точности аппроксимации эксперимен-
тальных кривых напряжения при различных значениях t
1
показала,
что приемлемые результаты достигают при t
1
= 0,2 с. В этом случае
максимальное расхождение расчетных экспериментальных кривых на
участке времени до 0,7 с не превышает 1 %.
В результате экспериментальных исследований батареи, со-
стоящих из различного числа n аккумуляторов типа ТНЖ-350-У5 и
ТНЖШ-500-У5, выполненных в соответствии с изложенной методи-
кой установлено, что на значения параметров батареи определяющее
влияние оказывает их степень заряженности и продолжительность
эксплуатации, а батарею в целом можно рассматривать как совокуп-
ность усредненных типовых аккумуляторов, параметры которых свя-
заны с соответствующими параметрами ТАБ соотношениями:
,;;;
n
к
кTTTTкк
А
ББАПБПАБА
====
(4.13)
30
которые представляют практический интерес при выборе параметров
объекта для расчетов САР тока и напряжения ЗУ и ЗРУ, предназна-
ченных для заряда-разряда батарей с различным числом аккумулято-
ров. Зависимости параметров усредненных аккумуляторов исследуе-
мого типа от степени заряженности для новых вводимых в эксплуа-
тацию, и старых, подлежащих изъятию из эксплуатации, батарей ил-
люстрированы на рисунке 4.32 из которого видно, что параметры
АПАА
TTк ,,
являются плавно возрастающими, а параметр
А
α
− плавно
убывающей функцией степени заряженности. Причем, значения
АПАА
TTк ,,
для новых аккумуляторов больше, чем для старых, а сте-
пень дифференцирования, определяемая
А
α
,меньше.
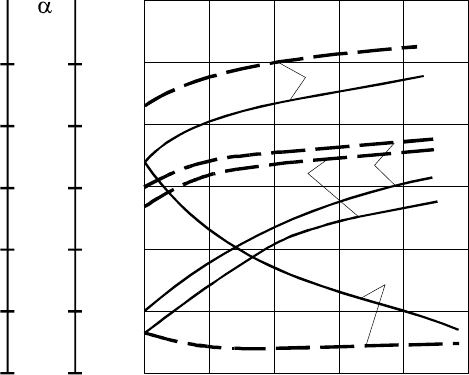
С
З
/С
Н
– степень заряженности; С
З
– фактическая емкость;
С
Н
– номинальная емкость; 1 – постоянная времени
ПА
T ;
2 – постоянная времени
А
T ; 3 – передаточный коэффициент
А
к
;
4 – коэффициент кратности
А
α
; ____ – старый аккумулятор;
----- – новый аккумулятор.
Рисунок 4.32 − Зависимости параметров усредненных аккумуляторов
типа ТНЖ-350-У5 от степени заряженности
Из экспериментальных данных следует, что параметры акку-
муляторов и, следовательно, батареи как объекта автоматического ре-
гулирования существенно перемены: величина
А
к
изменяется в 1,6
раза,
А
T − в 2,7 раза,
ПА
T − в 1,5 раза, а
А
α
− в 1,8 раза. В подобных слу-
чаях при синтезе САР рациональное использование минимаксного
8000,12 2,7
7200,10 2,4
6400,08 2,1
5600,06 1,8
4800,04 1,5
4000,02 1,2
0
4
3
2
1
0,2 0,4 0,6 0,8
С /С
К А/В
Т ,с
Т ,с
А
АА
ЗИ
ПА
