Валишев М.Г., Повзнер А.А. Лекции по оптике
Подождите немного. Документ загружается.

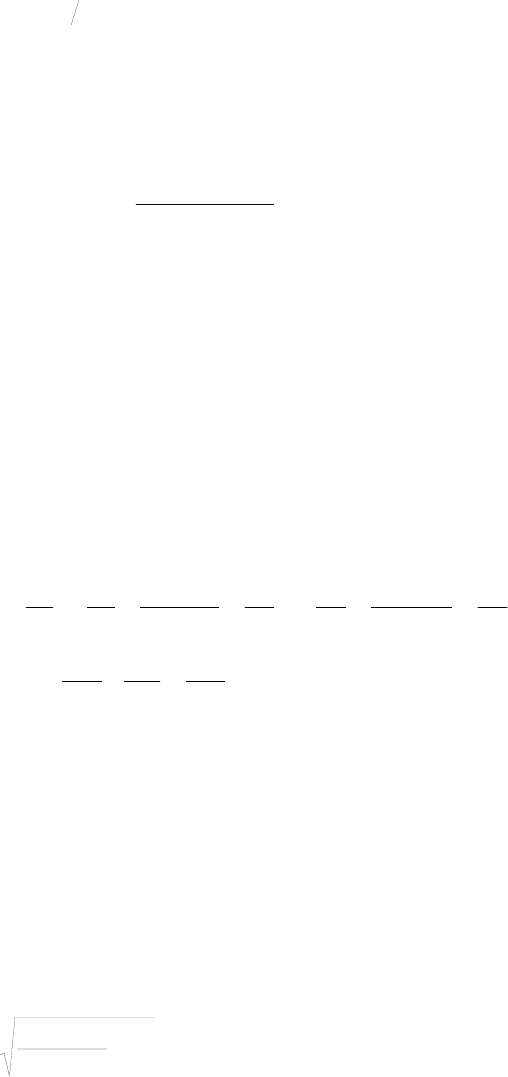
31
1) волны, приходящие в точку наблюдения от соседних зон Френеля имеют
оптическую разность хода разность
2
0
λ
или разность фаз, равную π;
2) при не слишком больших значениях номера m зоны площади зон примерно
одинаковы;
3) для амплитуды волн, приходящих от разных зон Френеля в точку
наблюдения, справедливы следующие соотношения
1
A
>
2
A
>
3
A
>
4
A
>
5
A
…,
2
11 +−
+
=
ii
i
AA
A
. (7.23)
Чем больше будет номер зоны Френеля, тем дальше она будет отстоять от
точки наблюдения и тем меньше будет ее угловой размер, под которым она
видна из точки наблюдения. Это приводит к тому, что с увеличением номера
зоны будет уменьшаться амплитуда волны, приходящая в точку наблюдения,
что подтверждает записанная выше
формула (7.23).
Введение зон Френеля позволяет найти результирующую амплитуду в точке
наблюдения через амплитуды волн от всех зон Френеля. Так, вместо интеграла
(7.22) для
P
A можно записать знакопеременный ряд, который можно
просуммировать учитывая формулу (7.23)
=++
+
−++
+
−+=−+−+−==
∫
...)
222
()
222
(
2
...
5533331
11
54321
AAAAAAA
AA
AAAAAdAA
P
222
11
A
A
A
N
≈±= . (7.24)
В формуле (7.24) учтено, что при значении N, стремящемся к бесконечности
(
∞→N ), вкладом зоны Френеля с номером N можно пренебречь по сравнению
с вкладом от первой зоны Френеля.
Итак, в точке наблюдения результирующая амплитуда всех вторичных волн,
испущенных от всех точек фронта волны, равна половине амплитуды
вторичной волны, приходящей в точку наблюдения от первой зоны Френеля.
Для радиусов
m
r
зон Френеля (см. рис.7.16,б) в случае сферической волны
несложно получить формулу, из которой следует, что радиус первой зоны
Френеля определяется формулой (m=1):
m
PCSC
PCSC
r
m 0
λ
+
⋅
= , (7.25)
что для видимого диапазона излучения (
0
λ
=500 нм) и расстояний от
источника S излучения до фронта волны (SC=1 м) и от фронта волны до точки
наблюдения Р (РС=1 м) дает
1
r =0,5 мм.
Следовательно, в видимой области излучения первая зона Френеля имеет
малые размеры. К тому же для различных положений фронта волны первые
зоны Френеля располагаются на прямой линии, соединяющей источник S
излучения и точку наблюдения P (рис.7.16,в). Все это доказывает
прямолинейность распространения света в волновой теории. Действительно,
интенсивность волны в
точке наблюдения определяется малыми участками

32
фронта волны, расположенными на прямой линии, соединяющей источник
излучения и точку наблюдения.
3. Амплитудная и фазовая зонные пластинки. Метод зон Френеля
позволяет достаточно просто предложить способы для получения значений
амплитуды результирующей волны в точке наблюдения, превышающих
значение
2/
1
A . Так, если закрыть непрозрачным экраном все зоны Френеля,
кроме первой, то тогда можно увеличить амплитуду результирующей волны в
два раза (
1
AA
P
=
) , а интенсивность – в четыре раза.
Для дальнейшего увеличения
P
A можно на пути волны поставить
амплитудную зонную пластинку, которая закрывает все четные зоны Френеля,
что приводит к следующему результату:
...
7531
+
+
+
+
=
AAAAA
P
,
а максимальное увеличение амплитуды
P
A можно получить с помощью
фазовой зонной пластинки, которая изменяет на фазу волны, идущие в точку
наблюдения от четных зон Френеля, на значение, равное
π
:
...
7654321
+
+
+
+
+
+
+
=
AAAAAAAA
P
.
Амплитудные и фазовые зонные пластинки достаточно легко создать для
электромагнитных волн в области сверхвысоких частот (СВЧ диапазон). В этом
случае размеры зон Френеля будут достаточно большими. Так, из формулы для
радиусов зон Френеля (7.25) в случае СВЧ-диапазона (
0
λ
≈1 см, SC=PC=1 м)
можно получить следующие оценки:
1
r = 7 см;
2
r =10 см,
3
r =12 см и т.д.
7.3.2. Дифракция Френеля на круглом диске и круглом отверстии
Рассмотрим конкретные примеры расчета дифракционной картины с
использованием метода зон Френеля. Этот метод достаточно просто позволяет
понять ее основные особенности, хотя не позволяет оценить интенсивности
получаемых максимумов.
1.Круглый диск. Пусть на круглый диск падает сферическая
монохроматическая волна, испущенная точечным источником S
монохроматического излучения (
0
const
λ
=
). За диском находится экран, на
котором наблюдается результат прохождения волной диска (рис.7.17,а).
Необходимо ответить на вопрос, что наблюдается на экране и в точке О,
расположенной в центре экрана. Для ответа используем метод зон Френеля
Разобьем фронт волны, занимающий положение в области диска, на зоны
Френеля относительно точки О. Пусть
диск закрывает первые i зон. Применяя
описанную выше методику разбиения видимой части фронта волны на зоны и
суммируя знакопеременный ряд для амплитуд волн, приходящих в точку
наблюдения от зон Френеля, получим
222
...
11
4321
++
++++
≈±=+−+−=
iNi
iiiiP
AAA
AAAAA
. (7.26)
Из полученного выражения следует, что в центре картины, в точке О будет
наблюдаться светлое пятно, которое получило название пятна Пуассона, а на
33
экране будет наблюдаться дифракционная картина в виде светлых (окрашенных
в один цвет) и темных колец (рис.7.17,в).
Рис.7.17
Дифракционная картина наблюдаться не будет, если диск закрывает менее
чем одну зону Френеля или закрывает достаточно большое количество зон
Френеля. В этих случаях на экране наблюдается монотонное падение
интенсивности света от центра картины к ее краям (рис.7.17,д).
2. Круглое отверстие. Пусть точечный источник монохроматического
излучения посылает волну на
преграду, в которой имеется круглое отверстие
(рис.7.17,б). Необходимо ответить на вопрос, что наблюдается на экране и в
точке О, расположенной напротив источника излучения.
Для ответа на этот вопрос применим метод зон Френеля, а именно: разобьем
видимую часть фронта волны на зоны Френеля. Пусть отверстие открывает
первые
i
зон. Применяя деление фронта волны на зоны Френеля относительно
точки О и суммируя знакопеременный ряд, получим в итоге следующее
выражение для амплитуды результирующей волны:
22
...
1
4321
i
P
AA
AAAAA
±=+−+−= . (7.27)
Как видно из полученного выражения, здесь возможны два случая.
1.Если число i является малым и нечетным, то тогда в точке О будет
наблюдаться светлое пятно, так как все зоны, кроме одной, разбиваются на
пары, которые гасят друг друга. Остается непогашенной одна зона, которая и
дает свет в точке О
. На экране будет наблюдаться дифракционная картина,
состоящая из светлых (окрашенных в один цвет) и темных колец (рис.7.17,в).
Если же число I будет малым и четным, то тогда все зоны разбиваются на
пары, которые гасят друг друга, и в точке О будет наблюдаться темное пятно.
На экране, как и в
первом случае, будет наблюдаться дифракционная картина,
состоящая из светлых (окрашенных в один цвет) и темных колец (рис.7.17,г).
34
Дифракционная картина будет отсутствовать, если отверстие открывает менее
чем одну зону Френеля или достаточно большое число зон Френеля. В этом
случае на экране наблюдается монотонная картина падения интенсивности
света от центра картины к краям (см. рис.7.17,д).
7.3.3. Дифракция Фраунгофера на одной щели (дифракция в
параллельных лучах). Изменение картины дифракции
при
изменении ширины щели
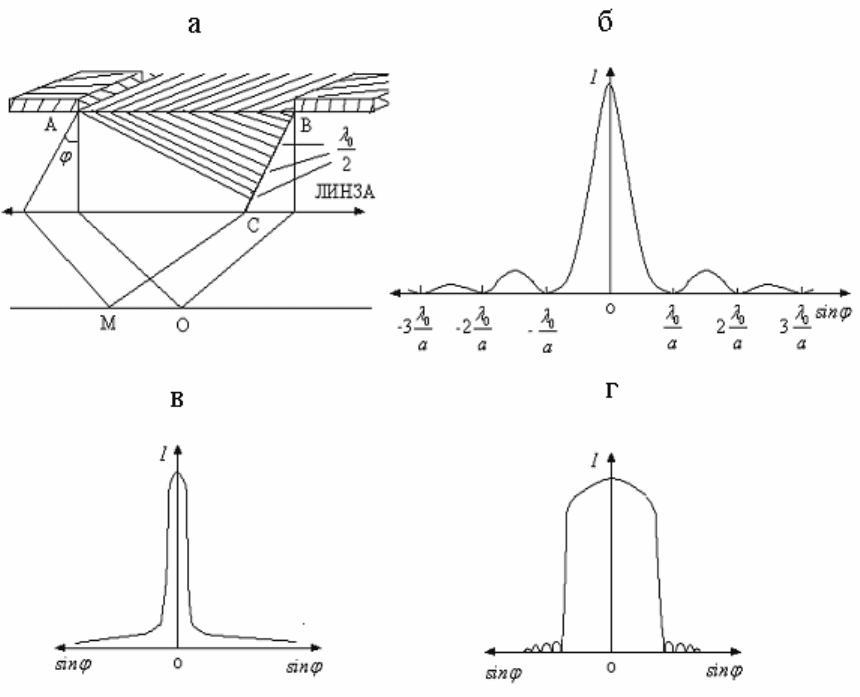
Пусть плоская монохроматическая волна (
0
const
λ
= ) падает
перпендикулярно на поверхность щели шириной а (
aAB
=
). С помощью линзы
в одной точке на экране, расположенном в фокальной плоскости линзы,
собираются все параллельные лучи, испущенные каждой точкой фронта волны
под углом φ к первоначальному направлению падения лучей на щель
(рис.7.18,а). В этом состоит отличие дифракции Фраунгофера от дифракции
Френеля. Так, в дифракции Френеля не принимается никаких
мер для
собирания лучей, они сами приходят в точку наблюдения, поэтому ее можно
назвать дифракцией в сходящихся лучах.
Для расчета дифракционной картины, наблюдаемой на экране, используем
метод зон Френеля. Разобьем фронт волны на зоны Френеля. Отметим, что на
линии АВ оптическая разность хода вторичных волн, испущенных каждой
точкой фронта волны
равна нулю, после линии АС она не изменяется. Поэтому
оптическая разность хода возникает при переходе вторичных волн от линии АВ
к линии ВС, т.е. отрезок ВС дает оптическую разность хода вторичных волн.
Разделим его на участки длиной
2
0
λ
, затем проведем через границы этих
участков прямые, параллельные линии АС. Это приведет к делению фронта
волны на прямоугольные полоски одинаковой ширины, которые и
представляют собой зоны Френеля. Для соседних зон оптическая разность хода
волн будет равна
2
0
λ , что является главным свойством зон Френеля.
Если на отрезке ВС укладывается четное число зон Френеля, то тогда все
зоны открытой части фронта волны делятся на пары зон, причем волны,
приходящие в точку наблюдения от каждой пары зон, гасят друг друга и на
экране в точке М наблюдается темная полоса
00
sin
2
22
ВС а
m
ϕ
λλ
==⇒
0
sin 2 , 1, 2,...
2
amm
λ
ϕ
=± = , (7.28)
т.е. уравнение (7.28) дает условие наблюдения минимумов дифракционной
картины на экране.
Если на отрезке ВС укладывается нечетное число зон Френеля, то тогда все
зоны открытой части фронта волны делятся на пары зон, кроме одной. Волны,
приходящие в точку наблюдения от каждой пары зон, гасят друг друга, остается
только одна
зона, которая и дает на экране светлую полосу
0
00
sin
2 1 sin (2 1) , 1, 2, ...
22 2
ВС a
ma mm
λ
ϕ
ϕ
λλ
==+⇒ =±+ = (7.29)
35
Уравнение (7.29) дает условие наблюдения на экране максимумов
дифракционной картины.
В связи с приближенным характером расчетов c помощью метода зон
Френеля (в общем случае необходимо проводить точное вычисление интеграла
в формуле (7.22), разбивая щель на бесконечное число узких полосок)
полученная формула является приближенной. Более точные расчеты дают
следующую формулу для наблюдения максимумов:
(sin/) sin/tg a a
π
ϕλ π ϕλ
=
. (7.30)
Рис.7.18
На рис.7.18,б приведена дифракционная картина, отражающая зависимость
интенсивности I не от координаты r точек экрана, а от значения
ϕ
sin , что
является удобным, так как на этом графике можно точно обозначить положение
минимумов и максимумов дифракционной картины.
В центре картины, для угла
0
=
ϕ
, наблюдается центральный максимум
нулевого порядка, который не описывается формулой (7.29). Как показывают
расчеты, интенсивность первых (
1
±
=
m ) максимумов в 22 раза меньше
интенсивности центрального максимума. В связи с этим картина дифракции на
экране получается достаточно слабой по интенсивности - на фоне яркой
светлой полосы (центрального максимума) другие максимумы практически не
видны и является нечеткой – наблюдаются плавные переходы между соседними
максимумами и минимумами.

36
Представляет интерес рассмотреть, как изменяются условия наблюдения
дифракционной картины при изменении ширины щели. Здесь возможны три
случая.
1. Узкая щель: ширина щели значительно меньше длины волны падающего
света:
0
λ<<a ⇒
)12(
2
sin
0
+
λ
=ϕ m
a
>1. Это приводит к тому, что все максимумы и
минимумы дифракционной картины уходят от центра картины на большие
расстояния и картина дифракции не наблюдается (рис.7.18,в).
2. Размеры щели сопоставимы с длиной волны падающего
излучения:
a ~
0
λ . В этом случае максимумы и минимумы приходят из
бесконечности - на экране наблюдается дифракционная картина.
3. Широкая щель: ширина щели значительно превышает длину волны
падающего излучения
0
λ>>a ⇒
1)12(
2
sin
0
<<+
λ
=ϕ m
a
. Все максимумы и
минимумы сходятся в окрестности одной точки пространства. Картина
дифракции наблюдаться не будет - практически невозможно наблюдать близко
расположенные максимумы и минимумы на фоне яркого центрального
максимума (рис.7.18,г).
Рассмотренный пример позволяет еще раз привести доводы в пользу
известного вывода о том, что дифракционные явления наблюдаются тогда,
когда размеры
препятствий сопоставимы с длиной волны падающего
излучения (
r
~
0
λ ).
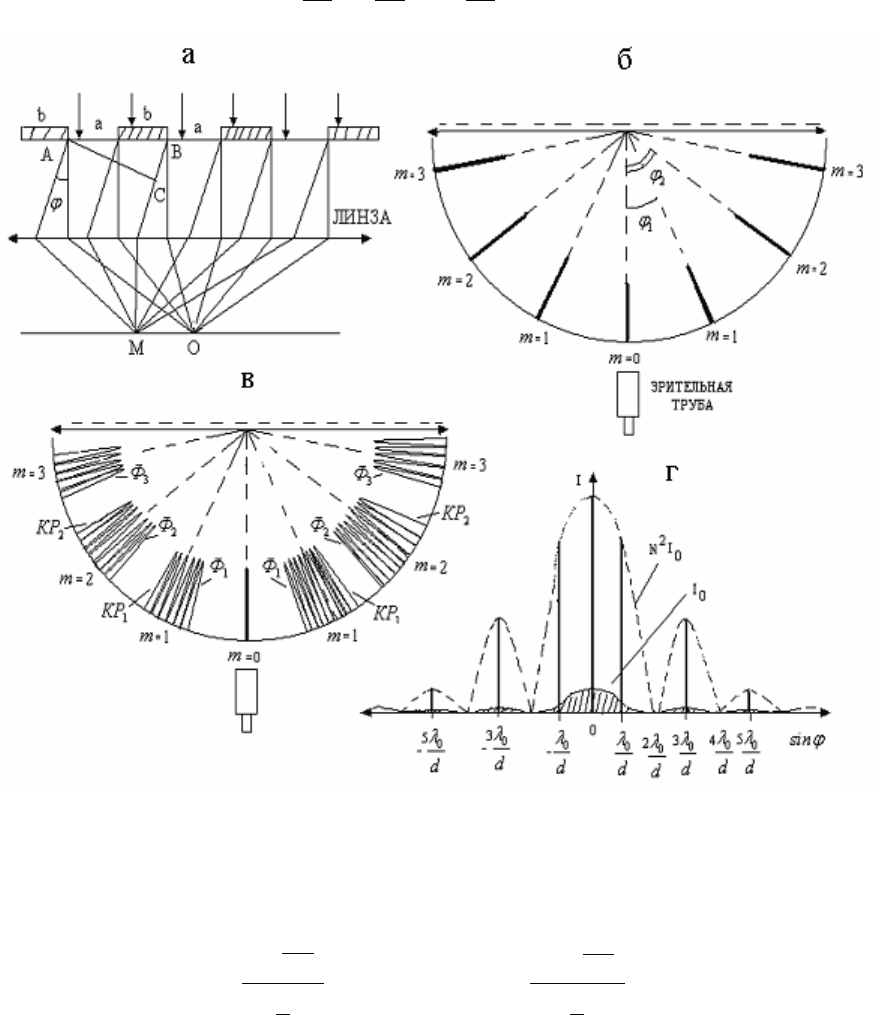
7.3.4. Одномерная дифракционная решетка. Условия наблюдения
главных максимумов
Одномерная дифракционная решетка представляет собой совокупность
большого числа N одинаковых щелей ширины a, отстоящих друг от друга на
одном и том же расстоянии b (рис.7.19,а). Расстояние
d , равное )( bad
+
= ,
называют периодом или постоянной дифракционной решетки.
Пусть на дифракционную решетку падает плоская монохроматическая волна.
С помощью линзы в одной точке на экране, расположенном в ее фокальной
плоскости, собираются все параллельные лучи, испущенные каждой щелью
дифракционной решетки (см. рис.7.19,а). В результате в каждой точке экрана
наблюдается сложение N одинаково направленных
одной и той же частоты
гармонических колебаний вектора
E
G
, начальные фазы которых образуют
арифметическую прогрессию с шагом
δ
:
11 0 2 2 0
:
1- : cos( ) , 2- : cos( ) ,ящель EA t ящель EA t
ωϕ ωϕδ
=+ =++
33 0 0
:
3- : cos( 2 ) ,..., : cos( ( 1) )
NN
ящель EA t Nщель EA t N
ωϕ
δω
ϕ
δ
=++ = ++−
.
Здесь
i
A
( ,...3,2,1=i ) обозначает амплитуду волны, приходящей в точку
наблюдения от одной щели. Входящий в фазу колебаний параметр
δ
дает
разность фаз волн, идущих от соседних щелей. Он связан с оптической
37
разностью хода ∆ этих волн, равной расстоянию ВС (см. рис.7.19,а),
соотношением
ϕ
λ
π
=
λ
π
=∆
λ
π
=δ sin
222
000
dBC . (7.31)
Рис.7.19
Такой случай сложения колебаний был рассмотрен в параграфе 5.7.2, где
была получена для результирующей амплитуды колебаний формула (5.31). Она
позволяет записать следующее выражение:
)
2
(
)
2
(
0
δ
δ
=
N
sin
AA
P
,
I
~
2
A
)
2
(
)
2
(sin
2
0
δ
δ
=⇒
N
II
P
. (7.32)
В этой формуле под интенсивностью
0
I понимают интенсивность волны,
приходящей в точку наблюдения от одной щели. Отметим, что
0
I также, как и
параметр
δ , зависит от угла ϕ .
Формула (7.32) полностью описывает дифракционную картину, определяя
расположение максимумов и минимумов на экране и их интенсивность.
Оказывается, что на экране наблюдаются только главные максимумы.
Найдем из формулы (7.32) условие наблюдения главных максимумов. Для
этого нужно одновременно приравнять нулю числитель и знаменатель
выражения (7.32):

38
⇒π=ϕ
λ
π
⇒π=δ⇒π=
δ
π=
δ
⇒=
δ
=
δ
mdmmm
NN
2sin
2
2
2
,
2
0
2
sin,0
2
sin
0
...,3,2,1,0,sin
0
=λ=ϕ mmd (7.33)
Из этого уравнения можно найти углы, под которыми наблюдаются главные
максимумы.
Найдем интенсивность главных максимумов. Для этого подставим в формулу
(7.32) параметр
δ , равный mπ2 , и раскроем дробь с использованием правила
Лопиталя
2
2
2
cos
)cos(
)(sin
))(sin(
)
2
cos
2
sin
2
1
(
)
2
cos
2
sin
2
2(
)
2
(sin
)
2
(sin
N
NNNNN
NNNN
=
δ
δ⋅
=
′
δ
′
δ
=
′
δδ
′
δ
δ
=
′
δ
′
δ
,
2
0ГЛ
I
IN= . (7.34)
Как следует из формулы (7.34), интенсивность главных максимумов в
2
N раз
больше интенсивности света от одной щели. Это связано с тем, что в случае
дифракционной решетки складывается в N раз большее число когерентных
волн, это приводит к более резкому перераспределению энергии световой
волны в пространстве.
На основе формулы (7.32) можно показать, что между двумя главными
максимумами находится (N-1) минимумов и (N
-2) побочных максимумов.
Интенсивность побочных максимумов в 22 раза меньше интенсивности
главных максимумов, и поэтому побочные максимумы на дифракционной
картине не видны.
В итоге картина дифракции будет резкой и яркой, а именно, наблюдаются
яркие узкие линии главных максимумов, разделенные большими
темными промежутками. На рис.7.19,б приведена картина дифракции,
наблюдаемая с помощью зрительной
трубы при ее повороте от центра картины
вправо и влево на углы, достигающие значения
0
90=ϕ
.
Из условия (7.32) следует, что главные максимумы дифракционной картины
наблюдаются при углах, равных
0
0=ϕ (главный максимум нулевого порядка,
m=0),
10
arcsin( )d
ϕ
λ
=± (главные максимумы первого порядка, m=±1),
20
arcsin(2 )d
ϕ
λ
=± (главные максимумы второго порядка, m=±2) и т.д.
Наибольший порядок главного максимума, который можно наблюдать на
дифракционной решетке, определяется из условия
0
max
0
sin 1
m
d
m
d
λ
ϕ
λ
=≤⇒ ≤, (7.35)
а общее число главных максимумов будет равно
)12(
max
+
=
mN
ГЛ
. Например,
при
0
λ
d =3,98 3
max
=m , 7=
ГЛ
N .
При падении на дифракционную решетку белого света все главные
максимумы, кроме центрального максимума, будут разлагаться в спектр.
Причем, в спектре разных порядков фиолетовые линии (Ф) будут располагаться
ближе к центру картины, чем красные линии (КР, рис.7.19,в).

39
Действительно, при m=0 для всех волн белого света из уравнения (7.33)
следует, что угол дифракции
ϕ равен нулю (
0
0=ϕ ). Следовательно, все волны с
разной длиной волны приходят в центр экрана и при сложении дают белую
полосу. Для
0≠m ( ,...3,2,1 ±±±=m ) угол наблюдения )(
0
dmarcsin λ=
ϕ
будет
зависеть от длины волны, и так как
Ф
λ
<
КР
λ
, то и
КРФ
ϕ
<
ϕ
в спектре любого
порядка.
Построим картину дифракции для дифракционной решетки, отражающую
зависимость интенсивности
I
света в разных точках экрана от значения
ϕ
sin
(рис.7.19,г).
Для этого на горизонтальной оси будем откладывать значения
ϕsin с шагом
d
0
λ . Затем нанесем на этой оси точки, в которых наблюдаются минимумы
интенсивности света при дифракции от одной щели (
0
I =0). Возьмем, например,
отношение ширины щели
a к постоянной d дифракционной решетки, равное
2=ad
и используем условие (7.26) . Тогда
,...6,4,22sin...,2,1,2
2
sin
000
0
0
ddd
dmmma
λ
±
λ
±
λ
±=λ=ϕ⇒=
λ
=ϕ
.
Это позволяет представить дифракционную картину от одной щели в виде
кривой зависимости
0
I от значений
ϕ
sin . Как видно из рис.7.19,г, эта
зависимость будет малой интенсивности и размытой.
Затем увеличиваем картину дифракции от одной щели в
2
N раз (на одном
поле это можно показать только качественно, так как N может достигать
значений порядка
4
105 ⋅ ) и наносим при всех значениях d
0
λ главные
максимумы в виде узких линий с интенсивностью
2
0
NI
(см. рис. 7.19,г).
Отметим, что в данном конкретном случае, для отношения
ad , равного двум,
пропадают главные максимумы для значений m, равных (
,...6,4,2 ±±±=m ).
В итоге, из рис.7.19,г наглядно видно, как размытая малой интенсивности
картина дифракции от одной щели за счет сложения в N раз большего числа
когерентных волн переходит в резкую дифракционную картину большой
яркости для решетки. Это позволяет использовать дифракционные решетки для
наблюдения спектров излучения различных веществ, т.е. в качестве
спектральных приборов.
40
7.3.5. Характеристики дифракционной решетки (угловая дисперсия
D , разрешающая способность R)
Для количественного описания качества дифракционной решетки вводят
такие понятия, как угловую дисперсию D и разрешающую способность R,
которые независимы друг от друга и взаимно дополняют друг друга.
Угловая дисперсия определяет расстояние по углам
ϕd двух близко
расположенных по длинам волн
λ
d спектральных линий и рассчитывается по
формуле
λ
ϕ
=
d
d
D
. (7.36)
Используя условие наблюдения главных максимумов (7.33), можно записать
⇒λ=ϕ⋅ϕ⇒λ=ϕ mdddmd cossin
0
)(
cos
10063,2)(
cos
5
нм
"
м
рад
ϕ
⋅=
ϕ
=
d
m
d
m
D
. (7.37)
Как видно из формулы (7.37) угловая дисперсия D определяется периодом d
дифракционной решетки, т.е. определяется числом щелей решетки,
приходящихся на единицу ее длины (
Nd /A
=
, где N-число щелей, A -ширина
используемой рабочей части решетки). Чем меньше будет d, тем лучше будет
решетка, тем дальше по углам будут отстоять две близко расположенные
спектральные линии, и тем легче их будет наблюдать.
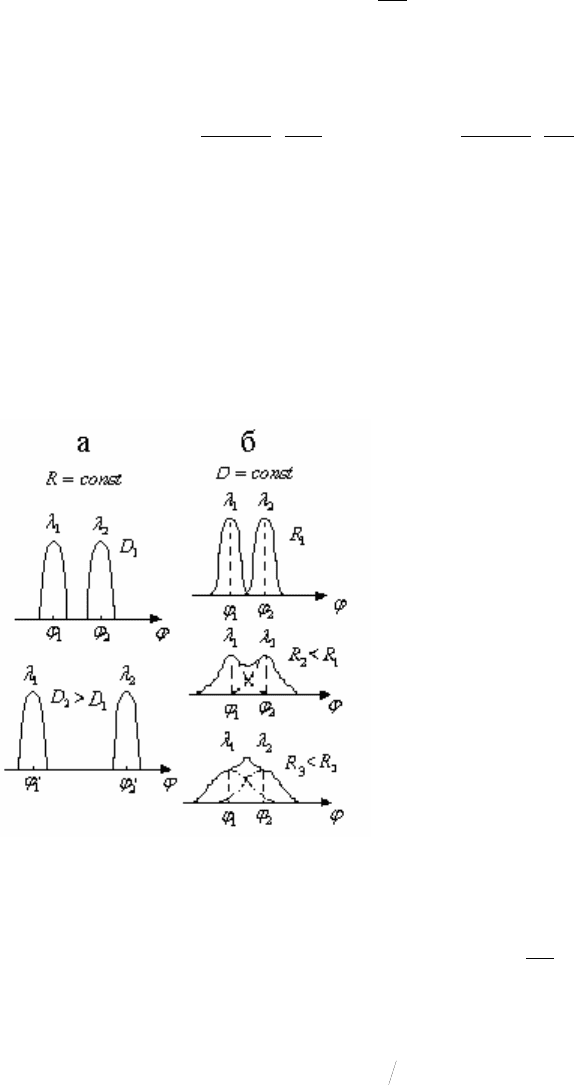
На рис. 7.20,а приведены две спектральные линии (
21
, ϕϕ ), наблюдаемые в
спектре порядка m для решеток с разным
периодом d, но с одинаковым числом
используемых щелей (
21
NN = ,
12
dd
<
).
Видно, что расстояние
ϕ∆ по углам
растет при переходе к решетке с
меньшим периодом d. При одинаковом
же числе используемых щелей (при
одинаковой разрешающей способности
R) в спектре одного порядка ширина
линий остается неизменной.
Под разрешающей способностью
R
дифракционной решетки понимают ее
способность видеть раздельно,
разрешать две близко расположенные по
длинам волн спектральные линии. Она
определяется по формуле:
δ
λ
λ
=R , (7.38)
где под длиной волны
λ понимают среднее значение длин волн спектральных
линий, а под
δλ – их разность
2)(
12
λ
+λ=λ , )(
12
λ
−
λ
=
δ
λ .
Рис. 7.20
