Валиев Ф.С. Сопротивление материалов: основы теории и примеры выполнения индивидуальных расчетных заданий (часть 1)

Подождите немного. Документ загружается.

100

а)

max

ext

б)

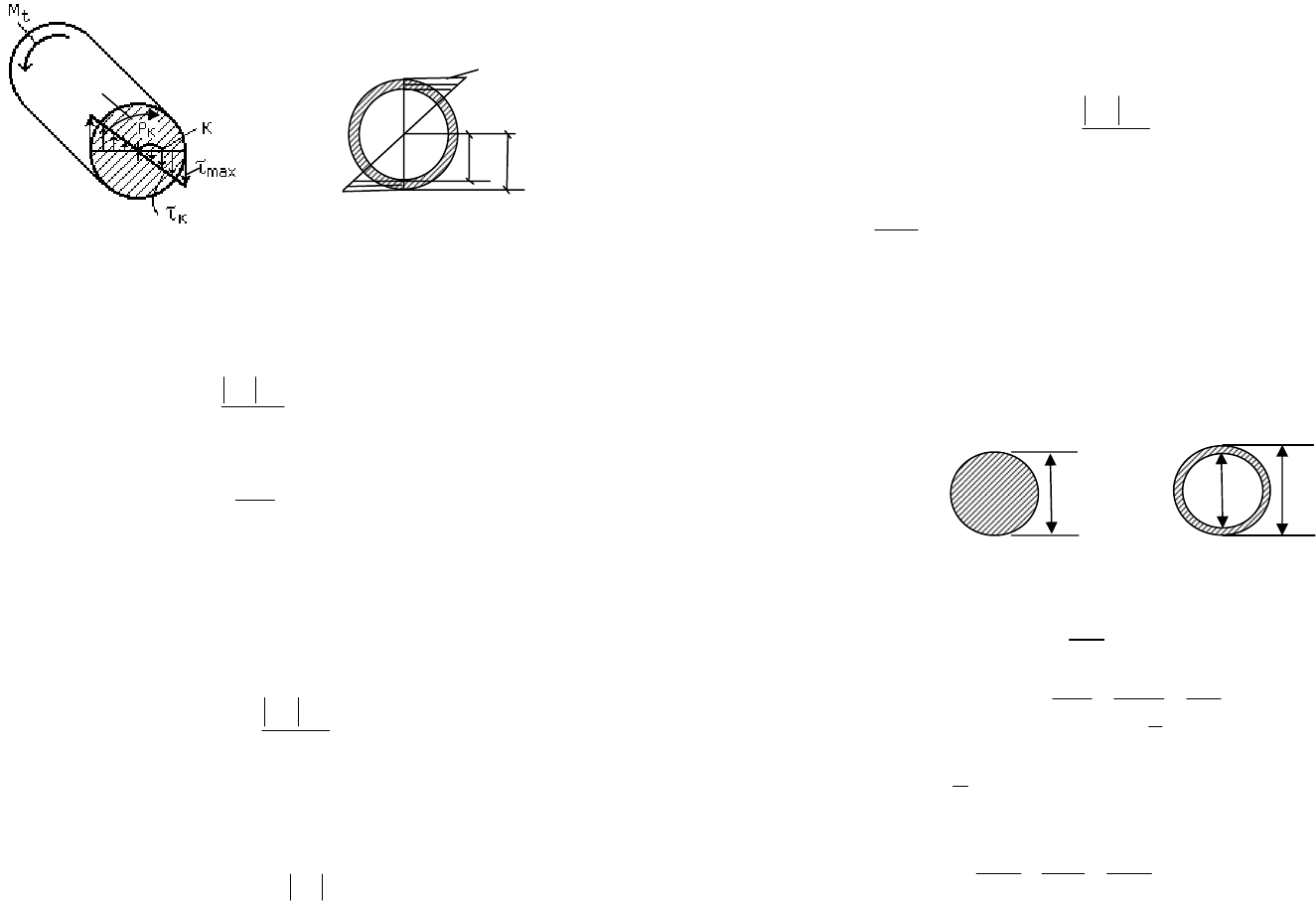
Рис. 6.1

Эпюры τ , построенные по формуле (6.1) для круглого

сплошного и кольцевого сечений, представлены на рис. 6.1а, б.

Наибольшие касательные напряжения в поперечных сече-

ниях определяются по формуле:

max

max max

τ= ⋅ρ (6.2)

Введем следующее обозначение:

max

W,=

(6.3)

где

– называется полярным моментом сопротивления попе-

речного сечения (см

, м

);

max

ρ – расстояние от центра тяжести

до наиболее удаленной точки сечения, оно равняется радиусу

круга

).r(

max

=ρ

Условие прочности при кручении запишется:

max

≤=τ (6.4)

где R

– расчетное сопротивление материала при сдвиге.

Используя условие прочности (6.4), можно решать следую-

щие задачи на кручение:

1. Проверочная задача, т.е. проверка прочности. Подстав-

ляя в формулу (6.4) величины

max

из эпюры крутящих мо-

101

ментов и W

, определенную по формуле (6.3), проверяем, вы-

полняется ли условие прочности.

2. Проектная задача, т.е. подбор сечения. В этом случае из

условия прочности (6.4), предполагая, что

max S

, определя-

ется значение

требуемого полярного момента сопротивления:

;

max

= (6.5)

Затем значение

W приравнивается выражению

;

max

т.е.

.WW

Из этого равенства определяется неизвестный диаметр

стержня.

Ниже приведены формулы для определения полярных мо-

ментов сопротивления для стержней круглого поперечного се-

чений:

а) сплошное круглое сечение

(рис. 6.2а):

а)

б)

int

Рис. 6.2

= (6.6)

max

ππ

== =

⋅

(6.7)

здесь

;

max

=ρ

б)

кольцевое сечение (рис. 6.2б):

444

ext int ext

ddd

I(1К );

32 32 32

πππ

=−=⋅− (6.8)

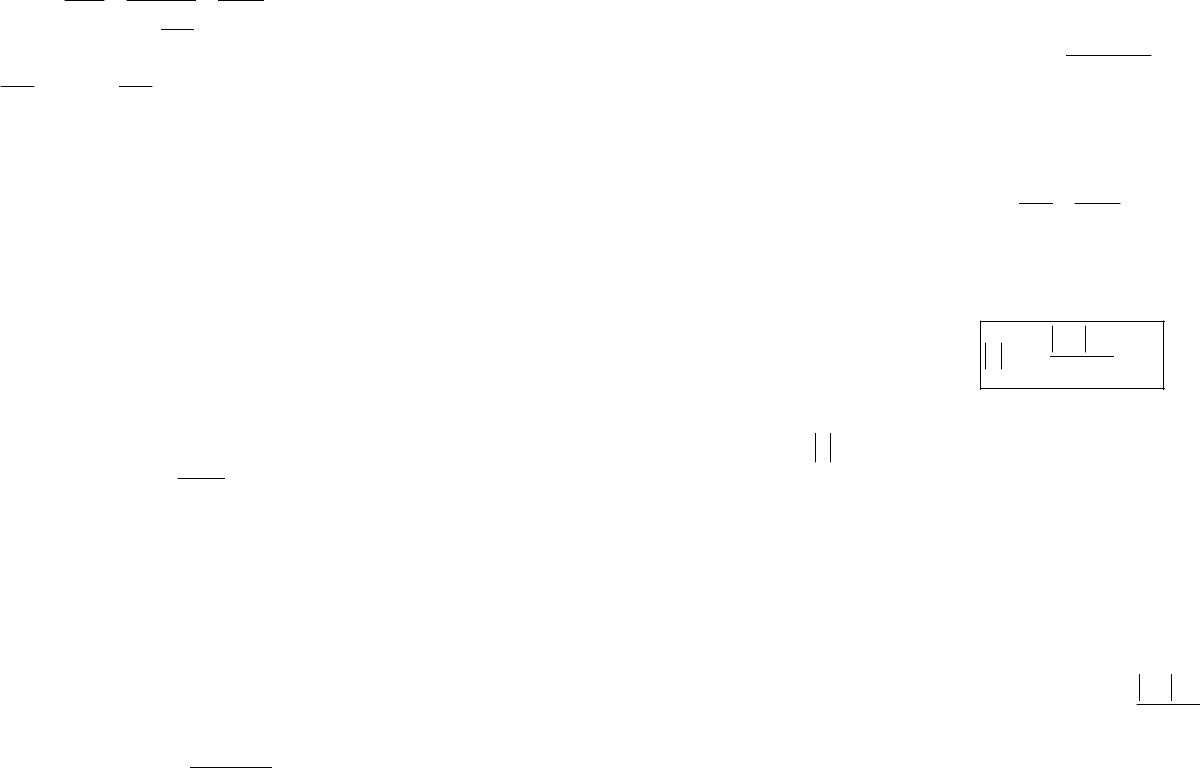
102

ext ext

ext

max

W(1К ),

ππ

== = ⋅−

⋅

(6.9)

Здесь

int

ext

К ;

ext

max

ρ=

3. Определение допускаемого значения крутящего момента

для стержня заданного диаметра и из заданного материала.

Из условия прочности (6.4), которое берем со знаком равен-

ства, т.е.

max S

Rτ=, определяем значение допускаемого крутяще-

го момента:

[]

tSP

MRW.= (6.10)

6.2. Определение углов закручивания брусьев круглого

поперечного сечения и расчеты на жесткость

Угол взаимного закручивания

ϕ концевых сечений участка

стержня длиной

определяется по формуле:

ϕ=

(6.11)

здесь

M – крутящий момент, постоянный по длине участка; l –

длина участка; G – модуль упругости материала при сдвиге (мо-

дуль упругости 2-го рода).

Произведение

GI называется жесткостью поперечного

сечения при кручении.

Если крутящий момент по длине участка M

(x) есть величи-

на переменная, то взаимный угол закручивания концевых сече-

ний участка определится по формуле:

M(x)dx

ϕ=

∫

. (6.12)

Чтобы определить полный угол закручивания

какого-либо

сечения j бруса по отношению к закрепленному сечению (там

угол закручивания равен нулю), нужно взять сумму углов закру-

103

чивания на всех n участках, заключенных между неподвижным

(закрепленным) и рассматриваемым j-м сечениями:

in in

i0 i0

M(x)dx

G I

α= ϕ=

∑∑

∫

(6.13)

Относительный угол закручивания

, т.е. угол закручива-

ния, приходящийся на единицу длины, определяется по сле-

дующей формуле:

t i

dx G I

θ= = (6.14)

Условие жесткости бруса, работающего на кручение, если

ограничен относительный угол закручивания

, запишется в

виде

[]

max

G I

=≤θ (6.15)

где

[

]

– допускаемый относительный угол закручивания

(рад/м);

max

θ – наибольший по модулю относительный угол за-

кручивания по длине бруса.

Используя условие жесткости (6.15), можно решать сле-

дующие задачи:

1. Проверить жесткость бруса, т.е. проверить выполнение

условия (6.15).

2. Определить диаметр бруса из условия жесткости (подбор

сечения).

Для этого из формулы (6.15) вычисляем требуемое значение

полярного момента инерции:

[]

ТР

max

Приравнивая требуемую величину

ТР

I к выражению (6.6)

или (6.8), т.е. I

ТР

I, определим диаметр поперечного сечения d

или d

ext

3. Вычислить допускаемое значение крутящего момента для

бруса заданного диаметра при известном значении G:

104

[] []

MG I.=θ

Если ограничен полный угол закручивания сечения [α] (в

радианах) для всего стержня, то условие жесткости запишется в

следующем виде:

[]

max

α≤α. (6.15)'

Здесь

max

α – наибольший полный угол закручивания сечения по

отношению к закрепленному, который берется из эпюры α.

При подборе сечения по данному условию жесткости эпюра

α строится при неизвестном диаметре, при GI

= const.

Используя условие жесткости (6.15)', также можно решать

приведенные выше три типа задач.

ПРИМЕР 6.1

Требуется

подобрать диаметр бруса кольцевого сечения,

(рис. 6.3), по условиям прочности и жесткости при следующих

исходных данных:

int

ext

К 0,8 ;

R40 МПа;=

[]

град

0,5 ;

θ=

G0,810 МПа.=⋅

int

ext

Рис. 6.3

а) б)

в)

105

РЕШЕНИЕ

Построение эпюры крутящих моментов. Наметим два

грузовых участка и в пределах каждого проводим произвольное

сечение.

Рассматривая от каждого сечения правую отсеченную часть

(так как там нет опоры), вычисляем величины крутящих момен-

тов, используя следующее рабочее правило, вытекающее из ме-

тода сечений:

Крутящий момент в любом сечении бруса численно равен

алгебраической сумме моментов всех внешних сил, действующих

по одну сторону от сечения относительно продольной оси бру-

са в месте сечения.

Правило знаков для крутящих моментов:

Крутящий момент будем считать

положительным, если при взгляде на се-

чение со стороны внешней нормали он

будет закручивать отсеченную часть по

ходу часовой стрелки. В этом случае

внешний закручивающий момент М

бу-

дет действовать против хода часовой

стрелки

(рис. 6.4). Знак М

будет отри-

цательным, если направление момента

будет противоположным.

MM0,8 кН м;

=⋅

t12

MMM0,821,2 кН м.

−=−=− ⋅

На обоих участках крутящие моменты постоянны. По этим

значениям строим эпюру

M (см. рис. 6.3в), из которой получа-

ем:

max

M1,2 кН м.

⋅

Подбор сечения из условия прочности.

Определяем требуемый полярный момент сопротивления из

условия прочности:

TP 3 3 3

max

1, 2 кН м

W0,0310 м 30 см .

R4010 кПа

−

⋅

== =⋅=

⋅

Рис. 6.4

106

Используем соотношение (6.8) для бруса кольцевого сече-

ния:

ext

W(1K).

=−

Приравниваем

;WW

ext

30 cм (1 K ) .

=−

Отсюда при заданном К = 0,8 находим d

ext

= 6,37 см.

Подбор сечения по условию жесткости. Из условия же-

сткости (6.15)

[]

;

I G

max

θ≤=θ определим требуемое зна-

чение полярного момента инерции по следующей формуле:

[]

max

G I

=θ Откуда

[]

max

В это соотношение

[]

подставляется в радианах, поэтому

заданный угол выразим в радианах:

[]

0,5 рад

0,00875 ;

180 180 м

⎡⎤

θπ

⋅π

⎣⎦

θ= = =

TP 44 4

1, 2 кН м

I 0,01712 10 м 171,2 см .

0,8 10 кПа 0,00875 рад/м

−

⋅

==⋅=

⋅⋅

Из условия

получим:

ext

171,2 см (1 К ).

=−

Отсюда определяем d

ext

(по условию задачи К = 0,8):

171,2 =

ext

(1 0, 8 );

−

ext

171, 2 32

d 7,374см.

(1 0, 8 )

⋅

π⋅ −

После округления примем d

ext

= 7,4, тогда

int

= 0,8 ⋅ d

ext

= 0,8 ⋅ 7,4 = 5,92 см.

По результатам расчетов на прочность и жесткость видно,

что по условию жесткости диаметр бруса требуется больше, чем

по условию прочности (7,4 см > 6,37 см).

Окончательно принимаем больший диаметр:

ext

= 7,4 см, d

int

= 5,92 см.

107

Проверим прочность и жесткость подобранного сечения.

Предварительно определим полярный момент сопротивле-

ния и полярный момент инерции подобранного сечения:

23 4

(7,4 10 ) (1 0,8 )

W 46,92 10 м ;

−

π⋅ ⋅−

==⋅

24 4

(7,4 10 ) (1 0,8 )

I173,610м ;

−

π⋅ ⋅−

==⋅

max

max S

1, 2

25,6 10 кПа R;

W 46,92 10

−

τ= = = ⋅ <

⋅

[]

max

884

max

1, 2

G I 0,8 10 кПа 173,6 10 м

рад

0,00857 .

−

== =

⋅⋅⋅

=<θ

Условия прочности и жесткости выполняются.

6.3. Деформация кручения брусьев прямоугольного сечения

Испытания стержней некруглого сечения на кручение пока-

зывают, что поперечные сечения таких стержней после дефор-

мации перестают быть плоскими. Это явление,

связанное с вы-

ходом точек поперечного сечения из плоскости, называется де-

планацией сечения.

Когда депланация всех поперечных сечений

одинакова, она считается свободной и не приводит к появлению

нормальных напряжений в продольных волокнах. В противном

случае депланация является стесненной и сопровождается появ-

лением нормальных напряжений в продольных волокнах. В дан-

ной части курса мы не будем учитывать влияние стесненности

депланации, т.е. будем рассматривать свободное

кручение

стержней.

Распределение касательных напряжений при кручении

стержней прямоугольного сечения более сложное, чем стержней

круглого сечения из-за наличия депланации. Эта задача была

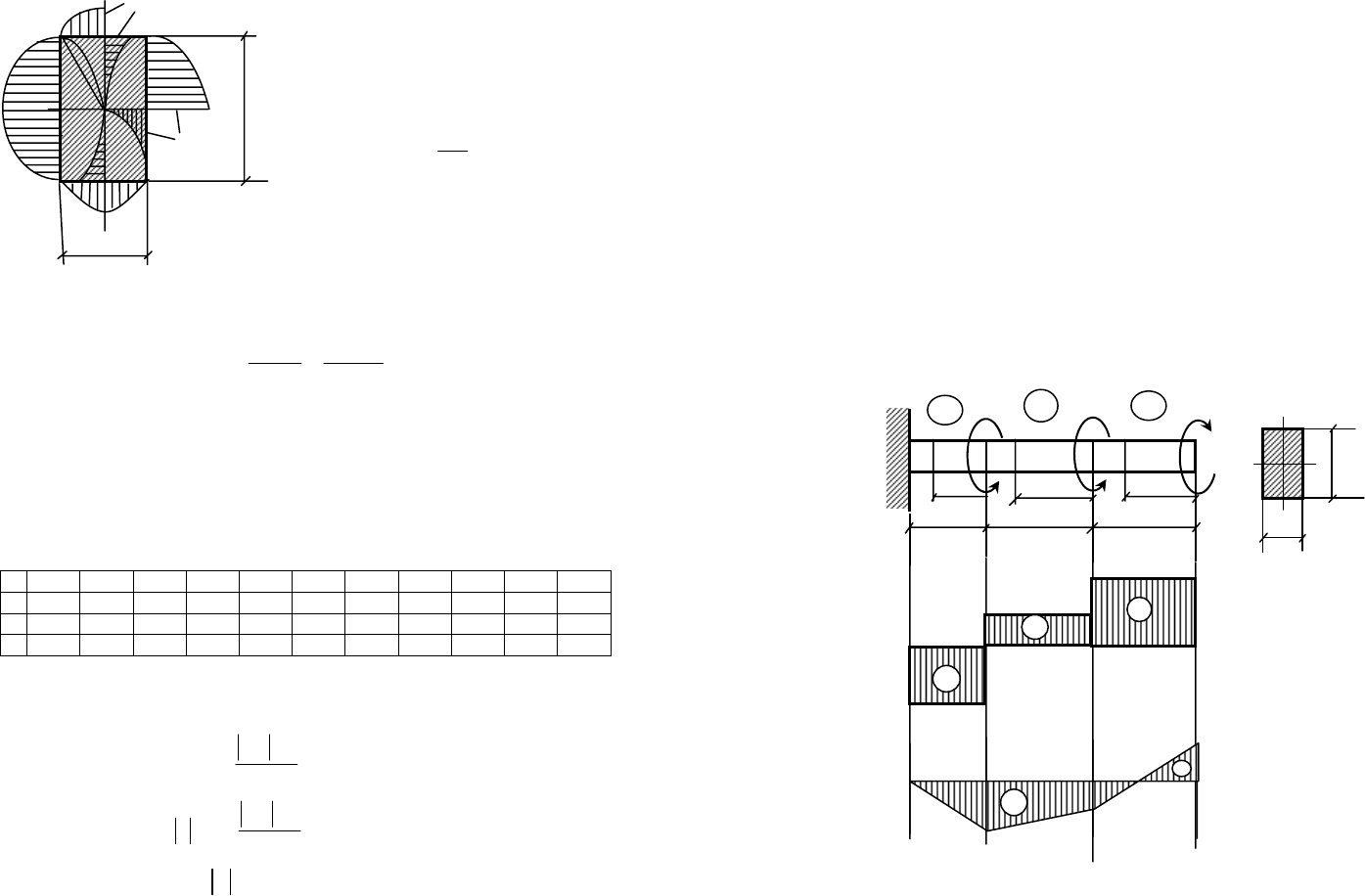
впервые решена Сен-Венаном в теории упругости. На рис. 6.5

108

показана картина распределения

касательных напряжений в попе-

речном сечении прямоугольной

формы. Величина максимального

касательного напряжения опре-

деляется по формуле:

max

τ= . (6.16)

Здесь W

= αhb

– момент сопро-

тивления сечения при кручении.

Дифференциальное уравнение

для углов закручивания анало-

гично уравнению для стержня

круглого сечения и имеет вид:

M(x)

d(x)

dx GI (x)

= ,

где I

= βhb

– момент инерции при кручении стержня прямо-

угольного сечения. Величины α, β, γ называют коэффициентами

Сен-Венана, их используют при расчете брусьев прямоугольно-

го сечения на кручение. Данные коэффициенты зависят от соот-

ношения h/b и приведены в табл. 6.1.

Таблица 6.1

h/b 1,0 1,5 1,75 2,0 2,5 3,0 4,0 6,0 8,0 10,0

∞

α 0,208 0,231 0,239 0,246 0,256 0,267 0,282 0,299 0,307 0,313 0,333

β 0,141 0,196 0,214 0,229 0,249 0,263 0,281 0,299 0,307 0,313 0,333

γ 1,0 0,859 0,820 0,795 0,766 0,753 0,745 0,743 0,742 0,742 0,743

Условия прочности и жесткости записываются аналогично

(6.4), (6.15), (6.15)'.

max

max S

τ= ≤

(6.17)

[]

max

;

G I

=≤θ (6.18)

[]

max

≤α

. (6.19)

max

γτ

≤

γ ≤ 1

max

Рис. 6.5

109

Здесь α – полный угол закручивания сечения по отношению к

защемленному сечению, определяется по тем же формулам, что

и для круглого сечения, заменяя в них I

на I

Подбор сечения выполняется в том же порядке, как и для

стержней круглого сечения.

ПРИМЕР 6.2

Для бруса, изображенного на рис. 6.6 требуется:

– построить эпюру крутящих моментов;

– из условия прочности при кручении подобрать размеры

прямоугольного поперечного сечения;

– построить эпюру углов закручивания сечений при сле-

дующих исходных данных:

= 2,1 кН

⋅

м; М

= 1,2 кН

⋅

м; М

= 2,7 кН

⋅

м;

h/b = 2; R

= 70 МПа; G = 8

⋅

МПа.

а)

в)

h=2b

1,8

–

0,9

2,1

Эп. М

(кН

⋅

м)

б)

0,0138

Эп.

(рад)

0,0211

0,0086

–

1,1 м

1,3 м

1 м

Рис. 6.6

г)

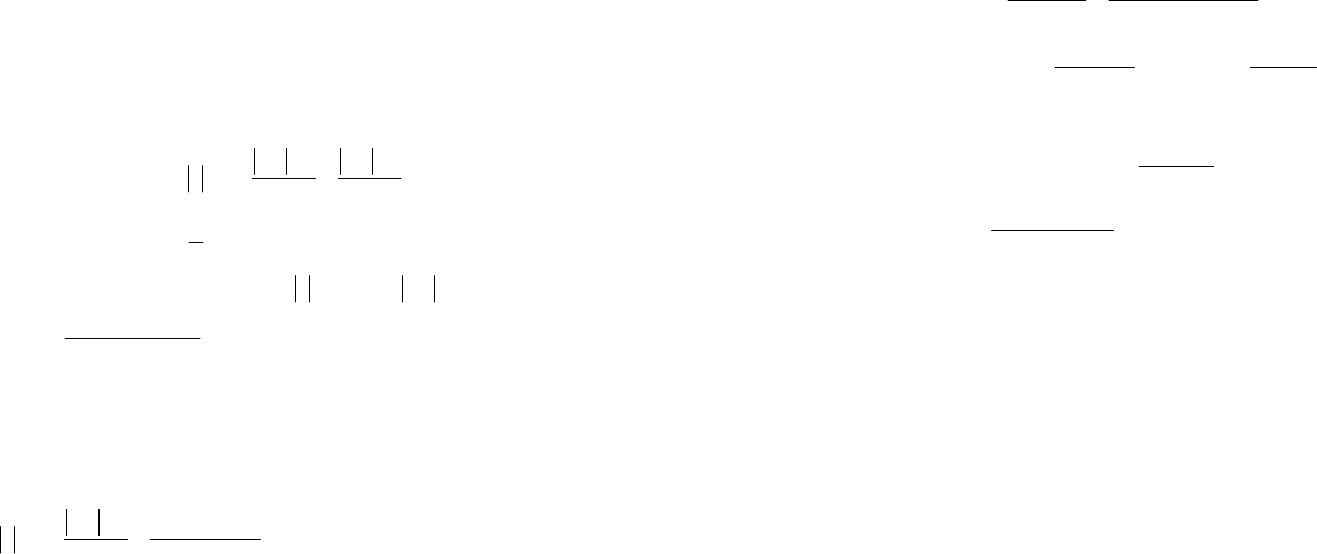
110

РЕШЕНИЕ

1. Построим эпюры крутящих моментов М

Рассматривая

правую отсеченную часть стержня для каждого грузового участ-

ка получим:

(1)

= М

= 2,1 кН

⋅

м;

(2)

= М

– М

= 2,1 – 1,2 = 0,9 кН⋅ м;

(3)

= М

– М

= 2,1 – 1,2 – 2,7 = –1,8 кН

⋅

м.

Эпюра М

показана на рис. 6.6б.

2. Определим необходимые размеры сечения, из условия

прочности (6.17):

max max

max

Whb

τ= = ≤

Для отношения

из табл. 6.1 находим α = 0,246.

При h = 2b и при условии

max

= R

max

= 2,1 кН⋅м по-

лучим

2,1 кН м

70 10 кПа

0, 246 (2b) b

⋅

=⋅

⋅⋅

. Отсюда находим:

b = 3,935

⋅ 10

–2

м.

После округления окончательно принимаем:

b = 4 см, h = 2b = 2

⋅ 4 = 8 см.

Проверим прочность подобранного сечения:

hbα = 0,246

84⋅⋅ = 31,5 см

;

max

2,1 кН м

W31,510м

−

⋅

τ= =

⋅

= 66,67

⋅

кПа < R

= 70

⋅

кПа.

3. Построим эпюру полных углов закручивания.

Предварительно определим момент инерции при кручении

и значение жесткости поперечного сечения при кручении GI

= βhb

= 0,229⋅8⋅4

= 117,25 см

= 117,25

⋅

–8

(при h/b = 2 β = 0,229 (табл. 6.1));

G = 0,8

⋅ 10

МПа = 0,8 ⋅10

кПа.

= 0,8⋅ 10

кН/м

⋅ 117,25 ⋅ 10

–8

= 93,8 кН⋅м

111

Определим полные углы закручивания сечений А, В, С, D

как сумму углов взаимного закручивания концов участков, за-

ключенных между рассматриваемым и защемленным сечениями.

= 0 (здесь стержень защемлен);

= α

+ ϕ

t(3) 3

1, 8 кН м 1,1 м

0,0211 рад;

GI 93,8 кН м

⋅

−⋅⋅

== =−

⋅

t(2) 2

С 32 3

0,9 1,3

0,0211

GI 93,8

0,0211 0,0125 0,0086 рад;

⋅

=ϕ +ϕ =ϕ + =− + =

=− + =−

t(1) 1

D32132

2,1 кН м 1 м

0,0086 0,0086 0,0224 0,0138 рад.

93,8 кН м

⋅

α=ϕ+ϕ+ϕ=ϕ+ϕ+ =

⋅⋅

=− + =− + =

⋅

Эпюра полных углов закручивания α показана на рис. 6.6в.

6.4. Статически неопределимые задачи

при деформации кручения

Как было отмечено ранее, статически неопределимыми на-

зываются брусья и системы, внутренние усилия или реакции

опор в которых нельзя определить с помощью одних лишь урав-

нений равновесия.

Поэтому при их расчете необходимо состав-

лять дополнительные уравнения –

уравнения совместности де-

формаций или перемещений. Число дополнительных уравнений,

необходимых для расчета системы, характеризует степень ее

статической неопределимости.

Важным этапом расчета статически неопределимых систем

является составление дополнительных (к уравнениям равнове-

сия) уравнений перемещений. Способ их составления поясним

на следующем примере.

Рассмотрим стержень, защемленный обоими концами и на-

груженный моментом М

, действующим в плоскости, перпенди-

кулярной продольной оси стержня (рис. 6.7).

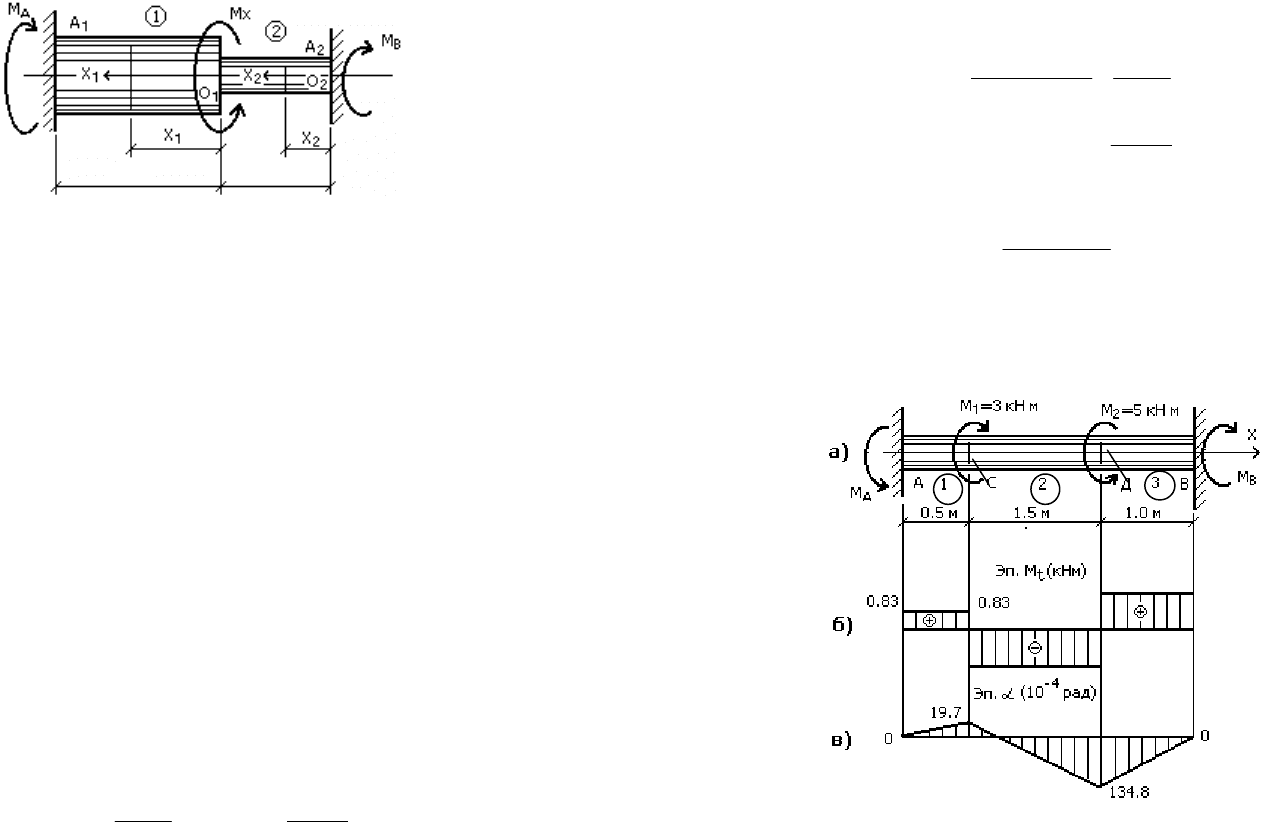
112

Рис. 6.7

В этом случае в заделках могут возникать только опорные

моменты М

и М

относительно продольной оси, которые требу-

ется определить. Направления неизвестных опорных реакций

показываются произвольно.

Статическая сторона задачи для определения этих неиз-

вестных дает только одно уравнение равновесия:

M0;

∑

AXB

MMM0.−+= (6.20)

Получили одно уравнение с двумя неизвестными, значит

степень статической неопределимости данной задачи равна еди-

нице. Для составления дополнительного уравнения рассмотрим

геометрическую сторону задачи, т.е. составим условие совме-

стности деформаций: полный угол закручивания сечения право-

го конца бруса

(сечения В) по отношению к левому защемленно-

му концу равен нулю, т.е.

=α

Полный угол закручивания

α равен сумме углов закручи-

вания двух участков:

B12

=ϕ +ϕ = (6.21)

Физическая сторона задачи. Углы закручивания отдельных

участков

определим по формуле (6.11):

t 1

;

G I

ϕ=

t 2

ϕ=

(6.22)

В этих формулах выражения для М

и M

записываем по

методу сечений, рассматривая правую отсеченную часть:

= M

– M

; M

= M

. (6.23)

113

Подставляя выражения (6.22) с учетом (6.23) в уравнение

(6.21), получим:

BX1 B2

1P 2P

(M M ) M

GI GI

−

=+=

Отсюда при

1P 2P

GI GI

имеем:

В случае

II,

≠

получаем

X1P

1P2 2P

(6.24)

ПРИМЕР 6.3

Брус, изображенный на рис. 6.8а, защемлен с двух концов:

R40 МПа 40 10 кПа;==⋅

G0,810 кПа.=⋅

Рис. 6.8

2,83

2,17

Требуется:

– определить реакции опор и построить эпюры крутящих

моментов;

114

– подобрать диаметр бруса сплошного круглого сечения;

– построить эпюру углов закручивания сечений.

РЕШЕНИЕ

А. Раскрытие статической неопределимости

и построение эпюры крутящих моментов

1. Статическая сторона задачи.

M0;

∑

;0MMMM

B21A

−

+−

AB12

MMMM352 кНм.

−

=+=−=−

Здесь М

и М

– опорные реакции в заделках, действующие в

плоскостях, перпендикулярных оси стержня. Их направление

выбрано произвольно.

Получили одно уравнение, содержащее два неизвестных,

т.е. рассматриваемая задача один раз статически неопределима.

Геометрическая сторона задачи.

Для получения дополнительного уравнения рассмотрим ус-

ловие совместности деформаций отдельных участков.

Определим полный угол закручивания правого концевого

сечения бруса по отношению к левому сечению. Он определяет-

ся как сумма углов закручивания трех участков и равен нулю.

B123

=ϕ +ϕ +ϕ =

Физическая сторона задачи.

Используем закон Гука при кручении для определения ϕ

;

ϕ=

t 2

;

ϕ=

t 3

ϕ=

Методом сечений получим выражения для определения

крутящих моментов

M из условия равновесия правой отсечен-

ной части:

t12B B B

MMMM35M 2M;=−+ =−+ =−+

t2B B

MMM5M;=− + =− +

= М

Эти выражения подставим в соотношение α

= ϕ

+ ϕ

= 0:

B1 B 2

PPP

(2 M) (5 M)

G I G I G I

−

+−+

α= + + =

115

Отсюда найдем значение опорной реакции M

BBB

(2 M)0,5 (5 M)1,5 M 1 0.

−

+⋅+−+⋅+⋅=

= 2,83 кН·м.

Построение эпюры крутящих моментов.

Зная величину опорной реакции, определяем значения кру-

тящих моментов на всех грузовых участках:

M 2 2,83 0,83 кН м;

−+ = ⋅

M 5 2,83 2,17 кН м;

−+ =− ⋅

M 2,83 кН м.

⋅

Эпюра

M изображена на рис. 6.8б.

Б. Подбор сечения

Используя условие прочности при кручении по формуле

(6.4) определяем требуемый полярный момент сопротивления

поперечного сечения.

TP 3 3 3

max

2,83 кН м

W0,007210 м 72 см .

R4010 кПа

−

⋅

== =⋅=

⋅

Полярный момент сопротивления круглого сплошного се-

чения определяется по формуле (6.6):

Из равенства

WW = определяем d:

72 см ;

= d = 7,17 см.

Округляя по ГОСТ 2590-88, примем d = 7,2 см.

Проверим прочность по формуле (6.4):

363

d 7,2

W73,3 см 73,3 10 м ;

16 16

−

ππ

== = =⋅

max

max S

2,83

38,6 10 кПа R4010 кПа .

W73,310

−

τ= = = ⋅ < =⋅

⋅

Недонапряжение 3,5 % объясняется округлением требуемо-

го диаметра в большую сторону.

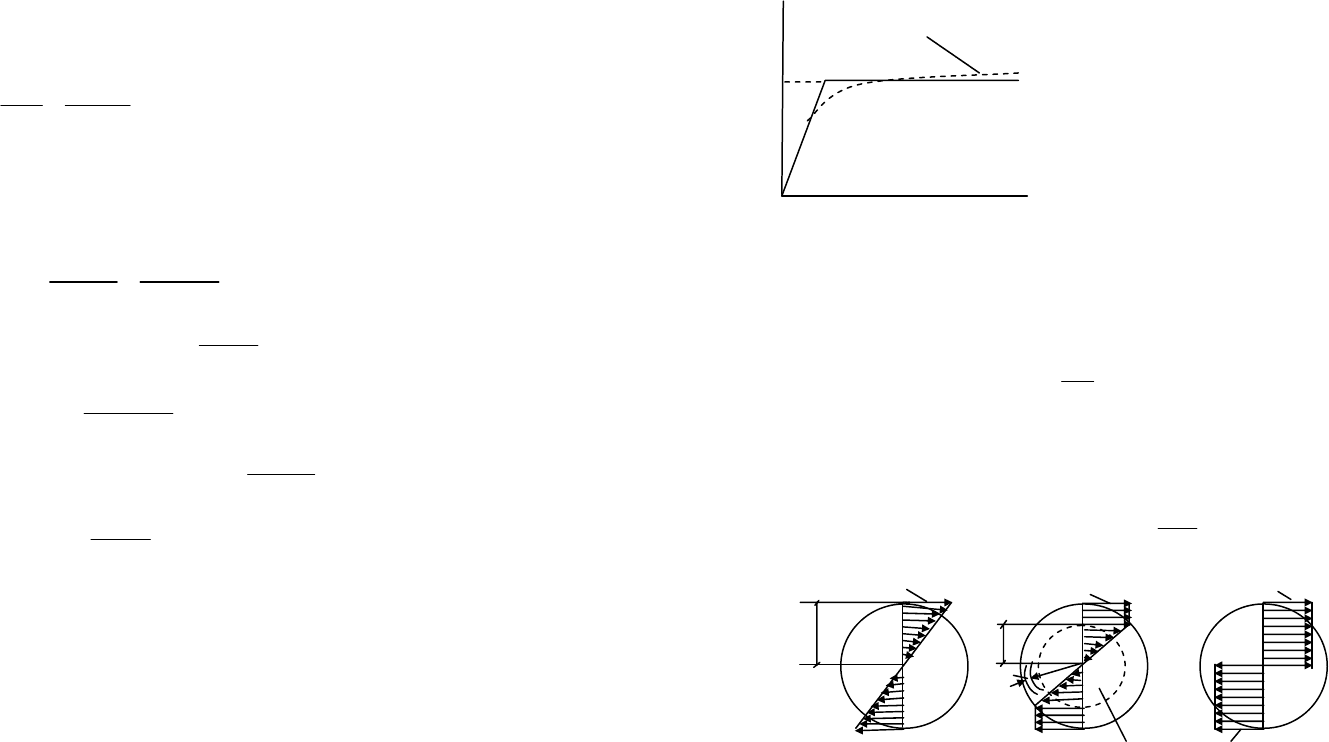
116

В. Построение эпюры углов закручивания сечений

Предварительно определим полярный момент инерции се-

чения и жесткость бруса при кручении:

484

d7,2

I264 см 264 10 м ;

32 32

−

ππ⋅

== = =⋅

8-842

G I 0,8 10 кПа 264 10 м 211 кН м .=⋅ ⋅ ⋅ = ⋅

Полные углы закручивания сечений определяем, используя

формулу (6.11).

=α (защемление, начало отсчета);

С 1

M t

0,83 0.5

19,7 10 рад.

G I 211

−

⋅

α=ϕ= = = ⋅

Д 12

19,7 10

2,17 1,5

19,7 10 134.8 10 рад;

211

−

−−

⋅

α=ϕ+ϕ= ⋅ + =

−⋅

=⋅+ =− ⋅

B123

134 10

2,83 1

134 10 0.

211

−

⋅

α =ϕ+ϕ+ϕ=− ⋅ + =

⋅

=− ⋅ + =

Равенство нулю угла закручивания в сечении В (в правом

опорном защемлении) подтверждает выполнение поставленного

в начале задачи условия.

По вычисленным значениям строим эпюру углов закручи-

вания (рис. 6.8в).

6.5. Кручение бруса круглого сечения

в упругопластической стадии

Заменим реальную криволинейную диаграмму сдвига (на

рис. 6.9 она показана пунктирной линией) – диаграммой Пран-

дтля при сдвиге, т.е. будем считать, что при τ < τ

(

– предел

текучести при сдвиге) справедлив закон Гука и материал дефор-

мируется линейно-упруго. При напряжениях τ = τ

возникают

117

пластические деформации сдвига,

значения которых неогра-

ниченны, а напряжения остаются

постоянными и равными τ

Выясним, как будет видоиз-

меняться эпюра касательных на-

пряжений в сечении при посте-

пенном возрастании крутящего

момента М

с учетом упругопла-

стической работы материала.

В упругой стадии напряжения τ распределены вдоль диа-

метра бруса по линейному закону. При возрастании момента М

пропорционально возрастают и все напряжения. Конец этой ста-

дии определяет равенство

max

τ (6.25)

когда в точках по краю сечения начинает появляется текучесть

(рис. 6.10а). Крутящий момент, соответствующий данному со-

стоянию, обозначим М

и получим из соотношения (6.25):

= τ

⋅

(6.26)

max

=τ

dρ

Уп

ру

гое яд

а)

)

в)

Рис. 6.10. Образование пластического шарнира

при кручении

При дальнейшем возрастании крутящего момента пластиче-

ская зона будет все больше проникать вглубь сечения бруса

(рис. 6.10б), а все сечение разделится на 2 зоны: упругое ядро,

где τ ≤ τ

с радиусом r

и пластическую кольцевую зону

Из эксперимента

Рис. 6.9

118

≤ ρ ≤ R, где τ = τ

. Суммарный крутящий момент представим

как сумму:

= M

+ M

, (6.27)

где момент упругого ядра М

= τ

(6.28)

найден по формуле (6.26) (R заменено на r

), а момент пластиче-

ской кольцевой зоны равен

SS SS

dA 2 d (R r ).

τ ⋅ ⋅ρ= τ πρ⋅ ρ⋅ρ= πτ ⋅ −

∫∫

(6.29)

При вычислении момента пластической кольцевой зоны

элементарная площадь dA равна площади кольца толщиной d

т.е. dA = 2 d .πρ ⋅ ρ

Из формулы (6.29) видно, что при r

→ 0 пластическая зона

стремится охватить все сечение (рис. 6.10в) и внутренний мо-

мент стремится к своему предельному значению:

пред

πτ (6.30)

Поперечное сечение стержня, в котором во всех точках

возникают пластические деформации, называется пластиче-

ским шарниром.

Cтержень превращается как бы в пластический

механизм, в котором углы закручивания неограниченно растут

при постоянном моменте М

пред

Соотношение

пред

2R4

R/ 1,33

М 323

⎛⎞

=πτ τ ==

⎜⎟

⎝⎠

показы-

вает, что от момента первого появления пластических деформа-

ций в наиболее напряженных точках бруса до полного исчерпа-

ния несущей способности крутящий момент должен возрасти в

1,33 раза, то есть это соотношение выражает резерв несущей

способности за счет учета упругопластических свойств материала.

119

6.6. Контрольные вопросы по теме

При каком нагружении прямой брус испытывает только де-

формацию кручения?

Как определяется величина крутящего момента в любом се-

чении бруса? Каков порядок построения эпюр крутящих

моментов?

Какие напряжения возникают в поперечном сечении бруса

при деформации кручения и как они определяются?

Как распределены напряжения в сечении при кручении бру-

са круглого сечения?

Запишите условие прочности при кручении.

Каков порядок подбора размеров поперечного сечения бру-

са при кручении по условию прочности?

Что называется полярным моментом сопротивления попе-

речного сечения?

Как определяется полярный момент сопротивления для

круглого сплошного и кольцевого сечений?

Какие задачи кручения брусьев решаются с использованием

условия прочности?

10.

Что называется жесткостью сечения при кручении?

11.

Как определяется взаимный угол закручивания сечений на

участке бруса длиной

12.

Как определяется относительный угол закручивания?

13.

Как определяется полный угол закручивания сечения по от-

ношению к неподвижному или начальному сечению?

14.

Как записываются условия жесткости при кручении через

полный и относительный углы закручивания?

15.

Поясните порядок подбора сечений при кручении из усло-

вий жесткости.

16.

Каков порядок решения статически неопределимых задач

при кручении?

17.

Как распределяются касательные напряжения при кручении

бруса прямоугольного сечения?

18.

Запишите условие прочности при кручении бруса прямо-

угольного поперечного сечения.