Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей

Подождите немного. Документ загружается.

Найти

матрицу

обратную

матрице

2 3 5

7 1 4

9 8 6

−

 

 

− −

 

− −

 

Проверить

выполнимость

равенства

-1

⋅А

АА

-1

Ответ

38 22 17

6 33 27

231

65 11 23

−

 

 

− − −

 

 

Решить

систему

помощью

формул

Крамера

матричным

методом

1 2 3

2 3 3

2 6 9 11

4 3 8 2

x x x

+ − = −





− + + = −





− − + = −



Ответ

(

)

4, 2,1

−

Исследовать

систему

на

совместность

найти

ее

решение

1 2 3 4

1 2 4

1 3 4

1 2 3 4

3 2 2 3

3 2 3

4 0

3 3 6

x x x x

x x x

x x x x

+ − + = −





− − + = −





− + =



− + + =



Ответ

система

не

совместна

Уровень II

Решить

уравнение

2 0 3

1 7 3 0

5 3 6

− − =

−

Ответ

: {5}.

Вычислить

используя

свойства

определителей

2 2

sin cos 1

α α

β β

γ γ

Ответ

: {0}.

Вычислить

-1

1 2 3 4

5 6 7 2

1 0 1 2

3 4 5 6

−

 

 

−

 

−

 

 

Ответ

1 1 61 23

6 5 60 60

1 3 11 11

3 10 15 30

1 1 1

6 12 12

1 1 3

10 20 20

 

− − −

 

−

 

−

 

− −

 

 

Найти

ранг

матрицы

приведением

ступенчатому

виду

2 0 8 1 5

3 1 7 2 4

8 2 6 3 13

11 3 13 5 17

− −

 

 

−

 

− − − −

 

−

 

Ответ

: {3}.

Исследовать

систему

на

совместность

определенность

слу

чае

совместности

найти

решение

1 2 3 4 5

2 2 3 2

6 3 2 5 3

6 3 4 8 13 9

4 2 2 4

x x x x x

− + + + =





− + + + =





− + + + =



− + + + =



Ответ

совместна

неопределенна

, (

; 5 –

+ 4

; –3; 1 + 2

–

Решить

однородную

систему

1 2 3 4 5

5 6 2 7 4 0

2 3 4 2 0

5 9 3 6 0

7 9 3 5 6 0

x x x x x

+ − + + =





+ − + + =





+ − + + =



+ − + + =



Ответ

: (0;

– 2

; 3

; 0; 3

Уровень III

Найти

ранг

матрицы

)

n n n

n n n n

 

 

 

…

⋮ ⋮ ⋮ ⋱ ⋮

…

;

)

0 1 1 1

1 0 1 1

1 1 0 1

1 1 1 0

 

 

 

⋯

⋮ ⋮ ⋮ ⋱ ⋮

⋯

Ответ

)

;

)

Решить

матричное

уравнение

1 2 3 1 2 3 1 2 3

2 3 1 4 5 6 4 5 6

0 2 1 7 8 0 7 8 0

−

     

     

− ⋅ ⋅ =

     

−

     

Ответ

1 4

7 7

2 1

7 7

4 2

7 7

 

−

 

− −

 

− −

 

 

Вычислить

определители

приведением

треугольному

виду

)

1 2 2 1

1 2 3 1 0

2 3 4 0 0

2 1 0 0 0

1 0 0 0 0

n n n

− − − − −

− − − −

− − −

− −

−

…

⋮ ⋮ ⋮ ⋱ ⋮ ⋮

…

Ответ

( )

(

)

1 .

n n

−

)

1 1 1 1

−

…

⋮ ⋮ ⋮ ⋱ ⋮

…

Ответ

: 0.

Числа

255, 391, 578

делятся

на

17.

Не

вычисляя

значение

определи

теля

2 5 5

3 9 1

5 7 8

доказать

что

он

тоже

делится

на

17.

Исследовать

систему

на

совместность

определенность

Найти

решение

1 2

1 3

1 2 4

1 2 1

... 2

... 3

....................................

... 3

x x x n

x x x x n

x x x n

−

+ + + = −





+ + + = −



+ + + + = −





+ + + = −





Ответ

система

совместна

определенна

единственное

решение

(

)

1;1;1;...;1

−

ГЛОССАРИЙ

Матрица – прямоугольная

таблица порядка m ×

××

× n,

обозначаемая

11 12 1

21 22 2

1 2

...

... ... ... ...

...

m m mn

a a a

 

 

 

прямоугольная таблица из m× n элементов,

где первое число m равно числу строк, а n –

числу столбцов матрицы А; кратко матрица А

обозначается

(

)

mn ij

A a

Элементы матрицы

числа

, из которых состоит матрица; ин-

дексы определяют положение элемента в таб-

лице: первый индекс – число строк; второй ин-

декс – число столбцов

Квадратная матрица поряд-

ка n

матрица, число строк которой равно числу ее

столбцов и равно числу n

Главная диагональ квад-

ратной матрицы

образуется элементами с одинаковыми индек-

сами а

, а

, …, a

Симметричная матрица

квадратная матрица, элементы которой, симмет-

ричные относительно главной диагонали, равны

, 1,2,..., ; 1,2,...,

ij ji

a a i m j n

= = =

Единичная матрица (Е)

квадратная матрица, на главной диагонали кото-

рой стоят единицы, а остальные элементы нуле-

вые

Произведение матрицы A

mхn

(порядка m ×

××

× n) на матрицу

nхk

(порядка n ×

××

× k)

матрица C

(порядка m × k), элементы кото-

рой вычисляются по формуле

1 1 2 2

...

ij i j i j in nj

C a b a b a b

= ⋅ + ⋅ + + ⋅

1,2,..., ; 1,2,...,

i m j k

= =

Определитель квадратной

матрицы

число, которое ставится в соответствие матри-

це А и вычисляется по ее элементам

Алгебраическое дополне

ние

элемента

величина

( )

i j

ij ij

A M

= −

, где

– определи-

тель порядка (n – 1), полученный вычеркива-

нием i-той строки и j-того столбца, на пересе-

чении которых стоит элемент

Вырожденная матрица

матрица, у которой определитель равен нулю.

Обратная матрица для

матрицы А.

квадратная матрица

−

, которая удовлетворяет

условию

1 1

A A A A E

− −

⋅ = ⋅ =

; обратная мат

рица

−

существует тогда и только тогда, когда исход-

ная матрица невырожденная,

det 0

≠

Ранг матрицы А

наибольший из порядков миноров данной мат-

рицы, отличных от нуля

Элементарные преобразо-

вания матрицы А

− перестановка местами двух параллельных

рядов матрицы;

− умножение всех элементов ряда матрицы

на число, отличное от нуля;

− прибавление ко всем элементам ряда мат-

рицы соответствующих элементов параллель-

ного ряда, умноженных на одно и то же число

Ступенчатая матрица

матрица, обладающая следующими свойством:

если в i-той строке матрицы левее элемента a

стоят только нули (a

- первый отличный от

нуля элемент в i-той строке), то ниже этого

элемента в j-том столбце стоят только нули

Метод Гаусса

метод приведения произвольной матрицы к

ступенчатому виду с помощью элементарных

преобразований

Угловые элементы ступен-

чатой матрицы

первые отличные от нуля элементы каждой

строки, «стоящие на углах» ступенчатой мат-

рицы; число угловых элементов ступенчатой

матрицы равно рангу исходной матрицы

Система из m линейных

уравнений с n неизвестны-

ми

система вида

11 1 12 2 1 1

21 1 22 2 2 2

1 1 2 2

...

............................................

...

n n

m m mn n m

a x a x a x b

+ + + =





+ + + =





+ + + =



где

(

)

1 2

; ;...;

x x x x

– вектор неизвестных,

подлежащих определению

Матрица системы

матрица коэффициентов при неизвестных

11 12 1

21 22 2

1 2

m m mn

a a a

 

 

 

…

… … … …

…

Расширенная матрица

системы

матрица, полученная присоединением столбца

из свободных членов

1 2

, , ...,

b b b

к матрице

системы

11 12 1 1

21 22 2 2

1 2

m m mn m

a a a b

 

 

 

…

… … … … …

…

Векторно-матричная за-

пись системы

запись системы в виде

Ax b

Однородная система

Система уравнений, в которых вектор правых

частей является нулевым вектором:

;

Неоднородная система

уравнений

система, в которой хотя бы в одном уравнении

справа стоит ненулевой элемент:

≠

Решение системы

такой вектор

(

)

1 2

, , ,

x x x x

…

, что при под-

становке чисел

1 2

, , ,

x x x

…

в уравнения сис-

темы, получаются верные равенства

Совместная система

система, у которой существует решение

Несовместная система

система, у которой нет решений

Критерий (необходимое

и достаточное условие)

совместности системы

равенство рангов основной и расширенной

матрицы

Общее решение системы

совокупность всех решений системы

Частное решение системы

решение, которое получается из общего реше-

ния путем подстановки вместо свободных пе-

ременных конкретных численных значений

Метод Гаусса для решения

системы уравнений

метод, состоящий из прямого и обратного хода:

1. прямой ход метода Гаусса – приведение

системы к ступенчатому виду с помощью эле-

ментарных преобразований;

2. обратный ход – выбор свободных и базис-

ных переменных и получение формул общего

решения

Общее решение неоднород-

ной системы

решение, состоящее из суммы общего решения

однородной системы и некоторого частного

решения неоднородной

Определенная система или

имеющая единственное ре-

шение

система, которая имеет единственное решение

(у которой число угловых элементов в ступенча-

той форме равно числу переменных, т.е. ранг

системы равен числу переменных)

УЧЕБНЫЙ МОДУЛЬ 2.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Введение

Математический анализ – общее название для ряда математи-

ческих дисциплин, основанных на понятиях функции и предельного

перехода. К нему относятся дифференциальное и интегральное

исчисления, теория рядов, дифференциальных уравнений и др.

ДИДАКТИЧЕСКИЕ ЦЕЛИ ОБУЧЕНИЯ

Студент должен знать Студент должен уметь

− определение функции, способы

ее задания ;

− определение предела числовой

последовательности;

− определение предела функции по

Гейне и по Коши;

− определения бесконечно малой,

бесконечно большой функции;

− связь между бесконечно малой и

бесконечно большой функциями;

− необходимое и достаточное ус-

ловие существования предела

функции;

− теоремы о предельном переходе

в равенствах;

− теоремы о предельном переходе

в неравенствах;

− первый замечательный предел;

− второй замечательный предел;

− три определения функции, не-

прерывной в точке;

− основные свойства непрерывных

на отрезке функций

− узнавать основные классы эле-

ментарных функций;

− строить графики основных эле-

ментарных функций;

− доказывать по определению, что

существует предел числовой по-

следовательности;

− выделять неопределенности;

− пользоваться правилами раскры-

тия неопределенностей;

− выделять первый замечательный

предел;

− выделять второй замечательный

предел;

− пользоваться таблицей эквива-

лентных бесконечно малых функ-

ций, бесконечно больших функций

при вычислении пределов;

− исследовать на непрерывность

различные функции;

− определять характер точек раз-

рыва;

− схематически изображать пове-

дение функции в окрестностях то-

чек разрыва

УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА МОДУЛЯ 2

Название вопросов,

которые изучаются на лекции

Номер

практи-

ческого

занятия

Нагляд-

ные и

методи-

ческие

пособия

Формы

кон-

троля

знаний

1. Множество действительных чисел.

Функция. Область ее определения. Спосо-

бы задания. Сложные и обратные функ-

ции, их графики. Основные элементарные

функции. Гиперболические функции, их

графики

1, 2, 4, 7,

Опрос,

ПДЗ

2. Числовые последовательности. Спо-

собы задания и виды последовательности.

Существование предела монотонной огра-

ниченной последовательности

II, III 2, 4, 7, 8

Опрос,

ПДЗ

3. Предел функции в точке. Предел

функции в бесконечности. Односторонние

пределы, их связь с пределом функции.

Свойства функций, имеющих предел. Пре-

дел суммы, произведения и частного

функций. Предел сложной функции

IV 2, 4, 7, 8 ПДЗ

4. Первый и второй замечательные пре-

делы, их следствия

V, VI 2, 4, 7, 8

Опрос,

ПДЗ

5. Бесконечно малые и бесконечно

большие функции, их свойства и взаимо-

связь. Эквивалентность функций, их ис-

пользование при вычислении пределов

VII 2, 4, 7, 8

Опрос,

ПДЗ

6. Непрерывность функции в точке. Не-

прерывность основных элементарных

функций. Свойства функций, непрерыв-

ных не отрезке: ограниченность, сущест-

вование наибольшего и наименьшего зна-

чений

VIII, IX 2, 4, 7, 8 КР

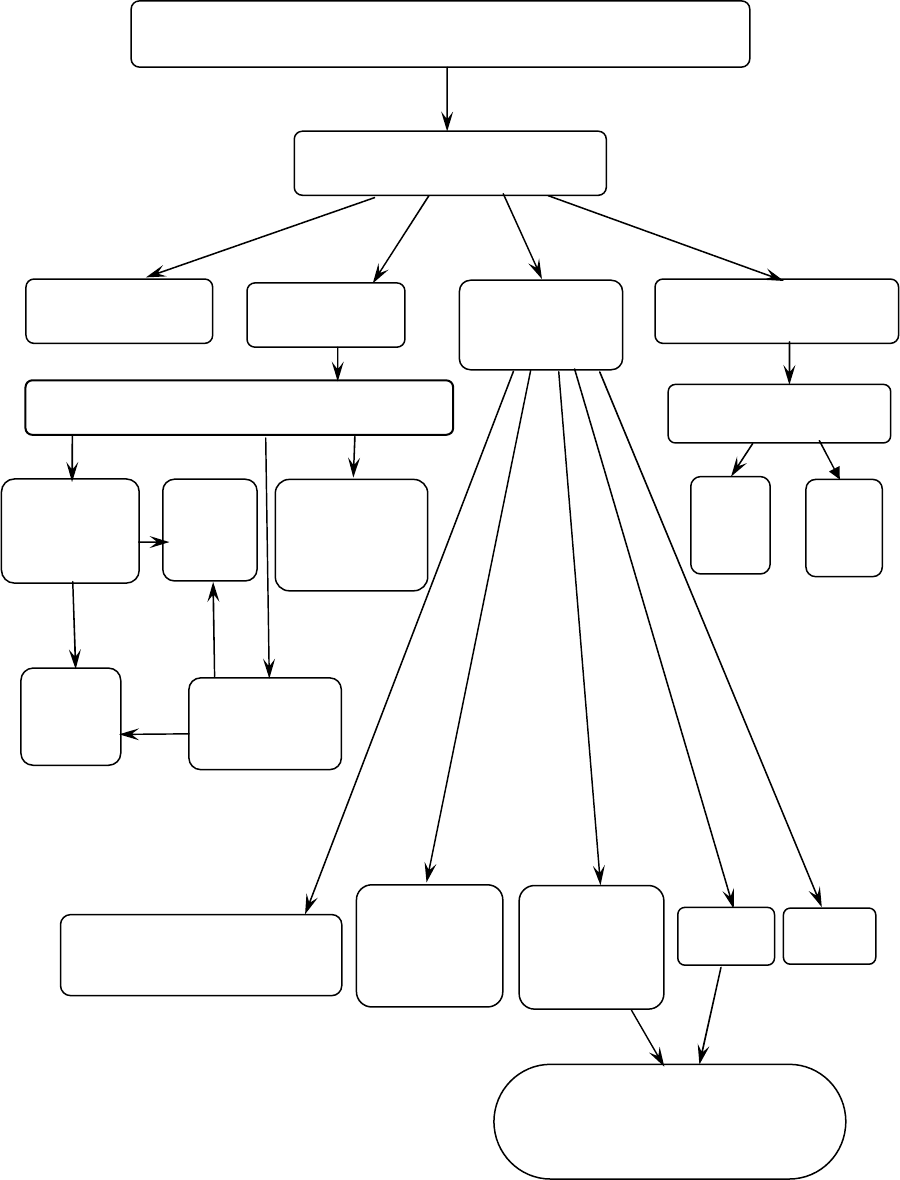
ГРАФИЧЕСКАЯ СХЕМА МОДУЛЯ 2

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Основные понятия

Множество

Функция

Предел

функции

Непрерывность

Аналитический способ задания

Явно

заданные

да

Неявно

заданные

ДПС

ПСК

Заданные

парамет-

рически

Точки разрыва

Числовая

последова

тел

ность

Предел

функции

по Гейне

БМФ

Предел

функции

по Коши

ББФ

Критерий существова-

ния предела функции

Информационная таблица «Введение в математический анализ»

Переменная величина y называется функцией

от независимой переменной x (аргумента),

если указан закон (правило), по которому каж-

дому элементу x некоторого множества ставит-

ся в соответствие единственный элемент y того

же или другого множества.

Способы задания: аналитический, табличный,

графический, словесный, программой на ЭВМ

Правый (левый) односторонний предел:

( )

(

)

(

)

lim 0

x x

f x f x A

→

= ± =

Бесконечно малые функции

(

)

lim 0

x x

→

α =

Бесконечно большие функции

(

)

lim

x x

f x

→

= ∞

Правила вычисления пределов

(

)

lim

x x

f x A

→

(

)

lim

x x

f x B

→

lim ,

x x

c c c const

→

= =

;

(

)

(

)

1 2

lim

x x

f x f x A B

→

± = ±

 

 

(

)

(

)

(

)

lim

x x

f x g x A B

→

⋅ = ⋅

;

(

)

lim

x x

c f x c A

→

⋅ = ⋅

;

(

)

( )

lim

x x

f x

f x B

→

, B

≠

НЕПРЕРЫВНОСТЬ

Опр.1

(

)

{ }

f x C

∈ ⇔

∃f

(

); 2)

(

)

(

)

lim

x x

f x f x

→

Опр.2

(

)

{ }

f x C

∈ ⇔

∃f

(

); 2)

(

)

lim 0

f x

∆ →

∆ =

Опр.3

(

)

{ }

f x C

∈ ⇔

(

)

(

)

(

)

0 0

lim lim

x x x x

f x f x f x

→ − → +

< >

= =

ПРЕДЕЛ ФУНКЦИИ

(

)

lim

x a

f x A

→

(

По Гейне

)

Число

называется

пределом

функции

(

)

y f x

при

x x

→ ,

если

для

любой

числовой

последовательности

{

}

n N

∈

сходящейся

соответствующая

последовательность

значений

функции

(

)

{

}

n N

f x

∈

сходится

(

По Коши

Число

является

пределом

функции

(

)

y f x

при

x x

→ ,

если

для

любого

сколь

угодно

малого

числа

ε >

существует

число

δ >

(

зависящее

от

ε),

такое

что

для

всех

x x

≠

удовлетворяющих

неравенству

x x

− < δ

выполняется

неравенство

( )f x A

− <ε

– точка разрыва

не

вы

полняется

хотя

бы

одно

условие

непрерывности

– точка разрыва I рода

оба

односторонних

предела

сущест

вуют

конечны

– точка разрыва II рода

хотя

бы

один

из

односторонних

преде

лов

равен

∞

или

не

существует

(

)

y f x

Возрастающая

(

)

y f x

Убывающая

y x

= +

Четная

(

)

(

)

f x f x

= −

y x

Нечетная

(

)

(

)

f x f x

= − −

(

)

y f u

(

)

u x

= ϕ

(

)

(

)

(

)

y f x F x

= ϕ =

–

независимая

переменная

–

промежуточная

переменная

Множества

Числовые множества

натуральных чисел –

ℕ

ℕℕ

ℕ

целых чисел –

ℤ

ℤℤ

ℤ

рациональных чисел –

ℚ

ℚℚ

ℚ

действительных чисел –

ℝ

ℝℝ

ℝ