Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей
Подождите немного. Документ загружается.

21
ход позволяет открыть решение заданий повышенных уровней сложности
всей аудитории. Предлагаемая модель «подтягивает» студентов до приклад-
ного и творческого уровней обучения. Работая на протяжении занятия с за-
даниями I уровня, слабые студенты приобретают базовые знания и умения.
Тем самым, создаются предпосылки для освоения методики решения более
сложных заданий студентам, желающим перейти на другой уровень обуче-
ния; для развития, в конечном счете, потенциала всей аудитории.
0.4. Методические рекомендации работы
в информационном поле модуля
В самом общем виде процесс познания новой информации состоит
из следующих этапов: первичное восприятие → изучение основных ее
элементов → углубление, обобщение, систематизация полученной инфор-
мации → включение познанного нового знания в систему имеющихся
представлений, знаний, мировоззрения в целом. Исходя из этих психолого-
методологических соображений, предлагается следующая последователь-
ность этапов работы в информационном поле модуля.
0. С помощью методической карты изучить содержание разделов
лекционного материала.
1. Вход в модуль целесообразно осуществить с помощью графиче-
ской схемы и информационной таблицы. Граф-схема и информационная
таблица определенного раздела математики представляют собой макси-
мально сжатый, компактно составленный справочный материал. Справоч-
ный материал информационной таблицы раскрывает основные блоки гра-
фической схемы рассматриваемого раздела.
Предложенные методические средства помогают при изучении но-
вой информации увязать различные понятия, теоремы, формулы в единое
целое; позволяют проследить логику построения теорий; служат эффек-
тивному прохождению всех этапов восприятия, усвоения, обобщения, сис-
тематизации, и в конечном итоге, логической организации новой инфор-
мации. Структурированная наглядность содержания представленной ин-
формации облегчает ее усвоение за счет целостности представления и вос-
приятия изучаемого объекта, направляет избирательность внимания и па-
мяти. Все это способствует более глубокому уровню усвоения предмета,
помогает находить главное и производное в изучаемом материале, анали-
зировать его, учит рационально работать с новой информацией любого со-
держания.

22
2. Изучение теоретической части модуля следует начинать с бегло-
го чтения всей информации. На втором этапе этой познавательной дея-
тельности рекомендуется проработать каждый раздел, отдельные фрагмен-
ты при этом разумно параллельно проделать своей рукой. На третьем эта-
пе, просмотрев еще раз графическую схему, отработав основные положе-
ния теоретической части модуля с помощью информационной таблицы,
целесообразно прочитать еще раз весь теоретический материал с целью его
целостного восприятия, большей систематизации, логической организации
и обобщения.
3. Практическая часть модуля представляет собой методически
спроектированные практические занятия. Отметим, что они содержат как
методические рекомендации преподавателям, так и методические реко-
мендации студентам. В этой связи, обратим внимание на наличие обучаю-
щих задач, решение нулевых вариантов аудиторных и внеаудиторных кон-
трольных работ. Все это дополняет задачи и примеры, приведенные в тео-
ретической части модуля, и создает предпосылки для овладения соответст-
вующим математическим аппаратом, по крайней мере, на уровне воспро-
изводящей познавательной деятельности, позволяет освоить студенту
практическую часть информации модуля либо самостоятельно, либо под
руководством преподавателя.
4. На выходе из модуля следует еще раз провести обобщение, сис-
тематизацию полученных знаний путем повторного изучения графической
схемы, информационной таблицы, глоссария и выводов. Кроме того, прак-
тическая часть содержит в себе возможности для проведения контроля и
самоконтроля результатов обучения: тесты трех уровней сложности, нуле-
вой вариант аудиторной или внеаудиторной контрольной работы, индиви-
дуальные домашние задания. Поэтому на выходе из модуля рекомендует-
ся, как минимум, выполнить тест первого уровня сложности. Тесты перво-
го уровня сложности рекомендуется выполнить и непосредственно при
подготовке к экзамену, зачету либо коллоквиуму.
Желаем успехов!

23
УЧЕБНЫЙ МОДУЛЬ 1.
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Введение
В данном учебном модуле рассматриваются матрицы и действия над
ними, изучаются свойства и методы вычисления определителей, большое
внимание уделяется теории решения систем линейных уравнений. Матрич-
ная алгебра дает возможность оперировать с целыми группами однотипных
величин, выполняя различные математические преобразования (сложение,
умножение и т.д.) аналогично тому, как это делается в обычной алгебре.
Использование матриц не только открывает новые возможности, но и уп-
рощает решение многих задач. Матричная формулировка задачи облегчает
ее программированное решение. При этом оказывается возможным исполь-
зование стандартного математического программного обеспечения.
ДИДАКТИЧЕСКИЕ ЦЕЛИ ОБУЧЕНИЯ
Студент должен знать Студент должен уметь
−
−−
−
основные определения, связан-
ные с понятием матриц;
−
−−
−
основные определения, связан-
ные с понятием определителей;
−
−−
−
основные определения, связан-
ные с понятием систем линейных
уравнений;
−
−−
− свойства линейных операций над
матрицами;
−
−−
− определение и свойства умноже-
ния матриц;
−
−−
− свойства определителей;
−
−−
− матричный метод и правило Кра-
мера решения невырожденных сис-
тем линейных уравнений;
−
−−
− теорему Кронекера – Капелли;
−
−−
− метод Гаусса
−
−−
− выполнять линейные операции
над матрицами;
−
−−
− выполнять умножение матриц;
−
−−
− вычислять обратную матрицу;
−
−−
− вычислять определители 2, 3, n
порядка разложением по элементам
произвольного ряда;
−
−−
− использовать эффективные спо-
собы вычисления определителей;
−
−−
− исследовать системы линейных
уравнений на совместность;
−
−−
− применять матрицы и определи-
тели к решению систем линейных
уравнений матричным методом, по
формулам Крамера;
−
−−
− использовать метод Гаусса

24
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА МОДУЛЯ 1
Название вопросов,
которые изучаются на лекции
Номер
практи-
ческого
занятия
Нагляд-
ные и
методи-
ческие
пособия
Формы
контроля
знаний
1. Матрицы, основные понятия. Линейные
операции над матрицами и их свойства.
Определители n-ного порядка и их свойст-
ва. Алгебраическое дополнение. Вычисле-
ние определителя разложением по строке
(столбцу). Вычисление определителя при-
ведением к треугольному виду.
I
1, 2, 3,
4, 5
ПЛ,
ВДЗ
2. Умножение матриц, свойства операции
умножения. Обратная матрица, ее вычисле-
ние. Решение систем линейных уравнений
матричным методом. Правило Крамера.
II, III
1, 2, 3,
4, 5
ПЛ,
ВДЗ
3. Ранг матрицы. Теорема Кронекера-
Капелли. Решение произвольных систем
линейных уравнений методом Гаусса
IV, V
1, 2, 3,
4, 5
Опрос,
ПДЗ
Перечень тем практических занятий приведен в практической части
модуля.
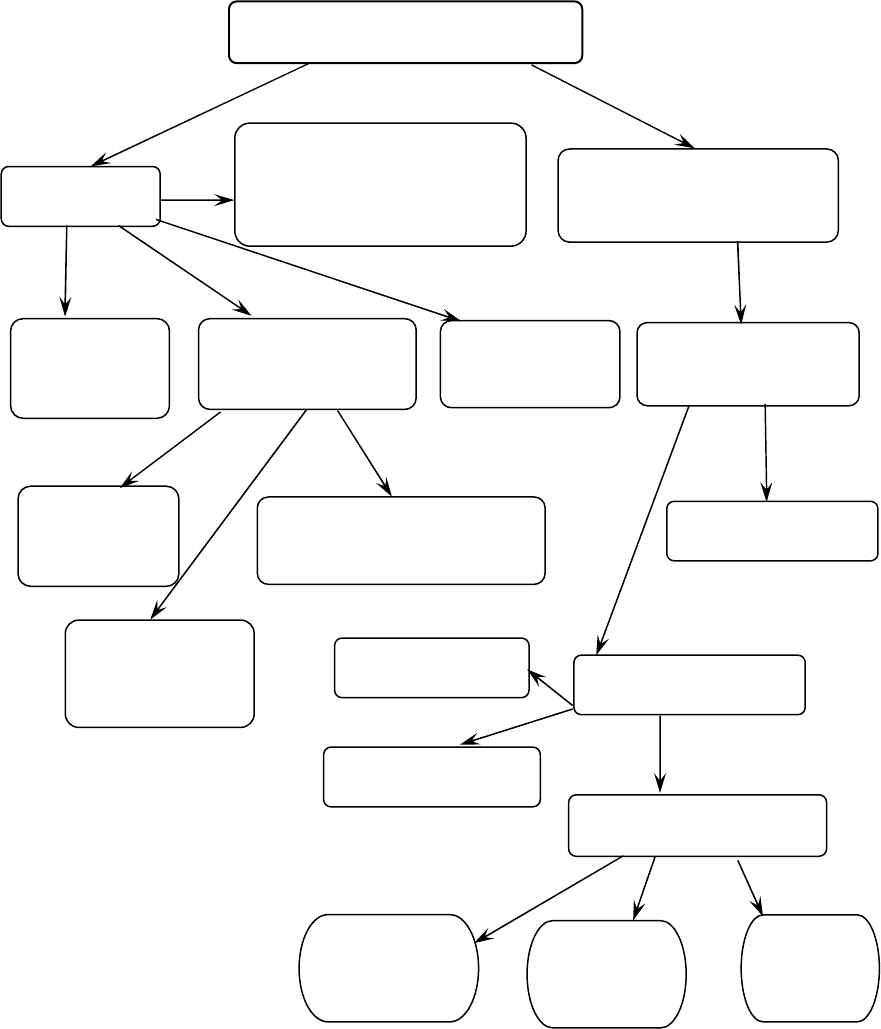
25
ГРАФИЧЕСКАЯ СХЕМА МОДУЛЯ 1
ЛИНЕЙНАЯ АЛГЕБРА
Матрицы
Определители,
их свойства,
методы вычисле-
ний
Системы линей-
ных уравнений
Основные
понятия
Операции над
матрицами
Ранг
матрицы
Критерий
совместн
о
сти
Линейные
свойства
Умножение матриц,
свойства
Обратная
матрица
Несовместные
Совместные
Однородные
Неоднородные
Методы решения
Матрич-
ный
Правило
Крамера
Метод
Гаусса

26
Информационная таблица «Элементы линейной алгебры»
Матрица А
m ×
××
× n
– прямоугольная таблица
из m строк и n столбцов, состоящая из эле-
ментов произвольной природы.
(
)
m n ij
m n
A a
×
×
=
.
А
m × n
+ B
m × n
= (a
ij
)
m × n
+ (b
ij
)
m × n
α
⋅
A = (α a
ij
)
m × n
А
m × к
⋅ B
к × n
=
1
k
il lj
l
a b
=
⋅
∑
∃A и В, что A⋅B≠В⋅A, ∃A≠0, B≠0, что A⋅B = 0
А
-1
– обратная матрица для А
n × n
,
если AА
-1
= А
-1
А = E.
Если ∆А
n×n
≠0, то
11 21 1
12 22 2
1
1 2
...
...
1
... ... ... ...
...
n
n
n n nn
A A A
A A A
A
A A A
−
∃ =
∆
Эффективные методы вычисления ∆А:
1) получение среди элементов произвольно-
го ряда максимального количества нулей;
2) приведение ∆А к «треугольному» виду.
Элемент строки матрицы – крайний, если
он не равен 0, а все элементы этой строки,
находящиеся левее него, равны 0.
Матрица – ступенчатая, если крайний
элемент каждой матрицы находится правее
крайнего элемента предыдущей строки.
1
0
.
1 3 4 2
0 0 2 0
0 1 3 1
−
2
0
.
1 2 3 2
0 2 0 1
0 0 0 0
−
.
неступенчатая ступенчатая
Ранг матрицы – наибольший из порядков
ее миноров, не равных 0.
Базисным минором называется любой из
отличных от нуля миноров матрицы А, по-
рядок которого равен r(A).
(1)
1 1
m n n m
A X b
× × ×
⋅ = – матричная запись систе-
мы из m линейных уравнений с n неизвестными.
Решение системы (1) – такой набор чисел
(с
1
,…, с
n
), что при его подстановке в систему
вместо соответствующих неизвестных каждое
из уравнений системы обращается в тождество.
Система называется определенной, если
она имеет единственное решение, и неопре-
деленной, если она имеет более одного ре-
шения.
Система совместна, если она имеет
хотя бы одно решение.
Система, не имеющая ни одного ре-
шения, называется несовместной.
Элементарные преобразования
матрицы:
1) перемена местами двух параллель-
ных рядов;
2) умножение элементов ряда на чис-
ло, отличное от нуля;
3) прибавление к элементам одного
ряда соответствующих элементов
другого, параллельного ему ряда.
При элементарных преобразованиях
ранг матрицы не изменяется
Ранг ступенчатой матрицы равен ко-
личеству ее ненулевых строк
Система (1) совместна тогда и толь-
ко тогда, кода ранг матрицы системы
равен рангу расширенной матрицы
системы
(
)
( ), ( )
r A r A A A b
= =
Если
∆А
≠ 0,
то
система
имеет
един
-
ственное
решение
.
i
i
x
∆
=
∆
(
формулы
Крамера
)
Если
∆А ≠
0,
то
система
имеет
един
-
ственное
решение
.
1
X A b
−
= ⋅
(
мат
-
ричный
метод
решения
системы
)
Суть метода Гаусса:
1)
привести
с
помощью
элементарных
преобразований
над
строками
A
к
ступенчатому
виду
;
2)
вычислить
и
сравнить
r
(
A
),
( )
r A
:
- если
(
)
( )
r A r A
≠ ,
то
система
несо
-
вместна
;
- если
(
)
( )
r A r A
= ,
то
система
со
-
вместна
;
3)
выбрать
базисный
минор
;
4)
выделить
свободные
и
базисные
неизвестные
.
Получить
решение
.
27
КРАТКОЕ СОДЕРЖАНИЕ
ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
1.1. Матрицы. Основные понятия.
Линейные операции над матрицами
Определение 1.1.1. Матрицей размера m ×
××
× n называется прямо-
угольная таблица чисел или объектов какой-либо другой природы, запи-
санных в m строк и n столбцов.
Определение 1.1.2. Числа или другие объекты, составляющие
матрицу, называются элементами матрицы.
Элементы матрицы удобно снабжать двумя индексами: a
ij
– элемент,
стоящий в i-той строке и j-том столбце.
Обозначение матрицы:
11 12 1
21 22 2
1 2
...
...
...
n
n
m m mn
a a a
a a a
A
a a a
=
−−−− −−−−−−
A = (a
ij
)
m×n
A = [a
ij
]
m×n
A = ||a
ij
||
m×n
Определение 1.1.3. Матрица, у которой число строк и столбцов
одинаково, называется квадратной.
Определение 1.1.4. Элементы а
11
, а
22
, …, a
nn
составляют главную
диагональ матрицы.
Определение 1.1.5. Матрица, у которой все элементы, кроме, мо-
жет быть, диагональных, равны нулю, называется диагональной.
Например,
1 0 0
0 2 0
0 0 0
A
=
Определение 1.1.6. Матрица, у которой все элементы равны нулю,
называется нулевой.
Например,
0 0 0
0 0 0
0 0 0
A
=
Определение 1.1.7. Диагональная матрица, у которой все диаго-
нальные элементы равны единице, называется единичной.
Определение 1.1.8. Матрица, у которой все элементы, стоящие
ниже главной диагонали равны нулю, называется верхнетреугольной.
28
Определение 1.1.9. Две матрицы называются равными, если их
размеры совпадают и совпадают все элементы, стоящие на одинаковых по-
зициях.
Определение 1.1.10. Матрица, в которой строки переставлены со
столбцами, называется транспонированной.
11 21 1
12 22 2
1 2
...
...
...
m
m
m m mm
a a a
a a a
A
a a a
∗
=
−−−−−− −−−−
.
Определение 1.1.11. Элементарными преобразованиями матриц
называются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих эле-
ментов параллельного ряда, умноженных на одно и то же число.
Определение 1.1.12. Элемент матрицы называется крайним, если
он не равен 0, а все элементы этой строки, стоящие левее его, равны 0.
Определение 1.1.13. Матрица называется ступенчатой, если
крайний элемент каждой матрицы находится правее крайнего элемента
предыдущей строки.
Определение 1.1.14. Матрица называется канонической, если в на-
чале главной диагонали ее стоят подряд несколько единиц, а все остальные
элементы равны нулю.
Определение 1.1.15. Две матрицы называются эквивалентными,
если одна из них получается из другой с помощью элементарных преобра-
зований. Записывается А∼
∼∼
∼В.
Замечание. При помощи элементарных преобразований любую
матрицу можно привести к эквивалентной ей ступенчатой или канониче-
ской матрице.
1.2. Линейные операции над матрицами и их свойства
Определение 1.2.1. Суммой двух матриц одной размерности на-
зывается матрица той же размерности, каждый элемент которой равен
сумме соответствующих элементов исходных матриц.
(a
ij
)
m×n
+ (b
ij
)
m×n
= (c
ij
)
m×n
29
Определение 1.2.2. Произведением матрицы на число (или на-
оборот) называется матрица той же размерности, в которой каждый эле-
мент умножен на это число.
Например, А =
1 2
3 4
; В
=
1 2
1 0
−
;
С
=
1
2
.
А + В
=
2 4
2 4
; (–1)
А
=
1 2
3 4
− −
− −
;
А + С
не
∃.
Определение 1.2.3
.
Матрица
(-1)
А
= -
А
называется
противопо-
ложной матрице
А
.
Свойства линейных операций:
1.
А + В
=
В + А
;
2.
(
А + В
) +
С
=
А +
(
В + С
);
3.
α(
А + В
) =
α
А +
α
В
;
4.
А
m× n
+
(–
А
) = 0
m×n
;
5.
А
m×n
+
0 =
А
m×n
;
1.
0 ⋅
А
m×n
= 0
m×n
;
2.
(α⋅β)
А
= α (β
А
) = αβ
А
;
3.
α
А
=
А
α;
4.
1⋅
А
=
А
.
1.3. Определители 2-го, 3-го, n-ного порядков
Квадратной
матрице
А можно
сопоставить
число
|
А
|, det
A
, ∆
A
,
на
-
зываемое
определителем
.
Определение 1.3.1. Определителем матрицы 2-го порядка
назы
-
вается
число
11 12
11 22 12 21
21 22
a a
a a a a
a a
= − .
Определение 1.3.2. Определителем матрицы 3-го порядка
назы
-
вается
число
11 12 13
21 22 23
31 32 33
a a a
a a a
a a a
=
а
11
а
22
а
33
+
а
21
а
32
а
13
+
а
12
а
23
а
31
–
а
31
а
22
а
13
–
а
21
а
12
а
33
–
а
32
а
23
а
11
.
Вычисление
определителя
3-
го
порядка
иллюстрируется
схемой
:
«+»
«–»
30
Замечание. Определитель
матрицы
А
также
называют
ее
детер-
минантом.
Правило
вычисления
детерминанта
для
матрицы
произвольно
-
го
порядка
является
довольно
сложным
для
восприятия
и
применения
.
Од
-
нако
известны
методы
,
позволяющие
вычисление
определителей
высокого
порядка
свести
к
вычислению
определителей
более
низких
порядков
.
Один
из
таких
методов
основан
на
свойстве
разложения
определителя
по
эле
-
ментам некоторого
ряда
.
Определение 1.3.3
.
Минором M
ik
, соответствующим
элементу
а
ik
,
называется
определитель
,
полученный
из
исходного
вычеркиванием
i
-
той
строки
и
k
-
того
столбца
.
Например
,
1 2 3
0 1 2
1 1 2
∆ =
−
.
Тогда
23
1 2
1 1
M =
−
.
Определение 1.3.4
.
Алгебраическим дополнением элемента а
ik
называется
его
минор
,
взятый
со
знаком
«+»,
если
сумма
индексов
строки
и
столбца
четна
,
и
«–»,
если
указанная
сумма
нечетна
.
A
ik
= (–1)
i+k
M
ik
.
Например
,
A
23
= –
1 2
1 1
−
= 3.
Определение 1.3.5. Определитель n-ного порядка
равен
сумме
произведений
элементов
его
произвольного
ряда
на
их
алгебраические
до
-
полнения
.
Определение 1.3.6. Определителем матрицы n-ного порядка
А
= (
а
ij
)
n
=
11 12 1
21 22 2
1 2
..............................
n
n
n n nn
a a a
a a a
a a a
…
…
…
,
полученным разложением по i-той строке
,
называется
число
det
A
=
a
i1
A
i1
+ a
i2
A
i2
+ ... + a
in
A
in
,
где
а
i1
,
a
i2
, …,
a
in
–
элементы
i
-
той
строки
A
,
A
i1
, A
i2
,
... ,
A
in
– их
алгебраические
дополнения
.
Например
,
по
определению
1.3.5
определителем
det
А
матрицы
3-
го
порядка
называется
число
det
A = a
11
A
11
+ a
12
A
12
+a
13
A
13
.
