Устинов В.П., Соловьев Л.Ю. Методические указания к курсовому проекту автодорожного железобетонного моста. Расчет пролетных строений (часть 2)
Подождите немного. Документ загружается.


624.2
Ó624
ÌÈÍÈÑÒÅÐÑÒÂÎ ÏÓÒÅÉ ÑÎÎÁÙÅÍÈß ÐÔ
ÑÈÁÈÐÑÊÈÉ ÃÎÑÓÄÀÐÑÒÂÅÍÍÛÉ
ÓÍÈÂÅÐÑÈÒÅÒ ÏÓÒÅÉ ÑÎÎÁÙÅÍÈß
Â.Ï. Óñòèíîâ, Ë.Þ. Ñîëîâüåâ
ÌÅÒÎÄÈ×ÅÑÊÈÅ ÓÊÀÇÀÍÈß
Ê ÊÓÐÑÎÂÎÌÓ ÏÐÎÅÊÒÓ ÀÂÒÎÄÎÐÎÆÍÎÃÎ ÆÅËÅÇÎÁÅÒÎÍÍÎÃÎ
ÌÎÑÒÀ
×àñòü 2
ÐÀÑ×ÅÒ ÏÐÎËÅÒÍÛÕ ÑÒÐÎÅÍÈÉ
ÍÎÂÎÑÈÁÈÐÑÊ 2003
2
ÓÄÊ 624.2
Ó ñ ò è í î â Â.Ï., Ñ î ë î â ü å â Ë.Þ. Ìåòîäè÷åñêèå óêàçàíèÿ ê
êóðñîâîìó ïðîåêòó àâòîäîðîæíîãî æåëåçîáåòîííîãî ìîñòà. ×àñòü 2. Ðàñ-
÷åò ïðîëåòíûõ ñòðîåíèé. Íîâîñèáèðñê: ÑÃÓÏÑ (ÍÈÈÆÒ), 2003. 41 ñ.
Âî âòîðîé ÷àñòè ìåòîäè÷åñêèõ óêàçàíèé ïðèâåäåíû îñíîâíûå íåîáõîäèìûå äàííûå ïî
ðàñ÷åòàì ïðîåçæåé ÷àñòè è ãëàâíûõ áàëîê æåëåçîáåòîííûõ ïðîëåòíûõ ñòðîåíèé àâòîäîðîæ-
íûõ, ãîðîäñêèõ è ïåøåõîäíûõ ìîñòîâ. Íàèáîëüøåå âíèìàíèå óäåëÿåòñÿ ðàñ÷åòó âàðèàíòîâ
êîíñòðóêöèé ìàññîâîãî ïðèìåíåíèÿ, êîòîðûå ÷àùå âñåãî óêàçûâàþòñÿ â çàäàíèÿõ íà êóðñî-
âîå ïðîåêòèðîâàíèå.
Ìåòîäè÷åñêèå óêàçàíèÿ îðèåíòèðîâàíû íà èñïîëüçîâàíèå ìåòîäèêè ïðåäåëüíûõ ñîñòî-
ÿíèé ïî ÑÍèÏ 2.05.03-84.* Ìîñòû è òðóáû. Ïðåäíàçíà÷åíû ñòóäåíòàì ôàêóëüòåòà Ìîñòû
è òîííåëè ñïåöèàëèçàöèè Ìîñòû è Ãîðîäñêèå òðàíñïîðòíûå ñîîðóæåíèÿ äíåâíîé è
çàî÷íîé ôîðì îáó÷åíèÿ.
Àâòîðû âûðàæàþò îñîáóþ áëàãîäàðíîñòü èíæåíåðó êàôåäû "Ìîñòû" Í.Â. Ìîëîêîâîé çà
âêëàä â ñîçäàíèå ýòèõ ìåòîäè÷åñêèõ óêàçàíèé.
Ðàññìîòðåíû è óòâåðæäåíû ê ïå÷àòè íà çàñåäàíèè êàôåäðû Ìîñòû 26
ìàðòà 2003 ãîäà.
Îòâåòñòâåííûé ðåäàêòîð ä.ò.í., ïðîô. Ã.Ì. Âëàñîâ
Ðåöåíçåíòû:
Êàôåäðà Ñòðîèòåëüíûå êîíñòðóêöèè è çäàíèÿ íà æåëåçíîäîðîæíîì
òðàíñïîðòå ÑÃÓÏÑ (çàâ. êàôåäðîé ä-ð òåõí. íàóê, ïðîô. Â.Ñ. Êàçàðíîâñ-
êèé)
Äèðåêòîð ÍÔ ÎÀÎ "Ãèïðîñòðîéìîñò" Ñ.È. Àðàõòèí
ÓñòèíîâÂ.Ï., Ñîëîâüåâ Ë.Þ. 2003
Ñèáèðñêèé ãîñóäàðñòâåííûé óíèâåðñèòåò ïóòåé ñîîáùåíèÿ, 2003
3
ÂÂÅÄÅÍÈÅ
Öåëüþ ðàñ÷åòà æåëåçîáåòîííûõ ïðîëåòíûõ ñòðîåíèé ÿâëÿåòñÿ îáîñíî-
âàíèå ïðèíÿòûõ ðàçìåðîâ ýëåìåíòîâ êîíñòðóêöèè ñ ó÷åòîì îáåñïå÷åíèÿ
ïðî÷íîñòè, òðåùèíîñòîéêîñòè, æåñòêîñòè è îïòèìèçàöèÿ èõ îñíîâíûõ
ðàçìåðîâ ïðè ðàöèîíàëüíîì ðàñõîäå áåòîíà, íàïðÿãàåìîé è íåíàïðÿãàåìîé
àðìàòóðû.
Ïðè êóðñîâîì ïðîåêòèðîâàíèè, êàê ïðàâèëî, îïðåäåëåíèå âíóòðåííèõ
óñèëèé, ïîäáîð ðàçìåðîâ ñå÷åíèé è èõ ïðîâåðêà ïî ïðî÷íîñòè, âûíîñëèâî-
ñòè, òðåùèíîñòîéêîñòè è æåñòêîñòè âûïîëíÿþòñÿ âðó÷íóþ. Ðàáîòû ïî
îïòèìèçàöèè çàïðîåêòèðîâàííûõ ýëåìåíòîâ ïðîèçâîäÿòñÿ â àâòîìàòèçè-
ðîâàííîì ðåæèìå ïîñëå çàâåðøåíèÿ ðó÷íîãî ðàñ÷åòà.
Âíóòðåííèå óñèëèÿ â ýëåìåíòàõ ïðîëåòíûõ ñòðîåíèé îïðåäåëÿþòñÿ
ìåòîäàìè ñòðîèòåëüíîé ìåõàíèêè íà îñíîâå ïðèíÿòûõ ðàñ÷åòíûõ ñõåì ñ
ó÷åòîì êîíñòðóêòèâíîãî ðåøåíèÿ è îñîáåííîñòåé ìîíòàæà. Ñóùåñòâóåò
ìíîãî ñïîñîáîâ, ïîçâîëÿþùèõ ñ ðàçëè÷íîé ñòåïåíüþ òî÷íîñòè îïðåäåëÿòü
âíóòðåííèå óñèëèÿ. Â êóðñîâîì ïðîåêòå äîïóñêàåòñÿ ïðèìåíÿòü ïðèáëè-
æåííûå ðàñ÷åòíûå ñõåìû, ïî êîòîðûì ïðîëåòíîå ñòðîåíèå óñëîâíî ðàñ÷ëå-
íÿåòñÿ íà ïëèòó ïðîåçæåé ÷àñòè è ãëàâíûå áàëêè, ðàññ÷èòûâàåìûå íåçàâè-
ñèìî äðóã îò äðóãà ñ ïðèáëèæåííûì ó÷åòîì èõ ñîâìåñòíîé ðàáîòû.
Ðàñ÷åòû â êóðñîâîì ïðîåêòå ñëåäóåò ïðîèçâîäèòü â åäèíèöàõ èçìåðåíèÿ
ÑÈ: ì, ì
2
, êÏà, ÌÏà, êÍ, ÌÍ.
1. ÐÀÑ×ÅÒ ÏËÈÒÛ ÏÐÎÅÇÆÅÉ ×ÀÑÒÈ
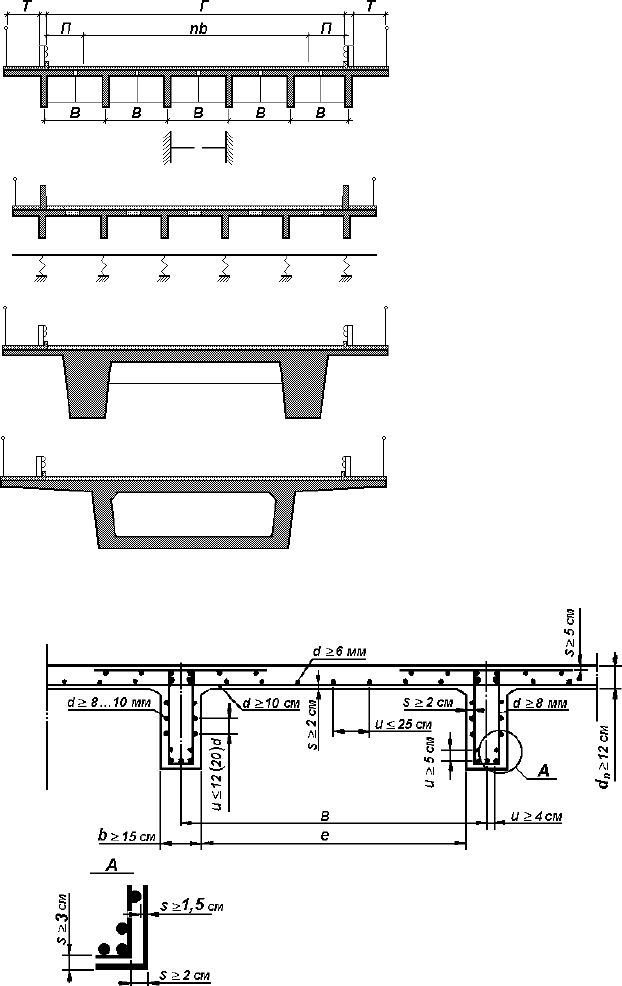
1.1. ÊÎÍÑÒÐÓÊÖÈß ÏËÈÒÛ ÏÐÎÅÇÆÅÉ ×ÀÑÒÈ ÀÂÒÎÄÎÐÎÆÍÛÕ
ÆÅËÅÇÎÁÅÒÎÍÍÛÕ ÌÎÑÒÎÂ
Ïëèòà ÿâëÿåòñÿ îñíîâíûì íåñóùèì ýëåìåíòîì êîíñòðóêöèè ïðîåçæåé
÷àñòè. Ñóùåñòâóþò òðè îñíîâíûõ ñõåìû óñòðîéñòâà ïëèòû (ðèñ. 1.1). Â
òàâðîâûõ áàëêàõ ñ äèàôðàãìàìè (ðèñ. 1.1, à) ïëèòó ÷àñòî íå îáúåäèíÿþò ñ
ïëèòàìè ñîñåäíèõ áàëîê, ò.å. ïëèòà ïðîåçæåé ÷àñòè êàæäîé áàëêè ðàáîòàåò
êàê êîíñîëü, çàùåìëåííàÿ â ðåáðå. Òîëùèíà íà êîíöå êîíñîëüíîé ïëèòû
íàçíà÷àåòñÿ íå ìåíåå 8 ñì. Àðìèðóåòñÿ òàêàÿ ïëèòà ðàáî÷åé àðìàòóðîé
òîëüêî â âåðõíåé ðàñòÿíóòîé çîíå. Äèàìåòð ñòåðæíåé ðàáî÷åé àðìàòóðû
ïðèíèìàþò íå ìåíåå 10 ìì, à ðàññòîÿíèå ìåæäó ñîñåäíèìè ïàðàëëåëüíûìè
ñòåðæíÿìè íå áîëåå 20 ñì. Ñòåðæíè ðàñïðåäåëèòåëüíîé àðìàòóðû ðàñïîëà-
ãàþò ïåðïåíäèêóëÿðíî ê ñòåðæíÿì ðàáî÷åé àðìàòóðû, äèàìåòð ñòåðæíåé
ðàñïðåäåëèòåëüíîé àðìàòóðû ïðèíèìàþò íå ìåíåå 6 ìì. Øàã ñòåðæíåé
ðàñïðåäåëèòåëüíîé àðìàòóðû ïðèíèìàþò íå áîëåå 25 ñì. Çàùèòíûé ñëîé
ñòåðæíåé ðàáî÷åé àðìàòóðû ïðèíèìàåòñÿ íå ìåíåå 5 ñì.
4
 áåçäèàôðàãìåííûõ ïðî-
ëåòíûõ ñòðîåíèÿõ (ðèñ. 1.1, á)
áàëêè îáúåäèíÿþòñÿ çà ñ÷åò
îìîíîëè÷èâàíèÿ âûïóñêîâ àð-
ìàòóðû ïëèò è ïëèòà ïðîåç-
æåé ÷àñòè òàêèõ ïðîëåòíûõ
ñòðîåíèé ðàáîòàåò êàê íåðàç-
ðåçíàÿ áàëêà íà óïðóãèõ îïî-
ðàõ. Íåîáõîäèìîå êîëè÷åñòâî
ñòåðæíåé íèæíåé è âåðõíåé
ðàáî÷åé àðìàòóðû â ñåðåäèíå
ïðîëåòà ïëèòû è íàä åå îïîðà-
ìè îïðåäåëÿåòñÿ èç ðàñ÷åòîâ
ïëèòû ïðè ñîáëþäåíèè âñåõ
êîíñòðóêòèâíûõ îãðàíè÷åíèé
íîðì [1, ïï. 3.117...3.136], îñ-
íîâíûå èç íèõ ïðèâåäåíû íà
ðèñ. 1.2.
Ðàññòîÿíèå ìåæäó áàëêà-
ìè áåçäèàôðàãìåííûõ ïðîëåò-
íûõ ñòðîåíèé îáû÷íî íàçíà-
÷àþò â ïðåäåëàõ 1,5...2,5 ì. Â
ýòîì ñëó÷àå ïëèòó àðìèðóþò
íåíàïðÿãàåìîé àðìàòóðîé, à
åå âûñîòà â ñåðåäèíå ïðîëåòà
Ðèñ. 1.1. Âèäû ïëèò ïðîåçæåé ÷àñòè
à)
á)
â)
Ðèñ. 1.2. Ðàñïîëîæåíèå àðìàòóðû ïëèòû è
íåíàïðÿãàåìûõ ãëàâíûõ áàëîê:
d äèàìåòðû àðìàòóðû; u ðàññòîÿíèÿ ïî
îñÿì ñòåðæíåé; s âåëè÷èíû çàùèòíîãî ñëîÿ
5
ìåæäó áàëêàìè íàçíà÷àåòñÿ â çàâèñèìîñòè îò ðàññòîÿíèÿ ìåæäó áàëêàìè â
ñâåòó å è ïðèíèìàåòñÿ îáû÷íî ðàâíîé 15...20 ñì èëè (1/121/18) å, íî íå
ìåíåå 12 ñì.
Ïðè áîëüøèõ ðàññòîÿíèÿõ ìåæäó áàëêàìè ìîæåò ïîòðåáîâàòüñÿ óâåëè-
÷åíèå òîëùèíû ïëèòû äî 2550 ñì è ñîçäàíèå ïðåäâàðèòåëüíîãî íàïðÿæå-
íèÿ â ïîïåðå÷íîì íàïðàâëåíèè.
Ïðè ïåðåêðûòèè áîëüøèõ ïðîëåòîâ øèðîêî èñïîëüçóþòñÿ ïëèòíî-ðåá-
ðèñòûå è êîðîá÷àòûå ïðîëåòíûå ñòðîåíèÿ (ðèñ. 1.1, â), â êîòîðûõ ïëèòà
ðàáîòàåò àíàëîãè÷íî ïëèòå áåçäèàôðàãìåííûõ ïðîëåòíûõ ñòðîåíèé, êàê
çàùåìëåííàÿ â ïîääåðæèâàþùèõ åå ãëàâíûõ áàëêàõ èëè ñòåíêàõ êîðîá÷à-
òûõ êîíñòðóêöèé. Òîëùèíà ïëèòû òàêæå çàâèñèò îò ðàññòîÿíèÿ ìåæäó
çàùåìëåíèÿìè.
1.2. ÐÀÑ×ÅÒÍÛÅ ÏÐÎÂÅÐÊÈ ÏËÈÒÛ ÏÐÎÅÇÆÅÉ ×ÀÑÒÈ
Ðàñ÷åò ïëèòû ïðîåçæåé ÷àñòè â êóðñîâîì ïðîåêòå âûïîëíÿåòñÿ â ñëåäó-
þùåì ïîðÿäêå:
íàõîäÿòñÿ íîðìàòèâíûå çíà÷åíèÿ ïîñòîÿííûõ è âðåìåííûõ âåðòè-
êàëüíûõ íàãðóçîê;
îïðåäåëÿþòñÿ ðàñ÷åòíûå çíà÷åíèÿ âíóòðåííèõ óñèëèé (èçãèáàþùèõ
ìîìåíòîâ è ïîïåðå÷íûõ ñèë) â õàðàêòåðíûõ ñå÷åíèÿõ ïëèòû äëÿ ðàñ÷åòîâ
ïî ïðî÷íîñòè, íà âûíîñëèâîñòü è ïî òðåùèíîñòîéêîñòè;
íàçíà÷àþòñÿ ðàçìåðû ðàñ÷åòíîãî ñå÷åíèÿ ïëèòû è ïëîùàäü ðàáî÷åé
àðìàòóðû;
âûïîëíÿþòñÿ ïðîâåðêè íîðìàëüíûõ ñå÷åíèé ïëèòû ïî ïðî÷íîñòè,
âûíîñëèâîñòè, òðåùèíîñòîéêîñòè è íàêëîííîãî ñå÷åíèÿ ïî ïðî÷íîñòè, à
ïðè íåîáõîäèìîñòè êîððåêòèðóþòñÿ ïðèíÿòûå ðàçìåðû ñå÷åíèé è êîëè÷å-
ñòâî ñòåðæíåé àðìàòóðû.
1.2.1. Îïðåäåëåíèå íîðìàòèâíûõ çíà÷åíèé ïîñòîÿííûõ è
âðåìåííûõ íàãðóçîê
Ïîñòîÿííûå íàãðóçêè íà 1 ì
2
ãîðèçîíòàëüíîé ïðîåêöèè ïëèòû ïðîåçæåé
÷àñòè, ÷èñëåííî ðàâíûå ïîãîííîé íàãðóçêå âäîëü ïðîëåòà ïëèòû øèðèíîé
1 ì, ñêëàäûâàþòñÿ îáû÷íî èç ñîáñòâåííîãî âåñà ïëèòû g
1
, âåñà âûðàâíèâà-
þùåãî, çàùèòíîãî è èçîëÿöèîííîãî ñëîåâ ìîñòîâîãî ïîëîòíà g
2
è âåñà
ïîêðûòèÿ åçäîâîãî ïîëîòíà g
3
.
Íàãðóçêà îò ñîáñòâåííîãî âåñà ïëèòû ïðîåçæåé ÷àñòè îïðåäåëÿåòñÿ êàê
g
1
= γ
1
d
1
, ãäå γ
1
= 24,5 êÍ/ì
3
óäåëüíûé âåñ æåëåçîáåòîíà, d
1
òîëùèíà
ïëèòû, êîòîðóþ â ïåðâîì ïðèáëèæåíèè ìîæíî ïðèíÿòü d
1
= 0,15 ì.
Àíàëîãè÷íî âû÷èñëÿþòñÿ íîðìàòèâíûå íàãðóçêè îò ñîáñòâåííîãî âåñà
îäåæäû åçäîâîãî ïîëîòíà g
2
è g
3
. Â êóðñîâîì ïðîåêòå ìîæíî âîñïîëüçî-
âàòüñÿ ñïðàâî÷íûìè äàííûìè, ïðèâåäåííûìè â [4, ïðèë. 8].

6
Äëÿ íàðóæíûõ êîíñîëüíûõ ó÷àñòêîâ ïëèòû íàãðóçêè îò ñîáñòâåííîãî
âåñà êîíñòðóêöèé ïåðèë g
6
, îãðàæäåíèÿ ïðîåçæåé ÷àñòè g
7
, òðîòóàðîâ g
4
, èõ
ïîêðûòèÿ g
5
, è êîììóíèêàöèé g
8
îïðåäåëÿþòñÿ ïî èõ ãåîìåòðè÷åñêèì
ðàçìåðàì èç ïðîåêòíîé äîêóìåíòàöèè. Â êóðñîâîì ïðîåêòå ìîæíî âîñïîëü-
çîâàòüñÿ äàííûìè, ïðèâåäåííûìè â [11]. Ïî ñîãëàñîâàíèþ ñ ðóêîâîäèòå-
ëåì êóðñîâîãî ïðîåêòèðîâàíèÿ ðàñ÷åò êîíñîëüíûõ ó÷àñòêîâ ïëèòû ìîæåò
íå ïðîèçâîäèòüñÿ.
Âðåìåííóþ âåðòèêàëüíóþ íàãðóçêó íà ïëèòó ñëåäóåò ïðèíèìàòü ïî [1,
ï. 2.12]:
îò àâòîòðàíñïîðòíûõ ñðåäñòâ â âèäå ïîëîñ ðàâíîìåðíî ðàñïðåäåëåí-
íîé íàãðóçêè ÀÊ ñ èíòåíñèâíîñòüþ v = 0,98Ê, êÍ/ì (íà îáå êîëåè êàæäîé
ïîëîñû) è äâóõîñíûõ òåëåæåê, ðàçìåùàåìûõ ïî îäíîé íà êàæäîé ïîëîñå, ñ
îñåâîé íàãðóçêîé Ð = 9,81Ê, êÍ, ãäå Ê = 8, 11 èëè 14 (â ñîîòâåòñòâèè ñ
çàäàíèåì);
îò òÿæåëîé îäèíî÷íîé êîëåñíîé íàãðóçêè ÍÊ-80 ñ äàâëåíèåì íà êàæäóþ
îñü Ð
ÍÊ
= 196 êÍ èëè ãóñåíè÷íîé íàãðóçêè ÍÃ-60 îáùèì âåñîì 589 êÍ ñ
äëèíîé ðàñïðåäåëåíèÿ 5 ì âäîëü ìîñòà.
1.2.2. Îïðåäåëåíèå ðàñ÷åòíûõ çíà÷åíèé âíóòðåííèõ óñèëèé
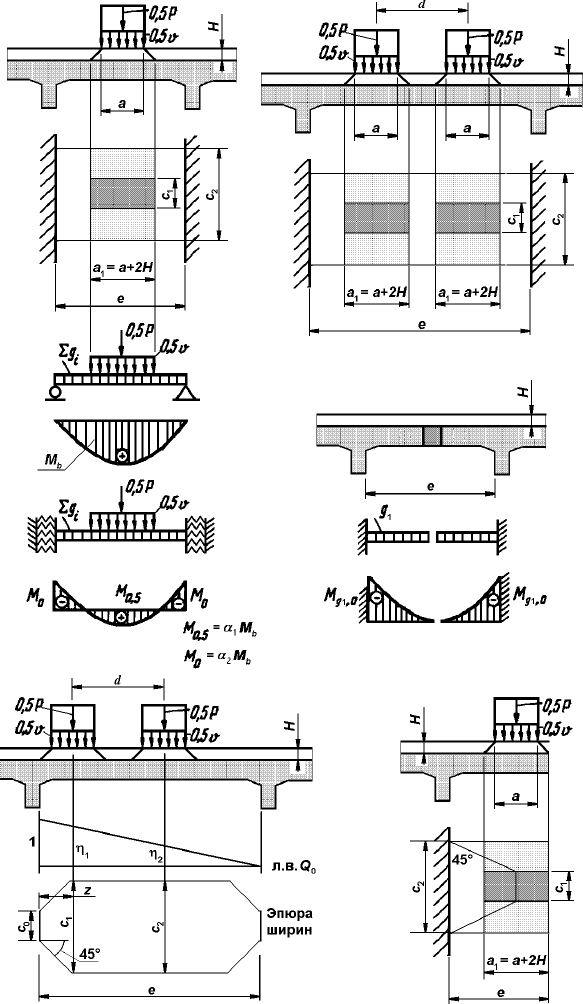
 áîëüøèíñòâå ñîâðåìåííûõ êîíñòðóêöèé ïëèòà ëèáî îìîíîëè÷èâàåòñÿ
íà ìîíòàæå (ðèñ. 1.3, â), ëèáî âûïîëíÿåòñÿ ïîëíîñòüþ ìîíîëèòíîé (ðèñ.
1.3, à, á).  ïîñëåäíåì ñëó÷àå åå ðåàëüíàÿ ðàñ÷åòíàÿ ñõåìà ïðåäñòàâëÿåò
ñîáîé íåðàçðåçíóþ áàëêó íà óïðóãî çàùåìëåííûõ ïðîñåäàþùèõ îïîðàõ.
Îäíàêî â èíæåíåðíîé ïðàêòèêå ñíà÷àëà íàõîäÿò èçãèáàþùèå ìîìåíòû M
b
â ñåðåäèíå ïðîëåòà ïëèòû å êàê â ðàçðåçíîé áàëêå íà äâóõ îïîðàõ, à çàòåì
ñ ïîìîùüþ ïîïðàâî÷íûõ êîýôôèöèåíòîâ îïðåäåëÿþò èñêîìûå ìîìåíòû â
ñåðåäèíå ïðîëåòà
b
MM
15,0
α=
è ó îïîð
b
MM
20
α=
óïðóãî çàùåìëåííîé
áàëêè (ðèñ. 1.3, à). Óñèëèÿ îïðåäåëÿþò íà 1 ïîã. ì øèðèíû ïëèòû.
 îáùåì âèäå äëÿ ìîíîëèòíîé ïëèòû (ðèñ. 1.3, à, á) áàëî÷íûé ìîìåíò
îïðåäåëÿåòñÿ ïî ôîðìóëå
bpbbgb
MMMM
++=
v
, (1.1)
ãäå
∑
=
=
γ=
3
1
2
8
i
i
ifgibg
egM
, M
b
v
, M
bp
ñîîòâåòñòâåííî áàëî÷íûå ìîìåíòû îò
ïîñòîÿííûõ íàãðóçîê g
i
, îò ðàâíîìåðíî ðàñïðåäåëåííîé ïîëîñîâîé íàãðóç-
êè (íà îáå êîëåè) v è îò äâóõîñíîé òåëåæêè ñ îñåâûìè íàãðóçêàìè Ð; γ
fgi
êîýôôèöèåíòû íàäåæíîñòè ê ñîîòâåòñòâóþùåé ïîñòîÿííîé íàãðóçêå g
i
[1,
ï. 2.10]. Âåëè÷èíû g
i
ïðèíèìàþòñÿ: g
1
ïîñòîÿííàÿ íàãðóçêà îò ñîáñòâåí-
íîãî âåñà ïëèòû, êÍ/ì; g
2
òî æå, îò âåñà âûðàâíèâàþùåãî, èçîëÿöèîííî-
ãî è çàùèòíîãî ñëîåâ, êÍ/ì; g
3
òî æå, îò âåñà ïîêðûòèÿ (àñôàëüòîáåòîíà)
åçäîâîãî ïîëîòíà, êÍ/ì. Äëÿ ïëèòû ïî ñõåìå 1.3, â îïîðíûé èçãèáàþùèé
ìîìåíò ñîñòàâëÿåò
8
2
10,
11
egM
fgg
γ−=
.
7
Ðèñ. 1.3
à) á)
â)
ã)
ä)
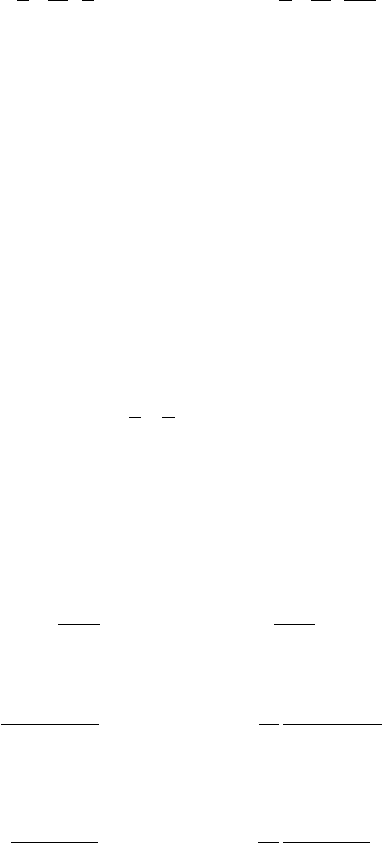
8
Âåëè÷èíû ìîìåíòîâ îò âðåìåííîé íàãðóçêè äëÿ ðàñ÷åòà ïî ïðî÷íîñòè
ïðèíèìàþòñÿ â çàâèñèìîñòè îò ïðîëåòà ïëèòû.
Ïðè íåáîëüøîì ïðîëåòå ïëèòû (å < 1,8...2,0 ì., ðèñ. 1.3, à) ìåæäó
ãðàíÿìè ðåáåð ìîæåò ðàçìåñòèòüñÿ òîëüêî îäíî êîëåñî. Òîãäà
() ()
,
4
1
42
1;
4
1
42
1
2
11
c
ae
PM
ae
M
fpbpfb
−µ+γ=
−µ+γ=
v
vv
(1.2)
ãäå v ðàâíîìåðíî ðàñïðåäåëåííàÿ ïîëîñîâàÿ íàãðóçêà (íà îáå êîëåè);
Ð îñåâàÿ íàãðóçêà îò äâóõîñíîé òåëåæêè; γ
f
v
êîýôôèöèåíò íàäåæíîñòè
ê ïîëîñîâîé íàãðóçêå (γ
f
v
= 1,2 [1, ï. 2.23]); γ
fp
êîýôôèöèåíò íàäåæíîñòè
ê íàãðóçêå îò òåëåæêè (γ
fp
= 1,5); (1+µ) äèíàìè÷åñêèé êîýôôèöèåíò [1, ï.
2.22] ïðè óñëîâíîé äëèíå çàãðóæåíèÿ λ
= 0; å ðàññòîÿíèå â ñâåòó ìåæäó
âíóòðåííèìè ãðàíÿìè ðåáåð áàëîê.
Çäåñü ñ ó÷åòîì ðàñïðåäåëÿþùåãî äåéñòâèÿ îäåæäû åçäîâîãî ïîëîòíà
ïîä óãëîì 45° èìååì
,2;2
11
HccHaa +=+=
(1.3)
ãäå H ïîëíàÿ òîëùèíà ïîêðûòèÿ åçäîâîãî ïîëîòíà (îáû÷íî H ≥0,15 ì);
a = 0,6 ì øèðèíà êîëåñà ïîëîñîâîé íàãðóçêè èëè êîëåñà òåëåæêè; ñ = 0,2 ì
äëèíà ñîïðèêàñàíèÿ êîëåñà ñ ïîêðûòèåì âäîëü äâèæåíèÿ [1, ï. 2.12].
Ñ ó÷åòîì âêëþ÷åíèÿ â ðàáîòó íà èçãèá ñìåæíûõ ó÷àñòêîâ ïëèòû ïîëó-
÷àåì ðàáî÷óþ øèðèíó ïëèòû
.
3
2
3
12
e
e
cc ≥+=
(1.4)
Ïðè áîëüøåì ïðîëåòå ïëèòû (å >1,8....2,0 ì) ñëåäóåò ðàññìàòðèâàòü
ñõåìó çàãðóæåíèÿ åå ïîëîñîâûìè íàãðóçêàìè ïî äâóì êîëåÿì è äâóìÿ
êîëåñàìè òåëåæåê ñî ñìåæíûõ ïîëîñ äâèæåíèÿ ñ ðàññòîÿíèÿìè ìåæäó íèìè
d = 1,1 ì (ðèñ. 1.3, á).  êóðñîâîì ïðîåêòå ïðè ðàñ÷åòå ïëèòû äîïóñêàåòñÿ
ïðèíèìàòü êîýôôèöèåíòû ïîëîñíîñòè s
1
= s
2
= 1 [1, ï. 2.14].
Òîãäà ïðè d + a
1
≤ e è H ≤ 0,25 ì
() ()
;
4
1;
4
1
2
c
de
PM
de
M
fpbpfb
−
µ+γ=
−
µ+γ=
v
v
v
(1.5)
ïðè d + a
1
> e è H ≤ 0,25 ì
()
()
()
()
.
16
1;
16
1
1
2
1
21
2
1
a
ade
c
P
M
a
ade
M
fpbpfb
+−
µ+γ=
+−
µ+γ=
v
vv
(1.6)
Ïðè d + a
1
≤ e è H > 0,25 ì ó÷àñòêè çàãðóæåíèÿ a
1
ìîãóò ïåðåêðûâàòü äðóã
äðóãà. Òîãäà
() ()
.
8
2
1;
8
2
1
1
2
1
ade
c
P
M
ade
M
fpbpfb
−−
µ+γ=
−−
µ+γ=
v
vv
(1.7)
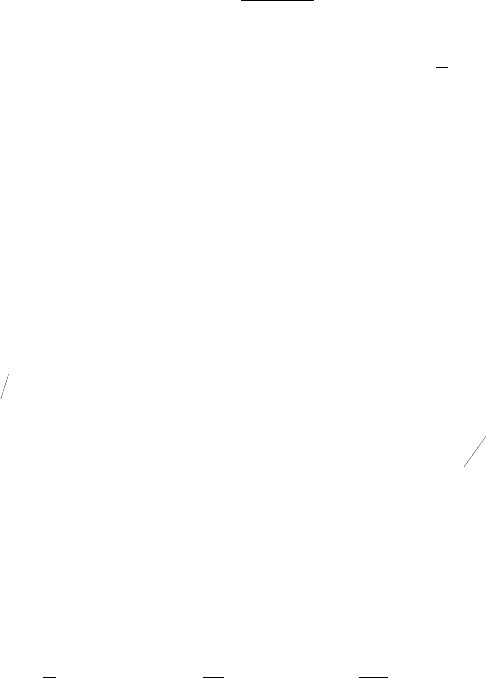
9
Ïðè ïðîëåòå ïëèòû å > 2,2....2,4 ì è H > 0,25 ì âîçìîæíî âçàèìíîå
ïåðåêðûòèå âäîëü ìîñòà ó÷àñòêîâ ñ
2
îò êîëåñ òåëåæêè. Òîãäà â ïðèâåäåííûõ
ôîðìóëàõ âåëè÷èíó ñ
2
ñëåäóåò çàìåíèòü âåëè÷èíîé ñ
3
= (ñ
2
+ u)/2 ≥ e/3+u/2,
ãäå u = 1,5 ì (ðàññòîÿíèå ìåæäó îñÿìè òåëåæêè).
Ïðè çàãðóæåíèè ïëèòû êîëåñíîé íàãðóçêîé ÍÊ-80 îñíîâíîé ÿâëÿåòñÿ
ñõåìà ñ ðàñïîëîæåíèåì êîëåè êîëåñ ïîñåðåäèíå ïðîëåòà ïëèòû (êàê íà ðèñ.
1.3, a). Òîãäà
()
,
8
5,0
1
2
1
ÍÊ
ÍÊ
ÍÊ,
c
ae
PMM
bgb
′
′
−
µ++=
(1.8)
ãäå (1+µ)
HK
= 1,3 (äëÿ λ = 0); Ð
ÍÊ
= 196 êÍ;
.ì2,1
3
2;28,0
21
≤++=
′
+=
′
e
HccHa
Êàê óæå ãîâîðèëîñü, äàëåå ñëåäóåò îïðåäåëèòü ðàñ÷åòíûå çíà÷åíèÿ
èçãèáàþùèõ ìîìåíòîâ â ñåðåäèíå ïðîëåòà Ì
0,5
è ó îïîðû ïëèòû Ì
0
ñ ó÷åòîì
åå óïðóãîãî çàùåìëåíèÿ â ðåáðàõ ãëàâíûõ áàëîê. Äëÿ ýòîãî èñïîëüçóþòñÿ
ïîïðàâî÷íûå êîýôôèöèåíòû α
1
è α
2
, ó÷èòûâàþùèå ñòåïåíü çàùåìëåíèÿ
ïëèòû â çàâèñèìîñòè îò âåëè÷èíû ï
1
, õàðàêòåðèçóþùåé îòíîøåíèå öèëèí-
äðè÷åñêîé æåñòêîñòè ïëèòû ê êðóòèëüíîé æåñòêîñòè ïîääåðæèâàþùåãî
åãî ðåáðà. Â ðàìêàõ êóðñîâîãî ïðîåêòà êîýôôèöèåíòû α
1
è α
2
ìîãóò áûòü
ïðèíÿòû ñîãëàñíî [5, ï.ï. 5.2, òàáë. 5.1 è 5.3] èëè [9, òàáë. 18].
Ïðè ñáîðíûõ áàëêàõ ñî øâîì ìåæäó êîíñîëÿìè ïëèòû (ðèñ. 1.3, â) â
âûðàæåíèÿõ (1.1) è (1.8) äëÿ Ì
bg
ñëåäóåò ó÷èòûâàòü òîëüêî íàãðóçêè g
2
è g
3
,
à ìîìåíò îò ñîáñòâåííîãî âåñà ïëèòû g
1
ó÷èòûâàåòñÿ òîëüêî â åå îïîðíîì
ñå÷åíèè äîáàâëåíèåì ê âåëè÷èíå ðàñ÷åòíîãî ìîìåíòà Ì
0
çíà÷åíèÿ
8
2
10,
11
egM
fgg
γ−=
.
Èçãèáàþùèå ìîìåíòû Ì
0,5,f
è Ì
0,f
äëÿ ðàñ÷åòîâ íà âûíîñëèâîñòü òàêæå
îïðåäåëÿþòñÿ ïî ïðèâåäåííûì ôîðìóëàì, ïðèíèìàÿ γ
fgi
= γ
f
v
= 1 è
()
µ+
3
2
1
âìåñòî (1+µ) [1, ï. 2.3, òàáë. 6]. Ïðè ðàñ÷åòå íà âûíîñëèâîñòü ðåäêî
îáðàùàþùàÿñÿ íàãðóçêà ÍÊ-80 èëè ÍÃ-60 íå ó÷èòûâàåòñÿ. Äëÿ ðàñ÷åòîâ ïî
òðåùèíîñòîéêîñòè îïðåäåëÿþòñÿ ìîìåíòû Ì
0,5,n
è Ì
0,n
ïî ôîðìóëàì
(1.1)...(1.8), ïðèíèìàÿ γ
fgi
= γ
f
v
= γ
fð
= 1 è (1+µ) = 1.
Ìàêñèìàëüíîå çíà÷åíèå ïîïåðå÷íîé ñèëû â îïîðíîì ñå÷åíèè ïëèòû
âû÷èñëÿåòñÿ êàê â ïðîñòîé ðàçðåçíîé áàëêå ñ ïðîëåòîì e (ðèñ. 1.3, ã). Òîãäà
â ðàñ÷åòàõ ïî ïðî÷íîñòè ïîïåðå÷íàÿ ñèëà îò íàãðóçêè ÀÊ èìååò âèä:
() ()
,
2
1
2
1
2
2
1
2
1
3
1
0
∑∑∑
=
=
=
=
=
=
η
µ+γ+
η
µ+γ+γ=
i
i
i
i
fp
i
i
i
if
i
i
ifgi
c
Ps
e
gQ
v
v
(1.9)
ãäå η
i
îðäèíàòû ëèíèè âëèÿíèÿ ïîïåðå÷íîé ñèëû Q
0
ïîä êîëåñàìè èëè
êîëåÿìè; s
i
êîýôôèöèåíò ïîëîñíîñòè (äëÿ îäíîé ïîëîñû íàãðóçêè ó
îïîðû s
1
= 1, à äëÿ äðóãîé â ïðîëåòå s
2
= 0,6); c
i
ðàñ÷åòíàÿ øèðèíà ïëèòû,
âîñïðèíèìàþùàÿ íàãðóçêó îò êîëåñà.
10
Ïðè ýòîì äëÿ ñðåäíèõ ó÷àñòêîâ ïëèòû ïðèíèìàþò ðàíåå ïîäñ÷èòàííóþ
âåëè÷èíó ñ
2
, ó ãðàíè îïîðû c
0
= c + 2H ≥ e/3, à äëÿ ïðîìåæóòî÷íûõ çíà÷åíèé
c
i
= c
0
+ 2z
i
≤ ñ
2
, ãäå z
i
ðàññòîÿíèå îò êîëåñà äî îïîðû (ãðàíè ðåáðà ãëàâíîé
áàëêè).
 ðàñ÷åòàõ íà íàãðóçêó ÍÊ-80 (îò îäíîãî êîëåñà) ïðè c
i
≤ 1,2 ì ôîðìóëà
èìååò âèä:
()
.
2
1
ÍÊ
ÍÊ
0,0
i
i
g
c
PQQ
η
µ++=
(1.10)
 êîíñîëüíîé ïëèòå (ðèñ. 1.3, ä) ïðè íàãðóçêå ÀÊ âîçíèêàþò ñëåäóþùèå
âíóòðåííèå óñèëèÿ:
;;
2
1
3
1
2
0,
Haa
e
gM
i
i
ifgig
+=γ=
∑
=
=
(1.11)
()
;ïðè
4
1
1
1
2
0,
ea
a
e
M
f
>µ+γ=
v
vv
(1.12)
()
.ïðè
2
5,0
1
1
1
0,
ea
ae
M
f
≤
−
µ+γ=
v
vv
(1.13)
Äëÿ òåëåæêè ôîðìóëû èìåþò òàêîé æå âèä, êàê ôîðìóëû (1.11)...(1.13),
íî ïðè êîýôôèöèåíòå íàäåæíîñòè äëÿ òåëåæêè γ
fð
(âìåñòî γ
f
v
) è ïðè
íàãðóçêå Ð/ñ
2
(âìåñòî v). Âåëè÷èíà ñ
2
îïðåäåëÿåòñÿ ñ ó÷åòîì ðàñïðåäåëåíèÿ
ñèëû Ð â ïëàíå ïîä óãëîì 45° îò öåíòðà òÿæåñòè ãðóçîâîé ïëîùàäêè, òîãäà
ñ
2
= ñ
1
+ å (ïðè a
1
≥ å) èëè ñ
2
= ñ
1
+ 2å a
1
(ïðè a
1
< å). Ïðè êîëåñíîé íàãðóçêå
ÍÊ-80 âìåñòî Ð è à
1
ñëåäóåò ïðèíÿòü Ð
ÍÊ
è
Haa +
′
=
′
1
ñ îãðàíè÷åíèåì
ñ
2
≤ 1,2 ì.
1.2.3. Íàçíà÷åíèå ðàçìåðîâ ðàñ÷åòíûõ ñå÷åíèé
Ïî ïîëó÷åííûì çíà÷åíèÿì óñèëèé íàçíà÷àþò ðàñ÷åòíîå ñå÷åíèå ïëèòû è
ïîäáèðàþò ïëîùàäü ðàáî÷åé àðìàòóðû äëÿ ñåðåäèíû ïðîëåòà è íàä îïîðîé
ïëèòû, à çàòåì ïðîèçâîäÿò ïðîâåðêó ïðî÷íîñòè, âûíîñëèâîñòè è òðåùèíîñ-
òîéêîñòè ïëèòû êàê èçãèáàåìîãî ýëåìåíòà ïðÿìîóãîëüíîãî ñå÷åíèÿ. Ðåêîìåí-
äóåòñÿ òàêàÿ ïîñëåäîâàòåëüíîñòü âûïîëíåíèÿ ýòèõ ðàñ÷åòíûõ îïåðàöèé:
à) â ïåðâîì ïðèáëèæåíèè ïðèíèìàåì òîëùèíó ïëèòû d
1
= 0,15 ì,
äèàìåòð ðàáî÷åé àðìàòóðû d
s
= 0,012 ì è òîëùèíó çàùèòíîãî ñëîÿ s = 0,05 ì;
á) äëÿ êàæäîãî èç ñå÷åíèé âû÷èñëÿåì ïîëåçíóþ (ðàáî÷óþ) âûñîòó
ïëèòû (ðèñ. 1.4):
,5,0
0
sii
dshh
−−=
(1.14)
ïðè÷åì äëÿ ñå÷åíèÿ 2-2 â ñåðåäèíå ïðîëåòà òîëùèíà ïëèòû
,
12
dhh
i
== (1.15)
