Устинов В.П., Соловьев Л.Ю. Методические указания к курсовому проекту автодорожного железобетонного моста. Расчет пролетных строений (часть 2)
Подождите немного. Документ загружается.

31
y
b1
, y
t1
, A
red 1
, I
red 1
äëÿ ñòàäèè èçãîòîâëåíèÿ áåç ó÷åòà íàïðÿãàåìîé
àðìàòóðû, íî ñ ó÷åòîì îñëàáëåíèÿ êàíàëàìè äëÿ íåå;
y
b2
, y
t2
, A
red 2
, I
red 2
äëÿ ñòàäèè ýêñïëóàòàöèè ñ ó÷åòîì âñåãî ñå÷åíèÿ
áåòîíà è âñåé àðìàòóðû.
Ïðè íàòÿæåíèè àð-
ìàòóðû íà óïîðû èñ-
ïîëüçóþòñÿ åäèíûå
õàðàêòåðèñòèêè ñå÷å-
íèÿ áàëêè äëÿ âñåõ
ñòàäèé ðàáîòû êîíñò-
ðóêöèè y
b
= y
b2
, y
t
= y
t2
,
A
red
= A
red 2
, I
red
= I
red 2
.
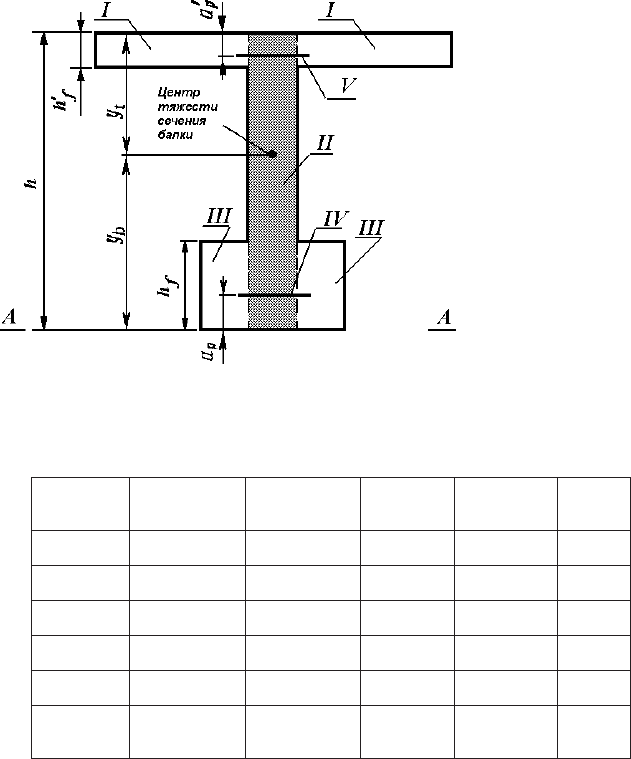
Äëÿ óïðîùåíèÿ
ðàñ÷åòîâ ìîæíî îïðå-
äåëÿòü ãåîìåòðè÷åñ-
êèå õàðàêòåðèñòèêè â
òàáëè÷íîé ôîðìå, íà-
ïðèìåð, äëÿ äâóòàâðî-
âîãî ñå÷åíèÿ ñ íàòÿ-
æåíèåì àðìàòóðû íà
óïîðû (ðèñ. 2.10)
ïî òàáë. 2.2.
Òàáëèöà 2.2
Îïðåäåëåíèå ãåîìåòðè÷åñêèõ õàðàêòåðèñòèê ñå÷åíèÿ
òíåìåëÝ
ÿèíå÷åñ
A
i
ì,
2
y
ÀÀ
,
i
ì,
S
AA
,
i
ì,
3
I
AA
,
i
ì,
4
I
,.c
i
ì,
4
I
A
1
(=
b
f
b'
)
h
f
'y
1
=
h
5,0
h
f
'S
1
=
A
1
y
1
I
1
=
S
1
y
1
I
c
1.
II
A
2
=
hby
2
5,0=
hS
2
=
A
2
y
2
I
2
=
S
2
y
2
I
c
2.
III
A
3
(=
b
f
b
)
h
f
y
3
5,0=
h
f
S
3
=
A
3
y
3
I
3
=
S
3
y
3
I
c
3.
VI
A
4
(=
n
p
)1
A
p
y
4
=
a
p
S
4
=
A
4
y
4
I
4
=
S
4
y
4
V
A
5
(=
n
p
)1
A
p
'y
5
=
ha
p
'S
5
=
A
5
y
5
I
5
=
S
5
y
5
åñÂ
åèíå÷åñ
A
der
=
Σ
A
i
y
b
Σ
S
i,AA
Σ
I
i,AA
Σ
I
.c
i
 òàáë. 2.2 îáîçíà÷åíî: n
p
êîýôôèöèåíò ïðèâåäåíèÿ íàïðÿãàåìîé
àðìàòóðû ê áåòîíó; À
i
ïëîùàäü i-ãî ýëåìåíòà; S
AA, i
ñòàòè÷åñêèé
ìîìåíò ýëåìåíòà îòíîñèòåëüíî îñè ÀÀ; I
AA, i
ìîìåíò èíåðöèè ýëåìåíòà
îòíîñèòåëüíî îñè ÀÀ; I
ñ., i
ìîìåíò èíåðöèè ýëåìåíòà îòíîñèòåëüíî
ñîáñòâåííîé îñè; ΣÀ
i
, ΣS
AA, i
, ΣI
AA, i
ñóììû ïëîùàäåé, ñòàòè÷åñêèõ
Ðèñ. 2.10. Ñõåìà ê îïðåäåëåíèþ
ãåîìåòðè÷åñêèõ õàðàêòåðèñòèê ñå÷åíèÿ
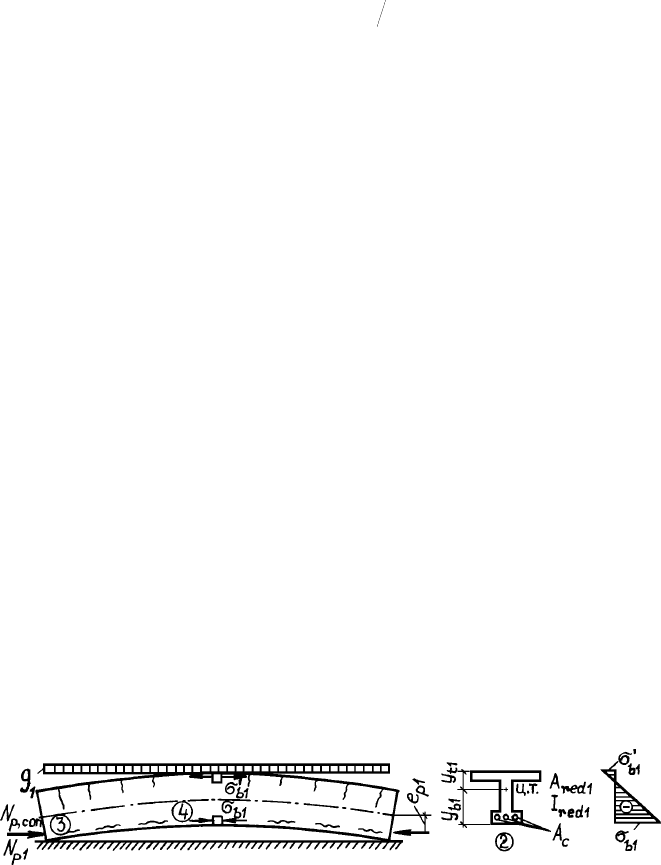
32
ìîìåíòîâ è ìîìåíòîâ èíåðöèè ýëåìåíòîâ ïîïåðå÷íîãî ñå÷åíèÿ îòíîñè-
òåëüíî îñè ÀÀ; y
b
ïîëîæåíèå öåíòðà òÿæåñòè ñå÷åíèÿ îòíîñèòåëüíî îñè
ÀÀ, îïðåäåëÿåìîå èç âûðàæåíèÿ
.
,
rediAAb
ASy
∑
=
Ïðè ýòîì ðàññòîÿíèå îò öåíòðà òÿæåñòè ñå÷åíèÿ äî âåðõíåé ôèáðû
y
t
= h y
b
.
Òîãäà ìîìåíò èíåðöèè âñåãî ïðèâåäåííîãî ñå÷åíèÿ îòíîñèòåëüíî åãî
öåíòðà òÿæåñòè ìîæíî îïðåäåëèòü ïî ôîðìóëå
.
,,c.
∑∑∑
−+=
iAAbiAAired
SyIII
Ïðè ó÷åòå íåíàïðÿãàåìîé àðìàòóðû â òàáë. 2.2 ñëåäóåò ââåñòè äîïîëíè-
òåëüíî çíà÷åíèÿ À
6
= (n
s
1)À
s
è À
7
= (n
s
1)À'
s
, ãäå À
s
è À'
s
ïëîùàäè
íåíàïðÿãàåìîé ðàñòÿíóòîé è ñæàòîé àðìàòóðû, n
s
êîýôôèöèåíò ïðèâåäå-
íèÿ íåíàïðÿãàåìîé àðìàòóðû ê áåòîíó.
Îêîí÷àòåëüíî äëÿ ñòàäèè ýêñïëóàòàöèè (ïðè íàòÿæåíèè àðìàòóðû è íà
óïîðû, è íà áåòîí) ïðèíèìàåì y
b2
= y
b
, y
t2
= y
t
, À
red 2
= À
red
, I
red 2
= I
red
.
Ïðè íàòÿæåíèè àðìàòóðû íà áåòîí íåîáõîäèìî êðîìå òîãî îïðåäåëèòü
ãåîìåòðè÷åñêèå õàðàêòåðèñòèêè ñå÷åíèÿ â ñòàäèè èçãîòîâëåíèÿ y
b1
, y
t1
,
À
red1
, I
red 1
. Äëÿ ýòîãî ñîñòàâëÿåì àíàëîãè÷íóþ òàáëèöó, ïîäñòàâëÿÿ â íåå
çíà÷åíèÿ À
4
= À
c
è À
5
= À
c
' , ãäå À
c
è À
c
' ïëîùàäè îñëàáëåíèé ñå÷åíèÿ
ïðîäîëüíûìè êàíàëàìè â íèæíåé è âåðõíåé ïîëêàõ áàëêè.
 ïðåäñòàâëåííîé ôîðìå ðàñ÷åòû ëåãêî àâòîìàòèçèðóþòñÿ, ÷òî ïîçâî-
ëÿåò çíà÷èòåëüíî ñîêðàòèòü òðóäîåìêîñòü îïðåäåëåíèÿ îïòèìàëüíûõ ðàç-
ìåðîâ ñå÷åíèÿ.
Íà 3 ýòàïå ðàñ÷åòà (ðèñ. 2.11) îïðåäåëÿþò íåîáõîäèìûå çíà÷åíèÿ
íà÷àëüíûõ êîíòðîëèðóåìûõ íàïðÿæåíèé σ
p, con
â íàïðÿãàåìîé àðìàòóðå
À
ð
è
p
A
′
. Ïðè ðàáîòå íàä êóðñîâûì ïðîåêòîì âåëè÷èíó σ
p, con
äîïóñêàåò-
ñÿ ñíà÷àëà ïðèíÿòü ðàâíîé åå ïðåäåëüíîìó çíà÷åíèþ (σ
p,con
= 1,1R
p
äëÿ àðìàòóðíûõ ýëåìåíòîâ èç ñòåðæíåé èëè âûñîêîïðî÷íîé ïðîâîëîêè
è σ
p,con
= 1,05R
p
äëÿ àðìàòóðíûõ êàíàòîâ êëàññà Ê-7 [1, ï. 3.37*;
3.43]), à ïîòîì ïðè íåîáõîäèìîñòè óòî÷íèòü â ïðîöåññå äàëüíåéøèõ
ðàñ÷åòîâ.
Ðèñ. 2.11. Ñõåìà ê 2, 3 è 4 ýòàïàì ðàñ÷åòà

33
Íà 4 ýòàïå âûïîëíÿåòñÿ ðàñ÷åò ïî òðåùèíîñòîéêîñòè áàëêè â ñòàäèè
îáæàòèÿ áåòîíà [5, ï. 3.2]. Ýòîò ðàñ÷åò ïîçâîëÿåò îöåíèòü ïðèíÿòóþ íà
ïðåäûäóùåì ýòàïå âåëè÷èíó íàïðÿæåíèÿ σ
p, con
. Äëÿ ýòîãî îïðåäåëÿþò
íàïðÿæåíèÿ σ
ð1
è σ'
ð1
ñîîòâåòñòâåííî â àðìàòóðå À
ð
è
p
A
′
ñ ó÷åòîì ïîòåðü
íàïðÿæåíèé ïåðâîé ãðóïïû ∆σ
ð1
.;
1con ,11con ,1
pppppp
σ
′
∆−σ
′
=σ
′
σ∆−σ=σ
(2.18)
 êóðñîâîì ïðîåêòå ïîòåðè íàïðÿæåíèÿ â íàïðÿãàåìîé àðìàòóðå ïðè
íàòÿæåíèè íà áåòîí ìîæíî îïðåäåëèòü êàê
,5,0
4311
σ+σ+σ=σ∆
p
ïðè íàòÿæåíèè íà óïîðû
,5,0
6543211
σ+σ+σ+σ+σ+σ=σ∆
p
ãäå ó÷òåíû ñîîòâåòñòâåííî ïîòåðè [1, ïðèë. 11; 5, ï. 3.4, ñòð. 101106]:
σ
1
îò ðåëàêñàöèè àðìàòóðû; σ
2
îò ðàçíîñòè òåìïåðàòóð íàãðåòîé
àðìàòóðû è óïîðîâ; σ
3
îò äåôîðìàöèè òÿãîâûõ àíêåðîâ; σ
4
îò òðåíèÿ
àðìàòóðû î ñòåíêè êàíàëîâ èëè îá îòêëîíÿþùèå ïðèñïîñîáëåíèÿ; σ
5
îò
äåôîðìàöèè ñòàëüíîé ôîðìû; σ
6
îò áûñòðîíàòåêàþùåé ïîëçó÷åñòè
. Ïðè
ýòîì íóæíî ó÷åñòü, ÷òî ñæèìàþùèì íàïðÿæåíèÿì â áåòîíå σ
bp
ñîîòâåòñòâó-
þò ïîëîæèòåëüíûå çíà÷åíèÿ ïîòåðü σ
6
.
 êóðñîâîì ïðîåêòå ïðè íàòÿæåíèè íà óïîðû ìîæíî ïðèíÿòü σ
4
= 0.
Äëÿ ðàñ÷åòîâ â ñòàäèè îáæàòèÿ áåòîíà íåîáõîäèìî íàéòè âíóòðåííèå
óñèëèÿ îò íàïðÿãàåìîé àðìàòóðû (ñ ó÷åòîì åå íàêëîíà):
( )
,
;
11111
111
ppppppp
ppppp
eAeAM
AAN
σ−
′′
σ
′
=
′
σ
′
+σ−=
(2.19)
ãäå
1p
e
′
è
1p
e
ðàññòîÿíèÿ îò öåíòðà òÿæåñòè ïðèâåäåííîãî ñå÷åíèÿ À
red1
áàëêè äî ðàâíîäåéñòâóþùèõ óñèëèé â âåðõíåé è íèæíåé àðìàòóðå.
 îáùåì ñëó÷àå ïðè íàòÿæåíèè àðìàòóðû íà áåòîí íàïðÿæåíèÿ â áåòîíå
(â ñåðåäèíå ïðîëåòà) ïðè ïåðâîì óðîâíå çàãðóæåíèÿ
,
1
1
1
1
1
1
1
y
I
M
y
I
M
A
N
red
g
red
p
red
p
b
++=σ
(2.20)
ãäå M
g1
ìîìåíò â ñåðåäèíå ïðîëåòà îò ñîáñòâåííîãî âåñà îáæèìàåìîãî
áëîêà (îò ïåðâîé ÷àñòè ïîñòîÿííûõ íàãðóçîê); äëÿ ðàçðåçíûõ áàëîê
M
g1
= g
1
l
2
/8, g
1
ñîáñòâåííûé âåñ áàëêè; l ðàñ÷åòíûé ïðîëåò áàëêè.
Ïðè èñïîëüçîâàíèè ôîðìóë (2.19) è (2.20) íåîáõîäèìî ñîáëþäàòü ñëå-
äóþùèå ïðàâèëà:
íàïðÿæåíèÿ â àðìàòóðå è áåòîíå, à òàêæå ïðîäîëüíûå óñèëèÿ ïîäñòàâ-
ëÿþò â ôîðìóëû ñî ñâîèìè çíàêàìè è ñ÷èòàþòñÿ ïîëîæèòåëüíûìè ïðè
ðàñòÿæåíèè;
34
èçãèáàþùèå ìîìåíòû ïîëîæèòåëüíû, åñëè îíè âûçûâàþò ðàñòÿæåíèå
íà íèæíèõ ãðàíÿõ;
êîîðäèíàòà ó ðàññìàòðèâàåìîé òî÷êè ïîïåðå÷íîãî ñå÷åíèÿ ïîëîæè-
òåëüíà, åñëè îíà ðàñïîëîæåíà íèæå öåíòðà òÿæåñòè ñå÷åíèÿ áàëêè.
Ðàñ÷åòíûå ïðîâåðêè ïî òðåùèíîñòîéêîñòè â ñòàäèè îáæàòèÿ áåòîíà
ñâîäÿòñÿ ê âûïîëíåíèþ óñëîâèé:
1,max,1 mcbpb
R
≤σ
äëÿ íèæíåé ãðàíè áàëêè ïðîòèâ îáðàçîâàíèÿ ïðî-
äîëüíûõ ìèêðîòðåùèí;
serbtpb
R
,max,1
8,0
≤σ
′
äëÿ âåðõíåé ãðàíè áàëêè ïðîòèâ îáðàçîâàíèÿ ïîïå-
ðå÷íûõ òðåùèí.
Çäåñü ðàñ÷åòíûå ñîïðîòèâëåíèÿ áåòîíà ïðèíèìàþò ñîãëàñíî [1, ï.ï.
3.24, 3.31], ó÷èòûâàÿ ïåðåäàòî÷íóþ (ôàêòè÷åñêóþ) ïðî÷íîñòü áåòîíà â
ìîìåíò åãî îáæàòèÿ.
Åñëè óêàçàííûå ïðîâåðêè íå óäîâëåòâîðÿþòñÿ, òî ñëåäóåò âûÿñíèòü
âîçìîæíîñòü óìåíüøåíèÿ âåëè÷èíû σ
p, con
, ïîâûøåíèÿ ïåðåäàòî÷íîé ïðî÷-
íîñòè èëè ïðîåêòíîãî êëàññà áåòîíà, à òàê æå óâåëè÷åíèÿ ñå÷åíèÿ áàëêè.
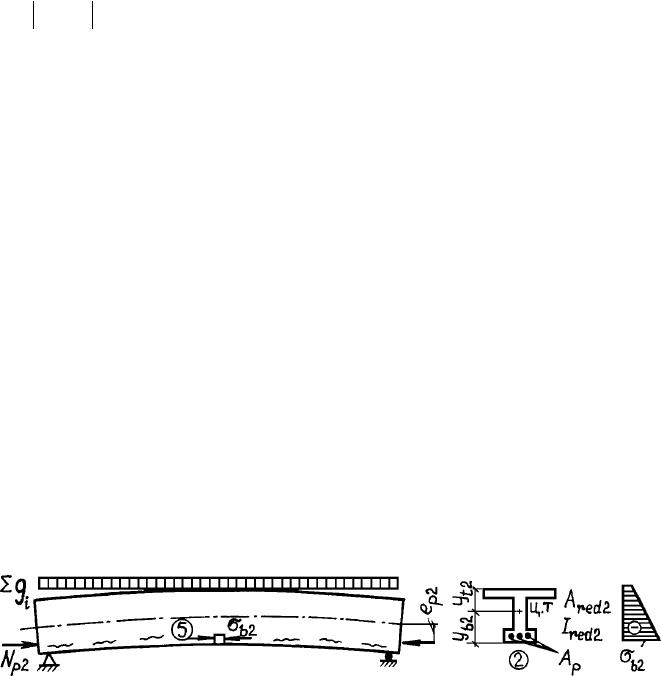
Íà 5 ýòàïå ïðè ðàñ÷åòå ïî òðåùèíîñòîéêîñòè áàëêè â ñòàäèè ýêñïëóà-
òàöèè áåç âðåìåííîé âåðòèêàëüíîé íàãðóçêè íà ìîñòó (ðèñ. 2.12) íåîáõîäè-
ìî çíàòü íàïðÿæåíèÿ â íàïðÿãàåìîé àðìàòóðå, óñòàíîâèâøèåñÿ ê ñòàäèè
ýêñïëóàòàöèè (ñ ó÷åòîì ïîòåðü ïåðâîé è âòîðîé ãðóïï):
,
212
ppp
σ∆−σ=σ
(2.21)
ãäå
1098712
5,0
σ+σ+σ+σ+σ=σ∆
p
ïðè íàòÿæåíèè íà áåòîí;
8712
5,0
σ+σ+σ=σ∆
p
ïðè íàòÿæåíèè íà óïîðû; ïîòåðè íàïðÿæåíèé â
íàïðÿãàåìîé àðìàòóðå: σ
7
îò óñàäêè áåòîíà; σ
8
îò ïîëçó÷åñòè áåòîíà;
σ
9
îò ñìÿòèÿ áåòîíà ïîä âèòêàìè ñïèðàëüíîé èëè êîëüöåâîé àðìàòóðû;
σ
10
îò äåôîðìàöèé îáæàòèÿ ñòûêîâ ìåæäó áëîêàìè, êîòîðûå îïðåäåëÿ-
þòñÿ ïî [1, ïðèë. 11; 5, ï. 3.4, ñòð. 101106].
 êóðñîâîì ïðîåêòå, êàê ïðàâèëî, ïðèíèìàåòñÿ σ
9
= σ
10
= 0.
Äëÿ áàëîê ñ íàòÿæåíèåì àðìàòóðû íà áåòîí ìîæíî ïðèíÿòü, ÷òî âñå
âòîðûå ïîòåðè ïðîòåêàþò â îìîíîëè÷åííîé êîíñòðóêöèè. Òîãäà äîïîëíè-
òåëüíûå âíóòðåííèå óñèëèÿ, âîçíèêàþùèå ïîñëå îáæàòèÿ áåòîíà, ìîæíî
íàéòè ïî ôîðìóëàì:
Ðèñ. 2.12. Ñõåìà ê 5 ýòàïó ðàñ÷åòà
35
,
;
2222
22
ppppppp
ppppp
eAeAM
AAN
′′
σ
′
∆−σ∆=∆
′
σ
′
∆+σ∆=∆
(2.22)
ãäå å
ð2
, å'
ð2
ðàññòîÿíèÿ îò àðìàòóðû À
ð
è
p
A
′
äî öåíòðà òÿæåñòè ïðèâåäåí-
íîãî ñå÷åíèÿ À
red 2
.
Íàïðÿæåíèÿ â áåòîíå (â ñåðåäèíå ïðîëåòà) îò âñåõ ïîñòîÿííûõ íàãðóçîê
è âîçäåéñòâèé â ñòàäèè ýêñïëóàòàöèè (âòîðîé óðîâåíü çàãðóæåíèÿ) íàõî-
äÿòñÿ ïî ôîðìóëå:
,
222
12
y
I
M
y
I
M
A
N
red
g
red
p
red
p
bb
∆
+
∆
+
∆
+σ=σ
(2.23)
ãäå σ
b1
íàïðÿæåíèå â áåòîíå, âîçíèêàþùåå íà ñòàäèè îáæàòèÿ è îïðåäå-
ëÿåìîå ïî ôîðìóëå (2.20) äëÿ òîé æå òî÷êè ñå÷åíèÿ áàëêè ñ îðäèíàòîé ó;
∆M
g
èçãèáàþùèé ìîìåíò îò ïîñòîÿííûõ íàãðóçîê g
2
g
8
â ñòàäèè ýêñïëó-
àòàöèè (ñì. ï. 2.2.1).
Äëÿ ïðåäîòâðàùåíèÿ îáðàçîâàíèÿ ïðîäîëüíûõ òðåùèí äëÿ íèæíåé ãðà-
íè áàëêè (ïðè ó = y
b2
) äîëæíî áûòü âûïîëíåíî óñëîâèå
,
2,max,2
mcbb
R
≤σ
ãäå
2,mcb
R
ïðèíèìàåòñÿ ïî [1, ï.ï. 3.24, 3.31].
Äîïîëíèòåëüíî ïðè íàëè÷èè íàïðÿãàåìîé âûñîêîïðî÷íîé ïðîâîëîêè
äèàìåòðîì 4 ìì è áîëåå íåîáõîäèìî îáåñïå÷èòü çàæàòèå ïîÿâèâøèõñÿ
ïîïåðå÷íûõ òðåùèí ïðè äåéñòâèè ïîñòîÿííûõ íàãðóçîê, îãðàíè÷èâ íàïðÿ-
æåíèÿ â áåòîíå:
bb
R
1,0
max,2
≥σ
ïðè áåòîíàõ êëàññà Â30 è íèæå;
ÌÏà6,1
max,2
≥σ
b
ïðè áåòîíàõ êëàññà Â35 è âûøå.
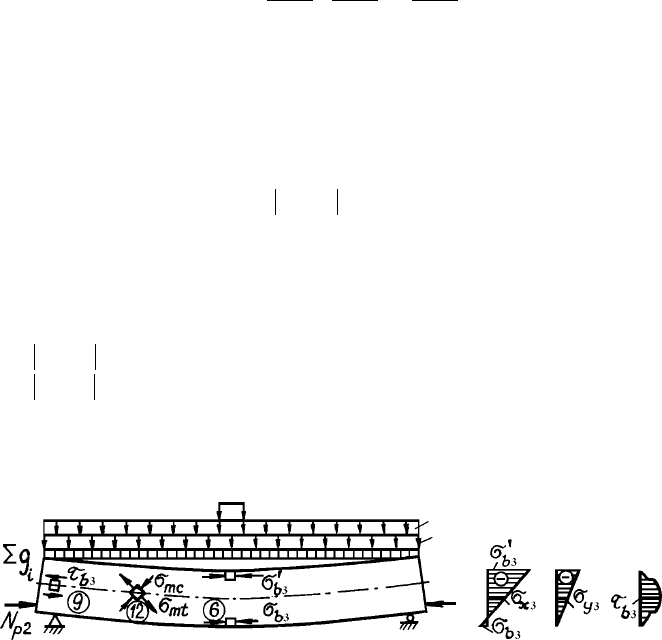
Íà 6 ýòàïå (ðèñ. 2.13) âûïîëíÿåòñÿ ðàñ÷åò ïî òðåùèíîñòîéêîñòè â
ñòàäèè ýêñïëóàòàöèè ñ ïîäâèæíîé íàãðóçêîé íà ìîñòó (òðåòèé óðîâåíü
çàãðóæåíèÿ).
Íàïðÿæåíèÿ σ
b3
ìîæíî íàéòè ñ èñïîëüçîâàíèåì íàïðÿæåíèÿ σ
b2
, îïðåäå-
ëåííîãî ïî ôîðìóëå (2.23) äëÿ òîé æå òî÷êè ñ îðäèíàòîé ó.
Ðèñ. 2.13. Ñõåìà ê 6, 9 è 12 ýòàïàì ðàñ÷åòà
ff
pk
v
v
k
Pk
p

36
Ðàñ÷åò ïî òðåùèíîñòîéêîñòè ïðîèçâîäèòñÿ ïî íîðìàëüíûì íàïðÿ-
æåíèÿì â áåòîíå â ñåðåäèíå ïðîëåòà ñ ó÷åòîì äåéñòâèÿ èçãèáàþùåãî
ìîìåíòà Ì
âð3
îò íîðìàòèâíûõ âðåìåííûõ âåðòèêàëüíûõ íàãðóçîê, âêëþ-
÷àþùèõ íàãðóçêó v è ð îò àâòîòðàíñïîðòíûõ ñðåäñòâ ÀÊ (Ì
v
,j
è Ì
p,j
),
íàãðóçêó îò ïåøåõîäîâ p
f
(Ì
f,j
) (Ì
âð3
= Ì
v
,j
+ Ì
p,j
+ Ì
f,j
) èëè îò íàãðóçêè
ÍÊ-80 (Ì
âð3
= Ì
ÍÊ,j
). Òîãäà
.
2
âð3
23
y
I
M
red
bb
+σ=σ
(2.24)
Âñå âåëè÷èíû Ì
v
,j
, Ì
p,j
, Ì
f,j
è Ì
ÍÊ,j
ïîäñ÷èòûâàþòñÿ ïî ôîðìóëàì (2.2),
(2.4) èëè (2.5) ïðè
fpfff
γ=γ=γ
v
= 1 è (1+µ) = (1+µ)
ÍÊ
= 1.
Ïðè ýòîì íåîáõîäèìî âûïîëíåíèå óñëîâèé:
à) ïî íîðìàëüíûì ñæèìàþùèì íàïðÿæåíèÿì äëÿ âåðõíåé ãðàíè áàëêè
(ïðè ó = ó
t2
) [1, ï. 3.24]
;
2,max,3
mcbb
R
≤σ
′
á) ïî íîðìàëüíûì ðàñòÿãèâàþùèì íàïðÿæåíèÿì äëÿ íèæíåé ãðàíè
áàëêè (ó = ó
b2
), àðìèðîâàííîé
íàïðÿãàåìîé ïðîâîëîêîé äèàìåòðîì 3 ìì èëè êàíàòàìè êëàññà Ê-7
äèàìåòðîì 9 ìì [1, ï. 3.95]
serbtb
R
,max,3
4,0
≤σ
;
íàïðÿãàåìîé ïðîâîëîêîé äèàìåòðîì 4 ìì è áîëåå èëè êàíàòàìè
êëàññà Ê-7 äèàìåòðîì áîëåå 9 ìì
;4,1
,max,3
serbtb
R
≤σ
â) ïî ðàñ÷åòíîé øèðèíå ðàñêðûòèÿ òðåùèí äëÿ íèæíåé ãðàíè áàëêè,
àðìèðîâàííîé
íàïðÿãàåìîé ïðîâîëîêîé äèàìåòðîì 4 ìì è áîëåå èëè êàíàòàìè
êëàññà Ê-7 äèàìåòðîì áîëåå 9 ìì
;ñì 015,0=∆≤
crcr
a
íàïðÿãàåìîé ñòåðæíåâîé àðìàòóðîé
.ñì 020,0=∆≤
crcr
a
Ïðè îïðåäåëåíèè âåëè÷èíû ðàñêðûòèÿ òðåùèí ñëåäóåò èñïîëüçîâàòü
ôîðìóëû [1, ï. 3.105, 3.1083.110] ñ ó÷åòîì ðåêîìåíäàöèé [5, ñòð. 7882].
Åñëè ïåðå÷èñëåííûå íà ýòîì ýòàïå ïðîâåðêè íå îáåñïå÷èâàþòñÿ, òî
ñëåäóåò óâåëè÷èòü îáùåå óñèëèå îáæàòèÿ áåòîíà, äîáàâèâ íåîáõîäèìîå
êîëè÷åñòâî ñòåðæíåé èëè ïó÷êîâ àðìàòóðû.  òàêîì ñëó÷àå äîëæíû áûòü
çàíîâî ïðîâåäåíû ïðîâåðêè ïî òðåùèíîñòîéêîñòè â ñòàäèè îáæàòèÿ.
Íà 7 ýòàïå â æåëåçíîäîðîæíûõ ìîñòàõ ïðîèçâîäèòñÿ ðàñ÷åò íà âûíîñ-
ëèâîñòü. Ñîãëàñíî ÑÍèÏ 2.05.0384* [1] ãëàâíûå áàëêè àâòîäîðîæíûõ,
ãîðîäñêèõ è ïåøåõîäíûõ ìîñòîâ íà âûíîñëèâîñòü íå ðàñ÷èòûâàþòñÿ.

37
Íà 8 ýòàïå îïðåäåëÿþò ìåñòà ðàñïîëîæåíèÿ ïî äëèíå ïðîëåòà âíóòðåí-
íèõ àíêåðîâ, íà÷àëà îòãèáîâ ïó÷êîâ íàïðÿãàåìîé àðìàòóðû èëè ìåñò èçî-
ëÿöèè àðìàòóðû îò áåòîíà (ñì. ðèñ. 2.9). Ýòîò ýòàï ðàáîòû àíàëîãè÷åí
ïîñòðîåíèþ îãèáàþùèõ ýïþð èçãèáàþùèõ ìîìåíòîâ è ýïþð ìàòåðèàëîâ
[5, ï. 5.2, ñòð. 136].  êóðñîâîì ïðîåêòå ìîæíî îãðàíè÷èòüñÿ èñïîëüçîâà-
íèåì ìîìåíòîâ èç ðàñ÷åòà ïî ïðî÷íîñòè, ñîâìåùàÿ çíà÷åíèÿ M
0,5
ñ M
0,5,lim
ïðè ñîáëþäåíèè òðåáîâàíèé íîðì [1, ï.ï. 3.59; 3.129, 3.131; 3.134].
2.3.3. Ðàñ÷åò íàêëîííîãî ñå÷åíèÿ áàëêè íà ïðèîïîðíîì ó÷àñòêå
Íà 9 ýòàïå ïðîèçâîäèòñÿ ðàñ÷åò îïîðíîãî ñå÷åíèÿ áàëêè ïî îãðàíè÷å-
íèþ êàñàòåëüíûõ íàïðÿæåíèé [5, ï. 3.3, ñòð. 85]. Ïðè ýòîì ñëåäóåò îïðåäå-
ëèòü ãåîìåòðè÷åñêèå õàðàêòåðèñòèêè áàëêè â ñå÷åíèè, ðàñïîëîæåííîì ó
íà÷àëà óøèðåíèÿ ñòåíêè.
 îáùåì ñëó÷àå ïðè íàòÿæåíèè àðìàòóðû íà áåòîí êàñàòåëüíûå íàïðÿ-
æåíèÿ ìîæíî îïðåäåëèòü ïî ôîðìóëå (òðåòèé óðîâåíü çàãðóæåíèÿ ïðè
τ
t
= 0)
( ) ( )
,
2
2âð3
1
11
bI
SQQQ
bI
SQQ
red
redpg
red
redpg
b
+∆+∆
+
+
=τ
(2.25)
ãäå Q
g1
ïîïåðå÷íàÿ ñèëà îò ïîñòîÿííûõ íàãðóçîê ïåðâîé ñòàäèè ðàáîòû;
g
Q
∆
ïîïåðå÷íàÿ ñèëà îò ïîñòîÿííûõ íàãðóçîê âòîðîé ñòàäèè ðàáîòû;
∑
ασ=
sin
1
pipp
AQ
ïîïåðå÷íàÿ ñèëà îò óñèëèé â îòîãíóòîé íàïðÿãàåìîé
àðìàòóðå, ïåðåñåêàþùåé ïðèîïîðíîå ñå÷åíèå ïîä óãëîì α ê îñè áàëêè ñ
ó÷åòîì ïåðâûõ ïîòåðü;
()
∑
ασ−σ=∆
sin
21
pippp
AQ
èçìåíåíèå ïîïåðå÷-
íîé ñèëû îò óñèëèé â îòîãíóòîé íàïðÿãàåìîé àðìàòóðå ñ ó÷åòîì âòîðûõ
ïîòåðü; S
red 1
, S
red 2
ñòàòè÷åñêèå ìîìåíòû îòñå÷åííîé ÷àñòè ïðèâåäåí-
íîãî îïîðíîãî ñå÷åíèÿ, ðàñïîëîæåííîé âûøå öåíòðà òÿæåñòè ñå÷åíèÿ
áàëêè; I
red 1
, I
red 2
ìîìåíòû èíåðöèè ïðèâåäåííîãî îïîðíîãî ñå÷åíèÿ
áàëêè; Q
âð3
= Q
v
,j
+ Q
p,j
+ Q
f,j
èëè Q
âð3
= Q
ÍÊ,j
, ãäå âåëè÷èíû Q
v
,j
, Q
p,j
, Q
f,j
èëè
Q
ÍÊ,j
ïîäñ÷èòûâàþòñÿ ïî ôîðìóëàì (2.3) è (2.6) ïðè
fpfff
γ=γ=γ
v
= 1 è
(1+µ) = (1+µ)
ÍÊ
= 1.
 ôîðìóëó (2.25) íàäî ïîäñòàâëÿòü Q
ð
ñî çíàêîì ìèíóñ, à
p
Q
∆
ñî
çíàêîì ïëþñ. Ïðè îòñóòñòâèè îòãèáàåìîé àðìàòóðû Q
ð
=
p
Q
∆
= 0.
Ïðè íàòÿæåíèè íà óïîðû ôîðìóëà (2.25) óïðîùàåòñÿ
( )
.
2
2âð31
bI
SQQQQQ
red
redpgpg
b
+∆+∆++
=τ
(2.26)
Âåëè÷èíà êàñàòåëüíûõ íàïðÿæåíèé â áåòîíå îãðàíè÷èâàåòñÿ çíà÷åíèåì
,
,6
shbbb
Rm
≤τ
(2.27)
ãäå
shbb
Rm
,6
ðàñ÷åòíîå ñîïðîòèâëåíèå áåòîíà [1, ï.ï. 3.24, 3.27].
Åñëè ïðîâåðêà íå âûïîëíÿåòñÿ, òî íóæíî óâåëè÷èòü òîëùèíó ñòåíêè.
38
 áîëåå òî÷íûõ ðàñ÷åòàõ ñòåíîê áàëîê ñëåäóåò ó÷èòûâàòü êðó÷åíèå (τ
t
)
è èçãèá ñòåíîê èç èõ ïëîñêîñòè â ñîîòâåòñòâèè ñ íîðìàìè [1, ï.ï. 3.9, 3.25,
3.104].
Íà 10 ýòàïå ðàñ÷åòà (ñì. ðèñ. 2.9) îïðåäåëÿåòñÿ õàðàêòåð ïîïåðå÷íîãî
àðìèðîâàíèÿ ñòåíêè áàëêè, ïðåæäå âñåãî, â ïðèîïîðíîì ñå÷åíèè. Äëÿ
ïðàâèëüíîãî àðìèðîâàíèÿ ñòåíêè áàëêè íåîáõîäèìî ðóêîâîäñòâîâàòüñÿ
òðåáîâàíèÿìè íîðì [1, ï.ï. 3.24; 3.25; 3.27; 3.37; 3.40; 3.48; 3.773.79], à
òàêæå ðåêîìåíäàöèÿìè [5, ï. 2.3]. Äëÿ ñðåäíåé ÷àñòè ïðîëåòà ïîïåðå÷íóþ
àðìàòóðó (õîìóòû) ìîæíî ñòàâèòü êîíñòðóêòèâíî â ìèíèìàëüíîì êîëè÷å-
ñòâå, ñîáëþäàÿ ñîîòâåòñòâóþùèå îãðàíè÷åíèÿ íîðì [1, ï. 3.143*], äëÿ
ïðèîïîðíîãî ó÷àñòêà èç ðàñ÷åòà, à äëÿ ïðîìåæóòî÷íûõ ó÷àñòêîâ
ïðèíÿòü ïîïåðå÷íîå àðìèðîâàíèå ïî èíòåðïîëÿöèè.
 êóðñîâîì ïðîåêòå ñëåäóåò âûïîëíèòü ðàñ÷åòû ïî ïðî÷íîñòè (ïðè
÷åòâåðòîì óðîâíå çàãðóæåíèÿ) íàêëîííîãî ñå÷åíèÿ áàëêè [1, ï. 3.78*] è ïî
ïðî÷íîñòè áåòîíà ìåæäó íàêëîííûìè òðåùèíàìè [1, ï. 3.77*].
 õîäå ðàñ÷åòîâ â îáùåì ñëó÷àå ðàññìàòðèâàþò íåñêîëüêî íàêëîííûõ
ñå÷åíèé, âûÿâëÿÿ íàèáîëåå îïàñíûå [1, ï. 3.79*; 5, ï. 2.3].  êóðñîâîì
ïðîåêòå äîñòàòî÷íî âûïîëíèòü ðàñ÷åò íàêëîííîãî ñå÷åíèÿ, ïðîõîäÿùåãî
îò êðàÿ âåðõíåé ïëèòû îïîðíîé ÷àñòè ïîä óãëîì 60° ê âåðòèêàëüíîé îñè [1,
ï. 3.78*, ÷åðò. 7; 5, ï. 2.3, ðèñ. 2.14] (â ïîëíîì îáúåìå ïî âñåì âàðèàíòàì
ðàñ÷åò ìîæåò áûòü âûïîëíåí ëèøü ïðè èñïîëüçîâàíèè ÝÂÌ).
 îáùåì âèäå óñëîâèå ïðî÷íîñòè íàêëîííîãî ñå÷åíèÿ íà äåéñòâèå
ðàñ÷åòíîé ïîïåðå÷íîé ñèëû ìîæíî çàïèñàòü â âèäå:
bwwij
QQQQQ
+++≤
ãõ
, (2.28)
ãäå Q
j
ðàñ÷åòíàÿ ïîïåðå÷íàÿ ñèëà â ñå÷åíèè ó êîíöà òðåùèíû, ïðîõîäÿ-
ùåì ÷åðåç öåíòð ñæàòîé çîíû (â êóðñîâîì ïðîåêòå ìîæíî ïðèíÿòü Q
j
= Q
0
);
Q
i
ïîïåðå÷íàÿ ñèëà, âîñïðèíèìàåìàÿ îòîãíóòûìè ïó÷êàìè (â êóðñîâîì
ïðîåêòå ìîæíî ïðèíÿòü Q
i
= 0);
∑
=
swsww
ARQ
õ
ïîïåðå÷íàÿ ñèëà, âîñïðè-
íèìàåìàÿ õîìóòàìè; R
sw
ðàñ÷åòíîå ñîïðîòèâëåíèå àðìàòóðû õîìóòîâ [1,
ï. 3.78*], îïðåäåëÿåìîå ñ ó÷åòîâ êîýôôèöèåíòà m
a 4
[1, ï. 3.40]; À
sw
ïëîùàäü ñå÷åíèÿ õîìóòîâ;
ã
w
Q
ïîïåðå÷íàÿ ñèëà, âîñïðèíèìàåìàÿ ãî-
ðèçîíòàëüíîé ðàáî÷åé àðìàòóðîé (â êóðñîâîì ïðîåêòå ìîæíî ïðèíÿòü
ã
w
Q
= 0); Q
b
ïîïåðå÷íàÿ ñèëà, âîñïðèíèìàåìàÿ áåòîíîì ñæàòîé çîíû.
Íà 11 ýòàïå ïðîèçâîäèòñÿ ðàñ÷åò ïî ðàñêðûòèþ íàêëîííûõ òðåùèí
ñîãëàñíî óêàçàíèÿì [1, ï. 3.105, 3.107*3.110] (òðåòèé óðîâåíü çàãðóæåíèÿ).
Íà 12 ýòàïå (òðåòèé óðîâåíü çàãðóæåíèÿ) âûïîëíÿåòñÿ ðàñ÷åò ïî îáðà-
çîâàíèþ íàêëîííûõ òðåùèí îò äåéñòâèÿ ãëàâíûõ ðàñòÿãèâàþùèõ σ
mt
è
ãëàâíûõ ñæèìàþùèõ íàïðÿæåíèé σ
mc
. Ðàñ÷åòíîå ñå÷åíèå íàçíà÷àþò íàä
îïîðîé èëè â ÷åòâåðòè ïðîëåòà (ïî óêàçàíèþ ïðåïîäàâàòåëÿ), ãäå çíà÷è-
òåëüíû îáå âåëè÷èíû è ïîïåðå÷íîé ñèëû è èçãèáàþùåãî ìîìåíòà (ñì.
ðèñ. 2.13). Íàïðÿæåíèÿ σ
mt
è σ
mc
îïðåäåëÿþò ïî ôîðìóëàì [1, ï. 3.104*]:

39
()()
()()
,45,0
;45,0
2,
2
2
,
2
2
mcbbbybxbybxmc
serbtmtbbybxbybxmt
R
R
≤
τ+σ−σ−σ+σ=σ
α≤
τ+σ−σ+σ+σ=σ
(2.29)
ãäå
;
;;
,6
2
2âð3
2
2
âð3
2
shbbt
red
red
btqb
i
i
by
red
bbx
Rm
bI
SQ
ba
Q
y
I
M
≤τ++τ=τ+τ=τ
−=σ+σ=σ
∑
σ
b2
, τ
b2
íàïðÿæåíèÿ â áåòîíå äëÿ ðàññìàòðèâàåìîé òî÷êè, ðàñïîëîæåííîé
íà ðàññòîÿíèè ó îò öåíòðà òÿæåñòè ïðèâåäåííîãî ñå÷åíèÿ (ñ ó÷åòîì çíàêà),
îò âñåõ ïîñòîÿííûõ íàãðóçîê è óñèëèé ïðåäíàïðÿæåíèÿ; Ì
âð3
, Q
âð3
âíóòðåííèå óñèëèÿ â ñå÷åíèè, ñîîòâåòñòâóþùèå îäíîìó è òîìó æå çàãðóæå-
íèþ ïðîëåòíîãî ñòðîåíèÿ âðåìåííûìè íàãðóçêàìè; Q
i
ïîïåðå÷íàÿ ñèëà
íà ó÷àñòêå áàëêè íàïðÿãàåìûõ õîìóòîâ, íàêëîííîé àðìàòóðû è îïîðíîé
ðåàêöèè (â êóðñîâîì ïðîåêòå, êàê ïðàâèëî, ó÷èòûâàåòñÿ òîëüêî îäíà ñî-
ñòàâëÿþùàÿ, ïî óêàçàíèþ ïðåïîäàâàòåëÿ); à
i
âåëè÷èíà ðàñïðåäåëåíèÿ
ñèëû Q
i
âäîëü áàëêè; b òîëùèíà ñòåíêè áàëêè â ðàññìàòðèâàåìîì
ñå÷åíèè; τ
t
êàñàòåëüíîå íàïðÿæåíèå â ñå÷åíèè îò êðó÷åíèÿ áàëêè (â
êóðñîâîì ïðîåêòå äîïóñêàåòñÿ ïðèíèìàòü τ
t
= 0).
 êóðñîâîì ïðîåêòå ìîæíî îãðàíè÷èòüñÿ ïðîâåðêîé òðåùèíîñòîéêîñòè
íà óðîâíå öåíòðà òÿæåñòè ñå÷åíèÿ (ïðè ó = 0).
Âåëè÷èíà α
mt
R
bt, ser
çàâèñèò îò íàçíà÷åíèÿ ìîñòà (æåëåçíîäîðîæíîãî èëè
àâòîäîðîæíîãî), ñîîòíîøåíèÿ
2,mcbmc
R
σ
è îïðåäåëÿåòñÿ ñîãëàñíî [1, ï.
3.103*]. Ïðè ýòîì max σ
mt
äëÿ àâòîäîðîæíûõ è ãîðîäñêèõ ìîñòîâ íå äîëæíî
ïðåâûøàòü 2,15 ÌÏà, à âåëè÷èíà σ
mñ
çíà÷åíèÿ R
b,mc2
.
 îáùåì ñëó÷àå íåîáõîäèìî òàêæå ïðîèçâåñòè ðàñ÷åò áåòîíà êîíñòðóê-
öèè â çîíå ïåðåäà÷è íà íåãî ñîñðåäîòî÷åííûõ óñèëèé (â òîì ÷èñëå ïîä
àíêåðàìè íàïðÿãàåìîé àðìàòóðû) ïî ïðî÷íîñòè íà ìåñòíîå ñæàòèå (ñìÿ-
òèå) è ïî òðåùèíîñòîéêîñòè íà ìåñòíûå íàïðÿæåíèÿ. Ïîðÿäîê ðàñ÷åòà
ïðèâåäåí â [1, ï.ï. 3.89; 3.90; 3.111*].  êóðñîâîì ïðîåêòå ýòîò ðàñ÷åò
ìîæíî íå ïðîèçâîäèòü.
2.3.4. Îïðåäåëåíèå ïðîãèáà áàëêè â ñåðåäèíå ïðîëåòà
Íà 13 ýòàïå ïðîâåðÿåòñÿ ðàñ÷åòíûé ïðîãèá ãëàâíîé áàëêè îò âðåìåí-
íûõ âåðòèêàëüíûõ íàãðóçîê. Ðàñ÷åò èìååò öåëüþ îãðàíè÷èòü âîçíèêíîâå-
íèå çíà÷èòåëüíûõ ïðîãèáîâ îò äåéñòâèÿ âðåìåííûõ íàãðóçîê. Äëÿ àâòîäî-
ðîæíûõ ìîñòîâ ìàêñèìàëüíûé ïðîãèá îò âðåìåííîé íàãðóçêè äîëæåí
óäîâëåòâîðÿòü óñëîâèþ [1, ï. 1.43]

40
,
400
1
max
lf ≤
(2.30)
ãäå l ðàñ÷åòíûé ïðîëåò, ì.
Äëÿ áàëî÷íûõ ïðîëåòíûõ ñòðîåíèé âåëè÷íèó f
max
äîïóñêàåòñÿ óâåëè÷è-
âàòü íà 20%.
Ëèòåðàòóðà
1. ÑÍèÏ 2.05.03-84*. Ìîñòû è òðóáû. Ì.: Ìèíñòðîé Ðîññèè, ÃÏ ÖÏÏ,
1996. 210 ñ.
2. Ðàñ÷åò æåëåçîáåòîííûõ ìîñòîâ / Ïîä ðåä. Ê.Ê. ßêîáñîíà. Ì.: Òðàíñïîðò,
1977. 352 ñ.
3. Ìåòîäè÷åñêèå óêàçàíèÿ ê êóðñîâîìó ïðîåêòó æåëåçîáåòîííîãî ìîñòà /
Ñîñò. Â.Ï. Óñòèíîâ. Íîâîñèáèðñê, 1993. 40 ñ.
4. Ìåòîäè÷åñêèå óêàçàíèÿ ê êóðñîâîìó ïðîåêòó àâòîäîðîæíîãî æåëåçîáå-
òîííîãî ìîñòà. ×.1. / Ñîñò. Â.Ï. Óñòèíîâ. Íîâîñèáèðñê, 1995. 68 ñ.
5. Âëàñîâ Ã.Ì., Óñòèíîâ Â.Ï. Ðàñ÷åò æåëåçîáåòîííûõ ìîñòîâ, Ì.: Òðàíñ-
ïîðò, 1992. 256 ñ.
6. Ìîñòû è ñîîðóæåíèÿ íà äîðîãàõ. Â 2-õ ÷. / Ïîä ðåä. Ï.Ì. Ñàëàìàõèíà.
Ì.: Òðàíñïîðò, 1991. ×.1, 344 ñ.
7. Ãèáøìàí Ì.Å. Òàáëèöû äëÿ ðàñ÷åòà ïðîëåòíûõ ñòðîåíèé òðàíñïîðòíûõ
ñîîðóæåíèé. Ì.: Òðàíñïîðò, 1985. 447 ñ.
8. Ãèáøìàí Ì.Å., Ïîïîâ Â.È. Ïðîåêòèðîâàíèå òðàíñïîðòíûõ ñîîðóæåíèé.
Ì.: Òðàíñïîðò, 1988. 447 ñ.
9. Ïîëèâàíîâ Í.È. Ïðîåêòèðîâàíèå è ðàñ÷åò æåëåçîáåòîííûõ è ìåòàëëè÷åñ-
êèõ àâòîäîðîæíûõ ìîñòîâ. Ì.: Òðàíñïîðò, 1970. 516 ñ.
10. Ïðîåêòèðîâàíèå äåðåâÿííûõ è æåëåçîáåòîííûõ ìîñòîâ / Ïîä ðåä. À.
Ïåòðîïàâëîâñêîãî. Ì.: Òðàíñïîðò, 1978. 360 ñ.
11. Ëèâøèö ß.Ä., Îíèùåíêî Ì.Ì., Øêóðàòîâñêèé À.À. Ïðèìåðû ðàñ÷åòà
æåëåçîáåòîííûõ ìîñòîâ. Êèåâ: Âèùà øêîëà, 1986. 263 ñ.
