Угринович Н., Босова Л., Михайлова Н. Практикум по информатике и информационным технологиям

Подождите немного. Документ загружается.

200

Глава

Проект

хранится

каталоге

\practicum\VB\Projects\project14\

CD-ROM

Для воспроизведения готовых анимационных файлов (типа

AVI) можно воспользоваться дополнительным управляющим

элементом Animation (Анимация), который входит в набор до-

Шр

полнительных компонентов

Visual

Basic

Microsoft

Windows

*~*-**~Common

Controls-2

5.0.

Проект

5.15. «Мультимедиа». Создадим проект, кото- .нц-

рый воспроизводит анимационные файлы типа AVI. ™

Проект

«Мультимедиа»

Установить набор дополнительных компонентов

Visual

Basic

Microsoft

Windows

Common

Controls-2

5.0 и поместить на фор-

му управляющий элемент Animation. Присвоить ему имя

animl.

2 Разместить на форме управляющий элемент

dlgl

(Общий

диалог)

3 Поместить на форму кнопку cmdStart и создать для нее про-

цедуру

открытия анимационного файла (с использованием

элемента

Общий

диалог)

и запуска его на воспроизведение:

Private

Sub cmdStart_Click()

dlgl.ShowOpen

animl.Open

dlgl.filename

animl.Play

End Sub

4 Поместить на форму кнопку cmdClose и создать для нее про-

цедуру

закрытия анима-

ционного

файла:

Private

Sub cmdClo-

se_Click()

; .,-- & ^

animl. Close "_ I i \_j

End Sub

5 Запустить проект и щел-

кнуть по кнопке

Старт.

На

появившейся панели

Открытие

файла

выбрать файл с расширением AVI. Напри-

мер,

файл

filecopy.avi,

который на CD-ROM находится в ката-

логе

. Мультимедиа

ЯЕШО

Старт

арт

Объектно-ориентированное программирование

на

языке Visual

Basic

201

\practicum\VB\Projects\project15\.

Для окончания воспроизведения щелкнуть по кнопке

Стоп.

6 Сохранить проект в файле

prj15.vbp.

Проект

хранится

каталоге

\practicum\VB\Projects\project15\.

Задания

для

самостоятельного

выполнения

5.53. Создать проект, реализующий работу стрелочных часов. Стрелки

(часовая,

минутная

секундная) должны вращаться

использова-

нием

эффекта анимации.

5.54. Создать проект, реализующий работу стрелочных

электронных

часов. Стрелки (часовая, минутная

секундная) должны вращаться

использованием эффекта анимации синхронно

системным време-

нем

компьютера.

5.55. Усовершенствовать проект

5.15

«Мультимедиа»

заменить кнопки

на

меню.

5.12.

Отладка программных кодов

В процессе разработки проектов программный код может со-

держать ошибки. Ошибки бывают

двух

видов:

синтаксические

Microsoft

Visual Basic

Рис.

5.4

Сообщение

об

ошибке

х^^^кш^у^^^

логические.

Синтаксические

ошибки.

Синтаксические ошибки в процес-

се ввода программы в окне

Программный

код система

Visual

Basic

обнаруживает автоматически и сообщает о них разработ-

чику.

Например,

если в операторе цикла со счетчиком

отсутствует

служебное слово Next, то строка с ошибкой

будет

выделена и

появится

информационная панель с сообщением об ошибке.

Если

причина ошибки ясна, то можно щелкнуть по кнопке

ОК и исправить ошибку.

202

Глава

Рис.

5.5

Справка

H Visual Basic

Reference

МШШ1

For without

Every

For

statement

must have a matching

statement.

This

error

has the following cause and

solution:

• A For

statement

is used without a

corresponding

statement.

Check

for an incorrectly matched For...Next

structure

inside the outer For...Next

structure.

For additional information,

select

the

item

question

and press F1.

ill

В противном

случае

следует

обратиться за помощью к спра-

вочной

системе

Visual

Basic,

для чего щелкнуть по кнопке

Справка,

(в версии VB 5.0 ССЕ отсутствует).

Если

при переходе к следующей строке программы система

Visual

Basic

не обнаружила синтаксических ошибок, то встро-

енный

редактор автоматически выделит ключевые слова (опе-

раторы, методы и др.) синим цветом, а комментарии — зеле-

ным.

Справочную систему можно вызвать в любой момент. Для

этого необходимо установить курсор на ключевое слово и на-

жать клавишу {F1}.

Логические

ошибки.

После запуска проекта

могут

обнару-

житься логические ошибки, содержащиеся в программном

коде. Например, если в цикле по условию условие сформулиро-

вано

неверно, то может произойти зацикливание (программа

начинает выполняться бесконечное множество раз). Для выхо-

да из цикла необходимо одновременно нажать клавиши

{Ctrl}+{Break}

после чего в окне программного кода система ав-

томатически выделит желтым цветом последнюю выполненную

строку программы.

Если

причина логической ошибки неясна, то можно исполь-

зовать специальную возможность и запустить

Отладчик

про-

граммы

(Debug).

Одной из важнейших возможностей отладчика

является выполнение программы по шагам, когда разработчик

может проследить последовательность выполнения программы

проследить процесс присваивания переменным их значений.

Объектно-ориентированное

программирование

на

языке

Visual

Basic

203

•|

Проект

5.16.

«Использование

отладчика

программы».

*^хЗапустить проект «Перевод чисел

из

римской системы

счисления

десятичную»

режиме отладки

проследить

ход выполнения программы.

Проект

«Использование

отладчика

программы»

1 Открыть проект

prj16.vbp,

хранящийся

папке \practicum\

VB\Projects\project16\,

запустить отладчик командой [De-

bug-Step

Into].

2 Выполнять программу по шагам, нажимая клавишу {F8}.

Текущая (выполняемая) строка программы отмечается жел-

|сп*И

'•':

•"

ШШШШШШШШШШШШШЗШ^й

Dim

bytl As

Byte,

intA,

intN,

intM,

intNi"7"

ivate

Sub

cmdil

С1

ick

()

intNuro(l)

•

intNure(2)

••

intNum(3)

•

intNmn(4)

intNun»(5)

intNura(6)

intNvun(7)

•

intNum(7)-50|)

intNum(9) •

intNuin(lO)

intNum(ll)

intNum(12)

intNu«(13)

strRire(l) =

strRiro(2) •

strRim(3) «

•

1000

•

900 •'

•

500

•

400

•

100

90 _J

•50

•

-5

:=•'

1 •••

•-

"M"

•

"CM"

•-

"D" |

тым цветом.

Подвести курсор

имени любой переменной выше исполняе-

мой строки.

Появится

надпись

информацией

значении, присвоенном

переменной.

Глава

Моделирование

формализация

В процессе изучения темы CD-ROM

рекомендуется установить: "

•

систему программирования

Visual

Basic

(VB5.0

ССЕ -

Visual

Basic

5.0

Control

Creation

Edition);

•

электронные таблицы StarCalc,

входящие в состав интегрированного

офисного

приложения StarOffice;

•

систему компьютерного черчения KOMIIAC-3D;

•

геоинформационную модель Карта Москвы (MosMap);

•

компьютерную модель периодической

системы элементов Д. И. Менделеева Table.

Процесс

разработки моделей и их исследование на компью-

тере можно разделить на несколько основных этапов.

На

первом этапе исследования объекта или процесса обычно

строится

описательная

информационная

модель.

Такая модель

выделяет существенные, с точки зрения целей проводимого ис-

следования, параметры объекта, а несущественными парамет-

рами пренебрегает.

На

втором этапе создается

формализованная

модель,

то есть

описательная информационная модель записывается с помо-

щью какого-либо формального языка. В такой модели с помо-

щью формул, уравнений, неравенств и так

фиксируются

формальные соотношения

между

начальными и конечными

значениями

свойств объектов, а также накладываются ограни-

чения

на допустимые значения этих свойств.

На

третьем этапе необходимо формализованную информаци-

онную модель преобразовать в

компьютерную

модель,

то есть

выразить ее на понятном для компьютера языке. Существуют

два принципиально различных пути построения компьютерной

модели:

•

построение алгоритма решения задачи и его кодирование на

одном из языков программирования;

•

построение компьютерной модели с использованием одного

из

приложений (электронных таблиц, СУБД и так далее).

Моделирование

формализация

205

Четвертый этап исследования информационной модели со-

стоит в проведении

компьютерного

эксперимента.

Если

компьютерная модель

существует

в виде программы на одном

из

языков программирования, ее нужно запустить на выполне-

ние

и получить результаты.

Если

компьютерная модель исследуется в приложении, на-

пример,

в электронных таблицах, можно провести сортировку

или

поиск данных, построить диаграмму или график и так да-

лее

Пятый

этап состоит в

анализе

полученных

результатов

корректировке

исследуемой

модели.

случае

различия резуль-

татов, полученных при исследовании информационной модели,

с измеряемыми параметрами реальных объектов, можно сде-

лать вывод, что на предыдущих этапах построения модели

были допущены ошибки или неточности.

6.1. Исследование математических

моделей

Алгебра-9,

Геометрия-7 И51Г

Исследование математических моделей начинается с записи

формальной

модели на языке определенной области математи-

ки:

алгебры, геометрии и так далее.

6.1.1.

Приближенное

решение

уравнений

На

языке алгебры формальные модели записываются с по-

мощью уравнений, точное решение которых основывается на

поиске

равносильных преобразований алгебраических выраже-

ний,

позволяющих выразить переменную величину с помощью

формулы. Точные решения

существуют

только для некоторых

уравнений определенного вида (линейные, квадратные, триго-

нометрические и др.)» поэтому для большинства уравнений

приходится использовать методы приближенного решения с за-

данной

точностью (графические, числовые и др.).

Графический

метод.

Построение графиков функций может

использоваться для

грубо

приближенного решения уравне-

ний.

Для не имеющего точного алгебраического решения урав-

нения

вида fi(x) =

(x)>

где fi(x) = f

(x) — некоторые непрерыв-

ные

функции, корень (или корни) этого уравнения являются

точкой (или точками) пересечения графиков этих функций.

Задача. Найти графическим методом корень уравнения

= sin*, которое не имеет точного алгебраического решения.

206

Глава

Формальная

модель задана уравнением, для нахождения

корня

уравнения разработаем компьютерную модель на языке

Visual

Basic.

*£%$ Проект «Графическое решение уравнения»

Открыть проект «Построение графика функции» (файл

prj13.vbp). Поместить на форму кнопку cmd2 и создать для нее

событийную процедуру построения графика функции у = х

Private Sub cmd2_Click()

For

sngX

= -10 To 10 Step 0.01

picGraph.PSet

(sngX,

sngX

3), vbRed

sngX

End

Sub

2 Для более точного решения уравнения добавить в существую-

щую процедуру построения графика первой функции у = sinx

координатную сетку:

'Координатная

сетка

For

bytl = -10 То 10

picGraph.Line (bytl, 2)-(bytl, -2), vbCyan

Next bytl

For

bytl = -2 To 2 Step 0.2

picGraph.Line (-10, bytl)-(10, bytl)

Next bytl

3 Запустить проект и щелкнуть по кнопкам

График

1 и Гра-

фик 2.

Координаты

х точек пересечения графиков и

будут

корнями

данного уравнения: х

= -1, х

= О, х

= 1.

Проект

хранится

каталоге

гп опм

\practicum\VB\Projects\prj6-1\

iu-ким

Моделирование

формализация

207

Числовой

метод

половинного

деления.

Для решения уравне-

ний

заданной точностью можно применить разработанные

вычислительной математике числовые итерационные методы

решения

уравнений. Если мы знаем отрезок, на котором суще-

ствует

корень,

функция

на

краях этого отрезка принимает

значения

разных знаков,

то

можно использовать метод поло-

винного деления.

Идея

метода состоит

выборе точности решения

сведении

первоначального отрезка

[А;£],

на

котором

существует

корень

уравнения,

отрезку заданной точности. Процесс сводится

по-

следовательному делению отрезков пополам точкой

= (А+Б)/2

отбрасыванию той половины отрезка

([А;С]

или

[С;В]),

на кото-

ром корня нет.

Выбор нужной половины отрезка основывается

на

проверке

знаков

значения функции на его краях. Выбирается

та

полови-

на,

на которой произведение значений функции на краях отри-

цательно,

то

есть когда функция имеет разные знаки

пересе-

кает

ось

абсцисс.

Процесс продолжается

до тех

пор, пока длина отрезка

не

станет меньше удвоенной точности. Деление этого отрезка по-

полам

дает

значение корня

заданной точностью

= (А+Б)/2.

Ц|

Проект

«Числовое

решение

уравнения

заданной

*^*Й1

точностью»

1 Открыть проект «Графическое решение уравнения» (файл

prj6-1

.vbp). Вместо

двух

событийных процедур построения

графиков функций

х и

sinx

создать событийную процедуру

построения графика

х -

siruc.

2 Поместить на форму текстовые поля

txtA

txtB для ввода

числовых значений концов отрезка А и

(переменные

dblA

dblB), поле txtE для ввода точности вычислений (перемен-

ная

dblE)

поле

txtx

для вывода значений корня.

3 Поместить на форму кнопку

создать событийную процеду-

ру, вычисляющую корень уравнения методом половинного

деления

использованием цикла

послеусловием:

Dim

dblA,

dblB, dblE

Double

Private

Sub

cmdNum_C1i с k()

dblA

dblB

dblE

dblC

Then

Val(txtA.

Val(txtB.

Val(txtE.

(dblA

.Text)

dblB)

ЗЫА^З

Sin(dblA)

dblB

dblC

(dblC

3 - Sin(dblC))<0

208

Глава

Else

dblA

= dblC

End

Loop

While (dblB - dblA) / 2 > dblE

txtX.Text

= (dblA + dblB) / 2

End

Sub

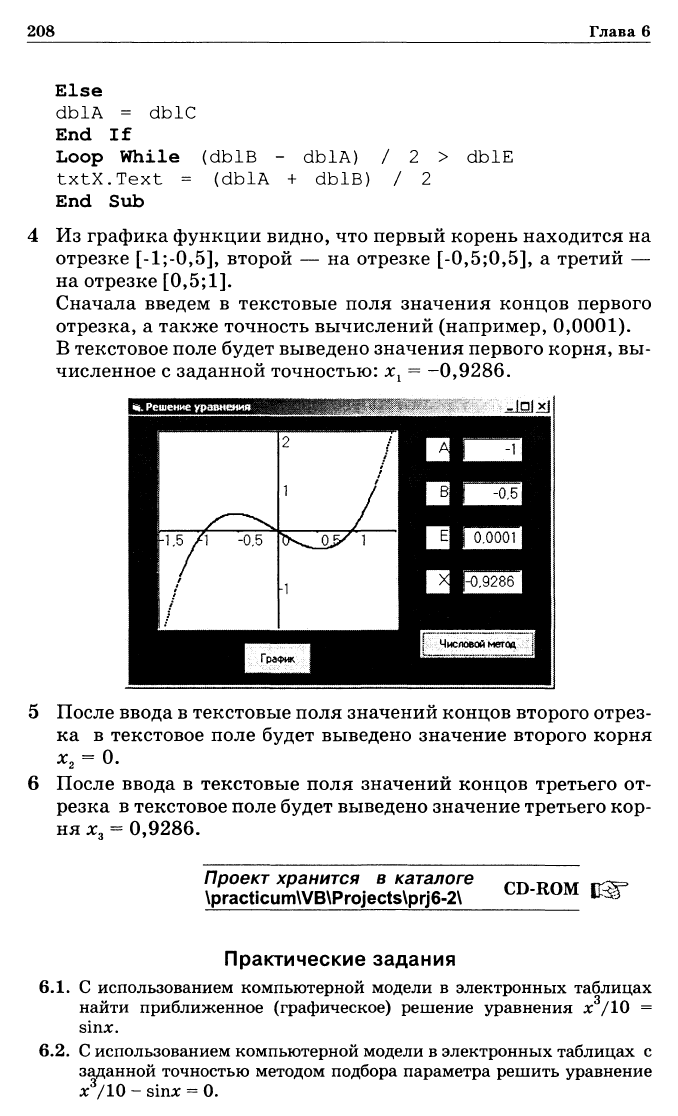
Из

графика функции видно, что первый корень находится на

отрезке

[-1;-0,5],

второй — на отрезке

[-0,5;0,5],

а третий —

на

отрезке [0,5;1].

Сначала введем в текстовые поля значения концов первого

отрезка, а также точность вычислений (например, 0,0001).

В текстовое поле

будет

выведено значения первого корня, вы-

численное с заданной точностью: х

= -0,9286.

После

ввода в текстовые поля значений концов второго отрез-

ка

в текстовое поле

будет

выведено значение второго корня

После

ввода в текстовые поля значений концов третьего от-

резка в текстовое поле

будет

выведено значение третьего кор-

ня

0,9286.

Проект хранится в каталоге

\practicum\VB\Projects\prj6-2\

CD-ROM

Практические задания

6.1.

использованием компьютерной модели

электронных таблицах

найти приближенное (графическое) решение уравнения

х /10 =

sinx.

6.2.

использованием компьютерной модели

электронных таблицах

заданной точностью методом подбора параметра решить уравнение

/Ю

sin*

= 0.

Моделирование

формализация

209

6.1.2.

Вероятностные

модели

Вероятностные модели базируются на использовании боль-

ших серий испытаний со случайными параметрами, причем

точность полученных результатов зависит от количества прове-

денных опытов. Воспользуемся методом Монте-Карло для ис-

следования вероятностной модели бросания монеты.

2.2.

Количество

информации как

мера

уменьшения неопределенности знаний

Учебник

Вероятностная

модель

бросания

монеты.

При введении по-

нятия

«количество информации» рассматривался опыт по бро-

санию монеты. Если бросить симметричную монету на ровную

поверхность, то можно предположить, что с равной вероятно-

стью произойдет одно из

двух

возможных событий — монета

окажется в одном из

двух

положений:

«орел»

или «решка». До-

казательство этого утверждения можно получить при проведе-

нии

большой серии опытов, когда количества выпадений

«орла»

и «решки» постепенно сближаются.

Сначала построим качественную вероятностную модель бро-

сания

монеты:

• поместим квадрат со стороной равной 1 в центр координат и

разделим его на две равные части по оси Y, назовем эти час-

ти

«орел»

и «решка»;

• заменим бросание монеты на «бросание» точек в этот квад-

рат с помощью генератора случайных чисел, который

будет

задавать точкам случайные координаты внутри квадрата;

•

будем

считать, что количество точек, попавших в

левую

часть квадрата, соответствует выпадению

«орла»,

а попада-

ние

в правую половину квадрата— выпадению «решки».

Формальная

модель.

Пусть

— количество точек, которые

случайным образом генерируют-

ся

внутри квадрата. Случайный

выбор координат точек, которые

попадают внутрь квадрата (N то-

чек),

должен производиться так,

чтобы координаты точек х и у

удовлетворяли условиям:

-1 < х < 1 и -н у а .

-1 1 X

-1

Рис.

6.1. Квадрат,

разделенный на две части