Tsoulfanidis N. Measurement and detection of radiation

Подождите немного. Документ загружается.

478

MEASUREMENT

AND

DETECTION

RADIATION

atoms-see Sec. 14.2.1). The decrease in sensitivity may be halted, to a certain

extent, if the counter wall is coated with a mixture of fertile and fissile materials.

One such combination is 90 percent

234~

and 10 percent 235~. The

235~

artiall replenished with new atoms produced by neutron capture in

234~.

23x

U-

U combination will have a similar effect, thanks to

239~~

produced as a

result of neutron capture in

238~.

Fission counters are used extensively for both out-of-core and in-core

measurements of neutron flux in nuclear flux in nuclear reactors. In out-of-core

situations, they monitor the neutron population during the early stages of power

ascension when the neutron flux level is very low. For in-core measurements,

fission counters are used for flux mapping (and consequently, determination of

the core power distribution). They are manufactured as long thin cylindrical

probes that can be driven in and out of the core with the reactor in power.

Typical commercial fission counters for in-core use have diameters of about 1.5

mm (0.06 in), use uranium enriched to at least 90 percent in

235~

as the sensitive

material, and can be used to measure neutron fluxes up to 1018 neutrons/(m2

[1014 neutrons/(cm2

dl.

Another method of measuring fission rates is by using fission track detec-

tors, as discussed in Sec. 16.9.3.

14.4

NEUTRON DETECTION

FOIL ACTIVATION

14.4.1

Basic Equations

Neutron detection by foil activation is based on the creation of a radioisotope by

neutron capture, and subsequent counting of the radiation emitted by that

radioisotope. Foil activation is important not only for neutron flux measure-

ments but also for neutron activation analysis, which is the subject of Chap. 15.

This section presents the basic equations involved.

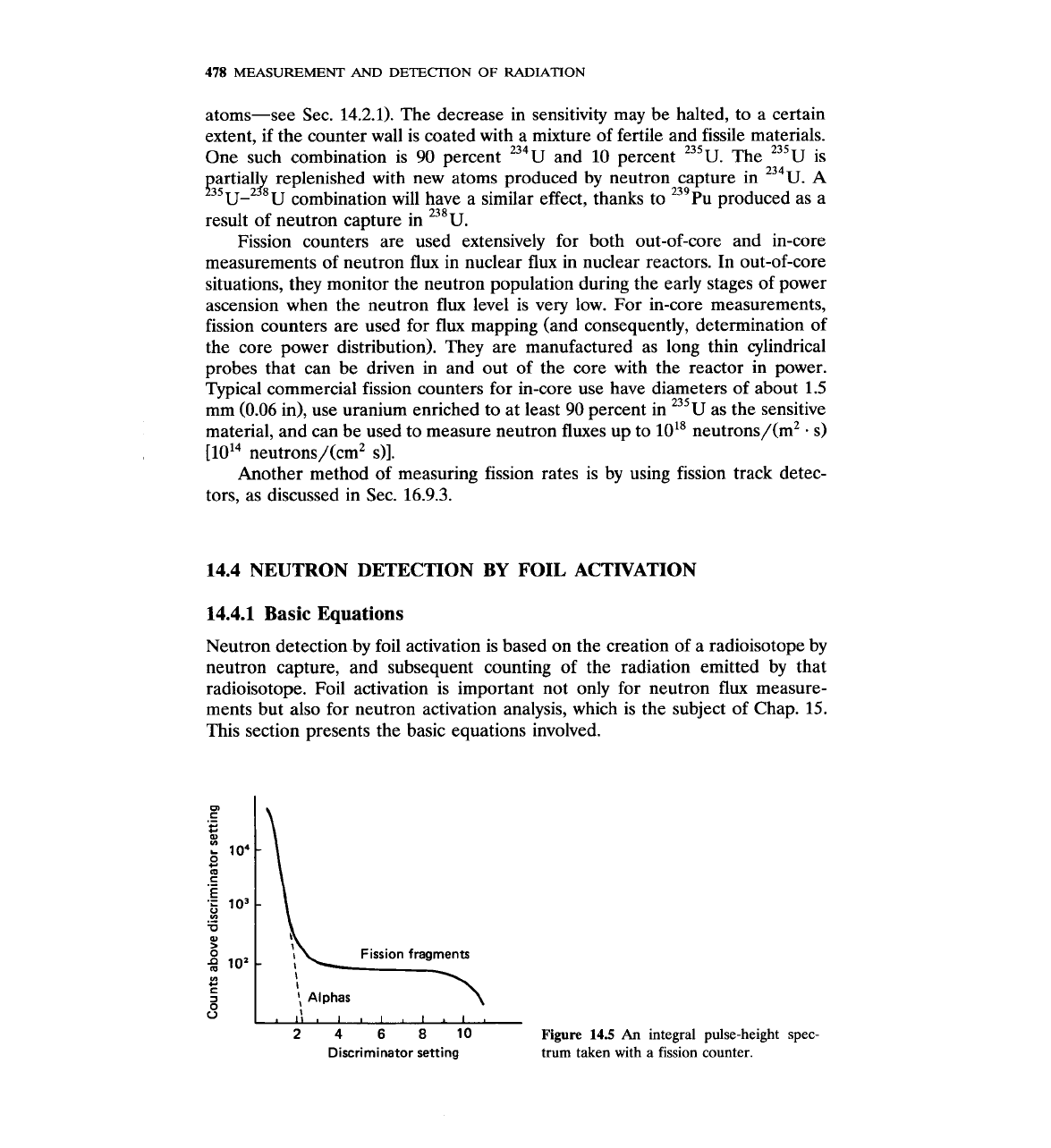
Fission fragments

246810

Figure

14.5

integral pulse-height spec-

Discriminator setting

trum taken with

fission counter.

NEUTRON

DETECTION

AND

SPECTROSCOPY

479

Consider a target being irradiated in a neutron

flux

+(E), where

ui(

neutron absorption cross section of isotope

at neutron energy

A,,

decay constant of isotope with atomic mass number

A,,

u,,

,(El

neutron absorption cross section of isotope

A,,

at neutron energy

)

number of atoms of nuclide with atomic mass number

A,,

present at time

mass of target (normally this is the mass of the element whose isotope

captures the neutron)

weight fraction in the sample of isotope

As a result of neutron absorption, the following processes take place:

1. Target atoms of atomic mass number

are destroyed.

2. Atoms with atomic mass number

A,,

are produced.

3. Atoms of type

A,,

decay.

4. Atoms of type

A,,,

may be destroyed by absorbing a neutron.

For the target isotope

($:x),

the reaction involved is

2:~

The destruction of these atoms proceeds according to the equation

In Eq. 14.12 and all others in this section, it is assumed that the presence of the

target does not disturb the

flux;

i.e., the foil does not cause depression of the

flux.

Corrections that take into account foil self-absorption can be found in

Chap. 11 in Beckurts and Wirtz and in Ref. 12. The integral over energy in Eq.

14.12 is usually expressed as

That is, an average cross section is used, even though the overbar that indicates

averaging is normally dropped. From now on, Eq. 14.13 will be used without the

overbar, but the reader should keep in mind that

is an average over the

neutron energy spectrum.

The solution of

Eq.

14.12 is, using Eq. 14.13,

N,(t)

N,(0)ep"~4' (14.14)

where

airnNA

Ago)

number of atoms of isotope

480

MEASUREMENT

AND DETECTION

RADIATION

The net production of the A,+

isotope is expressed by

dN,+

,(t)

production-destruction-decay

With initial condition

N,.+

,(t)

0, the solution of Eq. 14.15 is

The activity of this target, A,+ ,(t), is, after irradiation for time t,

-exp[-(Ai+,

ui+,+)tll (14.17)

Equation 14.17 refers to the most general case. In practice, targets are selected

in such a way that

The fraction of target nuclei destroyed is negligible, i.e., ui+t

The radioisotope produced has a neutron absorption cross section such that

hi+,

mi+,+.

If conditions (1) and

(2)

are met, Eq. 14.17 takes the form

A,+ ,(t)

ui4(0)+[l

exp (-Ai+,t)l

(14.18)

which is the more familiar form of the activity or activation equation.

If one plots activity as a function of irradiation time, the result is Fig. 14.6.

Two regions are observed.

1. For irradiation times that are short compared to the half-life of the radioiso-

tope produced, the activity increases linearly with time. Indeed, if

A,+

then

e-"+I'

A,+,t

and

where

T,+

is the half-life of the isotope produced.

For irradiation times many times longer than the half-life of the radioisotope,

the activity reaches a saturation value (A,). Theoretically, the saturation

activity

u,&(O)+ (14.19)

NEUTRON

DETECTION

AND

SPECTROSCOPY

481

Saturation

Figure

14.6

Activity versus irradi-

ation time (shown as a fraction of

Irradiation time saturation activity).

is reached for t

In practice, the activity produced is taken as equal to

for

6-7

half-lives.

Table 14.2 gives the fraction of saturation activity produced for several irradia-

tion times.

197

Example

14.3

The isotope

Au is irradiated in a thermal neutron

flux

1018

neutrons/(m2. s). The cross section for neutron capture is 99

and the

half-life of the radioactive I9'~u produced is

2.7

days. (a)

How

long does the

sample have to be irradiated for 0.1 percent of the target atoms to be destroyed?

(b)

What is the irradiation time necessary to produce

percent of saturation

activity? (c) If the mass of the sample

lop6

kg, what is the irradiation

time necessary to produce

7.4

lo4

pCi) of activity?

Answer

(a) Using

Eq.

14.14,

N(t)

N(0)

0.999

epU4' or

ln-

0.999

Table

14.2

Fraction of Saturation Activity

Produced

a Function of Irradiation Time

Irradiation time

(in

half-lives) A;+, (t)/A,

482

MEASUREMENT

AND

DETECTION

RADIATION

(b) Using Eq. 14.18, the irradiation time t should be such that

exp

At)

0.95 or

It is useful to evaluate A, first, because if A, is less than the activity desired, it

is impossible to obtain such activity under the conditions given.

The saturation activity is

In this example, A, is greater than

A(t) and the required irradiation time t is

A(t) 2.7 days

I--

=--

1-1 In 2

[

As]

In 2

1.21

10"

14.4.2

Determination of the Neutron Flux

Counting the Foil Activity

shown in Eq. 14.18, the activity of the irradiated foil is proportional to the

neutron

flux.

Determination of the

flux

requires measurement of the activity, a

task accomplished as follows.

Let the irradiation time be

to.

In practice, counting of the foil starts some

time after irradiation stops, and it is customary to consider the end of irradiation

as time

0 (Fig. 14.7). At time t after irradiation stops, the activity is, using

Eq. 14.18,

Ai+ I(t)

N,(0)ui+[l

exp

(

-A~+

lto)leh+l' (14.20)

If the sample is counted between t, and t,, the number of disintegrations in that

Figure

14.7

Timescale for counting an irradiated sample. Time

coincides with the end of the

irradiation period.

-Irradiation-

;--counting+; Time after

irradiation stops

NEUTRON

DETECTION

AND

SPECTROSCOPY

483

period is

Assuming that one counts particles with energy

for which

is the probabil-

ity of emission per decay, and the counting system is such that

the efficiency of the detection of particles with energy

solid angle

background counts recorded in time

then the gross counts recorded, G,, will be

The factor

Eq.

14.22 takes into account any other corrections (i.e.,

backscattering, foil self-absorption) that may be necessary (see Sec. 8.3). If

dead-time correction is necessary, it should be applied to

G,.

The

flux

is determined from

Eq.

14.22 if all the other factors are known.

There are two types of factors in

Eq.

14.22:

1. Factors that depend on the sample

[N,(O),

a,,

hi+

e,], which are assumed to

be known with negligible error

2. Factors that depend on the counting system

(E,

B),

which are the main

sources of error

To determine the

flux

distribution only, not the absolute value of the

flux,

foils are placed at known positions

and are irradiated for a time

to.

The foils

are then counted using the same detector. At any point

x,,

the

flux

may be

written as

where the subscript

indicates position of the foil and

mass of foil at position

includes all the factors that are common to all the foils.)

484

MEASUREMENT

AND

DETECTION

RADIATION

The title of this section includes the word

foil

because the sample to be

irradiated is used in the form of a thin foil of the order of

mm thick or less.

The mass of the foil is only a few milligrams. Small thin foils are used because

thick sample will absorb so many neutrons that the radiation field will be

perturbed and the measurement will not give the correct

flux.

thick sample will cause a depression of the

flux

in its interior. In such a

case, correction factors will have to be applied to all the equations of this

section that contain the

flux

If the radioisotope emits

particles, increased thickness will not necessarily

increase the counting rate, because only particles emitted close to the surface

within a thickness less than the range will leave the target and have a chance

to be recorded.

4. There is no purpose in producing more activity than is necessary.

Foil activation may be used for detection of the number of either fast or

thermal neutrons. The use of foils for fast-neutron energy measurements is

discussed in Sec. 14.6. Foil activation is not used generally for measurement of

the energy of thermal neutrons.

14.5

MEASUREMENT OF A NEUTRON ENERGY SPECTRUM

PROTON RECOIL

Detection of neutrons by proton recoil is based on collisions of neutrons with

protons and subsequent detection of the moving proton. Since neutrons and

protons have approximately the same mass, a neutron may, in one collision,

transfer all its kinetic energy to the proton. However, there is a possibility that

the struck proton may have any energy between zero and the maximum possible,

as a result of which the relationship between a neutron energy spectrum and a

pulse-height distribution of the struck protons is not simple. It is the objective of

this section to derive a general expression for this relationship. The sections that

follow show its application for specific detectors.

Consider the case of a neutron with kinetic energy

colliding with a

proton at rest (Fig. 14.8). To calculate the proton kinetic energy after the

collision, one must apply the equations of conservation of energy and linear

momentum

(Eqs. 3.81-3.83) using

0 and

Mp.

The result for

E,,

the

proton kinetic energy as a function of the recoil angle

In a neutron-proton collision, the maximum value of angle

is 90°, and the

minimum 0"; therefore, the limits of the proton energy are

En.

For

neutron energies up to about 14 MeV, the

-p)

collision is isotropic in the

center-of-mass system; as a consequence, there is an equal probability for the

NEUTRON DETECTION

AND

SPECTROSCOPY

485

Neutron

Figure

14.8

Neutron-proton collision

Before collision

After collision

kinematics.

proton to have any energy between zero and

in the laboratory system. That

is, if p(E) dE is the probability that the proton energy is between

and

dE, after the collision, then

The function p(E) is shown in Fig.

14.9.

What is important for the observer is

not p(E) but the proton pulse-height distribution produced by the detector. The

relationship between the pulse-height distribution and the neutron spectrum is

derived as follows. Let

En) dEn

neutron energy spectrum

=flux

of neutrons with energy

between

and En

dEn

Ep) dEp

proton recoil energy spectrum

number of protons produced (by

collisions with neutrons) with energy between

and

dE,

E, Ep) dE

response function of the detector

probability that a proton

of energy

will be recorded as having energy between E and

(defined before in Sec.

11.5)

M(E) dE

measured spectrum

number of protons measured with energy

between

and E

The measured spectrum M(E) is the pulse-height distribution in energy

scale. The response function

R(E, Ep) takes into account the finite energy

Figure

14.9

The proton energy distribu-

tion after a

(n,p)

collision that

isotropic in the center of mass system of

the two particles.

486

MEASUREMENT

AND

DETECTION

RADIATION

resolution of the detector and the relationship between energy deposition and

pulse height.

Assuming isotropic scattering in the center of mass system, the proton

energy spectrum is

where

number of hydrogen atoms exposed to the neutron beam

time of measurement of the recoil protons

H(En

E,)

step function; H(En

E,)

lIEn

zero otherwise

u(En)

elastic scattering cross section for

(n,

collisions

The measured energy spectrum is then given by

In Eqs. 14.26 and 14.27, the energy

Em,,

is the upper limit of the neutron energy

spectrum. Equation 14.27 may be rewritten in the form

where

Equation 14.28 has the form of the folding integral (see also

Sec. 11.51, while

Eq. 14.29 gives the "composite" response function for the proton recoil spec-

trometer.

Example

14.4

As a first application of Eq. 14.28, consider the case of a

monoenergetic neutron spectrum and a detector with a Gaussian response

function. What is the measured spectrum?

Answer

Substituting the Gaussian response function

into Eq. 14.29 and performing the integration, assuming E/u

1, one obtainst

h here

are two a's involved here: u(E) is the cross section at energy

without an

argument is the standard deviation of the Gaussian.

NEUTRON

DETECTION

AND

SPECTROSCOPY

487

where

Substituting the value of k(E, En) and the monoenergetic

flux

+(En)

S6(En

E,) into Eq. 14.28 and performing the integration, one obtains

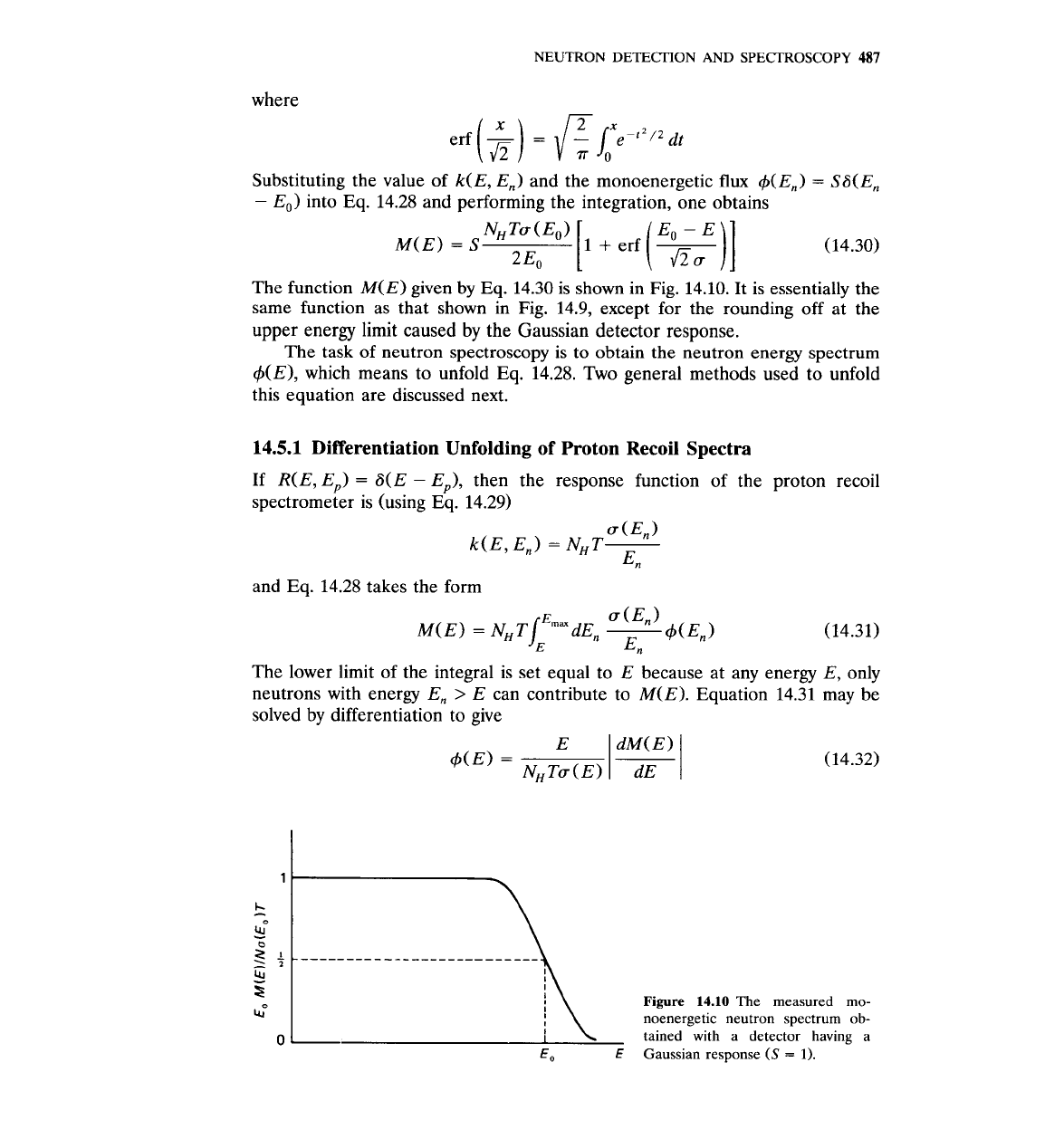
The function

M(E)

given by

Eq.

14.30 is shown in Fig. 14.10. It is essentially the

same function as that shown in Fig. 14.9, except for the rounding off at the

upper energy limit caused by the Gaussian detector response.

The task of neutron spectroscopy is to obtain the neutron energy spectrum

4(E), which means to unfold Eq. 14.28. Two general methods used to unfold

this equation are discussed next.

14.5.1

Differentiation Unfolding of Proton Recoil Spectra

If R(E,

6(E

EJ then the response function of the proton recoil

spectrometer is (using Eq. 14.29)

and Eq. 14.28 takes the form

The lower limit of the integral is set equal to E because at any energy E, only

neutrons with energy En

E can contribute to M(E). Equation 14.31 may be

solved by differentiation to give

Figure

14.10

The measured mo-

noenergetic neutron spectrum

ob-

tained with a detector having a

Gaussian response

1).