Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

ГЛ АВА 7

Осциллятор с изменяющимися параметрами

Примеры осцилляторов с переменными параметрами: колеба-

тельный контур, маятник с вибрирующим подвесом, качели.

Параметрический резонанс. Теория Флоке. Параметрическая

неустойчивость в модельной системе. Уравнение Матье. Ме-

тод Ван-дер-Поля для основного параметрического резонан-

са. Влияние затухания. Параметрическая неустойчивость в

двухконтурной схеме. Соотношения Мэнли-Роу. Медленное

изменение п араметров осциллятора. Аадиабатический инва-

риант. Движение в быстро осциллирующем поле. Маятник

Капицы. Лазер на свободных электронах.

§ 1. Вводные замечания

Существует несколько способов, которыми можно сообщить энергию

колебательной системе. С тремя из них м ы уже познакомились в предыду-

щих главах. Во-первых, можно сделать это в начальный момент времени,

выведя осциллятор из положения равновесия ил и толкнув его, т. е. ис-

пользовать начальные условия. Во-вторых, можно реализовать систему

с отрицательным трением, когда положение равновесия станет неустой-

чивым. Третий способ состоит в действии на осциллятор внешней си-

лы, находящейся с ним в резонансе. Оказывается, что существует еще

один способ, заключающийся в изменении параметров осциллятора во

времени. При определенных условиях это может приводить к появлению

неустойчивости в системе, а также к ряду других интересных физических

эффектов.

Рассмотрим колебательный контур, емкость которого меняется во вре-

мени (рис. 7.1,а), что можно обеспечить, например, механически изменяя

расстояние между пластинами конденсатора

. Мгновенное значение за-

ряда на конденсаторе Q(t) связано с напряжением на нем V

(t) соотно-

В современных радиотехнических схемах роль переменной емко с ти обычно играет

заряженный слой свободных носителей в области p − n- перехода полупроводникового

112

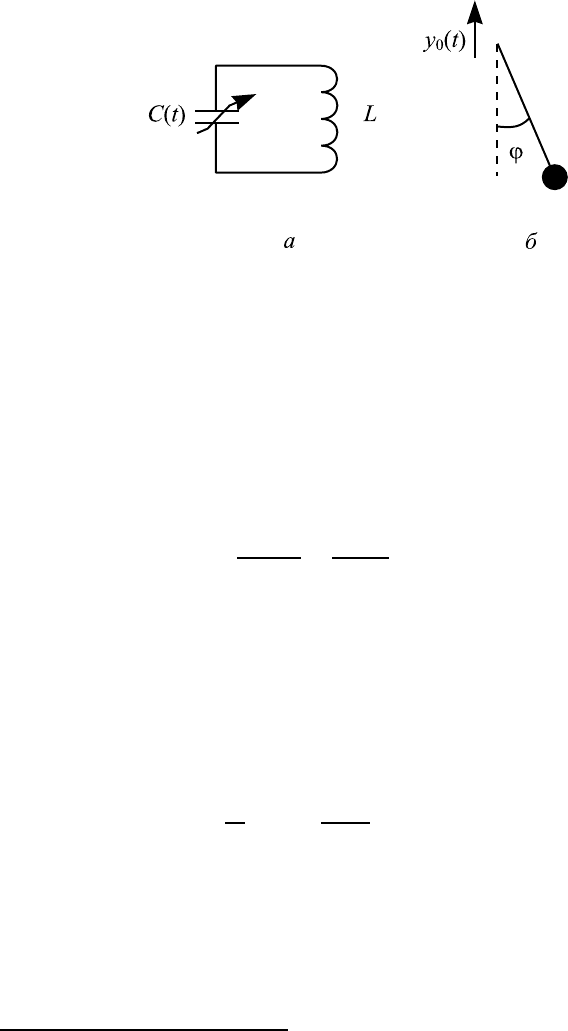
Рис. 7.1. Примеры осцилляторов с переменными парамет-

рами: колебательный контур с меняющейся емкостью (а)

и маятник, точка подвеса которого движется с ускорением

в вертикальном направлении (б).

шением Q(t) = C(t)V

(t), а уравнение К иргхофа для контура имеет вид

I(t) + V

(t) = 0. Учитывая, что I(t) =

Q(t), получаем уравнение

Q(t)

LC(t)

Q(t) = 0 . (7.1)

Это уравнение имеет вид уравнения гармонического осциллятора, частота

колебаний которого меняется во времени. С математической точки зре-

ния, мы имеем дело с линейным дифференциальным уравнением с пере-

менными коэффициентами. Отметим, что если в к ачестве динамической

переменной выбрать не заряд, а ток в контуре, то вместо (7.1) получается

уравнение



LC(t)

dI(t)



+ I(t) = 0 . (7.2)

Это означает, что уравнения (7.1) и (7.2) эквивалентны и могут быть

получены друг из друга заменой переменных.

Другой пример осцилля тора с переменными параметрами дает маят-

ник, точка подвеса которого совершает движение с ускорением в верти-

кальном направлении по заданному закону y = y

(t) (рис. 7.1,б). Переход

диода, а изменение емкости во времени обеспечивается изменением постоянного напря-

жения смещения на диоде.

113

в неинерциальную систему отсчета, в которой точка подвеса покоится,

позволяет записать уравнение маятника:

¨ϕ = −mglϕ − m¨y

(t)lϕ ,

где ϕ — угол отклонения маятника от положения равновесия, который

считается малым. Второе слагаемое в правой части есть момент силы

инерции F

ин

= −m¨y

(t), действующей в вертикальном направлении в

неинерциальной системе отсчета. Последнее уравнение преобразуется к

виду

¨ϕ +



¨y

(t)



ϕ = 0 . (7.3)

Видно, что (7.3) с точностью до переобозначений совпадает с уравнением

(7.1) (здесь ω

= g/l).

Третий пример хорошо знаком читателю с детства: это качели. Для

того, чтобы увеличивать амплитуду качания, мальчик на качелях должен

приседать и выпрямлять ноги в определенные моменты времени согласо-

ванно с движением самих качелей. При этом происходит изменение во

времени положения центра тяжести и момента инерции системы в целом.

Не записывая соответствующего уравнения, скажем, что после некоторых

упрощений оно также может быть приведено к виду (7.1).

В этих примерах изменению подвергается частота колебательной си-

стемы. Можно, однако, рассмотреть систему, в которой меняется во вре-

мени также и величина потерь, например колебательный контур с пере-

менными сопротивлением и емкостью. В этом случае уравнение осцилля-

тора имеет вид

¨x(t) + 2γ(t) ˙x(t) + ω

(t)x(t) = 0 . (7.4)

Заменой переменных

x(t) = exp





−

γ(t

) dt





y(t) , (7.5)

такое уравнение преобразуется в уравнение

¨y(t) +



(t) − γ

(t) − ˙γ(t)



y(t) = 0 , (7.6)

114

в котором слагаемое с первой производной от y(t) по времени отсутству-

ет. Таким образом, в наиболее общем случае линейное дифференциаль-

ное уравнение второго порядка с переменными коэффициентами можно

привести к канонической форме:

¨x(t) + ω

(t)x(t) = 0 . (7.7)

Это уравнение будет основным объектом исследования в данной главе.

С физической т очки зрения наибольший интерес представляют такие

системы, которые в некотором смысле близки по своим свойствам к гар-

моническому осциллятору. Так происходит, если ω(t) - функция, близкая

к константе, тогда в нулевом приближении можно считать, что в системе

существуют колебания с периодом 2π/ω(t). Свойства системы оказывают-

ся существенно зависящими от соотношения двух характерных времен-

ных масштабов: периода колебаний и характерного времени изменения

функции ω(t), назовем его τ. Можно выделить три случая:

1) Оба временных масштаба имеют один порядок, т.е. τ ∼ 2π/ω(t).

При этом говорят о параметрических колебаниях. На иболее ва-

жен случай, когда ω(t) — периодическая функция c периодом T , то-

гда возможно возникновение параметрической неустойчивости, ко-

гда малое начальное отклонение системы от положения равновесия

будет приводить к нарастанию колебаний. Именно это происходит

при раскачивании качелей.

2) Функция ω(t) мало меняется за время одного колебания, т. е. τ 

2π/ω(t). Это соответствует адиабатически медленному изменению

параметров системы.

3) Параметры системы меняются значительно быстрее, чем характер-

ный период колебаний осциллятора. В этом случае также возможны

интересные физические эффекты, связанные с дополнительной си-

лой, возникающей за счет эффекта усреднения быстрых колебаний

в неоднородных пространственных полях.

Анализу всех этих ситуаций посвящена настоящая глава.

§ 2. Параметрическая неустойчивость

Пусть к вадрат частоты осциллятора в уравнении (7.7) можно пред-

ставить в виде ω

(t) = ω

f(t), где f(t + T ) = f (t), f (t) — безразмерная

периодическая функция, которую мы будем считать мало уклоняющейся

115

от единицы, T — ее период, ω

— величина с размерностью частоты.

Если ω(t) близка к константе ω

то мы ожидаем, чт о решения близки к

гармоническим колебаниям с периодом T

= 2π/ω

. Подчеркнем, что па-

раметры T и T

независимы, и наибольший интерес представляет случай,

когда они относятся как небольшие целые или полуце лые числа. Почему

это так, можно понять на примере все того же колебательного контура с

переменной емкостью.

Пусть в контуре возбуждены колебания, а емкость конденсатора ме-

няется следующим образом. В момент, когда заряд на пластинах конден-

сатора максимален, пластины резко раздвигают, делая емкость равной

значению C

, при этом напряжение на конденсаторе скачком увеличива-

ется. Через чет верть периода свободных колебаний в получившемся кон-

туре, т.е. через время π

√

/2, заряд на пластинах оказывается равным

нулю. В этот момент пластины резко сдвигают, так что емкость стано-

вится равной значению C

> C

. Еще через время π

√

/2, когда заряд

конденсатора снова оказывается максимальным, но противоположным по

знаку заряду в начальный момент, пластины снова раздвигают, еще раз

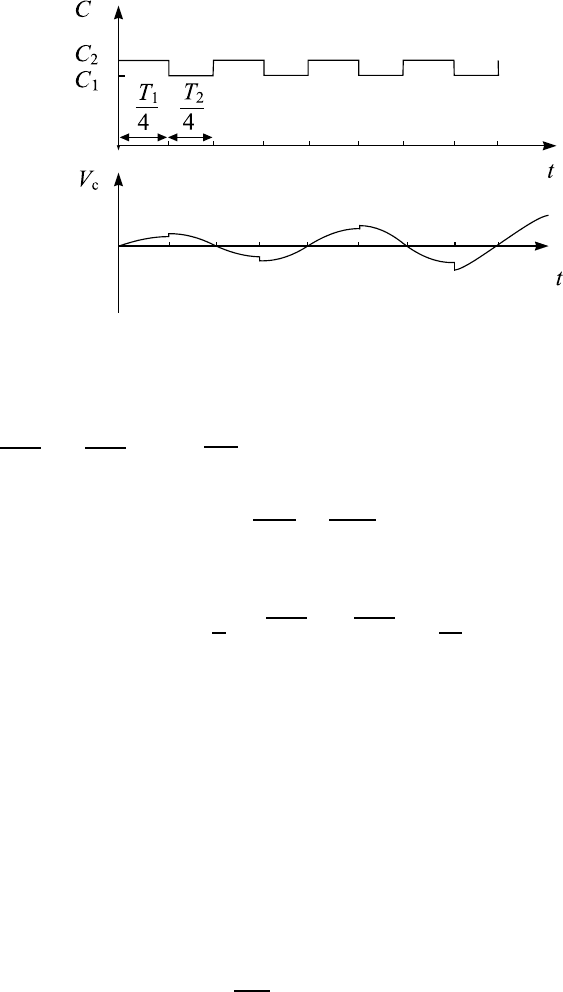
увеличивая напряжение, и так далее. Графики изменения емкости кон-

денсатора и напряжения на нем в зависимости от времени показаны на

рис. 7.2. Нетрудно понять, что в таком процессе будет постоянно совер-

шаться работа, которая пойдет на увеличение энергии осциллятора т. е.

на рост амплитуды колебаний. Такое возрастание амплитуды колебаний

при периодическом изменении параметров гармонического осцилл ятора

называется параметрическим резонансом.

Можно сделать и количественные оценки. Пусть в момент перед раз-

двиганием пластин напряжение на них равно V

, а энергия в системе

W = C

/2 (вся энергия сосредоточена в этот момент в конденсато-

ре). При резком увеличении расстояния между пластинами заряд на них

не успевает измениться, а напряжение скачком увеличивается до значе-

ния V

, которое можно найти из закона сохранения заряда C

= C

Энергия в контуре становится равной W

= C

/2. Собирая эти соот-

ношения вместе, получаем для изменения энергии

∆W = W

− W = W



− 1



≈ W

∆C

где ∆C = C

−C

, C = (C

)/2 (считаем, что ∆C/C  1). Поскольку

за один цикл пластины раздвигаются дважды, для энергии, закачивае-

мой в систему за время одного "периода"колебаний осциллятора, равного

116

Рис. 7.2. Изменение емкости в колебательном контуре и

напряжения на ней в зависимости от времени

π(

√

) ≈ 2π

√

LC, можно записать

∆W

≈

2∆C

. (7.8)

Для периода изменения параметра T выполняется соотношение

T =





≈

. (7.9)

Это значит, что наиболее эффективно энергия закачивается в систему,

когда период изменения параметра примерно равен половине собственного

периода колебаний о сциллятора.

Можно, однако, раздвигать пластины не каждый раз, когда заряд на

конденсаторе максимален, а через раз, энергия все равно будет посту-

пать в систему, хотя и в меньшем количестве. Условие такого резонанса

вместо (7.9) примет вид T ≈ T

. Очевидно, чт о в общем случае мож-

но раздвигать пластины только в каждый n-й благоприятный для этого

момент, что позволяет обобщить условие параметрического резонанса, за-

писав его следующим образом:

T ≈

, n = 1, 2, . . . . (7.10)

Для n = 1 говорят об основном резонансе, для произвольного значения n

— о резонансе n-го порядка.

117

Проведенное рассмотрение не учитывает потерь в системе, что легко

сделать. Если потери малы, то оба эффекта — параметрическую неустой-

чивость и влияние затухания — можно рассматривать независимо друг

от друга. За счет затухания потери энергии за период равны ∆W ≈ −

−2γT

W , где γ — коэффициент затухания. С учетом (7.8), общее изме-

нение энергии есть

∆W = W



2∆C

− 2γT



откуда получаем, что если ∆C/C > γ

= d = π/Q (d — логарифми-

ческий декремент, Q — добротность осциллятора), то в целом колебания

нарастают. Таким образом при конечных потерях в системе параметриче-

ская неустойчивость возникает только при достаточно большой глубине

модуля ции параметра.

Отметим, что для развития неустойчивости требуется, чтобы изна-

чально колебания в системе уже существовали. Если осцил лятор покоит-

ся, то изменение его параметров не приводит к появлению колебаний.

Проще и удобнее сделать так, чтобы параметры системы менялись

непрерывным образом, а не скачками. Пусть, например, емко сть в кон-

туре меняется по закону C(t) = C

+ ∆C cos(2ω

t), где ω

= 1/

√

∆C  C

(предполагается, что реал изован наиболее благоприятный слу-

чай основного резонанса). Так как значение емкости мало отклоняется

от своего среднего, то можно считать, что в течение одного периода ам-

плитуда колебаний почти не меняется и напряжение на емкости равно

(t) =

cos(ω

t + ϕ), ϕ — сдвиг фазы. При изменении емкости кон-

денсатора на малую величину ∆C совершается работа ∆A = −W

∆C/C,

= CV

/2 — энергия, запасенная в конденсаторе. Поэтому за один

период колебаний совершается работа

A = −

t+2π/ω

)

C(t

) dt

Подставляя выражения для C(t) и V

(t), получаем

A = ∆Cω

t+2π/ω

sin 2ω

cos

(ω

+ ϕ) dt

= −

π∆C

W sin 2ϕ .

Вся эта работа идет на приращение энергии системы. Максимальным

прирост энергии будет, если ϕ = −π/4 или ϕ = 3π/4, при этом ∆W/W =

= π∆C/C. Если в системе есть потери, то, как и в предыдущем случае,

118

глубина модуляции должна быть достаточно большой для возникновения

неустойчивости:

∆C

. (7.11)

Этот анализ является приближенным, так как в нем не учитывались

некоторые важные факторы. На пример, условие резонанса может выпол-

няться только приближенно, или частота колебаний в контуре на самом

деле может немного отличаться от ω

, и так далее. Однако сам результат

(7.11) оказывается верным, что будет показано ниже.

Задача 7.1. Предположим, что мальчик раскачивает качели, дважды за

период качания резко приседая и резко выпрямляя ноги. В какие именно

моменты он должен э то делать, чтобы качели раскачивались наиболее эф-

фективно? Как нужно действовать, если процесс приседания и вставания

растянут во времени?

Итак, проведенное качественное рассмотрение позволяет выделить

основные особенности параметрического резонанса:

1) Параметрический резонанс может появляться в колебательной си-

стеме при периодическом изменении ее параметров, если выполня-

ются определенные соотношения (7.10) между периодом изменения

параметров и собственным периодом колебаний системы.

2) Для развития неустойчивости необходимо, чтобы колебания в си-

стеме уже суще ствовали. Если осциллятор покоится в положении

равновесия, то изменение параметров не ведет к возникновению ко-

лебаний.

3) При конечных потерях в системе глубина модуляции параметров

должна быть достаточно большой, чтобы неустойчивость появилась.

§ 3. Теория Флоке

Линейное дифференциальное уравнение второго порядка с периоди-

ческими коэффициентами можно привести к виду

¨x(t) + ω

(t)x(t) = 0 , (7.12)

119

где ω

(t) — периодическая функция с периодом T . Для произвольной

функции ω

(t) это уравнение называется уравнением Хилла [1]. Суще-

ствует общая теория линейных дифференциальных уравнений с периоди-

ческими коэффициентами, результаты которой, применительно к уравне-

нию второго порядка (7.12), будут даны здесь без строгих доказательств.

Их можно найти, например, в [1–3].

У уравнения (7.12) существует два линейно независимых решения

(t) и x

(t), так что любое решение представимо в виде их линейной

комбинации. С другой стороны, делая в (7.12) замену t → t + T , мы

вновь получаем то же самое уравнение, следовательно функции x

(t + T )

и x

(t + T ) также должны являться решениями исходного уравнения.

Поэтому, используя матричные обозначения, можно записать



(t + T )







(t)









(t)



, (7.13)

где коэффициенты a

i,j

— постоянные, причем в каждой строке матрицы





хотя бы один из коэффициентов не равен нулю. Матрица





назы-

вается матрицей отображения за период, и она играет главную роль

при анализе параметрических систем.

Детерминант матрицы





равен единице, что можно показать следу-

ющим образом. Запишем уравнение (7.12) для решений x

1,2

(t):

¨x

(t) + ω

(t)x

(t) = 0 , ¨x

(t) + ω

(t)x

(t) = 0 .

Умножим первое из этих уравнений на x

(t), а второе — на x

(t),и вычтем

одно из другого. В результате получим ¨x

−x

¨x

= d( ˙x

−x

˙x

)/dt =

= 0, т. е. ˙x

− x

˙x

= const. Приравнивая эти комбинации в моменты

времени t и t + T , и, используя (7.13), непосредственно получаем

− a

= det





= 1 . (7.14)

Собственные числа матрицы отображения за период называются мульти-

пликаторами, они определяются из уравнения

det [A − µI] =



− µ a

− µ



= 0 , (7.15)

или, с учетом (7.14) ,

− (a

+ a

)µ + 1 = 0 . (7.16)

120

Корни к вадратного уравнения (7.16) равны

1,2











− 4



, (7.17)

где Sp





= a

+ a

- след матрицы, то есть сумма ее диагональ-

ных элементов. Та к как мы полагаем функцию ω

(t) действительной, то

коэффициенты матрицы





также будут действительными числами. В

зависимости от величины Sp





возможны три случая:

1) |Sp





| < 2, при этом мультипликаторы являются комплексно со-

пряженными величинами, причем µ

= 1, то есть оба мультипли-

катора лежат на единичной окружности в комплексной плоскости

µ. Матрица





при этом может быть с помощью преобразования

подобия









−1







(





— квадратная невырожденная

матрица) приведена к диагональному виду, так что на главной диа-

гонали матрицы





лежат собственные значения. Отсюда легко

показать (см. [3]), что д ва линейно независимых решения уравне-

ния (7.12) вида



(t)







−1



(t)



(7.18)

обладают следующим свойством: u

1,2

(t + T ) = µ

1,2

(t). Общее

решение этого функционального уравнения есть

1,2

(t) = e

1,2

Φ(t) , λ

1,2

ln µ

1,2

, (7.19)

где Φ

1,2

(t) — периодические с периодом T функции.

На больших временах эти решения остаются ограниченными. Дей-

ствительно, для произвольного t имеем |u

(t + nT )| = |µ

(t)| =

= |µ

||u

(t)| = |u

(t)|. То же самое справедливо и для u

(t). Так как

произвольное решение представляется в виде линейной суперпози-

ции решений u

1,2

(t), то отсюда вытекает ограниченность решения.

Неустойчивости в системе нет.

2) Если |Sp





| > 2, то из соотношения (7.17) получаются два дей-

ствительных мультипликатора, один из которых по модулю обяза-

тельно больше, а другой — меньше единицы. В этом случае опять

можно так выбрать д ва л инейно независимых решения, что для них

будут выполняться формулы (7.19). Однако теперь ограниченности