Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Tomography methods of recovering the image of medium 363

where x

, and x

are the source and receiver positions respectively; p

, p

and

are the vectors of the tomographic functionals, which corresponds to the next

perturbations of the medium δλ, δµ and δρ respectively. Under assumption of the

linear relation between perturbations of parameters of the elastic medium (δλ, δµ,

δρ):

δλ(x) = c

δµ(x), δρ(x) = c

δµ(x), (11.67)

the integral equation (11.66) can be written as follows

u (x

, x

, t) ≈



(x, x

, x

, t) + p

(x, x

, x

, t)

+ c

(x, x

, x

, t)] δµ(x)dx. (11.68)

After digitization of the equation (11.68) the system of linear equations relatively

to the vector d

of the desired values δµ(x) can be written as

P d

= d

, (11.69)

where d

are the samples of the ﬁeld scattered by the inhomogeneity. The solution

of the system of linear equations (11.69) we obtain by the minimizing of the sum

of squares of the deviations between left hand side and right hand side of (11.69),

that, after introducing regularizing terms, leads the system of linear equations

P + α

+ B

) + α

C + α

D]d

= P

. (11.70)

In equation (11.70) α

, α

are the regularizing coeﬃcients; matrices B

and B

are ﬁnite diﬀerences images of second partial derivatives with respect to x and z

respectively; C and D are penalty matrices for non-zero values of the desired values

) in the boundary point and the ‘near’ boundary point of the recovery region S

respectively.

Minimizing of the sum of squares of the deviations between the left hand side

and the right hand side of (11.69) permits to ﬁnd the coeﬃcients c

and c

. In

this case the system of equations (11.70) is solved iteratively, and the minimum of

such deviation (connected with the values of c

, c

and δµ(x)) can be found, for

example, by the gradient method.

The parameters of inhomogeneity can be determined using the parametric repre-

sentation of inhomogeneity. In this case for the minimization of the sum of squares

of the deviations between left hand side and right hand side of (11.69) the gradient

method can be used also.

The accuracy of the direct problem solution is estimated on the intrinsic con-

vergence for the following local inhomogeneity

δµ(x) =











0.25µ

1 + cos



x−ˆx

∆

ih

1 + cos



z−ˆz

∆

i

if |x − ˆx| < ∆

and |z − ˆz| < ∆

0, if |x − ˆx| > ∆

or |z − ˆz| > ∆

(11.71)

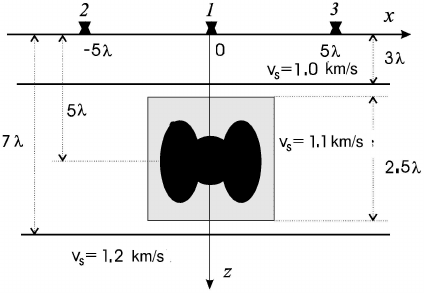
364 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Fig. 11.5 Seismic model and observation scheme: 1–3 are the source and receiver location; S is

the recovery region; λ ≡ λ

= 0.02 km.

where (ˆx, ˆz) is the location of the maximum deviation µ

the value µ(x) from the

value µ

(x) in the reference medium, ∆

and ∆

determine inhomogeneity sizes in

horizontal (e

) and vertical directions (e

) respectively. The solution of the direct

problem is implemented with a net for which in the case of ∆

= ∆

≈ λ

= v

decreasing of the distance between nodes on two times leads to the deviation between

signal amplitudes approximately of 2–5 %.

The recovered inhomogeneities are described by the formula (11.71). The re-

covery region S and the desired inhomogeneity are represented in Fig. 11.5. The

inhomogeneity with a complex geometry is obtained by the superposition of the

simple shapes (11.71). So, the model, which is marked in Fig. 11.5 by more dark

color, is constructed using three shapes (11.71) with the next parameters:

ˆx

= ˆx

, ˆz

= ˆz

(∆

= ∆

= 0.45λ

ˆx

= ˆx

+ 0.5λ

, ˆz

= ˆz

(∆

= 0.5λ

, ∆

= λ

ˆx

= ˆx

− 0.5λ

, ˆz

= ˆz

(∆

= 0.5λ

, ∆

= λ

ˆx

= 0, ˆz

= 5.0λ

, µ

m 1

= µ

m 2

= µ

m 3

= 1.2.

(11.72)

An asymmetric inhomogeneity described by the parameters

ˆx

= ˆx

− 0.25λ

, ˆz

= ˆz

+ 0.6λ

(∆

= ∆

= 0.5λ

ˆx

= ˆx

+ 0.25λ

, ˆz

= ˆz

+ 0.1λ

(∆

= ∆

= 0.5λ

ˆx

= ˆx

+ 0.25λ

, ˆz

= ˆz

− 0.5λ

(∆

= ∆

= 0.45λ

ˆx

= 0, ˆz

= 5.0λ

m 1

= µ

m 2

= µ

m 3

= 1.2

(11.73)

is considered also. The inhomogeneity is located in the uniform space (v

1.1 km/s), which contacts with the half-space (v

= 1.2 km/s) and with the uni-

form layer (v

= 1.0 km/s), which is bounded by the free surface (z = 0). The

maximum velocity contrast of the inhomogeneity is 20 % (δv

p max

= 0.37 km/s,

δv

s max

= 0.21 km/s). The observation points and the source points (1–3 Fig. 11.5)

are placed under the free surface (z = 0) with the depth ∼ 3 m.

Tomography methods of recovering the image of medium 365

The parameters of the inhomogeneities (11.72), (11.73) are recovered by the

solution of the system of linear equations (11.70) and with the help of the optimizing

methods together with the parametric representation of inhomogeneities using more

wade function set than one given by the formula (11.71). In the last case the desired

parameters are found by minimizing of the sum of squared diﬀerences of the left

hand side and right hand side of the equation (11.69). The elementary test function

δµ(x) =







0, r > ∆ + ∆

0.5µ



1 + cos



r−∆

∆



, ∆

< r < ∆ + ∆

, r < ∆

r =

(x − ˆx)

+ (z − ˆz)

+ (x − ˆx)(z − ˆz)h

(11.74)

is determined by the seven parameters: the location of its center ˆx, ˆz; the values

∆ and ∆

, which determine an ellipse with the constant value of δµ = µ

and the

region of a smooth change of δµ from the value µ

to zero value; the maximum value

of the shear module µ

; multipliers h

and h

. The restoration of the parameters

is implemented using one, two or three functions of the form (11.74). For ﬁnding

from 9 to 23 desired values (including c

and c

from the integral equation (11.68))

a gradient method is used. The convergence of the gradient method to the values

close to true values occurs, when the deviation of the initial values is not greater

than 50 %, and the deviation for ˆx and ˆz is 0.25–0.3 λ

Before consideration of the results of the numerical simulation, we make a few

remarks. The system of the linear equations (11.70) is solved at nonzero values of

the regularizing coeﬃcients α

and α

. As it follows from the numerical simulation

the smoothness condition, for recovered parameters of the medium, assigned as a

restriction on the value of the second derivative, leads to the better result than the

application of the ﬁrst derivative. The regularization using a penalty function on

the nonzero value of the desired parameters in the boundary points of the recovery

region S is a very natural procedure for the recovered region with a limited size.

Similar regularization (α

6= 0) leads to decrement by 10–20 % of the error of the

parameters (for example, the velocity of the p-wave) recovery. The penalty func-

tion connected with the regularizing coeﬃcient α

6= 0 can be used as a way for

introducing a priori information about the location and sizes of the desired inhomo-

geneity. A choice of the regularization parameter α

does not involve diﬃculties,

because in the great size of its changing (1–3 orders), after the transition from the

bad conditionality of the system of equation (11.70), the recovered function is a

very stable and tends to more smooth one with increasing of α

. The parameter

is chosen so that the recovered values in the boundary of the recovered region S

(see Fig. 11.5) are much smaller then their maximum value.

The number of nodes in the recovery region S is equal to 25×25. The represented

below examples of the parameters recovery are obtained using two (x- and z-)

component of the wave ﬁeld, “observed” in the points 1–3 (see Fig. 11.5). The wave

ﬁeld is excited at the same points (9 source-receiver pairs). Let’s not, that recovery

366 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

of the inhomogeneity parameters using only z-component of the wave ﬁeld leads to

increasing of the recovery error by 10–20 %.

Let us consider the results of recovery of the inhomogeneities (11.72) and (11.73)

(which are represented on Fig. 11.6(a) and 11.7(a) respectively) with the maximum

velocity perturbation of p-wave v

p max

= 0.37 km/s when the velocity of p-wave in

the reference medium is equal to v

= 1.9 km/s. In Fig. 11.6(b) (11.7(b)) are

Fig. 11.6 The recovery of v

for the inhomogeneity (11.72):

(a) is the model; (b) – (d) are the results of recovery: (b), (c) the recovery by the solution of the

system of equations (11.70) with α

= 0 and α

6= 0 respectively; (d) the recovery with the use of

the parametric representation of the inhomogeneity.

represented the results of recovery (the maximum value v

p max

= 0.31 (v

p max

0.29)), which are obtained by the solution of the system of linear equations (11.70)

together with the calculation of c

and c

(from the equation (11.68)) at α

= 0. The

values c

and c

corresponds to the minimum value of the sum of squared diﬀerences

of the left hand side and the right hand side of the equation (11.69), which is ﬁnding

by gradient method. The eﬀect of the introducing of penalty functions (α

6= 0,

equation (11.70)), is demonstrated on Fig. 11.6(c) (v

p max

= 0.30). As a rule, four

or ﬁve iteration are enough for calculation of c

and c

with error not greater than

1 %, if initial values (c

λ 0

and c

ρ 0

), diﬀer from the true values by 50 % at least.

In the considered cases the errors of recovery c

and c

are not greater of 10 %

Tomography methods of recovering the image of medium 367

Fig. 11.7 Recovery of v

for inhomogeneity (11.73): (a) is the model of inhomogeneity; (b)–(d)

are the results of recovery: (b) recovery by the solution of the system of equations (11.70) with

= 0; (c) and (d) recovery with the use of the parametric representation of inhomogeneity with

the help of three and one function (11.74) correspondingly.

and 90 % respectively. Let’s note, that c

always is overstated. Such considerable

error of the δρ recovery can be explained so that the part of the wave ﬁeld scattered

by the perturbation of δρ, “at the average” has a small contribution to the full

scattering ﬁeld.

Similar errors are obtained for the values c

and c

in the case of the para-

metric representation of inhomogeneities using the formula (11.74). The results of

the recovery of inhomogeneity (11.72) (see Fig. 11.6(a)) with the help of the one

function of (11.74) are represented in Fig. 11.6(d) (v

p max

= 0.337 km/s). The re-

covered inhomogeneity of the form (11.73) is represented in Fig. 11.7(c) and 11.7(d)

correspondingly for the cases of three and one function (11.74).

The calculation of c

allows as to recover γ = v

. In the considered model is

assumed λ = µ, and recovery error of γ is about 1 %.

From the results of numerical simulation, it follows that in the case of the velocity

contrast 40–80 % of the target inhomogeneity relatively to the reference medium,

the recovery error can be 40–50 %. In the cases of the symmetric target objects the

satisfactory result can be obtained using three or even two source-receiver pairs.

Let us consider the results of the numerical simulation of the recovery of pertur-

368 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

bation of an electrical conductivity using a nonstationary wave ﬁeld. The algorithm

of the recovery in this case is very close to considered above algorithm. The ex-

pression for the tomographic functional p

, which is connected with a scattering

by the perturbation of the electrical conductivity σ, has a form of the tomographic

functional, which is connected with the perturbation of the mass density (see an ex-

pression (10.19)). The tomographic functional p

is expressed through the electric

intensities E

out

and E

= E

out

⊗

∂

∂t

Let us note, that the tomographic functional p

, which is connected with the pertur-

bation of the electric permittivity ε accurate within the name of variables coincide

the mentioned above tomographic functional for the mass density:

= E

out

⊗

∂

∂t

With the help of the tomographic functional, the integral equation For the de-

sired perturbation of the electric permittivity δσ can be written as

δE =

δσp

dx, (11.75)

where δE is the diﬀerence ﬁeld. In Fig. 11.8 it is represented the result of recovery

of the inhomogeneity with a simple shape. The inhomogeneity size is equal approx-

imately the wavelength in the reference medium with ε =10. The inhomogeneity

Fig. 11.8 The recovery of the electrical conductivity.

is determined by the function (11.71) with a maximum quantity of the electrical

conductivity 10

−3

S/m. Sounding is implemented by the signal with apparent fre-

quency 5 · 10

Hz. The observation scheme is similar the considered above scheme

Tomography methods of recovering the image of medium 369

of the elastic case. The distance between the inhomogeneity and the observation

line is equal to 10 λ (λ=20 m). The system of linear equations (11.70) is solved at

zero values of the regularizing coeﬃcients α

and α

As in the case of the elastic medium, the recovery error is approximately equal

to the value of the maximum contrast of inhomogeneity relatively to the reference

medium.

This page intentionally left blankThis page intentionally left blank

Chapter 12

Methods of transforms and analysis of the

geophysical data

12.1 Fourier Transform

12.1.1 Fourier series

If the integral

T/2

−T/2

|f(τ)|dτ (12.1)

exists, the real function f (t) in the interval −T/2 < t < T/2 generates the Fourier

series, which is inﬁnite trigonometric series

∞

n=1

cos nω

t + b

sin nω

t) ≡

+∞

n=−∞

exp{inω

t}, (12.2)

where ω

= 2π/T ,

T/2

−T/2

f(τ) cos nω

τdτ, b

T/2

−T/2

f(τ) sin nω

τdτ,

= c

− ib

) =

T/2

−T/2

f(τ) exp{nω

τ}dτ. (12.3)

If the Fourier series is created for the interval (a, a + T ), then the integration in

(12.3) should be implemented between a and a + T .

If the integral

T/2

−T/2

[f(τ)]

dτ,

exists, then the mean square error

T/2

−T/2

[f(τ) −P

(τ)]

dτ,

371

372 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

where

(t) =

n=1

(α

cos nω

t + β

sin nω

is an arbitrary trigonometric polynomial, which for every n has a minimum value,

if it is a partial sum

(t) =

n=1

cos nω

t + b

sin nω

of the Fourier series of the function f(t). The coeﬃcients a

and b

are calculated

by the formula (12.3).

If the trigonometric series (12.2) converges uniformly to f(t) inside interval

(−T/2, T/2), then its coeﬃcients are the Fourier coeﬃcients (12.3) of the function

f(t) with the necessity.

The real coeﬃcients a

, b

and complex coeﬃcients c

are connected by the

formulas

= c

+ c

−n

, b

= i(c

− c

−n

− ib

), c

+ ib

) (n = 0, 1, 2 . . . ), (12.4)

where b

= 0. Fourier series (12.3) for the even function or the odd function f(t)

reduces to the sine Fourier series or cosine Fourier series correspondingly.

The necessary conditions for the expansion of the function f(t) in the Fourier

series consist in the absolute convergence and the constrained variation of f(t) (12.1)

(a ﬁnite interval contains a ﬁnite number of extremum points). Last condition is

always applied in practice.

12.1.2 Fourier integral

Let us show transformation of the Fourier series to Fourier integral in the case of

T → ∞. Substituting the expression (12.3) to the right hand side of equalities

(12.4), we obtain

f(t) =

∞

n=−∞







T/2

−T/2

f(t) exp{−inωt}dt







exp{inω

t}(1/T ).

If T tends to the inﬁnity, then 1/T tends to zero, hence

1/T → dν

= dω

/2π.

The diﬀerence between neighboring harmonics nω

and (n+1)ω

becomes inﬁnitely

small, i.e. nω

transforms to continuous variable ω. So, the discrete spectrum nω

which is connected with the Fourier series, transforms to the continuous spectrum.