Тронин А.В. Решение контрольных и самостоятельных работ по геометрии за 10 класс

124

С-3.

1.

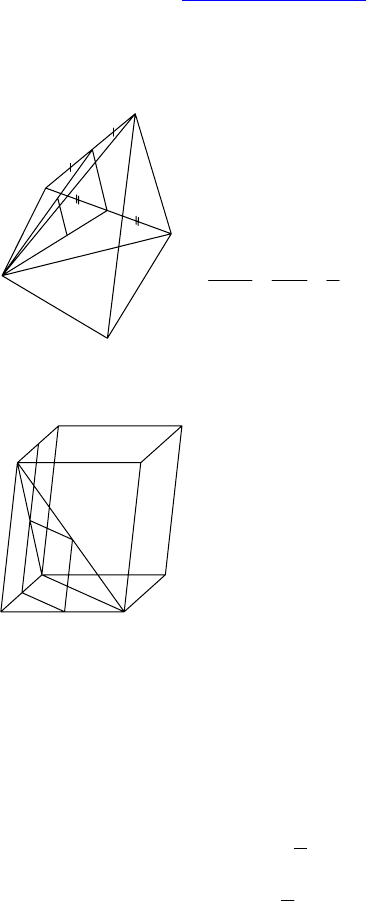
Дано: M

1

и M — точки пересечения ме-

диан ∆AHB и ∆ABC.

Найти: параллельны ли AHC и MM

1

.

Решение:

Проведем в ∆AHB и ∆ABC медианы AK и

AL соответственно.

1

2

1

==

ML

AM

KM

AM

.

Значит, MM

1

|| KL. А KL — средняя ли-

ния ∆BHC. Значит, KL || HC.

Значит, MM

1

|| HC. Значит, MM

1

|| (AHC).

Ответ: параллельна.

2.

Дано: ABCD — параллелограмм,

AA

1

=BB

1

=CC

1

=DD

1

, AA

1

||BB

1

||CC

1

|| DD

1

,

K, M, P — середины AB, A

1

B, AD соот-

ветственно, AA

1

= 20, BD = 40,

∠(BD, CC

1

) = 90°.

1) Построить: линии пересечения плос-

кости MKP с плоскостями AA

1

B, BA

1

D,

AA

1

D

1

и ABC.

2) Найти: площадь четырехугольника, образованного построен-

ными линиями.

Решение:

1) Пусть N — середина A

1

B

1

. Значит, (MKP) ∩ (AA

1

B) = KN.

Пусть L — середина A

1

D. (PL || MK). Значит, (MKP) ∩ (A

1

BD) = ML.

(MKP) ∩ (AA

1

D) = PL.

(MKP) ∩ (ABC) = KP.

2) MK || PL и ML || KP ⇒ MLPK — параллелограмм.

KM — средняя линия ∆AA

1

B. KM =

2

1

AA

1

= 10.

KP — средняя линия ∆ABD. KP =

2

1

BD = 20.

Т к. BD ⊥ CC

1

и KP || BD. Значит, KP ⊥ CC

1

.

Т к. KM || CC

1

, то KP ⊥ KM. Значит, KMLP — прямоугольник.

S

сеч

= KM ⋅ KP = 10 ⋅ 20 = 200.

Ответ: 200.

A

B

C

D

M

H

K

L

A

B

C

D

A

1

B

1

C

1

D

1

P

M

K

L

N

http://alexbooks.ucoz.com

125

С-4.

1.

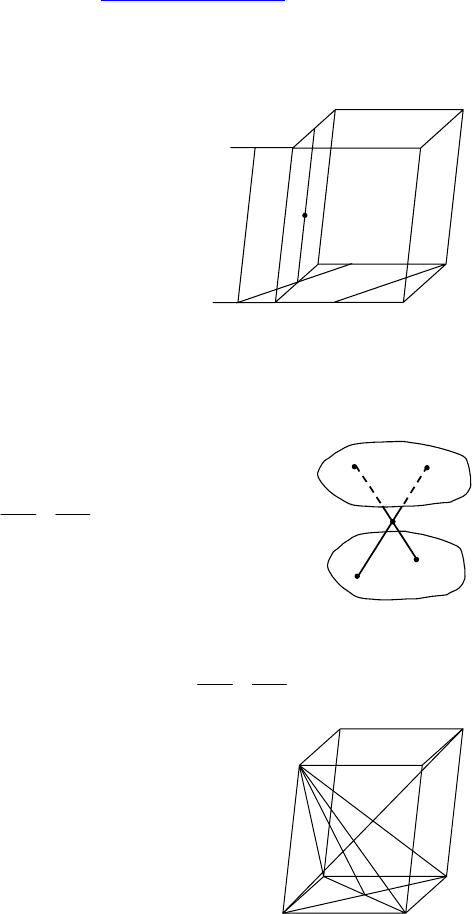
Дано: AA

1

|| BB

1

|| CC

1

|| DD

1

,

AA

1

=BB

1

=CC

1

= DD

1

, M ∈ AA

1

B

1

.

Через точку M проведена плос-

кость, параллельная CC

1

E.

Построить: линию пересечения

этой плоскости с AA

1

D

1

.

Построение:

Проведем через точку M пря-

мую, параллельную AA

1

.

Пусть она пересекает AB и A

1

B

1

в точках S и S

1

соответственно.

Проведем через точку S прямую SK, параллельную CE, K ∈ пря-

мой AD. Через точку K проведем прямую KK

1

, параллельную AA

1

.

KK

1

∩ A

1

D

1

= K.

KK

1

— искомая прямая.

2.

Дано: α || β, AB ∩ CD=M; A, C ∈ α, D, B ∈ β.

Доказать:

MD

CM

MB

AM

=

.

Доказательство:

AC || β; DB || α.

Т к. AC и DB лежат в одной плоскости,

то AC || DB.

Значит, ∠CAM = ∠MBD и ∠ACM = ∠MDB.

Значит, ∆ACM ∼ ∆BDM. Значит,

MD

CM

MB

AM

=

. Ч.т.д.

С-5.

1.

Дано: ABCDA

1

B

1

C

1

D

1

— параллелепипед.

Доказать: AC

1

проходит через точку

пересечения медиан ∆BDA

1

.

Доказательство:

(BDA

1

) ∩ (AA

1

C

1

) = A

1

O, где O — точка

пересечения диагоналей ABCD.

AC

1

∩ A

1

O = M; (AC

1

∩ (A

1

DB)) = M.

Пусть (A

1

C ∩ AC

1

) = K. Тогда AK и A

1

O — медианы ∆AA

1

C.

Значит, A

1

M : MO = 2 : 1.

Значит, M — точка пересечения медиан ∆A

1

BD. Ч.т.д.

A

B

C

D

A

1

B

1

C

1

D

1

E

M

S

1

K

1

K

A

B

β

α

D

C

M

A

B

C

D

A

1

B

1

C

1

D

1

O

M

K

http://alexbooks.ucoz.com

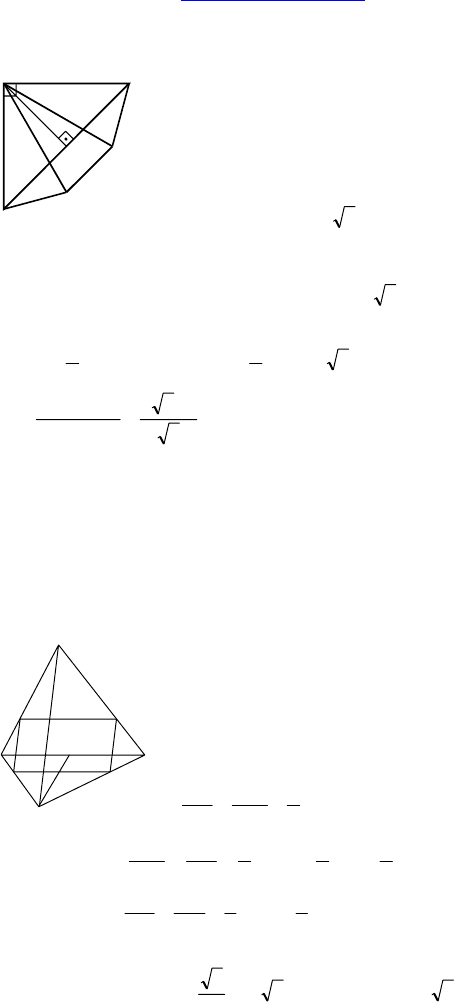
126

2.

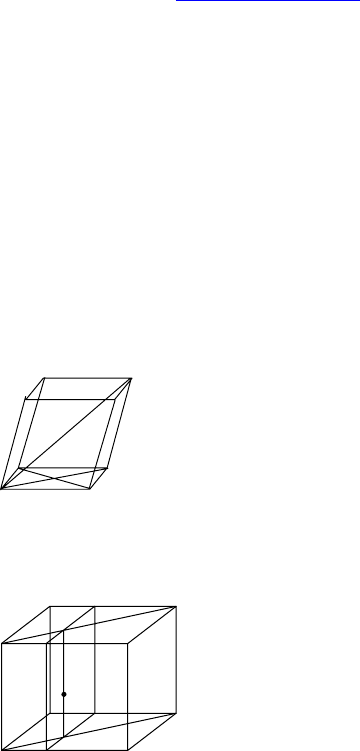
Дано: DABC — тетраэдр, угол при основа-

нии боковых граней равен 70°. Точка начи-

нает двигаться по грани ADC, затем по CDB,

затем по ADB и возвращается в исходное

положение. Наименьший путь, который она

проходит, равен

312 .

Найти: длину бокового ребра.

Решение: Сделаем развертку.

AA

1

— наименьший путь. DH ⊥ AA

1

, AA

1

= 312 .

∠ADA′ = 3 ⋅ (180° – 140°) = 120°.

∠ADH =

2

1

∠ADA′ = 60°. AH =

2

1

AA′ = 36 .

AD =

3

236

sin

⋅

=

∠ADH

AH

= 12 см.

Ответ: 12 см.

С-6.

1. Дано: DABC — тетраэдр, AC = 12, DB = 9, O — точка пересе-

чения медиан ∆ABC, ∠(AC; DB) = 60°.

Построить: сечение тетраэдра плоскостью, проходящей через

точку O параллельно прямым AC и DB.

Найти: S

сеч

Построение:

1) Через т. O проведем прямую KM, парал-

лельную AC.

2) Через точки K и M проведем прямые KL

и MN, параллельные BD.

3) KLNM — искомое сечение.

1

2

1

==

OB

BO

KA

BK

.

∆BKM ∼ ∆BAC;

3

2

==

AB

BK

AC

KM

; KM =

3

2

AC =

3

2

⋅ 12 = 8.

∆AKL ∼ ∆ABD;

3

1

==

AB

AK

BD

KL

; KL =

3

1

BD = 3.

Т к. KL || BD и KM || AC, то ∠LKM = 60°.

S

сеч

= 8 ⋅ 3 ⋅ sin60° = 24 ⋅

2

3

=

312

. Ответ:

312

.

A

B

C

A

′

D

H

B

A

C

D

O

M

K

L

N

B

1

http://alexbooks.ucoz.com

127

2.

B

A

C

D

M

L

O

Y

G

X

J

K

E

P

T

S

I

A

1

B

1

C

1

D

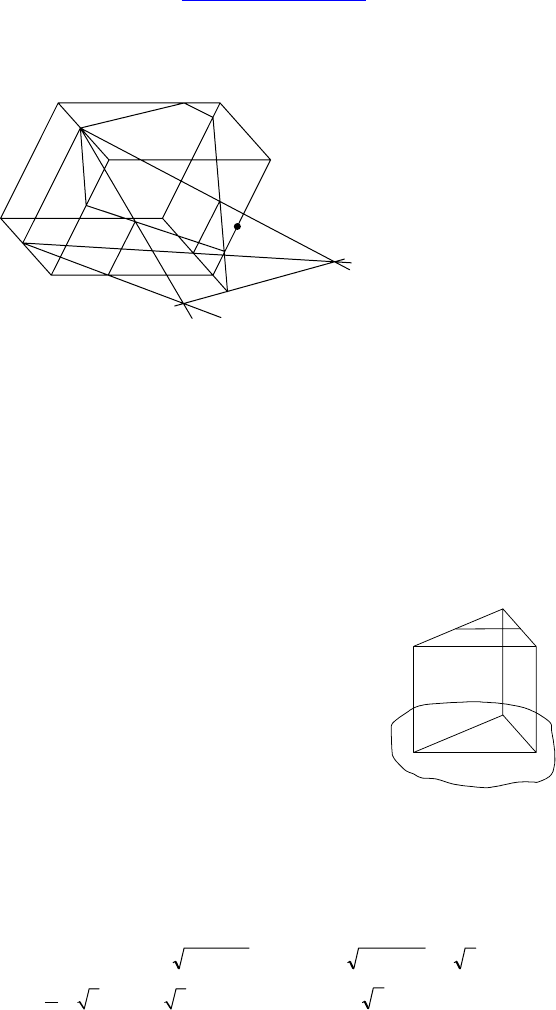
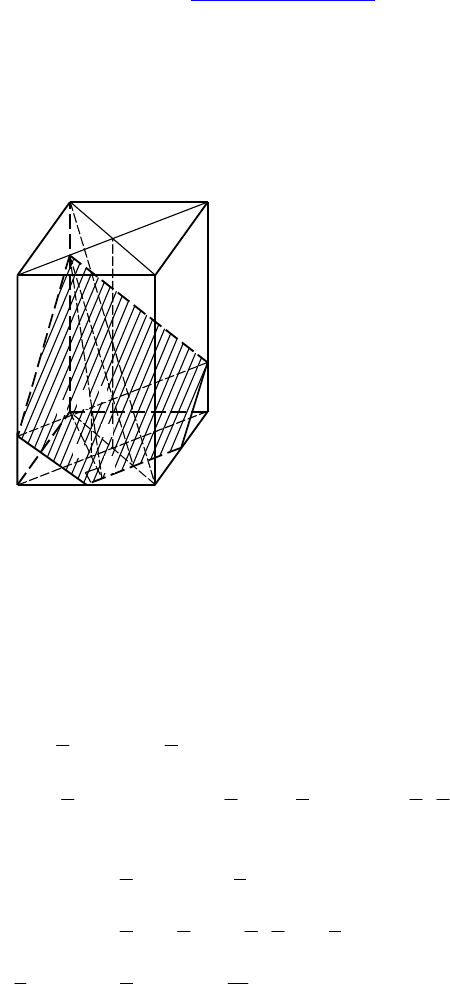
Дано: ABCDA

1

B

1

C

1

D

1

— параллелепипед, T ∈ A

1

B

1

, M ∈ DD

1

,

K ∈ DD

1

C

1

C, E ∈ AA

1

D

1

D.

Построить: сечение плоскостью, параллельной TEK и проходя-

щей через точку M.

Построение: TL || AA

1

, KH || AA

1

, LH ∩ TK = X.

EO || AA

1

, OL ∩ TE = Y. TS || XY, CD ∩ XY = G.

GK ∩ C

1

C = I, GK ∩ D

1

D = J, JE ∩ AA

1

= P. ⇒ TSIJP — сечение

плоскостью TEK.

Чтобы построить искомое сечение, проведите сечение, парал-

лельное построенному, через т. M. На рисунке не изображено,

чтобы не перегружать его.

С-7.

1. Дано: ∆ABC — прямоугольный, MN —

средняя линия ∆ABC,

α || MN, AA

1

⊥ α, BB

1

⊥ α, CC

1

⊥ α,

C

1

B

1

= 11 см, C

1

A

1

= 12 см, A

1

B

1

= 19 см.

Найти: S(∆ABC).

Решение: Т.к. MN || AB, то AB || α.

Значит, AB = A

1

B

1

= 19 см.

Проведем через точку C плоскость β (β || α).

β ∩ BB

1

= B

2

; β ∩ AA

1

= A

2

.

CB

2

= C

1

B

1

= 11 см; CA

2

= C

1

A

1

= 12 см; A

2

B

2

= A

1

B

1

= 19 см.

∆CB

2

B и ∆CA

2

A — прямоугольные.

Пусть BB

2

= AA

2

= x. CB

2

= x

2

+ 121, CA

2

= x

2

+ 144,

AB

2

= CA

2

+ CB

2

; x

2

+ 121 + x

2

+ 144 = 361.

Значит, x

2

= 48; CB = 12148 + = 13; CA = 3814448 =+ .

S

ACB

=

1

8 3 13 52 3

2

⋅⋅= см

2

. Ответ: 352 см

2

.

C

1

A

1

B

1

A

B

C

α

N

M

http://alexbooks.ucoz.com

128

2. Дано: α, точки A и B.

Найти: множество точек, принадлежащих α и равноудаленных от

A и B.

Решение: Заметим, что любая точка плоскости, проходящей через

середину AB и перпендикулярно AB, равноудалена от точек A и B,

и никакая другая точка пространства не обладает этим свойством.

Значит, искомым множеством точек будет пересечение этой

пло

ско

сти (обозначим ее за β) с плоскостью α. Т.е. это m, если α

∩ β = m; ∅ если α || β; α, если α = β.

Ответ: m, если α ∩ β = m; ∅ если α || β; α, если α = β.

С-8.

1.

Дано: MPKHM

1

P

1

K

1

H

1

— параллелепипед,

∠M

1

MH + ∠M

1

MP = 180°, все грани ромбы.

Доказать: P

1

H ⊥ MK.

Доказательство:

Очевидно, что все ромбы равны между со-

бой.

Значит, ∠P

1

PM = ∠P

1

PK. Значит, P

1

проецируется на PH.

Т к. PH ⊥ MK, то по ТТП P

1

H ⊥ MK. Ч.т.д.

2.

A

B

C

D

A

1

B

1

C

1

D

1

M

S

K

N

T

P

R

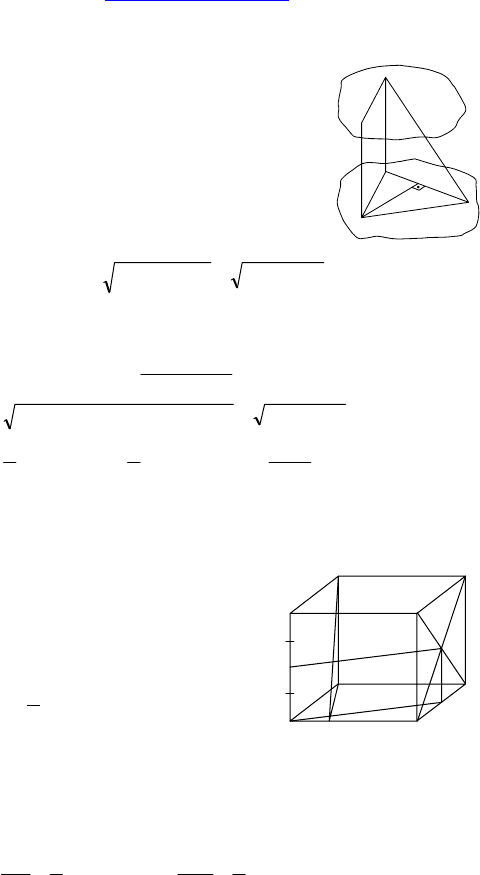
Дано: ABCDA

1

B

1

C

1

D

1

— параллелепипед, все грани —

прямоугольники, M — внутренняя точка грани AA

1

C

1

C.

Построить: сечение параллелепипеда плоскостью, проходящей

через точку M и перпендикулярной BC.

Построение:

1) Через точку M проведем прямую a, a || AA

1

.

a ∩ A

1

C

1

= K, a ∩ AC = N.

2) Через точки K и N проводим прямые b и c, параллельные AB.

b ∩ A

1

D

1

= P, b ∩ B

1

C

1

= R;

c ∩ AD = S, c ∩ BC = T.

(PRTS) — искомое сечение.

H

M

P

K

H

1

M

1

P

1

К

http://alexbooks.ucoz.com

129

С-9.

Дано: α || β; A, C ∈ α; B, D ∈ β; AB ⊥ α;

AB = 20; CD = 25; AC = 14; BD = 13.

Найти: р(AB, CD) — ?

Решение:

Т к. α || β и AB ⊥ α. то AB ⊥ β.

Из точки C проведем отрезок CC

1

, перпенди-

кулярный α.

CC

1

= AB = 20. C

1

D =

222

1

2

2025 −=− CCCD = 15.

Т к. C

1

D — проекция CD на плоскость β,

то р(AB, CD) = р(B, C

1

D) = BH, где BH — высота ∆BC

1

D.

BC

1

= AC = 14. P(BC

1

D) =

2

131514 ++

= 21.

S(BC

1

D) = 86721)1321)(1521)(1421(21 ⋅⋅⋅=−−− = 84.

S(BC

1

D) =

2

1

⋅ BH ⋅ C

1

D =

2

1

⋅ 15BH. BH =

15

284 ⋅

= 11,2.

Ответ: 11,2.

С-10.

1.

Дано: ABCDA

1

B

1

C

1

D

1

— прямоуголь-

ный параллелепипед, K — середина

AA

1

, L — точка пересечения диагона-

лей грани DD

1

C

1

C, E ∈ AD, AD = 4,

CD = 2, AE =

2

1

.

Доказать: B

1

E ⊥ KL.

Доказательство:

Пусть LL

1

⊥ CD. L

1

— середина CD.

AL

1

— проекция KL на (ABC), параллельная KL.

BE — проекция B

1

E.

tg∠ABE =

4

1

=

AB

AE

. tg∠DAL

1

=

4

1

=

AD

DL

.

∆ADL

1

∼ ∆BAE, т.к. ∠ABE = ∠DAL

1

.

Пусть AL

1

∩ BE = O.

∆AOE ∼ ∆BAE, т к. ∠OAE = ∠ABE и ∠OEA = ∠AEB.

Значит, ∠AOE = 90°.

Значит, BE ⊥ AL

1

⇒ B

1

E ⊥ KL. Ч.т.д.

B

D

C

1

β

H

A

α

A

B

C

D

A

1

B

1

C

1

D

1

L

1

O

E

K

http://alexbooks.ucoz.com

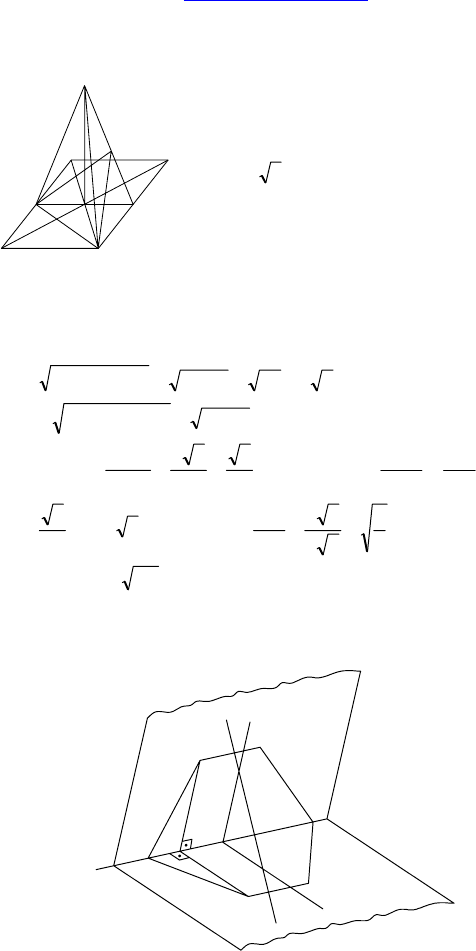
130

2.

Дано: ABCD — квадрат, O — точка пере-

сечения его диагоналей,

MO ⊥ ABC, F — середина AB, AB = 4.

MO =

32 .

Найти: ∠(FD, (DMC)) — ?

Решение:

M

1

— середина CD. DC ⊥ FM

1

;

DC ⊥ MM

1

(MM

1

— медиана и высота в равнобедренном ∆DMC).

Значит, DC ⊥ (FMM

1

). FH ⊥ MM

1

; т.к. DC ⊥ (FMM

1

), то DC ⊥ FH.

Значит, FH ⊥ (DMC).

Значит, ∠(DF, (DMC)) = ∠FDH. ∠FHD = 90°.

FD =

5220416

22

==+=+ AFAD .

MM

1

= 4124

22

1

=+=+ MOOM .

sin∠MM

1

O =

2

3

4

32

1

==

MM

MO

. sin∠MM

1

O =

4

1

FH

FM

FH

=

.

FH =

324

2

3

=⋅ . sin∠FDH =

5

3

52

32

==

FD

FH

.

∠FDH = arcsin

6,0 ≈ 50°46′. Ответ: ≈50°46′.

С-11.

1.

E

B

C

D

m

O

A

F

a

l

Y

X

Дано: ABCD, ADEF — равнобедренные трапеции, a ⊥ AD, a ∩ β = X.

Построить: a ∩ α = ?

O

B

C

D

H

M

A

M

1

F

http://alexbooks.ucoz.com

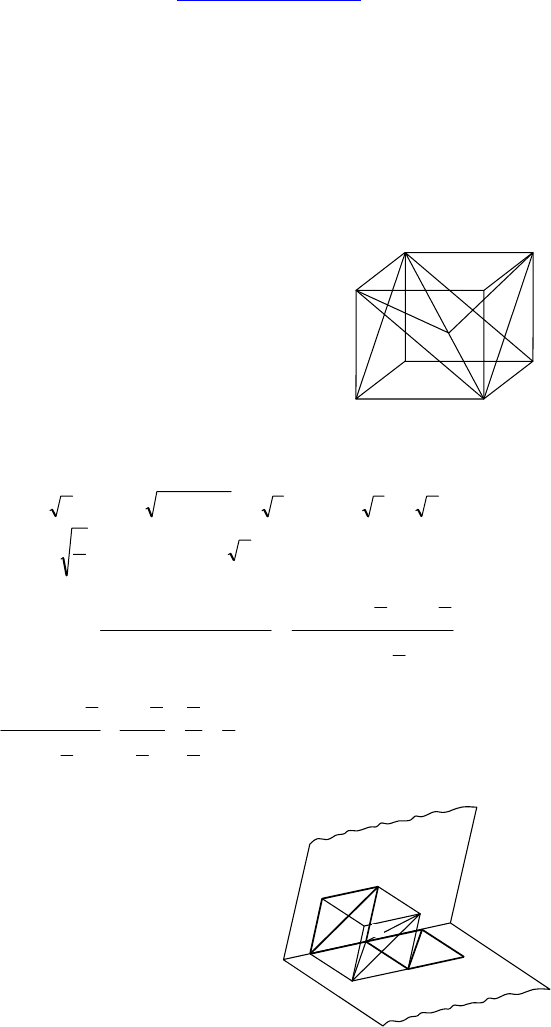
131

Построение: Через точку X проведем прямую m, параллельную

высоте трапеции ADEF. m ∩ AD = O.

Через точку O проведем прямую l, параллельную высоте трапе-

ции ABCD.

AD перпендикулярна плоскости, проходящей через прямые l и m.

Т к. AD ⊥ a и X лежит в плоскости, проходящей через l и m, то

если a ∩ l = Y, то Y — искомая то

ч

ка.

2.

Дано: ABCDA

1

B

1

C

1

D

1

— параллелепи-

пед, у которого все грани квадраты.

Найти: величину двугранного угла,

образованного сечениями AB

1

C

1

D и

CB

1

A

1

D.

Решение:

B

1

D — ребро двугранного угла.

∆A

1

B

1

D = ∆C

1

B

1

D. A

1

H и C

1

H — высоты.

∠A

1

HC

1

— линейный угол двугранного угла.

Пусть ребро — a.

A

1

D = 2a . B

1

D = 32

22

aaa =+ . A

1

H ⋅ 3a = 2a ⋅ a.

A

1

H =

3

2

⋅a

= C

1

H. A

1

C

1

= 2a .

cos∠A

1

HC

1

=

11

2

1

2

1

2

11

2 HCHA

HCHACA

⋅

−−

=

3

2

3

2

3

2

222

⋅⋅

⋅−⋅−

a

aaa

=

3

4

3

4

2

22

⋅

⋅−

a

aa

=

3

4

3

4

2 −

=

3

4

3

2

=

2

1

. ∠A

1

HC

1

= 120°. Ответ: 120°.

С-12.

1.

Дано: α ⊥ β, ABCD ∈ α,

CEFK ∈ β, ABCD = CEFK.

Найти: ∠(BD, EK) — ?

Решение:

Построим квадрат DCKM как

показано на рисунке.

CM || EK.

A

B

C

D

A

1

B

1

C

1

D

1

H

E

B

D

T

β

A

M

K

α

P

F

C

http://alexbooks.ucoz.com

132

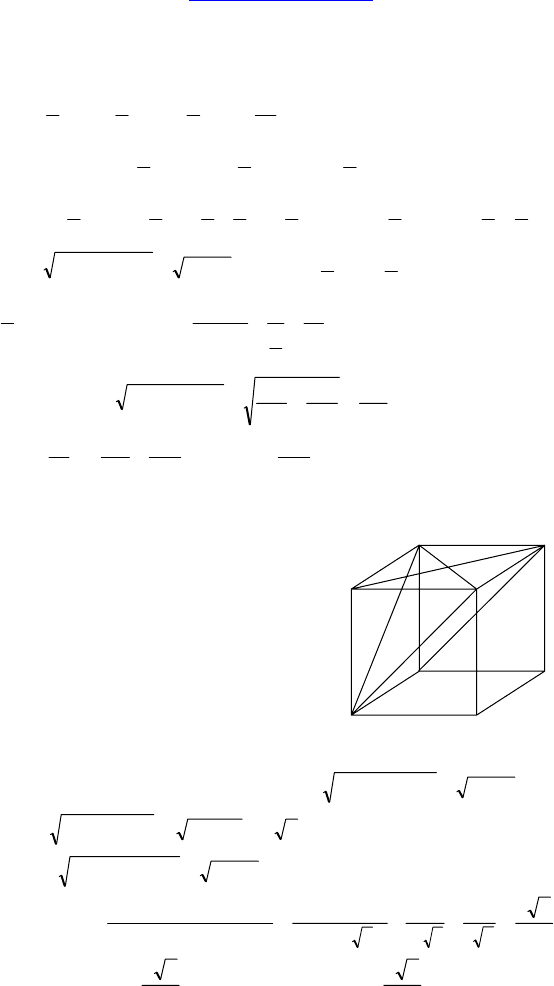
Построим куб на квадрате DCKM.

MT || DB.

∆MTC — равносторонний ⇒ ∠CMT = 60°.

Т к. CM || EK и MT || DB, то ∠(BD, EK) = ∠(MT, CM) = 60°.

Ответ: 60°.

2.

Дано: ABCDA

1

B

1

C

1

D

1

— параллеле-

пипед (основание — прямоуголь-

ник), AD = 4, CD = 3, CC

1

= 14, E —

середина AD, F — середина DC.

Построить: сечение, проходящее

через точки E, F, параллельное B

1

D.

Найти: S

сеч

.

Построение:

1) Проведем EF.

2) EF ∩ BD = N.

3) В плоскости BB

1

D проведем пря-

мую MN, параллельную B

1

D.

MN ∩ BB

1

= M.

4) MN ∩ OO

1

= S

(OO

1

— прямая, проведенная через точки пересечения диагона-

лей граней ABCD и A

1

B

1

C

1

D

1

).

5) Через точку S проведем прямую KL, параллельную AC.

6) KL ∩ AA

1

= K; KL ∩ CC

1

= L.

7) MKEFL — искомое сечение.

Решение:

Построим BP ⊥ EF. MP ⊥ EF и MP ⊥ KL; MP ∩ KL = Q.

S

сеч

= S

KML

+ S

EKLF

.

S

KML

=

2

1

KL ⋅ QM =

2

1

AC ⋅ QM.

S

EKLF

=

2

1

(KL + EF) ⋅ QP =

⎟

⎠

⎞

⎜

⎝

⎛

+ ACAC

2

1

2

1

⋅ QP =

2

1

⋅

2

3

AC ⋅ QP.

Прямоугольные ∆MPB и ∆QPT подобны.

Значит, MQ =

3

2

MP и QP =

3

1

MP.

Значит, S

сеч

=

2

1

AC ⋅

3

2

MP +

2

1

⋅

2

3

AC ⋅

3

1

MP =

=

3

1

AC ⋅ MP +

4

1

AC ⋅ MP =

12

7

AC ⋅ MP.

A

D

B

1

C

1

D

1

K

F

E

M

L

A

1

C

N

O

1

T

B

O

P

Q

S

http://alexbooks.ucoz.com

133

∆B

1

BD ∼ ∆MBN.

MB =

4

3

BB

1

=

4

3

CC

1

=

4

3

⋅ 14 =

2

21

.

S

BEF

= AB ⋅ AD –

2

1

AB ⋅ AE –

2

1

ED ⋅ DF –

2

1

BC ⋅ CF =

= 3 ⋅ 4 –

2

1

⋅ 3 ⋅ 2 –

2

1

⋅ 2 ⋅

2

3

–

2

1

⋅ 4 ⋅

2

3

= 12 – 3 –

2

3

– 3 = 6 –

2

3

=

2

9

.

AC =

916

22

+=+ CDAD

= 5. EF =

2

1

AC =

2

5

.

2

1

EF ⋅ BP = S

BEF

. BP =

5

18

2

5

9

2

==

EF

S

BEF

.

Значит, MP =

10

111

25

324

4

441

22

=+=+ BPMB .

S

сеч

=

8

259

10

111

5

12

7

=⋅⋅

. Ответ:

8

259

.

С-13.

1.

Дано: ABCA

1

B

1

C

1

— прямая призма,

∆ABC — прямоугольный (∠C = 90°),

AC = 4, BC = 3, B

1

B = 4.

Найти: ∠(AC

1

, B

1

C) — ?

Решение:

Достроим до прямого параллелепи-

педа ACBDA

1

C

1

B

1

D

1

.

Основание — прямоугольник ACBD.

AD

1

|| CB

1

.

Значит, ∠(AC

1

; B

1

C) = ∠D

1

AC

1

. AD

1

= 916

2

11

2

1

+=+ DAAA = 5.

AC

1

= 241616

2

1

2

=+=+ CCAC .

D

1

C

1

= 169

2

11

2

11

+=+ CADA = 5.

cos∠D

1

AC

1

=

11

2

1

2

1

2

11

2 ACAD

ACADCD

⋅

++−

=

2452

322525

⋅⋅

++−

=

240

32

=

25

4

=

5

22

.

∠D

1

AC

1

= arccos

5

22

≈ 55°33′. Ответ: arccos

5

22

≈ 55°33′.

A

C

B

D

A

1

C

1

B

1

D

1

http://alexbooks.ucoz.com

Тронин А.В. Решение контрольных и самостоятельных работ по геометрии за 10 класс

Подождите немного. Документ загружается.