Тронин А.В. Решение контрольных и самостоятельных работ по геометрии за 10 класс
Подождите немного. Документ загружается.

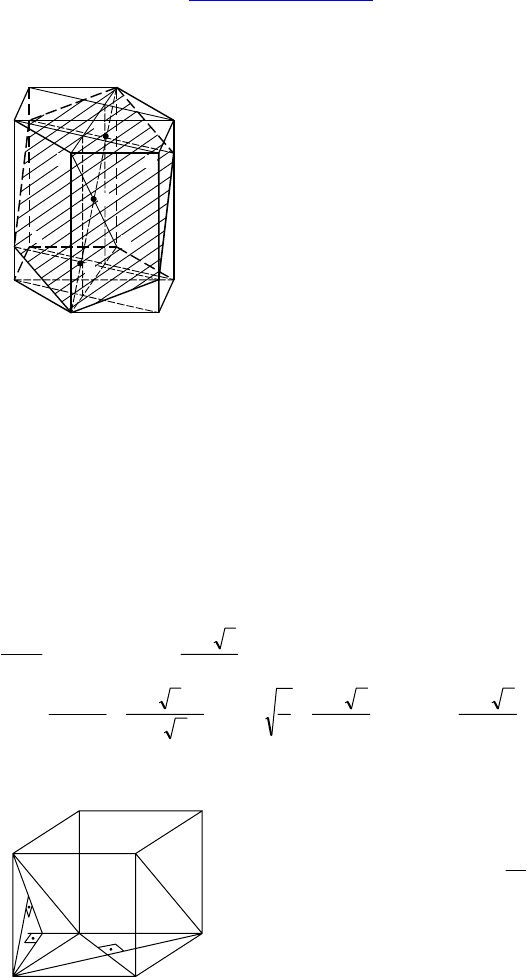
134
2.
Дано: ABCDEFA
1
B
1
C
1
D
1
E
1
F
1
— правиль-
ная призма, a — сторона основания,
2a — боковое ребро, O — середина F
1
C.
Построить: через O перпендикулярно
F
1
C сечение.
Найти: площадь сечения.
Построение:
Т.к. ABCDEF — правильный шести-
угольник, то FC = 2a.
Значит, FF
1
C
1
C — квадрат.
Значит, F
1
C ⊥ FC
1
.
Пусть L — точка пересечения FC
1
и прямой, проведенной через
точку пересечения AE и FC параллельно FF
1
.
Через точку L проведем прямую PQ параллельно AE.
PQ ∩ AA
1
= P; PQ ∩ EE
1
= Q.
Пусть K — точка пересечения FC
1
и прямой, проведенной через
точку пересечения F
1
C
1
и B
1
D
1
параллельно CC
1
.
Через точку K проведем прямую MT параллельно B
1
D
1
.
MT ∩ BB
1
= M, MT ∩ DD
1
= T.
MC
1
TQFP — искомое сечение.
(F
1
C ⊥ FC
1
; F
1
C ⊥ AE, а т.к. PQ || AE, то F
1
C ⊥ PQ)
Угол между плоскостью сечения и плоскостью основания —
∠C
1
FC = 45°.
сеч
осн
S
S
= cos45°. S
осн
=
2
33
2
a
.
S
сеч
=
°45cos
осн
S
=
22
233
2
⋅
⋅
a
= 3a
2
⋅
2
3
=
2
63
2
a
. Ответ:
2
63
2
a
.
С-14.
Дано: ABCDA
1
B
1
C
1
D
1
— прямой па-
раллелепипед, ABCD — ромб, ∠BAD
= 60°, AA
1
= 4 см, р(AD, D
1
C) =
5
12
см.
Найти: S
п п
— ?
Решение:
р(AD, D
1
C) = р(AD, (A
1
D
1
CB)).
AM ⊥ BC, AK ⊥ A
1
M, BC ⊥ AA
1
и
BC ⊥ AM, значит, BC ⊥ (AA
1
M).
A
P
D
A
1
B
1
C
1
D
1
M
F
E
T
F
1
C
B
L
O
E
K
Q
A
B
C
D
A
1
B
1
C
1
D
1
M
K
http://alexbooks.ucoz.com
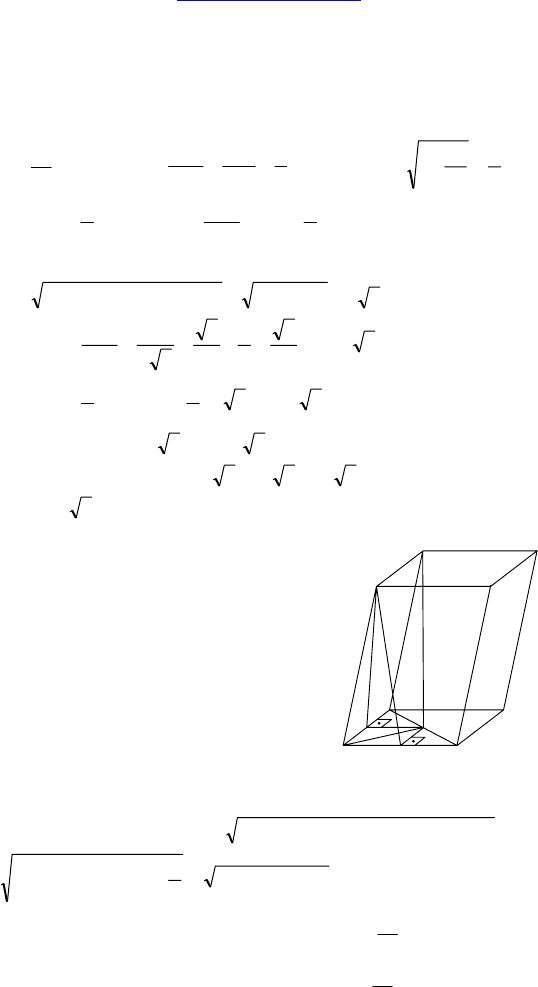
135
Т к. AK ∈ (AA
1
M), то AK ⊥ BC.
Т к. AK ⊥ A
1
M, то AK ⊥ (BA
1
D
1
).
Длина AK — расстояние между AD, D
1
C.
AK =
5
12
. sin∠KA
1
A =
5
3
45
12
1
=
⋅
=
AA
AK
. cos∠KA
1
A =
5
4
25
9
1 =−
.
tg∠KA
1
A =
4
3
. tg∠KA
1
A =
1
AA
AM
; AM =
4
3
⋅ 4 = 3.
Пусть сторона ромба a. Т.к. ∠BAD = 60°, то BD = a.
AC =
32120cos2
22222
aaaaaa =+=°−+
. ∠BCA = 30°.
sin∠BCA =
a
a
AC
AM
3
3
3
==
.
a
3
2
1
=
; a = 32 см; AC = 6 см.
S(ABCD) =
2
1
BD ⋅ AC =
2
1
⋅
32
⋅ 6 =
36
см
2
.
S
б п
= 4a ⋅ AA
1
= 4 ⋅ 32 ⋅ 4 = 332 см
2
.
S
п п
= S
б п
+ 2S(ABCD) = 332 + 312 = 344 см
2
.
Ответ:
344
см
2
.
С-15.
1.
Дано: ABCDA
1
B
1
C
1
D
1
— наклонный
параллелепипед, ABCD — параллело-
грамм, AD = 15, BD = 7, ∠BDA = 60°,
∠A
1
AD = ∠A
1
AB < 90°, ∠(A
1
D; (ABC))
= 45°, A
1
проектируется на BO.
Найти: S
б п
.
Решение:
Пусть A
1
K — высота параллелепипеда. K ∈ BD.
Т к. ∠A
1
AD = ∠A
1
AB, то AK — биссектриса ∆ABD.
По теореме косинусов AB =
°⋅⋅−+ 60cos2
22
BDADBDAD =
=
2
1
715249225 ⋅⋅⋅−+
= 10549225 −+ = 13.
По свойству биссектрисы треугольника KD =
4
15
.
∠(A
1
D; (ABC)) = ∠A
1
DK = 45°. Значит, A
1
K =
4
15
; KF ⊥ AD.
A
B
C
D
A
1
B
1
C
1
D
1
N
K
F
http://alexbooks.ucoz.com
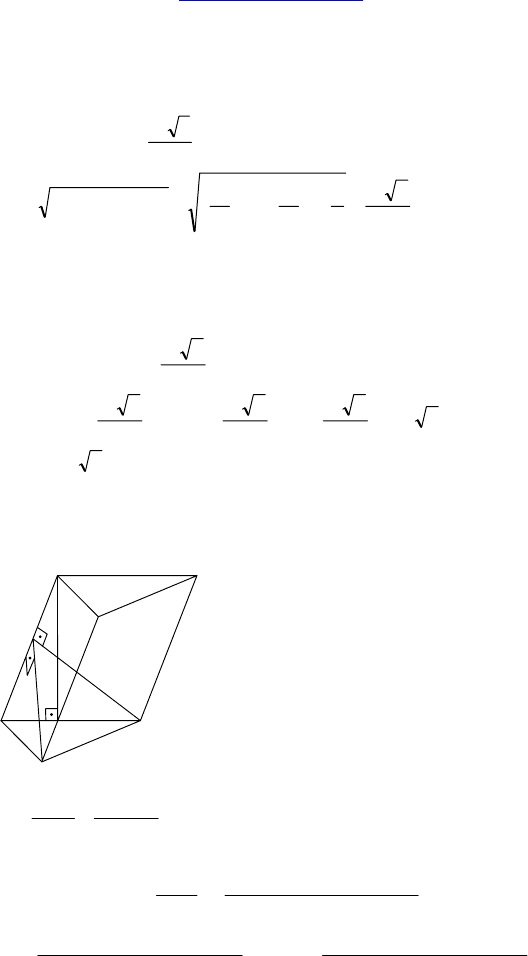
136
Т к. A
1
K ⊥ (ABC), KF ⊥ AD ⇒ по ТТП A
1
F ⊥ AD.
Значит, A
1
F — высота грани AA
1
D
1
D.
KF = KD ⋅ sin60° =
8
315
.
A
1
F =
8
715
4
3
4
15
4
15
)(
22
22
1
=⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=+ KFKA
.
KN ⊥ AB. AB ⊥ (A
1
KN) ⇒ A
1
N ⊥ AB.
∆ANK = ∆AFK (по гипотенузе и острому углу).
Значит, NK = KF.
Значит, ∆A
1
KN = ∆A
1
KF (по двум катетам).
Значит, A
1
N = A
1
F =
8
715
.
S
б п
= 2 ⋅ 15 ⋅
8
715
+ 2 ⋅ 13 ⋅
8
715
= 56 ⋅
8
715
= 7105 .
Ответ:
7105 .
2. Дано: ABCDA
1
B
1
C
1
D
1
— наклонная призма, ∆ABC — прямо-
угольный, ∠C = 90°, B
1
проектируется на середину BC, AA
1
= l,
∠(AA
1
; (ABC)) = ϕ, двугранный угол с ребром BB
1
равен α.
Найти: S
б п
— ?
Решение:
Пусть H — середина BC, B
1
H — вы-
сота призмы, ∠B
1
BC = ϕ.
По ТТП BB
1
⊥ AC. CF ⊥ BB
1
,
BB
1
⊥ (ACF), ∠ACF = 90°.
Из ∆BB
1
H: BH = l ⋅ cosϕ. BC = 2lcosϕ.
Из ∆FBC: FC = BC ⋅ sinϕ =
= 2lsinϕcosϕ = lsin2ϕ.
Из ∆ACF: AC = FC ⋅ tgα = lsin2ϕ ⋅ tgα.
AF =
sin 2
cos cos
FC l ⋅
ϕ
=
αα
.
Периметр перпендикулярного сечения равен:
P = lsin2ϕ
⎟
⎠
⎞
⎜
⎝
⎛
α
+α+
cos
1
tg1
=
α
α+α+ϕ
cos
)sincos1(2sinl
.
S
б п
=
α
α+α+ϕ
cos
)sincos1(2sin
2
l
. Ответ:
α
α+α+ϕ
cos
)sincos1(2sin
2
l
.
A
F
B
A
1
B
1
C
1
H
C
http://alexbooks.ucoz.com
137
С-16.
1.
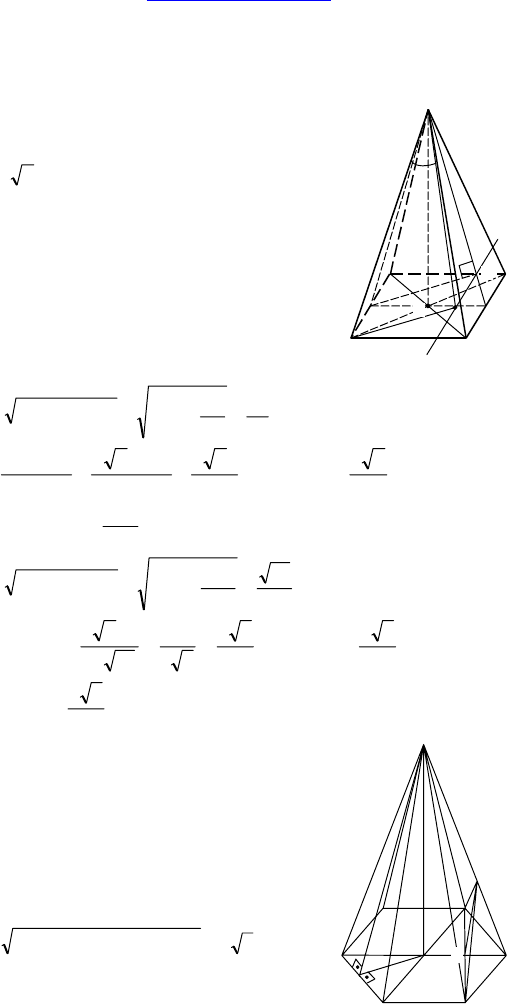
Дано: MABCD — правильная четырех-
угольная пирамида, a — сторона основа-
ния,
2a — высота.
Найти: ∠(MA; (DMC)) — ?
Решение: MO — высота пирамиды.
Пусть E — середина AB.
EK ⊥ (CMD) (EK ⊥ MF, EK ⊥ CD).
(ABK) пересекает плоскость (CMD) по
прямой параллельно AB;
AP || EK; т.к. EK ⊥ (CMD), то AP ⊥ (CMD).
Значит, ∠(MA; (DMC)) = ∠AMP.
MF =
2
3
4
2
2
222
aa
aOFMO =+=+
, MO ⋅ EF = EK ⋅ MF.
EK =
3
22
3
22
a
a
aa
MF
EFMO
=
⋅⋅
=
⋅
. AP = EK =
a
3
22
.
Из ∆AMP: sinα =
AM
AP
.
AM =
a
a
aAOMO
2
10
4
2
2
2
222
=+=+ .
Значит, sinα =
15
54
53
4
103
222
==
⋅
⋅
. α = arcsin
15
54
≈ 36°36′.
Ответ: arcsin
15
54
≈ 36°36′.
2.
Дано: SABCDEF — правильная пирами-
да, a — сторона основания, угол между
смежными боковыми гранями — ϕ.
Найти: S
б п
— ?
Решение:
CM ⊥ SD; EM ⊥ SD; ∠CME = α;
∠CDE = 120°.
CE =
3120cos2
222
aaaa =°⋅−+ .
NM ⊥ SD; ∆NMD ∼ ∆SOD.
A
C
B
E
P
F
M
D
O
α
K
A
C
B
S
N
M
D
E
F
L
O
http://alexbooks.ucoz.com
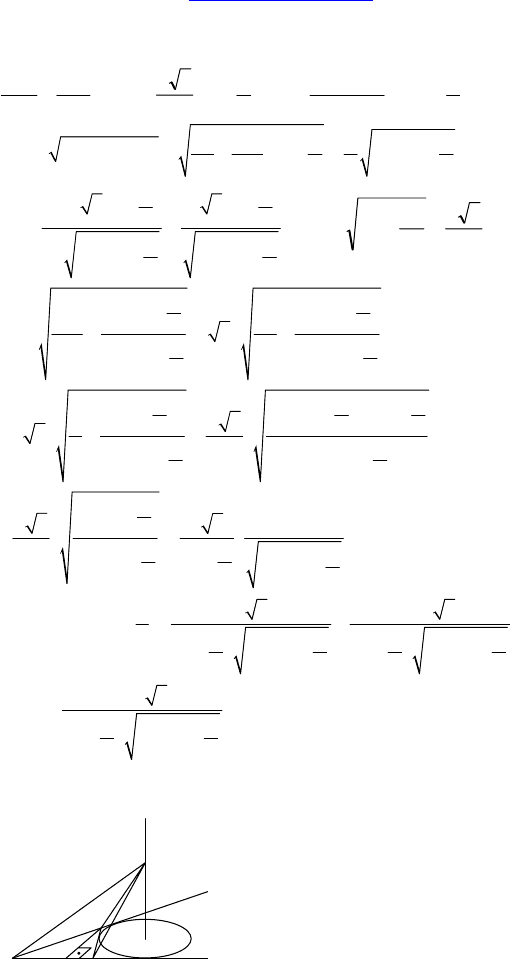
138
MD
OD
NM
SO
=
; NM =
2
3a
⋅ ctg
2
ϕ
; SO =
MD
ODNM ⋅
; ND =
2
a
.
MD =
22
22 2
3
ctg
44 2
aa
ND NM
ϕ
−=−⋅
=
2
13ctg
22
a
ϕ
− .
SO =
2
2
23ctg
2
213ctg
2
a
a
ϕ
⋅
ϕ
−
=
2
3ctg
2
13ctg
2
a
ϕ
⋅
ϕ
−
. LO =
4
2
2
a
a −
=
2
3a
.
SL =
22
2
2
3ctg
3
2
4
13ctg
2
a
a
ϕ
+
ϕ
−
=
22
2
2
ctg
2
3
4
13ctg
2
a
a
ϕ
⋅+
ϕ
−
=
=
2
2
ctg
1
2
3
4
13ctg
2
a
ϕ
⋅+
ϕ
−
=
22
2
1 3ctg 4ctg
3
22
2
13ctg
2
a
ϕϕ
−+
⋅
ϕ
−
=
=
2
2
1ctg
3
2
2
13ctg
2
a
ϕ
+
⋅
ϕ
−
=
2
31
2sin
13ctg
2
2
a
⋅
ϕ
ϕ
−
.
Значит, S
б п
=
2
13
6
2
2sin 1 3ctg
22
a
a⋅⋅
ϕϕ
⋅−
=
2
2
33
2sin 1 3ctg
22
a
ϕϕ
⋅−
.
Ответ:
2
2
33
2sin 1 3ctg
22
a
ϕϕ
⋅−
.
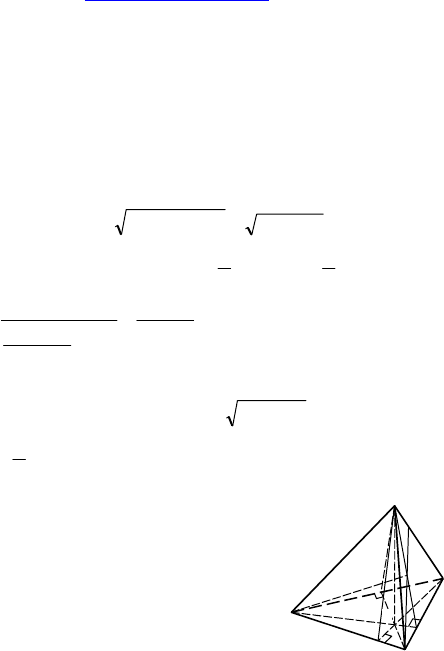
С-17.
1. Дано: MABC — пирамида, ∆ABC —
равнобедренный, AB = AC, BC = 24,
AK = 5, MH = 12, высоты боковых гра-
ней, проведенных из точки M, равны
между собой, ∠MAB ≠ ∠MAC.
Найти: S
б п
.
Решение:
Т к. высоты боковых граней равны, то вершина пирамиды одина-
ково удалена от сторон основания или от прямых, на которых
A
C
B
H
K
M
http://alexbooks.ucoz.com
139
лежат эти основания. В таком случае вершина проектируется ли-
бо в центр вписанной в основание окружности, либо в один из
центров вневписанных окружностей.
Т к. ∠MAB ≠ ∠MAC, то вершина пирамиды может проектиро-
ваться только в центр вневписанных окружностей, которые каса-
ются равных сторон основания.
BK = KC = 12. AB = AC =
14425
22
+=+ BKAK = 13.
P(ABC) = 13 + 13 + 24 = 50. S(ABC) =
2
1
AK ⋅ BC =
2
1
⋅ 5 ⋅ 24 = 60.
Значит, r =
1325
60
2
)(
)(
−
=
− AB
ABCP
ABCS
= 5 — радиус вневписанной
окружности.
Тогда высота боковых граней: h
бок гр
= 2512
2
+ = 13.
Значит, S
б п
=
2
1
P
осн
⋅ h
бок гр
= 25 ⋅ 13 = 325. Ответ: 325.
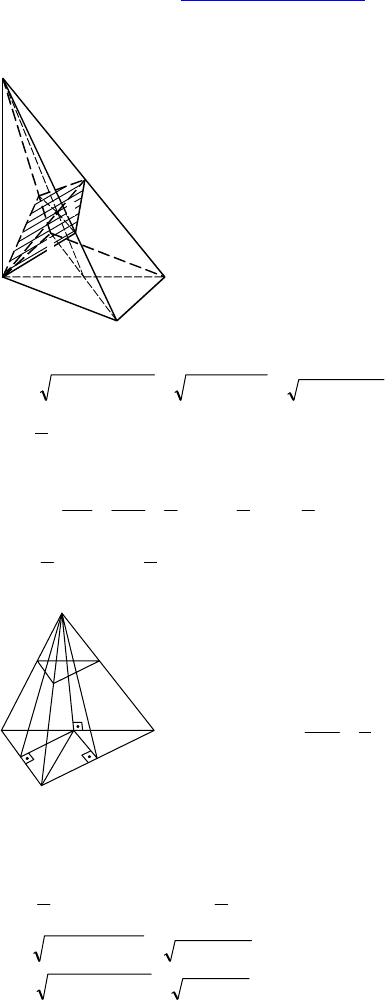
2. Дано: MABC — пирамида, O — точка
пересечения высот ∆ABC, MO — высота
пирамиды.
Доказать: если AK ⊥ (MBC), K ∈ МВС, то
К — точка пересечения высот грани MBC.
Доказательство:
Пусть AK ⊥ ME, покажем, что AK — вы-
сота.
По ТТП ME ⊥ BC. AK ⊥ ME (по построению).
Значит, BC ⊥ (AME). Значи
т,
BC ⊥ AK. Значит, AK ⊥ (MBC).
CK — проекция на плоскость (MBC) наклонной AC.
MO ⊥ AC и BP ⊥ AC. Значит, AC ⊥ (MBP). Значит, AC ⊥ MB.
По ТТП CK ⊥ MB ⇒ CF ⊥ MB.
Значит, K — точка пересечения высот грани MBC. Ч.т.д.
С-18.
1. Дано: MABCD — пирамида, ABCD — ромб, AC = 32 см,
BD = 18 см, грани проходящие через стороны AB и AD основания,
перпендикулярны к плоскости основания, их общее ребро —
24 см, K — середина MC.
Провести плоскость через точки A и K, параллельно BD.
Найти: S
сеч
.
A
C
B
F
K
T
M
E
P
O
http://alexbooks.ucoz.com
140
Построение:
Т.к. грани, проходящие через стороны AB
и AD основания, перпендикулярны к
плоскости основания, то MA ⊥ (ABC).
MA = 24 см.
Пусть O — точка пересечения диагона-
лей ромба ABCD.
Пусть P = MO ∩ AK.
Через точку P проведем прямую EF, па-
раллельную BD.
EF ∩ MB = E; EF ∩ MD = F; (AEKF) —
иско
мое сечение.
AK ⊥ EF (по ТТП).
MC =
57610242432
2222
+=+=+ AMAC = 40 см.
AK =
2
1
MC = 20 см.
P — точка пересечения медиан в ∆AMC и в ∆BMD.
Значит,
3
2
==
MO
MP
BD
EF
. EF =
3
2
BD =
3
2
⋅ 18 = 12 см.
S
сеч
=
2
1
AK ⋅ EF =
2
1
⋅ 20 ⋅ 12 = 120 см
2
. Ответ: 120 см
2
.
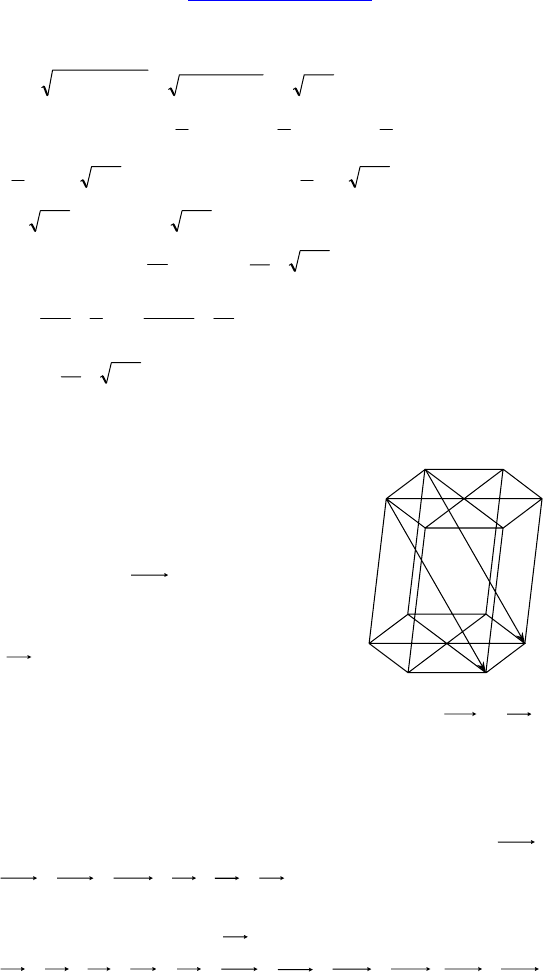
2.
Дано: SABC — пирамида, ∆ABC — пря-
моугольный, ∠C = 90°, AC = 10 см,
BC = 32 см, боковые ребра равнонаклоне-
ны к плоскости основания, SH — высота,
SH = 12 см,
3
1
1
1
=
BB
SB
. Через B
1
проведена
плоскость (A
1
B
1
C
1
), параллельная ABC.
Найти: S
б п ус пир
.
Решение: Т к. боковые ребра равнонаклонены к плоскости осно-
вания, то H — центр описанной окружности ∆ABC.
H — середина AB, SK и SM — высоты граней (ACS) и (CSB).
HK =
2
1
BC = 16 см. HM =
2
1
AC = 5 см.
SK =
256144
22
+=+ HKSH = 20.
SM =
25144
22
+=+ HMSH = 13 см.
A
C
B
F
K
E
M
O
D
P
C
A
B
S
M
K
H
A
1
B
1
C
http://alexbooks.ucoz.com
141
AB =
28121024100
22
=+=+ CBAC
.
S
бок пов полной пирамиды
=
2
1
SH ⋅ AB +
2
1
SK ⋅ AC +
2
1
SM ⋅ BC =
=
2
1
(12 ⋅ 2812 + 10 ⋅ 20 + 13 ⋅ 32) =
2
1
( 28124 + 200 + 416) =
=
28112 + 308 = 4( 2813 + 77) см
2
.
S
бок пов ус пирамиды
=
16
15
S
бок п п
= )772813(
4
15
+ см
2
.
(т.к.
1
1
4
SB
SB
=
, то
11
1
16
SC B
SCB
S
S
=
).
Ответ:
)772813(
4
15
+ см
2
.
С-19.
1.
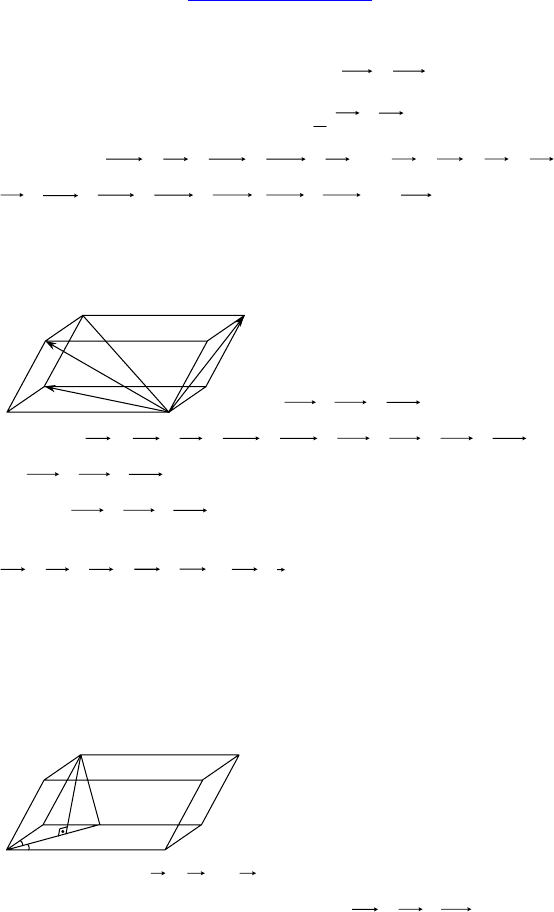
Дано: ABCDEFA
1
B
1
C
1
D
1
E
1
F
1
— пра-
вильная призма, O
1
— центр верхнего
основания.
1) Найти: а) векторы, противоположно
направленные
11
FO с началом и кон-
цом в вершинах призмы;
б) векторы, имеющие длины, равные
|| FC , началом и концом в вершинах
призмы.
2) От точки A
1
отложить векторы, равные векторам DB
1
и OE .
Решение:
1)
а) Т к. A
1
B
1
C
1
D
1
E
1
F
1
— правильный шестиугольник, то A
1
B
1
||
F
1
C
1
|| E
1
D
1
.
Значит, векторы, противоположно направленные вектору
11
FO :
11
BA ;
11
CF ;
11
DE ; AB ;
FC
;
E
D .
б) Т к. ABCDEF — правильный шестиугольник, то AD = FC = BE.
Значит, имеющие равные
FC длины:
CF ;
B
E ;
E
B ; AD ; DA ;
11
CF ;
11
FC ;
11
DA ;
11
AD ;
11
EB ;
11
BE .
2) Т к. A
1
B
1
= ED и A
1
B
1
|| ED, то A
1
B
1
DE — параллелограмм.
B
A
C
D
E
F
O
A
1
B
1
C
1
D
1
E
1
F
1
O
1
http://alexbooks.ucoz.com
142
Значит, A
1
E = B
1
D и A
1
E || B
1
D. Значит, EA
1
= DB
1
.
BE || A
1
F
1
, BE = 2A
1
F
1
. Значит,
11
AF
u
uuur
=
2
1
B
E = OE .
Ответ: 1) а)
11
CF ; FC ;
11
BA ;
11
DE ; AB ; б) CF ; AD ; DA ;
B
E ;
E
B ;
11
FC ;
11
CF ;
11
DA ;
11
AD ;
11
EB ;
11
BE ; 2) EA
1
и
11
AF
u
uuur
.
С-20.
1.
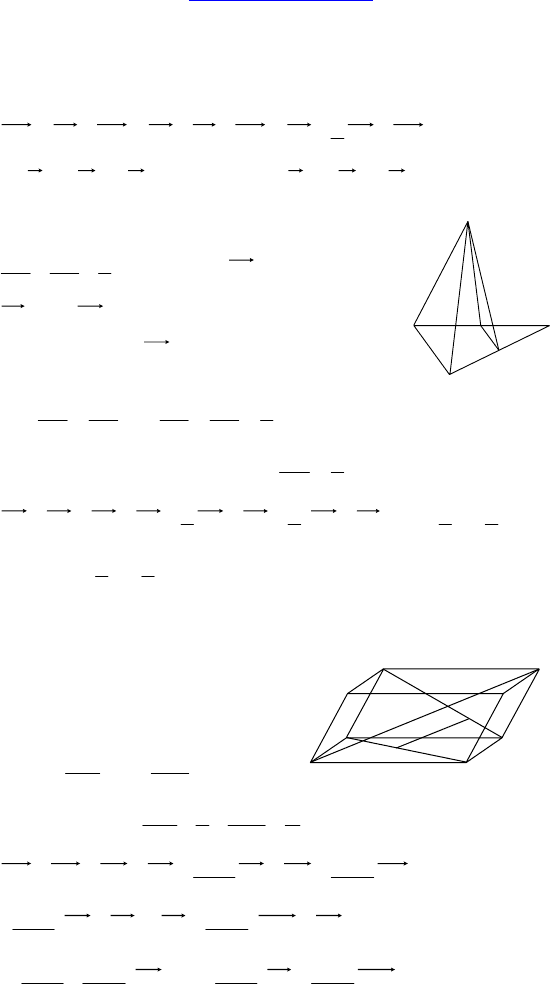
Дано: ABCDA
1
B
1
C
1
D
1
— парал-
лелепипед.
Представить вектор
DB
u
uur
как ал-
гебраическую сумму векторов
1
DA ,
1
DB ,
1
DC .
Решение:
CBDCDB +=
=
11
BA +
11
BC =
1
DB –
1
DA +
1
DB –
1
DC =
= 2
1
DB –
1
DA –
1
DC .
Ответ: 2
1
DB –
1
DA –
1
DC .
2. Дано: EABCDF — правильный октаэдр,
KE
+
K
A +
K
B + KC +
K
D +
KF
= 0 .
Найти: точку K.
Решение: Очевидно — это центр октаэдра.
Ответ: центр октаэдра.
С-21.
1.
Дано: ABCDA
1
B
1
C
1
D
1
— парал-
лелепипед, ∠A
1
AD = ∠A
1
AB,
AD = a, AB = b, a > b, AA
1
= c,
A
1
M — высота, AM ∩ BC = P.
Выразить вектор
1
AP
u
uuur
через еди-
ничные векторы
1
e ,
2
e и
3
e , отложенные от вершины и сона-
правленные соответственно с векторами
AD ; AB ;
1
AA .
Решение:
Т к. ∠A
1
AD = ∠A
1
AB, то AP — биссектриса угла ∠BAD.
Т к. AD || BC, то ∠BPA = ∠PAD = ∠BAP.
A
B
C
D
A
1
B
1
C
1
D
O
A
B
C
D
A
1
B
1
C
1
D
1
P
M
http://alexbooks.ucoz.com
143
Значит, ∆BAP — равнобедренный.
Значит, AB = BP = b.
1111
AAAD
a
b
ABAABPABAAAPPA
−+=−+=−= =
= b
1
e + b
2
e – c
3
e . Ответ: b
1
e + b
2
e – c
3
e .
2.
Дано: ∆ABC, E ∈ AB, F ∈ BC,
2
3
==
FB
CF
EB
AE
, O ∉ (ABC), mOE
r
= ,
pOA
r
= , kOC
r
= .
Выразить вектор
OF через векторы m
r
, p
r
, k
r
.
Решение:
Т к.
FB
CF
EB
AE
= , то
5
2
==
CB
BF
AB
BE
и ∠B — общий.
Значит, ∆ABC ∼ ∆EBF. Значит,
5
2
=
AC
EF
.
OF
= )(
5
2
5
2
OAOCOEACOEEFOE −+=+=+ = pkm
r
r
r
5
2
5
2
−+
.
Ответ:
pkm
r
r
r
5
2
5
2
−+
.
С-22.
1.
Дано: ABCDA
1
B
1
C
1
D
1
— парал-
лелепипед, M ∈ BD, N ∈ B
1
C,
MN || AC
1
.
Найти:
MD
BM
— ?
NC
NB
1
— ?
Решение: Пусть
MD
BM
=
b
a
,
NC
NB
1
=
d
c
.
1
CB
dc
d
DCBD
ba
b
CNDCMDMN
+
++
+
=++=
=
=
)()(
11
ADAA
dc
d
ABABAD
ba
b
−
+
++−
+
=
=
11
1 AA
dc
d
AB
ba
b
AD
dc
d
ba
b
+
+
⎟
⎠
⎞
⎜
⎝
⎛
+
−+
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+
C
A
B
O
E
F
A
B
C
A
1
B
1
C
1
D
1
M
D
N
http://alexbooks.ucoz.com
