Тронин А.В. Решение контрольных и самостоятельных работ по геометрии за 10 класс
Подождите немного. Документ загружается.

94
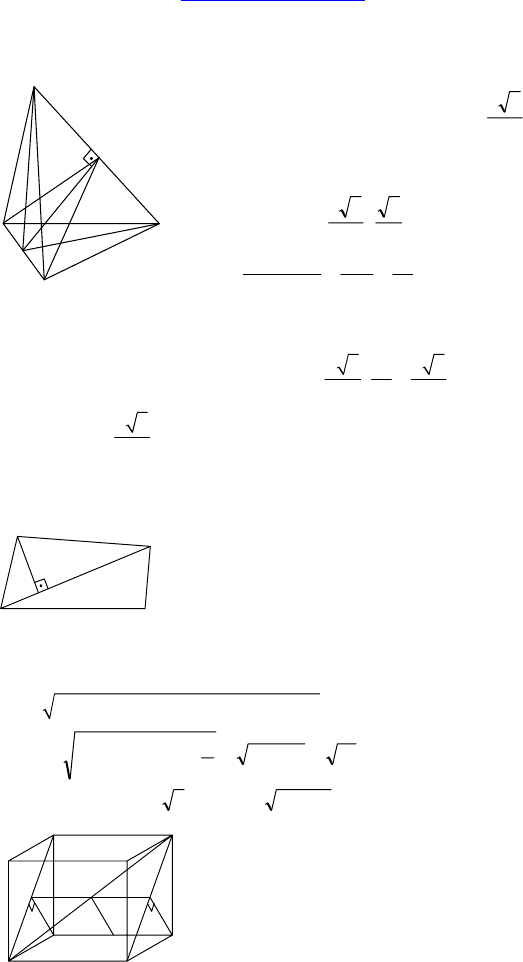
2.
Дано: ∆ABC — правильный, AC =
3
38
,
O — середина AC, OD ⊥ ABC, OD = 3.
Найти: ∠(ABD, CBD).
Решение:
2
3
3
38
⋅=BO = 4. OH ⊥ DB.
OH =
5
12
5
43
)(2
=
⋅
=
DB
DOBS
,
∠(ADB, CDB) = ∠AHC, т.к. ∆AHC равнобедренный, то HO —
биссектриса ∠AHC
⇒ ∠(ADB, CDB) = 2∠OHC;
43 5 53
tg
312 9
OHC
∠=⋅=.
Ответ:
53
2arctg
9
⎛⎞
⎜⎟
⎜⎟
⎝⎠
.
С-12.
1.
Дано: ABCD — параллелограмм, AB = 4,
AC = 5, ∠BAC = 60°. Сгибаем вдоль AC так,
чтобы ABC ⊥ ACD.
Найти: BD.
Решение: BH ⊥ AC ⇒ AH = ABcos ∠BAC = 2 ⇒ HC = 3 ⇒ по тео-
реме косинусов, т.к. ∠ACD = ∠BAC получим
22
2cos
H
DHCCD HCCD ACD=+−⋅∠ ⇒
⇒ HD =
2
1
432169 ⋅⋅⋅−+
=
1225 −
=
13
,
BH
⋅
ABsin∠BAC = 32 ⇒ BD = 1312 + = 5. Ответ: 5.
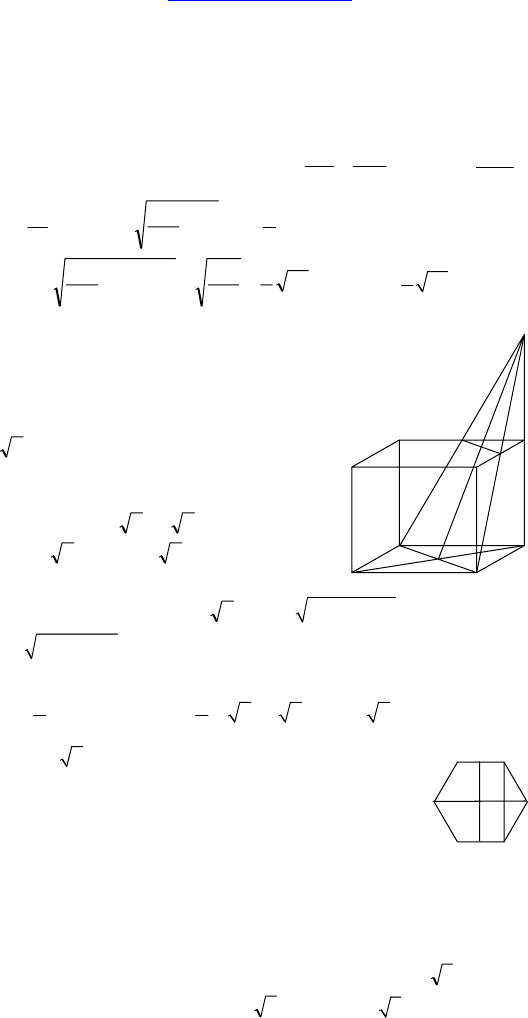
2. Дано: ABCDA
1
B
1
C
1
D
1
— прямоуголь-
ный параллелепипед, ABCD — квадрат,
AB = 5 см,
ρ
(AC
1
, BC) = 4 см.
Найти: AC
1
. Изобразить: общий перпен-
дикуляр BС и AС
1
.
Решение: Проводим C
1
D, B
1
A.
CL ⊥ C
1
D, BK ⊥ B
1
A, BK ⊥ AB
1
, CL ⊥
DC
1
, KL ∩ AC
1
= F, FM || KB, M ∈ BC. т к. параллелепипед прямо-
C
A
B
D
O
H
C
B
A
D
H
A
B
C
D
A
1
B
1
C
1
D
1
K
F
L
M
http://alexbooks.ucoz.com
95
угольный, то BC ⊥ AA
1
B
1
B ⇒ BC ⊥ KB ⇒ т.к. BC || KL, то KL ⊥
KB, т к. KB ⊥ AB
1
, то KB ⊥ AB
1
C
1
D ⇒ KB ⊥ AC
1
⇒ FM ⊥ AC
1
⇒
FM — искомый общий перпендикуляр.
LC = 4 ⇒ LD = 3, ∆DLC ∼ ∆CLC
1
⇒
1
DL LC
L
CLC
= ⇒
2
1
L
C
LC
D
L
=
⇒
C
1
L =
3
16
⇒ C
1
C = 25
9
625
− = 5 ⋅
3
4
⇒
⇒ AC
1
=
34
3
5
9
850
2525
9
400
==++
. Ответ:
5
34
3
см.
С-13.
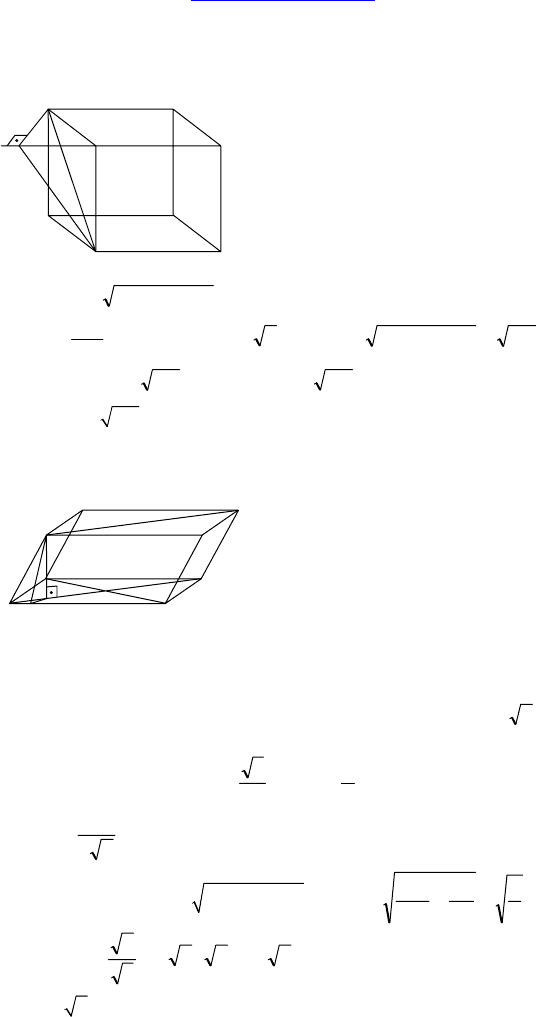
1.
Дано: ABCDA
1
B
1
C
1
D
1
— правильная че-
тырехугольная призма, AD = 8 см, C
1
C
=
23 см, через AC проведена плоскость,
составляющая 45° с основанием.
Найти: S
сеч
.
Решение: OC =
2324 > ⇒ SC =
= OC =
24 ⇒ SC
1
= 2 .
SD ∩ D
1
C
1
= M, SB ∩ B
1
C
1
= N.
Из подобия следует MN =
22 .
22
8OS OC CS
=
+=.
11
H
SHCCS=+, т.к. ∠SOC=∠SHC
1
= 45° то HC
1
= SC
1
⇒ HS = 2
⇒ HO = 6, т к. HO — высота равнобокой трапеции BNMD, то
()
()
сеч
11
22 82 6 302
22
SMNBDOH=+⋅= +⋅=
.
Ответ:
30 2 см
2
.
2. Дано: ABCDEFA
1
B
1
C
1
D
1
E
1
F
1
— правильная
шестиугольная призма, S
бок
= Q.
Найти: S
сеч
, которое перпендикулярно AD и де-
лит эту диагональ пополам.
Решение: Т.к. CE ⊥ AD ⇒ PR || CE (PR — линия пересечения се-
чения и нижней грани, O — середина AD) ⇒ площадь искомого
сечения равна площади прямоугольника CC
1
E
1
E.
Пусть AB = a. AA
1
= h ⇒ Q = ah.
Т к. ABCDEF — правильный шестиугольник, CE =
a3 (по тео-
реме косинусов) ⇒ S(CC
1
E
1
E) = Q3 . Ответ: 3Q .
A
B
C
D
A
1
B
1
C
1
D
1
N
O
M
S
H
A
B
C
D
E
F
P
O
R
http://alexbooks.ucoz.com
96
С-14.
Дано: ABCDA
1
B
1
C
1
D
1
— прямой
параллелепипед, AD = 17, DC = 28,
CA = 39, ∠(DA
1
, DD
1
C
1
C) = 45°.
Найти: S
полн
.
Решение:
A
1
K ⊥ D
1
C
1
, KD — проекция A
1
D ⇒
⇒ ∠KA
1
D = ∠KDA
1
= 45° ⇒
⇒ A
1
K = KD.
S(A
1
D
1
C
1
) = 2514342 ⋅⋅⋅ = 5 ⋅ 42 = 210 ⇒
⇒ AK =
28
420
= 15 ⇒ A
1
D
1
= 215 ⇒ AA
1
= 2892225 −⋅ = 161 ⇒
S
полн
=4 ⋅ 210 + 1612 (17 + 28) =
)281613(30 +
.
Ответ:
()
30 3 161 28+ .
С-15.
1.
Дано: ABCDA
1
B
1
C
1
D
1
— наклон-
ный параллелепипед, все его реб-
ра равны, ∠AA
1
B = ∠A
1
AB < 90°,
ABCD — квадрат, S(BB
1
D
1
D) = Q,
∠(AA
1
, ABC) = 60°.
Найти: S
бок
.
Решение:
Т к. ∠A
1
AB = ∠A
1
AD, то A
1
проецируется на AC в т. H, и т к. AC ⊥
BD, то AA
1
⊥ BD ⇒ B
1
BDD
1
— прямоугольник ⇒ Q =
2
2a =
BB
1
·BD (где a — ребро куба).
A
1
H = AA
1
·sin 60°⇒ A
1
H =
2
3
a
, а AH =
2
a
⇒
⇒ HK =
22
a
(где HK — перпендикуляр к AD, ∠HAK = 45° по
ТПП A
1
K ⊥ AD,
22
11
AK AH HK=+
)⇒A
1
K= a
aa
8
7
84
3
22
=+ ⇒
⇒ S
бок
= Qaaa 772
8
7
4
2
=⋅=⋅ .
Ответ:
7Q .
A
B
C
D
A
1
B
1
C
1
D
1
K
A
B
C
A
1
B
1
C
1
D
1
O
D
K
H
http://alexbooks.ucoz.com
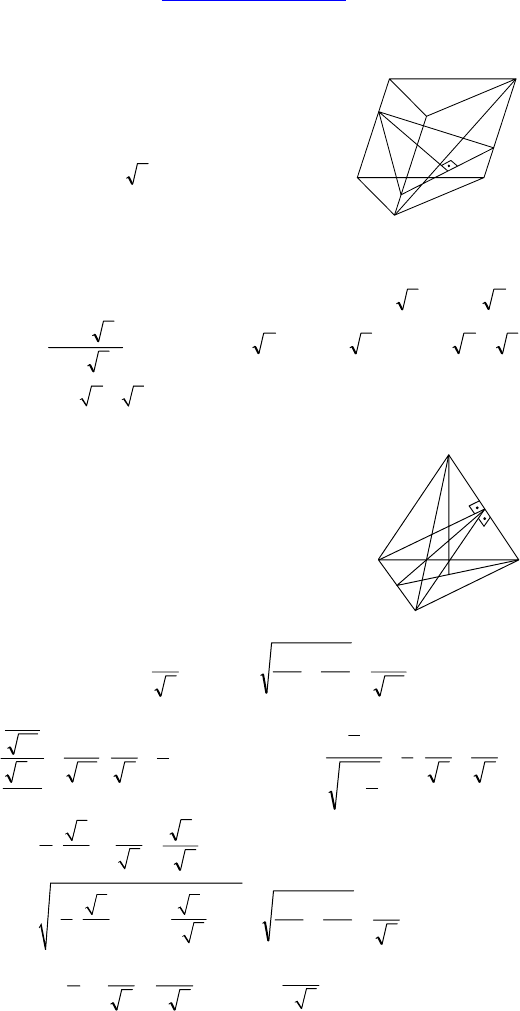
97
2.
Дано: ABCA
1
B
1
C
1
— наклонная призма,
р(AA
1
, CB
1
) = 1, ∠(AA
1
C
1
C, C
1
CBB
1
) = 45°,
∠(C
1
CBB
1
, B
1
BAA
1
) = 30°,
S(C
1
CBB
1
) = 4(1 + 3 ).
Найти: S
бок
.
Решение:
Пусть MNO — перпендикулярное сечение.
MH ⊥ NO ⇒
ρ
(AA
1
, CB
1
) =
ρ
(AA
1
, CC
1
B
1
B) т.к. AA
1
|| BB
1
и
AA
1
|| CC
1
B
1
B ⇒ MH = 1 ⇒ NH = 1, MO = 2, HO = 3 , MN = 2 ⇒
⇒ CC
1
=
31
)31(4
+
+
=4 ⇒ S
бок
= 4( 3122 +++ ) = 4( 323 ++ ).
Ответ:
()
43 2 3++ .
С-16.
1. Дано: SABC — правильная пирамида,
∠(ASC, BCS) = 120°, AB = m.
Найти: S
бок
.
Решение:
AH ⊥ SC, BH ⊥ SC ⇒ ∠AHB = 120°.
(по теореме косинусов)
Пусть HA=HB=x ⇒ m
2
= 2x
2
(1 – cos120°) ⇒
⇒ m
2
= 3x
2
⇒x=
3
m
⇒KH =
43
22
mm
−
=
12
m
⇒sin∠HCK =
=
2
3
12
m
m
=
3
2
12
1
⋅
=
3
1
⇒ tg∠HCK =
8
1
8
3
3
1
9
1
1
3
1
=⋅=
−
⇒
⇒ SO =
23 1
32
8
m⋅⋅= m⋅
83
3
⇒
⇒ SK =
22
13 3
32
38
mm
⎛⎞⎛⎞
⋅+
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
=
2412
22
mm
+
=
8
m
⇒
⇒ S
бок
=
82
3
8
2
1
3
2
mm
m
=⋅⋅ . Ответ:
2
3
28
m
.
A
C
B
A
1
B
1
C
1
O
M
N
H
B
A
C
S
H
K
O
http://alexbooks.ucoz.com
98
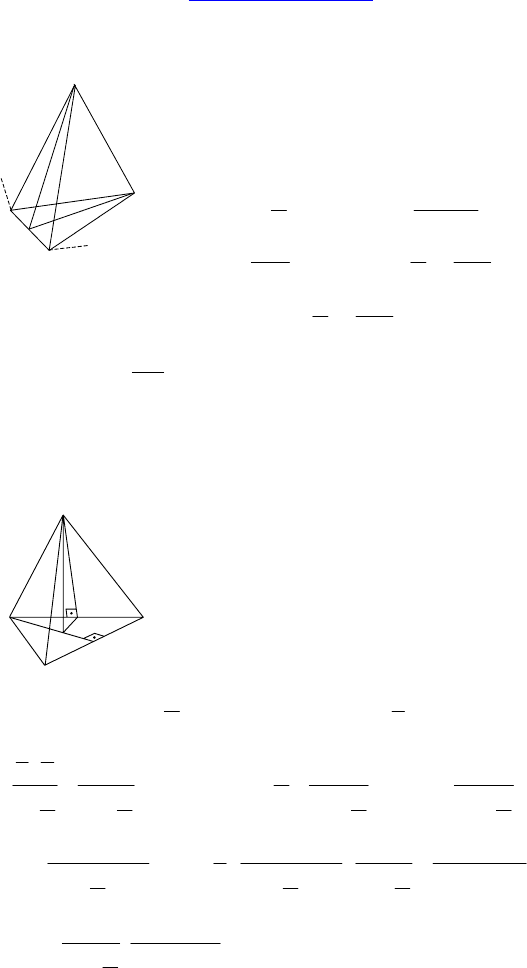
2. Дано: SA
1
A
2
...A
20
— правильная пирамида,
∠A
1
SA
2
= 10°.
Найти: ∠(A
1
SA
2
, A
1
A
2
A
3
).
Решение: Пусть O — центр основания, SH —
высота грани SA
1
A
2
⇒ OH — высота ∆OA
1
A
2
,
HA
2
= tg
2
SH
α
.
12
2
ctg
2
AOA
OH HA
∠
=
.
12
360 180
tg ctg
2
AOA OH SH
nn
°α°
∠=⇒=
.
∠(A
1
SA
2
, A
1
OA
2
) = ∠SHO =
180
arccos tg ctg
2
n
α
°
⎛⎞
⎜⎟
⎝⎠
.
т.к.
cos
H
O
SHO
SH
∠=.
α = 10°, n = 20 ⇒ ∠(A
1
SA
2
, A
1
OA
2
) = arccos(tg 5°ctg 9°).
Ответ: arccos(tg 5°ctg 9°).
С-17.
1. Дано: MABC — пирамида, ребра равнона-
клонены, AC = AB, BC = a, ∠BAC = α,
∠(AMB, ABC) = ∠(AMC, ABC) = ϕ.
Найти: высоту пирамиды и площади равно-
наклоненных граней.
Решение: Т к. ребра равнонаклонены, то M
проецируется в т. O — центр описанной ок-
ружности и O ∈ AH (AH ⊥ CB), т к. AC = АB
и ∠CAH = ∠BA
H =
2
α
. OK ⊥ AB ⇒ AK = KB =
2
1
AB =
=
2
sin
22
1
α
⋅
a
=
2
sin4
α
a
⇒ OK =AK ⋅ tg
2
α
=
2
cos4
α
a
⇒ MO =
2
cos4
α
a
tgϕ,
MK =
ϕ
α
cos
2
cos4
a
⇒ S =
2
1
⋅
ϕ
α
cos
2
cos4
a
⋅
2
sin2
α
a
=
ϕαcossin8
2
a
.
Ответ:
2
tg
;
8sin cos
4cos
2
aaϕ
α
αϕ
.
A
1
S
H
O
A
2
C
A
B
M
O
K
H
http://alexbooks.ucoz.com
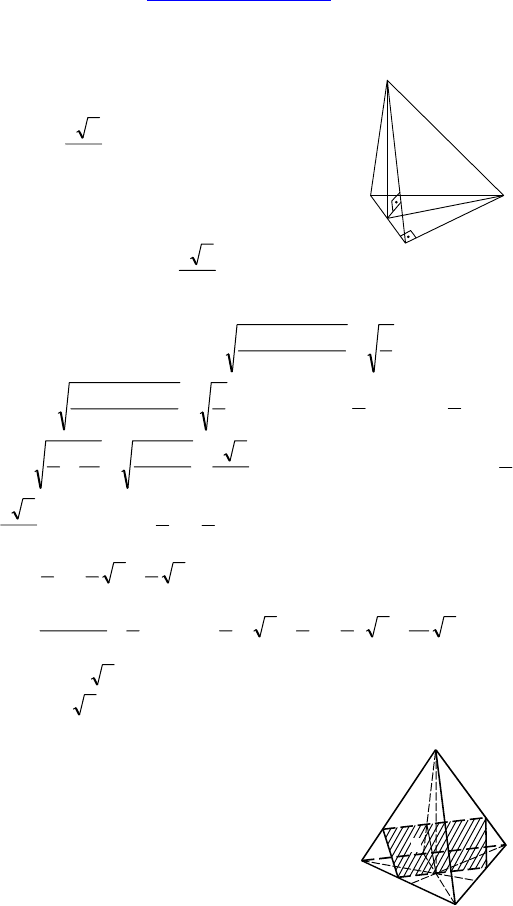
99
2. Дано: MABC — пирамида, MAC ⊥ ABC,
остальные грани равнонаклонены, ∠C = 90°,
р(H, BMC) =
4
23
. AC = 4 см, BC = 3 см.
Найти: S
бок
.
Решение:
HK ⊥ MC ⇒ по теореме о трех перпендику-
лярах HK ⊥ BMC ⇒ HK =
4
23
.
Из равнонаклоненности ⇒ BH — биссектриса ⇒ cos∠ABC =
= 1 – 2sin
2
∠HBC ⇒ sin∠HBC =
5
1
2
cos1
=
∠−
ABC
.
cos∠HBC =
5
4
2
cos1
=
∠+ ABC
⇒ tg∠HBC =
2
1
⇒ HC =
2
3
⇒
⇒ KC =
4
23
16
1836
16
18
4
9
=
−
=−
⇒ ∠MCH = 45° ⇒ MH =
2
3
,
MC=
2
23
⇒ S(AMC) =
2
3
4
2
1
⋅⋅
= 3.
S(MCB) =
2
4
9
2
2
3
3
2
1
=⋅⋅ .
S(AMB) =
2
4
15
2
2
5
3
2
1
2
2
3
343
2
1
45cos
)(
=⋅⋅⋅=⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅−⋅=
°
AHBS
⇒
⇒ S
бок
= 3(1 + 22 ).
Ответ: 3(1 +
22 ).
С-18.
1. Дано: MABC — правильная пирамида,
AB = a, боковые грани наклонены к плос-
кости основания под 60°, через центр осно-
вания проведена плоскость, параллельная
стороне основания и перпендикулярная
грани, проходящей через эту сторону.
Найти: S
сеч
.
Решение:
O — центр основания. EF||AB, O∈EF; CD⊥AB, D ∈ AB; OK ⊥ DM,
K ∈ DM; PT || EF, T ∈ MB, P ∈ AM ⇒ PTEF — искомое сечение.
Т к. ∠(AMB, ACB) = 60°, то ∠(PTFE, ABC) = 30° = ∠KOD ⇒
C
A
B
M
H
K
C
A
B
O
K
P
T
F
E
M
D
http://alexbooks.ucoz.com
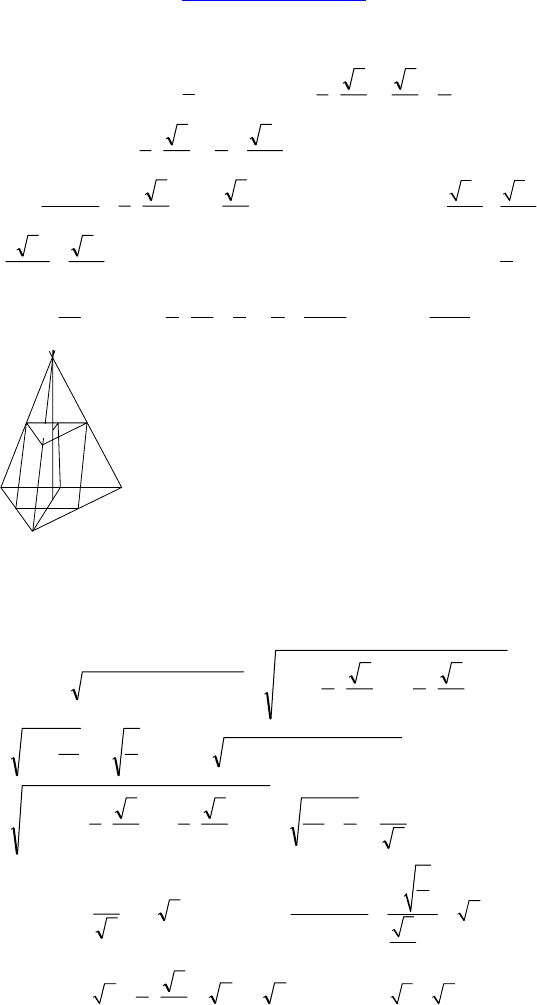
100
⇒ KO = DO ⋅ cos30° =
3
1
CD ⋅ cos30° =
42
3
2
3
3
1 a
a =⋅⋅
,
DK = DOsin30° =
12
3
2
1
2
3
3
1 a
a =⋅⋅
,
DM =
°60cos
DO
= aa
3
3
2
2
3
3
1
=⋅⋅ ⇒ MK = DM – KD =
33
312
aa
−
=
=
12
33 a
=
4
3a
⇒ из ∆PMT ∼ ∆AMB ⇒ PT : AB = MK : MD =
4
3
⇒
⇒ PT =
4
3a
⇒ S
сеч
=
96
17
43
2
4
3
2
1
2
aa
a
a
=
⎟
⎠
⎞
⎜
⎝
⎛
+
. Ответ:
2
17
96
a
.
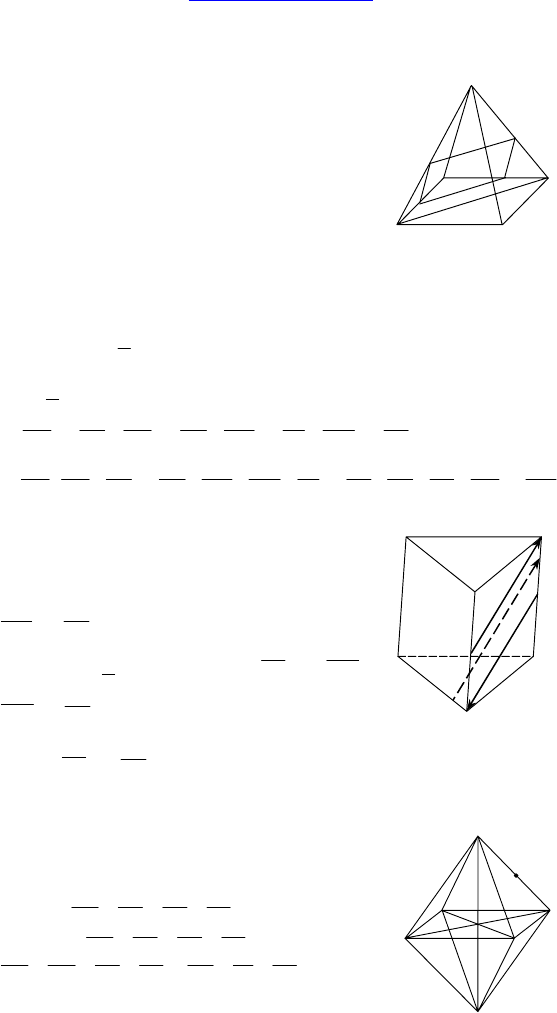
2. Дано: MNPABC — правильная усеченная
пирамида, MP = 2, через MP параллельно NS
проведена плоскость, S
сеч
= 8.
Найти: S
бок
, высоту полной пирамиды, частью
которой является данная усеченная.
Решение:
PQ || NS, MR || NS ⇒ MPQR — данное сечение.
Т.к. плоские углы при вершине нижнего осно-
вания равны, то NS проецируется а биссектри-
су ⇒ на высоту ⇒ NS ⊥ AC ⇒ MPQR — прямоугольник ⇒ NS =
= PQ = MR = 4 ⇒ PC = CQ = MA = AR =
4.
Пу
сть S — вершина нашей пирамиды. Пусть S проецируется в
т. O и O
1
верхнего и нижнего основания ⇒
⇒ OO
1
=
2
1
2
)( POOCPC −− =
2
2
2
3
3
2
6
2
3
3
2
16
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅⋅−⋅⋅− =
=
3
2
4
3
16
16 =−
. B
1
B
2
=
2
211
2
1
)( BOOBOO −+ =
=
2
2
1
2
2
3
3
1
6
2
3
3
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅⋅−⋅⋅+OO
=
3
6
3
4
3
32
=+
.
S
бок
= 3 ⋅ 4 ⋅
3
6
= 324 . tg∠PCO =
1
1
2
4
3
2
3
4
3
OO
OC O P
==
−
⋅
⇒
⇒ SO = OC
2 = 26
2
3
3
2
⋅⋅
= 62 . Ответ:
24 3; 2 6
.
B
A
S
C
P
M
N
R
Q
O
O
1
B
1
B
2
http://alexbooks.ucoz.com
101
С-19.
1. Дано: PABCD — правильная пирамида,
K, M, T, E — середины AB, PA, PC, BC со-
ответственно.
Перечислить: 1) пары сонаправленных
векторов с концами в т. K, M, T, E. 2) пары
равных векторов с концами в т. K, M, T, E.
3) векторы, имеющие равные длины, с
концами в т. K, M, T, E.
Решение:
Замети
м, что MTEK —
параллелограмм, т к. MT — средняя линия
∆APC,
1
2
M
TAC=
, MT || AC, KE — средняя линия ∆ABC,
1
2
K
EAC= , KE || AC.
1)
MT
и
KE
, TM и
EK
,
MK
и T
E
,
K
M и
ET
.
2) те же.
3)
MT
,
TM
,
KE
и
EK
,
MK
,
K
M
,
T
E
и
ET
,
KT
,
T
K
,
ME
и
E
M
.
2.
Дано: ABCA
1
B
1
C
1
— правильная призма, E
и F — середины ребер C
1
C и B
1
B.
Найти: коллинеарные векторы из указанных.
Решение:
1
EB и
FC
. т к. EB
1
FC — параллелограмм
(
11
1
2
B
FEC BB== , B
1
F || CE)
1
E
B и DM ,
DM и
FC
не коллинеарны, т.к. иначе AC
и BB
1
лежали бы в одной плоскости, что противоречит условию.
Ответ:
1
E
B и FC .
С-20.
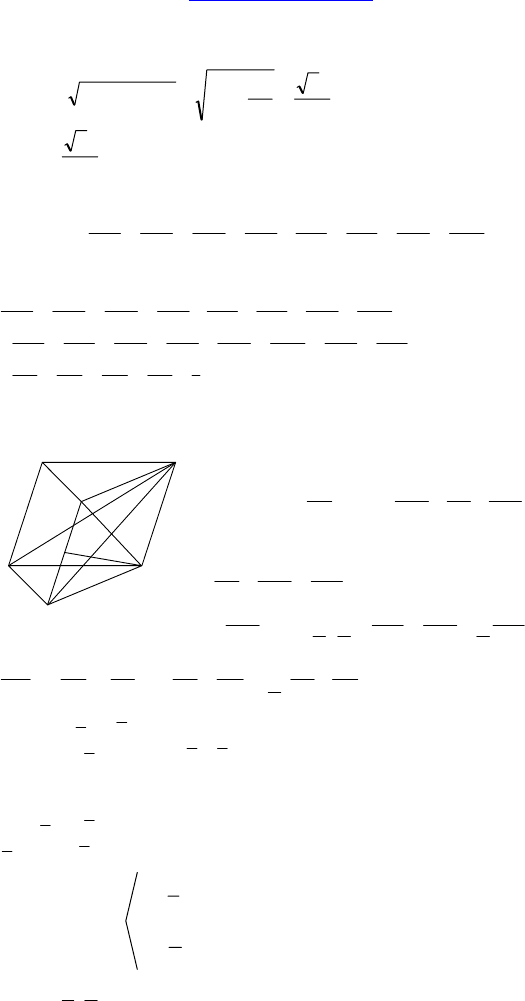
1.
Дано: PABCDT — правильный октаэдр, AB
= a, K — середина PC.
Найти:
|| CPCTABKD +++ .
Решение:
CPCTABKD +++ =
CPCTDCKD +++ =
K
ATA
K
T
=
+
.
∆APC — прямоугольный ⇒
P
B
C
D
A
K
E
T
M
C
M
A
B
A
1
B
1
D
F
C
E
P
B
C
D
A
K
T
http://alexbooks.ucoz.com
102
⇒ AK =
22
PKAP + =
4
2
2
a
a
+ =
2
5
a
.
Ответ:
2
5
a
.
2. Дано: ABCD, A
1
B
1
C
1
D
1
— два четырехугольника, произвольно
расположенных в пространстве.
Доказать:
1111
DACDBCAB +++
=
1111
DDCCBBAA +++
.
Доказательство:
Составим разность:
1111
DACDBCAB +++
–
1111
DDCCBBAA −−−
=
=
CCBCBBAB
1111
+++ + AADADDCD
1111
+++ =
=
0=+++ DACDBCAB , что и доказывает равенство.
С-21.
1. Дано: ABCA
1
B
1
C
1
— наклонная приз-
ма, E — середина BB
1
, C
1
B ∩ EC = P.
Выразить:
AP
через
1
AC , CB ,
1
CC .
Решение:
P — точка пересечения медиан ∆BB
1
C ⇒
AP
=
1
AC + PC
1
=
=
1
AC
+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
2
1
3
2
1
⋅
BC
1
=
1
AC
+ BC
1
3
2
;
1
1
C B CC CB=− + ⇒
(
)
11
2
3
AP AC CB CC=+ − .
2. Дано:
a
и b ненулевые и неколлинеарные.
(x + y –1)
a + (2x – y)
b
=
0
.
Найти: x и y.
Решение:
Т к.
a и
b
ненулевые и неколлинеарные, то коэффициенты при
a и при b равны 0.
⎩
⎨
⎧
=−
=+
02
1
yx
yx
⇒
3
2
3
1
=
=
y
x
.
Ответ:
12
;
33
.
A
B
C
A
1
C
1
B
1
P
E
http://alexbooks.ucoz.com
103
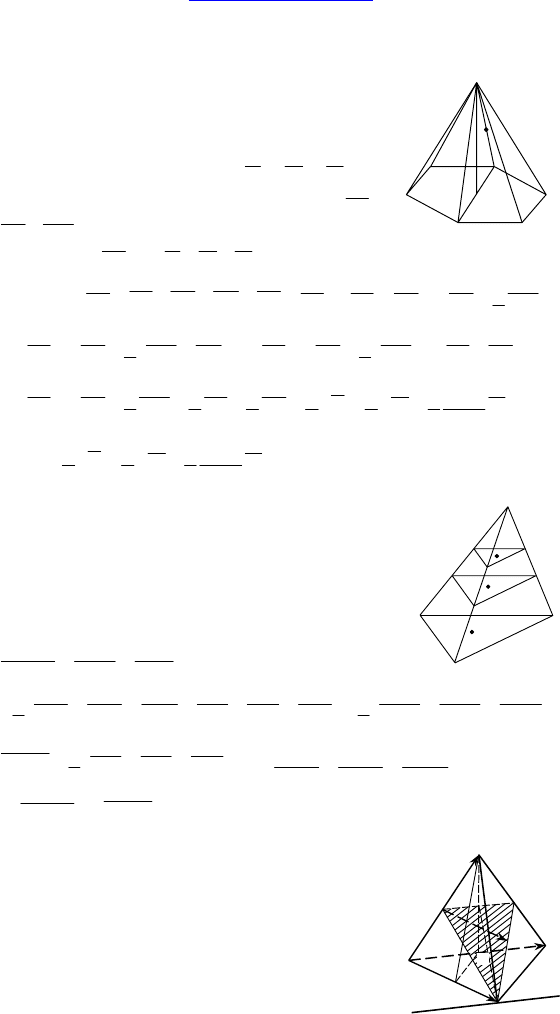
С-22.
1. Дано: MABCDEF — правильная пирами-
да, стороны основания равны a, P ∈ MC,
MP : PC = 2 : 3, боковые ребра сторон осно-
вания составляют угол ϕ,
1
e ,
2
e ,
3
e —
единичные векторы, сонаправленные с
FA
,
F
E
,
FM
.
Разложить:
FP по
1
e ,
2
e ,
3
e .
Решение:
FP = FA AB BC CP+++= FA +( FA + FE ) + FE + CM
5
3
=
= 2
FA +2 F
E
+ )(
5
3
FCFM − = 2 FA +2 F
E
+ ))(2(
5
3
FEFAFM +− =
= 2
FA +2 FE +
FEFAFM
5
6
5
6
5
3
−−
=
1
4
5
ae
+
2
5
4
ea
+
3
cos5
3
e
a
ϕ
.
Ответ:
1
4
5
ae +
2
5
4
ea +
3
cos5
3
e
a
ϕ
.
2.
Дано: MABC — пирамида, A
1
B
1
C
1
|| A
2
B
2
C
2
||
ABC, M
2
, M
1
, M — точки пересечения медиан
∆A
2
B
2
C
2
, ∆A
1
B
1
C
1
, ∆ABC.
Доказать: M, M
2
, M
1
— лежат на одной прямой.
Доказательство:
O — произвольная точка пространства:
1221
OMOMMM −= =
=
)(
3
1
111222
OCOBOAOCOBOA −−−++ = )(
3
1
212121
CCBBAA ++ .
13
M
M = )(
3
1
111
CCBBAA ++ , но k
CC
CC
BB
BB
AA
AA
===
1
21
1
21
1
21
⇒
⇒
21
MM
=
13
kM M ⇒точки M
1
, M
2
, M
3
лежат на одной прямой ч.т.д.
С-23.
Дано: DABC — пирамида, DA = DB = DC =
= AC = 2, AB = BC, ∠ABC = 90°, M, H —
середины AD, DC соответственно.
Найти: 1) S
бок
; 2) S(BMH); 3) ∠(BMH, ABC);
4) ∠(BD, BMH).
A
B
C
D
M
O
E
F
P
B
A
C
M
B
1
B
2
A
1
A
2 C
2
C
1
M
3
M
1
M
2
B
A
C
K
P
H
F
E
D
M
O
Q
http://alexbooks.ucoz.com
