Тронин А.В. Решение контрольных и самостоятельных работ по геометрии за 10 класс
Подождите немного. Документ загружается.

64
ВАРИАНТ 5.
С-1.
1.
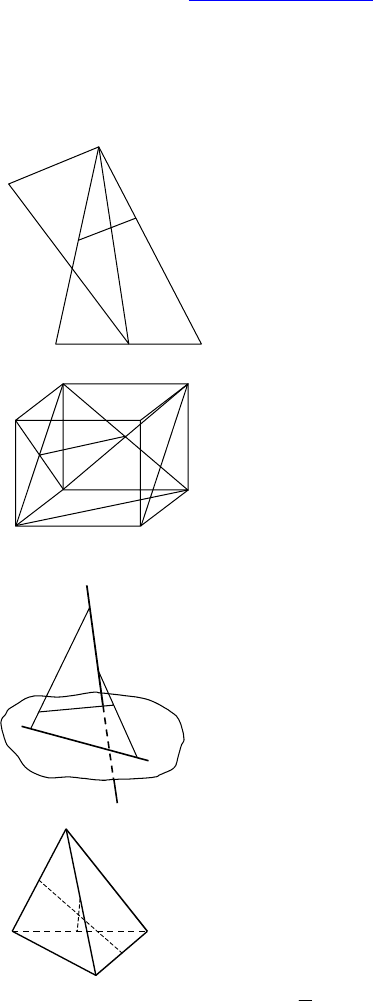
Дано: ABCD — трапеция, AD || BC,
AB∩CD=M, E — середина AD, O ∈ BC,
K ∉ (ABC).
Найти: при каком условии K, M, O и E
лежат в одной плоскости.
Решение:
O ∈ (KME), когда O ∈ ME, т.к. E —
середина AD, то O — середина BC.
Ответ: когда O — середина BC.
2.
Пос
троить линию пересечения плоско-
стей (AB
1
C) и (A
1
C
1
B).
Построение:
A
1
B∩AB
1
= M, B
1
C ∩ BC
1
= N, MN || AC,
MN || A
1
C
1
, MN — искомая прямая.
С-2.
1. Дано: a и b — скрещивающиеся прямые.
Найти: взаимное положение прямых EF и
a, EF и b.
Решение: Если прямые EF и a, EF и b
параллельны или пересекаются, то пря-
мые AA
1
и BB
1
лежат в одной плоскости.
Значит, прямые a и b лежат в одной
плоскости ⇒ противоречие. Значит, EF и
a, EF и b — скрещиваются.
Ответ: они попарно скрещиваются.
2.
Дано: ABCD — тетраэдр, E, F, P, M — сере-
дины AD, CD, BC, AB соответственно.
Доказать: EP и MF пересекаются и точкой
пересечения делятся по
полам.
Доказательство:
EM — средняя линия ∆ADM.
Значит, EM =
2
1
BD, EM || BD.
D
A
B
K
M
C
E
O
A
B
C
D
A
1
B
1
C
1
D
1
N
M
A
B
A
1
F
E
B
1
a
b
C
A
B
D
M
F
E
P
http://alexbooks.ucoz.com
65
FP — средняя линия ∆CDB. Значит, FP =
2
1
BD, FP || BD.
Значит, FP = EM и FP || BD. Значит MEFP — параллелограмм.
Его диагонали MF и EP пересекаются и точкой пересечения де-
лятся пополам. Ч.т.д.
С-3.
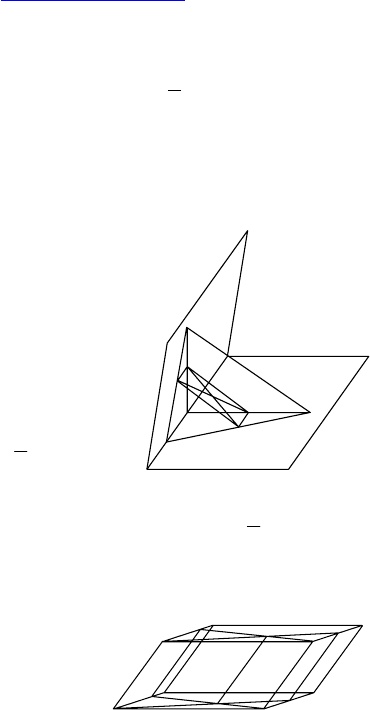
1. Дано: ∆ABC и ∆DBC не лежат в
одной плоскости, M — середина BD,
H — середина CD, K — середина
AC, (MKH) ∩ AB = P.
Доказать: PH и MK пересекаются и
точкой пересечения делятся пополам.
Доказательство:
MH — средняя линия ∆BCD.
Значит, MH || BC, MH =
2
1
BC.
Значит, (MKH) пересекает (ACB) по прямой, параллельной BC.
Значит, PK — средняя линия ∆BAC. PK || BC, PK =
2
1
BC.
Значит, PKHM — параллелограмм. Его диагонали PH и MK пере-
секаются и точкой пересечения делятся пополам. Ч.т.д.
2. Дано: ABCD — параллело-
грамм, ∠BCC
1
= 120°,
AA
1
= BB
1
= CC
1
= DD
1
,
AA
1
|| BB
1
|| CC
1
|| DD
1
.
1) Построить линию пересече-
ния OO
1
плоскостей, проходя-
щих через прямую AA
1
и точку M и прямую DD
1
и точку K.
2) Найти взаимное положение OO
1
и AA
1
.
3) ∠(OO
1
, AD) — ?
Решение: 1) Через т. M проведем прямую MH, параллельную DD
1
.
MH ∩ CD = H.
Через т. K проведем прямую KF, параллельную AA
1
.
KF ∩ AB = F, D
1
K ∩ A
1
M = O
1
, DF ∩ AH = O.
OO
1
— линия пересечения плоскостей (DDK) и (AA
1
M).
2) (AA
1
M) || CC
1
, (DD
1
K) || CC
1
. Значит, OO
1
|| CC
1
|| AA
1
.
3) OO
1
|| CC
1
, AD || BC.
∠(AD; OO
1
) = ∠(BC; CC
1
) = 180° – 120° = 60°.
Ответ: 2) OO
1
|| AA
1
; 3) 60°.
B
A
P
H
C
D
K
M
A
B
C
D
A
1
B
1
C
1
D
1
F
H
M
K
O
O
1
http://alexbooks.ucoz.com
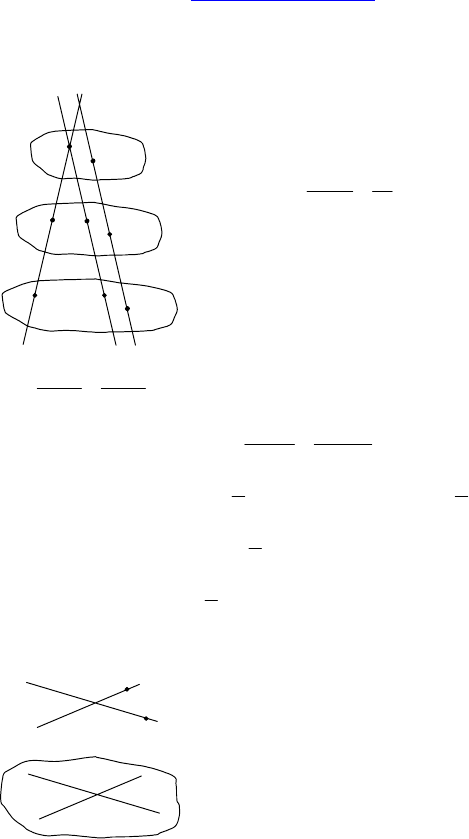
66
С-4.
1. Дано: α || β || γ, l
1
и l
2
— скрещивающиеся
прямые, l
1
∩ α = A
1
, l
1
∩ β = A
2
, l
1
∩ γ = A
3
,
l
2
∩ α=B
1
, l
2
∩β=B
2
, l
2
∩ γ = B
3
, B
1
B
2
= 5 см,
A
2
A
3
= 6 см,
15
8
32
21
=
BB
AA
.
Найти: A
1
A
3
— ? B
1
B
3
— ?
Решение:
Через точку A
1
проведем прямую l
3
, па-
раллельную l
2
.
l
3
∩ β = B′
2
, l
3
∩ γ = B′
3
.
Из подобия ∆A
2
A
1
B′
2
и ∆A
3
A
1
B′
3
следует,
что
31
21
31
21
BA
BA
AA
AA
′
′
=
, A
1
B′
2
= B
1
B
2
, A
1
B′
3
= B
1
B
3
.
Пусть A
1
A
2
= 8x, B
2
B
3
= 15x.
xx
x
155
5
86
8
+
=
+
.
30 + 40x = 40x + 120x
2
. x
2
=
4
1
, т.к. A
1
A
2
=8x > 0, то x =
1
2
.
Значит, A
1
A
3
= 6 + 8x = 6 +8 ⋅
2
1
= 10 см;
B
1
B
3
= 5 + 15x = 5 + 15 ⋅
2
1
= 12,5 см.
Ответ: 10 см; 12,5 см.
2.
A
B
C
α
p
q
Дано: p ⊂ α, q ⊂ α, p и q пересекаются, A ∉ α, AB || p, AC || q, A ∈
β, C ∈ β.
Найти: взаимное расположение плоскостей α и β.
Решение:
Если B ∈ β, то α || β.
Если B ∉ β, то α и β пересекаются.
Ответ: α || β ТИ
ТТ, когда B ∈ β.
A
3
l
1
γ
α
β
A
1
A
2
B
1
B
2
B
3
B
′
3
B
′
2
l
2
l
3
http://alexbooks.ucoz.com
67
С-5.
1.
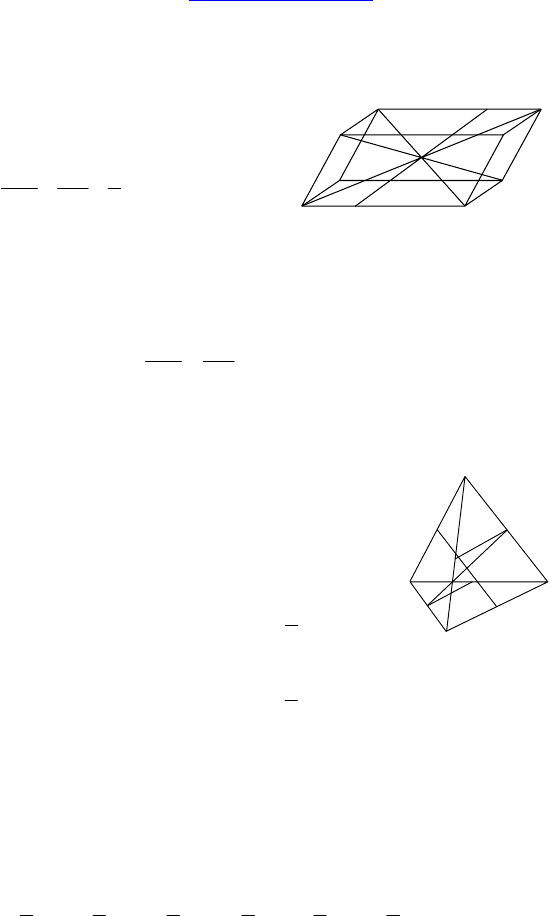
Дано: ABCDA
1
B
1
C
1
D
1
— парал-
лелепипед, E ∈ B
1
C
1
, F ∈ AD,
2
5
1
1
==
FA
DF
EC
EB
, O — точка пе-
ресечения диагоналей паралле-
лепипеда.
Доказать: E и F — симметричны относительно точки O.
Доказательство:
∆AOD = ∆C
1
OB
1
(по трем сторонам). Значит, ∠ODA = ∠OB
1
C
1
.
Т к. AD = B
1
C
1
и
FA
DF
EC
EB
=
1
1
, то FD = B
1
E.
Значит, ∆EB
1
O = ∆FDO (по двум сторонам и углу между ними).
Значит, EO = FO. Значит, E и F симметричны относительно точки
O. Ч.т.д.
2.
Дано: ABCD — тетраэдр, K, N, M, P, R, S —
середины AD, BD, BC, AC, AB, DC.
Доказать, что AD
2
+ BD
2
+ CD
2
+ AB
2
+
+ BC
2
+ AC
2
= 4(PN
2
+ KM
2
+ RS
2
).
Доказательство:
PR — средняя линия ∆ABC; PR =
2
1
BC,
PR || BC.
SN — средняя линия ∆DBC, SN =
2
1
BC, SN || BC.
Значит, PRNS — параллелограмм.
Аналогично PKNM — параллелограмм и KSMR параллелограмм.
По свойству параллелограмма: удвоенная сумма квадратов сто-
рон параллелограмма равна сумме квадратов диагоналей.
2PR
2
+ 2PS
2
= PN
2
+ RS
2
.
2KP
2
+ 2PM
2
= RN
2
+ KM
2
.
2KP
2
+ 2RM
2
= RS
2
+ KM
2
.
⎟
⎠
⎞
⎜
⎝
⎛
+++++
222222
4
1
4
1
4
1
4
1
4
1
4
1
2 ACBDABDCADBC
=
= 2PN
2
+ 2RS
2
+ 2KM
2
.
AD
2
+ BD
2
+ CD
2
+ AB
2
+ BC
2
+ AC
2
= 4(PN
2
+ KM
2
+ RS
2
). Ч.т.д.
A
B
C
A
1
B
1
C
1
D
1
O
D
F
E
C
A
B
D
M
P
K
N
R
S
http://alexbooks.ucoz.com
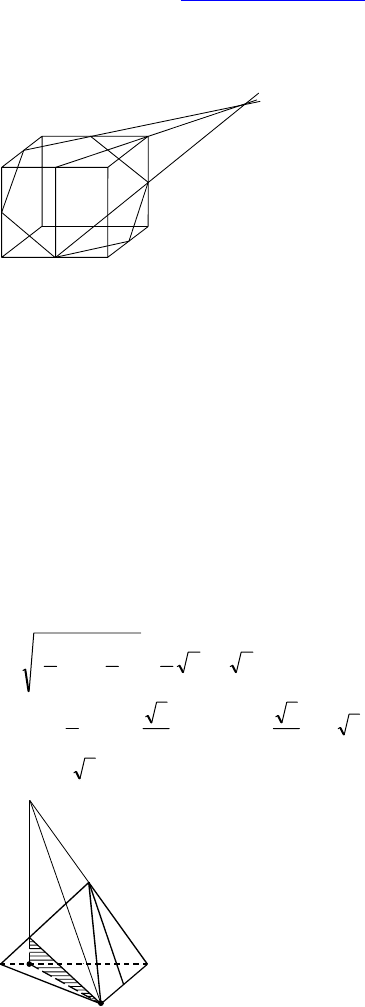
68
С-6.
1.
Дано: ABCDA
1
B
1
C
1
D
1
— куб,
ребра равны 8 см. P, M, T —
середины ребер A
1
B
1
, C
1
C, AD.
Построить сечение куба плоско-
стью, проходящей через P, M, T.
Найти: S
сеч
— ?
Построение:
Через точку T проведем прямую TT′, параллельную AA
1
, T′ —
середина A
1
D
1
; TT′ ∩ A
1
D
1
= T′.
Пусть TM ∩ T′C
1
= X. Пусть PX ∩ B
1
C
1
= K.
Проведем KM. В грани AA
1
D
1
D проведем прямую ET, параллель-
ную KM; TE ∩ AA
1
= E.
Проведем EP. В грани DD
1
C
1
C проведем прямую MR, параллель-
ную EP; MR ∩ CD = R.
Проведем TR.
(EPKMRT) — искомое сечение.
Из построения видно, что E — середина AA
1
; K — середина B
1
C
1
;
R — середина CD.
Т к. ABCDA
1
B
1
C
1
D
1
— куб, то EP = PK = KM = MK = TR = ET.
EM || AC; EM = AC. KT || C
1
D; KT = C
1
D. PR || A
1
D’ PR = A
1
D.
Значит, EM = KT = PR.
Значит, EPKMRT — правильный шестиугольник со стороной
242
2
8
2
8
2
8
22
==
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=a см.
S
сеч
= 6 ⋅
2
1
⋅ a ⋅ a ⋅
2
3
= 3 ⋅ 16 ⋅ 2 ⋅
2
3
= 348 см
2
.
Ответ:
348
см
2
.
2.
Дано: DABC — тетраэдр, P ∈ AB, DE —
медиана грани CDB.
Построить сечение тетраэдра плоскостью,
проходящей через точки C и P и парал-
лельной DE.
Построение:
В плоскости DBC через точку C проведем
прямую, параллельную DE. Она пересекает-
ся с прямой DB в точке X. Т.к. E — середина
A
B
C
D
A
1
B
1
C
1
D
1
M
E
T
T′
P
K
X
R
C
A
B
D
M
E
P
X
http://alexbooks.ucoz.com

69
BC и DE||CX, то DE — средняя линия ∆XBC. Значит, XD= DB.
Пусть XP ∩ AD = M. (MPC) — искомое сечение.
DE || (MPC), т.к. DE || XC и XC ∈ (MPC).
С-7.
1. Дано: ∆ABC; A ∈ α; BC || α; BB
1
⊥ α;
CC
1
⊥ α; CC
1
= 4; AC
1
= 209 ,
AB
1
= 33 , ∠BAC = 60°.
Найти: BC — ?
Решение: Т.к. BC || α, то BB
1
= CC
1
= 4. BB
1
⊥ α, CC
1
⊥ α.
Значит, B
1
BCC
1
— прямоугольник.
∆CC
1
A и ∆BB
1
A — прямоугольные.
CA =
20916
2
1
2
1
+=+ ACCC = 15.
AB =
3316
2
1
2
1
+=+ ABBB = 7.
По теореме косинусов:
BACABACABACBC ∠⋅⋅−+= cos2
22
=
2
1
715249225 ⋅⋅⋅−+
=
=
10549225 −+ = 13. Ответ: 13.
2. Дано: α || β; a ⊥ α; b ⊥ β; a ∩ α = A;
b ∩ β = B; PP
1
∩ α = M.
Построить: a ∩ β, b ∩ α.
Построение: Т.к. α|| β, и a ⊥ α, и b ⊥ β,
то a || b. Значит, они и прямая PP
1
ле-
жат в одной плоскости, которая пере-
секает α по прямой AM, а плоскость β
по прямой, параллельной AM.
Пусть AM ∩ b = B
1
; b
1
= b ∩ α.
Через точку B в плоскости β проведем
прямую BA
1
, параллельную AM. BA
1
∩ a = A
1
. A
1
= a ∩ β.
С-8.
1. Дано: DABC — тетраэдр, AB = BC,
∠DBC = ∠DBA.
Доказать: AC ⊥ DB.
Доказательство:
∆DBC = ∆DBA (по двум сторонам и углу
между ними).
A
B
C
α
B
1
C
B
1
A
P
M
a
b
α
β
A
1
B
P
C
A
B
D
M
http://alexbooks.ucoz.com
70
Значит, DA = DC.
Пусть M — середина AC, тогда DM и BM — медианы равнобед-
ренных ∆ADC и ∆ABC. Значит, AC ⊥ MB; AC ⊥ MD.
Значит, AC ⊥ (MBD). А т.к. DB ∈ (MBD), то AC ⊥ BD. Ч.т.д.
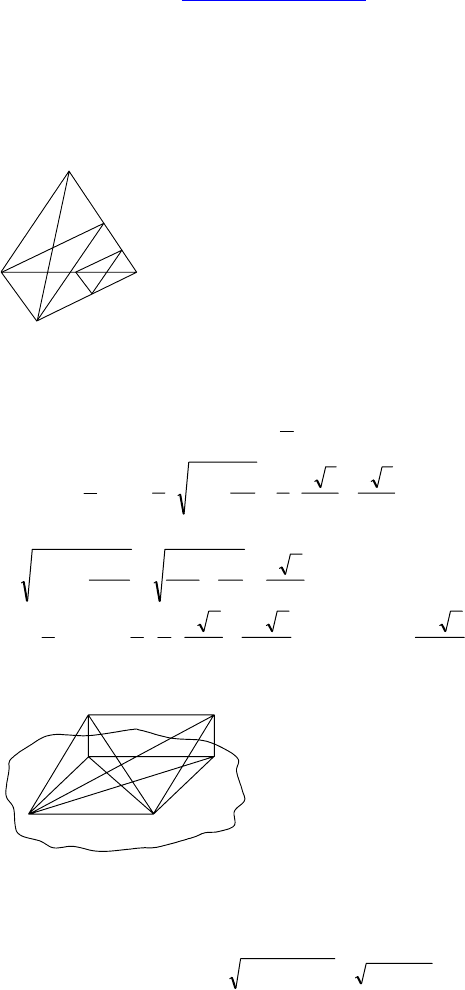
2.
Дано: DABC — тетраэдр, AB=BC= AC = DA =
= DB = DC = a, E — сере
д
ина BC.
Построить сечение тетраэдра плоскостью,
проходящей через точку E и перпендикуляр-
ной DB.
Найти S
сеч
.
Построение:
Пусть M — середина DB. Т к. все грани тетраэдра правильные
треугольники, то CM ⊥ BD и AM ⊥ DB.
Построим EK || CM и KN || AM. (EKN) — искомое сечение.
NE — средняя линия ∆ABC, NE =
2
a
.
EK = NK =
2
1
CM =
4
3
2
3
2
1
42
1
2
2
aaa
a =⋅=−⋅
.
Пусть высота ∆NKE h.
h =
4
2
1616
3
4
222
2
aaaNE
KE =−=−
.
S
сеч
=
2
1
NE ⋅ h =
2
1
⋅
2
a
⋅
4
2
a
=
16
2
2
a
. Ответ:
16
2
2
a
.
С-9.
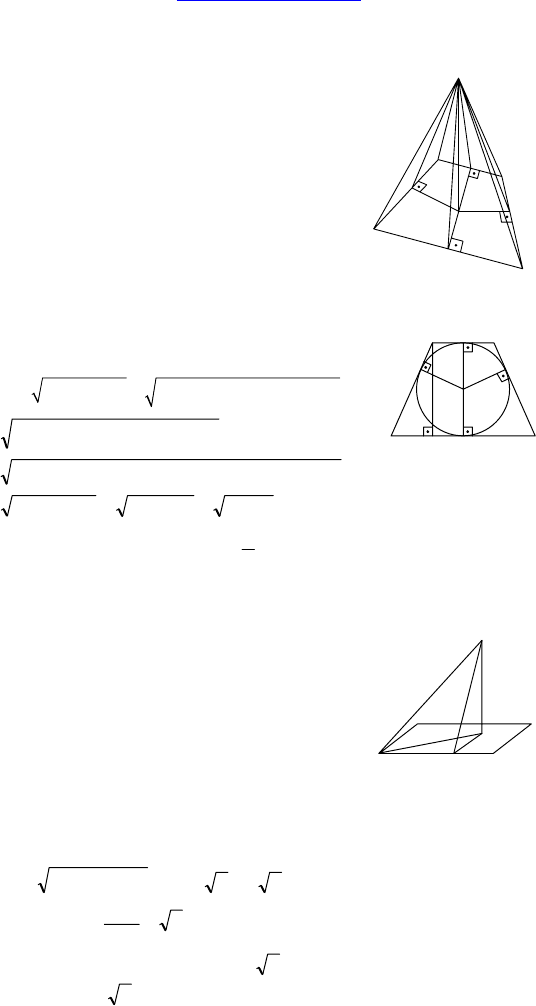
Дано: ABCD — параллелограмм,
A, D ∈ α, B, C ∉ α, AB = 15 см,
BC = 19 см, AC
1
и B
1
D — проек-
ции диагоналей AC и BD на α,
AC
1
=22 см, B
1
D = 20 см.
Найти: d(BC, α) — ?
Решение:
Т к. BC || AD и DA ∈ α, то BC || α. Значит, d(BC, α) = BB
1
= CC
1
.
B
1
C
1
|| BC, B
1
C
1
= BC. Значит, AD = B
1
C
1
; AD || B
1
C
1
.
Значит, AB
1
C
1
D — параллелограмм. По свойству параллелограмма
AC
1
2
+ B
1
D
2
= 2AB
1
2
+ 2AD
2
. 484 + 400 + 2AB
1
2
+ 722;
AB
1
2
= 81, AB
1
= 9 см. BB
1
= 81225
2
1
2
−=− ABAB = 12 см.
Значит, d(BC, α) = 12 см. Ответ: 12 см.
C
A
B
E
N
D
M
K
A
B
D
C
α
C
1
B
1
http://alexbooks.ucoz.com
71
С-10.
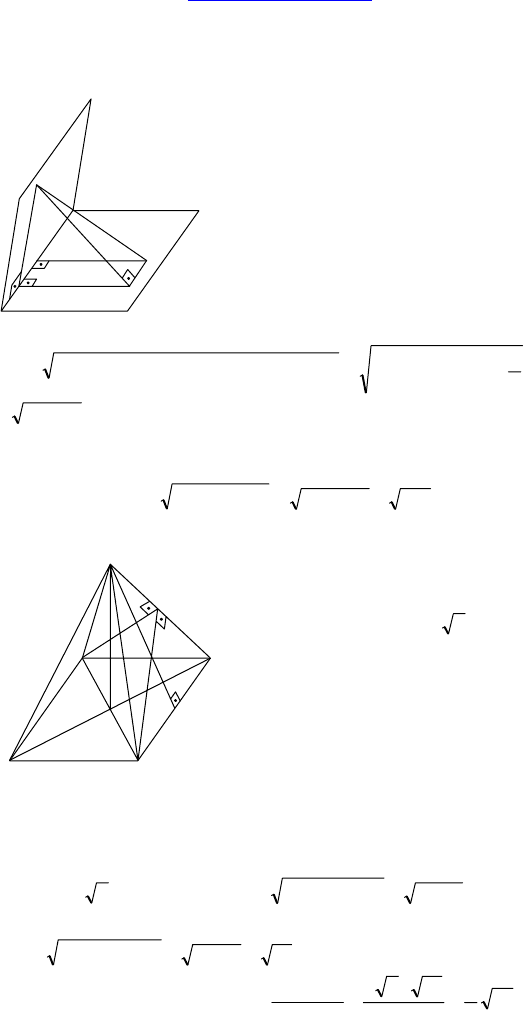
1.
Дано: ABCD — равнобедренная трапе-
ция, d(M, AB) = d(M, BC) = d(M, CD) =
=d(M, AD)=12 см, AD = 32 см, BC = 18 см.
Найти: d(M,(ABC)) — ?
Решение:
Пусть MH ⊥ (ABC). HP ⊥ AB; HR ⊥ BC;
HS ⊥ CD; HT ⊥ AD;
MP ⊥ AB; MR ⊥ BC; MS ⊥ CD; MT ⊥ AD.
∆MHP = ∆ MH
R =
∆MHS = ∆MHT (по гипотенузе и катету).
Значит, HT = HP = HR = HS.
Значит, H — центр вписанной окружности.
22 2 2
()()
B
KABAK APBP ATBR=−=+−−=
=
22
)()( BRATBRAT −−+ =
=
))(( BRATBRATBRATBRAT −+++−+ =
=
ATBR 22 ⋅ = ADBC ⋅ = 3218 ⋅ = 24 см.
Значит, HR = HP = HS = HT =
2
1
BH = 12 см.
Значит, M — лежит в плоскости трапеции.
Ответ: M — лежит в плоскости трапеции.
2. Дано: ABCD — прямоугольник, AM —
наклонная, ∠MAB = ∠MAD = 50°.
Найти: ∠(AM, (ABC)) — ?
Решение:
Пусть MH ⊥ (ABC). Т.к. ∠MAB = ∠MAD,
то H лежит на биссектрисе ∠BAD.
Пусть HE ⊥ AD. По ТТП ME ⊥ AD.
Пу
сть AM = a. Тогда AE
= AM ⋅ cos50° = acos50°.
Т к. AH — биссектриса ∠BAD, то ∠HAE = 45°. Значит, ∆AEH —
равнобедренный.
°⋅=⋅=+= 50cos22
22
aAEEHAEAH .
cos∠(MAH) =
°= 50cos2
AM
AH
.
Значит, ∠(AM, (ABC)) = arccos(
2 cos50°).
Ответ: arccos(
2 cos50°).
A
B
D
C
T
P
H
S
R
M
A
B
D
C
T
P
H
S
R
K
B
C
D
E
A
M
H
http://alexbooks.ucoz.com
72
С-11.
1.
Дано: концы отрезка AB = 25 см лежат
на гранях двугранного угла, равного
60°. Из точек A и B опущены перпен-
дикуляры AC и BD на ребра двугранно-
го угла. AC = 5 см, BD = 8 см.
Найти: CD — ?
Решение:
Через точку C в плоскости (BDC) про-
водим прямую, параллельную BD.
CK = BD, CK ⊥ CD. CDBK — пр
ямо
угольник. ∠ACK = 60°.
AK =
ACKCKACCKAC ∠⋅⋅−+ cos2
22
=
2
1
8526425 ⋅⋅⋅−+
=
=
4089 − = 7.
Т к. CD ⊥ AC и CD ⊥ CK, то CD ⊥ (ACK).
Значит, KB ⊥ (ACK) ⇒ KB ⊥ AK.
Значит, CD = KB =
22
AKAB − = 49625 − = 576 = 24 см.
Ответ: 24 см.
2.
Дано: ABCD — квадрат, AC ∩ BD= O,
OM ⊥ (ABC), OM = 3,
AB = BC = CD = AD =
24 .
Найти: ∠((BMC), (DMC)).
Решение:
Т.к. ABCD — квадрат, то AO = BO =
= CO = DO.
Значит, ∆OMB = ∆OMC = ∆OMD
(по двум катетам).
Значит, BM = MC = MD.
Значит, ∆MBC = ∆MCD (по трем сторонам).
Значит, если DH ⊥ MC, то BH ⊥ MC.
Значит, ∠((BMC), (DMC)) = ∠BHD.
BD = AD ⋅
2 = 8, OD = 4, MD = 169
22
+=+ ODMO = 5.
MK — высота и медиана ∆CDM.
MK =
17825
22
=−=− DKMD .
MK ⋅ CD = DH ⋅ CM; DH = BH =
CM
MKCD ⋅
=
5
1724
⋅
=
34
5
4
.
C
A
D
B
K
B
A
O
H
C
D
K
M
http://alexbooks.ucoz.com
73
По теореме косинусов
cos∠BHD =
HDBH
HDBHBD
⋅
++−
2
222
=
34
25
16
2
34
25
16
34
25
16
64
⋅⋅
⋅+⋅+−
=
17
8
−
.
Значит, ∠((BMC), (DMC)) = arccos
⎟
⎠
⎞
⎜
⎝
⎛
−
17
8
.
Ответ: arccos
⎟
⎠
⎞
⎜
⎝
⎛
−
17
8
.
С-12.
1.
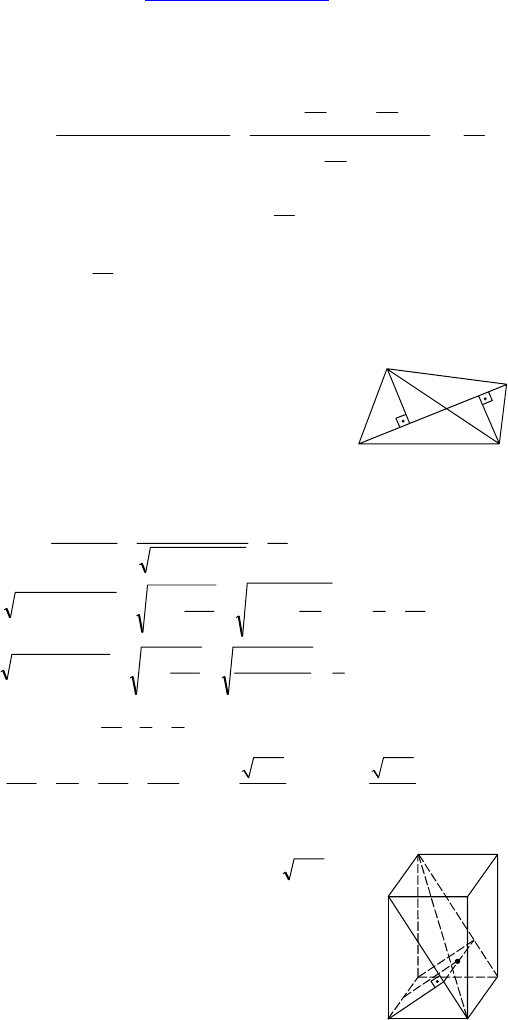
Дано: ABCD — прямоугольник, AB = 3,
AD = 4, прямоугольник перегнут по диаго-
нали AC так, что образовался прямой дву-
гранный угол.
Найти: BD.
Решение: BM ⊥ AC, DN ⊥ AC, BD
2
= BM
2
+ MN
2
+ ND
2
.
BM = ND =
5
12
22
=
+
⋅
=
⋅
BCAB
BCAB
AC
BCAB
.
MC =
5
16
5
4
4
25
9
116
25
144
16
22
=⋅=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=− BMBC
.
NC =
5
9
25
144225
25
144
9
22
=
−
=−=− NDCD .
MN = MC – NC =
16 9 7
555
−=
.
BD
2
=
25
337
25
144
25
49
25
144
=++
, BD =
337
5
. Ответ:
337
5
.
2.
Дано: ABCDA
1
B
1
C
1
D
1
— прямоугольный па-
раллелепипед, AB = 4, AB
1
= 15, B
1
D =
305
.
Найти: d(AB, B
1
D) — ?
Изобразить общий перпендикуляр этих пря-
мых.
Решение:
AB || (DA
1
B
1
), AE ⊥ A
1
D; AE ⊥ CD.
Значит, d(AB, B
1
D) = d(AB, (DA
1
B
1
)) = AE.
B
C
A
D
N
M
A
B
C
D
A
1
B
1
C
1
D
1
E
F
P
Q
http://alexbooks.ucoz.com
