Трофимова Т.И. Курс физики
Подождите немного. Документ загружается.


мгновенные силы) столь велики, что вне-
шними силами, действующими на них,
можно пренебречь. Это позволяет сис-
тему тел в процессе их соударения при-
ближенно рассматривать как замкну-
тую систему и применять к ней законы
сохранения.
Тела во время удара испытывают
деформацию. Сущность удара заключа-
ется в том, что кинетическая энергия
относительного движения соударяю-
щихся тел на короткое время преобра-
зуется в энергию упругой деформации.
Во время удара имеет место перерасп-
ределение энергии между соударяющи-
мися телами. Наблюдения показывают,
что относительная скорость тел после
удара не достигает своего прежнего зна-
чения. Это объясняется тем, что нет
идеально упругих тел и идеально глад-
ких поверхностей. Отношение нор-
мальных составляющих относительной
скорости тел после и до удара называ-
ется коэффициентом восстановле-
ния е:
Если для сталкивающихся тел е
=
О,
то такие тела называются абсолютно
неупругими, если
е
= 1 — абсолютно
упругими. На практике для всех тел
О <
е
< 1 (например, для стальных ша-
ров
е
«
0,56, для шаров из слоновой ко-
сти
£ «
0,89, для свинца
е
«
0). Однако
в некоторых случаях
тела
можно с боль-
шой степенью точности рассматривать
либо как абсолютно упругие, либо как
абсолютно неупругие.
Прямая, проходящая через точку
соприкосновения тел и нормальная к
поверхности их соприкосновения, на-
зывается линией удара. Удар называ-
ется центральным, если тела до удара
движутся вдоль прямой, проходящей
через их центры масс. Мы будем рас-
сматривать только центральные абсо-
лютно упругие и абсолютно неупругие
удары.
Абсолютно упругий удар — столк-
новение двух тел, в результате которо-
го в обоих взаимодействующих телах не
остается никаких деформаций и вся ки-
нетическая энергия, которой обладали
тела до удара, после удара снова превра-
щается в кинетическую энергию (под-
черкнем, что это идеализированный слу-
чай).
Для абсолютно упругого удара вы-
полняются закон сохранения импуль-
са и закон сохранения кинетической
энергии.
Обозначим скорости шаров массами
т
1
ит
2
до удара через
v
l
и
v
2
,
после уда-
ра — через
v[
и
v
2
(рис. 19). В случае
прямого центрального удара векторы
скоростей шаров до и после удара ле-
жат на прямой линии, соединяющей их
центры. Проекции векторов скорости
на эту линию равны модулям скорос-
тей. Их направления учтем знаками:
положительное значение припишем
движению вправо, отрицательное —
движению влево.
При указанных допущениях законы
сохранения имеют вид
Произведя соответствующие преоб-
разования в выражениях (15.1) и (15.2),
получаем
31
(15.3)
(15.4)
откуда
(15.5)
Решая уравнения (15.3) и (15.5), на-
ходим
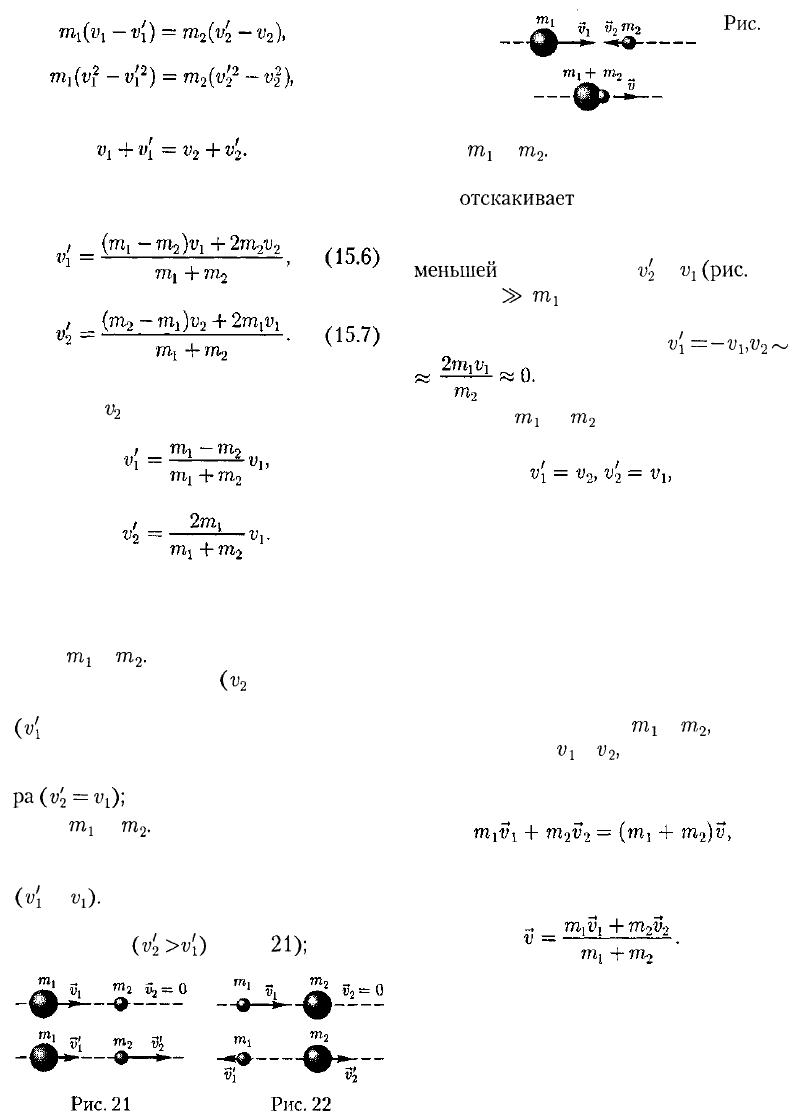
Разберем несколько примеров.
1. При
v
2
— О
(15.8)
(15.9)
Проанализируем выражения (15.8)
и (15.9) для двух шаров различных
масс:
а)
т
г
=
т
2
.
Если второй шар до уда-
ра висел неподвижно
(v
2
= 0) (рис. 20),
то после удара остановится первый шар
(v[
= 0), а второй будет двигаться с той
же скоростью и в том же направлении,
в котором двигался первый шар до уда-
ра(г;
2
=
г;
1
);
б)
т
х
>
т
2
.
Первый шар продолжа-
ет двигаться в том же направлении, как
и до удара, но с меньшей скоростью
(v'i
<
Vi).
Скорость второго шара после
удара больше, чем скорость первого
после удара
(v'
2
>
v[)
(рис.
21);
Рис.
23
в)
m
:
<
m2.
Направление движения
первого шара при ударе изменяется —
шар
отс^^акивает
обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с
мен^^ей
скоростыо, т. е. ^^^ <
^^i
(рис.
22);
г) m2 ^^^
m
:
(например, столкнове-
ние шара со стеной). Из уравнений
(15.8) и (15.9) следует, что
v[
=
—v
b
v
2
~
2. При
т
х
—
т
2
выражения (15.6) и
(15.7) будут иметь вид
т.е. шары равной массы «обменивают-
ся» скоростями.
Абсолютно неупругий удар — стол-
кновение двух тел, в результате которого
тела объединяются, двигаясь дальше как
единое целое. Продемонстрировать аб-
солютно неупругий удар можно с помо-
щью шаров из пластилина (глины), дви-
жущихся навстречу друг другу (рис. 23).
Если массы шаров
т
х
и
т
2
,
их ско-
рости до удара
у
г
и
v
2
,
то, используя за-
кон сохранения импульса, можно запи-
сать
где v — скорость движения шаров пос-
ле удара. Тогда
(15.10)
Если шары движутся навстречу друг
другу, то они вместе будут продолжать
двигаться в ту сторону, в которую дви-
гался шар, обладающий большим им-
пульсом. В частном случае, если массы
шаров равны (т
1
— m
2
), то
32

Выясним, как изменяется кинети-
ческая энергия шаров при центральном
абсолютно неупругом ударе. Так как в
процессе соударения шаров между
ними действуют силы, зависящие не от
самих деформаций, а от их скоростей,
то мы
имеем
дело с силами, подобны-
ми силам трения, поэтому закон сохра-
нения механической энергии не должен
соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю»
можно определить по разности кинети-
ческой энергии тел до и после удара:
Используя (15.10), получаем
Если ударяемое тело было первона-
чально неподвижно
(и
2
= 0), то
Когда
т
2
>•
т
х
(масса неподвижно-
го тела очень большая), то v
<C
v
h
и по-
чти вся кинетическая энергия тела при
ударе переходит в другие формы энер-
гии. Поэтому, например, для получения
значительной
деформации наковальня
должна быть массивнее молотка. На-
оборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей
{т
{
>
гп
2
),
тогда v
«
v
{
и
прак-
тически вся энергия затрачивается на
возможно большее перемещение гвоз-
дя, а не на остаточную деформацию
стены.
Абсолютно неупругий удар — при-
мер того, как происходит «потеря» ме-
ханической энергии под действием дис-
сипативных сил.
Контрольные вопросы
В чем различие между понятиями энергии и работы?
Как найти работу неременной силы?
Какую работу совершает равнодействующая всех сил, приложенных к телу, равномер-
но движущемуся по окружности?
Что такое мощность? Выведите ее формулу.
Дайте определения и выведите формулы для известных видов механической энергии.
Какова связь между силой и потенциальной энергией?
Чем обусловлено изменение потенциальной энергии?
Необходимо ли условие замкнутости системы для выполнения закона сохранения ме-
ханической энергии?
В чем заключается закон сохранения механической энергии? Для каких систем он вы-
полняется?
В чем
физическая
сущность закона сохранения и превращения энергии? Почему он яв-
ляется фундаментальным законом природы?
Что такое потенциальная яма? потенциальный барьер?
Какие заключения о характере движения тел можно сделать из анализа потенциальных
кривых?
Как охарактеризовать положения устойчивого и неустойчивого равновесия?
Чем отличается абсолютно упругий удар от абсолютно неупругого?
Как определить скорости тел после центрального абсолютно упругого удара? Следствием
каких законов являются эти выражения?
2 Курс финики
33
ЗАДАЧИ
3.1. Определите: 1) работу поднятия груза по наклонной плоскости; 2) среднюю и 3) мак-
симальную мощности подъемного устройства, если масса груза 10 кг, длина наклонной
плоскости 2 м, угол наклона к горизонту 45°, коэффициент трения 0,1 и время подъема 2 с.
[1) 173 Дж; 2) 86 Вт; 3) 173 Вт]
3.2. С башни высотой 35 м горизонтально
брошей
камень массой 0,3 кг. Пренебрегая
сопротивлением воздуха, определите: 1) скорость, с которой брошен камень, если через 1 с
после начала
движения
его кинетическая энергия составила 60 Дж; 2) потенциальную энер-
гию камня через 1 с после начала движения. [1) 17,4 м/с; 2)
88,6
Дж]
3.3. Пренебрегая трением, определите наименьшую высоту, с которой должна скаты-
ваться тележка с человеком по желобу, переходящему в петлю радиусом 10 м, чтобы она
сделала полную петлю и не выпала из желоба. [25 м]
3.4. Пуля массой т = 10 г, летевшая горизонтально со скоростью v = 500 м/с, попадает в
баллистический маятник длиной
/
— 1 м и массой М= 5 кг и застревает в нем. Определите
угол отклонения маятника.
[16°30
/
J
3.5. Зависимость потенциальной энергии частицы в центральном силовом поле от рас-
А В
стояния
г
до центра поля задается выражением
П(г)
= — , где А
и
В — положительные
Н
г
постоянные. Определите значение
г
0
,
соответствующее равновесному положению частицы.
Является ли это положение положением устойчивого равновесия?
[г
0
=
— ]
3.6. При центральном абсолютно упругом ударе движущееся тело массой
т
1
ударяется
о покоящееся тело массой
т
2
,
в результате чего скорость первого тела уменьшается в п =
= 1,5 раза. Определите: 1) отношение
^-;
2) кинетическую энергию
Т'
2
второго тела, если
первоначальная кинетическая энергия
первого
тела
Т
г
= 1000 Дж. [1) 5; 2) 555 Дж]
3.7. Тело массой
т
х
= 4 кг движется со скоростью
v
x
= 3 м/с
и
ударяется о неподвижное
тело такой же массы. Считая удар центральным и неупругим, определите количество теп-
лоты, выделившееся при ударе. [9 Дж]
Глава 4
МЕХАНИКА ТВЕРДОГО ТЕЛА
§ 16. Момент инерции
При изучении вращения твердых тел
пользуются понятием момента инер-
ции. Момент инерции тела — мера
инертности твердых тел при вращатель-
ном движении. Его роль такая же, что и
массы при поступательном движении.
Моментом инерции системы (тела)
относительно данной оси называется
физическая величина, равная сумме
произведений масс п материальных то-
чек системы на квадраты их расстоянии
до рассматриваемой оси:
Суммирование производится по
всем элементарным массам
пц,
на кото-
рые разбивается тело (рис. 24).
В случае непрерывного распределе-
ния масс эта сумма сводится к интегралу
34
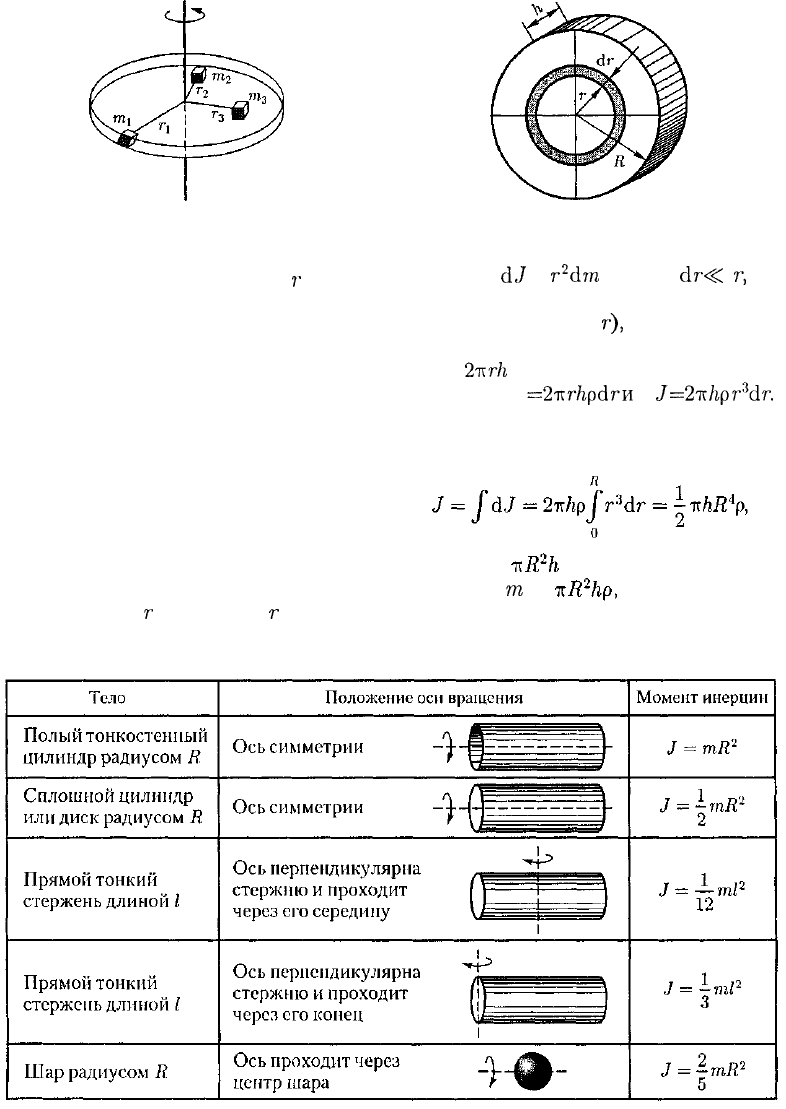
Рис. 24
Рис. 25
где интегрирование производится по
всему объему тела. Величина
г
в этом
случае есть функция положения точки
с координатами х, у, z. Момент инер-
ции — величина аддитивная: момент
инерции тела относительно некоторой
оси равен сумме моментов инерции ча-
стей тела относительно той же оси.
В качестве примера найдем момент
инерции однородного сплошного ци-
линдра высотой h и радиусом R отно-
сительно его геометрической оси (рис.
25). Разобьем цилиндр на отдельные
полые концентрические цилиндры бес-
конечно малой толщины dr с внутрен-
ним радиусом
г
и внешним
г
+ dr.
Момент инерции каждого полого
цилиндра
d,/
=
r
2
dm
(так как
dr
<§C
г,
то
считаем, что расстояние всех точек ци-
линдра от оси равно
г),
где dm — масса
всего элементарного цилиндра; его
объем
2ттr/i
dr. Если р — плотность мате-
риала, то dm
=
2-Krhpdrn
d
J=
2тс/фгМг.
Тогда момент инерции сплошного ци-
линдра
но так как — объем цилиндра, то
его масса
т
= а момент инер-
ции
Таблица 1
35
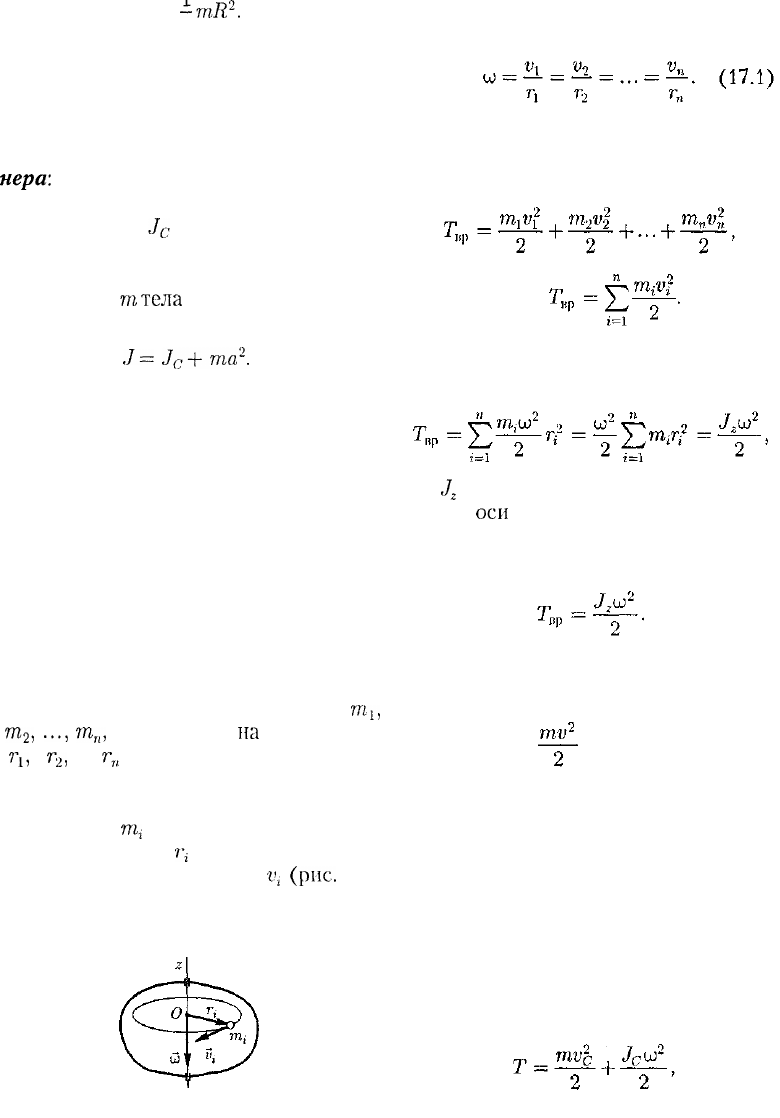
J =
~m.R
2
.
2
Если известен момент инерции тела
относительно оси, проходящей через
его центр масс, то момент инерции от-
носительно любой другой параллель-
ной оси определяется теоремой Штей-
нера:
момент инерции тела J относи-
тельно произвольной оси равен момен-
ту его инерции
«/
с
относительно парал-
лельной оси, проходящей через центр
масс С тела, сложенному с произведе-
нием массы
ттела
на квадрат расстоя-
ния а между осями:
J=
J
c
+ma
2
.
(16.1)
В заключение приведем значения
моментов инерции (табл. 1) для неко-
торых тел (тела считаются однородны-
ми, т — масса тела).
§ 17. Кинетическая энергия
вращения
Рассмотрим абсолютно твердое тело
(см. § 1), вращающееся около неподвиж-
ной оси z, проходящей через него. Мыс-
ленно разобьем это тело на маленькие
объемы с элементарными массами
т
и
т
2
,
••-,
т
п
,
находящиеся
на
расстоянии
7\,
г
2
,
...,
г
п
от оси. При вращении твер-
дого тела относительно неподвижной
оси отдельные его элементарные объе-
мы массами
т
г
опишут окружности раз-
личных радиусов
i\
и будут иметь раз-
личные линейные скорости
г\
(рис.
26).
Но так как мы рассматриваем абсолют-
Рис.
26
но твердое тело, то угловая скорость
вращения этих объемов одинакова:
Кинетическую энергию вращающе-
гося тела найдем как сумму кинетиче-
ских энергий его элементарных объемов:
или
Используя выражение (17.1), полу-
чим
где
J
z
— момент инерции тела относи-
тельно
оси
z.
Таким образом, кинетическая энер-
гия вращающегося тела
(17.2)
Из сравнения формулы (17.2) с вы-
ражением (12.1) для кинетической
энергии тела, движущегося поступа-
тельно ( Т = ), следует, что, как
уже указывалось (см. § 16), момент
инерции — мера инертности тела при
вращательном движении. Формула
(17.2) справедлива для тела, вращаю-
щегося вокруг неподвижной оси.
В случае плоского движения тела,
например цилиндра, скатывающегося с
наклонной плоскости без скольжения,
энергия движения складывается из
энергии поступательного движения и
энергии вращения:
36
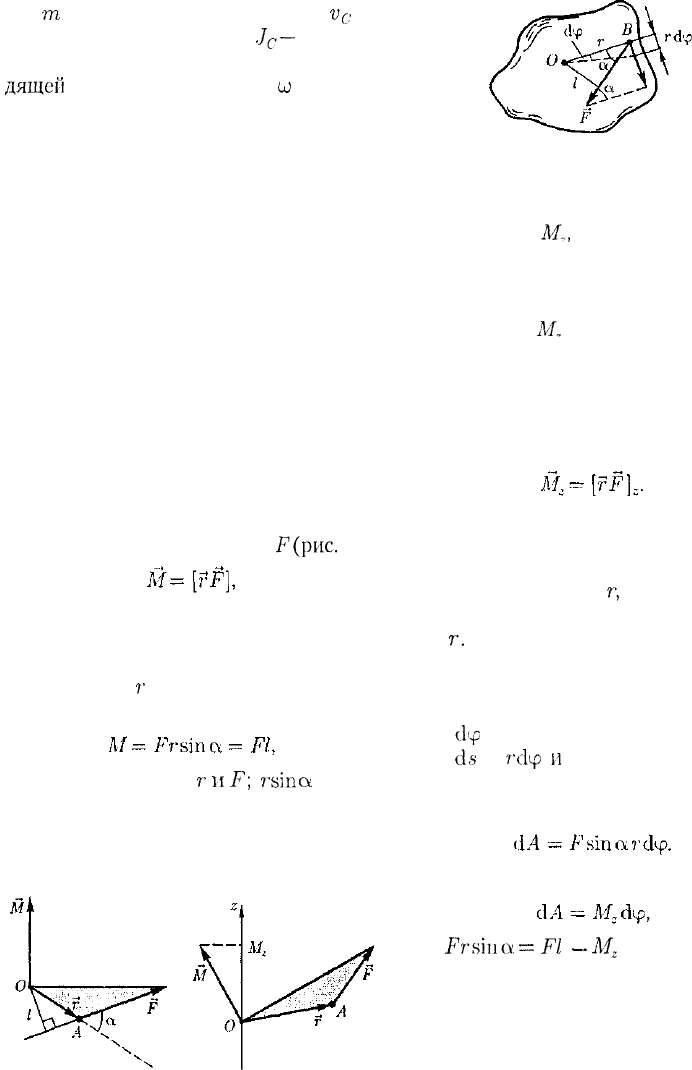
где
т
— масса катящегося тела;
v
c
—
скорость центра масс тела;
J
c
—
момент
инерции тела относительно оси, прохо-
дящей
через его центр масс;
ш
-- угло-
вая скорость тела.
Рис. 29
§ 18. Момент силы. Уравнение
динамики вращательного
движения твердого тела
Для характеристики вращательного
эффекта силы при действии ее на твер-
дое тело вводят понятие момента силы.
Различают моменты силы относитель-
но неподвижной точки и относительно
неподвижной оси.
Моментом силы относительно
неподвижной точки О называется фи-
зическая величина М, определяемая век-
торным произведением радиуса-векто-
ра г, проведенного из точки О в точку
Л приложения силы, на силу
F(pnc.
27):
где М— псевдовектор, его направление
совпадает с направлением поступатель-
ного движения правого винта при его
вращении от
г
к F.
Модуль момента силы
(18.1)
где а — угол между
г
и
F;
r
sin
а
= / —
кратчайшее расстояние между линией
действия силы и точкой О — плечо
силы.
Рис. 27
Рис.28
Моментом силы относительно
неподвижной оси z называется скаляр-
пая величина
М,,
равная проекции на
эту ось вектора Л/момента силы, опре-
деленного относительно произвольной
точки О данной оси z (рис. 28). Значе-
ние момента
М,
не зависит от выбора
положения точки О на оси z.
Если ось z совпадает с направлени-
ем вектора М, то момент силы представ-
ляется в виде вектора, совпадающего с
осью:
Найдем выражение для работы при
вращении тела (рис. 29). Пусть сила F
приложена в точке В, находящейся от
оси z на расстоянии
г,
а — угол между
направлением силы и радиусом-векто-
ром
т.
Так как тело абсолютно твердое,
то работа этой силы равна работе, за-
траченной на поворот всего тела. При
повороте тела на бесконечно малый
угол
(1ф
точка приложения В проходит
путь
ds
—
г
dip
и
работа равна произве-
дению проекции силы на направление
смещения на величину смещения:
(18.2)
Учитывая (18.1), можем записать
где
Frsiua
=
Fl
~
M
z
— момент силы
относительно оси z. Таким образом, ра-
бота при вращении тела равна произве-
дению момента действующей силы на
угол поворота.
Работа при вращении тела идет на
увеличение его кинетической энергии:
37
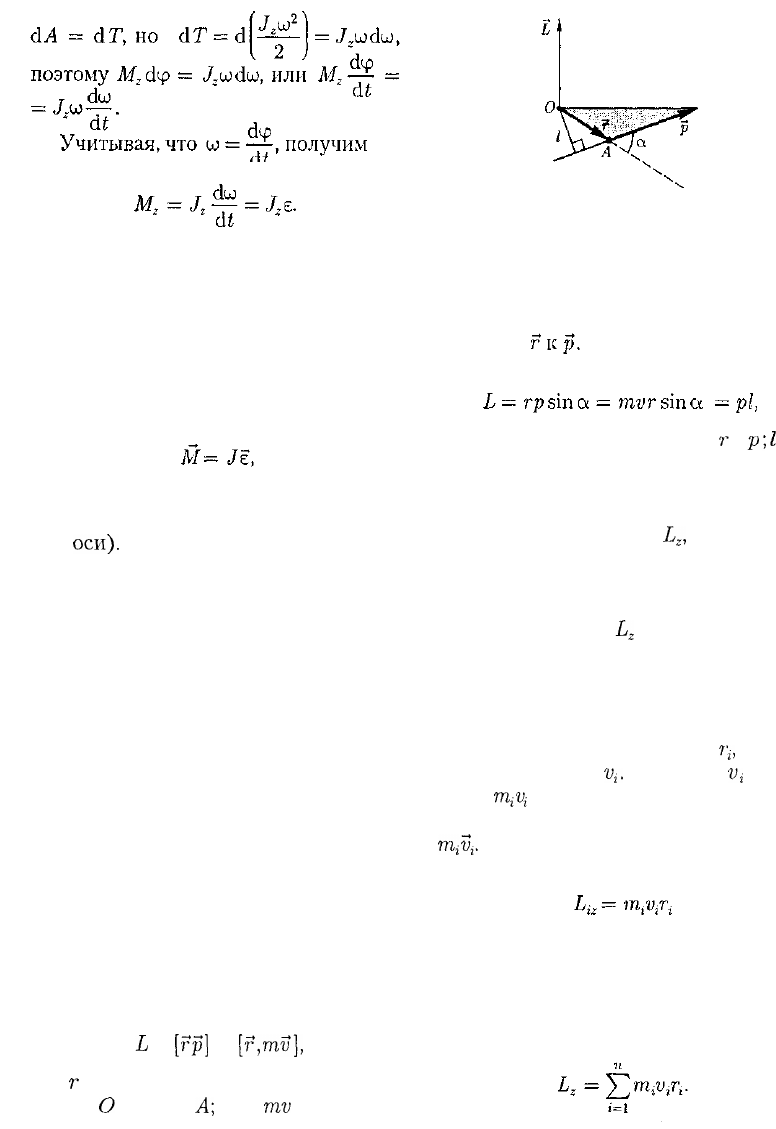
(18.3)
Уравнение (18.3) представляет со-
бой уравнение динамики вращатель-
ного движения твердого тела отно-
сительно неподвижной оси.
Можно показать, что если ось z со-
впадает с главной осью инерции (см.
§ 20), проходящей через центр масс, то
имеет место векторное равенство
(18.4)
где J — главный момент инерции тела
(момент инерции относительно глав-
ной
оси).
§ 19. Момент импульса
и закон его сохранения
При сравнении законов вращатель-
ного и поступательного движений про-
сматривается аналогия между ними,
только во вращательном движении вме-
сто силы «выступает» ее момент, а роль
массы «выполняет» момент инерции.
Какая же величина будет аналогом им-
пульса тела? Ею является момент им-
пульса тела относительно оси.
Моментом импульса (количества
движения) материальной точки А от-
носительно неподвижной точки О
называется физическая величина, опре-
деляемая векторным произведением:
L
=
[rp]
= [r,mv],
где
г
— радиус-вектор, проведенный из
точки
О
в точку
А;
р =
mv
— импульс
Рис. 30
материальной точки (рис. 30); L — псев-
довектор (см. § 4), его направление со-
впадает с направлением поступательно-
го движения правого винта при его вра-
щении от
Модуль вектора момента импульса
где а — угол между векторами
г
и
р;
/
—
плечо вектора р относительно точки О.
Моментом импульса относи-
тельно неподвижной оси z называет-
ся скалярная величина
Ь
г
,
равная про-
екции на эту ось вектора момента им-
пульса, определенного относительно
произвольной точки О данной оси.
Момент импульса
L
z
не зависит от по-
ложения точки О на оси z.
При вращении абсолютно твердого
тела вокруг неподвижной оси z каждая
отдельная точка тела движется по ок-
ружности постоянного радиуса
г
г
,
с неко-
торой скоростью
ц.
Скорость
Vi
и им-
пульс
т
г
ц
перпендикулярны этому ради-
усу, т. е. радиус является плечом вектора
тД.
Поэтому можем записать, что мо-
мент импульса отдельной частицы равен
(19.1)
и направлен по оси в сторону, опреде-
ляемую правилом правого винта.
Момент импульса твердого тела
относительно оси есть сумма моментов
импульса отдельных частиц:
38

Используя формулу (17.1)
получим
тельно оси равна моменту сил относи-
тельно той же оси.
Можно показать, что имеет место
векторное равенство
т.е.
(19.2)
Таким образом, момент импульса
твердого тела относительно оси равен
произведению момента инерции тела
относительно той же оси на угловую
скорость.
Продифференцируем уравнение
(19.2) по времени:
(19.3)
т.е.
Это выражение — еще одна форма
уравнения динамики вращательного
движения твердого тела относитель-
но неподвижной оси: производная мо-
мента импульса твердого тела относи-
В замкнутой системе момент вне-
шних сил М = 0 и — —
0,
откуда
dt
L = const. (19.4)
Выражение (19.4) представляет со-
бой закон сохранения момента им-
пульса: момент импульса замкнутой
системы сохраняется, т.е. не изменяет-
ся с течением времени.
Закон сохранения момента импуль-
са — фундаментальный закон природы.
Он связан со свойством симметрии
пространства — его изотропностью,
т.
е.
с инвариантностью физических зако-
нов относительно выбора направления
осей координат системы отсчета (отно-
сительно поворота замкнутой системы
в пространстве на любой угол).
Таблица
2
39
Piic. 31
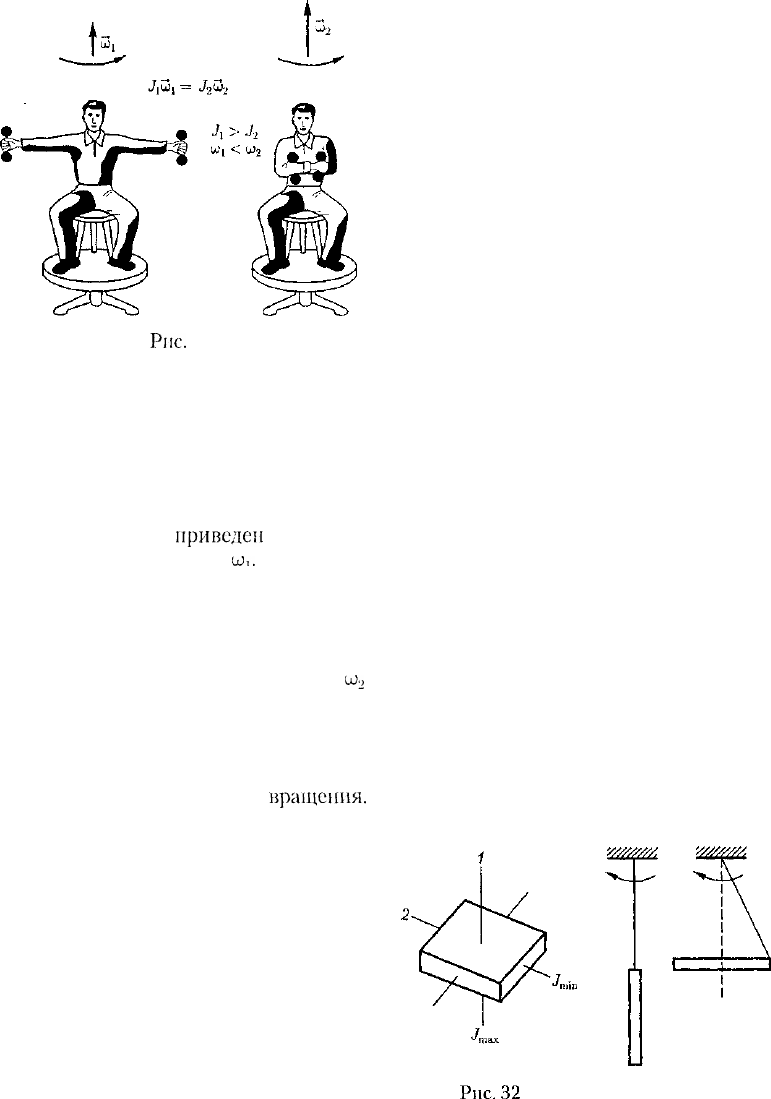
Продемонстрировать закон сохране-
ния момента импульса можно с помо-
щью скамьи Жуковского. Пусть чело-
век, сидящий на скамье, которая без
трения вращается вокруг вертикальной
оси, и держащий на вытянутых руках
гантели (рис. 31),
приведен
во враще-
ние с угловой скоростью
ш,.
Если чело-
век прижмет гантели к себе, то момент
инерции системы уменьшится. По-
скольку момент внешних сил равен
нулю, момент импульса системы сохра-
няется и угловая скорость вращения
ш
2
возрастает. Аналогично, гимнаст во вре-
мя прыжка через голову поджимает к
туловищу руки и ноги, чтобы умень-
шить свой момент инерции и увеличить
тем самым угловую скорость
вращения.
Сопоставим основные величины и
уравнения, определяющие вращение
тела вокруг неподвижной оси и его по-
ступательное движение (табл. 2).
§ 20. Свободные оси. Гироскоп
Для того чтобы сохранить положе-
ние оси вращения твердого тела с тече-
нием времени неизменным, использу-
ют подшипники, в которых она удержи-
вается. Однако существуют такие оси
вращения тел, которые не изменяют
своей ориентации в пространстве без
действия на нее внешних сил. Эти оси
называются свободными осями (или
осями свободного вращения).
Можно доказать, что в любом теле
существуют три взаимно перпендику-
лярные оси, проходящие через центр
масс тела, которые могут служить сво-
бодными осями (они называются глав-
ными осями инерции тела). Например,
главные оси инерции однородного пря-
моугольного параллелепипеда прохо-
дят через центры противоположных
граней (рис. 32).
Для однородного цилиндра одной из
главных осей инерции является его гео-
метрическая ось, а в качестве остальных
осей могут быть две любые взаимно
перпендикулярные оси, проведенные
через центр масс в плоскости, перпен-
дикулярной геометрической оси ци-
линдра. Главными осями инерции шара
являются любые три взаимно перпен-
дикулярные оси, проходящие через
центр масс.
Для устойчивости вращения боль-
шое значение имеет, какая именно из
свободных осей служит осью вращения
тела. Так, вращение вокруг главных
осей с наибольшим и наименьшим мо-
ментами инерции оказывается устойчи-
вым, а вращение около оси со средним
Рис. 33
40
