Трансформаторы и электрические машины
Подождите немного. Документ загружается.

71
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Òó ÷àñòü ñèíõðîííîé ìàøèíû, â îáìîòêå êîòîðîé íàâîäèòñÿ ÝÄÑ è
ïðîòåêàåò òîê íàãðóçêè, íàçûâàþò ÿêîðåì, à ÷àñòü ìàøèíû, ãäå
ðàñïîëîæåíà îáìîòêà âîçáóæäåíèÿ, íàçûâàåòñÿ èíäóêòîðîì. Â
ñèíõðîííîé ìàøèíå (ñì. ðèñ. 3.2) ñòàòîð ÿâëÿåòñÿ ÿêîðåì, à ðîòîð
èíäóêòîðîì.  íåêîòîðûõ ñëó÷àÿõ îáìîòêó ÿêîðÿ ðàñïîëàãàþò íà ðîòîðå,
à îáìîòêó âîçáóæäåíèÿ íà ñòàòîðå.
3.2. Õîëîñòîé õîä ñèíõðîííîãî ãåíåðàòîðà
Ðåæèì ðàáîòû ãåíåðàòîðà, ïðè êîòîðîì òîê â îáìîòêå ÿêîðÿ
(ñòàòîðà) ðàâåí íóëþ, íàçûâàåòñÿ õîëîñòûì õîäîì. Ïðè õîëîñòîì õîäå
ìàãíèòíûé ïîòîê Ô
0
ñîçäàåòñÿ òîëüêî ÌÄÑ îáìîòêè âîçáóæäåíèÿ. Ýòîò
ïîòîê, ïðîõîäÿ ÷åðåç âîçäóøíûé çàçîð, ñöåïëÿåòñÿ ñ îáìîòêîé ÿêîðÿ
è ïðè âðàùåíèè èíäóêòîðà íàâîäèò â êàæäîé ôàçå îáìîòêè ÿêîðÿ ÝÄÑ.
Ôîðìà êðèâîé ÝÄÑ, èíäóöèðîâàííîé â îáìîòêå ÿêîðÿ ïðè õîëîñòîì
õîäå, äîëæíà áûòü âîçìîæíî áëèæå ê ñèíóñîèäå. Äëÿ ïîëó÷åíèÿ áëèçêîé
ê ñèíóñîèäàëüíîé ôîðìû êðèâîé íàïðÿæåíèÿ (ÝÄÑ) íåîáõîäèìî, ÷òîáû
ðàñïðåäåëåíèå ìàãíèòíîãî ïîòîêà ïî îêðóæíîñòè ñòàòîðà ãåíåðàòîðà
áûëî áëèçêèì ê ñèíóñîèäàëüíîìó.
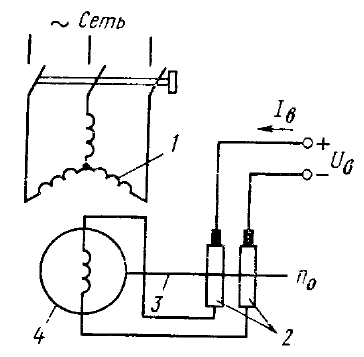
Íà ðèñ. 3.3 ïîêàçàíà ñõåìà ñèíõðîííîãî ãåíåðàòîðà, âàë ðîòîðà 3
êîòîðîãî âðàùàåòñÿ ñ ïîñòîÿííîé ÷àñòîòîé
0
n
. Òîê âîçáóæäåíèÿ
Â
I
,
ïîñòóïàþùèé â îáìîòêó ðîòîðà 4 îò èñòî÷íèêà ïîñòîÿííîãî òîêà ÷åðåç
êîíòàêòíûå êîëüöà 2, ìîæíî ðåãóëèðîâàòü, ÷òî ïîçâîëÿåò ïîëó÷àòü
ðàçëè÷íûå çíà÷åíèÿ ÝÄÑ, èíäóöèðóåìûõ â ôàçàõ îáìîòêè ñòàòîðà 1.
Äåéñòâóþùåå çíà÷åíèå ñèíóñîèäàëüíîé ÝÄÑ
E
0
, èíäóöèðóåìîé ïðè
Ðèñ. 3.3
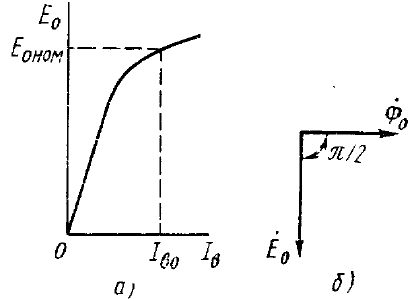
72
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
õîëîñòîì õîäå â ôàçå ñòàòîðà, ìîæåò áûòü ðàññ÷èòàíî, êàê è äëÿ
àñèíõðîííûõ ìàøèí, ïî ôîðìóëå
,44.4
010
Φ=
îáàa
kwfE
(3.3)
ãäå
îáà
k
îáìîòî÷íûé êîýôôèöèåíò ÿêîðÿ;
a
w
÷èñëî âèòêîâ â ôàçå ñòàòîðà, âêëþ÷åííûõ ïîñëåäîâàòåëüíî;
Φ
0
ìàêñèìàëüíûé ìàãíèòíûé ïîòîê ïîëþñà ðîòîðà ïðè òîêå
âîçáóæäåíèÿ
Â
I
;
1
f
÷àñòîòà ÝÄÑ ñòàòîðà, îïðåäåëÿåìàÿ ïî ôîðìóëå (3.1).
Áîëüøîå çíà÷åíèå ïðè àíàëèçå ðàáîòû ñèíõðîííîãî ãåíåðàòîðà
èìååò õàðàêòåðèñòèêà õîëîñòîãî õîäà, ïðåäñòàâëÿþùàÿ ñîáîé
çàâèñèìîñòü ÝÄÑ Å
0
îò òîêà âîçáóæäåíèÿ
Â
I
ïðè
constn =
0
(ðèñ. 3.4,à).
Íà ðèñ. 3.4,á ïðåäñòàâëåíà âåêòîðíàÿ äèàãðàììà, ñîîòâåòñòâóþùàÿ ýòîé
õàðàêòåðèñòèêå. Ñîãëàñíî (3.3), ïðè
const
n
=
0
(
const
f
=
1
) ÝÄÑ Å
0
ïðîïîðöèîíàëüíà Ô
0
, çíà÷èò, òîé æå êðèâîé ðèñ. 3.4,à (íî â äðóãîì
ìàñøòàáå) ìîæíî ïðåäñòàâèòü çàâèñèìîñòü
()
B
If
=Φ
0
.
Ðèñ. 3.4
Ïðè ìàëûõ çíà÷åíèÿõ òîêà âîçáóæäåíèÿ ìàãíèòíûé ïîòîê ìàë,
õàðàêòåðèñòèêà
()
BB
If
=Φ
èìååò ëèíåéíóþ çàâèñèìîñòü (ðèñ. 3.4,à),
ïî ìåðå âîçðàñòàíèÿ ìàãíèòíîãî ïîòîêà ñòàëüíûå ó÷àñòêè ìàãíèòîïðî-
âîäà íàñûùàþòñÿ è âîçðàñòàåò èõ ìàãíèòíîå ñîïðîòèâëåíèå, à ïðè
èíäóêöèè â ñòàëè áîëåå 1,71,8 Òë ñîïðîòèâëåíèå ýòèõ ó÷àñòêîâ íàñòîëü-
73
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
êî âåëèêî, ÷òî õàðàêòåðèñòèêà
()
BB
If
=Φ
(
()
B
I
f
E
=
0
) ñòàíîâèòñÿ
íåëèíåéíîé. Îáû÷íî íîìèíàëüíûé ðåæèì ñèíõðîííûõ ãåíåðàòîðîâ
ñîîòâåòñòâóåò êîëåíó êðèâîé
()
B
IfE
=
0
(íà ðèñ. 3.4, à òî÷êà ñ
êîîðäèíàòàìè
0Â
I
è
OÍÎÌ
E
).
3.3. Ðàáîòà ñèíõðîííîãî ãåíåðàòîðà ïîä íàãðóçêîé
Ðàññìîòðèì ðàáîòó òðåõôàçíîãî ñèíõðîííîãî ãåíåðàòîðà ïðè ñèì-
ìåòðè÷íîé íàãðóçêå, êîãäà îí ðàáîòàåò íåçàâèñèìî îò äðóãèõ ñèíõðîí-
íûõ ìàøèí. Ïðè ñèììåòðè÷íîé íàãðóçêå â ôàçíûõ îáìîòêàõ ïðîõîäÿò
îäèíàêîâûå òîêè, ñäâèíóòûå ïî ôàçå íà óãîë
3/2
π
, ñîçäàþò ìàãíèòíîå
ïîëå, êîòîðîå âðàùàåòñÿ îòíîñèòåëüíî ÿêîðÿ â òó æå ñòîðîíó è ñ òîé æå
÷àñòîòîé, ÷òî è ïîëå îáìîòêè âîçáóæäåíèÿ. Òàêèì îáðàçîì, ìàãíèòíûå
ïîòîêè âîçáóæäåíèÿ
â
Φ è ÿêîðÿ
à
Φ â ñèíõðîííîé ìàøèíå âçàèìíî
íåïîäâèæíû. Â ìàøèíå, ðàáîòàþùåé ïîä íàãðóçêîé, ðåçóëüòèðóþùèé
ìàãíèòíûé ïîòîê
ðåç
Φ
ñîçäàåòñÿ íå òîëüêî ÌÄÑ îáìîòêè âîçáóæäåíèÿ,
íî è ÌÄÑ îáìîòêè ÿêîðÿ. Âîçäåéñòâèå ÌÄÑ ÿêîðÿ íà ïîëå ñèíõðîííîé
ìàøèíû, ñîçäàâàåìîå îáìîòêîé âîçáóæäåíèÿ, íàçûâàåòñÿ ðåàêöèåé
ÿêîðÿ. Ñëåäîâàòåëüíî, ïîä äåéñòâèåì ðåàêöèè ÿêîðÿ èçìåíÿåòñÿ
ðåçóëüòèðóþùèé ìàãíèòíûé ïîòîê è íàïðÿæåíèå ãåíåðàòîðà.
Ìîæíî ïîêàçàòü, ÷òî â ñèíõðîííîì ãåíåðàòîðå ðåàêöèÿ ÿêîðÿ
çàâèñèò îò õàðàêòåðà íàãðóçêè (ïðè ðàçëè÷íûõ óãëàõ ñäâèãà ôàç
ψ
ìåæäó
ÝÄÑ Å
0
è òîêîì
I
â îáìîòêå ÿêîðÿ) è ïðè îòñòàþùåì òîêå ÿâëÿåòñÿ
ðàçìàãíè÷èâàþùåé, à ïðè îïåðåæàþùåì íàìàãíè÷èâàþùåé.
Ïðè ðàáîòå ñèíõðîííîãî ãåíåðàòîðà ïîä íàãðóçêîé ÝÄÑ â êàæäîé
ôàçå îáìîòêè ñòàòîðà
E
&
ñ ó÷åòîì ÿâëåíèÿ ðåàêöèè ÿêîðÿ áóäåò íåñêîëü-
êî îòëè÷àòüñÿ îò ÝÄÑ
0
E
&
ïðè õîëîñòîì õîäå. Ðåçóëüòèðóþùèé ìàãíèòíûé
ïîòîê â çàçîðå íåíàñûùåííîé ìàøèíû
,
0
àðåç
Φ+Φ=Φ
&&&
(3.4)
à ÝÄÑ, èíäóöèðóåìàÿ ïîòîêîì
ðåç
Φ
â ôàçå ñòàòîðà íåÿâíîïîëþñíîãî
ãåíåðàòîðà,
,
0
àðåç
EEE
&&&
+=
(3.5)
ãäå
0
E
&
êîìïëåêñíàÿ ÝÄÑ, èíäóöèðóåìàÿ â ôàçå ñòàòîðà ïîòîêîì
0
Φ
&
;
à
E
&
êîìïëåêñíàÿ ÝÄÑ, èíäóöèðóåìàÿ â ôàçå ñòàòîðà ïîòîêîì ðåàê-
öèè ÿêîðÿ
à
Φ
&
;
à
E
ïðîïîðöèîíàëüíà ïîòîêó
à
Φ , à â íåíàñûùåííîé
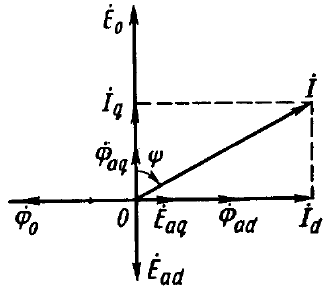
74
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
ìàøèíå è òîêó ÿêîðÿ
I
, ïîýòîìó åå ìîæíî ðàññìàòðèâàòü êàê ÝÄÑ
ñàìîèíäóêöèè, íàâåäåííóþ â îáìîòêå ÿêîðÿ, è ïðåäñòàâèòü â âèäå
àà
XIjE
&&
−=
, ãäå
à
X
èíäóêòèâíîå ñîïðîòèâëåíèå ñèíõðîííîé
ìàøèíû, îáóñëîâëåííîå ïîòîêîì ÿêîðÿ. ÝÄÑ ÿâíîïîëþñíîãî ãåíåðàòîðà
ïðè åãî ðàáîòå ïîä íàãðóçêîé ðàâíà
,
0
àdàq
EEEE
&&&&
++=
(3.6)
ãäå
àq
E
&
è
àd
E
&
ÝÄÑ, èíäóöèðóåìûå ñîîòâåòñòâåííî ïîòîêàìè
àq
Φ
è
àd
Φ . Äëÿ íåíàñûùåííîé ìàøèíû ìîæíî ñ÷èòàòü, ÷òî
;
àqqàq
XIjE
&&
−=
,
àddàd
XIjE
&&
−=
(3.7)
ãäå
àq
X
è
àd
X
èíäóêòèâíûå ñîïðîòèâëåíèÿ îáìîòêè ÿêîðÿ, ñîîòâåò-
ñòâåííî îáóñëîâëåííûå ïîëÿìè ïîïåðå÷íîé è ïðîäîëüíîé ðåàêöèé
ÿêîðÿ. Âñîîòâåòñòâèè ñ ðèñ. 3.5 òîê ÿêîðÿ
I
ìîæíî ïðåäñòàâèòü â âèäå
ïîïåðå÷íîé
ψ
cosII
q
=
è ïðîäîëüíîé
ψ
sin
II
d
=
ñîñòàâëÿþùèõ.
 ñèíõðîííûõ ìàøèíàõ ñ íåÿâíî âûðàæåííûìè ïîëþñàìè
ìàãíèòíîå ñîïðîòèâëåíèå âîçäóøíîãî çàçîðà îäèíàêîâî ïî âñåé
îêðóæíîñòè ðîòîðà è íå çàâèñèò îò âçàèìíîãî ðàñïîëîæåíèÿ ñòàòîðà è
ðîòîðà, ïîýòîìó îòïàäàåò íåîáõîäèìîñòü â ðàçäåëåíèè ìàãíèòíîãî
ïîòîêà, ïðîíèêàþùåãî èç ñòàòîðà â ðîòîð, íà ïîïåðå÷íóþ è ïðîäîëüíóþ
ñîñòàâëÿþùèå.  ýòîì ñëó÷àå ìàãíèòíîå ïîëå ðåàêöèè ÿêîðÿ
à
Φ
èíäóöèðóåò â îáìîòêå ÿêîðÿ ÝÄÑ
à
E
.
Ïîëó÷åííûå âûâîäû ñïðàâåäëèâû è äëÿ îáùåãî ñëó÷àÿ, êîãäà
íàãðóçêà ñìåøàííàÿ, ò.å. êîãäà óãîë ñäâèãà ôàç
ψ
ïî àáñîëþòíîìó
çíà÷åíèþ ìåíüøå 90°. Îòñòàþùèé òîê (àêòèâíî-èíäóêòèâíàÿ íàãðóçêà)
Ðèñ. 3.5
75
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
ðàçìàãíè÷èâàåò ìàøèíó, à îïåðåæàþùèé òîê (àêòèâíî-åìêîñòíàÿ
íàãðóçêà) ïîäìàãíè÷èâàåò åå.
3.3.1. Âåêòîðíûå äèàãðàììû, âíåøíèå
è ðåãóëèðîâî÷íûå õàðàêòåðèñòèêè ñèíõðîííîãî ãåíåðàòîðà
Âåêòîðíûå äèàãðàììû øèðîêî èñïîëüçóþòñÿ êàê ïðè êà÷åñòâåííîì,
òàê è ïðè êîëè÷åñòâåííîì àíàëèçå ðàáîòû ñèíõðîííûõ ãåíåðàòîðîâ è
äâèãàòåëåé. Ïðè êà÷åñòâåííîì àíàëèçå èñïîëüçóþò óïðîùåííûå
äèàãðàììû, ïðè êîëè÷åñòâåííîì óòî÷íåííûå.
Âåêòîðíàÿ äèàãðàììà íåÿâíîïîëþñíîãî ãåíåðàòîðà. ÝÄÑ,
íàâîäèìàÿ â ôàçå îáìîòêå ñòàòîðà,
àà
rIjXUE
&&&
++=
σ
, (3.8)
ãäå
U
íàïðÿæåíèå íà çàæèìàõ ôàçû ñòàòîðà;
à
X
σ
èíäóêòèâíîå ñîïðîòèâëåíèå îáìîòêè ñòàòîðà, îáóñëîâëåí-
íîå ïîòîêîì ðàññåÿíèÿ
à
σ
Φ ;
à
r
àêòèâíîå ñîïðîòèâëåíèå ôàçû îáìîòêè ÿêîðÿ.
Èç (3.8) ñ ó÷åòîì (3.5) èìååì
,
0
ààààà
rIXIjEErIjXEU
&&&&&&&
−−+=−−=
σσ
(3.9)
èëè
,
0
àñíààà
rIXIjUrIjIXXIjUE
&&&&&&&
++=+++=
σ
(3.10)
ãäå
ààñí
XXX
σ
+= ïîëíîå, èëè ñèíõðîííîå, èíäóêòèâíîå ñîïðîòèâëå-
íèå ìàøèíû;
àà
XIjE
&
−=
ÝÄÑ, íàâåäåííàÿ â ôàçå ñòàòîðà íåíàñûùåí-
íîé ìàøèíû ïîòîêîì ðåàêöèè ÿêîðÿ
à
Φ
&
. Àêòèâíîå ñîïðîòèâëåíèå öåïè
ÿêîðÿ
à
r
íåâåëèêî ïî ñðàâíåíèþ ñ ñîïðîòèâëåíèåì
ñí
X
, ïîýòîìó ïàäå-
íèåì íàïðÿæåíèÿ
à
Ir
â àêòèâíîì ñîïðîòèâëåíèè ìîæíî ïðåíåáðå÷ü,
òàê êàê îíî ñðàâíèòåëüíî íåâåëèêî. Òîãäà óðàâíåíèå (3.10) ïðèíèìàåò
âèä
.
0
ñíàà
XIjUjIXXIjUE
&&&&&
+=++=
σ
(3.11)
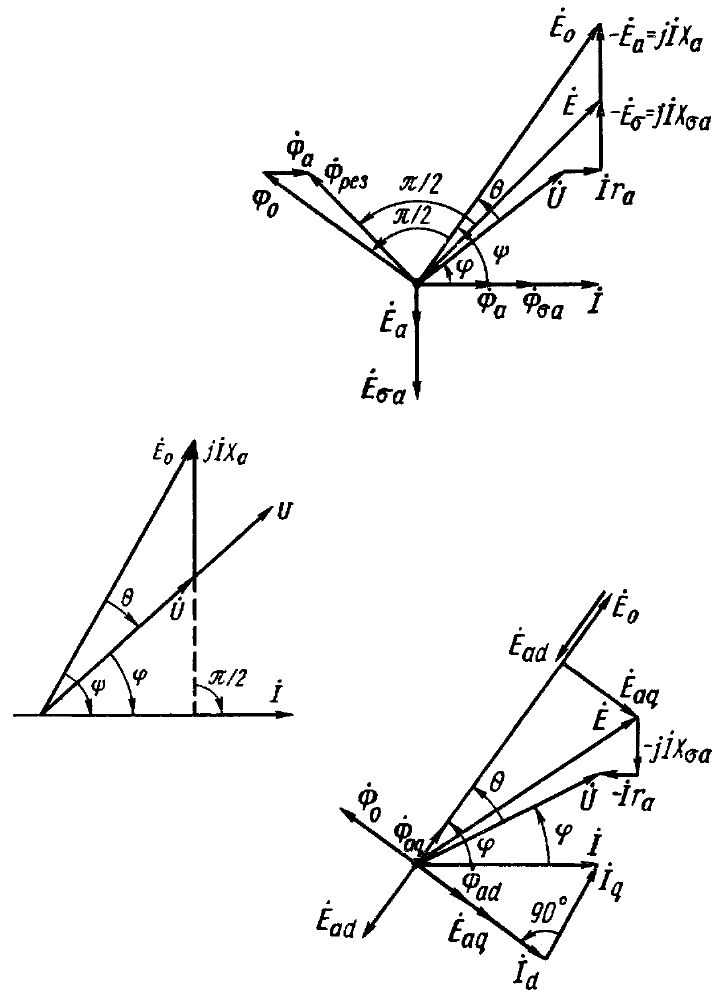
Íà ðèñ. 3.6 ïîêàçàíà âåêòîðíàÿ äèàãðàììà, ïîñòðîåííàÿ ñîãëàñíî
óðàâíåíèÿì (3.8) è (3.10) äëÿ íåíàñûùåííîãî íåÿâíîïîëþñíîãî ãåíå-
ðàòîðà. Ìàãíèòíûé ïîòîê ðàññåÿíèÿ
à
σ
Φ
&
ñîâïàäàåò ïî ôàçå ñ òîêîì
ÿêîðÿ, à ÝÄÑ ðàññåÿíèÿ
à
E
σ
&
îòñòàåò îò ýòîãî ïîòîêà è òîêà íà óãîë
2/
π
.
Îñíîâíûì ñîïðîòèâëåíèåì íà ïóòè ïîòîêà ðåàêöèè ÿêîðÿ
a
Φ
&
ÿâëÿåòñÿ
âîçäóøíûé çàçîð, ïîýòîìó ïîòîê
a
Φ
&
ñîâïàäàåò ïî ôàçå ñ òîêîì ÿêîðÿ
76
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Ðèñ. 3.6
Ðèñ. 3.7
Ðèñ. 3.8
77
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
I
&
è ïðîïîðöèîíàëåí åìó. ÝÄÑ
a
E
&
îòñòàåò îò èíäóöèðóþùåãî åå ïîòîêà
a
Φ
&
íà óãîë
2/
π
. Óãîë
ψ
åñòü óãîë ìåæäó âåêòîðàìè
0
E
&
è
I
, à óãîë
θ
óãîë ìåæäó âåêòîðàìè
0
E
&
è
0
U
&
, íàçûâàåìûé óãëîì íàãðóçêè. Ïðè
ðàáîòå ñèíõðîííîé ìàøèíû â êà÷åñòâå ãåíåðàòîðà âåêòîð íàïðÿæåíèÿ
U
&
âñåãäà îòñòàåò îò âåêòîðà ÝÄÑ
E
&
è
θ
ñ÷èòàåòñÿ ïîëîæèòåëüíûì. Ñ
óâåëè÷åíèåì íàãðóçêè
θ
óâåëè÷èâàåòñÿ.
Íà ðèñ. 3.7 ïîêàçàíà óïðîùåííàÿ âåêòîðíàÿ äèàãðàììà ñèíõðîí-
íîãî íåÿâíîïîëþñíîãî ãåíåðàòîðà, ïîñòðîåííàÿ â ñîîòâåòñòâèè ñ óðàâ-
íåíèåì (3.11). Ýòó äèàãðàììó øèðîêî èñïîëüçóþò ïðè êà÷åñòâåííîì
àíàëèçå ðàáîòû ñèíõðîííîé ìàøèíû.
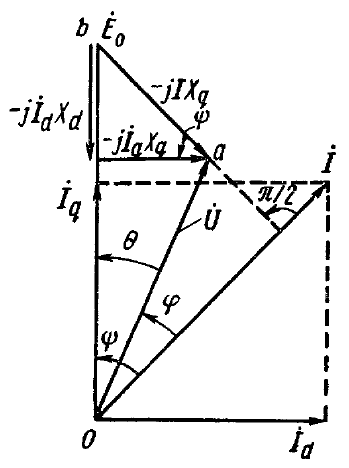
Âåêòîðíàÿ äèàãðàììà ÿâíîïîëþñíîãî ãåíåðàòîðà. Âåêòîðíóþ
äèàãðàììó ñèíõðîííîé ÿâíîïîëþñíîé ìàøèíû (ðèñ. 3.8) ìîæíî
ïîñòðîèòü ñîãëàñíî óðàâíåíèþ (3.9), êîòîðîå ñ ó÷åòîì (3.6) ïðèíèìàåò
âèä
.
0
àààqàdàà
rIXIjEEErIjXEU
&&&&&&&&
−−++=−−=
σσ
(3.12)
Åñëè ïðåíåáðå÷ü ñîïðîòèâëåíèåì
à
r
, êîòîðîå î÷åíü ìàëî, òî
óðàâíåíèå (3.12) ìîæíî ïåðåïèñàòü:
,
00
ààqàdààqàd
EEEEXIjEEEU
σσ
&&&&&&&&&
+++=−++=
(3.13)
ãäå
à
E
σ
&
ÝÄÑ ðàññåÿíèÿ, èíäóöèðóåìàÿ â îáìîòêå ÿêîðÿ ïîòîêîì
ðàññåÿíèÿ, êîòîðóþ ìîæíî ïðåäñòàâèòü â âèäå ñóììû äâóõ ñîñòàâëÿþ-
ùèõ, îðèåíòèðîâàííûõ ïî ïðîäîëüíîé è ïîïåðå÷íîé îñÿì:
,
àqàdà
EEE
σσσ
&&&
+=
(3.14)
;
àdàd
XIjE
σσ
&&
−=
.
àqàq
XIjE
σσ
&&
−=
(3.15)
Óðàâíåíèå (3.13) ñ ó÷åòîì (3.14) çàïèñûâàåòñÿ â âèäå
,
00
dqàqàdàqàd
EEEEEEEEU
&&&&&&&&&
++=++++=
σσ
(3.16)
ãäå
àdàdd
EEE
σ
&&&
+=
;
àqàqq
EEE
σ
&&&
+=
. Çàìåíèâ â (3.16) ÝÄÑ ñîîòâåò-
ñòâóþùèìè èíäóêòèâíûìè ïàäåíèÿìè íàïðÿæåíèÿ, ïîëó÷èì
,
00
qqddàqàdàqqàdd
XIjXIjEXIjXIjXIjXIjEU
&&&&&&&&&
−−=−−−−=
σσ
(3.17)
ãäå
ààdd
XXX
σ
+= ;
ààqq
XXX
σ
+=
ïîëíûå, èëè ñèíõðîííûå,
èíäóêòèâíûå ñîïðîòèâëåíèÿ îáìîòêè ÿêîðÿ ïî ïðîäîëüíîé è ïîïåðå÷íîé
îñÿì.
78
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Íà ðèñ. 3.9 ïðèâåäåíà âåêòîð-
íàÿ äèàãðàììà, ïîñòðîåííàÿ â
ñîîòâåòñòâèè ñ óðàâíåíèåì (3.17).
Âíåøíèå õàðàêòåðèñòèêè
ñèíõðîííîãî ãåíåðàòîðà. Õà-
ðàêòåðèñòèêè
()
IU
, îïèñûâàþ-
ùèå çàâèñèìîñòü íàïðÿæåíèÿ
ñèíõðîííîãî ãåíåðàòîðà
U
îò òîêà
íàãðóçêè
I
, íàçûâàþòñÿ âíåøíè-
ìè õàðàêòåðèñòèêàìè ãåíåðà-
òîðà. Ñîãëàñíî (3.11), íàïðÿæåíèå
íà çàæèìàõ êàæäîé ôàçû ñòàòîðà
ãåíåðàòîðà
.
0
ñí
XIjEU
&&&
−=
(3.18)
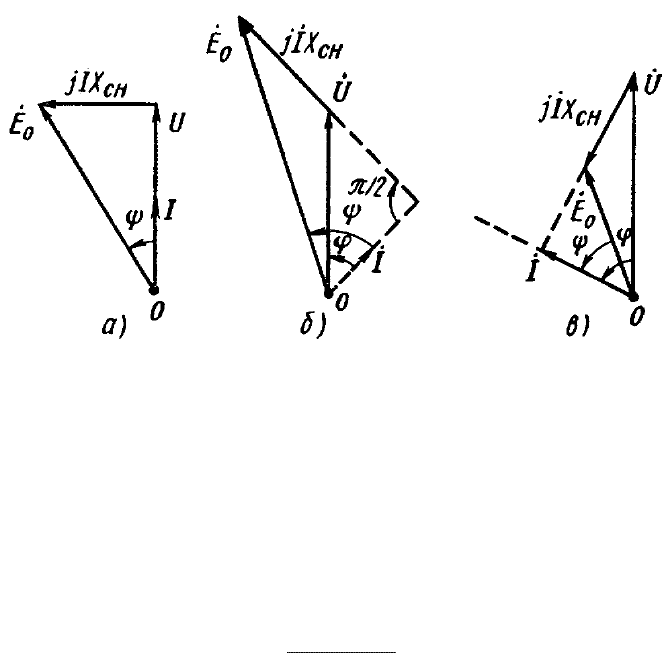
Íà ðèñ. 3.10 ïîêàçàíû óïðî-
ùåííûå âåêòîðíûå äèàãðàììû
ñèíõðîííîãî íåÿâíîïîëþñíîãî
ãåíåðàòîðà äëÿ àêòèâíîé (à),
àêòèâíî-èíäóêòèâíîé (á) è àêòèâíî-åìêîñòíîé (â) íàãðóçîê. Êàê âèäíî èç
äèàãðàìì, ïðè àêòèâíîé è àêòèâíî-èíäóêòèâíîé íàãðóçêàõ ÝÄÑ
ãåíåðàòîðà
0
E
áîëüøå íàïðÿæåíèÿ
U
íà çàæèìàõ êàæäîé èç åãî ôàç, à
ïðè àêòèâíî-åìêîñòíîé íàãðóçêå ÝÄÑ
0
E
ìåíüøå
U
. Òàêèì îáðàçîì, ñ
ðîñòîì íàãðóçêè ïðè àêòèâíîé è àêòèâíî-èíäóêòèâíîé íàãðóçêàõ
íàïðÿæåíèå ãåíåðàòîðà óìåíüøàåòñÿ, à ïðè àêòèâíî-åìêîñòíîé
óâåëè÷èâàåòñÿ.
Èç âåêòîðíûõ äèàãðàìì è óðàâíåíèÿ (3.18) ñëåäóåò, ÷òî íàïðÿæåíèå
U
çàâèñèò îò õàðàêòåðà íàãðóçêè è îò ÝÄÑ
0
E
. Ïîñëåäíÿÿ æå ÿâëÿåòñÿ
ôóíêöèåé ÷àñòîòû âðàùåíèÿ è òîêà âîçáóæäåíèÿ ãåíåðàòîðà. ×òîáû
èñêëþ÷èòü âëèÿíèå õàðàêòåðà íàãðóçêè, ÷àñòîòû âðàùåíèÿ ðîòîðà è òîêà
âîçáóæäåíèÿ ãåíåðàòîðà, ïîñòðîåíèå âíåøíèõ õàðàêòåðèñòèê ïðîèçâîäÿò
ïðè
const=
ϕ
cos
è
constI
B
=
.
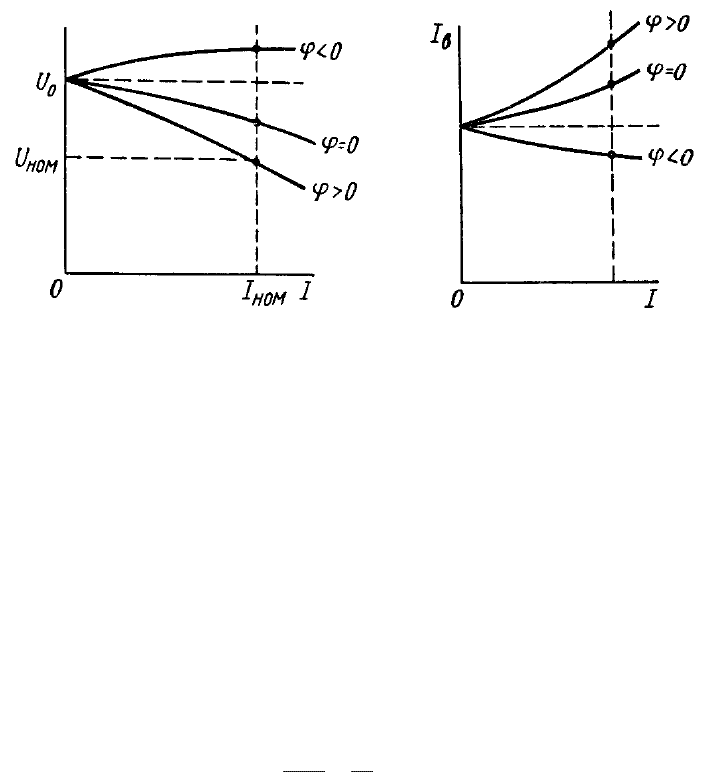
Íà ðèñ. 3.11 ïîêàçàíû âíåøíèå õàðàêòåðèñòèêè ñèíõðîííîãî ãåíå-
ðàòîðà äëÿ àêòèâíîé (ϕ = 0), àêòèâíî-èíäóêòèâíîé (ϕ > 0) è àêòèâíî-
åìêîñòíîé (ϕ < 0, êîãäà íàïðÿæåíèå
U
îòñòàåò îò òîêà
I
) íàãðóçîê.
Õàðàêòåðèñòèêè ïîñòðîåíû ïðè
constI
B
=
, èëè
const
E
=
0
, ò.å. êàæäàÿ
êðèâàÿ ñîîòâåòñòâóåò ñëó÷àþ, êîãäà ïðè èçìåíåíèè íàãðóçêè
ϕ
cos
îñòàåòñÿ íåèçìåííûì.
Ðèñ. 3.9
79
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
Äëÿ ïîëó÷åíèÿ íàïðÿæåíèÿ ãåíåðàòîðà
ÍÎÌ
U
ïðè íîìèíàëüíîé
íàãðóçêå (
ÍÎÌ
II
=
) ïðè ïîñòîÿííîì
ϕ
cos
íåîáõîäèìî óñòàíàâëèâàòü
îïðåäåëåííîå çíà÷åíèå ÝÄÑ
0
E
. Ñ èçìåíåíèåì
ϕ
cos
íåîáõîäèìî
óñòàíàâëèâàòü ñîîòâåòñòâåííî äðóãèå çíà÷åíèÿ ÝÄÑ
0
E
.
Îòíîñèòåëüíîå èçìåíåíèå íàïðÿæåíèÿ ãåíåðàòîðà â ïðîöåíòàõ ïðè
ïåðåõîäå îò ðåæèìà õîëîñòîãî õîäà ê ðåæèìó íîìèíàëüíîé íàãðóçêè
îïðåäåëÿåòñÿ ïî ôîðìóëå
,100
0
⋅
−
=∆
ÍÎÌ
ÍÎÌ
U
UU
U
(3.19)
ãäå
00
EU =
íàïðÿæåíèå ïðè õîëîñòîì õîäå;
ÍÎÌ
U
íàïðÿæåíèå ïðè íîìèíàëüíîì òîêå.
Ãåíåðàòîðû ÷àùå âñåãî ðàáîòàþò íà àêòèâíî-èíäóêòèâíóþ íàãðóçêó
ïðè
ϕ
cos
= 0,9 0,85. Ïðè ýòîì èçìåíåíèå íàïðÿæåíèÿ
U∆
= 25-35%.
Äëÿ òîãî ÷òîáû ïðè èçìåíåíèè íàãðóçêè ïîääåðæèâàòü íàïðÿæåíèå
ãåíåðàòîðà ïîñòîÿííûì, áëèçêèì ê íîìèíàëüíîìó, íåîáõîäèìî
ñîîòâåòñòâóþùèì îáðàçîì èçìåíÿòü ÝÄÑ ãåíåðàòîðà ïóòåì âîçäåéñòâèÿ
íà åãî òîê âîçáóæäåíèÿ. Äëÿ ñòàáèëèçàöèè íàïðÿæåíèÿ U ãåíåðàòîðà
ïðèìåíÿþò ñïåöèàëüíûå ðåãóëÿòîðû òîêà âîçáóæäåíèÿ.
Çàâèñèìîñòü òîêà âîçáóæäåíèÿ
B
I
îò òîêà íàãðóçêè
I
, ïîêàçûâàþ-
ùàÿ, êàê ñëåäóåò èçìåíÿòü òîê âîçáóæäåíèÿ ïðè èçìåíåíèè íàãðóçêè,
÷òîáû íàïðÿæåíèå áûëî ïîñòîÿííûì, íàçûâàåòñÿ ðåãóëèðîâî÷íîé
Ðèñ. 3.10
80
Ñîâðåìåííûé Ãóìàíèòàðíûé Óíèâåðñèòåò
õàðàêòåðèñòèêîé ñèíõðîííîãî ãåíåðàòîðà. Íà ðèñ. 3.12 ïîêàçàíû
ðåãóëèðîâî÷íûå õàðàêòåðèñòèêè äëÿ ðàçëè÷íîãî õàðàêòåðà íàãðóçêè.
×òîáû èñêëþ÷èòü âëèÿíèå õàðàêòåðà íàãðóçêè è ÷àñòîòû âðàùåíèÿ
ãåíåðàòîðà, ýòè õàðàêòåðèñòèêè ñòðîÿò ïðè
const=
ϕ
cos
è
constn =
.
Êàê âèäíî èç ðèñ. 3.12, äëÿ ïîääåðæàíèÿ íàïðÿæåíèÿ ãåíåðàòîðà
íåèçìåííûì ñ âîçðàñòàíèåì íàãðóçêè ïðè
ϕ
= 0 è
ϕ
> 0 íåîáõîäèìî
òîê âîçáóæäåíèÿ óâåëè÷èâàòü, à ïðè
ϕ
< 0 óìåíüøàòü.
Ðèñ. 3.11 Ðèñ. 3.12
3.3.2. Ìîùíîñòü è ýëåêòðîìàãíèòíûé ìîìåíò
ñèíõðîííîéìàøèíû
Ìîùíîñòü, ïîëó÷àåìàÿ ãåíåðàòîðîì îò ïåðâè÷íîãî äâèãàòåëÿ,
ïðåîáðàçóåòñÿ â íåì â ýëåêòðîìàãíèòíóþ ìîùíîñòü. Áàëàíñ ìîùíîñòåé
îäíîé ôàçû ãåíåðàòîðà îïèñûâàåòñÿ óðàâíåíèåì
,coscos
2
0
rIUIIE +=
ϕψ
(3.20)
ãäå
ψ
cos
0
IE
ýëåêòðîìàãíèòíàÿ ìîùíîñòü, ò.å. ìîùíîñòü, ïîëó÷àåìàÿ
îäíîé ôàçîé ÿêîðÿ îò èíäóêòîðà ýëåêòðîìàãíèòíûì ïóòåì;
ϕ
cosUI
àêòèâíàÿ ìîùíîñòü, îòäàâàåìàÿ îäíîé ôàçîé ãåíåðàòîðà â ñåòü;
rI
2
-
ïîòåðè ìîùíîñòè â îäíîé ôàçå îáìîòêè ÿêîðÿ. Ýëåêòðîìàãíèòíûé
ìîìåíò íà âàëó ãåíåðàòîðà
,cos
0
ψ
ωω
IE
m
P
M
ÝÌ
==
(3.21)
