Torrieri D. Principles of Spread-Spectrum Communication Systems
Подождите немного. Документ загружается.

428
APPENDIX C.
SIGNAL CHARACTERISTICS
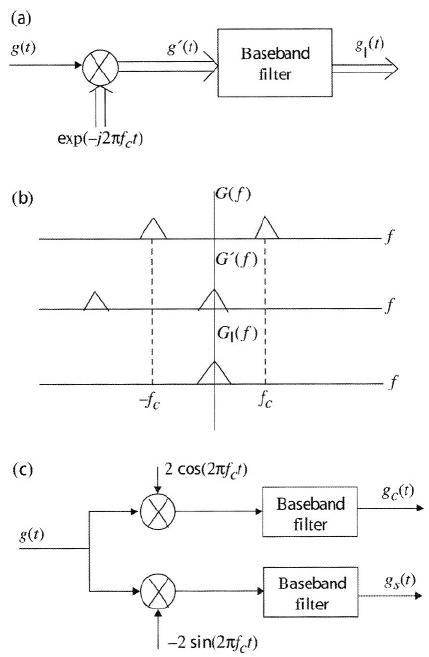
Figure C.1: Envelope extraction: (a) direct-conversion receiver, (b) associated
spectra, and (c) implementation with real-valued signals.
C.4.
DIRECT-CONVERSION RECEIVER
429
then evaluating the Fourier transform of both sides of (C-86) gives
Thus, if the subsequent filters have narrower bandwidths than W or if
then the autocorrelation of z(t) may be approximated by
This approximation permits major analytical simplifications. Equations (C-84)
and (C-83) imply that
Reasoning similar to that following (C-82) leads to
A complex-valued stochastic process that satisfies (C-91) is called a cir-
cularly symmetric process. Let and denote the real and imaginary
parts of respectively. Setting in (C-91) and (C-85), and then using
(C-86), Parseval’s identity, and (C-87), we obtain
Thus, and are zero-mean, independent Gaussian processes with the
same variance.
This page intentionally left blank

Appendix D
Probability Distributions
D.1
Chi-Square Distribution
Consider the random variable
where the are independent Gaussian random variables with means
and common variance The random variable Z is said to have a noncen-
tral chi-square distribution with N degrees of freedom and a noncentral
parameter
To derive the probability density function of Z, we first note that each
has the density function
From elementary probability, the density of is
where and Substituting (D-3) into (D-4),
expanding the exponentials, and simplifying, we obtain the density
The characteristic function of a random variable X is defined as

432
APPENDIX D. PROBABILITY DISTRIBUTIONS
where and is the density of X. Since is the conjugate
Fourier transform of
From Laplace or Fourier transform tables, it is found that the characteristic
function of is
The characteristic function of a sum of independent random variables is equal
to the product of the individual characteristic functions. Because Z is the sum
of the the characteristic function of Z is
where we have used (D-2). From (D-9), (D-7), and Laplace or Fourier transform
tables, we obtain the probability density function of noncentral random
variable with N degrees of freedom and a noncentral parameter
where is the modified Bessel function of the first kind and order This
function may be represented by
where the gamma function is defined as
The probability distribution function of a noncentral random variable is
If N is even so that N/2 is an integer, then and a change of variables
in (D-13) yield
D.2.
CENTRAL CHI-SQUARE DISTRIBUTION
433
where the generalized Marcum Q-function is defined as
and is an integer. Since it follows that is
an integral with finite limits that can be numerically integrated. However,
the numerical computation of the generalized Q-function is simplified if it is
expressed in alternative forms [2]. The mean, variance, and moments of Z can
be easily obtained by using (D-1) and the properties of independent Gaussian
random variables. The mean and variance of Z are
where is the common variance of the
From (D-9), it follows that the sum of two independent noncentral ran-
dom variables with and degrees of freedom, noncentral parameters
and respectively, and the same parameter is a noncentral random
variable with degrees of freedom and noncentral parameter
D.2
Central Chi-Square Distribution
To determine the probability density function of Z when the have zero
means, we substitute (D-11) into (D-10) and then take the limit as We
obtain
Alternatively, this equation results if we substitute into the characteristic
function (D-9) and then use (D-7). Equation (D-18) is the probability density
function of a central random variable with N degrees of freedom. The
probability distribution function is
If N is even so that
N
/2 is an integer, then integrating this equation by parts
N
/2 – 1 times yields
By direct integration using (D-18) and (D-12) or from (D-16) and (D-17), it is
found that the mean and variance of Z are
434
APPENDIX D.
PROBABILITY DISTRIBUTIONS
D.3
Rice Distribution
Consider the random variable
where and are independent Gaussian random variables with means
and respectively, and a common variance The probability distribution
function of R must satisfy where is a random
variable with two degrees of freedom. Therefore, (D-14) with N = 2 implies
that
where This function is called the Rice probability distribution
function. The Rice probability density function, which may be obtained by
differentiation of (D-24), is
The moments of even order can be derived from (D-23) and the moments of the
independent Gaussian random variables. The second moment is
In general, moments of the Rice distribution are given by an integration over
the density in (D-25). Substituting (D-11) into the integrand, interchanging
the summation and integration, changing the integration variable, and using
(D-12), we obtain a series that is recognized as a special case of the confluent
hypergeometric function. Thus,
where the confluent hypergeometric function is defined as
The Rice density function often arises in the context of a transformation
of variables. Let and represent independent Gaussian random variables
with common variance and means and zero, respectively. Let R and
be implicitly defined by and Then (D-23) and
describes a transformation of variables. A straightforward
calculation yields the joint density function of R and
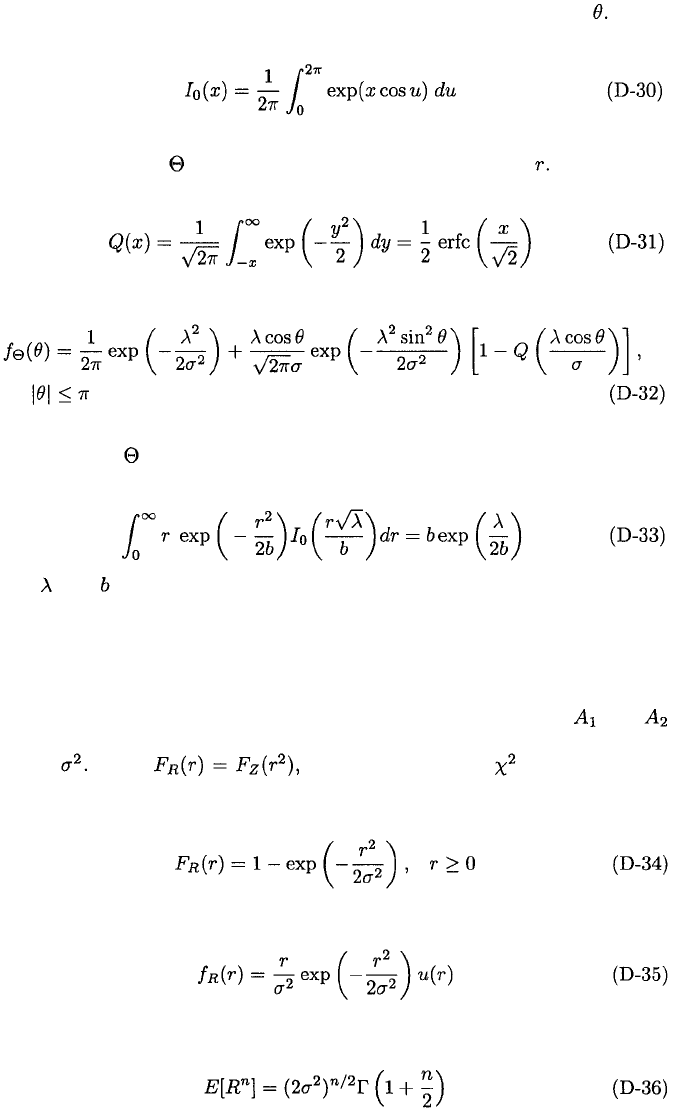
D.4.
RAYLEIGH DISTRIBUTION
435
The density function of the envelope R is obtained by integration over Since
the modified Bessel function of the first kind and order zero satisfies
this density function reduces to the Rice density function (D-25). The density
function of the angle is obtained by integrating (D-29) over Completing
the square of the argument in (D-29), changing variables, and defining
where erfc( ) is the complementary error function, we obtain
Since (D-29) cannot be written as the product of (D-25) and (D-32), the random
variables R and are not independent.
Since the density function of (D-25) must integrate to unity, we find that
where and are positive constants. This equation is useful in calculations
involving the Rice density function.
D.4
Rayleigh Distribution
A Rayleigh-distributed random variable is defined by (D-23) when and
are independent Gaussian random variables with zero means and a common
variance Since where Z is a central random variable
with two degrees of freedom, (D-20) with N = 2 implies that the Rayleigh
probability distribution function is
The Rayleigh probability density function, which may be obtained by differen-
tiation of (D-34), is
By a change of variables in the defining integral, any moment of R can be
expressed in terms of the gamma function defined in (D-12). Therefore,
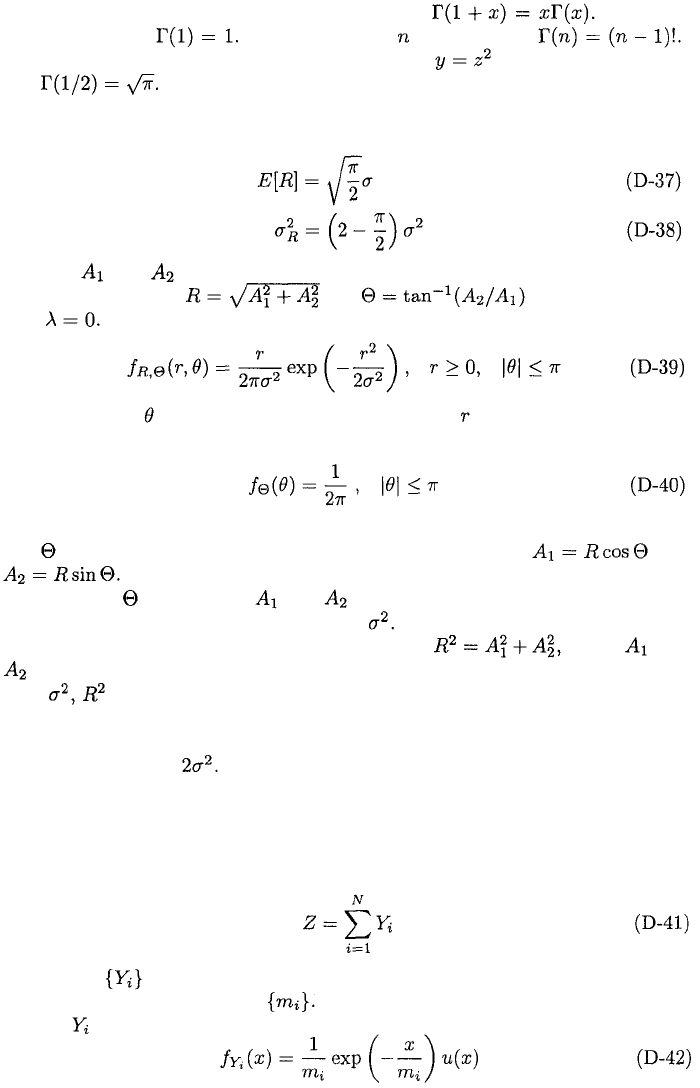
436
APPENDIX D.
PROBABILITY DISTRIBUTIONS
Certain properties of the gamma function are needed to simplify (D-36).
An integration by parts of (D-12) indicates that A direct
integration yields Therefore, when is an integer,
Changing the integration variable by substituting in (D-12), it is found
that
Using these properties of the gamma function, we obtain the mean and the
variance of a Rayleigh-distributed random variable:
Since and have zero means, the joint probability density function of
the random variables and is given by (D-29)
with Therefore,
Integration over yields (A-35), and integration over yields the uniform prob-
ability density function:
Since (D-39) equals the product of (D-35) and (D-40), the random variables R
and are independent. In terms of these random variables, and
A straightforward calculation using the independence and densi-
ties of R and verifies that and are zero-mean, independent, Gaussian
random variables with common variance Since the square of a Rayleigh-
distributed random variable may be expressed as where and
are zero-mean, independent, Gaussian random variables with common vari-
ance has the distribution of a central chi-square random variable with 2
degrees of freedom. Therefore, (D-18) with N = 2 indicates that the square of
a Rayleigh-distributed random variable has an exponential probability density
function with mean
D.5
Exponentially Distributed Random Variables
Consider the random variable
where the are independent, exponentially distributed random variables
with unequal positive means The exponential probability density func-
tion of is
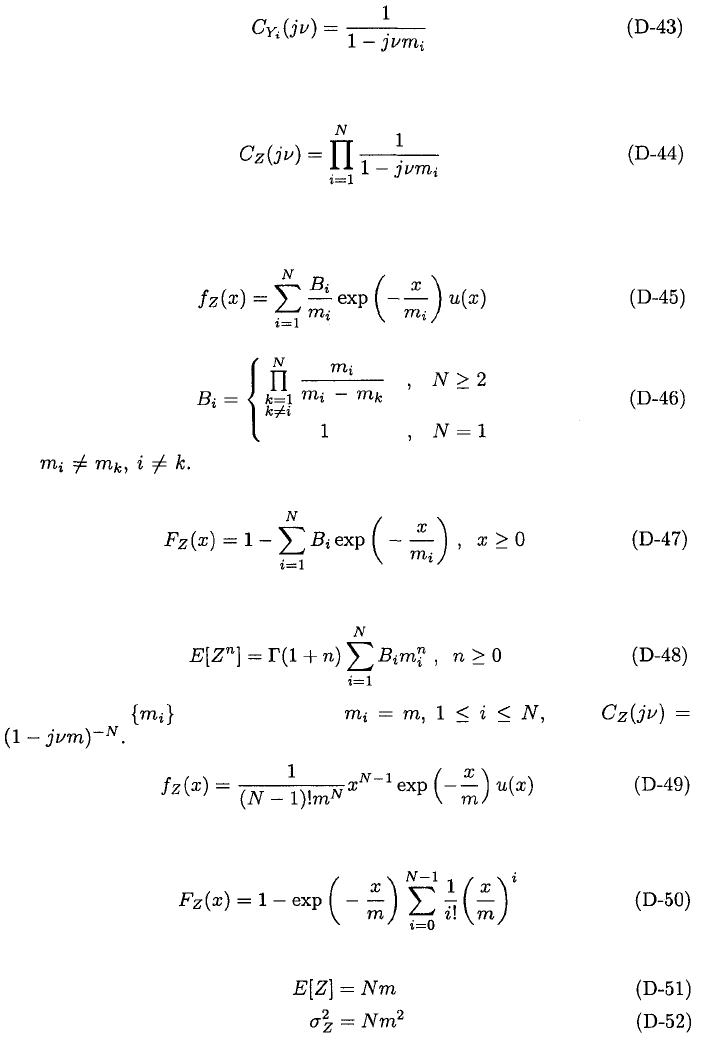
D.5.
EXPONENTIALLY DISTRIBUTED RANDOM VARIABLES
437
A straightforward calculation yields the characteristic function
Since Z is the sum of independent random variables, (D-43) implies that its
characteristic function is
To derive the probability density function of Z, (D-7) is applied after first
expanding the right-hand side of (D-44) in a partial-fraction expansion. The
result is
where
and A direct integration and algebra yields the probability
distribution function
Equations (D-45) and (D-12) give
When the are equal so that then
Therefore, the probability density function of Z is
which is a special case of the gamma density function. Successive integration
by parts yields
From (D-49) and (D-12), the mean and variance of Z are found to be
