Torrieri D. Principles of Spread-Spectrum Communication Systems
Подождите немного. Документ загружается.

388
CHAPTER 7.
DETECTION OF SPREAD-SPECTRUM SIGNALS
Consider the detection of a direct-sequence signal with PSK modulation:
where S is the average signal power, is the known carrier frequency, and is
the carrier phase assumed to be constant over the observation interval
The spreading waveform which subsumes the random data modulation,
is given by (2-76) with the modeled as a random binary sequence. To
determine whether a signal is present based on the observation of the
received signal, classical detection theory requires that one choose between the
hypothesis that the signal is present and the hypothesis that the signal
is absent. Over the observation interval, the received signal under the two
hypotheses is
where is zero-mean, white Gaussian noise with two-sided power spectral
density
The coefficients in the expansion of the observed waveform in terms of
orthonormal basis functions constitute the received vector
Let denote the vector of parameter values that characterize the signal to be
detected. The average likelihood ratio [1], which is compared with a threshold
for a detection decision, is
where is the conditional density function of r given hypothesis and
the value of is the conditional density function of r given hypothesis
and is the expectation over the random vector The coefficients in
the expansion of the Gaussian process in terms of the orthonorrnal basis
functions are uncorrelated and, hence, statistically independent. Since each
coefficient is Gaussian with variance
where the are the coefficients of the signal. Substituting these equations
into (7-3) yields
Expansions in the orthonormal basis functions indicate that if the
average likelihood ratio may be expressed in terms of the signal waveforms as
7.1.
DETECTION OF DIRECT-SEQUENCE SIGNALS
389
where is the energy in the signal waveform over the observation interval of
duration
T
.
If N is the number of chips, each of duration received in the observation
interval, then there are equally likely patterns of the spreading sequence.
For coherent detection, we set in (7-1), substitute it into (7-7), and then
evaluate the expectation to obtain
where is chip of pattern and
These equations indicate how is to be calculated by the ideal coherent
detector. The factor is irrelevant in the sense that it can be merged
with the threshold level with which the average likelihood ratio is compared.
For the more realistic noncoherent detection of a direct-sequence signal,
the received carrier phase is assumed to be uniformly distributed over
Substituting (7-1) into (7-7), using a trigonometric expansion, dropping the ir-
relevant factor that can be merged with the threshold level, and then evaluating
the expectation over the random spreading sequence, we obtain
where
and denotes the expectation with respect to
The modified Bessel function of the first kind and order zero is given by
Since the cosine is a periodic function and the integration is over the same
period, we may replace with for any in (7-13). A trigonometric
expansion with and then yields

390
CHAPTER 7.
DETECTION OF SPREAD-SPECTRUM SIGNALS
Using this relation and the uniform distribution of the average likelihood
ratio of (7-10) becomes
where
These equations define the optimum noncoherent detector for a direct-sequence
signal. The presence of the desired signal is declared if (7-15) exceeds a threshold
level.
The implementation of either the coherent or noncoherent optimum detector
would be very complicated, and the complexity would grow exponentially with
N, the number of chips in the observation interval. Calculations [2] indicate
that the ideal coherent and noncoherent detectors typically provide 3 dB and 1.5
dB advantages, respectively, over the far more practical wideband radiometer,
which is analyzed subsequently. The use of four or two wideband radiometers,
respectively, can compensate for these advantages with less complexity than the
optimum detectors. Furthermore, implementation losses and imperfections in
the optimum detectors are likely to be significant.
Radiometer
Among the many alternatives [3] to the optimum detector, the radiometer is
notable in that it requires virtually no detailed information about the signals
to be detected other than their rough spectral location. Not even whether the
modulation is binary or quaternary is required. Suppose that the signal to be
detected is approximated by a zero-mean, white Gaussian process. Consider
two hypotheses that both assume the presence of a zero-mean, bandlimited
white Gaussian process over an observation interval Under
only noise is present, and the one-sided power spectral density over the signal
band is while under both signal and noise are present, and the power
spectral density is over this band. Using orthonormal basis functions as
in the derivation of (7-4) and (7-5) and ignoring the effects of the bandlimiting,
we find that the conditional densities are approximated by
Calculating the likelihood ratio, taking the logarithm, and merging constants
with the threshold, we find that the decision rule is to compare
7.1.
DETECTION OF DIRECT-SEQUENCE SIGNALS
391
to a threshold. If we let and use the properties of orthonormal basis
functions, then we find that the test statistic is
where the assumption of bandlimited processes is necessary to ensure the finite-
ness of the statistic. A device that implements this test statistic is called an
energy detector or radiometer. Although it was derived for a bandlimited white
Gaussia
n
signal, the radiometer is a reasonable configuration for determining
the presence of unknown deterministic signals.
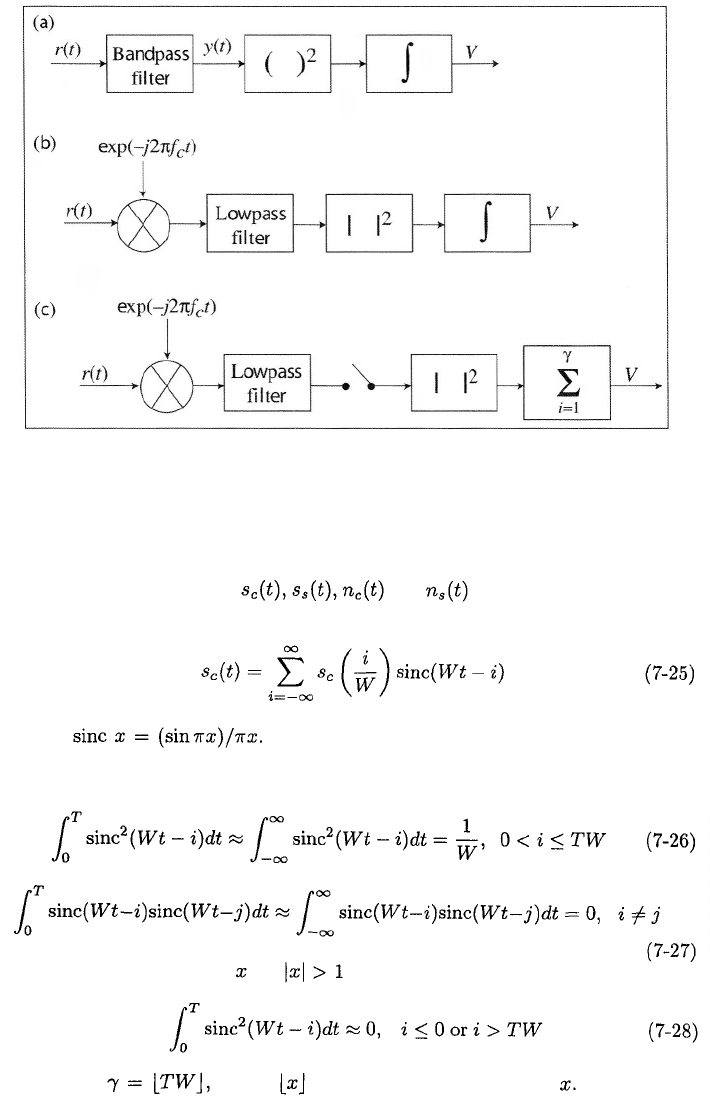
A radiometer may have one of the three equivalent forms shown in Figure
7.1. Consider the system of Figure 7.1 (a), which gives a direct realization of (7-
19). The bandpass filter is assumed to be an ideal rectangular filter that passes
the deterministic desired signal with negligible distortion while limiting the
noise. The filter has center frequency bandwidth W, and produces the
output
where is bandlimited white Gaussian noise with a two-sided power spectral
density equal to Squaring and integrating taking the expected value,
and observing that is a zero-mean process, we obtain
which indicates that the radiometer output is an unbiased estimate of the total
energy after the filtering.
A bandlimited deterministic signal can be represented as (Appendix C.1)
Since the spectrum of is confined within the filter passband, and
have frequency components confined to the band The Gaussian
noise emerging from the bandpass filter can be represented in terms of quadra-
ture components as (Appendix C.2)
where and have flat power spectral densities, each equal to over
Substituting (7-23) and (7-22) into (7-20), squaring and integrating
and assuming that and we obtain
A straightforward calculation verifies that the baseband radiometer of Figure
7.1(b) also produces this test statistic.
392
CHAPTER 7.
DETECTION OF SPREAD-SPECTRUM SIGNALS
Figure 7.1: Radiometers: (a) passband, (b) baseband with integration, and (c)
baseband with sampling at rate
1
/W and summation.
The sampling theorems for deterministic and stochastic processes (Appendix
C.3) provide expansions of and that facilitate a statistical
performance analysis. For example,
where Since the Fourier transform of the sinc function
is a rectangular function, using Parseval’s theorem from Fourier analysis and
evaluating the resulting integral yields the approximations:
We define where denotes the integer part of Substituting
expansion
s
similar to (7-25) into (7-24) and then using the preceding approxi-
The rapid decline of sinc for implies that

7.1.
DETECTION OF DIRECT-SEQUENCE SIGNALS
393
mations, we obtain
where it is always assumed that The error introduced by (7-28) at
and the error introduced by (7-26) at are both nearly 1/2W. For
other values of the errors caused by the approximations are much less than
1/2W and decrease as TW increases. Equation (7-29) becomes an increasingly
accurate approximation of (7-24) as increases. A test statistic proportional to
(7-29) can be derived for the baseband radiometer of Figure 7.1(c) and the sam-
pling rate 1/W without invoking the sampling theorems and the accompanying
approximations.
Since is a zero-mean Gaussian process and has a power spectral den-
sity that is symmetrical about and are zero-mean, independent
Gaussian processes (Appendix C.2). Thus, and are zero-
mean, independent Gaussian random variables. Equation (C-40) implies that
the power spectral densities of and are
The associated autocorrelation functions are
which indicates that is statistically independent of
and similarly for and Therefore, (7-29) becomes
where the and the are statistically independent Gaussian random
variables with unit variances and means
Thus, has a noncentral chi-squared distribution (Appendix D.1)
with degrees of freedom and a noncentral parameter
394
CHAPTER 7.
DETECTION OF SPREAD-SPECTRUM SIGNALS
The probability density function of is
wher
e
is the modified Bessel function of the first kind and order defined
by (D-11), and and Using the series
expansion in of the Bessel function and then setting in (7-36), we
obtain the probability density function for Z in the absence of the signal:
where is the gamma function defined by (D-12). The direct application of
the statistics of Gaussian variables to (7-32) yields
Equation (7-38) approaches the exact result of (7-21) as TW increases.
Let denote the threshold level to which V is compared. A false alarm
occurs if when the signal is absent. Application of (7-37) yields the
probability of a false alarm:
where the incomplete gamma function is defined as
and Integrating (7-40) by parts times yields the series
Since correct detection occurs if when the signal is present, (7-36)
indicates that the probability of detection is
The generalized Marcum Q-function is defined as

7.1.
DETECTION OF DIRECT-SEQUENCE SIGNALS
395
where is a nonnegative integer, and and are nonnegative real numbers.
A change of variables in (7-43) and the substitution of (7-35) yield
The threshold is usually set to a value that ensures a specified To
derive an easily computed closed-form expression for in terms of we first
approximate (7-40). When and the central limit theorem
for the sum of independent, identically distributed random variables with finite
means and variances indicates that the distribution of V given by (7-32) is
approximately Gaussian. Using (7-38) and (7-39) with and the Gaussian
distribution, we obtain
Inverting this equation, we obtain in terms of and Accordingly, if
the estimate of is and is specified, then the threshold should be
where denotes the inverse of the function
Q
( ). In the absence of a
signal, (7-21) indicates that Thus, can be estimated
by averaging sampled radiometer outputs when it is known that no signal is
present.
In some applications, one might wish to specify the false alarm rate, which is
the expected number of false alarms per unit time, rather than If successive
observation intervals do not overlap each other except possibly at end points,
then the false alarm rate is
For TW > 100, the generalized Marcum Q-function in (7-45) is difficult to
compute and to invert. If V is approximated by a Gaussian random variable,
then (7-38) and (7-39) imply that
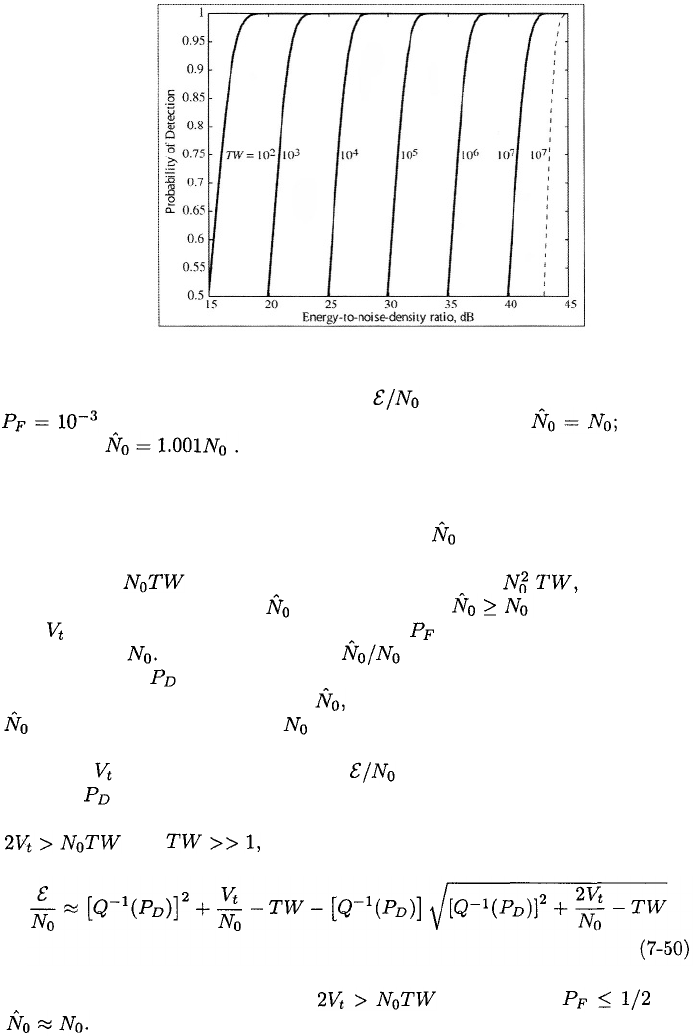
Figure 7.2 depicts versus for radiometers with and
Equations (7-47) and (7-49) are used to calculate and respectively.
The figure illustrates the increased energy required to maintain a specified as
TW increases. The figure also illustrates the impact of the imperfect estimation
of when and When the estimation uncertainty is
enough that the required value of for a specified is
increased considerably.
396
CHAPTER 7. DETECTION OF SPREAD-SPECTRUM SIGNALS
Figure 7.2: Probability of detection versus for wideband radiometer with
and various values of TW. Solid curves are the dashed
curve is for
The sensitivity of the radiometer to errors in when TW is large, which
has been observed experimentally [3], is due to the fact that E[V] contains a bias
term equal to and var(V) contains a term equal to as indicated
by (7-38) and (7-39). Setting high enough that is certain ensures
that will be large enough that the required is achieved regardless of the
exact value of It is important that is as close to unity as possible to
avoid degrading when TW is large. Consequently, the radiometer output
due to noise alone, which provides should be observed often enough that
closely tracks the changes in that might result from small changes in the
circuitry or the environmental noise.
When is specified, the value of necessary to achieve a specified
value of may be obtained by inverting (7-45), which is computationally
difficult but can be closely approximated by inverting (7-49). Assuming that
and we obtain the necessary value:
According to (7-47), the condition is satisfied if and
The substitution of (7-47) into (7-50) and a rearrangement of terms

7.1.
DETECTION OF DIRECT-SEQUENCE SIGNALS
397
Figure 7.3: Energy-to-noise-density ratio versus TW for wideband radiometer
with and various values of and
yields
where
As TW increases, the significance of the third term in (7-51) decreases, while
that of the second term increases if Figure 7.3 shows versus TW
for and various values of and
If the signal duration is then the detected signal power is
Equation (7-51) indicates that the detected power necessary to achieve specified
values of and either or F is
This equation indicates that increasing the observation interval T decreases the
required power only if Although a single radiometer is incapable of de-
