Torrieri D. Principles of Spread-Spectrum Communication Systems

Подождите немного. Документ загружается.

418

APPENDIX C.

IGNAL CHARACTERISTICS

Let and let Equations (C-l) and (C-4) and

the convolution theorem imply that

Because results from passing through two successive filters, each

with transfer function

provided that G(0) = 0.

Equation (C-6) indicates that taking the Hilbert transform corresponds to

introducing a phase sift of radians for all positive frequencies and radians

for all negative frequencies. Consequently,

These relations can be formally verified by taking the Fourier transform of the

left-hand side of (C-8) or (C-9), applying (C-6), and then taking the inverse

Fourier transform of the result. If for and the same

method yields

A bandpass signal is one with a Fourier transform that is negligible except

for where and is the center

frequency. If the bandpass signal is often called a narrowband signal.

A complex-valued signal with a Fourier transform that is nonzero only for

is called an analytic signal.

Consider a bandpass signal with Fourier transform The ana-

lytic signal associated with is defined to be the signal with Fourier

transform

which is zero for and is confined to the band when

The inverse Fourier transform of (C-12) and (C-6) imply that

The complex envelope of is defined by

where is the center frequency if is a bandpass signal. Since the Fourier

transform of is which occupies the band the complex

envelope is a baseband signal that may be regarded as an equivalent lowpass

C.2. STATIONARY STOCHASTIC PROCESSES

419

representation of Equations (C-13) and (C-14) imply that may be

expressed in terms of its complex envelope as

The complex envelope can be decomposed as

where and are real-valued functions. Therefore, (C-15) yields

Since the two sinusoidal carriers are in phase quadrature, and are

called the in-phase and quadrature components of respectively. These

components are lowpass signals confined to

Applying Parseval’s identity from Fourier analysis and then (C-6), we obtain

Therefore,

where denotes the energy of the bandpass signal

C.2

Stationary Stochastic Processes

Consider a stochastic process that is a zero-mean, wide-sense stationary

process with autocorrelation

where denotes the expected value of The Hilbert transform of this

process is the stochastic process defined by

where it is assumed that the Cauchy principal value of the integral exists for

almost every sample function of This equation indicates that is a

zero-mean stochastic process. The zero-mean processes and are jointly

wide-sense stationary if their correlation and cross-correlation functions are not

420

APPENDIX C. SIGNAL CHARACTERISTICS

functions of A straightforward calculation using (C-21) and (C-20) gives the

cross correlation

A similar derivation using (C-7) yields the autocorrelation

Equations (C-20), (C-22), and (C-23) indicate that and are jointly

wide-sense stationary.

The analytic signal associated with is the zero-mean process defined by

The autocorrelation of the analytic signal is defined as

where thee asterisk denotes the complex conjugate. Using (C-20) and (C-22)

which establishes the wide-sense stationarity of the analytic signal.

Since (C-20) indicates that is an even function, (C-22) yields

which indicates that and are uncorrelated. Equations (C-23), (C-26),

and (C-27) yield

The complex envelope of or the equivalent lowpass representation of

is the zero-mean stochastic process defined by

where is an arbitrary frequency usually chosen as the center or carrier fre-

quency of The complex envelope can be decomposed as

where and are real-valued, zero-mean stochastic processes.

Equations (C-29) and (C-30) imply that

Substituting (C-24) and (C-30) into (C-29) we find that

to (C-25), we obtain

C.2. STATIONARY STOCHASTIC PROCESSES

421

The autocorrelations of and are defined by

and

Using (C-32) and (C-33) and then (C-20), (C-23), and (C-24) and trigonometric

identities, we obtain

which shows explicitly that if is wide-sense stationary, then and

are wide-sense stationary with the same autocorrelation function. The variances

of and are all equal because

A derivation similar to that of (C-36) gives the cross correlation

Equations (C-36) and (C-38) indicate that and are jointly wide-sense

stationary. Equations (C-28) and (C-38) give

which implies that and are uncorrelated.

Equation (C-21) indicates that is generated by a linear operation on

Therefore, if is a zero-mean Gaussian process, and are

zero-mean jointly Gaussian processes. Equations (C-32) and (C-33) then imply

that and are zero-mean jointly Gaussian processes. Since they are

uncorrelated, and are statistically independent, zero-mean Gaussian

processes.

The power spectral density of a signal is the Fourier transform of its auto-

correlation. Let and denote the power spectral densities of

and respectively. We assume that occupies the band

and that Taking the Fourier

transform of (C-36), using (C-6), and simplifying, we obtain

Thus, if is a passband process with one-sided bandwidth W, then and

are baseband processes with one-sided bandwidths W/2. This property

and the statistical independence of and when is Gaussian make

(C-31) a very useful representation of

Similarly, the cross-spectral density of and can be derived by

taking the Fourier transform of (C-38) and using (C-6). After simplification,

the result is

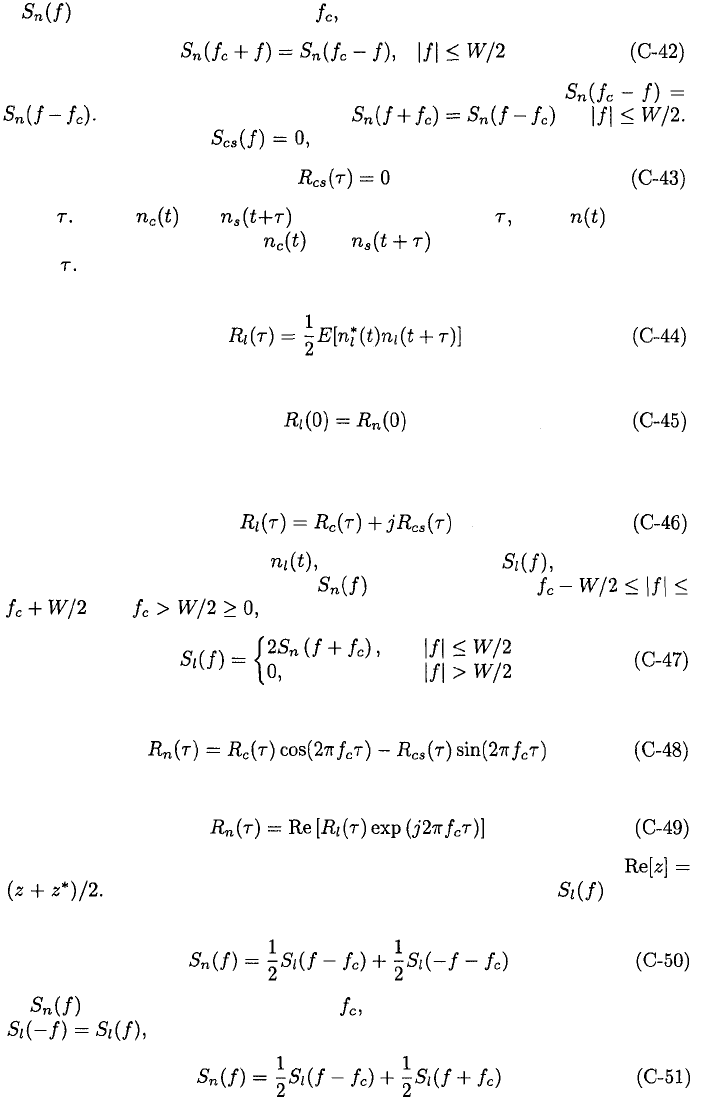
422

APPENDIX C. SIGNAL CHARACTERISTICS

If is locally symmetric about then

Since a power spectral density is a real-valued, even function,

Equation (C-42) then yields for

Therefore, (C-41) gives which implies that

for all Thus, and are uncorrelated for all and if is a zero-

mean Gaussian process, then and are statistically independent

for all

The autocorrelation of the complex envelope is defined by

where the 1/2 is inserted so that

which follows from (C-28) and (C-29). Substituting (C-30) into (C-44) and

using (C-36) and (C-38), we obtain

The power spectral density of which we denote by can be derived

from (C-46), (C-41), and (C-40). If occupies the band

and then

Equations (C-36) and (C-38) yield

Equations (C-48) and (C-46) imply that

We expand the right-hand side of this equation by using the fact that

Taking the Fourier transform and observing that is a real-

valued function, we obtain

If is locally symmetric about then (C-47) and (C-42) imply that

and (C-50) becomes

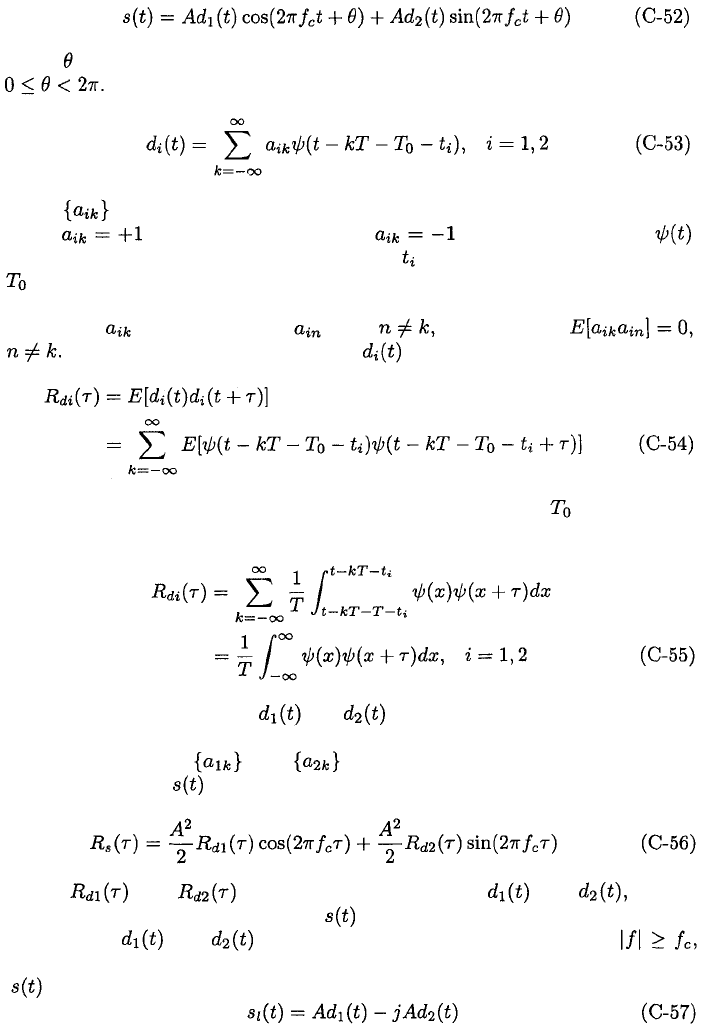
C.2. STATIONARY STOCHASTIC PROCESSES

423

Power Spectral Densities of Communication Signals

Many useful communication signals are modeled as having the form

where is an independent random variable that is uniformly distributed over

The modulations have the form

where is a sequence of independent, identically distributed random vari-

ables, with probability 1/2 and with probability 1/2,

is a pulse waveform, T is the pulse duration, is the relative pulse offset, and

is an independent random variable that is uniformly distributed over the

interval (0, T) and reflects the arbitrariness of the origin of the coordinate sys-

tem. Since is independent of when it follows that

Therefore, the autocorrelation of is

Expressing the expected value as an integral over the range of and changing

variables, we obtain

This equation indicates that and are wide-sense stationary processes

with the same autocorrelation.

If the sequences and are statistically independent, then the

autocorrelation of is

where and are the autocorrelations of and respec-

tively. This equation indicates that is wide-sense stationary. If the sample

functions of and have Fourier transforms that vanish for

then (C-10), (C-11), (C-24), and (C-29) indicate that the complex envelope of

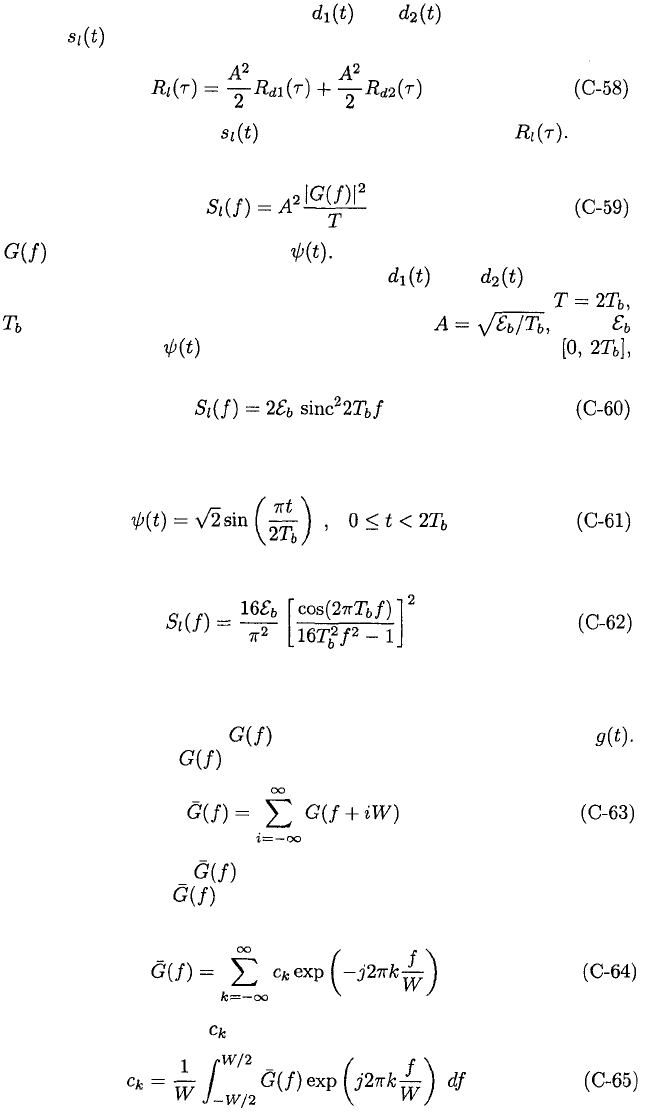
424

APPENDIX C. SIGNAL CHARACTERISTICS

Equation (C-44) and the independence of and imply that the auto-

correlation of is

The power spectral density of is the Fourier transform of From

(C-58) and (C-55), we obtain the density

where is the Fourier transform of

In a quadriphase-shift-keying (QPSK) signal, and are usually

modeled as independent random binary sequences with pulse duration

where is a bit duration. The component amplitude is where

is the energy per bit. If is rectangular with unit amplitude over

then (C-59) yields the power spectral density for QPSK:

which is the same as the density for PSK. For a binary minimum-shift-keying

(MSK) signal with the same component amplitude,

Therefore, the power spectral density for MSK is

C.3

Sampling Theorems

Consider the Fourier transform of an absolutely integrable function

The periodic extension of is defined as

where W is the period of and it is assumed that the series converges

uniformly. Suppose that has a piecewise continuous derivative so that it

can be represented as a uniformly convergent complex Fourier series:

where the Fourier coefficient is given by

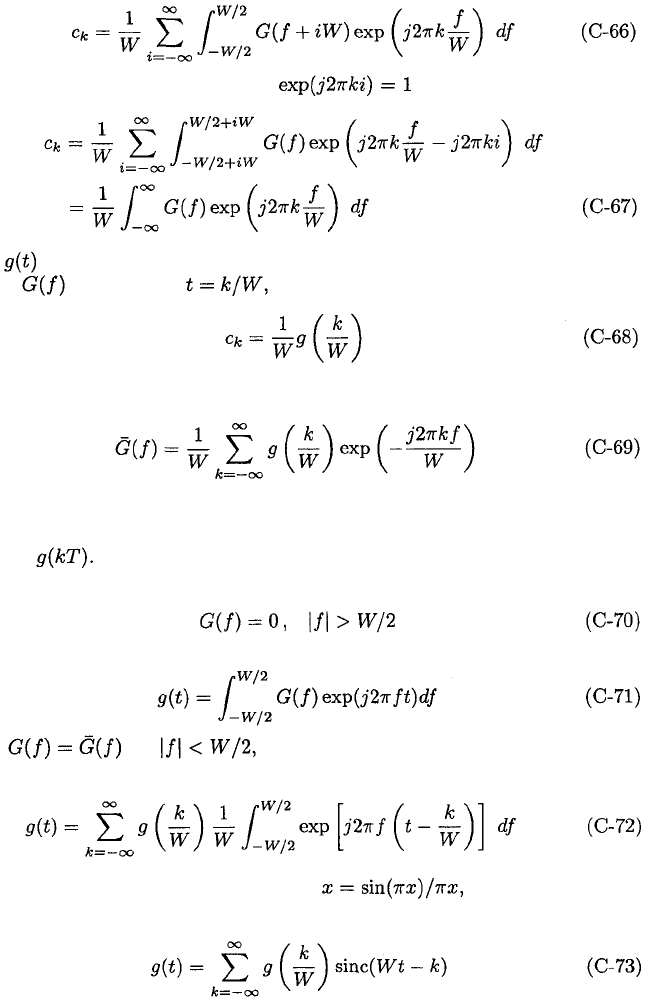
C.3. SAMPLING THEOREMS

425

Substituting (C-63) into (C-65) and interchanging the order of the summation

and the integration, which is justified because of the uniform convergence, we

obtain

We change variables and observe the to obtain

Since is absolutely integrable, the last integral is the inverse Fourier trans-

form of evaluated at and

Substituting (C-68) into (C-64) yields one version of the Poisson sum formula:

where the series converges uniformly. If we define T = 1/W, then the right-

hand side of (C-69) is proportional to the discrete-time Fourier transform of the

sequence

Suppose that the Fourier transform vanishes outside a frequency band:

It follows that

Since for (C-71) and (C-69) and the interchange of a

summation and integration yield

Evaluating this integral and defining sinc we obtain the sam-

pling theorem for deterministic signals:

where the samples are separated by T = 1/W.

426

APPENDIX C. SIGNAL CHARACTERISTICS

Consider a wide-sense stationary stochastic process with autocorrela-

tion and power spectral density which is the Fourier transform of

then it follows from the sampling theorem that

For an arbitrary constant the Fourier transform of is

which is zero for Therefore, (C-75) can be applied to

which gives

We define the stochastic process

The mean square difference between and is

Since the repeated use of (C-76) yields

which states that the mean square difference between and approaches

zero. With equality interpreted in the sense of this limit, the sampling theorem

for stationary stochastic process is

C.4

Direct-Conversion Receiver

Receivers often extract the complex envelope of the desired signal before apply-

ing it to a matched filter. The main components in a direct-conversion receiver

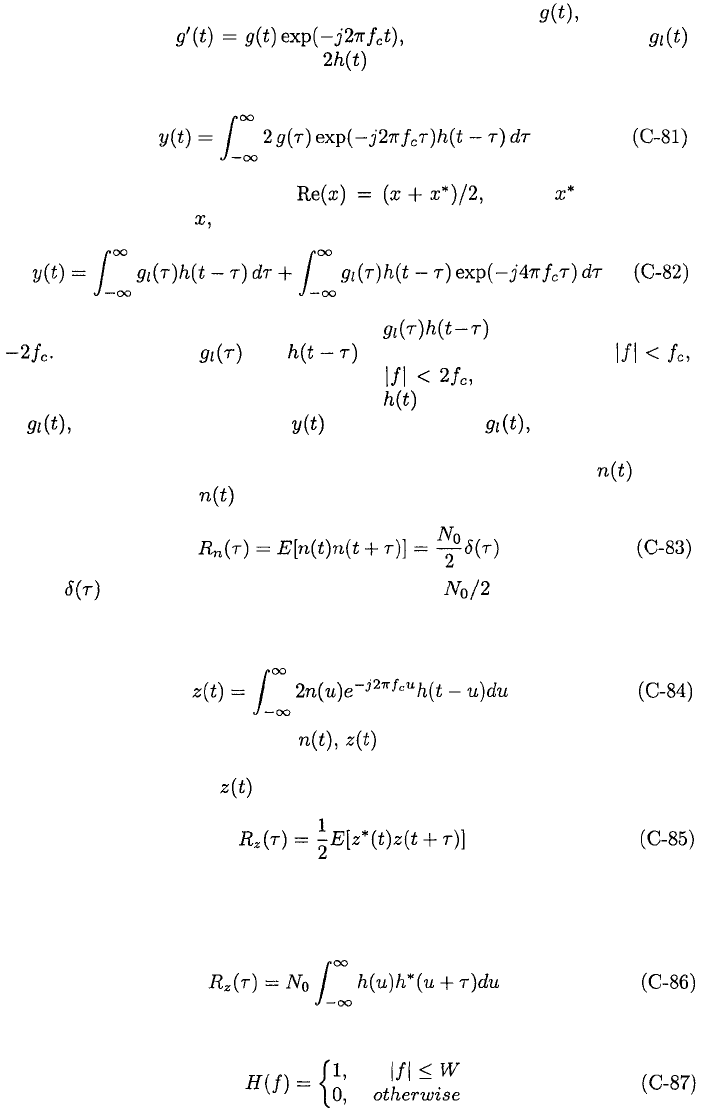
C.4.

DIRECT-CONVERSION RECEIVER

427

are shown in Figure C.1(a). The spectra of the received signal the input to

the baseband filter and the complex envelope

are depicted in Figure C.1(b). Let denote the impulse response of the

filter. The output of the filter is

Using (C-15) and the fact that where denotes the

complex conjugate of we obtain

The second term is the Fourier transform of evaluated at frequency

Assuming that and have transforms confined to

their product has a transform confined to and the second term in

(C-82) vanishes. If the Fourier transform of is a constant over the passband

of then (C-82) implies that is proportional to as desired. Figure

C.1(c) shows the direct-conversion receiver for real-valued signals.

The direct-conversion receiver alters the character of the noise enter-

ing it. Suppose that is a zero-mean, white Gaussian noise process with

autocorrelation

where denotes the Dirac delta function, and is the two-sided noise-

power spectral density. The complex-valued noise at the output of Figure C.1 (a)

Since it is a linear function of is zero-mean and its real and imagi-

nary parts are jointly Gaussian. The autocorrelation of a wide-sense stationary,

complex-valued process is defined as

Substituting (C-84), interchanging the expectation and integration operations,

using (C-83) to evaluate one of the integrals, and then changing variables, we

obtain

If the filter is an ideal bandpass filter with Fourier transform