Torrieri D. Principles of Spread-Spectrum Communication Systems
Подождите немного. Документ загружается.

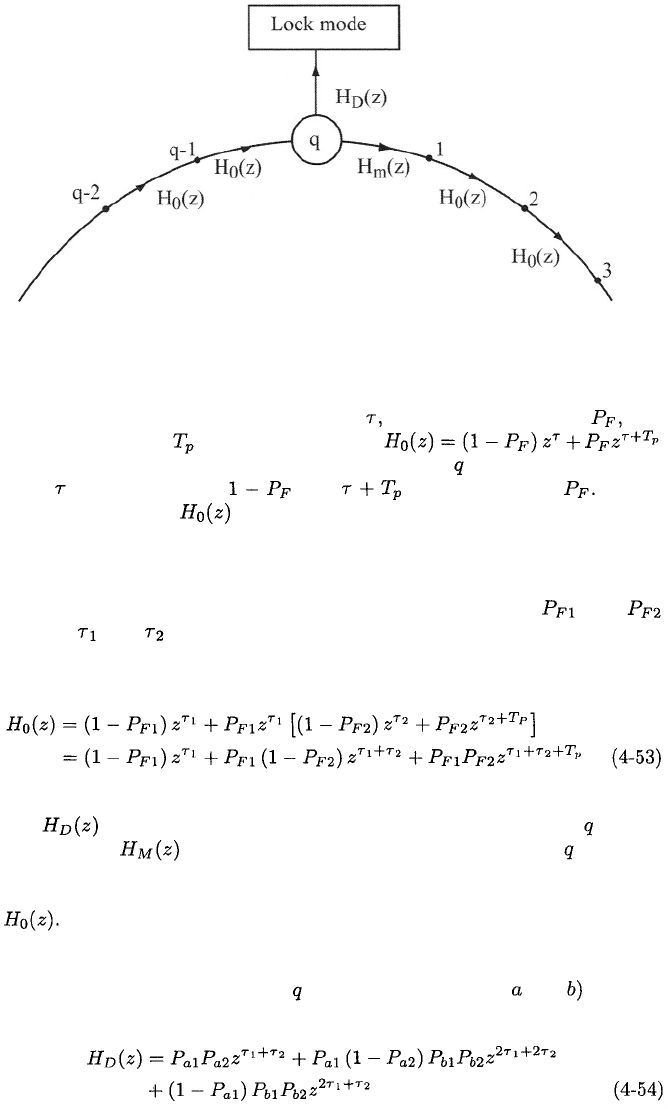
198
CHAPTER 4.
CODE SYNCHRONIZATION
Figure 4.9: Circular state diagram for serial-search acquisition.
time delay. A single-dwell system with dwell false-alarm probability and
constant penalty time has transfer function
for all branches that do not originate in collective state because the transition
delay is with probability and with probability For a
multiple-dwell system, is determined by first drawing a subsidiary state
diagram representing intermediate states and transitions that may occur as the
system progresses from one state to the next one in the original circular state
diagram. For example, Figure 4.10 illustrates the subsidiary state diagram
for a consecutive-count double-dwell system with false alarms and
and delays and for the initial test and the verification test, respectively.
Examination of all possible paths between the initial state and the next state
indicates that
Let denote the transfer function between the collective state and the
lock mode. Let denote the transfer function between state and state
1, which represents the failure to recognize code-phase offsets that are less than
a chip duration. These transfer functions may be derived in the same manner
as For example, consider a consecutive-count, double-dwell system with
a collective state that comprises two states. Figure 4.11 depicts the subsidiary
state diagram representing intermediate states and transitions that may occur
as the system progresses from state (with subsidiary states and to either
the lock mode or state 1. Examination of all possible paths yields

4.2.
SERIAL-SEARCH ACQUISITION
199
Figure 4.10: Subsidiary state diagram for determination of for
consecutive-count double-dwell system.
For a single-dwell system with a collective state that comprises N states,
where is the dwell time, is the false-alarm probability, and is the
detection probability of state within the collective state. To calculate the
statistics of the acquisition time, we seek the generating function defined as the
polynomial
where is the probability that the acquisition process will terminate in the
lock mode after seconds. If is known, then the mean acquisition time
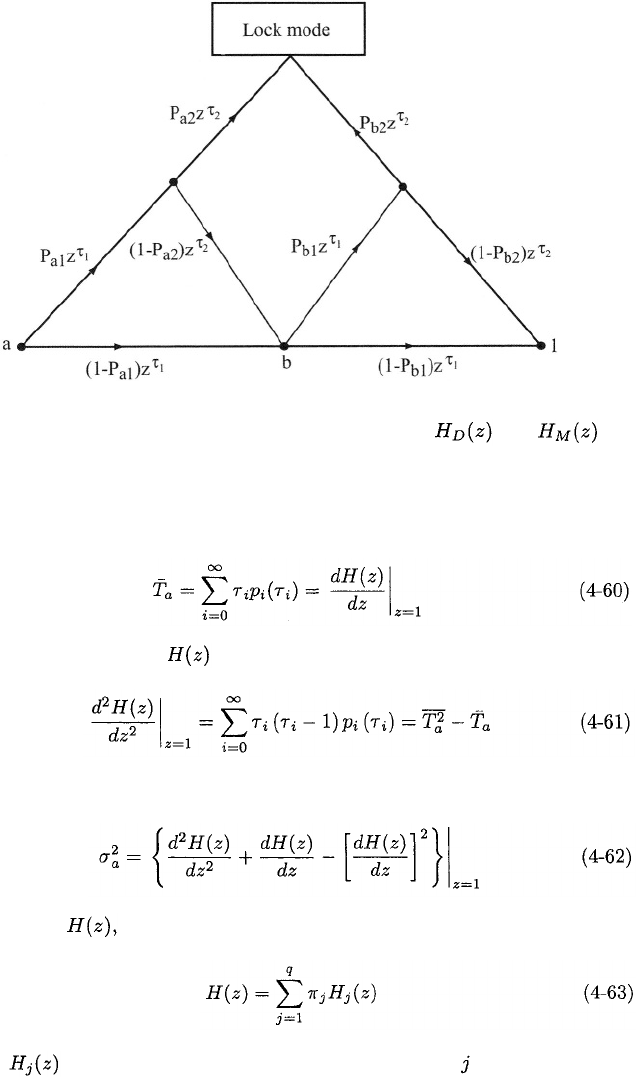
200
CHAPTER 4.
CODE SYNCHRONIZATION
Figure 4.11: Subsidiary state diagram for calculation of and for
consecutive-count double-dwell system with two-state collective state.
is
Therefore, the variance of the acquisition time is
To derive we observe that it may be expressed as
where is the transfer function from an initial state to the lock mode.
Since the circular state diagram of Figure 4.9 may be traversed an indefinite
The second derivative of gives
4.3.
ACQUISITION CORRELATOR
201
number of times during the acquisition process,
Substitution of this equation into (4-63) yields
The generating function may be expressed as the polynomial in (4-59) by means
of polynomial long division.
For the uniform a priori distribution given by (4-17),
Since the progression from one state to another is inevitable until the lock mode
is reached, Since (4-65) and (4-60) yield
where the prime indicates differentiation with respect to As an example,
consider a single-dwell system with a two-state collective state. The evaluation
of (4-67) using (4-56) to (4-58) with N = 2 yields (4-32) with if we set
and define by (4-26).
4.3
Acquisition Correlator
The noncoherent correlator of Figure 4.3 provides the approximate maximiza-
tion of given by (4-9). It is assumed that chip synchronization is
established by one of the standard methods of symbol synchronization. Conse-
quently, the test interval can be defined with boundaries that coincide with chip
boundaries, and we test code phases such that where is an integer.
Let denote the duration of the test interval, where M is a positive integer.
If the Doppler shift is not estimated, may be absorbed into in (4-9). If
the test interval begins with chip of the local spreading sequence, then (2-76)
and (4-9) imply that the decision variable for one test of a specific code phase
is
where
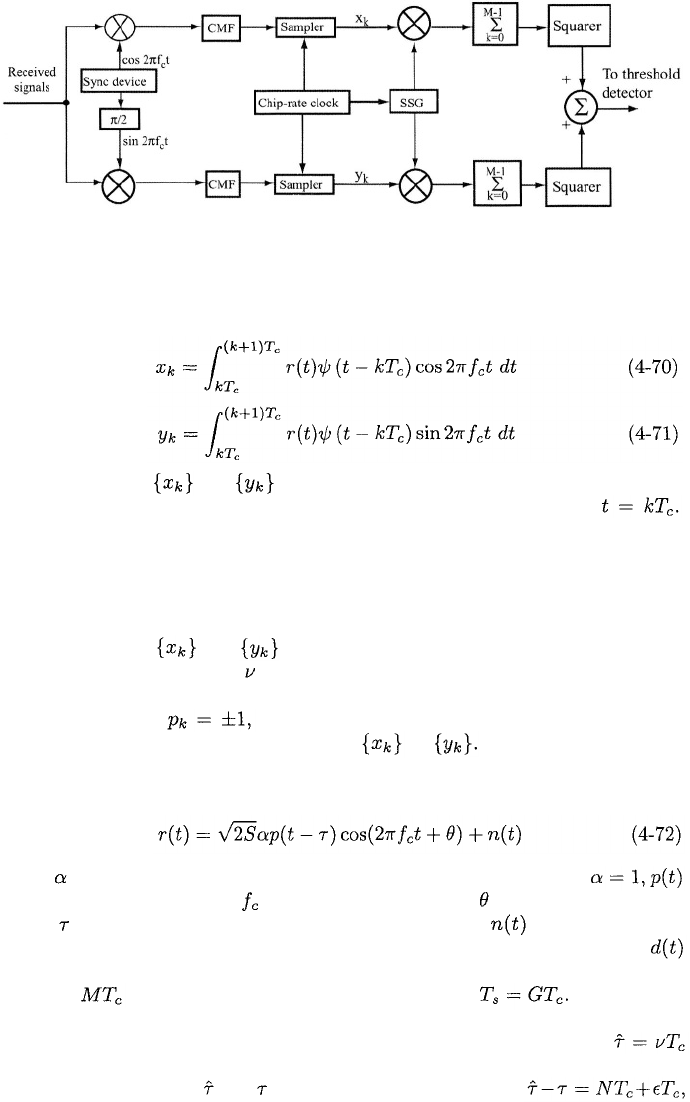
202
CHAPTER 4.
CODE SYNCHRONIZATION
Figure 4.12: Noncoherent correlator for acquisition system. CMF = chip
matched filter. SSG = spreading sequence generator.
The sequences and can be obtained by an in-phase and quadrature
downconversions followed by chip-matched filters sampled at times
Thus, the acquisition correlator has the form depicted in Figure 4.12. The
decision variable V is applied to a threshold detector to determine whether or
not a test of a particular code phase is passed. If a quaternary data modulation
is used instead of PSK, then the only modification necessary is to assign separate
spreading sequence generators to the two parallel branches of the correlator.
The sequences and can be applied to multiple parallel inner prod-
ucts with different values of simultaneously. This procedure allows a parallel
search of various code phases with a moderate amount of additional hardware
or software. Since each inner product may be computed by either
adding or subtracting each component of or
To analyze the performance of the acquisition correlator under fading con-
ditions, we assume that the received signal is
where is the attenuation due to fading,
S
is the average power when
is the spreading waveform, is the carrier frequency, is the random carrier
phase, is the delay due to the unknown code phase, and is the interference
plus noise modeled as additive white Gaussian noise. The data modulation
is omitted because either it is not transmitted during acquisition or the test
duration is much smaller than a symbol duration In the latter
case, the probability that a symbol transition occurs during a test is negligible,
and the squaring operations eliminate the symbol value from V. Let
denote the delay associated with the code phase of the local spreading sequence.
The difference between and may be expressed in the form
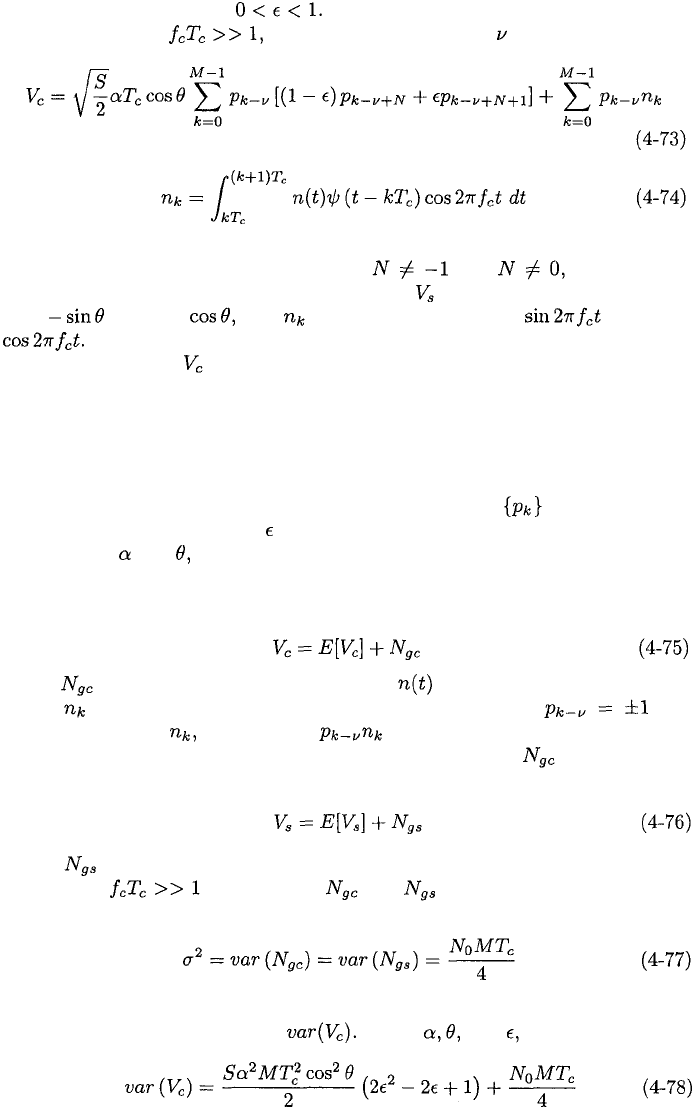
4.3.
ACQUISITION CORRELATOR
203
where N is an integer and For a rectangular chip waveform, (4-69),
(4-70), and (4-72), and the definition of chip yield
where
The alignment of the received and local spreading sequences is close enough
for acquisition if N = –1 or N = 0. If and then the cell
may be considered incorrect. The equation for is the same as (4-74) except
that replaces and is given by (4-74) with replacing
The first term of in (4-73) contributes self-interference that may cause a
false alarm. The self-interference is small if the autocorrelation of the spread-
ing sequence is sharply peaked. In a network of similar systems, interfering se-
quences are substantially suppressed if the cross-correlations among sequences
are small, as they are if all the sequences are Gold or Kasami sequences (Chapter
6).
In the performance analysis, the spreading sequence is modeled as a
random binary sequence and is modeled as a random variable. Thus, given
the values of and the self-interference varies with respect to its mean value
and, hence, degrades acquisition even when the noise term is negligible. If the
variable part the self-interference is negligible, then (4-73) can be approximated
by
where is the second term in (4-73). Since is zero-mean, white Gaussian
noise, is a zero-mean Gaussian random variable. Since and
is independent of the product is zero-mean and Gaussian. The
independence of the terms in the sum then indicates that is a zero-mean
Gaussian random variable. Similarly, we obtain the approximation
where is a zero-mean, Gaussian random variable. Straightforward calcula-
tions using indicate that and are statistically independent
with the same variance:
To determine the condition under which the self-interference is approximated
by its mean value, we calculate Given and (4-73) yields
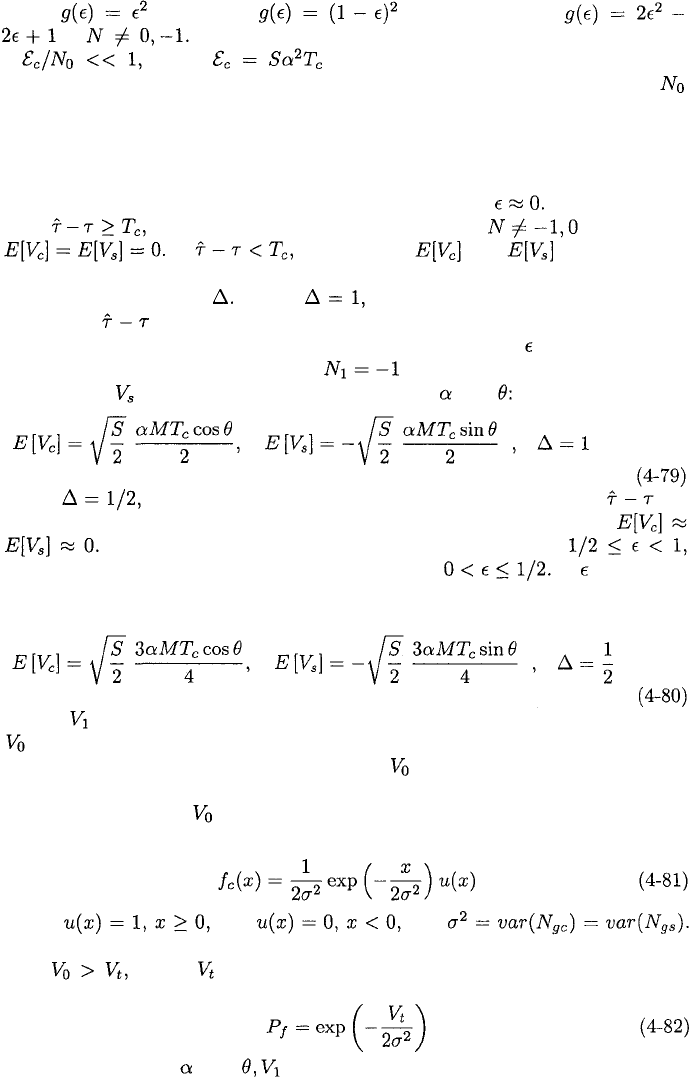
204
CHAPTER 4.
CODE SYNCHRONIZATION
where if N = 0, if N = –1, and
if The first term is much smaller than the second term
if where is the energy per chip. This condition
is satisfied with high probability in most practical systems, especially if
incorporates the power spectral densities due to multiple-access interference
and multipath signals. Accordingly, we proceed with the analysis using the
approximations (4-75) and (4-76). Without these approximations, alternative
approximations and assumptions are necessary or the analysis becomes much
more complicated [6]. A common approximation is that
If then a cell is incorrect and (4-73) with implies that
If the values of and depend on the
step size of the serial search. The step size is the separation in chips between
cells and is denoted by When two consecutive cells are considered
correct. If is increasing, then the cell corresponding to N = –1 occurs
first and is followed by the cell corresponding to
N
= 0. If is assumed to be
uniformly distributed over (0,1) and or 0, then (4-73) and the similar
equation for yield the conditional means given and
When the two consecutive cells with the smallest values of are
considered the two correct cells. For all the others, we assume that
The first correct cell corresponds to N = –1 and
whereas the second one corresponds to N = 0 and If is assumed
to be uniformly distributed over the latter intervals, then for both cells, we
obtain
Let denote the decision variable V when the correct cell is tested, and let
denote V when the incorrect cell is tested. Equations (4-68), (4-75), and (4-
76) and the preceding analysis indicate that is the sum of the squares of two
independent, zero-mean Gaussian random variables. The results of Appendix
D then indicate that has a central chi-square distribution with two degrees
of freedom and probability density function
where and and
The false-alarm probability for a test of an incorrect cell is the probability
that where
is the threshold. The integration of (4-81) gives the
false-alarm probability:
Similarly, given and is the sum of the squares of two independent
Gaussian random variables with nonzero means. The results of Appendix D

4.3.
ACQUISITION CORRELATOR
205
then indicate that has a noncentral chi-square distribution with two degrees
of freedom and probability density function
where
and
The detection probability for a test of a correct cell is the probability that
The integration of (4-83) and the substitution of (4-84) give the
detection probability
where is the generalized Q-function defined by (D-15),
and is the signal energy per chip when fading is absent and
Combining (4-86) and (4-82) yields
Thus, if is specified, is given by (4-88). The threshold needed to realize
a specified is
which requires an accurate estimate of
In the presence of fast Rayleigh fading, has the Rayleigh probability den-
sity (Appendix D.4):
where so that S remains the average signal power in (4-72). It
is assumed that is approximately constant during a test, but independent
between one test and another. Since (4-86) is conditioned on the detection
probability in the presence of fast fading is
To evaluate this integral, we substitute the integral definition of given
by (D-15), interchange the order of integration in the resulting double integral,

206
CHAPTER 4.
CODE SYNCHRONIZATION
and then use (D-33) to evaluate one of the integrals. The remaining integration
over an exponential function is elementary. The final result is
For slow Rayleigh fading with a coherence time much larger than the acquisition
time, it is appropriate to use (4-86) in calculating the conditional mean acqui-
sition time and then integrate over the Rayleigh density to obtain the mean
acquisition time.
Let C denote the number of chips in the timing uncertainty. The normalized
mean acquisition time (NMAT) is defined as The normalized standard
deviation (NSD) is defined as
Example 1.
As an example of the application of the preceding results,
consider a single-dwell system with a uniform search and a uniform a priori
correct-cell location distribution. Let where M is the number of
chips per test, and where K is the number of chips in the mean
penalty time. It is assumed that there are two independent correct cells with
the common detection probability If (4-32) and (4-26)
yield the NMAT:
where
In a single-dwell system, which is given by (4-82). For step size
for In the absence of fading, (4-88) relates
and whereas (4-92) relates them in the presence of fast Rayleigh fading.
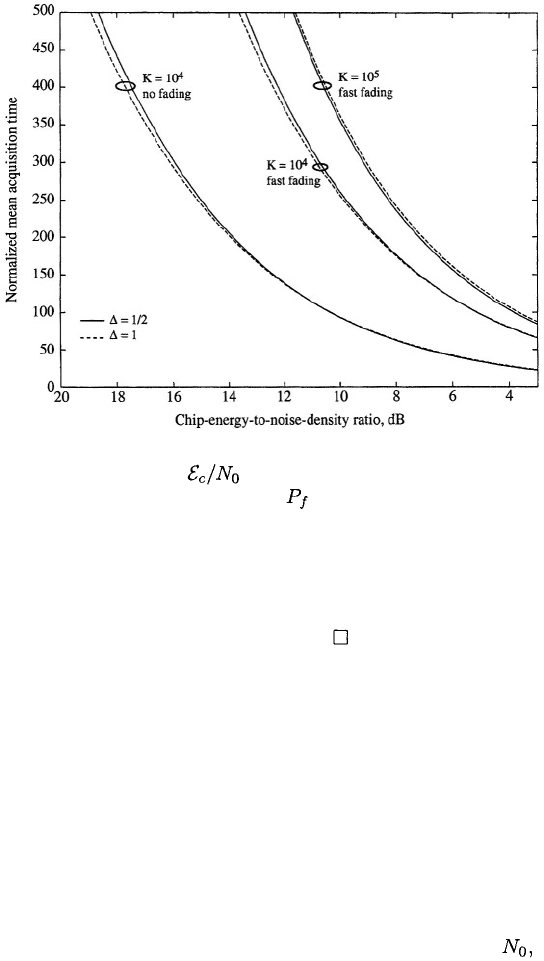
Figure 4.13 shows the NMAT as a function of for fast Rayleigh fading
and no fading. At each value of the values of and M are selected
to minimize the NMAT. The figure indicates the advantage of when
and the advantage of when The large increase in the
NMAT due to fast Rayleigh fading is apparent. From (4-25), it is found that
each plot of the NSD is similar to that of the corresponding NMAT.
Example 2. Consider double-dwell systems with a uniform search, a
uniform a priori correct-cell location distribution, and two independent correct
cells with and The test durations are
and If the NMAT is obtained from (4-24)
and (4-94), where is given by (4-28) for a consecutive-count system and
(4-36) for an up-down system. By replacing with and with the
probabilities and or 2, are related through (4-88) with for
no fading and (4-92) for fast Rayleigh fading.
Figure 4.14 shows the NMAT as a function of for double-dwell systems
in the presence of fast Rayleigh fading. The step size is which is
found to be advantageous for the parameter values chosen. At each value of
the values of and are selected to minimize the NMAT.
The figure illustrates the advantage of the up-down system in most practical
applications. From (4-25), it is found that each plot of the NSD is similar to
4.3.
ACQUISITION CORRELATOR
207
Figure 4.13: NMAT versus for single-dwell system in presence of fast
Rayleigh fading or no fading. Values of and M are optimized.
that of the corresponding NMAT. A comparison of Figure 4.14 with Figure
4.13 indicates that double-dwell systems are capable of significantly lowering
the NMAT relative to a single-dwell system.
The existence of two consecutive correct cells can be directly exploited in
joint two-cell detection, which can be shown to provide a lower NMAT than the
conventional cell-by-cell detection [7]. In the presence of frequency-selective
fading with a large number of resolvable multipath signals, the NMAT of serial-
search acquisition is usually increased because the increased self-interference is
more significant than the higher number of nonconsecutive correct cells with
correct phases. However, joint two-cell detection is more resistant to multiple-
access interference and more robust against variations in the detection thresh-
old, the power level of the desired signal, and the number of multipath signals.
The advantages of joint two-cell detection over cell-by-cell detection are the
result of the efficient combining of the energy of two adjacent correct-phase
samples.
The detection threshold of (4-89) depends on an estimate of the equiv-
alent noise-power spectral density. An accurate estimate usually requires a
long observation interval. However, in mobile communication systems and in
the presence of jamming, the instantaneous interference power may be rapidly
varying. To cope with this environment, an adaptive threshold may be set by
the instantaneous received power [8]. As a result, the mean acquisition time is
lowered relative to its value for nonadaptive schemes when Rayleigh fading or
