Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.


§
1.
Функції багатьох змінних та їх диференціювання
121
Якщо х
х
,х
2
,...,х
п
- незалежні змінні і функція и = /(х
]
,х
2
,...,х
п
)
має неперервні частинні похідні, то диференціал т -го порядку виражаєть-
ся символічною формулою:
І-
,=і 3*і
и, (2.17)
яка формально розкривається за біноміальним законом.
Зокрема,
п т д
2
и
а
2
и =
ХХт—г—ск,сіх
.
,=і
7=
і ах,д
Х]
Для функції двох змінних 2 = /(х,у) справедлива формула
сі
т
г = \і-ах + ~сіу
ах оу
(2.18)
При т = 2, /и = 3 маємо
^
2
2
=
-
3
-|-ал-
2
+2^-Ай>
+
-
3
-4а>
2
,
(2.19)
ох^
охоу Зі/
с/
3
г = ^А-ЧЗ-^ах
2
ф + 3-^
т
Аф
2
+ ^4ф
3
. (2.20)
дх
3
дх
2
ду ЗхЗ>>
2
ду
3
II. Контрольні питання та завдання
1. Дайте означення функції п змінних, її області визна-
чення та області значень.
2.
Дайте означення функції двох змінних та її області виз-
начення. Який геометричний зміст цих понять?
3.
Що називається лінією рівня функції г = /(х,у)?
4. Дайте означення поверхні рівня функції и = /(х,у,г).
5.
Побудуйте поверхню г = х
2
+ 4у
2
та її лінії рівня.
6. Запишіть вирази для повного та частинного приросту
ФУНКЦІЇ 2 = /(X, у).
7. Дайте означення границі функції и = /(Р) в точці Р
0
.
8. Дайте означення неперервності функції и = /(Р) в точ-
ці Р
0
.

122
Глава 2. Диференціальне числення функцій багатьох змінних
9. Визначіть частинні похідні функції и = /(Р) в точці Р
0
.
10.
Сформулюйте правило знаходження частинних похідних
функції и = Дх,,х
2
,...,х
п
).
11.Наведіть означення повного диференціала функції п
змінних; двох змінних.
12.
Як застосовується повний диференціал в наближених
обчисленнях?
13.
За якими формулами проводиться диференціювання
складних функцій?
14.
Запишіть формулу повної похідної.
15.
Дайте означення похідної за напрямом.
16.
Дайте означення градієнта функції.
17.
Як зв'язані похідна за напрямом і градієнт?
18.
Сформулюйте правило диференціювання неявно зада-
ної функції.
19.
Як проводиться диференціювання системи неявно зада-
них функцій?
20.
Які правила диференціювання параметрично заданих
функцій?
21.
Визначіть і вкажіть правила знаходження похідних і
диференціалів вищих порядків.
///. Приклади розв'язання задач
Прикладі. Знайти область визначення Б наступних функцій:
а) 2 = 1а
(4-
х
2
-4у
2
); б) и =
л]-х
2
-у
2
+2г .
• а) область визначення И даної функції г
—
1п (4 - х
2
- 4у
2
) - мно-
жина тих точок
(х,у),
для яких 4-х
2
- 4у
2
> 0, бо логарифмічна функція
визначена тільки для додатних значень аргумента.
Щоб зобразити область £> геометрично, знайдемо її межу
2 2
4-х
2
-4у
2
=0 або х
2
+4у
2
=4 або — + ?— = \.
4 1

§
1.
Функції багатьох змінних та їх диференціювання
123
Це рівняння визначає в площині хОу еліпс з півосями а = 2 та Ь = 1.
Даний еліпс ділить всю площину на дві частини. Для точок однієї з цих час-
тин 4-х
2
-4у
2
> 0 , для другої 4-х
2
-4у
2
< 0 .
Щоб виявити, яка з частин є областю визначення даної функції, тобто
задовольняє умові 4-х
2
-4у
2
> 0, достатньо перевірити цю умову для будь-
якої однієї точки, яка не лежить на еліпсі. Наприклад, точка 0(0,0) нале-
жить області О, бо 4 - О
2
- 4
•
О
2
= 4 > 0.
Отже,
внутрішніми точками області О даної функції є точки, обме-
жені еліпсом. Сам еліпс не належить області О тому, що для точок еліпса
4-х
2
-4у
2
= 0. Область И - відкрита область (рис.2.1). Нарис.2.1 межа
області позначена пунктиром.
Рис.2.1 Рис.2.2
б) область визначення О даної функції и = х
2
-у
2
+ 2г - мно-
жина точок
(х,у,г),
для яких -х
2
- у
2
+ 2г > 0 або х
2
+ у
2
<2г.
Межа цієї області х
2
+у
2
= 2г . Це рівняння параболоїда обертання.
Параболоїд обертання ділить весь простір на дві частини, для точок однієї з
яких X
2
+у
2
<2г , для іншої х
2
+ у
2
>2г .
Для виявлення, яка з частин задовольняє умові х
2
+ у
2
< 2г, візьме-
мо одну з точок, яка не лежить на параболоїді обертання, наприклад, точку
(0,0,1).
Ця точка належить області £>, бо О
2
+ О
2
< 2
•
1.
Отже,
областю й визначення даної функції є область, що міститься
всередині параболоїда обертання, включаючи і його межу (рис.2.2).
Приклад
2. Знайти лінії рівня функції г = 2х
+
у .
•
Лінії рівня визначаються рівнянням
2х + у = с.
Це сім'я паралельних прямих.
124
Глава 2. Диференціальне числення функцій багатьох змінних
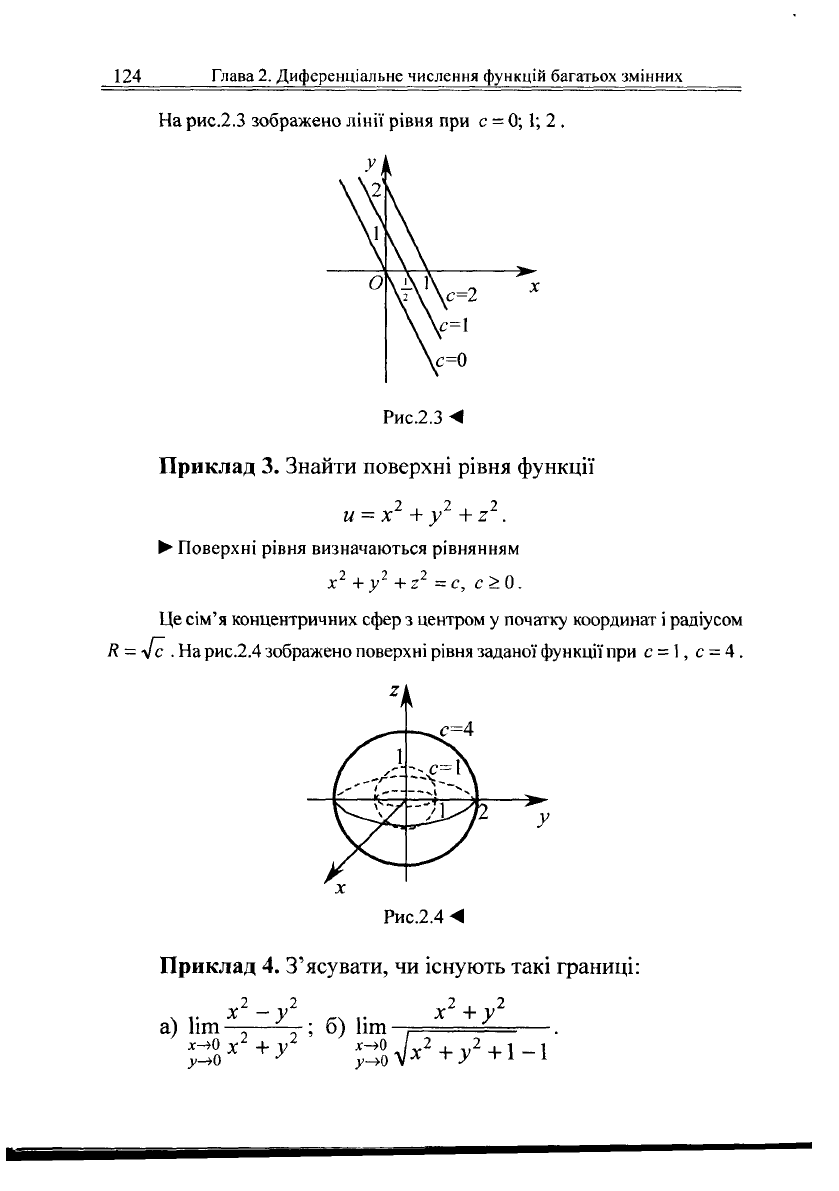
На рис.2.3 зображено лінії рівня при с = 0; 1; 2 .
Рис.2.3 М
Приклад
3.
Знайти поверхні рівня функції
2 2 2
и = х +у +2 .
• Поверхні рівня визначаються рівнянням
х
2
+у
2
+2
2
=с, с>0.
Це сім'я концентричних сфер з центром у початку координат і радіусом
Я = 4с . На рис.2.4 зображено поверхні рівня заданої функції при с = 1, с = 4.
2
>
/ 1
1 —
^Т
2
У
Рис.2.4 <
Приклад
4.
З'ясувати,
чи
існують такі
границі:
2 2 2,2
\У
х
~У РЛУ х +у
а) Ііт—з——\ о) ііт
*-»о х
2
+ у
2
у-*0
'
Х
->°у1х
2
+у
2
+\-\
у-+0

§ І. Функції багатьох змінних та їх диференціювання
125
х
1
-
2
•
а) розглядаємо Ііт ^—^г-.
х + у
Спосіб 1. Нехай точка Р(х,у) прямує до точки Р
0
(0,0). Розглянемо
зміну х та у вздовж прямої у = кх . Отримаємо
2
2
X
-У
*->°х
2
+ у
2
Ііт
у = кх , Ук
х ->0
х к, х .. 1 к.
Ііт — —— = нт
•
^х
2
+к
2
х
2
*->°
1
+&
2
\ + к
2
Результат має різні значення в залежності від вибраного к і тому функ-
ція границі не має.
Спосіб 2. Вважаємо, що при Р(х,у) -» Р(0,0), р = ^х
2
+ у
2
—»0 не-
залежно від того, за яким напрямком Р
—>
Р
0
. Цей напрямок характеризується
кутом ф нахилу прямої - напрямку наближення Р до Р
0
. Тому
2
2
..
X -у
Ііт ——
«»ґ
+у
X
= рС05ф,
у
=р5ІПф,
р
= /х
2
+ у
2
,
X
-» 0,
у —>
0 : •0 Уф.
..
р С052ф „
=
Ііт —
31
= сов2ф.
р^о р
2
Результат має різні значення в залежності від вибраного напрямку
прагнення Р до Р
0
, тобто кута ф . Звідси функція границі не має.
б) розглядаємо Ііт
х
2
+у
2
х
у
^х
2
+у
2
+\-\'
Спосіб І. Розглянемо зміну х та у вздовж прямої у = кх. Отримаємо
х
2
+у
2
Ііт .
^х
2
+
у
2
+
1-\
у = кх,Ук
х-»0
= Ііт
Х
2
(1
+ А:
2
)
х
^^х
2
(\
+ к
2
)+\-\
2
= 1іт
2
*<
1 +
* > = 1іт2^
2
(1 + ^) + 1=2
х(1 + Г)
х->0
7х
2
(1 + х
2
) +
1
При знаходженні границі скористались правилом Лопіталя.

126
Глава 2. Диференціальне числення функцій багатьох змінних
Спосіб2. Якщо Р(х,у)-> /"(0,0),то р = фс
2
+ у
2
->0,тому
2 2
X +у
Ііт .
х = р СОЗ ф,
у = рзіпф,
Р=у[х
2
~+~у
2
,
х->0,у-»0=>р->0 \/ф.
= Ііт = Ііт-
2р
Р-^д/р
2
+1 -1 Р-^° Р Р-*
0
= Ііт 2^|р
2
+ \ = 2 .
Тут при знаходженні границі застосовано правило Лопіталя. А
Приклад 5. Знайти точки розриву функції
1
- хуг
и =
2х + 3у - г + 4
• Функція не визначена в точках, в яких знаменник обертається в
нуль. Тому вона має поверхню розриву - площину 2х + 3у - 2 + 4 = 0.-^
Приклад 6. Знайти частинні похідні функції г = агсІ§
• Вважаючи у сталою, маємо
Зт_
Зх
У
1
+
2 2
X + у
Вважаючи х сталою, маємо
<к_ 1 1 х
Зу
1
+
2 2 2
у 1 X X +у
Приклад 7. Знайти повний диференціал функції
и = х
2
у + 3у
3
2-4г
3
+2.

§
1.
Функції багатьох змінних та їх диференціювання
127
^ _ . Зм ди ди
• Знаходимо частинні похідні ——, ——, ——:
Зх ду дг
Зм ди і
п
і ди „
2
.
~ 2
— = 2ху; — = х
2
+9у
2
г; — = 3у
2
-\2г
2
.
дх ду дг
Враховуючи,
що
, Зм , ди . ди ,
аи = —ах + —ау + —аг,
Зх Зу дг
маємо
сіи = 2хуах + {х
2
+9у
2
г)сіу + (3у
2
-\2г
2
)сіг.<
Приклад 8. Обчислити наближено за допомогою повного
диференціала
Л
/(4,05)
2
+ (2,97)
2
.
• Розглянемо функцію /(х, у) = ^х^ + у
2
і застосуємо до неї формулу
/(х + Ах,у + Ау) = /(х,у) + -^-Ах + ^-Ау,
дх ду
поклавши х = 4, у = 3, Ах = 0,05, Ау =
-0,03.
з/_
х , а/_ у .
Врахуємо,
що - , - ,
^
V*
2
+у
2
^ 7*
2
+/
/(4,3) = 7ЇЧр" = 5; Ж^Л.
Зх 5 ду 5
л
/(4,05)
2
+
(3,07)
2
,
5 +
1.0,05
+
1 (-0,03) = 5
+
°'
2
°"°'°
9
=
= 5 + ^- =5 + 0,022 =5,022.
Отже,
-у/(4,05)
2
+(3,07)
2
= 5,022. <
Приклад 9. Знайти —, якщо и = хуг, де х = І
2
+1,
.у = пи, г = ї§/.
• Скористаємося формулою
сій _
Зм
ах Зм сіу
+
ди аг
сії дх сії ду сії дг сії '

128
Глава 2. Диференціальне числення функцій багатьох змінних
Маємо
сій „ 1 1
= У2-21 + Х2 \-Ху — .
СІІ І С05
1
І
Далі, виразивши х,у,г через Дотримуємо
сій і 1 ч 1
= 2/1пМ§г + (/
2
+ 1)1§г-- + (ґ + 1)1п/-
сії
° І '
соз
2
1
Зауважимо, що результат буде той же самий, якщо попередньо підста-
вити замість х та у їхні значення, а потім знайти звичайну похідну по і. А
Приклад 10. Знайти — , якщо и = -у/х
2
+ у
2
+ г
2
, де
сіх
у = х
3
, г = зіп
2
х.
• Скористаємося формулою повної похідної
сій _ди ди сіу
+
Зм сіг
сіх дх ду сіх дг сіх
Послідовно знаходимо
ди х ди у ди 2
&
^х
2
+у
2
+г
2
' ^
^х
2
+у
2
+
2
2
'
92
уІх
2
+у
2
+2
2
'
А
Л
і і , • • „
-^ = 3х ; — = 2зіпхсозх = зіп2х.
ох аг
Підставивши ці вирази в формулу повної похідної, отримаємо
сій 1 , -і • ^ ч
— = • (х + у Зх +7-8іп2х).
Л
4х
2
+
У
2
+2
2
Далі підставимо замість у
та
г їхні задані вирази через х. Остаточно
#И
1 , , , 5 • 2 • ч ^
г(х + 3х + зіп х-зіп2х).-Ч
А
УІХ
2
+Х
Ь
+
8ІП
4
X
Приклад 11. Знайти і , якщо 2 = х
2
1п у, де х = —,
_у = «V .
• Скористаємося формулами
дг _дг дх дг ду дг _ дг дх дг ду
ди дх ди ду ди ' ду дх ду ду ду

§
1.
Функції багатьох змінних та їх диференціювання
129
Тоді
аг „ , їх
2
— = 2хЧп.у-- + У;
ди V у
дг ( и V х
2
— = 2х 1п
>>
•
—- + и .
ду V
у
/ У
Далі підставивши замість х та у їх вирази через и та V , отримаємо
о
2
и ,, , ... 32 м
2
„ ,
чч
^
— = — (1 +
21П(ИУ));
— =
—(1-21П(ИУ)).^
Зі/
у Зу у
Приклад 12. Знайти похідну функції и = ху
2
г
3
в точці
М(3,2,1) за напрямом вектора / = МИ, де N(5,4,2).
• Знайдемо вектор МN та його напрямні косинуси:
МЇЇ = 1
=(5-3)1
+ (4-2)] + (2-])к =2Ї + 2] + к; |/| = 3;
С05а = —, С05В = —,
С05у
= —.
з з з
Обчислимо значення частинних похідних функції в точці М :
Зи
Зх
2
з
І
. Зм
= у 2 =4 ; —
І« ду
м
= 2
*-У
2
,,
=12;
Т~
]
м дг
м
=3ху
2
г
2
\ =36.
7
ш
Отже,
ди
з7
м
„
2 2
1 68 ^
= 4-+12- +36- = —
З 3 3 3
Приклад
13.
Знайти градієнт функції г = х у в точці М(1,1).
• Обчислюємо частинні похідні функції в точці М(1,1):
32
Зг
Зх
=
2Х
У\
М
=
2
^
м оу
м
X
І
Ч =1
їм
Отже,
§гас12 = 2 / + _/'.
Приклад 14. Знайти похідну функції 2 = 1п(х
2
+,у
2
) в
точці М(3,4) за напрямом градієнта функції г.

130
Глава 2. Диференціальне числення функцій багатьох змінних
• Знайдемо §гасІ2:
2х
£гасІ2
=
х
2
+у
2
•і +
2у
м
2 2
X + у
М
-. 6
т
8 -
•) ~ —' + — ]
25 25
За умовою / = §гас12 .
дг
Отже,
-— = | ©гасі г |
=
о/
-Т
сіу
Приклад
15.
Знайти похідну
—
функції
у,
заданої
неяв-
ок
но
рівнянням
е
у
- е
х
+ 2ху = 0.
• Позначимо ліву частину заданого рівняння через Р(х, у). Скорис-
таємось формулою для визначення похідної функції у = у(х), заданої неяв-
но рівнянням Р(х,у) = 0:
дР_
<*У
=
Зх
ах Ь?_'
ду
дР х <ЬР V
де —— = -е +2у;
——
= е
у
+ 2х.
дх ду
Отже,
маємо
сіу _ -е
х
+2у _ е
х
- 2у
сіх
е
у
+ 2х е
у
+2х
Приклад
16.
Знайти похідні
та
функції
г,
заданої
дх ду
неявно рівнянням
х +2у +2 -
Зхуг
- 2у + З = 0 .
• Позначимо ліву частину заданого рівняння через Р(х,у, г). Скорис-
таємось формулами для визначення похідних функції г =
г(х,у),
заданої не-
явно рівнянням Р(х, у, г) = 0:
дР_
<к___дх_. 92 _ ду
дх дР_' ду дР '
дг дг
