Taylor M.E. Partial Differential Equations III: Nonlinear Equations
Подождите немного. Документ загружается.


258 14. Nonlinear Elliptic Equations
then follows from Corollary 12.12 and Proposition 12.14 of Chap. 13, just as in
(12b.93). Hence Corollary 12B.5 is applicable. This result, established by [Wen],
was an important precursor to Proposition 12.13 of Chap.13.
13. Elliptic regularity IV (Krylov–Safonov estimates)
In this section we obtain estimates for solutions to second-order elliptic equations
of the form
(13.1) Lu D f; Lu D a
jk
.x/ @
j
@
k
u C b
j
.x/ @
j
u C c.x/u;
on a domain R
n
. We assume that a
jk
;b
j
,andc are real-valued and that
a
jk
2 L
1
./, with
(13.2) jj
2
a
jk
.x/
j
k
ƒjj
2
;
for certain ;ƒ 2 .0; 1/.Wedefine
(13.3) D D det .a
jk
/; D
D D
1=n
:
A. Alexandrov [Al] proved that if jbj=D
2 L
n
./ and c 0 on ,then
(13.4) u 2 C.
/ \ H
2;n
loc
./; Lu f on ;
implies
(13.5) sup
x2
u.x/ sup
y2@
u
C
.y/ C C kD
1
f k
L
n
./
;
where C D C
n; diam ;kb=D
k
L
n
. We will not make use of this and will
not include a proof, but we will establish the following result of I. Bakelman [B],
essentially a more precise version of (13.5) for the special case b
j
D c D 0
(under stronger regularity hypotheses on u). It is used in some proofs of (13.5)
(see [GT]).
To formulate this result, set
(13.6)
C
Dfy 2 W u.x/ u.y/ C p .x y/; 8 x 2 ;
for some p D p.y/ 2 R
n
g:
If u 2 C
1
./,theny belongs to
C
if and only if the graph of u lies everywhere
below its tangent plane at
y; u.y/
.Ifu 2 C
2
./,thenu is concave on
C
,that
is, .@
j
@
k
u/ 0 on
C
.

13. Elliptic regularity IV (Krylov–Safonov estimates) 259
Proposition 13.1. If u 2 C
2
./ \ C./, we have
(13.7) sup
x2
u.x/ sup
y2@
u.y/ C
d
nV
1=n
n
D
1
.a
jk
@
j
@
k
u/
L
n
.
C
/
;
where d D diam , and V
n
is the volume of the unit ball in R
n
.
To establish this, we use the matrix inequality
(13.8) .det A/.det B/
1
n
Tr AB
n
;
for positive, symmetric, n n matrices A and B. (See the exercise at the end of
this section for a proof.) Setting
(13.9) A DH.u/ D
@
j
@
k
u.x/
;BD
a
jk
.x/
;x2
C
;
where H.u/ is the Hessian matrix, as in (3.7a), we have
(13.10) jdet H.u/jD
1
1
n
a
jk
@
j
@
k
u
n
on
C
:
Thus Proposition 13.1 follows from
Lemma 13.2. Fo r u 2 C
2
./ \ C./, we have
(13.11) sup
x2
u.x/ sup
y2@
u.y/ C
d
V
1=n
n
Z
C
jdet H.u/j dx
1=n
:
Proof. Replacing u by u sup
@
u, it suffices to assume u 0 on @.Define
./ to be
S
y2
.y/,where
(13.12) .y/ Dfp 2 R
n
W u.x/ u.y/ C p .x y/; 8 x 2 g;
so .y/ ¤;,y 2
C
. Also, if u 2 C
1
./ (as we assume here),
(13.13) .y/ DfDu.y/g; for y 2
C
:
Thus the Lebesgue measure of ./ is given by
(13.14) L
n
./
D L
n
.
C
/
D L
n
Du.
C
/
Z
C
jdet H.u/j dx:

260 14. Nonlinear Elliptic Equations
Thus it suffices to show that if u 2 C./ \ C
2
./ and u 0 on @,then
(13.15) sup
x2
u.x/
d
V
1=n
n
L
n
./
:
This is basically a comparison result. Assume sup u >0is attained at x
0
.Let
W
1
be the function on whose graph is the cone with apex at
x
0
; u.x
0
/
and
base @ f0g. Then, if
W
1
.y/ denotes the function (13.12) with u replaced by
W
1
,wehave
(13.16)
u
./
W
1
./:
Similarly, if W
2
is the function on B
d
.x
0
/ whose graph is the cone with apex at
x
0
; u.x
0
/
and base fx Wjx x
0
jDdgf0g,then
(13.17)
W
1
./
W
2
B
d
.x
0
/
:
Finally, the inequality
(13.18) sup W
2
d
V
1=n
n
L
n
W
2
.B
d
.x
0
//
is elementary, so we have (13.15), and hence Lemma 13.2 is proved.
We now make the assumption that
(13.19)
ƒ
;
jbj
2
;
jcj
;
and establish the following local maximum principle, following [GT].
Proposition 13.3. Let u 2 H
2;n
./; Lu f; f 2 L
n
./. Then, for any ball
B D B
2R
.y/ and any p 2 .0; n, we have
(13.20) sup
x2B
R
.y/
u.x/ C
8
<
:
1
Vol.B/
Z
B
.u
C
/
p
dx
1=p
C
R
kf k
L
n
.B/
9
=
;
;
where C D C.n;;R
2
;p/.
Proof. Translating and dilating, we can assume without loss of generality that
0 2 and B D B
1
.0/. We will also assume that u 2 C
2
./ \ H
2;n
./,since
if (13.20) is established in this case, the more general case follows by a simple
approximation argument.

13. Elliptic regularity IV (Krylov–Safonov estimates) 261
Given ˇ 1,define
(13.21) .x/ D
1 jxj
2
ˇ
; for jxj1:
Setting v D u on B,wehave
(13.22)
a
jk
@
j
@
k
v D a
jk
@
j
@
k
u C 2a
jk
.@
j
/.@
k
u/ C ua
jk
@
j
@
k
.f b
j
@
j
u cu/ C 2a
jk
.@
j
/.@
k
u/ C ua
jk
@
j
@
k
:
Let
C
v
be as in (13.6), but with u replaced by v,and replaced by B. Clearly,
u 0 on
C
v
.Wehave
(13.23) jDvj
v
1 jxj
on
C
v
;
so
(13.24)
jDujD
1
jDv uDj
1
v
1 jxj
C ujDj
2.1 C ˇ/
1=ˇ
u on
C
v
:
Hence
(13.25)
a
jk
@
j
@
k
v
n
16ˇ
2
C 2ˇ
ƒ
2=ˇ
C 2ˇjbj
1=ˇ
C c
o
v C f
C
2=ˇ
v C f;
on
C
v
,whereC D C.n;ˇ;;/. Of course, a
jk
@
j
@
k
v 0 on
C
v
.Ifˇ 2,we
have, upon applying Proposition 13.1 to v,
(13.26)
sup
B
v C
2=ˇ
v
C
L
n
.B/
C
1
kf k
L
n
.B/
C
1
sup
B
v
C
12=ˇ
.u
C
/
2=ˇ
L
n
.B/
C
1
kf k
L
n
.B/
:
Choose ˇ D 2n=p 2,sowehave
(13.27) sup
B
v C
1
sup
B
v
C
1p=n
ku
C
k
p=n
L
p
.B/
C
1
kf k
L
n
.B/
:
(Hereweallowp<1, in which case kk
L
p
is not a norm, but (13.27) is still
valid.) Using the elementary inequality
(13.28) a
1p=n
b
p=n
"a C "
n=p1
b; 8 " 2 .0; 1/;
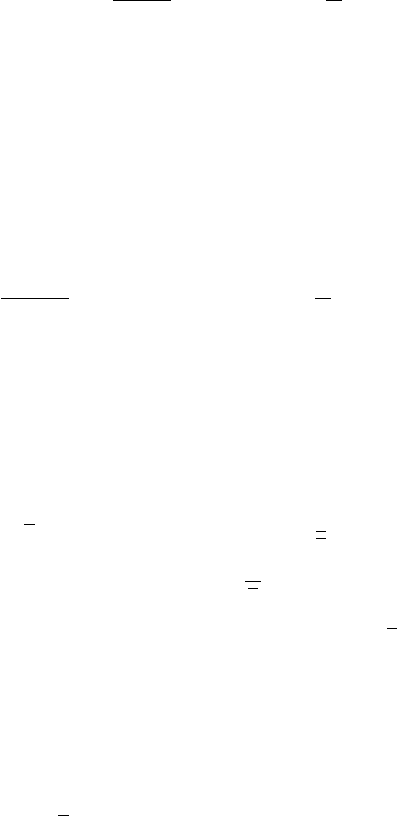
262 14. Nonlinear Elliptic Equations
and taking a D sup
B
v
C
;bDku
C
k
L
p
.B/
,and" D 1=2C
1
,wehave(theR D 1
case of) (13.20), so Proposition 13.3 is proved.
Replacing u by u,wehaveanestimateonsup
B
R
.y/
.u/ when Lu f .
Thus, when Lu D f and the hypotheses of Proposition 13.3 hold, we have
(13.29) sup
B
R
.y/
jujC
8
<
:
1
Vo l .B/
Z
B
juj
p
dx
1=p
C
R
kf k
L
n
.B/
9
=
;
:
Next we establish a “weak Harnack inequality” of [KrS], which will lead to
results on H¨older continuity of solutions of Lu D f . This result will also be
applied directly in the next section, to results on solutions to certain completely
nonlinear equations.
Proposition 13.4. Assume u 2 H
2;n
./; Lu f in ; f 2 L
n
./, and u 0
on a ball B D B
2R
.y/ .Then
(13.30)
0
B
@
1
Vol.B
R
/
Z
B
R
u
p
dx
1
C
A
1=p
C
inf
B
R
u C
R
kf k
L
n
.B/
;
for some positive p D p.n;; R
2
/ and C D C.n;;R
2
/.
As before, there is no loss of generality in assuming B D B
1
.0/. Also, replac-
ing L and f by
1
L and
1
f , we can assume D 1.
To begin the proof, take ">0and set
(13.31)
u D u C " Ckf k
L
n
.B/
;wD log
1
u
;
v D w; g D
f
u
;
where is given by (13.21). Note that w is large (positive) where
u is small. We
have
(13.32)
a
jk
@
j
@
k
v Da
jk
@
j
@
k
w 2a
jk
.@
j
/.@
k
w/ wa
jk
@
j
@
k
a
jk
.@
j
w/.@
k
w/ C b
j
@
j
w CjcjCg
2a
jk
.@
j
/.@
k
w/ wa
jk
@
j
@
k
2
a
jk
.@
j
/.@
k
/ wa
jk
@
j
@
k
C .jbj
2
CjcjCg/;
where the last inequality is obtained via Cauchy’s inequality, applied to the inner
product hV;W iDV
j
a
jk
W
k
.

13. Elliptic regularity IV (Krylov–Safonov estimates) 263
Now the form of implies that a
jk
@
j
@
k
0 provided 2.ˇ 1/a
jk
x
j
x
k
C
a
jj
jxj
2
a
jj
, and hence
(13.33) 2ˇjxj
2
nƒ H) a
jk
@
j
@
k
0:
Thus, if ˛ 2 .0; 1/,then
(13.34) ˇ
n
2˛
; jxj˛ H) a
jk
@
j
@
k
0:
Hence, on the set B
C
Dfx 2 B W w.x/ > 0g,wehave
(13.35)
a
jk
@
j
@
k
v 4ˇ
2
1 jxj
2
ˇ2
jxj
2
C v
B
˛
sup
B
˛
a
jk
@
j
@
k
!
C
jbj
2
CjcjCg
4ˇ
2
ƒ Cjbj
2
CjcjCg C
2nˇƒ
1 ˛
2
v
B
˛
:
Note that kgk
L
n
.B/
1. Thus Proposition 13.1 yields
(13.36) sup
B
v C
1 Ckv
C
k
L
n
.B
˛
/
;
with C D C.n;˛;;/.
Note that if u satisfies the hypotheses of Proposition 13.4 and t 2 .0; 1/,then
u=t satisfies L.u=t/ f=t, and the analogue of w in (13.31)isw k,where
k D log.1=t/. The function g in (13.31) is unchanged, and, working through
(13.32)–(13.36), we obtain the following extension of (13.36):
(13.37) sup
B
.w k/ C
1 Ck.w k/
C
k
L
n
.B
˛
/
; 8 k 2 R;
with constants independent of k.
The next stage in the proof of Proposition 13.4 will involve a decomposition
into cubes of the sort used for Calderon–Zygmund estimates in 5 of Chap. 13.
To set up some notation, given y 2 R
n
;R>0,letQ
R
.y/ denote the open cube
centered at y, of edge 2R:
(13.38) Q
R
.y/ Dfx 2 R
n
Wjx
j
y
j
j <R; 1 j ng:
If ˛<1=
p
n,thenQ
˛
D Q
˛
.0/ B.
The cube decomposition we will use in the proof of Lemma 13.5 below can
be described in general as follows. Let Q
0
be a cube in R
n
,let' 0 be an
element of L
1
.Q
0
/, and suppose
R
Q
0
'dx tL
n
.Q
0
/; t 2 .0; 1/. Bisecting
the edges of Q
0
, we subdivide it into 2
n
subcubes. Those subcubes that satisfy

264 14. Nonlinear Elliptic Equations
R
Q
'dx tL
n
.Q/ are similarly subdivided, and this process is repeated
indefinitely. Let F denote the set of subcubes so obtained that satisfy
Z
Q
'dx>tL
n
.Q/I
we do not further subdivide these cubes. For each Q 2 F, denote by
e
Q the
subcube whose subdivision gives Q.SinceL
n
.
e
Q/=L
n
.Q/ D 2
n
, we see that
(13.39) t<
1
L
n
.Q/
Z
Q
'dx 2
n
t; 8 Q 2 F:
Also, setting F D
S
Q2F
Q and G D Q
0
n F ,wehave
(13.40) ' t; a.e. in G:
This subdivision was also done in the proof of Lemma 5.5 in Chap. 13. Let us
also set
e
F D
S
Q2F
e
Q;sinceQ 2 F )
e
Q … F ,wehave
(13.41)
Z
e
F
'dx tL
n
.
e
F/:
In particular, when ' is the characteristic function
of a measurable subset
of Q
0
, of measure t L
n
.Q
0
/, we deduce from (13.40)–(13.41)that
(13.42) L
n
./ D L
n
. \
e
F/ tL
n
.
e
F/:
We have the following measure-theoretic result:
Lemma 13.5. Let Q
0
be a cube in R
n
;w2 L
1
.Q
0
/, and, for k 2 R,set
(13.43)
k
Dfx 2 Q
0
W w.x/ kg:
Suppose there are positive constants ı<1and C such that
(13.44) sup
Q
0
\Q
3r
.z/
.w k/ C
whenever k and Q D Q
r
.z/ Q
0
satisfy
(13.45) L
n
.
k
\ Q/ ıL
n
.Q/:

13. Elliptic regularity IV (Krylov–Safonov estimates) 265
Then, for all k 2 R,
(13.46) sup
Q
0
.w k/ C
1 C
log
L
n
.
k
/=L
n
.Q
0
/
log ı
!
:
Proof. We show by induction that
(13.47) sup
Q
0
.w k/ mC;
for any m 2 Z
C
and k 2 R such that L
n
.
k
/ ı
m
L
n
.Q
0
/.Thisistrueby
hypothesis if m D 1. Suppose that it holds for m D M 2 Z
C
and that L
n
.
k
/
ı
M C1
L
n
.Q
0
/.Define
e
k
by
(13.48)
e
k
D
[
˚
Q
3r
.z/ \ Q
0
W L
n
Q
r
.z/ \
k
ı L
n
Q
r
.z/
:
Applying the estimate (13.42), with t D ı, we see that either
e
k
D Q
0
or
(13.49) L
n
.
e
k
/ ı
1
L
n
.
k
/ ı
M
vol.Q
0
/;
and hence, replacing k by k C C , we obtain
(13.50) sup
Q
0
.w k/ .M C 1/C;
which verifies (13.47)form D M C 1.
Now, the estimate (13.46) follows by choosing m appropriately, and the lemma
is proved.
Returning to the estimation of the functions defined in (13.31), we see that
(13.36) implies
(13.51) sup
B
v C
1 Ckv
C
k
L
n
.Q
˛
/
C
1 C
vol.Q
C
˛
/
1=n
sup
B
v
C
;
where Q
˛
D Q
˛
.0/, as stated below (13.38), and
Q
C
˛
Dfx 2 Q
˛
W v.x/ > 0gDfx 2 Q
˛
W u.x/ < 1g:
Hence, if C is the constant in (13.36),
(13.52)
vol.Q
C
˛
/
vol.Q
˛
/
1
4˛C
n
D H) sup
B
v 2C:
Now choose ˛ D 1=3n,andtake D .4˛C /
n
,asin(13.52). Using the coor-
dinate change x 7! ˛.x z/=r, we obtain for any cube Q D Q
r
.z/ such that
B
3nr
.z/ B, the implication
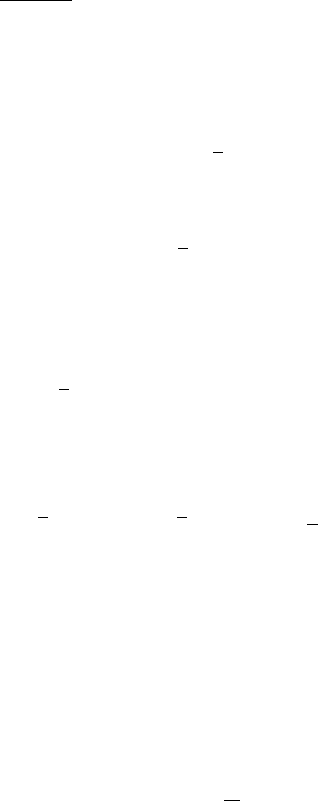
266 14. Nonlinear Elliptic Equations
(13.53)
vol.Q
C
/
vol.Q/
H) sup
Q
3r
.z/
w C.n;;/:
With ˛ and as specified above, take ı D 1 ; Q
0
D Q
˛
.0/, and note that
the estimate (13.53) holds also when w is replaced by w k,andQ
C
is replaced
by the set fx 2 Q W w.x/ k>0g, as a consequence of (13.37). Let
(13.54) .t/ D L
n
fx 2 Q
0
W u.x/ > tg
:
Setting k D log 1=t, we have from Lemma 13.5 the estimate
(13.55) .t/ C
inf
Q
0
t
1
u
; 8 t>0;
where C D C.n;;/; D .n;;/. Replacing the cube Q
0
by the inscribed
ball B
˛
.0/; ˛ D 1=3n, and using the identity
(13.56)
Z
Q
0
.u/
p
dx D p
Z
1
0
t
p1
.t/ dt;
we have
(13.57)
Z
B
˛
.u/
p
dx C
inf
B
˛
u
p
; for p D
2
:
The inequality (13.30) then follows by letting " ! 0 if we use a covering
argument to extend (13.57) to arbitrary ˛<1(especially, ˛ D 1=2) and use the
coordinate transformation x 7! .x y/=2R. Thus Proposition 13.4 is established.
Putting together (13.29)and(13.30), we have the following.
Corollary 13.6. Assume u 2 H
2;n
./; Lu D f on ; f 2 L
n
./, and u 0
on a ball B D B
4R
.y/ .Then
(13.58) sup
B
R
.y/
u.x/ C
1
inf
B
2R
.y/
u C
R
kf k
L
n
.B
4R
/
;
for some C
1
D C
1
.n;;R
2
/. In particular, if u 0 on ,
(13.59) Lu D 0 H) sup
B
R
.y/
u.x/ C
1
inf
B
2R
.y/
u.x/:
We can use this to establish H¨older estimates on solutions to Lu D f . We will
actually apply Corollary 13.6 to L
1
D a
jk
@
j
@
k
Cb
j
@
j
,soL
1
u D f
1
D f cu.
Suppose that
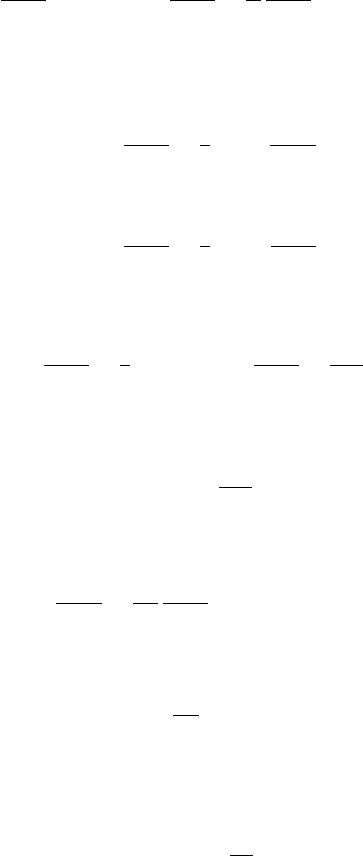
13. Elliptic regularity IV (Krylov–Safonov estimates) 267
(13.60) a D inf
B
4R
.y/
u sup
B
4R
.y/
u D b:
Then v D .ua/=.b a/ is 0 on B
4R
.y/,andL
1
v D f
1
=.b a/, so Corollary
13.6 yields
(13.61) sup
B
R
.y/
u a
b a
C
1
inf
B
2R
.y/
u a
b a
C
R
1
b a
kf cuk
L
n
.B
4R
/
:
Without loss of generality, we can assume C
1
1. Now given this, one of the
following two cases must hold:
(i) C
1
inf
B
2R
.y/
u a
b a
1
2
sup
B
R
.y/
u a
b a
;
(ii) C
1
inf
B
2R
.y/
u a
b a
<
1
2
sup
B
R
.y/
u a
b a
:
If case (i) holds, then either
sup
B
R
.y/
u a
b a
1
2
or inf
B
2R
.y/
u a
b a
1
4C
1
;
and hence (since we are assuming C
1
1)
(13.62) (i) H) osc
B
R
.y/
u
1
1
4C
1
osc
B
4R
.y/
u:
If case (ii) holds, then
sup
B
R
.y/
u a
b a
2R
1
b a
kf cuk
L
n
.B
4R
/
;
so
(13.63) (ii) H) osc
B
R
.y/
u
2R
kf cuk
L
n
.B
4R
/
;
which is bounded by C
2
R in view of the sup-norm estimate (13.29).Consequently,
under the hypotheses of Corollary 13.6, we have
(13.64) osc
B
R
.y/
u max
C
2
R;
1
1
C
1
osc
B
4R
.y/
u
;
