Tarek Ahmed. Reservoir engineering handbook

Подождите немного. Документ загружается.

where Q

= gas flow rate, Mscf/day

k = permeability, md

T = temperature, °R

z = gas compressibility factor

= gas viscosity, cp

It is recommended that the z-factor and gas viscosity be evaluated at

the average pressure p

avg

as defined by:

The method of calculating the gas flow rate by Equation 8-11 is called

the pressure-squared approximation method.

If both p

–

and p

are lower than 2000 psi, Equation 8-11 can be

expressed in terms of the productivity index J as:

with

where

Example 8-1

The PVT properties of a gas sample taken from a dry gas reservoir are

given in the following table:

g avg

1422 0 75( ) ln .m

(8 -14)

()

max

Q AOF J p

(8 -13)

QJpp

grwf

=-()

(8 -12)

avg

kh p p

rwf

g avg

()

( ) ln .

1422 0 75m

(8 -11)

538 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 538

p, psi m

, cp Z y, psi

/cp B

, bbl/scf

0 0.01270 1.000 0 —

400 0.01286 0.937 13.2 ¥ 10

0.007080

1200 0.01530 0.832 113.1 ¥ 10

0.00210

1600 0.01680 0.794 198.0 ¥ 10

0.00150

2000 0.01840 0.770 304.0 ¥ 10

0.00116

3200 0.02340 0.797 678.0 ¥ 10

0.00075

3600 0.02500 0.827 816.0 ¥ 10

0.000695

4000 0.02660 0.860 950.0 ¥ 10

0.000650

The reservoir is producing under the pseudosteady-state condition. The

following additional data is available:

k = 65 md h = 15¢ T = 600°R

= 1000¢ r

= 0.25¢ s = 0.4

Calculate the gas flow rate under the following conditions:

a. p

–

= 4000 psi, p

= 3200 psi

b. p

–

= 2000 psi, p

= 1200 psi

Use the appropriate approximation methods and compare results with

the exact solution.

Solution

a. Calculate Q

at p

–

= 4000 and p

= 3200 psi:

Step 1. Select the approximation method. Because p

–

and p

are both >

3000, the pressure-approximation method is used, i.e., Equation 8-9.

Step 2. Calculate average pressure and determine the corresponding gas

properties.

= 0.025 B

= 0.000695

p psi=

4000 3200

3600

Gas Well Performance 539

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 539

Step 3. Calculate the gas flow rate by applying Equation 8-9.

Step 4. Recalculate Q

by using the pseudopressure equation, i.e., Equa-

tion 8-1.

b. Calculate Q

at p

–

= 2000 and p

= 1058:

Step 1. Select the appropriate approximation method. Because p

–

and p

≤ 2000, use the pressure-squared approximation.

Step 2. Calculate average pressure and the corresponding m

and z.

= 0.017 z = 0.791

Step 3. Calculate Q

by using the pressure-squared equation, i.e., Equa-

tion 8-11.

Mscf day

()()( )

()(.)(.)ln

65 15 2000 1200

1422 600 0 017 0 791

1000

025

075 04

30 453

p psi=

2000 1200

1649

Q Mscf day

()()( . .)()()

()()ln

65 15 950 0 678 0 65 15 10

1422 600

1000

025

075 04

43 509

Mscf day

7 08 10 65 15 4000 3200

0 025 0 000695

1000

025

075 04

44 490

. ( )( )( )( )

(. )(. )ln

540 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 540

Step 4. Compare Q

with the exact value from Equation 8-1:

All of the mathematical formulations presented thus far in this chapter

are based on the assumption that laminar (viscous) flow conditions are

observed during the gas flow. During radial flow, the flow velocity

increases as the wellbore is approached. This increase of the gas velocity

might cause the development of a turbulent flow around the wellbore. If

turbulent flow does exist, it causes an additional pressure drop similar to

that caused by the mechanical skin effect.

As presented in Chapter 6 by Equations 6-164 through 6-166, the

semisteady-state flow equation for compressible fluids can be modified

to account for the additional pressure drop due the turbulent flow by

including the rate-dependent skin factor DQ

. The resulting pseu-

dosteady-state equations are given in the following three forms:

First Form : Pressure-Squared Approximation Form

where D is the inertial or turbulent flow factor and is given by Equation

6-160 as:

where the non-Darcy flow coefficient F is defined by Equation 6-156 as:

3 161 10

.( )

(8 -17)

FKh

1422

(8 -16)

kh p p

sDQ

g avg

(

)

-++

1422 0 75( ) ln .m

(8 -15)

Mscf day

()()( . .)

()()ln

65 15 304 0 113 1 10

1422 600

1000

025

075 04

30 536

Gas Well Performance 541

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 541

where F = non-Darcy flow coefficient

k = permeability, md

T = temperature, °R

= gas gravity

= wellbore radius, ft

h = thickness, ft

b=turbulence parameter as given by Equation 6-157 as

b = 1.88 (10

-10

) k

-1.47

-0.53

Second Form: Pressure-Approximation Form

Third Form: Real Gas Potential (Pseudopressure) Form

Equations 8-15, 8-18, and 8-19 are essentially quadratic relationships

in Q

and, thus, they do not represent explicit expressions for calculating

the gas flow rate. There are two separate empirical treatments that can be

used to represent the turbulent flow problem in gas wells. Both treat-

ments, with varying degrees of approximation, are directly derived and

formulated from the three forms of the pseudosteady-state equations, i.e.,

Equations 8-15 through 8-17. These two treatments are called:

• Simplified treatment approach

• Laminar-inertial-turbulent (LIT) treatment

The above two empirical treatments of the gas flow equation are pre-

sented on the following pages.

sDQ

rwf

-++

()

ln .

1422 0 75

(8 -19)

kh p p

sDQ

rwf

g g avg

-++

708 10

075

.( ) ( )

( ) ln .mb

(8 -18)

542 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 542

The Simplified Treatment Approach

Based on the analysis for flow data obtained from a large member of

gas wells, Rawlins and Schellhardt (1936) postulated that the relationship

between the gas flow rate and pressure can be expressed as:

where Q

= gas flow rate, Mscf/day

–

= average reservoir pressure, psi

n = exponent

C = performance coefficient, Mscf/day/psi

The exponent n is intended to account for the additional pressure drop

caused by the high-velocity gas flow, i.e., turbulence. Depending on the

flowing conditions, the exponent n may vary from 1.0 for completely

laminar flow to 0.5 for fully turbulent flow. The performance coefficient

C in Equation 8-20 is included to account for:

• Reservoir rock properties

• Fluid properties

• Reservoir flow geometry

Equation 8-20 is commonly called the deliverability or back-pres-

sure equation. If the coefficients of the equation (i.e., n and C) can be

determined, the gas flow rate Q

at any bottom-hole flow pressure p

can be calculated and the IPR curve constructed.

Taking the logarithm of both sides of Equation 8-20 gives:

log (Q

) = log (C) + n log (p

–

- p

) (8 - 21)

Equation 8-22 suggests that a plot of Q

versus (p

–

- p

) on log-log

scales should yield a straight line having a slope of n. In the natural gas

industry the plot is traditionally reversed by plotting (p

–

- p

) versus Q

on the logarithmic scales to produce a straight line with a slope of (1/n).

This plot as shown schematically in Figure 8-3 is commonly referred to

as the deliverability graph or the back-pressure plot.

QCpp

grwf

=-()

(8 - 20)

Gas Well Performance 543

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 543

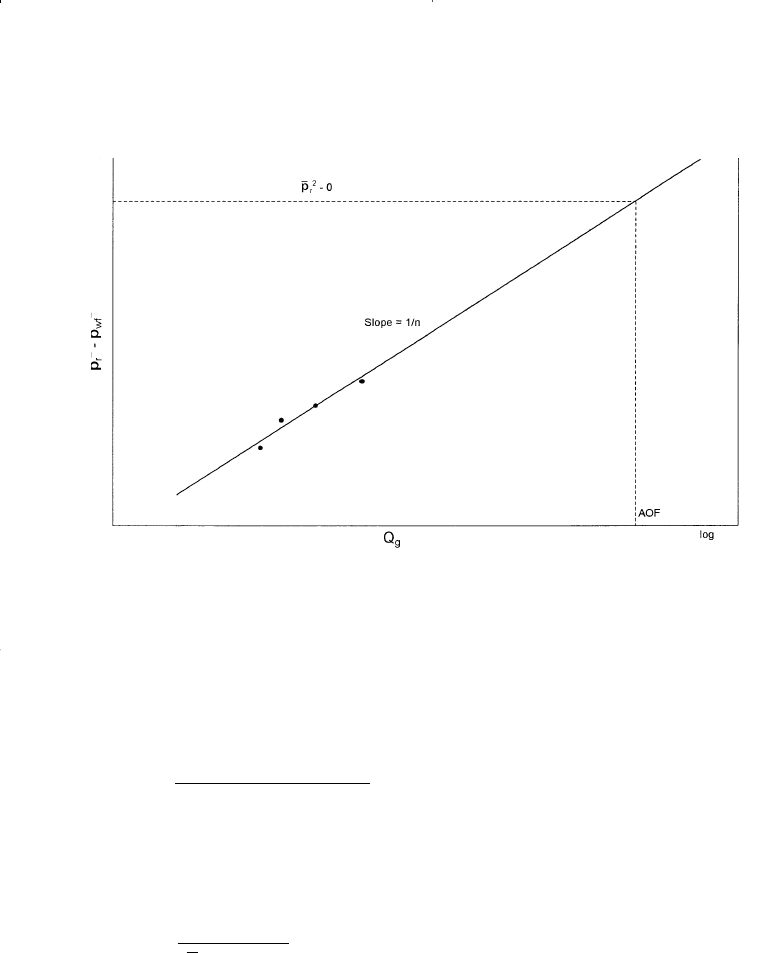
The deliverability exponent n can be determined from any two points

on the straight line, i.e., (Q

, Dp

) and (Q

, Dp

), according to the flow-

ing expression:

Given n, any point on the straight line can be used to compute the per-

formance coefficient C from:

The coefficients of the back-pressure equation or any of the other

empirical equations are traditionally determined from analyzing gas well

testing data. Deliverability testing has been used for more than sixty

years by the petroleum industry to characterize and determine the flow

potential of gas wells. There are essentially three types of deliverability

tests and these are:

rwf

-()

(8 - 23)

log( ) log( )

log( ) log ( )

(8 - 22)

544 Reservoir Engineering Handbook

Figure 8-3. Well deliverability graph.

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 544

• Conventional deliverability (back-pressure) test

• Isochronal test

• Modified isochronal test

These tests basically consist of flowing wells at multiple rates and

measuring the bottom-hole flowing pressure as a function of time. When

the recorded data is properly analyzed, it is possible to determine the

flow potential and establish the inflow performance relationships of the

gas well. The deliverability test is discussed later in this chapter for the

purpose of introducing basic techniques used in analyzing the test data.

The Laminar-Inertial-Turbulent (LIT) Approach

The three forms of the semisteady-state equation as presented by

Equations 8-15, 8-18, and 8-19 can be rearranged in quadratic forms for

the purpose of separating the laminar and inertial-turbulent terms com-

posing these equations as follows:

a. Pressure-Squared Quadratic Form

Equation 8-15 can be written in a more simplified form as:

with

where a = laminar flow coefficient

b = inertial-turbulent flow coefficient

= gas flow rate, Mscf/day

z = gas deviation factor

k = permeability, md

= gas viscosity, cp

1422 m

(8 - 26)

1422

075

ln . (8 - 25)

pp aQbQ

rwf g

22 2

-= + (8 - 24)

Gas Well Performance 545

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 545

The term (a Q

) in Equation 8-26 represents the pressure-squared

drop due to laminar flow while the term (b Q

) accounts for the pres-

sure-squared drop due to inertial-turbulent flow effects.

Equation 8-24 can be linearized by dividing both sides of the equa-

tion by Q

to yield:

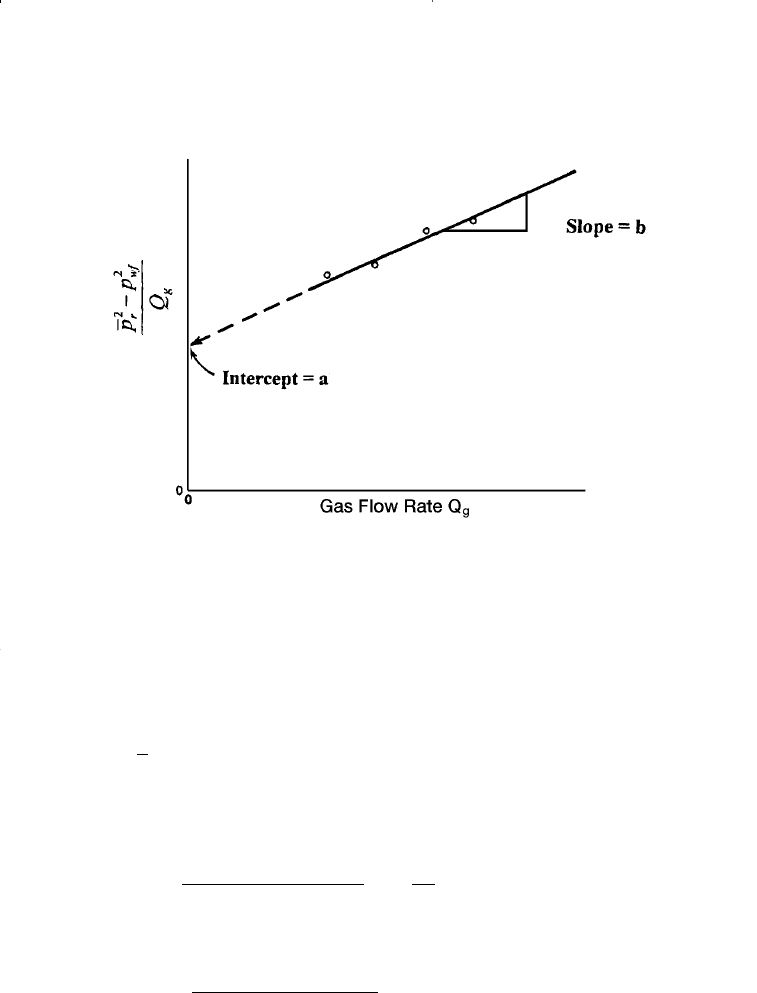
The coefficients a and b can be determined by plotting

versus Q

on a Cartesian scale and should yield a straight line with a

slope of b and intercept of a. As presented later in this chapter, data

from deliverability tests can be used to construct the linear relation-

ship as shown schematically in Figure 8-4.

Given the values of a and b, the quadratic flow equation, i.e., Equa-

tion 8-24, can be solved for Q

at any p

from:

Furthermore, by assuming various values of p

and calculating the

corresponding Q

from Equation 8-28, the current IPR of the gas well

at the current reservoir pressure p

–

can be generated.

It should be pointed out the following assumptions were made in

developing Equation 8-24:

• Single phase flow in the reservoir

• Homogeneous and isotropic reservoir system

• Permeability is independent of pressure

• The product of the gas viscosity and compressibility factor, i.e., (m

is constant.

This method is recommended for applications at pressures below

2000 psi.

aa bp p

-+ + -

(

)

(8 - 28)

rwf

abQ

rwf

=+ (8 - 27)

546 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 546

b. Pressure-Quadratic Form

The pressure-approximation equation, i.e., Equation 8-18, can be

rearranged and expressed in the following quadratic form.

where

The term (a

) represents the pressure drop due to laminar flow,

while the term (b

) accounts for the additional pressure drop due to

141 2 10

.( )( )m

(8 - 31)

141 2 10

075=

.( )( )

ln .

(8 - 30)

pp aQbQ

rwf g g

-= +

(8 - 29)

Gas Well Performance 547

Figure 8-4. Graph of the pressure-squared data.

Reservoir Eng Hndbk Ch 08 2001-10-24 11:13 Page 547