Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.

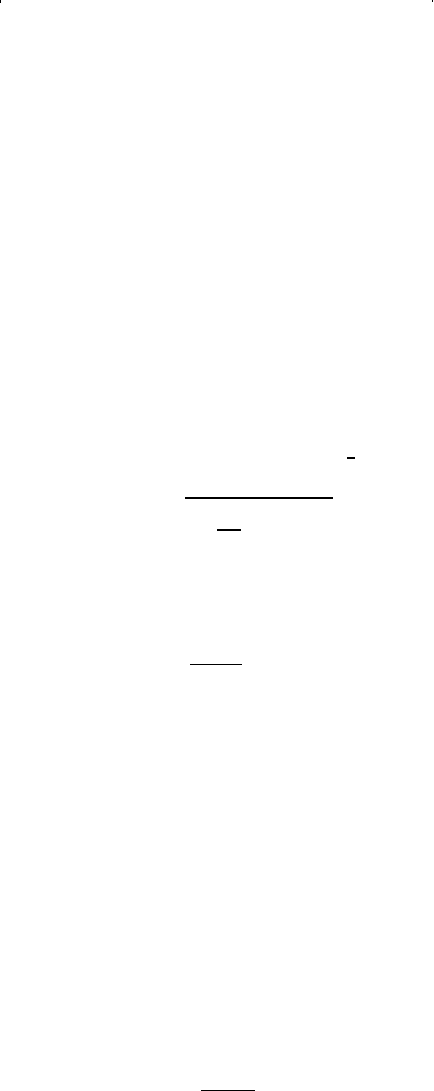
It should be noted that one of the main disadvantages of Standing’s
methodology is that it requires reliable permeability information; in addi-
tion, it also requires material balance calculations to predict oil satura-
tions at future average reservoir pressures.
Fetkovich’s Method
Muskat and Evinger (1942) attempted to account for the observed non-
linear flow behavior (i.e., IPR) of wells by calculating a theoretical pro-
ductivity index from the pseudosteady-state flow equation. They
expressed Darcy’s equation as:
where the pressure function f(p) is defined by:
where k
ro
= oil relative permeability
k = absolute permeability, md
B
o
= oil formation volume factor
m
o
= oil viscosity, cp
Fetkovich (1973) suggests that the pressure function f(p) can basically
fall into one of the following two regions:
Region 1: Undersaturated Region
The pressure function f(p) falls into this region if p > p
b
. Since oil rela-
tive permeability in this region equals unity (i.e., k
ro
= 1), then:
fp
B
oo
p
()=
Ê
Ë
Á
ˆ
¯
˜
1
m
(7 - 27)
fp
k
ro
oo
(
)
=
mb
(7 - 26)
Q
o
=
0.00708 kh
ln
r
e
r
w
- 0.75 +s
È
Î
Í
˘
˚
˙
f(p)
p
wf
p
r
Ú
dp (7 - 25)
498 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 498

Fetkovich observed that the variation in f(p) is only slight and the
pressure function is considered constant as shown in Figure 7-10.
Region 2: Saturated Region
In the saturated region where p < p
b
, Fetkovich shows that the (k
ro
/
m
o
B
o
) changes linearly with pressure and that the straight line passes
through the origin. This linear is shown schematically in Figure 7-10 can
be expressed mathematically as:
Where m
o
and B
o
are evaluated at the bubble-point pressure. In the
application of the straight-line pressure function, there are three cases
that must be considered:
fp
B
p
p
oo
p
b
b
()=
Ê
Ë
Á
ˆ
¯
˜
Ê
Ë
Á
ˆ
¯
˜
1
m
(7 - 28)
Oil Well Performance 499
Figure 7-10. Pressure function concept.
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 499

• p
–
r
and p
wf
> p
b
• p
–
r
and p
wf
< p
b
• p
–
r
> p
b
and p
wf
< p
b
All three cases are presented below.
Case 1: p
–
r
and p
wf
> p
b
This is the case of a well producing from an undersaturated oil reser-
voir where both p
wf
and p
–
r
are greater than the bubble-point pressure. The
pressure function f(p) in this case is described by Equation 7-27. Substi-
tuting Equation 7-27 into Equation 7-25 gives:
or
Q
o
= J (p
–
r
- p
wf
) (7 -30)
The productivity index is defined in terms of the reservoir parameters as:
where B
o
and m
o
are evaluated at (p
–
r
+ p
wf
)/2.
J
kh
B
r
r
s
oo
e
w
=
Ê
Ë
Á
ˆ
¯
˜
-+
È
Î
Í
Í
˘
˚
˙
˙
0 00708
075
.
ln .m
(7 - 31)
Q
kh
B
r
r
s
pp
o
oo
e
w
rwf
=
Ê
Ë
Á
ˆ
¯
˜
-+
È
Î
Í
Í
˘
˚
˙
˙
-
0 00708
075
.
ln .
()
m
(7 - 29)
Since is constant, then:
1
m
oo
B
Ê
Ë
Á
ˆ
¯
˜
Q
kh
r
r
s
B
dp
o
e
w
oo
p
wf
p
r
=
Ê
Ë
Á
ˆ
¯
˜
-+
Ê
Ë
Á
ˆ
¯
˜
Ú
0 00708
075
1.
ln .
m
500 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 500

Example 7-8
A well is producing from an undersaturated-oil reservoir that exists at
an average reservoir pressure of 3000 psi. The bubble-point pressure is
recorded as 1500 psi at 150°F. The following additional data are available:
• stabilized flow rate = 280 STB/day
• stabilized wellbore pressure = 2200 psi
• h = 20¢ r
w
= 0.3¢ r
e
= 660¢ s =-0.5
• k = 65 md
• m
o
at 2600 psi = 2.4 cp
• B
o
at 2600 psi = 1.4 bbl/STB
Calculate the productivity index by using both the reservoir properties
(i.e., Equation 7-31) and flow test data (i.e., Equation 7-30).
Solution
• From Equation 7-31
• From production data:
Results show a reasonable match between the two approaches. It
should be noted, however, that there are several uncertainties in the val-
ues of the parameters used in Equation 7-31 to determine the productivi-
ty index. For example, changes in the skin factor k or drainage area
would change the calculated value of J.
Case 2: p
–
r
and p
wf
< p
b
When the reservoir pressure p
–
r
and bottom-hole flowing pressure p
wf
are both below the bubble-point pressure p
b
, the pressure function f(p) is
J STB day psi=
-
=
280
3000 2200
035.//
J STB day psi=
Ê
Ë
ˆ
¯
--
È
Î
Í
˘
˚
˙
=
0 00708 65 20
24 14
660
03
075 05
042
.()()
(.)(.)ln
.
..
.//
Oil Well Performance 501
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 501

represented by the straight line relationship as expressed by Equation
7-28. Combining Equation 7-28 with Equation 7-25 gives:
Integrating gives:
Introducing the productivity index into the above equation gives:
QCpp
orwf
=-()
22
(7 - 34)
The term is commonly referred to as the
C, or:
J
p
b
2
Ê
Ë
Á
ˆ
¯
˜
performance coeffi -
cient
QJ
p
pp
o
b
rwf
=
Ê
Ë
Á
ˆ
¯
˜
-
-
1
2
22
( ) (7 - 33)
Q
kh
B
r
r
s
p
pp
o
oop
b
e
w
b
rwf
=
Ê
Ë
Á
ˆ
¯
˜
-+
È
Î
Í
Í
˘
˚
˙
˙
Ê
Ë
Á
ˆ
¯
˜
-
-
0 00708
075
1
2
22
.
( ) ln .
()
m
(7 - 32)
Q
kh
r
r
s
Bp
pdp
o
e
w
oop
b
b
p
wf
p
r
=
Ê
Ë
Á
ˆ
¯
˜
-+
È
Î
Í
Í
Í
Í
Í
˘
˚
˙
˙
˙
˙
˙
Ê
Ë
Á
ˆ
¯
˜
Ú
0 00708
075
11.
ln .
()m
Since the term is constant, then:
11
m
oo
p
b
b
Bp
Ê
Ë
Á
ˆ
¯
˜
Ê
Ë
Á
ˆ
¯
˜
È
Î
Í
Í
˘
˚
˙
˙
Q
kh
r
r
s
B
p
p
dp
o
e
w
oop
b
p
wf
p
r
b
=
Ê
Ë
Á
ˆ
¯
˜
-+
È
Î
Í
Í
Í
Í
Í
˘
˚
˙
˙
˙
˙
˙
Ê
Ë
Á
ˆ
¯
˜
Ú
0 00708
075
1.
ln .
()m
502 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 502

To account for the possibility of non-Darcy flow (turbulent flow) in oil
wells, Fetkovich introduced the exponent n in Equation 7-35 to yield:
The value of n ranges from 1.000 for a complete laminar flow to 0.5
for highly turbulent flow.
There are two unknowns in Equation 7-35, the performance coefficient
C and the exponent n. At least two tests are required to evaluate these
two parameters, assuming p
–
r
is known:
By taking the log of both sides of Equation 7-35 and solving for log
(p
2
r
- p
2
wf
), the expression can be written as:
A plot of p
–
2
r
- p
2
wf
versus Q
o
on log-log scales will result in a straight
line having a slope of 1/n and an intercept of C at p
–
2
r
- p
2
wf
= 1. The value
of C can also be calculated using any point on the linear plot once n has
been determined to give:
Once the values of C and n are determined from test data, Equation
7-35 can be used to generate a complete IPR.
To construct the future IPR when the average reservoir pressure
declines to (p
–
r
)
f
, Fetkovich assumes that the performance coefficient C is
a linear function of the average reservoir pressure and, therefore, the
value of C can be adjusted as:
(C)
f
= (C)
p
[(p
–
r
)
f
/(p
–
r
)
p
] (7-36)
where the subscripts f and p represent the future and present conditions.
Fetkovich assumes that the value of the exponent n would not change
as the reservoir pressure declines. Beggs (1991) presented an excellent
and comprehensive discussion of the different methodologies used in
constructing the IPR curves for oil and gas wells.
The following example was used by Beggs (1991) to illustrate
Fetkovich’s method for generating the current and future IPR.
C
Q
pp
o
rwf
n
=
-()
22
log ( ) log logpp
n
Q
n
C
rwf o
22
11
-= -
QCpp
orwf
n
=-()
22
(7 - 35)
Oil Well Performance 503
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 503

Example 7-9
A four-point stabilized flow test was conducted on a well producing
from a saturated reservoir that exists at an average pressure of 3600 psi.
Q
o
, STB/day p
wf
, psi
263 3170
383 2890
497 2440
640 2150
a. Construct a complete IPR by using Fetkovich’s method.
b. Construct the IPR when the reservoir pressure declines to 2000 psi.
Solution
Part A.
Step 1. Construct the following table:
Q
o
, STB/day P
wf
, psi (p
–
2
r
- p
2
wf
) ¥ 10
-6
, psi
2
263 3170 2.911
383 2890 4.567
497 2440 7.006
640 2150 8.338
Step 2. Plot (p
–
2
r
- p
2
wf
) verses Q
o
on log-log paper as shown in Figure
7-11 and determine the exponent n, or:
Step 3. Solve for the performance coefficient C:
C = 0.00079
n =
-
-
=
log( ) log( )
log ( ) log ( )
.
750 105
10 10
0 854
76
504 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 07 2001-10-24 16:49 Page 504
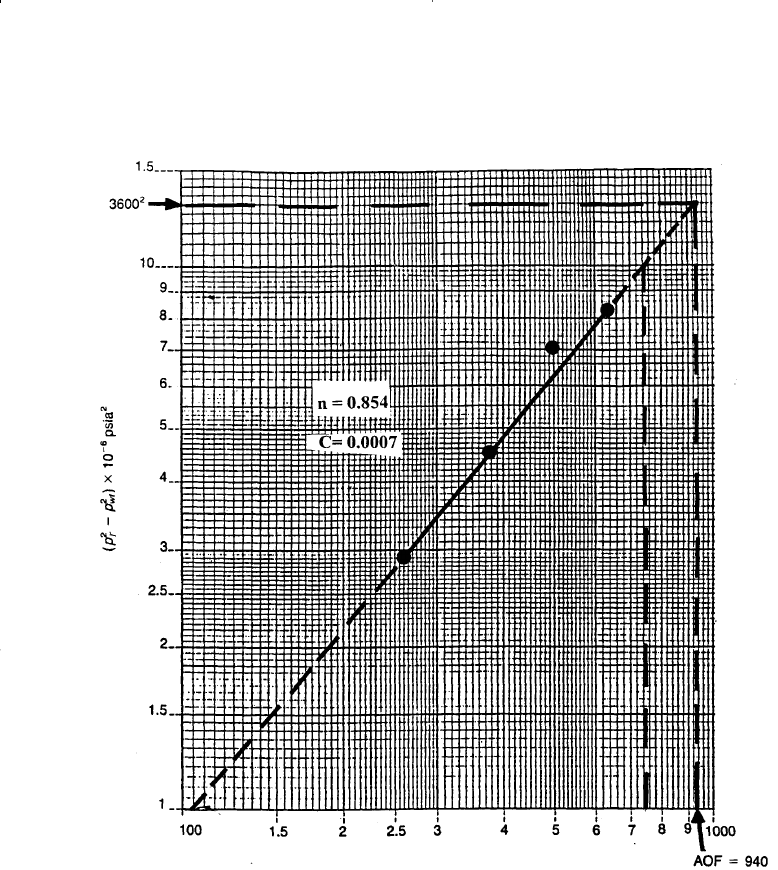
Step 4. Generate the IPR by assuming various values for p
wf
and calculat-
ing the corresponding flow rate from Equation 7-25:
Q
o
= 0.00079 (3600
2
- p
2
wf
)
0.854
Oil Well Performance 505
Figure 7-11. Flow-after-flow data for example 7-9 (After Beggs, D., “Production
Optimization Using Nodal Analysis,” permission to publish by the OGCI, copyright
OGCI, 1991.)
Reservoir Eng Hndbk Ch 07 2001-10-24 16:50 Page 505
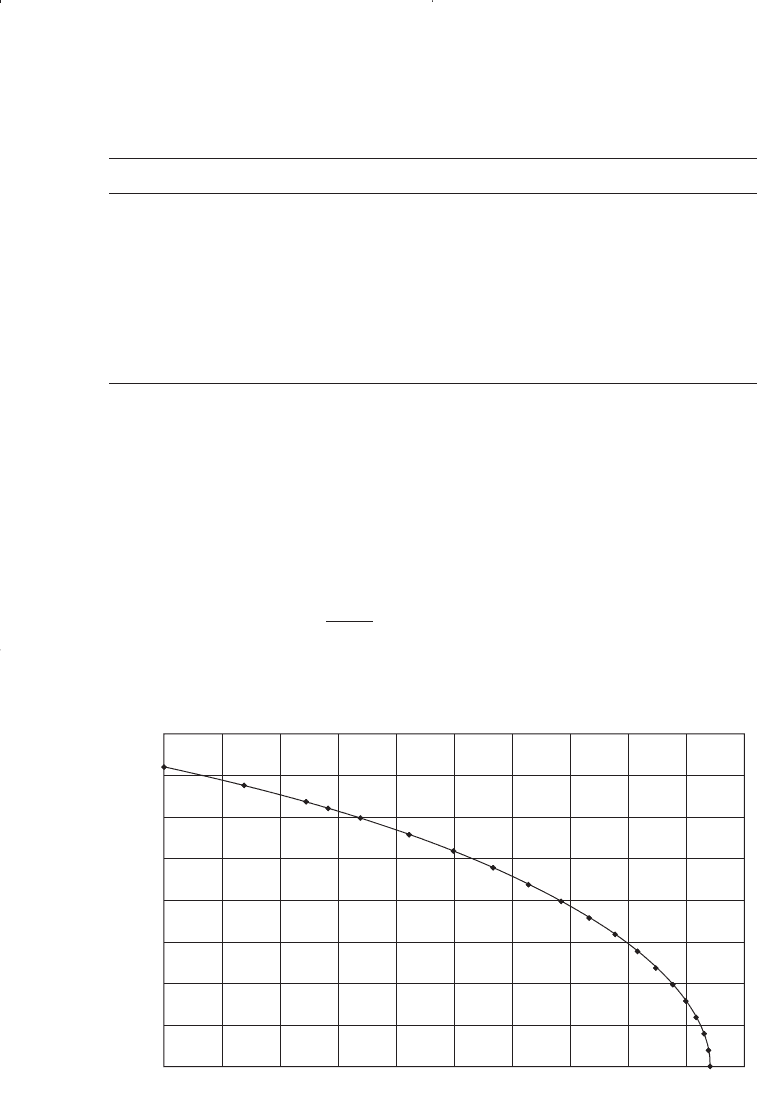
P
wf
Q
o
, STB/day
3600 0
3000 340
2500 503
2000 684
1500 796
1000 875
500 922
0 937
The IPR curve is shown in Figure 7-12. Notice that the AOF, i.e.,
(Q
o
)
max
, is 937 STB/day.
Part B.
Step 1. Calculate future C by applying Equation 7-36
() . .C
f
=
Ê
Ë
ˆ
¯
=0 00079
2000
3600
0 000439
506 Reservoir Engineering Handbook
500
0
0
1000
1500
2000
2500
3000
3500
4000
100 200 300 400 500 600 700 800 900 1000
Flow Rate (STB/Day)
Pressure (psi)
Figure 7-12. IPR using Fetkovich method.
Reservoir Eng Hndbk Ch 07 2001-10-24 16:50 Page 506
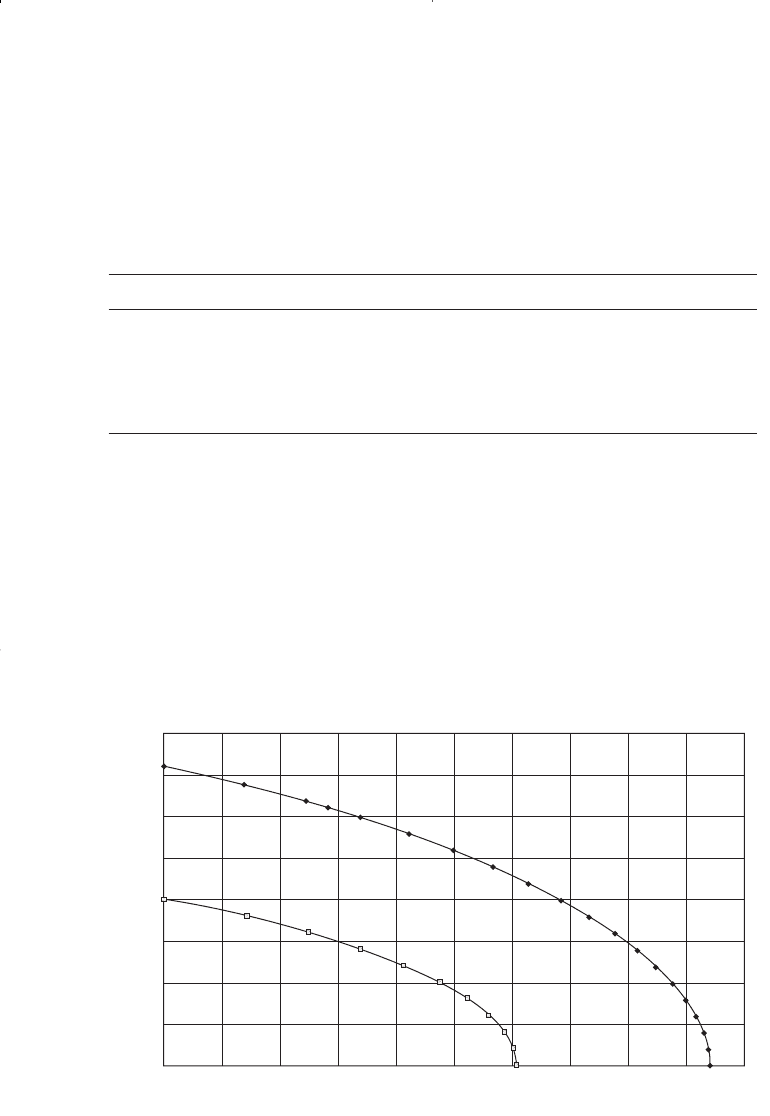
Step 2. Construct the new IPR curve at 2000 psi by using the new calcu-
lated C and applying the inflow equation.
Q
o
= 0.000439 (20002 - p
2
wf
)
0.854
p
wf
Q
o
2000 0
1500 94
1000 150
500 181
0 191
Both the present time and future IPRs are plotted in Figure 7-13.
Klins and Clark (1993) developed empirical correlations that correlate
the changes in Fetkovich’s performance coefficient C and the flow expo-
nent n with the decline in the reservoir pressure. The authors observed
the exponent n changes considerably with reservoir pressure. Klins and
Clark concluded the “future” values of (n)
f
and (C) at pressure (p
–
r
)
f
are
related to the values of n and C at the bubble-point pressure. Denoting C
b
Oil Well Performance 507
500
0
0
1000
1500
2000
2500
3000
3500
4000
100 200 300 400 500 600 700 800 900 1000
Flow Rate (STB/Day)
Pressure (psi)
Figure 7-13. Future IPR at 2000 psi.
Reservoir Eng Hndbk Ch 07 2001-10-24 16:50 Page 507
