Таран Т.А. Основы дискретной математики

Подождите немного. Документ загружается.

80 81

Ñïðàâåäëèâà è äâîéñòâåííàÿ ëåììà îòíîñèòåëüíî îáúåäèíåíèÿ.

Òåïåðü ìû ìîæåì äîêàçàòü òåîðåìó î òîì, ÷òî ëþáàÿ ðåøåòêà

ìîæåò ðàññìàòðèâàòüñÿ êàê àëãåáðà.

Òåîðåìà 6.3. Ëþáàÿ àëãåáðà L = <P, ∨, ∧ > ñ äâóìÿ áèíàðíûìè

îïåðàöèÿìè, óäîâëåòâîðÿþùèìè óñëîâèÿì L1  L4, ÿâëÿåòñÿ

ðåøåòêîé, è îáðàòíî.

Äîêàçàòåëüñòâî. Ñîãëàñíî ëåììå 6.6, ëþáàÿ ñèñòåìà L, îïåðàöèè

êîòîðîé óäîâëåòâîðÿþò óñëîâèÿì L1  L4, ÿâëÿåòñÿ ó-ìíîæåñòâîì,

â êîòîðîì x∧y=inf{x,y}, òàê ÷òî x ≤ y îçíà÷àåò, ÷òî x∧y=x.

Ðàññìîòðèì òåïåðü îïåðàöèþ x∨y. Åñëè x ≤ y, òî x∧y=x. Ïîäñòà-

âèì x∧yâìåñòî xâ x∨y; ïîëó÷èì x∨y=(x∧y)∨y=y (ïîñëåä-

íåå ðàâåíñòâî âûïîëíèìî â ñèëó çàêîíà ïîãëîùåíèÿ L4). Â ñèëó

äâîéñòâåííîñòè ñïðàâåäëèâî è îáðàòíîå óòâåðæäåíèå: åñëè x∨y=y,

òî x ≤ y. Ñëåäîâàòåëüíî, íåðàâåíñòâî x ≤ y ðàâíîñèëüíî òàêæå è

ðàâåíñòâó x∨y=y. Ïî ïðèíöèïó äâîéñòâåííîñòè ïîëó÷àåì, ÷òî

x∨y=sup{x,y} è, çíà÷èò, L ÿâëÿåòñÿ ðåøåòêîé.

Ïðèìåð.

Ïóñòü íà ìíîæåñòâå L = {a, b, c, d} çàäàíû áèíàðíûå îïåðàöèè ⊗ è ⊕:

Íåïîñðåäñòâåííî èç òàáëèö âèäíî,

÷òî îáå îïåðàöèè èäåìïîòåíòíû (ñì. çíà-

÷åíèÿ íà äèàãîíàëè òàáëèö) è êîììóòà-

òèâíû (òàáëèöû ñèììåòðè÷íû). Â àññî-

öèàòèâíîñòè îïåðàöèé òàêæå íåòðóäíî

óáåäèòüñÿ. Áóäåì ïîëàãàòü, ÷òî x ≤ y

âñÿêèé ðàç, êîãäà x⊗y=x. Òîãäà èç

ïåðâîé ñòðîêè òàáë. 6 ïîëó÷èì: a ≤ b,

a≤ c, a ≤ d, äàëåå: b ≤ d, òàê êàê b⊗d=b,

è c ≤ d, òàê êàê c⊗d=c. Èìååì òàêæå:

b⊗c=c⊗b=a, îòêóäà ñëåäóåò, ÷òî a ÿâëÿåòñÿ òî÷íîé íèæíåé

ãðàíüþ b è c, è, ó÷èòûâàÿ ïåðâóþ ñòðîêó, óíèâåðñàëüíîé íèæíåé

ãðàíüþ. Òîãäà, ïîñòðîèâ äèàãðàììû äâóõ öåïåé: a≤b, b≤ d, è a≤c,

c ≤d, ïîëó÷èì äèàãðàììó íà ðèñ. 6.3, ãäå îïåðàöèÿ ⊗ ÿâëÿåòñÿ

ïåðåñå÷åíèåì, à ⊕  îáúåäèíåíèåì ëþáûõ äâóõ ýëåìåíòîâ. Òàêèì

îáðàçîì, ìíîæåñòâî L ÿâëÿåòñÿ ðåøåòêîé.

6.3. Äèñòðèáóòèâíûå ðåøåòêè

Ìîæíî âûäåëèòü ðåøåòêè, îáëàäàþùèå äîïîëíèòåëüíûìè

ñâîéñòâàìè, è îïðåäåëèòü òèïû ðåøåòîê, ñîãëàñíî ýòèì ñâîéñòâàì.

Òàê, íàïðèìåð, äëÿ ëþáîé ðåøåòêè âûïîëíÿþòñÿ íåðàâåíñòâà

äèñòðèáóòèâíîñòè (6.1) è (6.1′), îäíàêî ñóùåñòâóþò è òàêèå, äëÿ

êîòîðûõ âûïîëíèìû ñòðîãèå ðàâåíñòâà.

Îïðåäåëåíèå 6.7. Ðåøåòêà íàçûâàåòñÿ äèñòðèáóòèâíîé, åñëè â

íåé äëÿ âñåõ x,y,z âûïîëíÿþòñÿ òîæäåñòâà:

x∧(y∨z)=(x∧y)∨(x∧z), L6

′′

′

x∨(y∧z)=(x∨y)∧(x∨z). L6

′′′′

′′

Ñëåäóåò îòìåòèòü, ÷òî âûïîëíèìîñòü L6

′′

′ äëÿ îòäåëüíûõ ýëåìåí-

òîâ ðåøåòêè íå âëå÷åò âûïîëíèìîñòè äëÿ íèõ L6

′′′′

′′ (ñâîéñòâî L6

′′′′

′′

äëÿ òåõ æå ýëåìåíòîâ ìîæåò íå âûïîëíÿòüñÿ, åñëè ðåøåòêà

íåäèñòðèáóòèâíà). Îäíàêî âûïîëíèìîñòü îäíîãî èç ñâîéñòâ äëÿ

âñåõ ýëåìåíòîâ ðåøåòêè âëå÷åò âûïîëíèìîñòü è äðóãîãî. Òîãäà

äëÿ ïðîâåðêè äèñòðèáóòèâíîñòè ðåøåòêè äîñòàòî÷íî óñòàíîâèòü

òîæäåñòâî L6

′′

′ (èëè L6

′′′′

′′) äëÿ âñåõ ýëåìåíòîâ, âòîðîå áóäåò ñëåäî-

âàòü ïî òåîðåìå 6.4.

Òåîðåìà 6.4. Åñëè â ðåøåòêå äëÿ âñåõ ýëåìåíòîâ âûïîëíÿåòñÿ

òîæäåñòâî L6

′′

′, òî âûïîëíÿåòñÿ òîæäåñòâî L6

′′′′

′′ è íàîáîðîò.

Äîêàçàòåëüñòâî. Ïîêàæåì, ÷òî èç L6

′′

′ ñëåäóåò L6

′′′′

′′. Èç L6

′′′′

′′ áóäåò

ñëåäîâàòü L6

′′

′ ïî ïðèíöèïó äâîéñòâåííîñòè. Äëÿ âñåõ x,y,z:

(x∨y)∧(x∨z)=

=[(x∨y)∧x]∨[(x∨y)∧z]= ñîãëàñíî L6

′′

′

=x∨[z∧(x∨y)]= ïî L4, L2

=x∨[(z∧x)∨(z∧y)]= ïî L6

′′

′

=[x∨(z∧x)∨(z∧y)]= ïî L3

=x∨(z∧y). ïî L4

Ëåììà 6.7. Ëþáàÿ öåïü ÿâëÿåòñÿ äèñòðèáóòèâíîé ðåøåòêîé.

Äîêàçàòü ñàìîñòîÿòåëüíî.

6.4. Ìîäóëÿðíîñòü

Îïðåäåëåíèå 6.8. Ðåøåòêà íàçûâàåòñÿ ìîäóëÿðíîé, åñëè â íåé

âûïîëíÿåòñÿ ìîäóëÿðíûé çàêîí L5:

åñëè x ≤ z, òî x∨(y∧z)=(x∨y)∧z. L5

Çàìåòèì, ÷òî ïî ïðèíöèïó äâîéñòâåííîñòè, åñëè z ≤ x, òî

x∧(y∨z)=(x∧y)∨z, ÷òî ñîâïàäàåò ñ L5, ò.å. çàêîí ìîäóëÿðíîñòè

ÿâëÿåòñÿ ñàìîäâîéñòâåííûì.

Ìîäóëÿðíûé çàêîí ìîæåò áûòü ïîëó÷åí èç L6", åñëè x ≤ z. Òàêèì

îáðàçîì, ìîäóëÿðíûé çàêîí L5 èìååò ìåñòî â ëþáîé äèñòðèáóòèâ-

Ãëàâà 6 Ðåøåòêè

⊗ abcd ⊕ abcd

aaaaa aabcd

babab bbbdd

caacc ccdcd

dabcd ddddd

Ðèñ. 6.3.

Ðåøåòêà L = {a, b, c, d}.

82 83

íîé ðåøåòêå. Îòñþäà ñëåäóåò, ÷òî åñëè ðåøåòêà äèñòðèáóòèâíà,

òî îíà è ìîäóëÿðíà.

Ïðèìåðû.

1. Ðàññìîòðèì ðåøåòêó N

(«ïåíòàãîí») íà ðèñ. 6.4. Äîêàæåì, ÷òî

îíà íåìîäóëÿðíà. Âñå öåïè â ðåøåòêå äèñòðèáóòèâíû, ñëåäîâà-

òåëüíî, äëÿ ëþáûõ äâóõ ýëåìåíòîâ, ëåæàùèõ íà îäíîé öåïè, óñëîâèå

ìîäóëÿðíîñòè âûïîëíÿåòñÿ. Âîçüìåì ýëåìåíòû a ≤ b è ýëåìåíò c,

íå ëåæàùèé ñ íèìè íà îäíîé öåïè. Ïðîâåðèì âûïîëíèìîñòü

ñâîéñòâà L5: a∨(c∧b)=(a∨c)∧b. Ïîëó÷èì: a∨(c∧b)=a∨0=a,

(a∨c)∧b=I∧b=b. Òàê êàê a ≠ b, òî çàêîí ìîäóëÿðíîñòè íå

âûïîëíÿåòñÿ. Ðàññìîòðèì, óäîâëåòâîðÿåòñÿ ëè ñâîéñòâî äèñòðèáó-

òèâíîñòè: a∨(c∧b)=(a∨c)∧(a∨b), íî a∨0≠I∧b, ñëåäîâà-

òåëüíî, ðåøåòêà N

íå äèñòðèáóòèâíà.

Îòñþäà ñëåäóåò âûâîä: åñëè ðåøåòêà íåìîäóëÿðíà, òî îíà íåäèñòðè-

áóòèâíà.

Ðèñ. 6.4. Ðåøåòêè N

(ïåíòàãîí), M

(äèàìàíò), N

2. Ðàññìîòðèì ðåøåòêó M

(«äèàìàíò») íà ðèñ. 6.4. Âñå öåïè

{0,a,I}, {0, b, I}, {0, c, I} äèñòðèáóòèâíû, ñëåäîâàòåëüíî, è ìîäóëÿðíû.

Âîçüìåì òðè ýëåìåíòà, íå ëåæàùèå íà îäíîé öåïè: a ≤ I è c. Óñëîâèå

ìîäóëÿðíîñòè äëÿ íèõ âûïîëíÿåòñÿ: a∨(c∧I)=(a∨c)∧I, òàê

êàê a∨c=I∧I, ò.å. I=I. Íåòðóäíî óáåäèòüñÿ â òîì, ÷òî óñëîâèå

ìîäóëÿðíîñòè â M

áóäåò âûïîëíÿòüñÿ äëÿ ëþáûõ òðåõ ýëåìåíòîâ,

äâà èç êîòîðûõ íàõîäÿòñÿ â îòíîøåíèè ïîðÿäêà, è, ñëåäîâàòåëüíî,

ðåøåòêà M

ìîäóëÿðíà. Ïðîâåðèì âûïîëíåíèå ñâîéñòâà äèñòðèáó-

òèâíîñòè äëÿ ýëåìåíòîâ a, b, c (âñå îñòàëüíûå òðîéêè ýëåìåíòîâ â

ýòîé ðåøåòêå äèñòðèáóòèâíû): a∨(b∧c)=(a∨b)∧(a∨c). Ðàâåí-

ñòâî íåâûïîëíåíî, òàê êàê a∨(b∧c) = a∨0 = a, íî (a∨b)∧(a∨c)=

= I∧I = I, è a≠I. Îòìåòèì, ÷òî âûïîëíåíî òîëüêî íåðàâåíñòâî

äèñòðèáóòèâíîñòè: a≤I. Òàêèì îáðàçîì, ðåøåòêà M

ìîäóëÿðíà,

íî íå äèñòðèáóòèâíà. Âñå ýëåìåíòû a, b, c íåñðàâíèìû, ñëåäîâà-

òåëüíî, äëÿ íèõ íå îïðåäåëåí çàêîí ìîäóëÿðíîñòè, íî äèñòðèáó-

òèâíûé çàêîí äîëæåí âûïîëíÿòüñÿ äëÿ âñåõ ýëåìåíòîâ, â òîì ÷èñëå

äëÿ a, b, c.

Îòñþäà ñëåäóåò âûâîä: ðåøåòêà ìîæåò áûòü ìîäóëÿðíîé, íî íåäè-

ñòðèáóòèâíîé.

Îáîáùàÿ âûâîäû, ïîëó÷åííûå íàìè ïðè èññëåäîâàíèè äèñòðè-

áóòèâíûõ è ìîäóëÿðíûõ ðåøåòîê, ìîæíî ñôîðìóëèðîâàòü ñëåäó-

þùóþ òåîðåìó.

Òåîðåìà 6.6.

à) Ðåøåòêà L ìîäóëÿðíà òîãäà è òîëüêî òîãäà, êîãäà îíà íå

ñîäåðæèò ïåíòàãîíîâ.

á) Ìîäóëÿðíàÿ ðåøåòêà L äèñòðèáóòèâíà òîãäà è òîëüêî òîãäà,

êîãäà îíà íå ñîäåðæèò äèàìàíòîâ.

â) Ðåøåòêà L äèñòðèáóòèâíà òîãäà è òîëüêî òîãäà, êîãäà îíà íå

ñîäåðæèò íè ïåíòàãîíîâ, íè äèàìàíòîâ.

Äîêàçàòåëüñòâî. à). Åñëè L ìîäó-

ëÿðíà, òî âñÿêàÿ åå ïîäðåøåòêà òîæå

ìîäóëÿðíà è, ñëåäîâàòåëüíî, L íå ñî-

äåðæèò ïîäðåøåòîê, èçîìîðôíûõ N

Åñëè L íåìîäóëÿðíà, òî îíà ñîäåðæèò

òðè ýëåìåíòà x,y,z òàêèå, ÷òî x ≤ z, è

x∨(y∧z)<(x∨y)∧z. Òîãäà ýëåìåíòû y,

x ∨ y, y∧ z, (x ∨ y) ∧ z, x ∨(y ∧ z) îáðàçóþò

ïåíòàãîí (ñì. ðèñ.6.5.). Äåéñòâèòåëüíî,

y ∧ z ≤ x ∨ (y ∧ z) <(x ∨ y) ∧ z ≤ x ∨ y. Äàëåå,

(x∨(y∧z))∨y=(x∨y)∨((y∧z)∨y)=

= x ∨ y. Äâîéñòâåííî, ((x∨y)∧z)∧y=

= z ∧ y. Ðàâåíñòâî y ∧ z= x ∨ (y ∧ z)

íåâîçìîæíî, òàê êàê òîãäà áûëî áû

x≤y ∧ z, îòêóäà (x∨y)∧z = x∨(y∧z), ÷òî ïðîòèâîðå÷èò óñëîâèþ.

Ñ äîêàçàòåëüñòâîì ïóíêòà á) ìîæíî ïîçíàêîìèòüñÿ â [ÃðåòöåðÃ.,

1982]; ïóíêò â) ñëåäóåò èç à) è á).

Îñíîâíûì ñâîéñòâîì ìîäóëÿðíûõ ðåøåòîê ÿâëÿåòñÿ ïðèíöèï

òðàíñïîçèöèè.

Òåîðåìà 6.7 (ïðèíöèï òðàíñïîçèöèè). Â ëþáîé ìîäóëÿðíîé

ðåøåòêå îòîáðàæåíèÿ ϕ

:x→x∧a è ψ

:y→y∨b ÿâëÿþòñÿ

âçàèìíî îáðàòíûìè èçîìîðôèçìàìè ìåæäó èíòåðâàëàìè.

[b,a∨b] è [a ∧ b, a].

Äîêàçàòåëüñòâî. Åñëè x∈[b, a∨b], òî ϕ

(x)∈ [a ∧ b, a]â

ñèëó èçîòîííîñòè ϕ

. Ñîãëàñíî L5, (x∧a) ∨ b = x∧(a∨b), òàê

êàê x∈[b, a∨b], Ýòî îçíà÷àåò, ÷òî ψ

(ϕ

(x))=x. Â ñèëó ïðèíöèïà

äâîéñòâåííîñòè ïîëó÷àåì, ÷òî ϕ

(ψ

(y))=y äëÿ âñåõ y∈[a ∧b,a].

Ãëàâà 6 Ðåøåòêè

Ðèñ. 6.5.

Ê äîêàçàòåëüñòâó

òåîðåìû 6.6.

84 85

Ñëåäñòâèå. Â ëþáîé ìîäóëÿðíîé ðåøåòêå, åñëè a ≠ b è îáà

ýëåìåíòà ïîêðûâàþò c, òî a ∨ b ïîêðûâàåò è a, è b (M1),

äâîéñòâåííî, åñëè a ≠ b è c ïîêðûâàåò îáà ýëåìåíòà, òî a è b îáà

ïîêðûâàþò a ∧ b (M2).

Ïðèìåð. Äëÿ ðåøåòêè N

íà ðèñ. 6.4 íå âûïîëíÿåòåñÿ óñëîâèå

M2: ýëåìåíòû b, e ïîêðûâàþòñÿ ýëåìåíòîì I, îäíàêî, íè b, íè e íå

ïîêðûâàåò b∧ e= 0. Îòñþäà ñëåäóåò, ÷òî ðåøåòêà N

íåìîäóëÿðíà.

Íåòðóäíî ïðîâåðèòü, ÷òî óñëîâèå M1 óäîâëåòâîðÿåòñÿ â ýòîé

ðåøåòêå. Òàêèå ðåøåòêè, â êîòîðûõ âûïîëíÿåòñÿ îäíî èç óñëîâèé

M1 èëè M2, íàçûâàþòñÿ ïîëóìîäóëÿðíûìè: åñëè â ðåøåòêå âûïîë-

íÿåòñÿ óñëîâèå M1, òî ðåøåòêà ïîëóìîäóëÿðíà ñâåðõó, à åñëè óñëî-

âèå M2  òî ïîëóìîäóëÿðíà ñíèçó. Ðåøåòêà N

ïîëóìîäóëÿðíà ñâåðõó.

6.5. Ìîäóëÿðíûå ðåøåòêè ñ äîïîëíåíèÿìè

Îïðåäåëåíèå 6.9. Äîïîëíåíèåì ýëåìåíòà x â ðåøåòêå ñ 0 è I

íàçûâàåòñÿ ýëåìåíò y òàêîé, ÷òî x∧y=0 è x∨y=I. Äîïîëíå-

íèå x áóäåì îáîçíà÷àòü x'.

Îïðåäåëåíèå 6.10. Ðåøåòêà íàçûâàåòñÿ ðåøåòêîé ñ äîïîëíåíè-

ÿìè, åñëè âñå åå ýëåìåíòû èìåþò äîïîëíåíèÿ.

Ïðèìåðû.

1. Ðåøåòêà íà ðèñ. 6.1 ÿâëÿåòñÿ ðåøåòêîé ñ äîïîëíåíèÿìè. Äîïîëíå-

íèå êàæäîãî ýëåìåíòà ñîîòâåòñòâóåò åãî òåîðåòèêî-ìíîæåñòâåííîìó

äîïîëíåíèþ äî ìíîæåñòâà {a, b, c}: äîïîëíåíèå ýëåìåíòà ∅ åñòü

{a,b,c}, äîïîëíåíèå {a} åñòü {b, c} è ò.ä. Â îáùåì ñëó÷àå ëþáîå

ìíîæåñòâî-ñòåïåíü ℘(U) ÿâëÿåòñÿ ðåøåòêîé ñ äîïîëíåíèÿìè.

2. Ðåøåòêà íà ðèñ. 5.11, èçîìîðôíàÿ ðåøåòêå ℘(A), òàêæå ÿâëÿåòñÿ

ðåøåòêîé ñ äîïîëíåíèÿìè. Äëÿ êàæäîãî ýëåìåíòà x ñóùåñòâóåò

äîïîëíåíèå x′ òàêîå, ÷òî ÍÎÄ(x,x′) =1, ò.å. íóëþ ðåøåòêè,

ÍÎÊ(x,x′)=30, ò.å. åäèíèöå ðåøåòêè. Íàïðèìåð, 1 åñòü äîïîë-

íåíèå 30 (è íàîáîðîò), 2 åñòü äîïîëíåíèå 15 (è íàîáîðîò):

ÍÎÄ(2,15) =1, ÍÎÊ(2,15)=30 è ò.ä., ò.å. äîïîëíåíèÿìè äðóã

äðóãà ÿâëÿþòñÿ âçàèìíî ïðîñòûå ÷èñëà.

Îïðåäåëåíèå 6.11. Ðåøåòêà L íàçûâàåòñÿ ðåøåòêîé ñ îòíîñè-

òåëüíûìè äîïîëíåíèÿìè, åñëè êàæäûé åå çàìêíóòûé èíòåðâàë

ÿâëÿåòñÿ ðåøåòêîé ñ äîïîëíåíèÿìè.

Äàâàÿ îïðåäåëåíèå ïîäðåøåòêè, ìû îïðåäåëèëè çàìêíóòûé

èíòåðâàë [a, b] ðåøåòêè êàê èíòåðâàë, ñîñòîÿùèé èç âñåõ ýëåìåíòîâ

x ∈ L, òàêèõ ÷òî a≤x≤ b. Òàêîé èíòåðâàë ðåøåòêè âñåãäà áóäåò

ïîäðåøåòêîé. Ýëåìåíò x′ÿâëÿåòñÿ îòíîñèòåëüíûì äîïîëíåíèåì

ýëåìåíòà x∈[a,b], åñëè x∧ x′=aè x∨x′=b.

Ïðèìåðû. Íà ðèñ. 6.4 ðåøåòêà N

 íåìîäóëÿðíàÿ ðåøåòêà ñ

äîïîëíåíèÿìè: äîïîëíåíèåì 0ÿâëÿåòñÿ I, äîïîëíåíèå a  c, äîïîë-

íåíèå b  c, c èìååò äâà äîïîëíåíèÿ: a è b. Îäíàêî ýòî ðåøåòêà áåç

îòíîñèòåëüíûõ äîïîëíåíèé: â èíòåðâàëå [0, b] ýëåìåíò aíå èìååò

äîïîëíåíèÿ. Ðåøåòêà M

ÿâëÿåòñÿ ïîäðåøåòêîé ñ äîïîëíåíèÿìè.

Ðåøåòêà N

 ðåøåòêà áåç äîïîëíåíèé: ýëåìåíò c íå èìååò

äîïîëíåíèÿ.

Äëÿ äèñòðèáóòèâíûõ ðåøåòîê èìååò ìåñòî ñëåäóþùàÿ òåîðåìà.

Òåîðåìà 6.8. Åñëè â äèñòðèáóòèâíîé ðåøåòêå äëÿ ôèêñèðîâàí-

íîãî c c ∨ x=c ∨ y è c ∧ x=c ∧ y, òî x=y.

Äîêàçàòåëüñòâî.

x=x ∧ (c ∨ x)= (çàêîí ïîãëîùåíèÿ)

=x ∧ (c ∨ y)= (ïî óñëîâèþ òåîðåìû)

=(x ∧ c) ∨ (x ∧ y)= (äèñòðèáóòèâíîñòü)

=(c ∧ y) ∨ (x ∧ y)= (L2 è ïî óñëîâèþ c ∧ x=c ∧ y)

=(c ∨ x) ∧ y=(c ∨ y) ∧ y=y.

Ñîãëàñíî ýòîé òåîðåìå â ëþáîì çàìêíóòîì èíòåðâàëå [a, b]

äèñòðèáóòèâíîé ðåøåòêè ýëåìåíò c ìîæåò èìåòü ñàìîå áîëüøåå

îäíî îòíîñèòåëüíîå äîïîëíåíèå.

Òåîðåìà 6.9. Ëþáàÿ ìîäóëÿðíàÿ ðåøåòêà ñ äîïîëíåíèÿìè

ÿâëÿåòñÿ ðåøåòêîé ñ îòíîñèòåëüíûìè äîïîëíåíèÿìè.

Äîêàçàòåëüñòâî. Ïóñòü M  ïðîèçâîëüíàÿ ìîäóëÿðíàÿ ðåøåòêà

ñ äîïîëíåíèÿìè. Ðàññìîòðèì èíòåðâàë [0, b] ⊂M. Åñëè 0 ≤ x ≤ b â

M, òî x ∧ (x' ∧ b)=(x ∧ x') ∧ b=0 ∧ b=0, òàê êàê M  ðåøåòêà ñ

äîïîëíåíèÿìè, à òàê êàê M  ìîäóëÿðíà, òî x∨(x'∧b)=(x∨x')∧b=

= I ∧ b=b. Ñëåäîâàòåëüíî, B=[0, b] ÿâëÿåòñÿ ìîäóëÿðíîé ïîäðå-

øåòêîé ñ äîïîëíåíèÿìè ðåøåòêè Ì. Åñëè âçÿòü òåïåðü [a, b] ⊂ B,

òî ýòî áóäåò ìîäóëÿðíàÿ ðåøåòêà ñ äîïîëíåíèÿìè â B. Ñëåäîâà-

òåëüíî, ïî îïðåäåëåíèþ, Ì ÿâëÿåòñÿ ìîäóëÿðíîé ðåøåòêîé ñ

îòíîñèòåëüíûìè äîïîëíåíèÿìè.

Íàïîìíèì, ÷òî â ó-ìíîæåñòâå Ð êîíå÷íîé äëèíû ñ 0 àòîìîì

íàçûâàåòñÿ ýëåìåíò õ, ïîêðûâàþùèé 0 (åãî âûñîòà h[x]=1).

Òåîðåìà 6.10. Â ðåøåòêå L êîíå÷íîé äëèíû ñ îòíîñèòåëüíûìè

äîïîëíåíèÿìè êàæäûé ýëåìåíò à ÿâëÿåòñÿ îáúåäèíåíèåì ñîäåð-

æàùèõñÿ â íåì àòîìîâ.

Äîêàçàòåëüñòâî. Åñëè à> 0, òî ëèáî a ÿâëÿåòñÿ àòîìîì, ëèáî

à> b > 0 äëÿ íåêîòîðîãî b∈ L. Ïóñòü c áóäåò îòíîñèòåëüíûì

äîïîëíåíèåì ýëåìåíòà b â [0, a]. Èíäóêöèåé ïî äëèíå èíòåðâàëà

[0, a] äîêàçûâàåòñÿ, ÷òî ýëåìåíòû b è c îáà ÿâëÿþòñÿ îáúåäèíåíèÿìè

àòîìîâ. Òîãäà ýòî ñïðàâåäëèâî è äëÿ a=b∨ c.

Ñëåäñòâèå. Â ìîäóëÿðíîé ðåøåòêå êîíå÷íîé äëèíû ñ äîïîëíå-

íèÿìè êàæäûé ýëåìåíò ÿâëÿåòñÿ îáúåäèíåíèåì ñîäåðæàùèõñÿ â

íåì àòîìîâ.

Ãëàâà 6 Ðåøåòêè

86 87

6.6. Áóëåâû ðåøåòêè

Îïðåäåëåíèå 6.12. Áóëåâîé ðåøåòêîé íàçûâàåòñÿ äèñòðèáóòèâ-

íàÿ ðåøåòêà ñ äîïîëíåíèÿìè.

Òåîðåìà 6.11. Â áóëåâîé ðåøåòêå ëþáîé ýëåìåíò õ èìååò îäíî

è òîëüêî îäíî äîïîëíåíèå x'. Ïðè ýòîì:

x ∧ x'=0, x ∨ x'=I; L7

(x')'=x;(èíâîëþöèÿ) L8

(x ∧ y)'=x' ∨ y',(x ∨ y)'=x'∧y'.(çàêîíû äå Ìîðãàíà) L9

Äîêàçàòåëüñòâî. Ïî òåîðåìå 6.8, åñëè â äèñòðèáóòèâíîé ðåøåòêå

c∨x=c ∨ y è c ∧ x=c ∧ y, òî x=y, ò.å. êàæäûé ýëåìåíò äèñòðè-

áóòèâíîé ðåøåòêè ñ äîïîëíåíèÿìè èìååò íå áîëåå îäíîãî

äîïîëíåíèÿ. L7 ÿâëÿåòñÿ îïðåäåëåíèåì äîïîëíåíèÿ. Äîêàæåì L8.

Äîïîëíåíèå ýëåìåíòà õ â äèñòðèáóòèâíîé ðåøåòêå åäèíñòâåííî,

ñëåäîâàòåëüíî, ñîîòâåòñòâèå x → x' îäíîçíà÷íî. Íî, ïî îïðåäåëå-

íèþ, åñëè õ' ÿâëÿåòñÿ äîïîëíåíèåì õ, òî õ ÿâëÿåòñÿ äîïîëíåíèåì

õ', ñëåäîâàòåëüíî, îáðàòíîå ñîîòâåòñòâèå òàêæå îäíîçíà÷íî, ò.å.

(õ')'=õ. L8 äîêàçàíî.

Äîêàæåì L9. Åñëè x è y èìåþò äîïîëíåíèÿ x' è y' ñîîòâåòñòâåííî,

òî ýëåìåíò x ∧ y èìååò ñâîèì äîïîëíåíèåì (x ∧ y)', à ýëåìåíò

x∨y (x ∨ y)'. Â ñèëó åäèíñòâåííîñòè äîïîëíåíèÿ äëÿ äîêàçàòåëü-

ñòâà ïåðâîãî ðàâåíñòâà L9 äîñòàòî÷íî ïîêàçàòü, ÷òî

(x ∧ y) ∨ (x' ∨ y') = I è (x ∧ y) ∧ (x' ∨ y') = 0.

Äåéñòâèòåëüíî, (x ∧ y) ∨ (x' ∨ y') = (x' ∨ y'∨ x) ∧ (x' ∨ y'∨ y)=I∧I=I.

(x ∧ y) ∧ (x' ∨ y') = (x ∧ y ∧ x')∨ (x ∧ y ∧ y') = 0 ∨ 0 =0.

Âòîðîå ðàâåíñòâî L9 äîêàçûâàåòñÿ äâîéñòâåííî.

Ëåììà 6.7. Â áóëåâîé ðåøåòêå x ∧ a=0 òîãäà è òîëüêî òîãäà,

êîãäà x ≤ a'.

Äîêàçàòåëüñòâî. Äåéñòâèòåëüíî, åñëè x≤a' òî x∧a≤a'∧a=0,

è, åñëè x∧a=0, òî x=x∧I=x∧(a∨a')=(x∧a)∨(x ∧ a')=

=0∨ (x ∧ a')=x ∧ a', ò. å. x=x ∧ a', îòêóäà ñëåäóåò, ÷òî x ≤ a'.

Èç ëåììû 6.7 ñëåäóåò, ÷òî ïðè a ≤ b, b' ≤ a', ò.å. âçàèìíî

îäíîçíà÷íîå ñîîòâåòñòâèå x → x' îáðàùàåò ïîðÿäîê (àíòèèçîòîííî).

Ñîîòâåòñòâèå x' → (x')' òàêæå àíòèèçîòîííî, ñëåäîâàòåëüíî, x→x'

ÿâëÿåòñÿ äóàëüíûì èçîìîðôèçìîì. Ñëåäîâàòåëüíî, ëþáàÿ áóëåâà

ðåøåòêà äóàëüíî èçîìîðôíà ñàìîé ñåáå, ò.å. ñàìîäâîéñòâåííà.

Ïîñêîëüêó äîïîëíåíèÿ â áóëåâîé ðåøåòêå åäèíñòâåííû, åå

ìîæíî ðàññìàòðèâàòü êàê àëãåáðó.

Îïðåäåëåíèå 6.13. Áóëåâîé àëãåáðîé B = <L, ∨, ∧, ′, 0, I>

íàçûâàåòñÿ àëãåáðà ñ äâóìÿ áèíàðíûìè îïåðàöèÿìè ∨ è ∧, îäíîé

óíàðíîé îïåðàöèåé ′ è äâóìÿ íóëüàðíûìè îïåðàöèÿìè 0 è I,

óäîâëåòâîðÿþùèìè óñëîâèÿì L1  L9. (Íóëüàðíûå îïåðàöèè

âûäåëÿþò ýëåìåíòû 0, Iìíîæåñòâà L, ýòè ýëåìåíòû íàçûâàþòñÿ

âûäåëåííûìè ýëåìåíòàìè).

Ðèñ. 6.6. Áóëåâû ðåøåòêè.

Íà ðèñ. 6.6 ïîêàçàíû áóëåâû ðåøåòêè 2, 2

, 2

Ëþáîå ïîëå ìíîæåñòâ è, â ÷àñòíîñòè, ìíîæåñòâî âñåõ ïîäìíî-

æåñòâ íåêîòîðîãî ìíîæåñòâà ÿâëÿåòñÿ áóëåâîé àëãåáðîé. Ëþáàÿ

ïîäàëãåáðà áóëåâîé àëãåáðû ñàìà ÿâëÿåòñÿ áóëåâîé àëãåáðîé.

Ïðÿìîå ïðîèçâåäåíèå áóëåâûõ àëãåáð ÿâëÿåòñÿ áóëåâîé àëãåáðîé.

6.7. Êâàçèïîðÿäêè

Îïðåäåëåíèå 6.14. Îòíîøåíèå êâàçèïîðÿäêà (ïðåäïîðÿäêà)

(îáîçíà÷èì åãî ∠) íà ìíîæåñòâå S îïðåäåëÿåòñÿ êàê îòíîøåíèå,

óäîâëåòâîðÿþùåå óñëîâèÿì

ðåôëåêñèâíîñòè: x ∠ x, P1

òðàíçèòèâíîñòè: åñëè x ∠ y è y ∠ z, òî x ∠ z, Ð3

íî íå îáÿçàòåëüíî óñëîâèþ àíòèñèììåòðè÷íîñòè Ð2.

Ïàðà <S, ∠> íàçûâàåòñÿ êâàçèóïîðÿäî÷åííûì (ïñåâäîóïîðÿäî-

÷åííûì) ìíîæåñòâîì.

Ðèñ. 6.7.

a) Êâàçèïîðÿäîê S. á) Ôàêòîð-ìíîæåñòâî [S/~].

Ãëàâà 6 Ðåøåòêè

88 89

Êâàçèóïîðÿäî÷åííîå ìíîæåñòâî èçîáðàæàåòñÿ â âèäå îðèåíòèðî-

âàíîãî ãðàôà, (ñì., íàïðèìåð, ðèñ. 6.7, a). Íà ãðàôå ñóùåñòâîâàíèå

îòíîøåíèÿ x∠y îçíà÷àåò, ÷òî ëèáî x=y, ëèáî ñóùåñòâóåò ïóòü èç

x â y â íàïðàâëåíèè ñòðåëîê. Íà ðèñ. 6.7,a) ïîêàçàíî, ÷òî èìååòñÿ

ïóòü èç b â e: b→d, d→e, ò.å. b∠e. Ñ äðóãîé ñòîðîíû, èìååòñÿ

ïóòü èç e â b: e→b, ò.å. e ∠ b. Òàêèì îáðàçîì, b ∠ e è e ∠ b, îäíàêî,

e≠b, ò.å. àíòèñèììåòðè÷íîñòü â äàííîì ñëó÷àå íå âûïîëíÿåòñÿ.

Àíàëîãè÷íî äëÿ d, e è d, b.

Ðàññìîòðèì îñíîâíóþ ëåììó î êâàçèóïîðÿäî÷åííûõ ìíîæå-

ñòâàõ, ñîãëàñíî êîòîðîé ëþáîå êâàçèóïîðÿäî÷åííîå ìíîæåñòâî

ìîæíî ïðåîáðàçîâàòü â óïîðÿäî÷åííîå. Ïî ëåììå, åñëè äëÿ êàêèõ-

òî äâóõ ýëåìåíòîâ âûïîëíÿåòñÿ x ∠ y è y ∠ x, è ïðè ýòîì x≠y, òî

ýòè ýëåìåíòû ïîëàãàþòñÿ ýêâèâàëåíòíûìè. Ìíîæåñòâî êëàññîâ

ýêâèâàëåíòíîñòè îáðàçóåò ó-ìíîæåñòâî. Íàïðèìåð, íà ðèñ. 6.7

ýëåìåíòû b, d, e áóäóò ýêâèâàëåíòíû è îáðàçóþò îäèí êëàññ ýêâèâà-

ëåíòíîñòè. Äâà äðóãèõ êëàññà ýêâèâàëåíòíîñòè áóäóò îáðàçîâàíû

îäíîýëåìåíòíûìè ïîäìíîæåñòâàìè {a} è {ñ}. Òåïåðü ëþáûå äâà

ýëåìåíòà áóäóò íàõîäèòüñÿ â îòíîøåíèè ïîðÿäêà x ∠ y òîëüêî â

òîì ñëó÷àå, åñëè îíè ïðèíàäëåæàò ðàçíûì êëàññàì ýêâèâàëåíòíîñòè.

Â äàííîì ïðèìåðå: a ∠ b, a ∠ d, a ∠ e, c ∠ b, c ∠ d, c ∠ e, è a

íåñðàâíèìî ñ c. Òîãäà ôàêòîð-ìíîæåñòâî [S/~] åñòü ó-ìíîæåñòâî,

ãäå êàæäûé ýëåìåíò ÿâëÿåòñÿ îäíèì èç êëàññîâ ýêâèâàëåíòíîñòè.

Íà ðèñ. 6.7, á) ïîêàçàíî ó-ìíîæåñòâî êëàññîâ ýêâèâàëåíòíîñòè {a},

{c}, {b, d, e}.

Äîêàæåì ýòó ëåììó.

Ëåììà 6.8. Â êâàçèóïîðÿäî÷åííîì ìíîæåñòâå Q=<S, ∠>

ïîëîæèì x ~ y, åñëè x ∠ y è y∠x. Òîãäà:

I. îòíîøåíèå ~ ÿâëÿåòñÿ îòíîøåíèåì ýêâèâàëåíòíîñòè íà S;

II. åñëè E è F  äâà êëàññà ýêâèâàëåíòíîñòè îòíîøåíèÿ ~, òî

ëèáî x ∠ y äëÿ âñåõ x ∈ E, y ∈ F, ëèáî ïîäîáíîå ñîîòíîøåíèå

íåâîçìîæíî íè ïðè êàêèõ x ∈ E, y ∈ F;

III. ôàêòîð-ìíîæåñòâî S/~ ñòàíîâèòñÿ ó-ìíîæåñòâîì, åñëè

ïîëîæèòü E ≤ F â ñëó÷àå, åñëè x ∠ y äëÿ íåêîòîðûõ (à çíà÷èò è

äëÿ âñåõ) x ∈ E, y ∈ F.

Äîêàçàòåëüñòâî.

I. Îòíîøåíèå x ∠ x âûïîëíÿåòñÿ äëÿ âñÿêîãî x∈S ïî P1,

ñëåäîâàòåëüíî, îòíîøåíèå ~ ðåôëåêñèâíî. Ñîãëàñíî îïðåäåëåíèþ,

èç x ~ y è y~z ñëåäóåò x ∠ y è y ∠ z, îòêóäà x ∠ z ïî P3. Àíàëîãè÷íî,

èç x~y è y~z ñëåäóåò z ∠ y è y ∠ x, ïîýòîìó z∠ x. Ñëåäîâàòåëüíî,

åñëè x~y è y~z, òî x~z, ò.å. îòíîøåíèå ~ òðàíçèòèâíî. Îòíîøåíèå

~ ñèììåòðè÷íî ïî îïðåäåëåíèþ. Ñëåäîâàòåëüíî, ýòî îòíîøåíèå

ýêâèâàëåíòíîñòè.

Ãëàâà 6

II. Â äâóõ êëàññàõ ýêâèâàëåíòíîñòè E è F, åñëè x ∠ y äëÿ

íåêîòîðûõ x∈E, y∈F, òî x

∠ x ∠ y ∠ y

äëÿ âñåõ x

∈ E, y

∈ F, è,

ñëåäîâàòåëüíî, x

∠ y

â ñèëó òðàíçèòèâíîñòè. Ýòî îçíà÷àåò, ÷òî

òîëüêî ýëåìåíòû, ïðèíàäëåæàùèå ðàçíûì êëàññàì ýêâèâàëåíòíîñòè,

ìîãóò íàõîäèòüñÿ â îòíîøåíèè ïîðÿäêà, ëèáî ýòè ýëåìåíòû

íåñðàâíèìû.

III. Â ôàêòîð-ìíîæåñòâå [S/~] êëàññ E ~ E (òàê êàê x ~ x) äëÿ

âñåõ E. Åñëè E ≤ F, è F ≤ G, òî x ∠ y ∠ z äëÿ âñåõ x ∈ E, y ∈ F, z ∈ G,

ñëåäîâàòåëüíî, x ∠ z ñîãëàñíî Ð3 äëÿ ∠. Çíà÷èò îòíîøåíèå ≤ òðàíçè-

òèâíî. È, åñëè E ≤ F, è F ≤ E, òî äëÿ âñåõ x ∈ E, y ∈ F x ∠ y è y ∠ x,

îòêóäà x~y, è çíà÷èò E=F.

Òàêèì îáðàçîì, ââåäåíèå êëàññîâ ýêâèâàëåíòíîñòè íà êâàçèóïî-

ðÿäî÷åííûõ ìíîæåñòâàõ ñâîäèò èõ ê y-ìíîæåñòâàì, ïîýòîìó êâàçè-

ïîðÿäîê ÷àñòî íàçûâàþò ïðåäïîðÿäêîì.

Ðåøåòêè

Ãëàâà 7. ÑÒÐÎÅÍÈÅ È ÏÐÅÄÑÒÀÂËÅÍÈÅ

ÐÅØÅÒÎÊ

7.1. Îïåðàöèè íàä ó-ìíîæåñòâàìè

Ðàññìîòðèì ïðîáëåìó ïîñòðîåíèÿ ðåøåòîê èç ìåíüøèõ

êîìïîíåíò. Äëÿ ýòîãî èñïîëüçóåì îïåðàöèè íàä ó-ìíîæåñòâàìè,

îáîáùàþùèå àðèôìåòè÷åñêèå îïåðàöèè ñëîæåíèÿ, óìíîæåíèÿ è

âîçâåäåíèÿ â ñòåïåíü. Ýòè îïåðàöèè íàä ìíîæåñòâàìè íàçûâàþòñÿ

êàðäèíàëüíûìè îïåðàöèÿìè.

Îïðåäåëåíèå 7.1. Ïóñòü X, Y  ó-ìíîæåñòâà. Êàðäèíàëüíàÿ

ñóììà X+Y  ýòî ìíîæåñòâî, ýëåìåíòàìè êîòîðîãî ÿâëÿþòñÿ

âñå ýëåìåíòû èç X è Y, ðàññìàòðèâàåìûå êàê íåïåðå-

ñåêàþùèåñÿ ìíîæåñòâà. Ïîðÿäîê ≤ ñîõðàíÿåò ñâîé ñìûñë

îòäåëüíî â X è â Y, è íè äëÿ êàêèõ x ∈ X, y ∈ Y íå ìîæåò áûòü

íè x≤y, íè y ≤ x.

Äèàãðàììà ñóììû äâóõ êîíå÷íûõ ìíîæåñòâ X + Y ñîñòîèò èç

äèàãðàììû äëÿ X è Y, ïîìåùåííûõ ðÿäîì, íàïðèìåð, äèàãðàììà

2+2 áóäåò âûãëÿäåòü òàê:

Îïðåäåëåíèå 7.2. Êàðäèíàëüíîå ïðîèçâåäåíèå X × Y (èëè XY) 

ýòî äåêàðòîâî (ïðÿìîå) ïðîèçâåäåíèå ó-ìíîæåñòâ X è Y.

Òåîðåìà 7.1. Ïðÿìîå ïðîèçâåäåíèå L×M ëþáûõ äâóõ ðåøåòîê

ÿâëÿåòñÿ ðåøåòêîé.

Äîêàçàòåëüñòâî. Äëÿ ëþáûõ äâóõ ýëåìåíòîâ <x

,y

> è

,y

> â L×M ýëåìåíò <x

∨x

, y

∨y

> ÿâëÿåòñÿ âåðõíåé

ãðàíüþ ýòîé ïàðû. Ëþáàÿ äðóãàÿ âåðõíÿÿ ãðàíü <u, v> îáîèõ

ýëåìåíòîâ <x

, y

> è <x

, y

> óäîâëåòâîðÿåò íåðàâåíñòâàì u ≥ x

v≥y

(i=1, 2), è çíà÷èò, ïî îïðåäåëåíèþ âåðõíåé ãðàíè,

u≥x

∨x

è v≥y

∨y

, òàê ÷òî <u, v> ≥ <x

∨x

, y

∨y

>. Ýòî

ïîêàçûâàåò, ÷òî <x

∨x

, y

∨y

>=<x

, y

>∨<x

, y

>, îòêóäà

ñëåäóåò, ÷òî îáúåäèíåíèå, ñòîÿùåå ñïðàâà, ñóùåñòâóåò. Äâîé-

ñòâåííî: <x

∧x

, y

∧y

>=<x

,y

>∧<x

,y

>. Ñëåäîâàòåëüíî,

L×M ÿâëÿåòñÿ ðåøåòêîé.

Òåîðåìà 7.2. Ïðÿìîå ïðîèçâåäåíèå X×Y äâóõ äèñòðèáóòèâíûõ

ðåøåòîê ÿâëÿåòñÿ äèñòðèáóòèâíîé ðåøåòêîé.

Äîêàçàòåëüñòâî. Ïîñêîëüêó X è Y  ðåøåòêè, òî ïî òåîðåìå 7.1

èõ ïðîèçâåäåíèå òîæå ðåøåòêà, ïîýòîìó èìåþò ìåñòî ðàâåíñòâà:

,y

>∨<x

,y

>=<x

∨x

,y

∨y

> è

,y

>∧<x

,y

>=<x

∧x

,y

∧y

Òîãäà <x

,y

>∨(<x

,y

>∧<x

,y

>)=

= <x

,y

>∨<x

∧x

, y

∧y

>=

=<x

∨(x

∧x

),y

∨(y

∧y

)>=

(ïîñêîëüêó êàæäàÿ èç èñõîäíûõ ðåøåòîê äèñòðèáóòèâíà,

ìîæåì ïðîäîëæèòü öåïî÷êó ðàâåíñòâ)

= <(x

∨ x

)∧(x

∨ x

),(y

∨ y

)∧(y

∨ y

)>=

= <(x

∨ x

),(y

∨ y

)>∧ <(x

∨ x

),(y

∨ y

)>=

= (<x

,y

>∨<x

,y

>)∧(<x

,y

>∨<x

, y

>).

Àíàëîãè÷íîäîêàçûâàåòñÿ,÷òî

, y

> ∧ (<x

,y

> ∨ <x

,y

>) =

= (<x

,y

> ∧ <x

,y

>) ∨ (<x

,y

> ∧ <x

,y

>).

Ñëåäñòâèå. Ïîñêîëüêó öåïü ÿâëÿåòñÿ äèñòðèáóòèâíîé ðåøåò-

êîé, òî, î÷åâèäíî, ÷òî ïðÿìîå ïðîèçâåäåíèå öåïåé åñòü äèñòðè-

áóòèâíàÿ ðåøåòêà.

Ïðèìåðû.

1. Ïðÿìîå ïðîèçâåäåíèå öåïè íà ñåáÿ ÷àñòî íàçûâàþò âåêòîðíîé

ðåøåòêîé, à îòíîøåíèå ÷àñòè÷íîãî ïîðÿäêà íà íåé  îòíîøåíèåì

äîìèíèðîâàíèÿ. Íà ðèñ. 7.1 ïîêàçàíà äèñòðèáóòèâíàÿ âåêòîðíàÿ

ðåøåòêà.

Ðèñ. 7.1. Äèñòðèáóòèâíàÿ âåêòîðíàÿ ðåøåòêà.

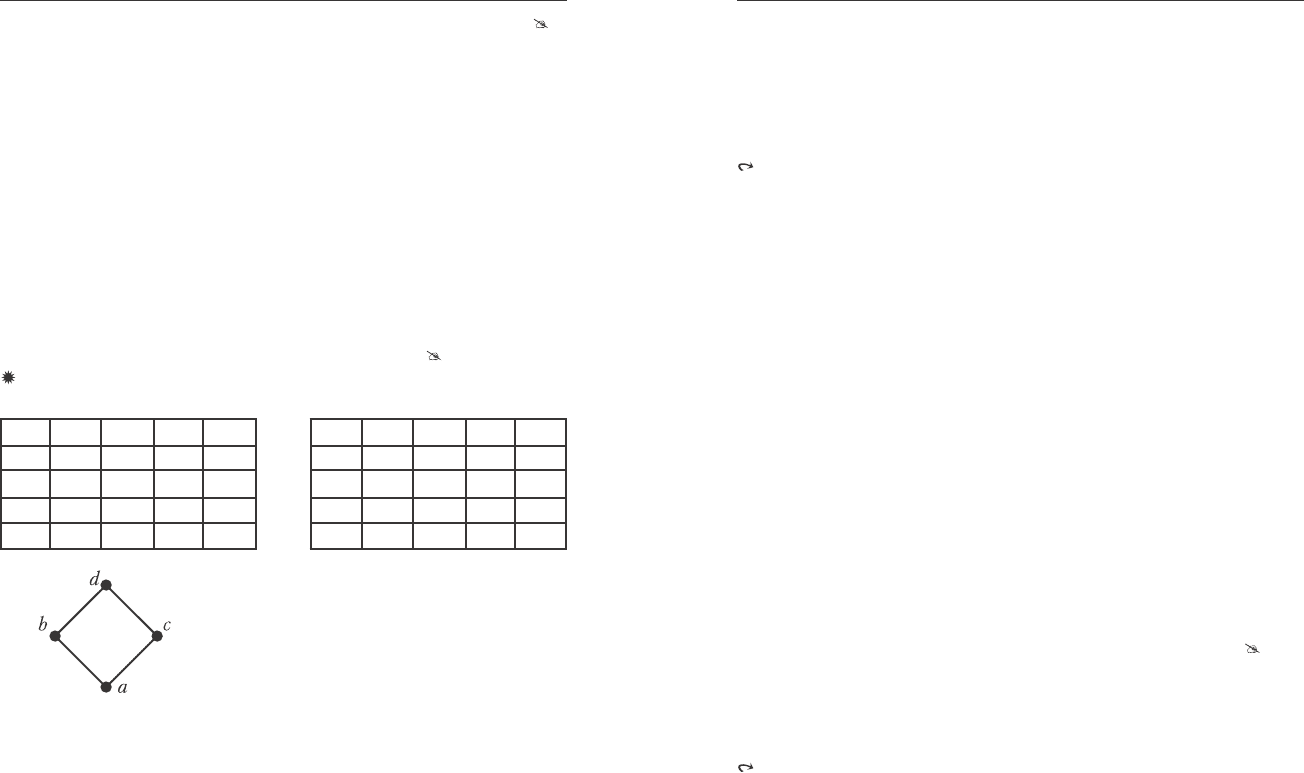
2. Ïóñòü X={0,1}, Y={0, 1, 2}  öåïè. Íà ðèñ. 7.2 ïðåä-

ñòàâëåíû äèàãðàììû ó-ìíîæåñòâ X, Y, X×Y, X×X×Y. Äåêàðòîâî

ïðîèçâåäåíèå öåïåé X×Y èìååò ïëîñêóþ äèàãðàììó è îáðàçóåò

äèñòðèáóòèâíóþ ðåøåòêó. Äåêàðòîâî ïðîèçâåäåíèå öåïè X è

ðåøåòêè X×Y ñ ïëîñêîé äèàãðàììîé èìååò ïðîñòðàíñòâåííóþ

äèàãðàììó.

Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê

92 93

Ðèñ. 7.2. Äåêàðòîâî ïðîèçâåäåíèå öåïåé.

7.2. Ñòåïåíü ìíîæåñòâ

Îïðåäåëåíèå 7.3. Êàðäèíàëüíîé ñòåïåíüþ Y

: X → Y ñ îñíî-

âàíèåì Y è ïîêàçàòåëåì X íàçûâàåòñÿ ìíîæåñòâî âñåõ èçîòîííûõ

ôóíêöèé y=f(x), çàäàííûõ íà X è ïðèíèìàþùèõ çíà÷åíèÿ â

Y, óïîðÿäî÷åííûõ îòíîøåíèåì f(x) ≤ g(x) äëÿ âñåõ x ∈ X.

Èññëåäóåì ñâîéñòâà ñòåïåíè ìíîæåñòâ.

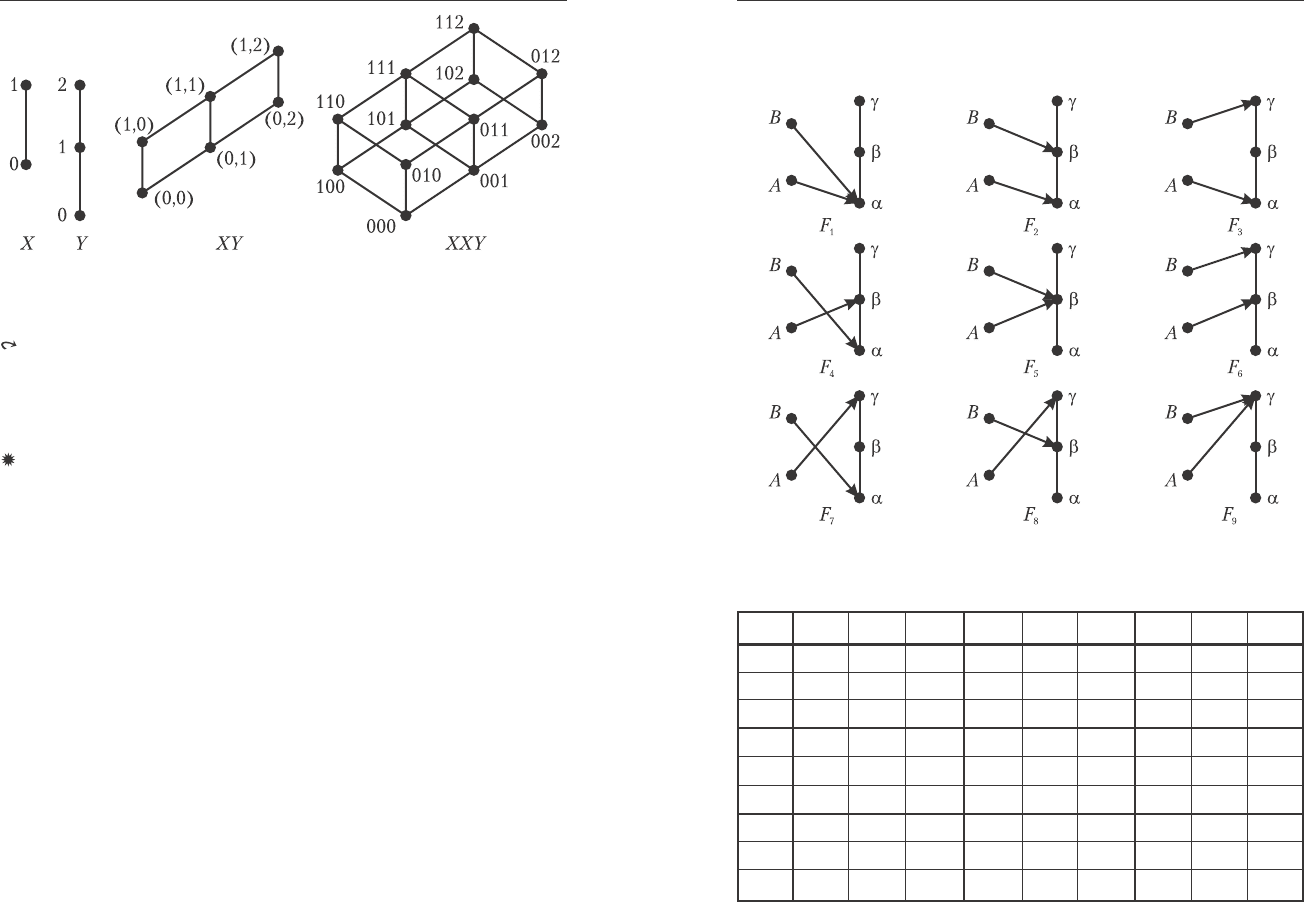
Ïðèìåð. Ïóñòü E={A, B}, L={α, β, γ}. Ìíîæåñòâî

ôóíêöèîíàëüíûõ îòîáðàæåíèé F:E→L èìååò ìîùíîñòü

cardL

=cardL

cardE

=3

=9 (ðèñ. 7.3). Ïåðå÷èñëèì âñå ôóíêöèè

(çàïèñü A/α îçíà÷àåò, ÷òî α  îáðàç ýëåìåíòà A):

={A/α,B/α}, F

={A/α,B/β}, F

={A/α,B/γ},

={A/β,B/α}, F

={A/β,B/β}, F

={A/β,B/γ},

={A/γ,B/α}, F

={A/γ,B/β},F

={A/γ,B/γ}.

Ïóñòü L ={α, β, γ}  öåïü, òîãäà íà L îïðåäåëåíû îïåðàöèè

îáúåäèíåíèÿ ∨ è ïåðåñå÷åíèÿ ∧. Â ýòîì ñëó÷àå íà ìíîæåñòâå âñåõ

ôóíêöèîíàëüíûõ îòîáðàæåíèé L

èíäóöèðóþòñÿ îïåðàöèè ñ òåìè

æå ñâîéñòâàìè. Äëÿ îïåðàöèè ïåðåñå÷åíèÿ èíäóöèðóåòñÿ îïåðàöèÿ

⊗ ñëåäóþùèì îáðàçîì:

⊗ F

={A/α,B/α} ∧ {A/α,B/β}= {A/(α ∧ α), B/(α ∧ β)}=

={A/α, B/α}=F

Âûïîëíÿÿ äàííóþ îïåðàöèþ äëÿ âñåõ F

∈ L

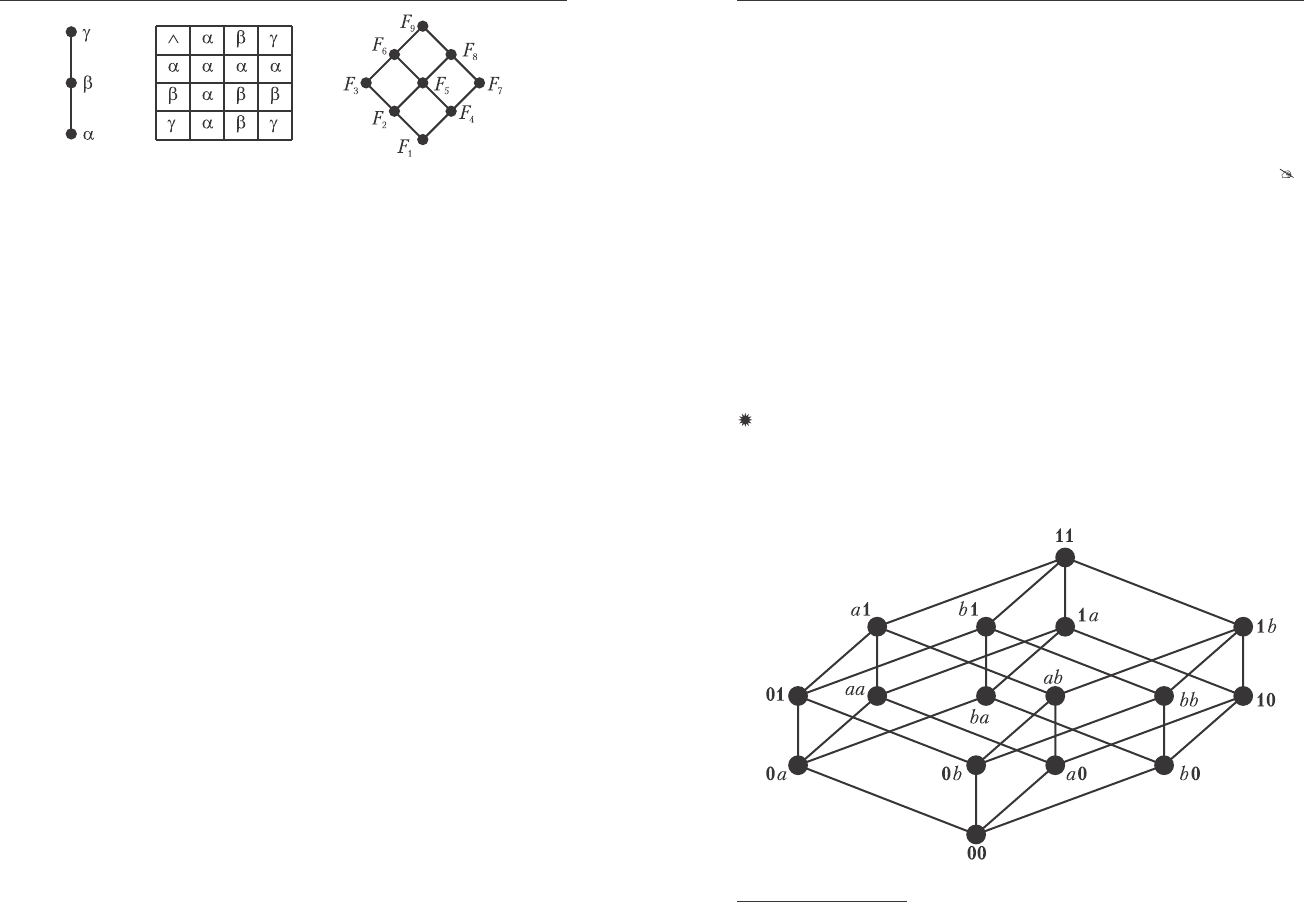
, ïîëó÷àåì òàáëèöó

äëÿ èíäóöèðîâàííîé îïåðàöèè ⊗ â L

(òàáë. 7.1).

Àíàëîãè÷íî ìîæíî ïîëó÷èòü òàáëèöó äëÿ îïåðàöèè ⊕, èíäóöè-

ðóåìîé â L

îïåðàöèåé îáúåäèíåíèÿ ∨ íà L. Âñå ñâîéñòâà îïåðàöèé

∧ è ∨: èäåìïîòåíòíîñòü, êîììóòàòèâíîñòü, àññîöèàòèâíîñòü,

äèñòðèáóòèâíîñòü,  ñîõðàíÿþòñÿ äëÿ èíäóöèðîâàííûõ îïåðàöèé

⊗ è ⊕. (Ïðîâåðèòü âûïîëíèìîñòü ýòèõ çàêîíîâ äëÿ äâóõ èíäóöèðî-

âàííûõ îïåðàöèé ïðåäîñòàâëÿåòñÿ ÷èòàòåëþ.) Â ðåçóëüòàòå ìíî-

æåñòâî âñåõ ôóíêöèîíàëüíûõ îòîáðàæåíèé L

îáðàçóåò ðåøåòêó

(ðèñ. 7.4).

Ðèñ. 7.3. Ìíîæåñòâî ôóíêöèîíàëüíûõ îòîáðàæåíèé.

Òàáëèöà 7.1.

Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê

⊗ F

94 95

Ðèñ. 7.4. Ñòåïåíü ìíîæåñòâ L

Ðàññìîòðåííûé ïðèìåð ïîçâîëÿåò îáîáùèòü ïîëó÷åííûé

ðåçóëüòàò ñëåäóþùåé òåîðåìîé.

Òåîðåìà 7.3. Êàðäèíàëüíàÿ ñòåïåíü L

èíäóöèðóåò íà ìíîæåñòâå

ôóíêöèîíàëüíûõ îòîáðàæåíèé E→L ìíîæåñòâî îïåðàöèé ñ

òåìè æå ñâîéñòâàìè, êîòîðûìè îáëàäàþò îïåðàöèè, îïðåäåëåí-

íûå íà L. Òîãäà

1) åñëè L  ó-ìíîæåñòâî, òî L

 ó-ìíîæåñòâî;

2) åñëè L  íèæíÿÿ/âåðõíÿÿ ïîëóðåøåòêà, òî L

 íèæíÿÿ/âåðõíÿÿ

ïîëóðåøåòêà;

3) åñëè L  ðåøåòêà, òî L

 ðåøåòêà.

Ïðè ýòîì åñëè L  äèñòðèáóòèâíàÿ ðåøåòêà, òî L

 äèñòðèáóòèâíàÿ

ðåøåòêà, åñëè L  áóëåâà ðåøåòêà, òî L

 áóëåâà ðåøåòêà.

Äîêàçàòåëüñòâî.

Ïóíêò 1) âûïîëíåí ïî îïðåäåëåíèþ êàðäèíàëüíîé ñòåïåíè (ñì.

îïðåäåëåíèå 7.3).

2). Ðàññìîòðèì L

, ãäå Lèìååò ñòðóêòóðó ∨-ïîëóðåøåòêè. Ïîëî-

æèì x

, x

, y

∈ L, A

, , A

∈ E. Ïóñòü F

={A

,, A

={A

,, A

}, F

={A

,, A

}. Òîãäà äëÿ ëþáûõ äâóõ

ýëåìåíòîâ F

, F

∈ L

ýëåìåíò {A

/(x

∨x

),, A

/(y

∨ y

)} áóäåò

âåðõíåé ãðàíüþ ýòîé ïàðû. Ëþáàÿ äðóãàÿ âåðõíÿÿ ãðàíü <u, v>

îáîèõ ýëåìåíòîâ <x

, y

> è <x

, y

> óäîâëåòâîðÿåò íåðàâåíñòâàì

u≥x

, v≥y

(i=1, 2), è çíà÷èò, ïî îïðåäåëåíèþ âåðõíåé ãðàíè,

u≥x

∨x

è v≥y

∨y

, òàê ÷òî <u, v> ≥ <x

∨x

, y

∨y

>. Ýòî

ïîêàçûâàåò, ÷òî {A

/(x

∨x

),, A

/(y

∨ y

)}={A

,.., A

}∨

∨{A/x

,.., A

}, îòêóäà ñëåäóåò, ÷òî îáúåäèíåíèå F

∨ F

ñóùåñòâóåò.

Ñëåäîâàòåëüíî, L

 ∨-ïîëóðåøåòêà.

Äâîéñòâåííî: F

∧ F

= {A

/(x

∧x

),, A

/(y

∧ y

)}=

={A

,..,A

}∧{A/x

,.., A

Ñëåäîâàòåëüíî, åñëè Lèìååò ñòðóêòóðó ðåøåòêè, òî L

 ðåøåòêà.

Ïðîâåðèì äèñòðèáóòèâíîñòü L

, åñëè L  äèñòðèáóòèâíàÿ

ðåøåòêà. Òîãäà

∨ (F

∧ F

)={ A

/(x

∨ (x

∧ x

)), , A

/(y

∨ (y

∧ y

))}=

={A

/((x

∨ x

) ∧ (x

∨ x

)), , A

/((y

∨ y

) ∧ (y

∨ y

))}=

= (F

∨ F

) ∧ (F

∨ F

)  çàêîí äèñòðèáóòèâíîñòè âûïîëíåí.

Ïðåäïîëîæèì, ÷òî L  áóëåâà ðåøåòêà. Ïîëîæèì F

′=

={A

′,, A

′}, ãäå F

′,x

′, y

′  äîïîëíåíèÿ F

,x

, y

ñîîòâåò-

ñòâåííî. Òîãäà F

∧F

′={A

/(x

∧ x

′),, A

/(y

∧ y

′)}=

={A

/0,,A

/0}. Àíàëîãè÷íî, F

∨F

′ = {A

/(x

∨x

′),,A

∨y

′}=

= {A

/I,,A

/I}. Îòîáðàæåíèå F

′ = {A

′,, A

′} ÿâëÿåòñÿ

äîïîëíåíèåì îòîáðàæåíèÿ F

={A

, , A

}. Òàêèì îáðàçîì, L

òàêæå îáëàäàåò ñòðóêòóðîé áóëåâîé ðåøåòêè ñ äîïîëíåíèÿìè.

Ñëåäñòâèå. Åñëè L  îáû÷íûé ïðåäïîðÿäîê, òî L

 îáû÷íûé

ïðåäïîðÿäîê;

Åñëè L èìååò ñòðóêòóðó ïðåäïîðÿäêà, òî â ýòîì ïðåäïîðÿäêå

ìîæíî îïðåäåëèòü ìíîæåñòâî êëàññîâ ýêâèâàëåíòíîñòè è òîãäà ýòè

êëàññû ñàìè ñîáîé îáðàçóþò ÷àñòè÷íûé èëè ïîëíûé ïîðÿäîê.

Óäàëÿÿ òðàíçèòèâíî çàìûêàþùèå äóãè íà ãðàôå êëàññîâ ýêâèâà-

ëåíòíîñòè, ïîëó÷èì äèàãðàììó Õàññå. Íàïðèìåð, åñëè êëàññû

ýêâèâàëåíòíîñòè ïðåäïîðÿäêà îáðàçóþò âåðõíþþ ïîëóðåøåòêó, òî

òàêæå îáðàçóåò âåðõíþþ ïîëóðåøåòêó äëÿ êëàññîâ ýêâèâàëåíò-

íîñòè, â êîòîðûõ òàêæå âûïîëíÿåòñÿ îòíîøåíèå ïðåäïîðÿäêà.

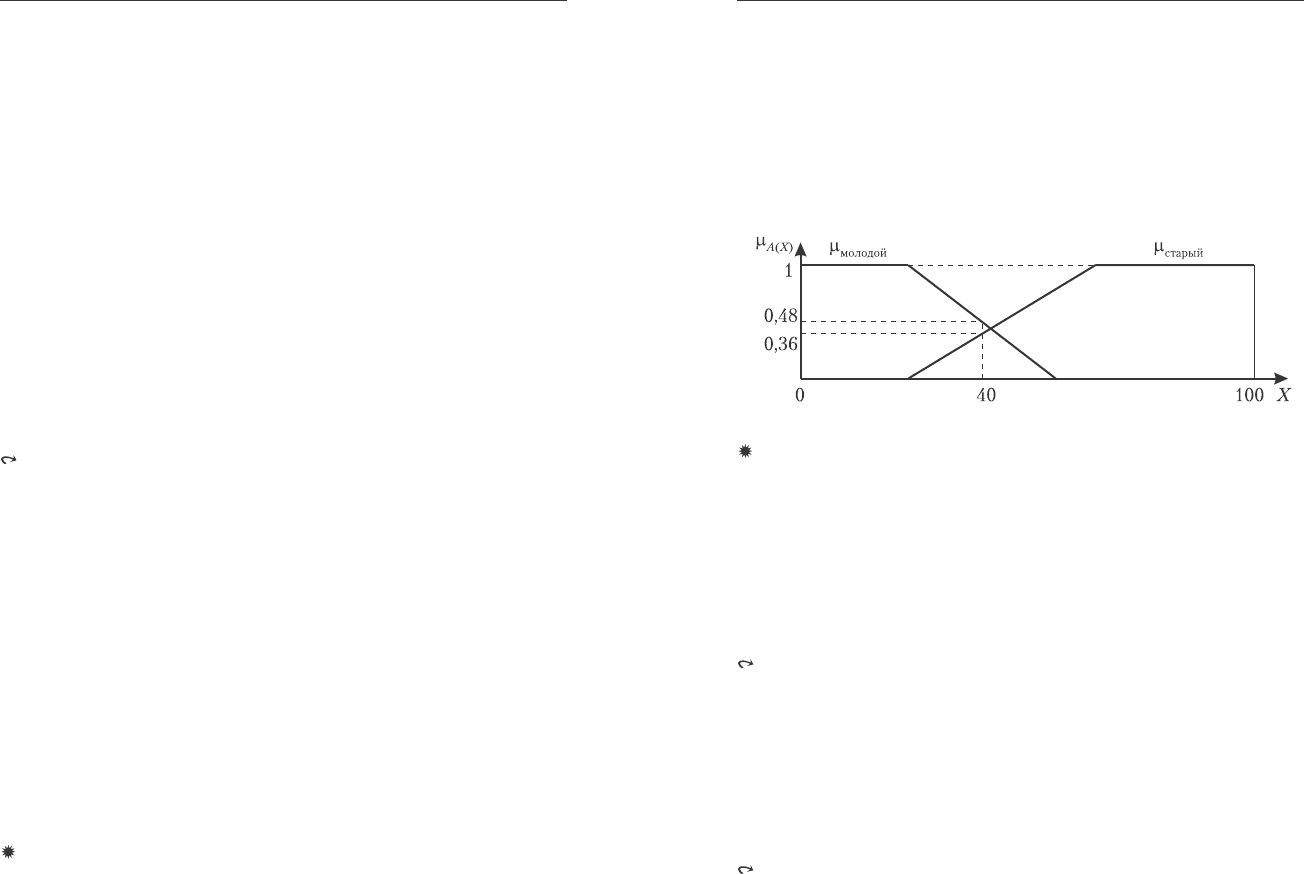
Ïðèìåð. Ïóñòü E={A, B} è L={0, a, b, 1}èìååò ñòðóêòóðó áóëåâîé

ðåøåòêè ñ íóëåì 0 è åäèíèöåé 1. Ñòðóêòóðà ôóíêöèîíàëüíûõ îòîáðàæåíèé

äëÿ L

èçîáðàæåíà íà ðèñ.7.5. Îíà èìååò cardL

=cardL

cardE

=4

=16

ýëåìåíòîâ

. Íà ðèñóíêå îáîçíà÷åíèå xy  ýòî îòîáðàæåíèå {A/x, B/y},

íàïðèìåð: 00  {A/0, B/0}, ab  {A/a, B/b} è. ò.ä.

Ðèñ. 7.5. Ðåøåòêà ôóíêöèîíàëüíûõ îòîáðàæåíèé 4

Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê

Äèàãðàììû Õàññå äëÿ 16-ýëåìåíòíûõ áóëåâûõ ðåøåòîê 2

×2

, 2

, 4

, (2

)

èìåþò îäèíàêîâóþ ñòðóêòóðó, íî ðàçëè÷àþòñÿ ñâîèìè ýëåìåíòàìè.

96 97

Ïóñòü òåïåðü L={0, a, b, 1}  öåïü, E={A, B}. Òîãäà L

òàêæå

èìååò 16 ýëåìåíòîâ, äèàãðàììà åãî ñîâïàäàåò ñ äèàãðàììîé äèñòðè-

áóòèâíîé âåêòîðíîé ðåøåòêè, ïðåäñòàâëåííîé íà ðèñ 7.1. Ðàçëè÷èå

çàêëþ÷àåòñÿ â òîì, ÷òî ñàìè ýëåìåíòû ðåøåòêè èìåþò äðóãîé ñìûñë.

Äëÿ äèàãðàììû L

îáîçíà÷åíèå xy íà ðèñóíêå ñëåäóåò ïîíèìàòü

êàê ôóíêöèîíàëüíîå îòîáðàæåíèå {A/x, B/y}, íàïðèìåð, a0 åñòü

îáîçíà÷åíèå äëÿ {A/a, B/0} è ò.ä. Ïîëó÷åííàÿ ðåøåòêà L

ÿâëÿåòñÿ

îáîáùåíèåì íå÷åòêîãî ìíîæåñòâà ïåðâîãî óðîâíÿ â ñìûñëå Çàäå.

7.3. Íå÷åòêèå ìíîæåñòâà

7.3.1. Îñíîâíûå ïîíÿòèÿ

Ðàññìîòðèì êîíå÷íîå ìíîæåñòâî E={x

, x

,..., x

} è L={0,1}.

Òîãäà L

=2

åñòü ìíîæåñòâî âñåõ õàðàêòåðèñòè÷åñêèõ ôóíêöèé

ïîäìíîæåñòâ ìíîæåñòâà E, âêëþ÷àÿ ∅, è îíî îáðàçóåò áóëåâó

ðåøåòêó. Ýëåìåíòàìè ýòîé ðåøåòêè áóäóò õàðàêòåðèñòè÷åñêèå âåê-

òîðà ïîäìíîæåñòâ ìíîæåñòâà E (ñì. ï. 4.6 ãëàâû 4). Êàæäûé ýëåìåíò

õàðàêòåðèñòè÷åñêîãî âåêòîðà ïîêàçûâàåò, ïðèíàäëåæèò ëè äàííûé

ýëåìåíò ìíîæåñòâà E äàííîìó ïîäìíîæåñòâó, èëè íåò. Îäíàêî, êàê

ìû ïîêàçàëè âûøå, ìíîæåñòâî Eìîæíî îòîáðàçèòü â ëþáóþ ðåøåò-

êó. Òîãäà ìû ïðèõîäèì ê íîâîìó ïîíÿòèþ.

Îïðåäåëåíèå 7.4. Ïóñòü E  óíèâåðñàëüíîå ìíîæåñòâî è L 

ðåøåòêà. Ïóñòü α∈L. Íå÷åòêîå ïîäìíîæåñòâî A ⊆ E, èëè, ÷òî

ýêâèâàëåíòíî, A∈L

, ýòî òàêîå ïîäìíîæåñòâî, ÷òî êàæäîìó

ýëåìåíòó x∈E ìîæíî ïîñòàâèòü â ñîîòâåòñòâèå ýëåìåíò α∈L.

Ýòè ýëåìåíòû îáîçíà÷àþò µ

(x) è íàçûâàþò ôóíêöèåé ïðèíàä-

ëåæíîñòè.

Â ñëó÷àå, åñëè ðåøåòêà L åñòü çàìêíóòûé èíòåðâàë [0, 1] íà

ìíîæåñòâå äåéñòâèòåëüíûõ ÷èñåë, ïðåäñòàâëÿþùèé ñîáîé öåïü,

âîçâåäåíèå åãî â ñòåïåíü ïðîèçâîëüíîãî ìíîæåñòâà E äàåò ìíîæåñòâî

íå÷åòêèõ ïîäìíîæåñòâ â ñìûñëå Çàäå. Òîãäà ôóíêöèÿ ïðèíàäëåæ-

íîñòè µ

(x) ïðèíèìàåò çíà÷åíèÿ èç èíòåðâàëà [0,1] è îïðåäåëÿåò

ñòåïåíü, ñ êîòîðîé ýëåìåíò x ïðèíàäëåæèò íå÷åòêîìó ìíîæåñòâó

A. Â ÷àñòíîñòè, åñëè µ

(x)=0, òî ýëåìåíò x íå ïðèíàäëåæèò íå÷åò-

êîìó ìíîæåñòâó A, åñëè µ

(x)=1, òî ýëåìåíò x ïðèíàäëåæèò íå÷åò-

êîìó ìíîæåñòâó A ñî ñòåïåíüþ 1, åñëè µ

(x)=0,6, òî ýëåìåíò x

ïðèíàäëåæèò íå÷åòêîìó ìíîæåñòâó A ñî ñòåïåíüþ 0,6 è ò.ä.

Òàêèì îáðàçîì, íå÷åòêîå ìíîæåñòâî â ñìûñëå Çàäå åñòü îòîáðà-

æåíèå [0, 1]

: E→[0,1].

Ïðèìåð 1. Ïóñòü ìíîæåñòâî E åñòü ìíîæåñòâî ÷èñåë, îáîçíà÷à-

þùèõ âîçðàñò ÷åëîâåêà, íàïðèìåð, â ïðåäåëàõ îò 0 äî 100. Ðàññìîò-

ðèì òàêèå ïîíÿòèÿ, êàê ìîëîäîé è ñòàðûé. Î÷åâèäíî, òðóäíî óñòàíî-

âèòü êàêóþ-òî òî÷íóþ ãðàíèöó, ãäå êîí÷àåòñÿ âîçðàñò ìîëîäîñòè è

íàñòóïàåò âîçðàñò ñòàðîñòè. Ìû ìîæåì óêàçàòü ýòè ãðàíèöû ïðèá-

ëèçèòåëüíî, è, îïðîñèâ, íàïðèìåð, íåêîòîðîå êîëè÷åñòâî ëþäåé,

óñòàíîâèòü, ñ êàêîé ñòåïåíüþ ìîæíî îòíåñòè òîò èëè èíîé âîçðàñò

ê êàòåãîðèè ìîëîäîé èëè ñòàðûé. Ðåçóëüòàòû ýòèõ îïðîñîâ ìîæíî

áóäåò èçîáðàçèòü â âèäå ãðàôèêîâ ôóíêöèé ïðèíàäëåæíîñòè µ

ìîëîäîé

è µ

ñòàðûé

(ðèñ. 7.6). Çíà÷åíèÿ ôóíêöèè ïðèíàäëåæíîñòè èç èíòåðâàëà

[0,1] ïîêàçûâàþò, ñ êàêîé ñòåïåíüþ òîò èëè èíîé âîçðàñò ïðèíàä-

ëåæèò âîçðàñòó ìîëîäûõ èëè ñòàðûõ. Íàïðèìåð, âîçðàñò 40ëåò ñî

ñòåïåíüþ 0,48 îòíåñåí ê ïîíÿòèþ ìîëîäîé è ñî ñòåïåíüþ 0,36  ê

ïîíÿòèþ ñòàðûé.

Ðèñ. 7.6. Ôóíêöèè ïðèíàäëåæíîñòè íå÷åòêèõ ìíîæåñòâ.

Ïðèìåð 2. Ïóñòü E={a, b, c}, è ïóñòü A, B∈ [0, 1]

: A={a/0,2,

b/0,6, c/0,8}, B={a/0,1, b/0,4, c/0,9}  äâà íå÷åòêèõ ìíîæåñòâà.

Ýëåìåíò a ïðèíàäëåæèò ìíîæåñòâó A ñî ñòåïåíüþ 0,2, ìíîæåñòâó

B ñî ñòåïåíüþ 0,1, è ò.ä.

Ïðèâåäåííîå âûøå îïðåäåëåíèå 7.4 ÿâëÿåòñÿ îáîáùåíèåì

ïîíÿòèÿ íå÷åòêîãî ìíîæåñòâà, ââåäåííîãî Çàäå. Ðàññìîòðèì îáîá-

ùåíèå ñâîéñòâ íå÷åòêèõ ìíîæåñòâ è îïåðàöèé íà íèõ, åñëè L

ðåøåòêà.

7.3.2. Îïåðàöèè íàä íå÷åòêèìè ìíîæåñòâàìè

Îïðåäåëåíèå 7.5. Åñëè ≤  îòíîøåíèå ïîðÿäêà íà ðåøåòêå L,E

íåêîòîðîå ìíîæåñòâî, A ∈L

, B ∈L

 íå÷åòêèå ìíîæåñòâà, òî

ãîâîðÿò, ÷òî A âêëþ÷åíî â B (A ⊆ B), åñëè

∀x

∈ E:µ

)≤µ

Òàêèì îáðàçîì, äâà íå÷åòêèõ ìíîæåñòâà ñðàâíèìû, åñëè ñðàâ-

íèìû ñîîòâåòñòâóþùèå çíà÷åíèÿ ôóíêöèé ïðèíàäëåæíîñòè è

ìåæäó äâóìÿ íå÷åòêèìè ïîäìíîæåñòâàìè ñóùåñòâóåò îòíîøåíèå

äîìèíèðîâàíèÿ. Íàïðèìåð, åñëè A={a/0,2, b/0,6, c/0,8},

B={a/0,3, b/0,8, c/0,9}, òî A⊂B.

Îïðåäåëåíèå 7.6. Äâà íå÷åòêèõ ìíîæåñòâà A è B ðàâíû òîãäà è

òîëüêî òîãäà, êîãäà

∀x

∈ E: µ

) = µ

Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê

98 99

Ïîíÿòèå äîïîëíåíèÿ â òåîðèè íå÷åòêèõ ìíîæåñòâ Çàäå è â

òåîðèè ðåøåòîê  ðàçíûå. Â ñëó÷àå, åñëè L  áóëåâà ðåøåòêà, L



òàêæå áóëåâà ðåøåòêà. Òîãäà äîïîëíåíèå íå÷åòêîãî ìíîæåñòâà A

îïðåäåëÿåòñÿ êàê íå÷åòêîå ìíîæåñòâî B, òàêîå ÷òî

∀x

∈ E: µ

) ∧µ

)=0 è µ

) ∨ µ

) =I,

ãäå 0  íóëü, à I  åäèíèöà áóëåâîé ðåøåòêè L.

Ó÷èòûâàÿ, ÷òî íå âñå ðåøåòêè èìåþò äîïîëíåíèÿ ñâîèõ

ýëåìåíòîâ, è, â ÷àñòíîñòè ðåøåòêà [0,1] íå èìååò äîïîëíåíèé, äëÿ

íå÷åòêèõ ìíîæåñòâ â ñìûñëå Çàäå ââîäèòñÿ ïñåâäîäîïîëíåíèå,

êîòîðîå íàçûâàþò äîïîëíåíèåì.

Îïðåäåëåíèå 7.7. Äîïîëíåíèå íå÷åòêîãî ìíîæåñòâà A∈[0,1]

åñòü íå÷åòêîå ïîäìíîæåñòâî B ñî çíà÷åíèÿìè ôóíêöèè

ïðèíàäëåæíîñòè, òàêèìè ÷òî

∀x

∈ E: µ

) =1 µ

Íàïðèìåð, åñëè A={a/0,2, b/0,6, c/0,8}, òî äîïîëíåíèå A 

íå÷åòêîå ìíîæåñòâî B={a/0,8, b/0,4, c/0,2}.

Îïðåäåëåíèå 7.8. Îïåðàöèÿ ïåðåñå÷åíèÿ íà ðåøåòêå L èíäó-

öèðóåò îïåðàöèþ ïåðåñå÷åíèÿ íå÷åòêèõ ìíîæåñòâ êàê

∀x

∈ E: µ

A∩B

) =µ

)∧µ

Äëÿ íå÷åòêèõ ìíîæåñòâ â ñìûñëå Çàäå ýòî îïðåäåëåíèå ñîâïàäàåò ñ

A∩B

) =min{µ

), µ

)}.

Íàïðèìåð, åñëè A={a/0,2, b/0,6, c/0,8}, B={a/0,1, b/0,4, c/0,9},

òî A ∩ B = {a/0,1, b/0,4, c/0,8}.

Îïðåäåëåíèå 7.9. Îïåðàöèÿ îáúåäèíåíèÿ íà ðåøåòêå L èíäóöè-

ðóåò îïåðàöèþ îáúåäèíåíèÿ íå÷åòêèõ ìíîæåñòâ êàê

∀x

∈ E: µ

A∪B

) =µ

)∨µ

Äëÿ íå÷åòêèõ ìíîæåñòâ â ñìûñëå Çàäå ýòî îïðåäåëåíèå ñîâïàäàåò ñ

A∪B

) = max{µ

),µ

)}.

Íàïðèìåð, åñëè A={a/0,2, b/0,3, c/0,8}, B={a/0,1, b/0,4, c/0,9},

òî A ∪ B = {a/0,2, b/0,4, c/0,9}.

Òàêèì îáðàçîì, åñëè L îáëàäàåò ñòðóêòóðîé äèñòðèáóòèâíîé

ðåøåòêè ñ îïåðàöèÿìè ∧ è ∨, â ÷àñòíîñòè, ïðåäñòàâëÿåò ñîáîé èíòåð-

âàë [0,1]⊂R, òî ñòåïåíü L

èíäóöèðóåò òàêæå äèñòðèáóòèâíóþ

âåêòîðíóþ ðåøåòêó îòíîñèòåëüíî îïåðàöèé ∩ è ∪ â ìíîæåñòâå

íå÷åòêèõ ïîäìíîæåñòâ.

Äëÿ íå÷åòêèõ ìíîæåñòâ â ñìûñëå Çàäå ìîæíî òàêæå îïðåäåëèòü

ñëåäóþùèå îïåðàöèè.

Îïðåäåëåíèå 7.10. Àëãåáðàè÷åñêîå ïðîèçâåäåíèå íå÷åòêèõ ìíî-

æåñòâ A è B (îáîçíà÷àåòñÿ AB) îïðåäåëÿåòñÿ êàê àðèôìåòè÷åñêîå

ïðîèçâåäåíèå èõ ôóíêöèé ïðèíàäëåæíîñòè:

(x) = µ

(x) µ

(x).

Îïðåäåëåíèå 7.11. Àëãåáðàè÷åñêàÿ ñóììà íå÷åòêèõ ìíîæåñòâ A

è B (îáîçíà÷àåòñÿ A + B) îïðåäåëÿåòñÿ êàê

A+B

(x)=µ

(x) + µ

(x)  µ

(x) µ

(x),

ãäå + è  åñòü îïåðàöèè àðèôìåòè÷åñêîãî ñëîæåíèÿ è âû÷èòàíèÿ

ñîîòâåòñòâåííî.

Îïåðàöèè êàðäèíàëüíîé ñòåïåíè è ïðîèçâåäåíèÿ ìíîæåñòâ

îáëàäàþò ñëåäóþùèìè ñâîéñòâàìè:

×E

)

=E

×E

)

=E

E2 × E3

Ýòè ñâîéñòâà ïîçâîëÿþò ïîëó÷èòü íåêîòîðûå íîâûå äîïîëíè-

òåëüíûå îáîáùåíèÿ è ðåçóëüòàòû. Ðàññìîòðèì ñòåïåíü ïðîèçâåäå-

íèÿ ìíîæåñòâ, íàïðèìåð, (L

×L

)

, ãäå L

,L

 ðåøåòêè (ïîëóðå-

øåòêè). Òîãäà L

×L

òàêæå îáëàäàåò ñòðóêòóðîé ðåøåòêè (ïîëóðå-

øåòêè), à ìíîæåñòâî (L

×L

)

 ìíîæåñòâî íå÷åòêèõ ïîäìíîæåñòâ

ñ äâóìåñòíîé ôóíêöèåé ïðèíàäëåæíîñòè. Íàïðèìåð, åñëè L

={a,b,c}

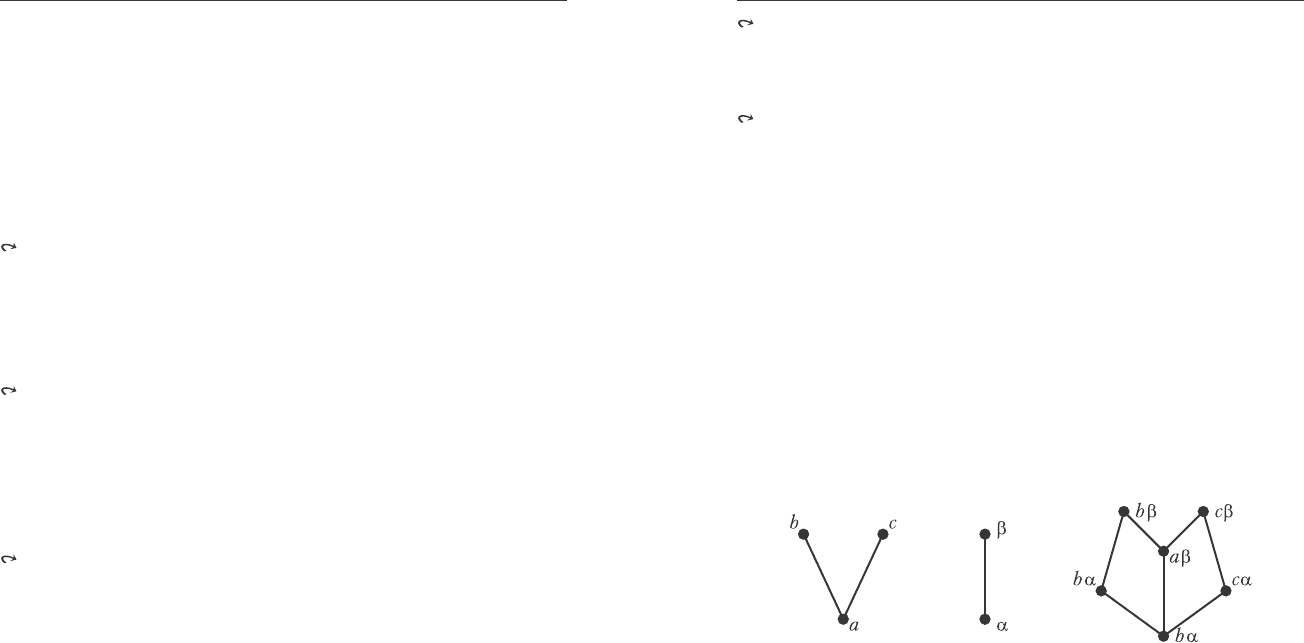
íèæíÿÿ ïîëóðåøåòêà, L

= {α, β}  ðåøåòêà 2, òî L

×L

òàêæå

îáëàäàåò ñòðóêòóðîé íèæíåé ïîëóðåøåòêè (ðèñ.7.7).

Ðèñ. 7.7. Ïðîèçâåäåíèå L

× L

Âîçüìåì ìíîæåñòâî E={A, B, C} è âîçâåäåì ïîëó÷åííóþ

ñòðóêòóðó L

×L

â ñòåïåíü E. Òîãäà: (L

×L

)

èìååò 6

=218

ýëåìåíòîâ, êîòîðûå îáðàçóþò ìíîæåñòâî íå÷åòêèõ ïîäìíîæåñòâ,

èìåþùåå ñòðóêòóðó íèæíåé ïîëóðåøåòêè ñ ýëåìåíòàìè: {A/(x

,y

B/(x

,y

), C/(x

,y

)}, ãäå x

=a, b, c; i=1, 2, 3; y

=α, β; j=1, 2.

Ïðåäïîëîæèì, ÷òî µ

) ïðèíèìàåò ñâîè çíà÷åíèÿ â L

i=1,2,...,n, òàê ÷òî êàæäîåx

i

∈L

. Òîãäà ìíîæåñòâî íå÷åòêèõ

ïîäìíîæåñòâ ìîæíî çàïèñàòü êàê

{} {}

{}

...

LL L

×××

, (*)

ãäå {x

} (i=1, ..., n)  îáû÷íûå îäíîòî÷å÷íûå ïîäìíîæåñòâà E. Òîãäà

ëþáîé ýëåìåíò âèäà (*) íàçûâàåòñÿ íå÷åòêèì íåîäíîðîäíûì

Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê