Таран Т.А. Основы дискретной математики

Подождите немного. Документ загружается.

Ãëàâà 5. ÎÒÍÎØÅÍÈÅ ÏÎÐßÄÊÀ

5.1. Îñíîâíûå îïðåäåëåíèÿ

Îïðåäåëåíèå 5.1. Îòíîøåíèå íà ìíîæåñòâå P, óäîâëåòâîðÿþùåå

ñâîéñòâàì

ðåôëåêñèâíîñòè: x ≤ x äëÿ âñåõ x, Ð1.

àíòèñèììåòðè÷íîñòè:

åñëè x ≤ y è y ≤ x, òî x = y äëÿ âñåõ x, y, Ð2.

òðàíçèòèâíîñòè:

åñëè x ≤ y è y ≤ z, òî x ≤ z äëÿ âñåõ x, y, z Ð3.

íàçûâàåòñÿ îòíîøåíèåì ïîðÿäêà.

Ñâîéñòâà, êîòîðûì óäîâëåòâîðÿåò ýòî îòíîøåíèå, ïðèâîäèò ê

ïîíÿòèþ óïîðÿäî÷åííîãî ìíîæåñòâà.

Îïðåäåëåíèå 5.2. Íåïóñòîå ìíîæåñòâî P, íà êîòîðîì çàäàíî

áèíàðíîå îòíîøåíèå ïîðÿäêà, óäîâëåòâîðÿþùåå ñâîéñòâàì P1,

P2, P3, íàçûâàåòñÿ ÷àñòè÷íî óïîðÿäî÷åííûì ìíîæåñòâîì.

Îòíîøåíèå ïîðÿäêà

óñëîâèìñÿ îáîçíà÷àòü ñèìâîëîì ≤, õîòÿ

äàëåêî íå âñåãäà ýòîò ñèìâîë áóäåò îáîçíà÷àòü îòíîøåíèå «ìåíüøå

èëè ðàâíî», îïðåäåëåííîå íà ìíîæåñòâå ÷èñåë. Çàïèñü x ≥ y áóäåò

îçíà÷àòü, ÷òî y ≤ x. Ïîñêîëüêó ñâîéñòâà P1, P2, P3 çàäàþò íàèáîëåå

îáùèé òèï ïîðÿäêà, ÷àñòè÷íî óïîðÿäî÷åííîå ìíîæåñòâî íàçûâàþò

ïðîñòî óïîðÿäî÷åííûì, èëè ó-ìíîæåñòâîì, â îòëè÷èå îò ëèíåéíî è

ñòðîãî óïîðÿäî÷åííûõ ìíîæåñòâ, êîòîðûå áóäóò îïðåäåëåíû íèæå.

Óïîðÿäî÷åííîå ìíîæåñòâî P ÷àñòî îáîçíà÷àþò â âèäå äâîéêè <P,

≤>. Îäíîýëåìåíòíîå ìíîæåñòâî ñ÷èòàåòñÿ ó-ìíîæåñòâîì.

Åñëè <P, ≤>  ó-ìíîæåñòâî è a, b∈ P, òî a è b íàçûâàþòñÿ

ñðàâíèìûìè ýëåìåíòàìè, åñëè a≤b èëè b ≤ a. Â ïðîòèâíîì ñëó÷àå

îíè íàçûâàþòñÿ íåñðàâíèìûìè. Íåñðàâíèìûå ýëåìåíòû áóäåì

îáîçíà÷àòü a||b. Â ÷àñòè÷íî óïîðÿäî÷åííûì ìíîæåñòâå åñòü êàê

ñðàâíèìûå, òàê è íåñðàâíèìûå ýëåìåíòû.

Îïðåäåëåíèå 5.3. Åñëè x ≤ y è x ≠ y, òî îòíîøåíèå íàçûâàåòñÿ

îòíîøåíèåì ñòðîãîãî ïîðÿäêà è îáîçíà÷àåòñÿ x < y.

Îòíîøåíèå ñòðîãîãî ïîðÿäêà íå ÿâëÿåòñÿ ðåôëåêñèâíûì: â

ëþáîì ñòðîãî óïîðÿäî÷åííîì ìíîæåñòâå íè äëÿ êàêîãî õ íå èìååò

ìåñòà ñîîòíîøåíèå õ < õ. Äëÿ îòíîøåíèÿ < âûïîëíèìî ñâîéñòâî

àñèììåòðè÷íîñòè: åñëè x < y, òî íå âûïîëíÿåòñÿ y < x. Âî âñåõ

ñëó÷àÿõ, êîãäà ðàçëè÷èå ìåæäó ñòðîãèì è íåñòðîãèì ïîðÿäêîì íå

èìååò ïðèíöèïèàëüíîãî çíà÷åíèÿ, ìû áóäåì ïîëüçîâàòüñÿ îáîçíà-

÷åíèåì ≤.

Îïðåäåëåíèå 5.4. Ó-ìíîæåñòâî <P, ≤ >, óäîâëåòâîðÿþùåå ñâîé-

ñòâó ëèíåéíîñòè:

íåîòðèöàòåëüíûõ ðàöèîíàëüíûõ ÷èñåë ÿâëÿåòñÿ ëèíåéíûì ïîðÿä-

êîì, íî íå ÿâëÿåòñÿ âïîëíå óïîðÿäî÷åíèåì, ýòî ìíîæåñòâî íå

èìååò íàèìåíüøåãî ýëåìåíòà. Àíàëîãè÷íî, ìíîæåñòâî öåëûõ ÷èñåë

ëèíåéíî óïîðÿäî÷åíî îòíîøåíèåì «ìåíüøå», íî íå âïîëíå óïîðÿäî-

÷åíî, òàê êàê íå èìååò íàèìåíüøåãî ýëåìåíòà.

Àêñèîìà âûáîðà ýêâèâàëåíòíà ïðèíöèïó ïîëíîãî óïîðÿäî÷åíèÿ,

ñîãëàñíî êîòîðîìó âñÿêîå ìíîæåñòâî ìîæåò áûòü âïîëíå óïîðÿäî-

÷åíî. Íàïðèìåð, ïåðåñ÷åò, ïîñòðîåííûé íàìè ïðè äîêàçàòåëüñòâå

ñ÷åòíîñòè ìíîæåñòâà íåîòðèöàòåëüíûõ ðàöèîíàëüíûõ ÷èñåë, âïîëíå

óïîðÿäî÷èâàåò ýòî ìíîæåñòâî (íå ïî âåëè÷èíå ÷èñåë, à â ïîðÿäêå

èõ ïåðåñ÷åòà). Îäíàêî ïî âîïðîñó î çàêîííîñòè ýòîãî ïðèíöèïà

âîçíèêëà ñåðüåçíàÿ ïîëåìèêà. Íàïðèìåð, Áèðêãîô ïèøåò: «Ýòî

âåäåò ê âåñüìà ñïåöèôè÷åñêîìó çàêëþ÷åíèþ î òîì, ÷òî R ìîæíî

âïîëíå óïîðÿäî÷èòü, à ýòî, ïî-âèäèìîìó, íåâîçìîæíî ñäåëàòü â

êàêîì-íèáóäü êîíñòðóêòèâíîì ñìûñëå Íèêîìó äî ñèõ ïîð íå

óäàëîñü «ïîñòðîèòü» êàêóþ-íèáóäü ÿâíî çàäàííóþ ôóíêöèþ, êîòî-

ðàÿ áû âïîëíå óïîðÿäî÷èâàëà íåñ÷åòíîå ìíîæåñòâî; ìû ñîâåðøåííî

íå ïðåäñòàâëÿåì ñåáå, êàê «âûãëÿäèò» íåñ÷åòíîå âïîëíå óïîðÿäî-

÷åííîå ìíîæåñòâî. Ïðîáëåìà «êîíñòðóêòèâíîãî» âïîëíå óïîðÿäî÷å-

íèÿ íåñ÷åòíîãî ìíîæåñòâà ÿâëÿåòñÿ îñíîâíîé ïðîáëåìîé òåîðèè

ìíîæåñòâ.» [Áèðêãîô, 1984. Ñ. 172273].

Ãëàâà 4

62 63

∀x∈A (à ≤ õ), à áóêâà ÿ, ïîñëåäíÿÿ áóêâà â àëôàâèòå, «áîëüøå»

âñåõ îñòàëüíûõ, ò.å. ∀x∈A (x ≤ ÿ).

5.Íà ìíîæåñòâå öåëûõ ïîëîæèòåëüíûõ ÷èñåë Z

ìîæíî çàäàòü

îòíîøåíèå ïîðÿäêà, òàêîå, ÷òî x≤ y îçíà÷àåò: «x äåëèòñÿ íà y».

Åãî ìîæíî îïðåäåëèòü êàê x/y=k, ãäå k∈N. Ýòî îòíîøåíèå ðå-

ôëåêñèâíî: x/x= 1, è 1∈N; àíòèñèììåòðè÷íî: åñëè x/y=k è

y/x=k, òî x/y=y/x, îòñþäà x = y; òðàíçèòèâíî: åñëè x/y=k

y/z= k

, òî x/z =k

, ãäå k

, k

∈ N. Äåéñòâèòåëüíî, åñëè x= k

y è

y=k

z, òî x= k

z, ò.å. x=k

z, ãäå k

= k

. Ñîâåðøåííî î÷åâèäíî,

÷òî íå âñÿêèå äâà öåëûå ÷èñëà x, y ∈ Z

íàõîäÿòñÿ â îòíîøåíèè

ïîðÿäêà «x äåëèòñÿ íà y», ñëåäîâàòåëüíî, ýòî îòíîøåíèå ÷àñòè÷íîãî

ïîðÿäêà. Òàêèì îáðàçîì, ìíîæåñòâî Z

ÿâëÿåòñÿ ëèíåéíî óïîðÿäî-

÷åííîì ìíîæåñòâîì ïî îòíîøåíèþ ≤ (ìåíüøå èëè ðàâíî), è ÿâëÿåò-

ñÿ ÷àñòè÷íî óïîðÿäî÷åííûì ïî îòíîøåíèþ «x äåëèòñÿ íà y».

5.2. Ñâîéñòâà ó-ìíîæåñòâ

Îïðåäåëåíèå 5.5. Ïîðÿäêîì n(P) ó-ìíîæåñòâà P íàçûâàåòñÿ

(êàðäèíàëüíîå) ÷èñëî åãî ýëåìåíòîâ. Åñëè ýòî ÷èñëî êîíå÷íî,

Ð íàçûâàåòñÿ êîíå÷íûì ó-ìíîæåñòâîì.

Îïðåäåëåíèå 5.6. Åñëè â ó-ìíîæåñòâå P ñóùåñòâóåò åäèíñòâåí-

íûé ýëåìåíò à∈P, òàêîé ÷òî ∀x∈P(à ≤ õ), òî à íàçûâàåòñÿ

íàèìåíüøèì ýëåìåíòîì ó-ìíîæåñòâà.

Ìîæíî ïîêàçàòü, ÷òî ó-ìíîæåñòâî Ð ìîæåò ñîäåðæàòü òîëüêî

îäèí íàèìåíüøèé ýëåìåíò a. Ýòî ñëåäóåò èç îïðåäåëåíèÿ: ýëåìåíò

a òàêîâ, ÷òî âñå îñòàëüíûå ýëåìåíòû ìíîæåñòâà P «áîëüøå» a. Ïî-

ýòîìó, åñëè ïðåäïîëîæèòü, ÷òî a è b  äâà íàèìåíüøèõ ýëåìåíòà,

òî a ≤ b, è, îäíîâðåìåííî, b≤ a, îòêóäà ñëåäóåò, ÷òî a=b, ò.å. ýòî

îäèí è òîò æå ýëåìåíò. Ñëåäîâàòåëüíî, íàèìåíüøèé ýëåìåíò ó-

ìíîæåñòâà, åñëè îí ñóùåñòâóåò, âñåãäà åäèíñòâåííûé. Åãî íàçûâàþò

íóëåì ó-ìíîæåñòâà è îáîçíà÷àþò ñèìâîëîì 0.

Îïðåäåëåíèå 5.7. Åñëè â ó-ìíîæåñòâå P ñóùåñòâóåò åäèíñòâåí-

íûé ýëåìåíò b∈P, òàêîé ÷òî ∀x∈P(x≤b), òî b íàçûâàåòñÿ

íàèáîëüøèì ýëåìåíòîì ó-ìíîæåñòâà.

Íàèáîëüøèé ýëåìåíò ó-ìíîæåñòâà P, åñëè îí ñóùåñòâóåò, òàêæå

âñåãäà åäèíñòâåííûé. Åãî îáîçíà÷àþò ñèìâîëîì I è íàçûâàþò

åäèíèöåé ó-ìíîæåñòâà.

Îïðåäåëåíèå 5.8. Ó-ìíîæåñòâî P, â êîòîðîì ñóùåñòâóþò

íàèáîëüøèé è íàèìåíüøèé ýëåìåíòû, íàçûâàþò óïîðÿäî÷åí-

íûì ìíîæåñòâîì ñ íóëåì è åäèíèöåé. Òîãäà ∀x∈P (0 ≤ x ≤ I),

ò.å. ëþáîé äðóãîé ýëåìåíò ó-ìíîæåñòâà ëåæèò ìåæäó íóëåì è

åäèíèöåé, ïîýòîìó ýëåìåíòû 0 è I, åñëè îíè ñóùåñòâóþò, íàçûâà-

þòñÿ óíèâåðñàëüíûìè ãðàíÿìè ìíîæåñòâà Ð.

Ãëàâà 5

x ≤ y èëè y ≤ x äëÿ âñåõ x, y∈P, P4.

íàçûâàåòñÿ ëèíåéíî óïîðÿäî÷åííûì ìíîæåñòâîì, èëè öåïüþ.

Â öåïè êàæäûå äâà ïðîèçâîëüíî âçÿòûå ýëåìåíòà ñðàâíèìû è

íåò íåñðàâíèìûõ ýëåìåíòîâ. Ó-ìíîæåñòâî, ÿâëÿþùååñÿ öåïüþ,

ìîæíî çàïèñàòü â âèäå: x

≤ x

≤ ... ≤ x

Ó-ìíîæåñòâî, â êîòîðîì âñå ýëåìåíòû íåñðàâíèìû, èíîãäà

íàçûâàþò àíòèöåïüþ.

Ñâîéñòâî àöèêëè÷íîñòè ïîðÿäêà: åñëè x

≤ x

≤ ... ≤ x

≤ x

, òî

=x

=...=x

, íåïîñðåäñòâåííî ñëåäóåò èç ñâîéñòâ òðàíçèòèâíî-

ñòè è àíòèñèììåòðè÷íîñòè.

Öåïüþ C â ó-ìíîæåñòâå P íàçûâàåòñÿ òàêîå åãî íåïóñòîå ïîä-

ìíîæåñòâî, êîòîðîå êàê ó-ìíîæåñòâî ÿâëÿåòñÿ öåïüþ. Öåïü

≤x

≤...≤x

â ó-ìíîæåñòâå P íàçûâàåòñÿ ìàêñèìàëüíîé öåïüþ,

åñëè â íåé îòñóòñòâóþò òðàíçèòèâíî çàìûêàþùèå äóãè. Ýòî îçíà-

÷àåò, ÷òî åñëè x

≤ x

, òî íè äëÿ êàêèõ x

, x

íå ñóùåñòâóåò òàêîãî y,

÷òî x

≤ y ≤ x

Ïðèìåðû.

1.Îòíîøåíèå âêëþ÷åíèÿ x ⊆ y, ò.å. «õ  ïîäìíîæåñòâî ó», çàäàííîå

íà ìíîæåñòâå âñåõ ïîäìíîæåñòâ íåêîòîðîãî ìíîæåñòâà U, åñòü

îòíîøåíèå ÷àñòè÷íîãî ïîðÿäêà. Äåéñòâèòåëüíî, ýòî îòíîøåíèå

ðåôëåêñèâíî: x⊆x, àíòèñèììåòðè÷íî: åñëè x ⊆ y è y ⊆ x, òî x = y,

è òðàíçèòèâíî: åñëè x ⊆ y è y ⊆ z, òî x ⊆ z. Ïóñòü äàíî ìíîæåñòâî

A={a, b, c}. Ìíîæåñòâî-ñòåïåíü <℘(A), ⊆ >  ÷àñòè÷íî óïîðÿäî-

÷åííîå ìíîæåñòâî. Ïîäìíîæåñòâî ∅ ⊆ {a} ⊆ {a, b}⊆ {a, b, c} ÿâëÿåòñÿ

ìàêñèìàëüíîé öåïüþ â <℘(A), ⊆ >. Ïîäìíîæåñòâî ∅⊆{a,b}⊆{a,b,c}

òàêæå ÿâëÿåòñÿ öåïüþ, íî íå ìàêñèìàëüíîé.

2.Íà ÷èñëîâûõ ìíîæåñòâàõ N, Z, Q, R óñòàíîâëåíû îòíîøåíèÿ

ïîðÿäêà ≤ (ìåíüøå ëèáî ðàâíî), < (ìåíüøå), ≥ (áîëüøå ëèáî ðàâíî),

> (áîëüøå). Ýòè îòíîøåíèÿ ÿâëÿþòñÿ îòíîøåíèÿìè ëèíåéíîãî

ïîðÿäêà, ïîýòîìó ýòè ìíîæåñòâà, à òàêæå ëþáûå èõ ïîäìíîæåñòâà

ÿâëÿþòñÿ öåïÿìè. Íàïðèìåð, ìíîæåñòâî {1, 2, 3, 4}  öåïü.

3.Îòíîøåíèå «x  ïðåäîê y», îïðåäåëåííîå íà ìíîæåñòâå âñåõ

ëþäåé, åñòü îòíîøåíèå ïîðÿäêà. Ýòî îòíîøåíèå ñòðîãîãî ïîðÿäêà,

òàê êàê îíî íå ðåôëåêñèâíî (íèêàêîé ÷åëîâåê íå ÿâëÿåòñÿ ïðåäêîì

ñàìîãî ñåáÿ); ýòî îòíîøåíèå ÷àñòè÷íîãî ïîðÿäêà, òàê â íåì åñòü

íåñðàâíèìûå ýëåìåíòû: íå êàæäûå äâà ÷åëîâåêà íàõîäÿòñÿ â

îòíîøåíèè ðîäñòâà.

4.Ìíîæåñòâî ñèìâîëîâ ðóññêîãî àëôàâèòà A={à, á, â, ..., ÿ}

öåïü. Â ýòîì ìíîæåñòâå îòíîøåíèå ≤ ìîæíî ÷èòàòü êàê «ïðåäøå-

ñòâóåò»: à ïðåäøåñòâóåò á, á ïðåäøåñòâóåò â, è òàê äàëåå. Òîãäà à,

êàê ïåðâàÿ áóêâà àëôàâèòà, ïðåäøåñòâóåò âñåì îñòàëüíûì, ò.å.

Îòíîøåíèå ïîðÿäêà

64 65

Äîêàçàòåëüñòâî. Ïóñòü Õ={x

,...,x

}. Ïîëîæèì m

=x

, à

=x

, åñëè x

<m

k1

, è m

=m

k1

â ïðîòèâíîì ñëó÷àå. Òîãäà ýëåìåíò

áóäåò ìèíèìàëüíûì. Àíàëîãè÷íî ìîæíî äîêàçàòü ñóùåñòâîâàíèå

â Õ ìàêñèìàëüíîãî ýëåìåíòà.

Â ëþáîé êîíå÷íîé öåïè ïîíÿòèÿ íàèìåíüøåãî è ìèíèìàëüíîãî

(íàèáîëüøåãî è ìàêñèìàëüíîãî) ýëåìåíòà ñîâïàäàþò. Òàêèì îáðà-

çîì, ëþáàÿ êîíå÷íàÿ öåïü ñîäåðæèò íàèìåíüøèé (ïåðâûé) è íàè-

áîëüøèé (ïîñëåäíèé) ýëåìåíòû.

Ìíîæåñòâî íàòóðàëüíûõ ÷èñåë {1, 2, ..., n} îáðàçóåò öåïü n (îðäè-

íàëüíîå ÷èñëî n) â ñâîåé åñòåñòâåííîé óïîðÿäî÷åííîñòè.

Îïðåäåëåíèå 5.11. Ïîäìíîæåñòâî Õ ìíîæåñòâà Ð íàçûâàþò îãðà-

íè÷åííûì, èëè èíòåðâàëîì, åñëè ∀a, b∈P ∀x∈X (a ≤ x≤b).

5.3. Äèàãðàììû ó-ìíîæåñòâ

Ãðàô îòíîøåíèÿ ïîðÿäêà, ïîñòðîåííûé ïî åãî ìàòðèöå, áóäåò

ñîäåðæàòü áîëüøîå ÷èñëî òðàíçèòèâíî çàìûêàþùèõ äóã. Ïîýòîìó

îí áóäåò âûãëÿäåòü ñëèøêîì ñëîæíûì (ñì., íàïðèìåð, ðèñ. 5.2,á).

Äëÿ îòíîøåíèÿ ïîðÿäêà îáû÷íî ñòðîèòñÿ äèàãðàììà Õàññå, êîòîðàÿ

îòîáðàæàåò îòíîøåíèå ïîêðûâàåìîñòè.

Îïðåäåëåíèå 5.12. Â óïîðÿäî÷åííîì ìíîæåñòâå ñ îòíîøåíèåì

ïîðÿäêà ≤ ýëåìåíò b ïîêðûâàåò a, åñëè a < b è íå ñóùåñòâóåò

òàêîãî ýëåìåíòà x, ÷òîáû a < x < b.

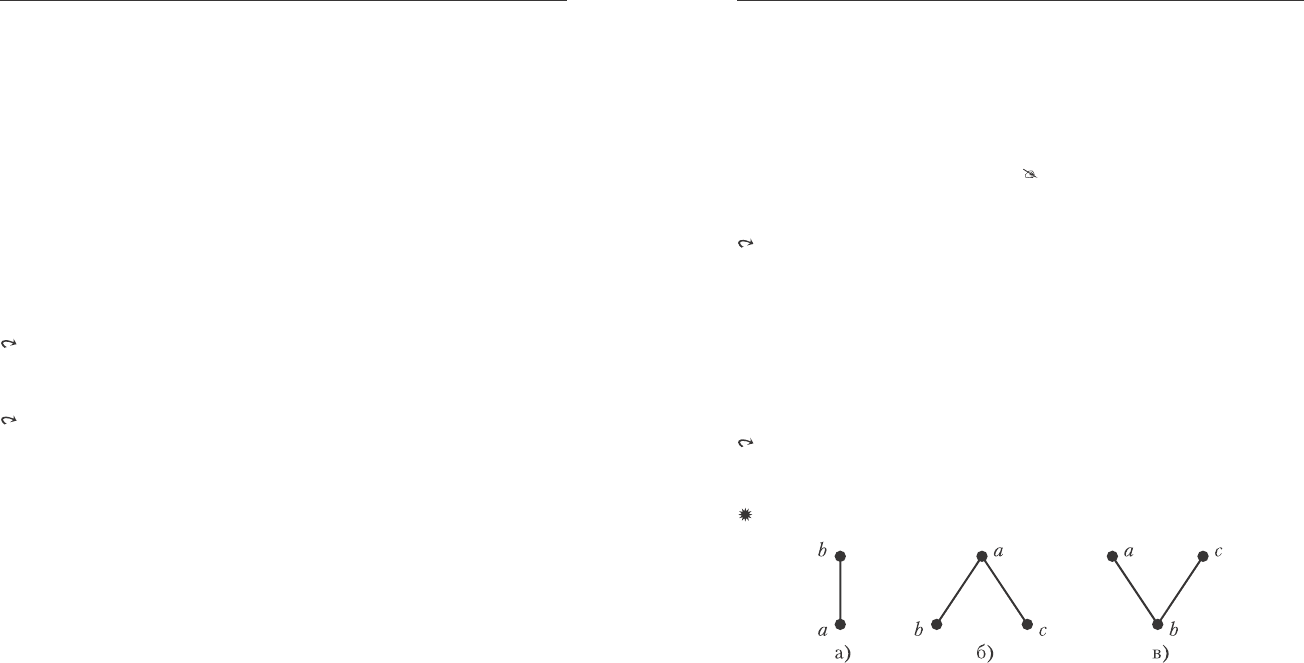
Ïðèìåð.

Ðèñ.5.1.

à) b ïîêðûâàåò a; á) à ïîêðûâàåò b è ñ; â) à, ñ ïîêðûâàþò b.

Òîãäà ó-ìíîæåñòâî ìîæíî èçîáðàçèòü â âèäå ãðàôà. Ïðèíÿòî

ãðàô ó-ìíîæåñòâà ñòðîèòü ñíèçó ââåðõ: åñëè ýëåìåíò b ïîêðûâàåò

ýëåìåíò a, òî îí ðàñïîëàãàåòñÿ âûøå ýëåìåíòà a è ñîåäèíÿåòñÿ ñ

íèì ïðÿìîé. Íåñðàâíèìûå ýëåìåíòû ðàñïîëàãàþòñÿ íà îäíîì

óðîâíå. Ïîëó÷åííûé ãðàô íàçûâàåòñÿ äèàãðàììîé ó-ìíîæåñòâà, èëè

äèàãðàììîé Õàññå (ñì. ðèñ. 5.1). Ãðàô îòíîøåíèÿ ïîêðûâàåìîñòè

íå ñîäåðæèò òðàíçèòèâíî çàìûêàþùèõ äóã è ïåòåëü, îòðàæàþùèõ

ðåôëåêñèâíîñòü îòíîøåíèÿ, ïîýòîìó äèàãðàììà ó-ìíîæåñòâà Ð

ìîæåò áûòü ïîëó÷åíà èç îðèåíòèðîâàííîãî ãðàôà îòíîøåíèÿ

Ãëàâà 5

Ìîæåò ïîêàçàòüñÿ, ÷òî íàèìåíüøèé è íàèáîëüøèé ýëåìåíòû

ñóùåñòâóþò â ëþáîì ó-ìíîæåñòâå. Îäíàêî ýòî íå òàê.

Ðàññìîòðèì ìíîæåñòâî A={2, 3, 6, 12, 24} ñ îïðåäåëåííûì íà

íåì îòíîøåíèåì ïîðÿäêà x ≤ y: «x äåëèò y», íàïðèìåð, 2 äåëèò 6,

12, 24; 3 äåëèò 6, 12, 24; 6 äåëèò 12, 24, è ò.ä. Â ýòîì ìíîæåñòâå

íàèìåíüøèé ýëåìåíò, åñëè îí ñóùåñòâóåò, äîëæåí äåëèòü âñå ñëåäó-

þùèå çà íèì ÷èñëà. Îäíàêî ýòèì ñâîéñòâîì íå îáëàäàþò íè 2, íè

3, êîòîðûå íå ñðàâíèìû ìåæäó ñîáîé ïî îòíîøåíèþ x äåëèò y, è

íè îäíî èç íèõ íå ÿâëÿåòñÿ íàèìåíüøèì, òàê êàê íå âñå ÷èñëà

«áîëüøå» 2 (èëè 3) ïî äàííîìó îòíîøåíèþ (2 íå äåëèò 3 è 3 íå

äåëèò 2). Ïîýòîìó â ýòîì ìíîæåñòâå íåò íàèìåíüøåãî ýëåìåíòà.

Îäíàêî ÷èñëà 2 è 3 îáëàäàþò òåì ñâîéñòâîì, ÷òî íèêàêîå äðóãîå

÷èñëî íå ìåíüøå èõ ïî äàííîìó îòíîøåíèþ, ò.å. íè îäíî äðóãîå

÷èñëî íå äåëèò 2 è 3. Òàêèå ýëåìåíòû, êîòîðûå ìåíüøå âñåõ îñòàëü-

íûõ ýëåìåíòîâ ó-ìíîæåñòâà, ÿâëÿþòñÿ ìèíèìàëüíûìè â ó-ìíîæåñòâå.

Îïðåäåëåíèå 5.9. Ìèíèìàëüíûì ýëåìåíòîì ó-ìíîæåñòâà P

íàçûâàåòñÿ òàêîé ýëåìåíò à∈P, ÷òî íè äëÿ êàêîãî x∈P íå

âûïîëíÿåòñÿ óñëîâèå x ≤ à.

Îïðåäåëåíèå 5.10. Ìàêñèìàëüíûì ýëåìåíòîì ó-ìíîæåñòâà P

íàçûâàåòñÿ òàêîé ýëåìåíò b∈P, ÷òî íè äëÿ êàêîãî x∈P íå

âûïîëíÿåòñÿ óñëîâèå b ≤ x.

Íåòðóäíî ïîêàçàòü, ÷òî íàèìåíüøèé ýëåìåíò âñåãäà ÿâëÿåòñÿ

ìèíèìàëüíûì â ó-ìíîæåñòâå, à íàèáîëüøèé  ìàêñèìàëüíûì, íî

îáðàòíîå âûïîëíèìî äàëåêî íå âñåãäà. Â ðàññìîòðåííîì âûøå

ïðèìåðå ÷èñëî 24 ÿâëÿåòñÿ íàèáîëüøèì ýëåìåíòîì, òàê êàê îíî

äåëèòñÿ íà âñå ïðåäøåñòâóþùèå ÷èñëà, è, â òî æå ñàìîå âðåìÿ,

ìàêñèìàëüíûì, à ÷èñëà 2 è 3 ÿâëÿþòñÿ ìèíèìàëüíûìè, â òî âðåìÿ,

êàê íàèìåíüøåãî ÷èñëà â ýòîì ó-ìíîæåñòâå íå ñóùåñòâóåò. Äàííîå

ìíîæåñòâî íå ÿâëÿåòñÿ òàêæå è öåïüþ, òàê êàê îíî ñîäåðæèò

íåñðàâíèìûå ýëåìåíòû 2 è 3.

Ðàññìîòðèì ïðîèçâîëüíîå ó-ìíîæåñòâî P. Ïóñòü S åñòü ïîäìíî-

æåñòâî P. Òîãäà, åñëè x ≤ y äëÿ x,y∈S, òî x ≤ y â P. Ïîñêîëüêó

ñâîéñòâà P1  P3 âûïîëíÿþòñÿ â P, òî îíè âûïîëíÿþòñÿ è â S.

Åñëè â Ð âûïîëíÿåòñÿ è Ð4, òî îíî âûïîëíÿåòñÿ è â S. Îòñþäà

ïðèõîäèì ê ñëåäóþùåìó çàêëþ÷åíèþ.

Òåîðåìà 5.1. Âñÿêîå ïîäìíîæåñòâî S ó-ìíîæåñòâà Ð ñàìî

ÿâëÿåòñÿ ó-ìíîæåñòâîì îòíîñèòåëüíî òîãî æå ñàìîãî ïîðÿäêà

(îãðàíè÷åííîãî íàS). Â ÷àñòíîñòè, ëþáîå ïîäìíîæåñòâî öåïè

ÿâëÿåòñÿ öåïüþ.

Òåîðåìà 5.2. Ëþáîå êîíå÷íîå íåïóñòîå ïîäìíîæåñòâî Õ ïðîèç-

âîëüíîãî ó-ìíîæåñòâà P èìååò ìèíèìàëüíûå è ìàêñèìàëüíûå

ýëåìåíòû.

Îòíîøåíèå ïîðÿäêà

66 67

ðàñïîëîæåííûå íèæå (äëÿ âåðõíèõ ãðàíåé  âûøå) îáîèõ

ýëåìåíòîâ.

Îïðåäåëåíèå 5.15. Ýëåìåíò õ íàçûâàåòñÿ íàèáîëüøåé íèæíåé

ãðàíüþ (òî÷íîé íèæíåé ãðàíüþ) ýëåìåíòîâ à è b, åñëè îí ÿâëÿåò-

ñÿ èõ íèæíåé ãðàíüþ è äëÿ ëþáîé íèæíåé ãðàíè u u ≤ x. Îáîçíà-

÷àåòñÿ x=inf{a, b} (infimum{a, b}).

Îïðåäåëåíèå 5.16. Ýëåìåíò y íàçûâàåòñÿ íàèìåíüøåé âåðõíåé

ãðàíüþ (òî÷íîé âåðõíåé ãðàíüþ) ýëåìåíòîâ a è b, åñëè îí ÿâëÿåò-

ñÿ âåðõíåé ãðàíüþ a è b è äëÿ ëþáîé âåðõíåé ãðàíè v y≤v.

Îáîçíà÷àåòñÿ y=sup{a, b} (supremum{a, b)}.

Ïðèìåðû.

1. Ðàññìîòðèì ìíîæåñòâî, ïðåäñòàâëåííîå äèàãðàììîé Õàññå íà

ðèñ. 5.3. Äëÿ ýëåìåíòîâ d, e íèæíèìè ãðàíÿìè áóäóò ýëåìåíòû b,

òàê êàê b ≤d, b ≤ e, è a, òàê êàê a≤d è a ≤e, îäíàêî, a≤b, ñëåäîâà-

òåëüíî, b ÿâëÿåòñÿ íàèáîëüøåé íèæíåé ãðàíüþ. Äëÿ ýëåìåíòîâ e è

c c≤e, a≤e, a≤c, ïîýòîìó a è c  íèæíèå ãðàíè ýëåìåíòîâ e è c,

íî a≤c, ñëåäîâàòåëüíî, c=inf{e,c}  íàèáîëüøàÿ íèæíÿÿ ãðàíü.

Àíàëîãè÷íî îïðåäåëÿþòñÿ è òî÷íûå âåðõíèå ãðàíè:sup{b, c}= e,

sup{d, e}= f,sup{e, c} = e.

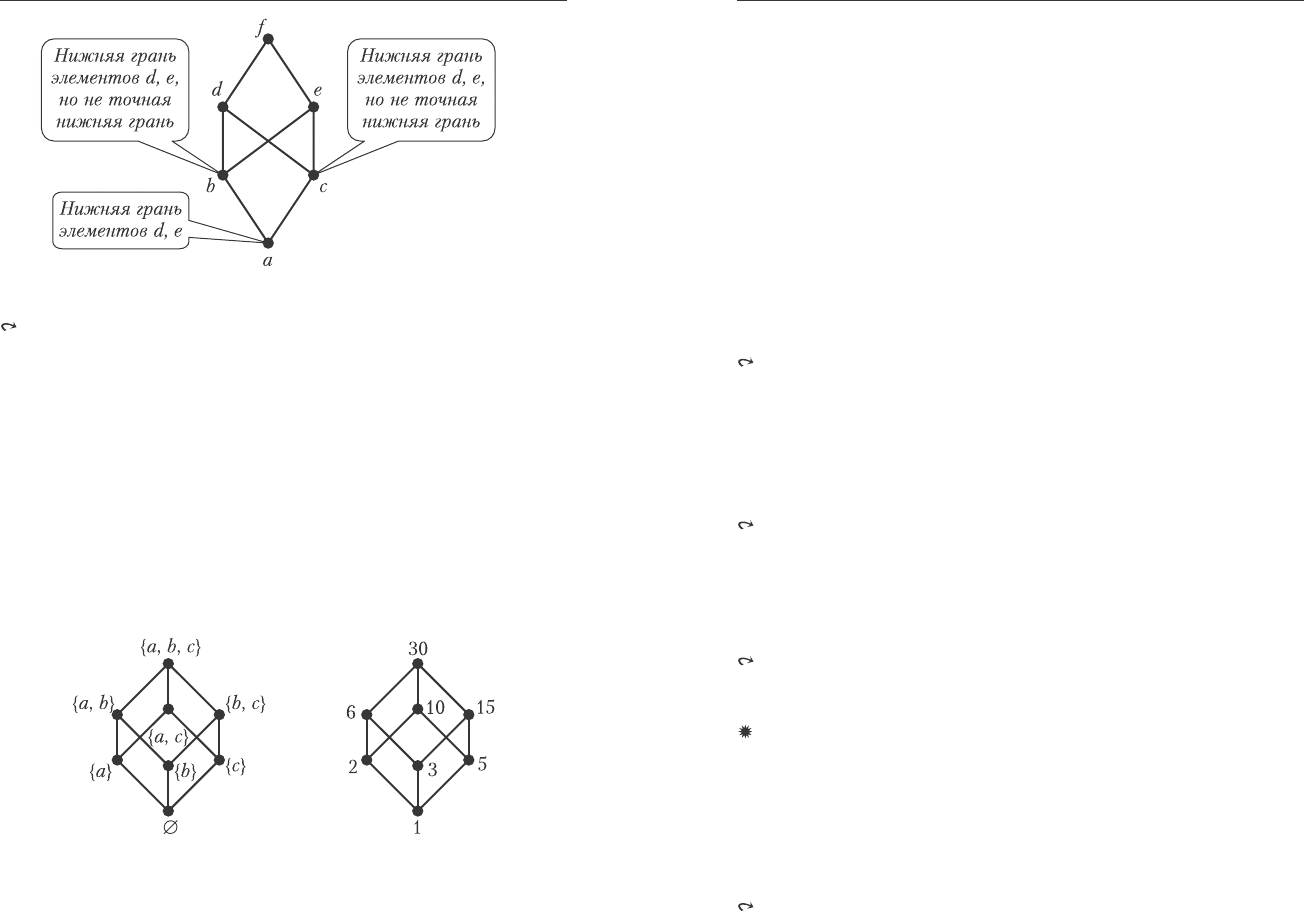
Ðèñ. 5.3. Òî÷íûå íèæíèå ãðàíè

2. Ðàññìîòðèì ìíîæåñòâî íà ðèñ. 5.4. Äëÿ ýëåìåíòîâ d, e íèæíèìè

ãðàíÿìè áóäóò ýëåìåíòû: b (b ≤d, b ≤ e), c (c ≤d, c ≤ e), è a (a≤d

è a ≤ e), ïðè ýòîì a≤ b è a ≤ c, îäíàêî, c||b (íåñðàâíèìû), ñëåäîâà-

òåëüíî, íè b, íè c íå ÿâëÿåòñÿ íàèáîëüøåé íèæíåé ãðàíüþ. Òî÷íîé

íèæíåé ãðàíüþ ýëåìåíòîâ b è c áóäåò ýëåìåíò a. Àíàëîãè÷íî, äëÿ

ýëåìåíòîâ b, c íå ñóùåñòâóåò òî÷íîé âåðõíåé ãðàíè. Òàêèì îáðàçîì,

â äàííîì ó-ìíîæåñòâå íå äëÿ âñÿêèõ äâóõ ýëåìåíòîâ ñóùåñòâóåò

òî÷íàÿ íèæíÿÿ è òî÷íàÿ âåðõíÿÿ ãðàíè.

Ãëàâà 5

ïîðÿäêà x ≤ y, ãäå x, y∈P, óäàëåíèåì ïåòåëü è òðàíçèòèâíî çàìûêà-

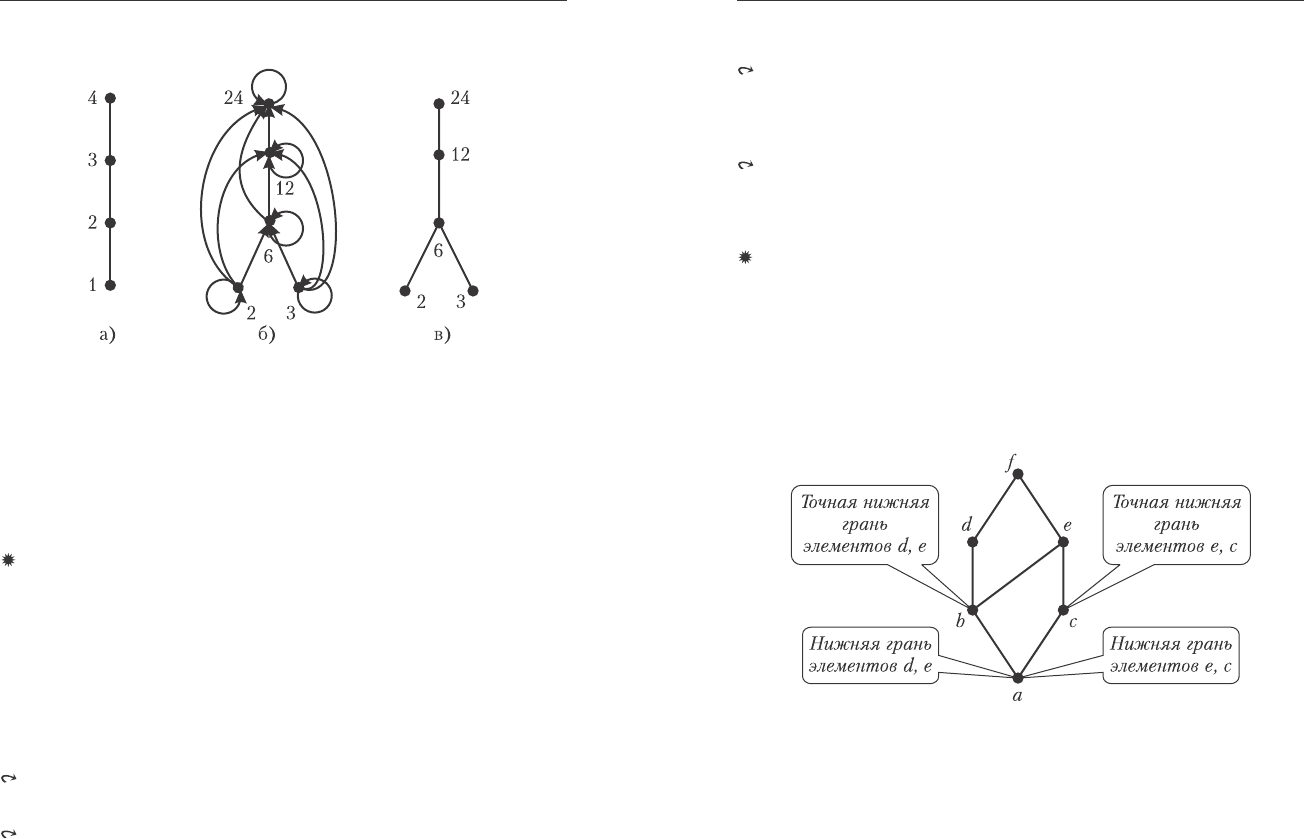
þùèõ äóã. Ïðèìåðû äèàãðàìì Õàññå ïðèâåäåíû íà ðèñ. 5.2.

Ðèñ. 5.2. Ïðèìåðû äèàãðàìì Õàññå:

a)  ëèíåéíî óïîðÿäî÷åííîå ìíîæåñòâî (öåïü);

á)  ãðàô îòíîøåíèÿ «x äåëèò y»;

â)  äèàãðàììà Õàññå ìíîæåñòâà, óïîðÿäî÷åííîãî îòíîøåíèåì

«x äåëèò y».

Åñëè äâà ýëåìåíòà a, b ∈ P íàõîäÿòñÿ â îòíîøåíèè ïîðÿäêà

a≤b, òî íà äèàãðàììå ñóùåñòâóåò ïóòü èç à â b. Òàêèì îáðàçîì,

ëþáîå êîíå÷íîå ó-ìíîæåñòâî ñ òî÷íîñòüþ äî èçîìîðôèçìà îïðåäå-

ëÿåòñÿ ñâîåé äèàãðàììîé.

Ïðèìåð.

Ïðîäîëæàÿ ïðåäûäóùèé ïðèìåð, ðàññìîòðèì äèàãðàììó Õàññå äëÿ

ìíîæåñòâà A={2, 3, 6, 12, 24} ñ îòíîøåíèåì «x äåëèò y» (ðèñ. 5.2,

â). Ýòà äèàãðàììà ïîëó÷åíà óäàëåíèåì êîëüöåâûõ è òðàíçèòèâíî

çàìûêàþùèõ äóã íà îðèåíòèðîâàííîì ãðàôå (ðèñ. 5.2, á). Ìû âèäèì,

÷òî êàæäûé âûøåëåæàùèé ýëåìåíò íà äèàãðàììå «áîëüøå» âñåõ,

ëåæàùèõ íèæå åãî. Òàêèì îáðàçîì, íåò íåîáõîäèìîñòè ñòðåëêàìè

óêàçûâàòü îòíîøåíèå ïîðÿäêà ìåæäó ýëåìåíòàìè: ýòî ëåãêî îïðå-

äåëèòü ïî óðîâíþ, êîòîðûé çàíèìàåò êàæäûé ýëåìåíò íà äèàãðàììå

Õàññå. Ïîýòîìó äèàãðàììà Õàññå îáû÷íî èçîáðàæàåòñÿ áåç ñòðåëîê.

Îïðåäåëåíèå 5.13. Ýëåìåíò u íàçûâàåòñÿ íèæíåé ãðàíüþ ýëå-

ìåíòîâ a è b, åñëè u ≤ a è u ≤ b.

Îïðåäåëåíèå 5.14. Ýëåìåíò v íàçûâàþò âåðõíåé ãðàíüþ ýëå-

ìåíòîâ a è b, åñëè a ≤ v è b ≤ v.

Ó äâóõ ýëåìåíòîâ ìîæåò áûòü íåñêîëüêî íèæíèõ è âåðõíèõ

ãðàíåé, ÷òî õîðîøî âèäíî íà äèàãðàììàõ Õàññå: ýòî âñå ýëåìåíòû,

Îòíîøåíèå ïîðÿäêà

68 69

Ãëÿäÿ íà äèàãðàììó ℘(A), ìîæíî ñäåëàòü âûâîä, ÷òî â èíòåðïðåòà-

öèè òåîðèè ìíîæåñòâ îïåðàöèè sup{x, y} ñîîòâåòñòâóåò îïåðàöèÿ

îáúåäèíåíèÿ, à îïåðàöèè inf {x, y}  ïåðåñå÷åíèÿ. Ýòà àíàëîãèÿ

ïîñëóæèëà îñíîâàíèåì äëÿ âûáîðà íàèìåíîâàíèÿ îïåðàöèè

íàõîæäåíèÿ òî÷íîé âåðõíåé ãðàíè  «îáúåäèíåíèå» (îáîçíà÷àåòñÿ

∨) è òî÷íîé íèæíåé ãðàíè  «ïåðåñå÷åíèå» (îáîçíà÷àåòñÿ ∧) â

òåîðèè ðåøåòîê. Òàêèì îáðàçîì îáîçíà÷åíèÿ inf{x, y} è x∧ y,

sup{x,y} è x∨ y ðàâíîçíà÷íû.

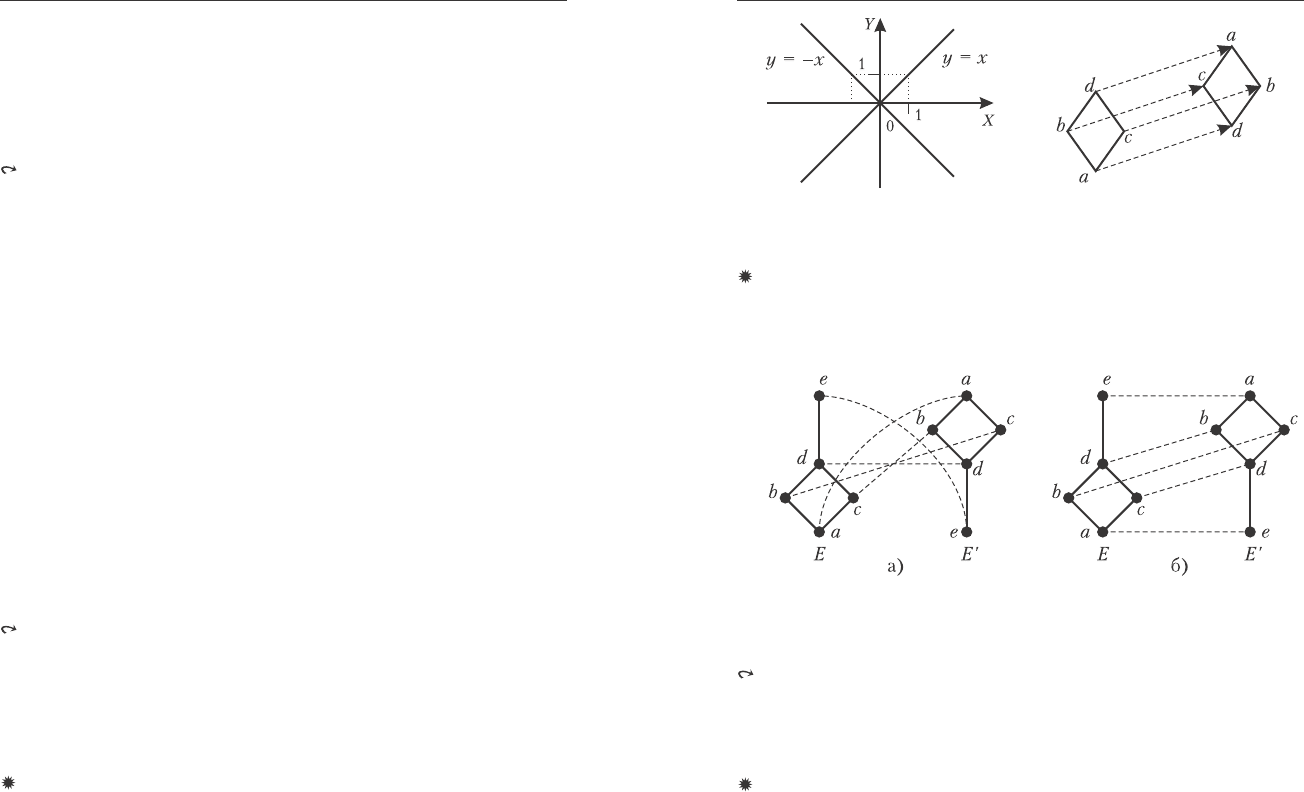
4. Ìíîæåñòâî X={1, 2, 3, 5, 6, 10, 15, 30} c çàäàííûì íà íåì îòíî-

øåíèåì «x  äåëèòåëü y» (ðèñ. 5.6) îáðàçóåò ðåøåòêó, â êîòîðîé

îïåðàöèè íàõîæäåíèÿ òî÷íîé íèæíåé ãðàíè x è y ñîîòâåòñòâóåò

íàõîæäåíèå ÍÎÄ (x, y) (íàèáîëüøèé îáùèé äåëèòåëü), à îïåðàöèè

íàõîæäåíèÿ òî÷íîé âåðõíåé ãðàíè x è y ñîîòâåòñòâóåò íàõîæäåíèå

ÍÎÊ (x, y) (íàèìåíüøåå îáùåå êðàòíîå).

5.4. Èçîìîðôèçì. Äâîéñòâåííîñòü

Îïðåäåëåíèå 5.18. Ôóíêöèÿ ϕ: P → Q, çàäàííàÿ íà ó-ìíîæåñòâå

P è ïðèíèìàþùàÿ çíà÷åíèÿ â ó-ìíîæåñòâå Q, íàçûâàåòñÿ ñîõðà-

íÿþùåé ïîðÿäîê, èëè èçîòîííîé, åñëè

èç x ≤ y ñëåäóåò, ÷òî ϕ(x) ≤ ϕ(y). (1)

Íàïðèìåð, åñëè P = {1, 2, 3}, òàêîå ÷òî 1 ≤ 2 ≤ 3, è Q = {a, b, c},

òàêîå ÷òî a ≤ b ≤ c, òî îòîáðàæåíèå ϕ(1)=a, ϕ(2)=b, ϕ(3)=c

ÿâëÿåòñÿ èçîòîííîé ôóíêöèåé.

Îïðåäåëåíèå 5.19. Èçîòîííàÿ ôóíêöèÿ, äîïóñêàþùàÿ èçîòîí-

íóþ îáðàòíóþ ôóíêöèþ, íàçûâàåòñÿ ϕ-èçîìîðôèçìîì. Èíûìè

ñëîâàìè, èçîìîðôèçì åñòü âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå

ìåæäó äâóìÿ ó-ìíîæåñòâàìè, óäîâëåòâîðÿþùåå óñëîâèþ (1) è

óñëîâèþ (1'):

èç ϕ(x) ≤ ϕ(y) ñëåäóåò, ÷òî x ≤ y.(1')

Îïðåäåëåíèå 5.20. Äâà ó-ìíîæåñòâà P è Q íàçûâàþòñÿ èçîìîðô-

íûìè (îáîçíà÷åíèå: P≅Q), åñëè ìåæäó íèìè ñóùåñòâóåò èçî-

ìîðôèçì.

Ïðèìåð. Íåòðóäíî çàìåòèòü, ÷òî äèàãðàììû ìíîæåñòâ ℘(A)

(ðèñ. 5.5) è Õ (ðèñ.5.6) èìåþò ñîâåðøåííî îäèíàêîâóþ ñòðóêòóðó,

õîòÿ ñîñòîÿò èç ðàçíûõ ýëåìåíòîâ. Çíà÷èò, ìåæäó íèìè ìîæíî

óñòàíîâèòü âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå (ñàìîñòîÿòåëüíî

îïðåäåëèòå èçîòîííóþ ôóíêöèþ ϕ, äîïóñêàþùóþ èçîòîííóþ

îáðàòíóþ ôóíêöèþ). Î÷åâèäíî, ÷òî ñîîòâåòñòâèå áóäåò ñîõðàíÿòü

ïîðÿäîê êàæäîãî óïîðÿäî÷åííîãî ìíîæåñòâà, ò.å. ýòè ó-ìíîæåñòâà

èçîìîðôíû.

Îïðåäåëåíèå 5.21. Èçîìîðôèçì ó-ìíîæåñòâà Ð ñ ñàìèì ñîáîé

íàçûâàåòñÿ àâòîìîðôèçìîì.

Ãëàâà 5

Ðèñ. 5.4. Ó-ìíîæåñòâî, íå ÿâëÿþùååñÿ ðåøåòêîé.

Îïðåäåëåíèå 5.17. Óïîðÿäî÷åííûå ìíîæåñòâà, â êîòîðûõ äëÿ

êàæäûõ äâóõ ýëåìåíòîâ ñóùåñòâóåò òî÷íàÿ âåðõíÿÿ è òî÷íàÿ

íèæíÿÿ ãðàíè, íàçûâàþòñÿ ðåøåòêàìè.

Òàêèì îáðàçîì, ìíîæåñòâî íà ðèñ. 5.3 ÿâëÿåòñÿ ðåøåòêîé, à ìíî-

æåñòâî íà ðèñ. 5.4  ó-ìíîæåñòâî, íî íå ðåøåòêà.

3. Ðàññìîòðèì ìíîæåñòâî âñåõ ïîäìíîæåñòâ ìíîæåñòâà A={a, b,c}:

℘(A)={∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}. Ýòî ìíîæåñòâî

óïîðÿäî÷åíî îòíîøåíèåì âêëþ÷åíèÿ è åãî ìîæíî ïðåäñòàâèòü íà

äèàãðàììå Õàññå (ðèñ. 5.5). Çäåñü òî÷íîé íèæíåé ãðàíüþ ïîäìíî-

æåñòâ ÿâëÿåòñÿ èõ òåîðåòèêî-ìíîæåñòâåííîå ïåðåñå÷åíèå, íàïðèìåð

äëÿ {a} è {b} ýòî ∅: {a}∩{b}=∅; äëÿ {a, b} è {b, c} ýòî {b} è ò. ä.

Òî÷íîé âåðõíåé ãðàíüþ äâóõ ïîäìíîæåñòâ ÿâëÿåòñÿ èõ òåîðåòèêî-

ìíîæåñòâåííîå îáúåäèíåíèå, íàïðèìåð, äëÿ {a} è {b}  ýòî {a, b},

äëÿ {a, b} è {b, c}  ýòî {a, b, c} è ò.ä.

Ðèñ. 5.5. Ðèñ. 5.6.

Äèàãðàììà ℘(A) Äèàãðàììà ó-ìíîæåñòâà

ñ îòíîøåíèåì «x  äåëèòåëü y».

Îòíîøåíèå ïîðÿäêà

70 71

Ðèñ. 5.7. Ðèñ. 5.8.

Àâòîìîðôèçì è Äóàëüíûé èçîìîðôèçì

äóàëüíûé àâòîìîðôèçì. (ñàìîäâîéñòâåííîå ìíîæåñòâî).

Ïðèìåð. Ìíîæåñòâà E è E′ íà ðèñ. 5.9. äâîéñòâåííû äðóã äðóãó.

Îòîáðàæåíèå ϕ ÿâëÿåòñÿ èçîìîðôèçìîì: ïðÿìîå è îáðàòíîå îòîáðàæåíèÿ

áèåêòèâíû è èçîòîííû. Îòîáðàæåíèå ψ íà ðèñ. 5.9, á íå ÿâëÿåòñÿ

èçîìîðôèçìîì, îíî íå ñîõðàíÿåò ïîðÿäîê, íàïðèìåð, b≤ d, íî ψ(b)|| ψ(d).

Ðèñ. 5.9.

à) Èçîòîííîå îòîáðàæåíèå, èçîìîðôèçì.

á) Íåèçîòîíîîå îòîáðàæåíèå.

Îïðåäåëåíèå 5.24. Ó-ìíîæåñòâî, äóàëüíî èçîìîðôíîå ñàìîìó

ñåáå, íàçûâàåòñÿ ñàìîäâîéñòâåííûì. Â ñàìîäâîéñòâåííîì ìíî-

æåñòâå äëÿ ëþáîãî x îáðàç ϕ(ϕ(x)) îáðàçà ϕ(x) ñîâïàäàåò ñ x:

ϕ(ϕ(x))=x. Òàêèå ñàìîäâîéñòâåííûå (äóàëüíûå) àâòîìîðôèçìû

íàçûâàþòñÿ èíâîëþöèÿìè.

Ïðèìåðû.

1. Ìíîæåñòâî íà ðèñ.5.8 ÿâëÿåòñÿ ñàìîäâîéñòâåííûì. Äåéñòâèòåëüíî,

îòîáðàæåíèå ϕ(a)=d, ϕ(b)=c, ϕ(c)=b, ϕ(d)=a ÿâëÿåòñÿ äóàëüíûì àâòî-

ìîðôèçìîì. Ïîâòîðíîå ïðèìåíåíèå ýòîãî îòîáðàæåíèÿ äàåò òå æå ñàìûå

ýëåìåíòû, ò.å. âûïîëíÿåòñÿ ñâîéñòâî ñàìîäâîéñòâåííîñòè: ϕ(ϕ(x))=x.

2. Ñâîéñòâîì ñàìîäâîéñòâåííîñòè îáëàäàåò ìíîæåñòâî-ñòåïåíü

℘(Ð) âñåõ ïîäìíîæåñòâ íåêîòîðîãî ìíîæåñòâà Ð, óïîðÿäî÷åííîå

Ãëàâà 5

Èç ñâîéñòâ Ð1  Ð3 ñëåäóåò ïðèíöèï äâîéñòâåííîñòè.

Òåîðåìà 5.3. Îòíîøåíèå, îáðàòíîå äëÿ îòíîøåíèÿ ïîðÿäêà, ñàìî

ÿâëÿåòñÿ óïîðÿäî÷åííîñòüþ.

Äåéñòâèòåëüíî, åñëè x ≤ y («x ìåíüøå y») , òî y ≥ x («y áîëüøå

x»). Íàïðèìåð, åñëè x ≤ y åñòü îòíîøåíèå «x äåëèò y», òî îáðàòíîå

åìó îòíîøåíèå y ≥ x åñòü «y äåëèòñÿ íà x».

Îïðåäåëåíèå 5.22. Äâîéñòâåííûì äëÿ ó-ìíîæåñòâà X íàçûâàåòñÿ

ìíîæåñòâîX′, îïðåäåëÿåìîå íà òåõ æå ýëåìåíòàõ îòíîøåíèåì,

îáðàòíûì ê óïîðÿäî÷åííîñòè â X. Ïðè ýòîì: X ≅ X′.

Èç òåîðåìû 5.3 ñëåäóåò, ÷òî êàæäîå ñâîéñòâî è êàæäàÿ òåîðåìà

îá ó-ìíîæåñòâàõ èìååò äâîéñòâåííûé àíàëîã, è åñëè íåêîòîðîå

óòâåðæäåíèå ñïðàâåäëèâî äëÿ âñåõ ó-ìíîæåñòâ, òî äâîéñòâåííîå

åìó óòâåðæäåíèå òàêæå ñïðàâåäëèâî äëÿ âñåõ ó-ìíîæåñòâ. Ýòî

ñâîéñòâî ó-ìíîæåñòâ îáû÷íî è íàçûâàåòñÿ ïðèíöèïîì

äâîéñòâåííîñòè.

Ñîãëàñíî ýòîìó ïðèíöèïó, óòâåðæäåíèå ψ ñïðàâåäëèâî â ó-

ìíîæåñòâå < X, ≤ >, òîãäà è òîëüêî òîãäà, êîãäà äâîéñòâåííîå åìó

óòâåðæäåíèå ñïðàâåäëèâî â ó-ìíîæåñòâå <X′, ≥ >. Äëÿ êàæäîãî

óòâåðæäåíèÿ îòíîñèòåëüíî ðåøåòêè ìîæíî ïîëó÷èòü äâîéñòâåííîå

åìó óòâåðæäåíèå, çàìåíèâ â íåì îïåðàöèþ ∨ íà ∧ è íàîáîðîò. Åñëè

â óòâåðæäåíèè ïðèñóòñòâóþò 0 è I ðåøåòêè, òî â äâîéñòâåííîì

óòâåðæäåíèè èõ òàêæå ñëåäóåò ïîìåíÿòü ìåñòàìè. Íàïðèìåð, äëÿ

óòâåðæäåíèÿ «ìíîæåñòâî < X, ≤ > èìååò íóëü» äâîéñòâåííûì áóäåò

óòâåðæäåíèå «ìíîæåñòâî <X′, ≥ > èìååò åäèíèöó».

Ñîãëàñíî ïðèíöèïó äâîéñòâåííîñòè, âñå ñâîéñòâà ðåøåòîê,

êîòîðûå áóäóò ðàññìîòðåíû â ñëåäóþùåé ãëàâå, ôîðìóëèðóþòñÿ â

âèäå äâóõ óòâåðæäåíèé, äâîéñòâåííûõ äðóã äðóãó.

Îïðåäåëåíèå 5.23. Ôóíêöèÿ ϕ: P → Q íàçûâàåòñÿ àíòèèçîòîí-

íîé (àíòèòîííîé), åñëè:

èç x ≤ y ñëåäóåò, ÷òî ϕ(x) ≥ ϕ(y), (2)

à âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå ϕ, óäîâëåòâîðÿþùåå óñëî-

âèþ (2) è (2'):

èç ϕ(x) ≤ ϕ(y) ñëåäóåò x ≥ y,(2')

íàçûâàåòñÿ äóàëüíûì èçîìîðôèçìîì.

Ïðèìåð.

Íà ðèñ.5.7 ïðÿìàÿy = x åñòü àâòîìîðôèçì R→R, êîòîðûé ÿâëÿ-

åòñÿ òîæäåñòâåííûì îòîáðàæåíèåì. Ïðÿìàÿ y=x åñòü äóàëüíûé

àâòîìîðôèçì; ýòî îòîáðàæåíèå áèåêòèâíî è àíòèòîííî: åñëè x

≤x

òî y

≥y

Ñèñòåìû <X′, ≥ >, äóàëüíî èçîìîðôíûå < X, ≤ >, ÿâëÿþòñÿ

äâîéñòâåííûìè ïî îòíîøåíèþ êX.

Îòíîøåíèå ïîðÿäêà

72 73

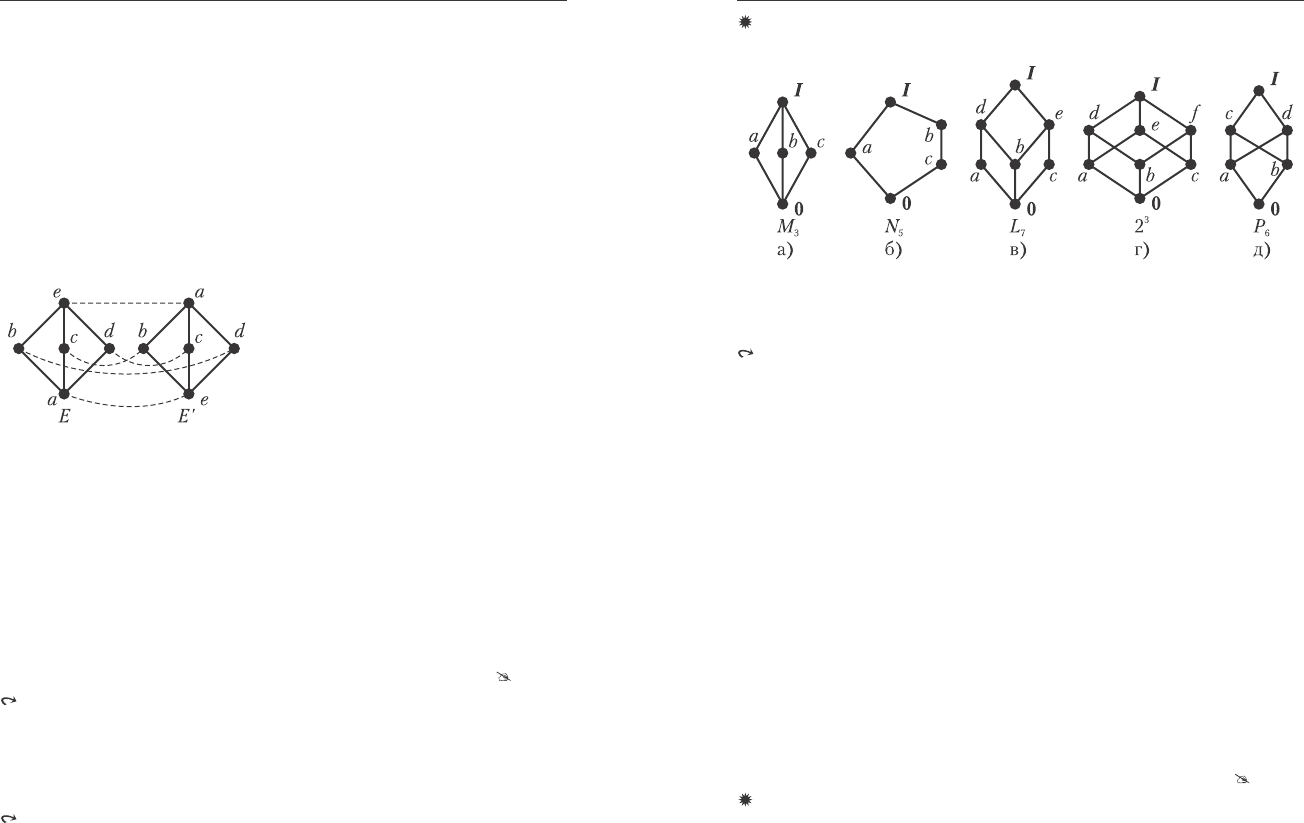
Ïðèìåðû. Íà ðèñ. 5.11 âûñîòà ìíîæåñòâà M

ðàâíà 2, à âûñîòà

ìíîæåñòâ N

, L

, 2

è P

ðàâíà 3.

Ðèñ. 5.11. Äèàãðàììû ó-ìíîæåñòâ.

Ïîíÿòèå âûñîòû òåñíî ñâÿçàíî ñ ïîíÿòèåì ãðàäóèðîâàííîãî

ìíîæåñòâà.

Îïðåäåëåíèå 5.27. Ãðàäóèðîâàííûì ó-ìíîæåñòâîì íàçûâàåòñÿ

ó-ìíîæåñòâî Ð ñ çàäàííîé íà íåì ôóíêöèåé g: P → Z, ïðèíèìà-

þùåé çíà÷åíèå â öåïè öåëûõ ÷èñåë, è òàêîé, ÷òî

åñëè x > y, òî g[x] > g[y], (ñòðîãàÿ èçîòîííîñòü); G1.

åñëè õ ïîêðûâàåò ó, òî g[x] = g[y] + 1. G2.

Óòâåðæäåíèå. Âî âñÿêîì ãðàäóèðîâàííîì ó-ìíîæåñòâå èìååò

ìåñòî öåïíîå óñëîâèå Æîðäàíà-Äåäåêèíäà: âñå ìàêñèìàëüíûå

öåïè ìåæäó äâóìÿ ôèêñèðîâàííûìè òî÷êàìè èìåþò îäèíàêîâóþ

äëèíó.

Òåîðåìà 5.5. Â ó-ìíîæåñòâå Ð ñ 0 è êîíå÷íûìè öåïÿìè òîãäà è

òîëüêî òîãäà âûïîëíÿåòñÿ öåïíîå óñëîâèå ÆîðäàíàÄåäåêèíäà,

êîãäà Ð ãðàäóèðóåòñÿ ôóíêöèåé âûñîòû h[x].

Òàêèå ìíîæåñòâà, â êîòîðûõ âûïîëíÿåòñÿ óñëîâèå Æîðäàíà

Äåäåêèíäà, íàçûâàþò åùå äåäåêèíäîâûìè ìíîæåñòâàìè.

Äîêàçàòåëüñòâî. Åñëè Ð ãðàäóèðóåòñÿ ôóíêöèåé h[x], òî óñëîâèå

ÆîðäàíàÄåäåêèíäà âûïîëíÿåòñÿ î÷åâèäíûì îáðàçîì: äëèíà

ìàêñèìàëüíîé öåïè, ñîåäèíÿþùåé òî÷êè à è b, òàêèå, ÷òî b>a,

ðàâíà h[b]h[a]. Îáðàòíî, åñëè èìååò ìåñòî óñëîâèå Æîðäàíà

Äåäåêèíäà, òî h[x] áóäåò äëèíîé ìàêñèìàëüíîé öåïè îò 0 äî x,

îòêóäà ñëåäóåò âûïîëíèìîñòü äëÿ h[x] óñëîâèé G1 è G2.

Ïðèìåð. Ðàññìîòðèì äèàãðàììû íà ðèñ.5.11. Ñðåäè ìíîæåñòâ,

èçîáðàæåííûõ íà ðèñ.5.11, ìíîæåñòâî N

âûäåëÿåòñÿ ñâîåé

«íåñèììåòðè÷íîñòüþ»: äëèíà ëåâîé öåïè ìåæäó 0 è I ðàâíà äâóì, à ïðàâîé

öåïè  òðåì. Ïîñêîëüêó íà äèàãðàììàõ Õàññå èçîáðàæàþòñÿ òîëüêî

ìàêñèìàëüíûå öåïè, óñëîâèå ÆîðäàíàÄåäåêèíäà íå âûïîëíÿåòñÿ â

äàííîì ìíîæåñòâå, îíî ÿâëÿåòñÿ íå ãðàäóèðîâàííûì (íå äåäåêèíäîâûì)

ìíîæåñòâîì. Âñå îñòàëüíûå ìíîæåñòâà  ãðàäóèðîâàííûå.

Ãëàâà 5

îòíîøåíèåì âêëþ÷åíèÿ. Îòîáðàæåíèå, ñòàâÿùåå â ñîîòâåòñòâèå

êàæäîìó ïîäìíîæåñòâó åãî äîïîëíåíèå äî ìíîæåñòâà Ð, âçàèìíî

îäíîçíà÷íî è îáðàùàåò âêëþ÷åíèå. Òàêèì îáðàçîì, ìíîæåñòâî-

ñòåïåíü ℘(Ð) ÿâëÿåòñÿ ñàìîäâîéñòâåííûì (ñì. ðèñ. 5.5).

3. Íà ðèñ. 5.9, à) ïîêàçàíû ìíîæåñòâà E è E′, äâîéñòâåííûå äðóã äðóãó.

Íà ðèñ. 5.9, á) ïîêàçàíî, ÷òî ìíîæåñòâî E íå ÿâëÿåòñÿ ñàìîäâîéñòâåí-

íûì. Äåéñòâèòåëüíî, îòîáðàæåíèå ψ íå ÿâëÿåòñÿ äóàëüíûì èçîìîðôèç-

ìîì: b ≤ d, îäíàêî ψ(b) = c è ψ(d) = b íåñðàâíèìû. Íåòðóäíî óáåäèòüñÿ,

÷òî äëÿ ýòèõ ìíîæåñòâ íå ñóùåñòâóåò äóàëüíîãî èçîìîðôèçìà.

4. Ìíîæåñòâî íà ðèñ. 5.10 íå ÿâëÿåòñÿ ñàìîäâîéñòâåííûì. Äåéñòâè-

òåëüíî, óñëîâèå ϕ(ϕ(x))=x âûïîëíÿåòñÿ íå äëÿ âñåõ ýëåìåíòîâ

ïðè ýòîì îòîáðàæåíèè:

Ðèñ. 5.10. Íåñàìîäâîéñòâåííîå ìíîæåñòâî.

5.5. Ãðàäóèðîâàííûå ìíîæåñòâà

Òåîðåìà 5.4. Ëþáàÿ êîíå÷íàÿ öåïü èç n ýëåìåíòîâ èçîìîðôíà

îðäèíàëüíîìó ÷èñëó n (öåïè öåëûõ ÷èñåë 1,...,n). Èíûìè ñëîâà-

ìè, ñóùåñòâóåò âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå ϕ ìåæäó

n-ýëåìåíòíîé öåïüþ X è ìíîæåñòâîì {1, 2, ..., n}, òàêîå, ÷òî

≤x

òîãäà è òîëüêî òîãäà, êîãäà ϕ(x

)≤ϕ(x

Äîêàçàòåëüñòâî. Ïóñòü ϕ îòîáðàæàåò íàèìåíüøèé ýëåìåíò x∈X

â 1, íàèìåíüøèé ýëåìåíò èç îñòàâøèõñÿ  â 2 è ò. ä. Òîãäà êàæäîìó

ýëåìåíòó öåïè áóäåò ñîîòâåòñòâîâàòü íàòóðàëüíîå ÷èñëî.

Îïðåäåëåíèå 5.25. Äëèíîé l[P] ó-ìíîæåñòâà Ð íàçûâàåòñÿ òî÷-

íàÿ âåðõíÿÿ ãðàíü äëèí öåïåé â Ð. Äëèíà êîíå÷íîé öåïè n ïî

îïðåäåëåíèþ ïîëàãàåòñÿ ðàâíîé n1 (ýòî î÷åâèäíî, åñëè

ïîñìîòðåòü íà äèàãðàììó öåïè). Åñëè l[P] êîíå÷íî, òî ãîâîðÿò,

÷òî ó-ìíîæåñòâî P èìååò êîíå÷íóþ äëèíó.

Îïðåäåëåíèå 5.26. Âûñîòîé, èëè ðàçìåðíîñòüþ, h[x] ýëåìåíòà x

íàçûâàåòñÿ òî÷íàÿ âåðõíÿÿ ãðàíü äëèí öåïåé 0<x

<x

<...<x

=x

ìåæäó 0 è õ. Åñëè Ð èìååò íàèáîëüøèé ýëåìåíò I, òî, î÷åâèäíî,

÷òî h[I]=l[P]. Ïîíÿòíî òàêæå, ÷òî h[x]=1 òîãäà è òîëüêî òîãäà,

êîãäà õ ïîêðûâàåò 0. Òàêèå ýëåìåíòû õ íàçûâàþòñÿ àòîìàìè,

èëè òî÷êàìè, ó-ìíîæåñòâà Ð.

Îòíîøåíèå ïîðÿäêà

ϕ(a) = e, ϕ(ϕ(a)) = ϕ(e) = a,

ϕ(b) = d, ϕ(ϕ(b)) = ϕ(d) = c,

ϕ(c) = b, ϕ(ϕ(c)) = ϕ(b) = d,

ϕ(d) = c, ϕ(ϕ(d)) = ϕ(c) = b,

ϕ(e) = a, ϕ(ϕ(e)) = ϕ(a) = e.

Ãëàâà 6. ÐÅØÅÒÊÈ

Èñòîðè÷åñêè òåîðèÿ ðåøåòîê ïîÿâèëàñü ïîçæå ôîðìàëèçàöèè

Äæîðäæåì Áóëåì ïðîïîçèöèîíàëüíîé ëîãèêè âûñêàçûâàíèé,

êîòîðîå ïðèâåëî ê ïîíÿòèþ áóëåâîé àëãåáðû. Èìåííî èññëåäîâàíèÿ

ïî àêñèîìàòèçàöèè áóëåâûõ àëãåáð ïîáóäèëè ×àðëüçà Ïèðñà è

Ýðíñòà Øð¸äåðà ââåñòè ïîíÿòèå ðåøåòêè â êîíöå äåâÿò-

íàäöàòîãî âåêà. Íåçàâèñèìî îò íèõ, Ðè÷àðä Äåäåêèíä â ñâîèõ

èññëåäîâàíèÿõ ïî èäåàëàì àëãåáðàè÷åñêèõ ÷èñåë ïðèøåë ê òîìó

æå ñàìîìó ïîíÿòèþ. Îäíàêî ýòè ðàáîòû íå ïðèâëåêëè âíèìàíèÿ

ìàòåìàòè÷åñêîé îáùåñòâåííîñòè â òî âðåìÿ. È òîëüêî èññëåäî-

âàíèÿ Ãàððåòòà Áèðêãîôà â ñåðåäèíå òðèäöàòûõ ãîäîâ äàëè

òîë÷îê ðàçâèòèþ òåîðèè ðåøåòîê. Â ñåðèè áëåñòÿùèõ ðàáîò îí

ïîêàçàë âàæíîñòü òåîðèè ðåøåòîê, êîòîðàÿ ñëóæèò êàðêàñîì

äëÿ îáîáùåíèÿ è óíèôèêàöèè ìíîãèõ ðåçóëüòàòîâ â ðàçëè÷íûõ

ìàòåìàòè÷åñêèõ äèñöèïëèíàõ. Ñîáðàâ è îáîáùèâ ñâîè ðåçóëüòàòû,

à òàêæå äîñòèæåíèÿ ìíîãèõ äðóãèõ ìàòåìàòèêîâ, ðàáîòàþùèõ

â ýòîé îáëàñòè, Ã. Áèðêãîô â 1940 ã. èçäàë ìîíîãðàôèþ «Lattice

Theory», ñîçäàâ ôàêòè÷åñêè îñíîâû îáùåé òåîðèè ðåøåòîê, ÷òî

ïîçâîëèëî âûäåëèòü åå â ñàìîñòîÿòåëüíóþ äèñöèïëèíó. Â äàëüíåé-

øèõ èçäàíèÿõ (1948, 1967ãã.) Ã.Áèðêãîô îòðàçèë ðàçâèòèå ýòîé

òåîðèè, è â íàñòîÿùåå âðåìÿ åãî ìîíîãðàôèÿ (íà ðóññêîì ÿçûêå

ñì. [Áèðêãîô, 1984]) ÿâëÿåòñÿ íàñòîÿùåé ýíöèêëîïåäèåé

êëàññè÷åñêîé òåîðèè ðåøåòîê.

6.1. Îñíîâíûå îïðåäåëåíèÿ

Îïðåäåëåíèå 6.1. Ðåøåòêîé

íàçûâàåòñÿ ó-ìíîæåñòâî L, â

êîòîðîì ëþáûå äâà ýëåìåíòà x è y èìåþò òî÷íóþ íèæíþþ ãðàíü,

íàçûâàåìóþ ïåðåñå÷åíèåì (îáîçíà÷àåòñÿ x∧y), è òî÷íóþ âåðõ-

íþþ ãðàíü, íàçûâàåìóþ îáúåäèíåíèåì (îáîçíà÷àåòñÿ x∨y).

Ðåøåòêà L íàçûâàåòñÿ ïîëíîé, åñëè ëþáîå åå ïîäìíîæåñòâî Õ

èìååò â L òî÷íûå âåðõíþþ è íèæíþþ ãðàíè.

Ïîëàãàÿ X=L, ìû âèäèì, ÷òî ëþáàÿ íåïóñòàÿ ïîëíàÿ ðåøåòêà

ñîäåðæèò íàèìåíüøèé ýëåìåíò 0 è íàèáîëüøèé ýëåìåíò I. Äåé-

ñòâèòåëüíî, åñëè êàæäûå äâà ýëåìåíòà èìåþò òî÷íóþ âåðõíþþ

ãðàíü, òî â ðåøåòêå èìååòñÿ òîëüêî îäèí ìàêñèìàëüíûé ýëåìåíò,

êîòîðûé áóäåò è óíèâåðñàëüíîé âåðõíåé ãðàíüþ, ò.å. åäèíèöåé

ó-ìíîæåñòâà. Àíàëîãè÷íî, ñóùåñòâîâàíèå òî÷íîé íèæíåé ãðàíè

äëÿ ëþáûõ äâóõ ýëåìåíòîâ îáåñïå÷èâàåò ñóùåñòâîâàíèå óíèâåð-

ñàëüíîé íèæíåé ãðàíè  íóëÿ ó-ìíîæåñòâà. Î÷åâèäíî, ÷òî ó-

ìíîæåñòâî, äâîéñòâåííîå ðåøåòêå, ñàìî ÿâëÿåòñÿ ðåøåòêîé, à ó-

ìíîæåñòâî, äâîéñòâåííîå ïîëíîé ðåøåòêå, áóäåò ïîëíîé ðåøåò-

êîé ñ âçàèìíîé çàìåíîé îáúåäèíåíèé è ïåðåñå÷åíèé. Èç îïðåäå-

ëåíèÿ ñëåäóåò òàêæå, ÷òî ëþáàÿ êîíå÷íàÿ ðåøåòêà ÿâëÿåòñÿ

ïîëíîé.

Óòâåðæäåíèå 6.1. Ëþáàÿ öåïü ÿâëÿåòñÿ ðåøåòêîé, â êîòîðîé

x∧y ñîâïàäàåò ñ ìåíüøèì, à x∨y  ñ áîëüøèì èç ýëåìåíòîâ

x,y.

Ýòî óòâåðæäåíèå î÷åâèäíî, òàê êàê â ëþáîé öåïè ëèáî x ≤ y,

ëèáî y ≤ x, ïîýòîìó ëèáî x∧ y = x, ëèáî x ∧ y= y. Äâîéñòâåííî äëÿ

îáúåäèíåíèÿ: ëèáî x ∨ y = x, ëèáî x ∨ y = y.

Ïðèìåðû.

1. Â ãëàâå 5 íà ðèñ. 5.11 èçîáðàæåíû äèàãðàììû Õàññå ó-ìíîæåñòâ,

ñðåäè êîòîðûõ ìíîæåñòâà M

, N

, L

, 2

ÿâëÿþòñÿ ðåøåòêàìè. Íå

âñÿêîå ó-ìíîæåñòâî ñ 0 è I ÿâëÿåòñÿ ðåøåòêîé. Ó-ìíîæåñòâî P

ÿâëÿåòñÿ äåäåêèíäîâûì ó-ìíîæåñòâîì ñ 0 è ², îäíàêî, îíî íå îáðàçó-

åò ðåøåòêó, òàê êàê â íåì íå äëÿ âñÿêèõ äâóõ ýëåìåíòîâ ñóùåñòâóåò

îáúåäèíåíèå è ïåðåñå÷åíèå: äëÿ ýëåìåíòîâ ñ è d íå ñóùåñòâóåò

ïåðåñå÷åíèÿ, à äëÿ ýëåìåíòîâ a, b  îáúåäèíåíèÿ.

2. Ó-ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë íå ÿâëÿåòñÿ ïîëíîé

ðåøåòêîé, òàê êàê â íåì îòñóòñòâóþò óíèâåðñàëüíûå ãðàíè 0 è

I. Â ó-ìíîæåñòâå äåéñòâèòåëüíûõ ÷èñåë óñëîâèÿ ïîëíîòû áóäóò

âûïîëíÿòüñÿ, åñëè ïðèñîåäèíèòü ê íèì â êà÷åñòâå óíèâåðñàëüíûõ

ãðàíåé ∞ è +∞.

Îïðåäåëåíèå 6.2. Ïîäðåøåòêîé ðåøåòêè L íàçûâàåòñÿ ïîäìíî-

æåñòâî X⊂L òàêîå, ÷òî åñëè a∈X, b∈X, òî a∧b∈X è

a∨b∈X.

Ïóñòîå ïîäìíîæåñòâî è ëþáîå îäíîýëåìåíòíîå ïîäìíîæåñòâî

ÿâëÿþòñÿ ïîäðåøåòêàìè. Ïîäðåøåòêà ðåøåòêè ñàìà ÿâëÿåòñÿ

ðåøåòêîé ñ òåìè æå îïåðàöèÿìè îáúåäèíåíèÿ è ïåðåñå÷åíèÿ.

Âîîáùå, åñëè a ≤ b â ðåøåòêå L, òî (çàìêíóòûé) èíòåðâàë [a, b],

ñîñòîÿùèé èç âñåõ ýëåìåíòîâ x∈L, êîòîðûå óäîâëåòâîðÿþò

óñëîâèþ a ≤ x ≤ b, âñåãäà áóäåò ïîäðåøåòêîé. Äëÿ öåïè è åå ýëåìåí-

òîâ a ≤ b ìîæíî îïðåäåëèòü ïîíÿòèÿ ïîëóîòêðûòûõ èíòåðâàëîâ:

(a,b]={x|a<x ≤ b} è [a, b) = {x| a ≤ x < b}, à òàêæå îòêðûòûé

èíòåðâàë (a, b) = {x| a < x < b}. Åñëè ýòè ìíîæåñòâà íåïóñòû, îíè

òàêæå ÿâëÿþòñÿ ïîäðåøåòêàìè.

Ïðèìåð. Â ðåøåòêå íà ðèñ. 6.1 ïîäìíîæåñòâî Y={∅, {b}, {c},

{b,c}} ÿâëÿåòñÿ ïîäðåøåòêîé. Äåéñòâèòåëüíî {b}∈Y, {c}∈Y,

{b}∧{c}=∅∈Y, {b}∨{c}={b,c}∈Y, {b}∨{b,c}={b,c}∈Y, ïåðå-

ñå÷åíèå {b}∧{à, c} = {b}∈Y è ò. ä. Ýòî ïîäìíîæåñòâî îáðàçóåò çàìê-

íóòûé èíòåðâàë [∅, {b, c}]. Ïîäìíîæåñòâî Z={∅, {a}, {a, b}, {a, c}, {c}}

íå ÿâëÿåòñÿ ïîäðåøåòêîé, òàê êàê {a, b}∨{à, c}={a, b, c}∉Z. Ýòî

Ðåøåòêè

1 Ïî-àíãëèéñêè lattice, ïî-íåìåöêè Verband; â íàøåé ëèòåðàòóðå ðåøåòêè èíîãäà

èìåíóþò ñòðóêòóðàìè.

76 77

ïîäìíîæåñòâî íå ÿâëÿåòñÿ òàêæå èíòåðâàëîì. Ïîäðåøåòêàìè áóäóò

òàêæå ïîäìíîæåñòâà: {∅, {a}}, {{c}, {a, c}}, {{a}, {a, b}}, è ò.ä., âñå

öåïè, íàïðèìåð, {∅, {b}, {∅, {b}, {b, c}}, à òàêæå âñå ýëåìåíòû

ðåøåòêè.

Ðèñ. 6.1. Ðåøåòêà è åå ïîäðåøåòêè.

Îïðåäåëåíèå 6.3. Âûïóêëûì ïîäìíîæåñòâîì â ó-ìíîæåñòâå Ð

íàçûâàåòñÿ ïîäìíîæåñòâî, êîòîðîå âìåñòå ñ ëþáûìè ñâîèìè

ýëåìåíòàìè a è b, ãäå a ≤ b, ñîäåðæèò âåñü èíòåðâàë [a, b].

Íà ðèñ. 6.1 ïîäìíîæåñòâî {∅, {b}, {c}, {b, c}}, âûïóêëîå, à

ïîäìíîæåñòâî {∅, {b}, {b, c}}  íåò. Ïîäìíîæåñòâî S ðåøåòêè L

ÿâëÿåòñÿ âûïóêëîé ïîäðåøåòêîé, åñëè äëÿ ëþáûõ a, b∈S [a∧b,

a∨b] ⊂ S.

Îïðåäåëåíèå 6.4. Ñâîéñòâî ïîäìíîæåñòâ ìíîæåñòâà S íàçûâà-

åòñÿ ñâîéñòâîì çàìûêàíèÿ, åñëè:

1) S îáëàäàåò ýòèì ñâîéñòâîì;

2) ëþáîå ïåðåñå÷åíèå ïîäìíîæåñòâ, îáëàäàþùèõ ýòèì ñâîé-

ñòâîì, ñàìî îáëàäàåò èì.

Ïîíÿòèå «ñâîéñòâî çàìûêàíèÿ» ðàâíîñèëüíî ïîíÿòèþ «îïåðà-

öèÿ çàìûêàíèÿ».

Îïðåäåëåíèå 6.5. Îïåðàöèåé çàìûêàíèÿ íà ìíîæåñòâå S íàçûâà-

åòñÿ îòîáðàæåíèå X→X′ íà ïîäìíîæåñòâàõ ýòîãî ìíîæåñòâà

òàêîå, ÷òî

X ⊂ X′ (ýêñòåíñèâíîñòü); Ñ1

X′ = X′′ (èäåìïîòåíòíîñòü); Ñ2

Åñëè X ⊂ Y, òî X′ ⊂ Y′ (èçîòîííîñòü). Ñ3

Ïîäìíîæåñòâî X⊂S, ïî îïðåäåëåíèþ, çàìêíóòî îòíîñèòåëüíî

äàííîé îïåðàöèè çàìûêàíèÿ, åñëè îíî ñîâïàäàåò ñî ñâîèì «çàìûêà-

íèåì» X′. Òåïåðü ïîäðåøåòêó ìîæíî îïðåäåëèòü êàê ëþáîå ïîäìíî-

æåñòâî ðåøåòêè, çàìêíóòîå îòíîñèòåëüíî îïåðàöèé îáúåäèíåíèÿ è

ïåðåñå÷åíèÿ.

6.2. Ðåøåòêè êàê àëãåáðû

Ðåøåòêó ìîæíî îïðåäåëèòü êàê àëãåáðàè÷åñêóþ ñèñòåìó:

L=<P,∨,∧,≤>, ñ äâóìÿ áèíàðíûìè îïåðàöèÿìè è îòíîøåíèåì

ïîðÿäêà, çàäàííûìè íà ìíîæåñòâå P. Ðåøåòî÷íûå îïåðàöèè ∨ è ∧

îáëàäàþò âàæíûìè àëãåáðàè÷åñêèìè ñâîéñòâàìè. Â ýòîì ðàçäåëå

ìû èññëåäóåì ñâîéñòâà îïåðàöèé ∨ è ∧ è ïîêàæåì, ÷òî îïåðàöèè,

îáëàäàþùèå ýòèìè ñâîéñòâàìè, îïðåäåëÿþò îòíîøåíèå ïîðÿäêà íà

ìíîæåñòâå P, ÷òî ïîçâîëÿåò ðàññìàòðèâàòü ðåøåòêè êàê àëãåáðû ñ

äâóìÿ îïåðàöèÿìè.

Ëåììà 6.1. Â ëþáîì ó-ìíîæåñòâå äëÿ îïåðàöèé ïåðåñå÷åíèÿ è

îáúåäèíåíèÿ âûïîëíÿþòñÿ (ïðè îïðåäåëåííûõ â íèõ âûðàæå-

íèÿõ) ñëåäóþùèå çàêîíû:

x∧x=x, x∨x=x (èäåìïîòåíòíîñòü); L1

x∨y=y∨x, x∧y=y∧x (êîììóòàòèâíîñòü); L2

x∧(y∧z)=(x∧y)∧z,

x∨(y∨z)=(x∨y)∨z (àññîöèàòèâíîñòü); L3

x∧(x∨y)=x, x∨(x∧y)=x (ïîãëîùåíèå). L4

Êðîìå òîãî, íåðàâåíñòâî x ≤ y ðàâíîñèëüíî êàæäîìó èç óñëîâèé:

x∧y=x è x∨y=y (óñëîâèå ñîâìåñòèìîñòè).

Äîêàçàòåëüñòâî. L1 è L2 âûïîëíÿþòñÿ î÷åâèäíî. Àññîöèàòèâ-

íûé çàêîí L3 òàêæå î÷åâèäåí: x∧(y∧z)=inf{x,inf{y,z}}=

=inf{inf{x,y}, z}=(x∧y) ∧z. Çàêîí ïîãëîùåíèÿ L4 âûïîëíèì â

ñèëó òîãî, ÷òî x∧(x∨y)=inf{x, sup{x, y}}. Åñëè x ≤ y, òî

sup{x,y}=y, è òîãäà inf{x, y} = x, à åñëè y ≤ x, òî sup{x, y} = x, è

òîãäà inf{x, x} = x. Óñëîâèå ñîâìåñòèìîñòè: x∧y=x, åñëè x ≤ y, è

x∨y=y, åñëè x ≤ y, âûïîëíÿåòñÿ òàêæå î÷åâèäíî.

Èç óñëîâèÿ ñîâìåñòèìîñòè ñëåäóþò âàæíûå ñâîéñòâà óíèâåð-

ñàëüíûõ ãðàíåé 0 è I.

Ëåììà 6.2. Åñëè ó-ìíîæåñòâî P èìååò 0, òî

0∧x=0 è 0∨x=x äëÿ âñÿêîãî x∈P,

è åñëè ó-ìíîæåñòâî P èìååò I, òî

x∧I=x è x∨I=I äëÿ âñÿêîãî x∈P.

Äîêàçàòåëüñòâî íå ïðåäñòàâëÿåò òðóäà.

Ëåììà 6.3. Âî âñÿêîé ðåøåòêå îïåðàöèè îáúåäèíåíèÿ è ïåðåñå-

÷åíèÿ èçîòîííû:

åñëè y ≤ z, òî x∧y ≤ x∧z è x∨y ≤ x∨z.

Äîêàçàòåëüñòâî. Ñîãëàñíî L1  L4, åñëè y ≤ z, òî x∧y=

=(x∧x)∧(y∧z)=(x∧y) ∧(x∧z). Ó÷èòûâàÿ, ÷òîx∧x=x

èy∧z=y, ïî óñëîâèþ ñîâìåñòèìîñòè ïîëó÷àåì x∧y ≤ x∧z.

Âòîðîå íåðàâåíñòâî äîêàçûâàåòñÿ äâîéñòâåííî.

Ãëàâà 6 Ðåøåòêè

78 79

Ëåììà 6.4. Âî âñÿêîé ðåøåòêå èìåþò ìåñòî ñëåäóþùèå íåðàâåí-

ñòâà äèñòðèáóòèâíîñòè:

x∧(y∨z) ≥ (x∧y)∨(x∧z), (6.1)

x∨(y∧z) ≤ (x∨y) ∧(x∨z). (6.1')

Äîêàçàòåëüñòâî. Î÷åâèäíî, ÷òî x∧y ≤ x è x∧y ≤ y ≤ y∨z,

îòêóäà x∧y ≤ x∧(y∨z). Àíàëîãè÷íî: x∧z ≤ x è x∧z≤z≤y∨z,

îòêóäà x∧z ≤ x∧(y∨z). Òàêèì îáðàçîì, x∧(y∨z) ÿâëÿåòñÿ âåðõ-

íåé ãðàíüþ äëÿ x∧y è x∧z è, ñëåäîâàòåëüíî, âûïîëíÿåòñÿ (6.1).

(6.1') äîêàçûâàåòñÿ äâîéñòâåííî.

Ëåììà 6.5. Ýëåìåíòû ëþáîé ðåøåòêè óäîâëåòâîðÿþò íåðàâåí-

ñòâó ìîäóëÿðíîñòè:

åñëè x≤z, òî x∨(y∧z) ≤ (x∨y) ∧z. (6.2)

Äîêàçàòåëüñòâî. x ≤ x∨y è x ≤ z, çíà÷èò x ≤ (x∨y)∧z. Àíàëî-

ãè÷íî, y∧z ≤ y ≤ x∨y è y∧z ≤ z, ñëåäîâàòåëüíî, y∧z≤(x∨y)∧z,

îòñþäà x∨(y∧z) ≤ (x∨y) ∧z.

Äàäèì ñëåäóþùèå îïðåäåëåíèÿ.

Îïðåäåëåíèå 6.6. Ñèñòåìà ñ îäíîé áèíàðíîé èäåìïîòåíòíîé,

êîììóòàòèâíîé è àññîöèàòèâíîé îïåðàöèåé íàçûâàåòñÿ ïîëóðå-

øåòêîé. Ó-ìíîæåñòâî P, â êîòîðîì ëþáûå äâà ýëåìåíòà èìåþò

ïåðåñå÷åíèå, ÿâëÿåòñÿ ïîëóðåøåòêîé îòíîñèòåëüíî áèíàðíîé

îïåðàöèè ∧. Òàêèå ïîëóðåøåòêè íàçûâàþòñÿ ∧-ïîëóðåøåòêàìè,

èëè íèæíèìè ïîëóðåøåòêàìè. Ó-ìíîæåñòâî P, â êîòîðîì ëþáûå

äâà ýëåìåíòà èìåþò îáúåäèíåíèå, ÿâëÿåòñÿ ïîëóðåøåòêîé

îòíîñèòåëüíî áèíàðíîé îïåðàöèè ∨. Òàêèå ïîëóðåøåòêè

íàçûâàþòñÿ ∨-ïîëóðåøåòêàìè, èëè âåðõíèìè ïîëóðåøåòêàìè.

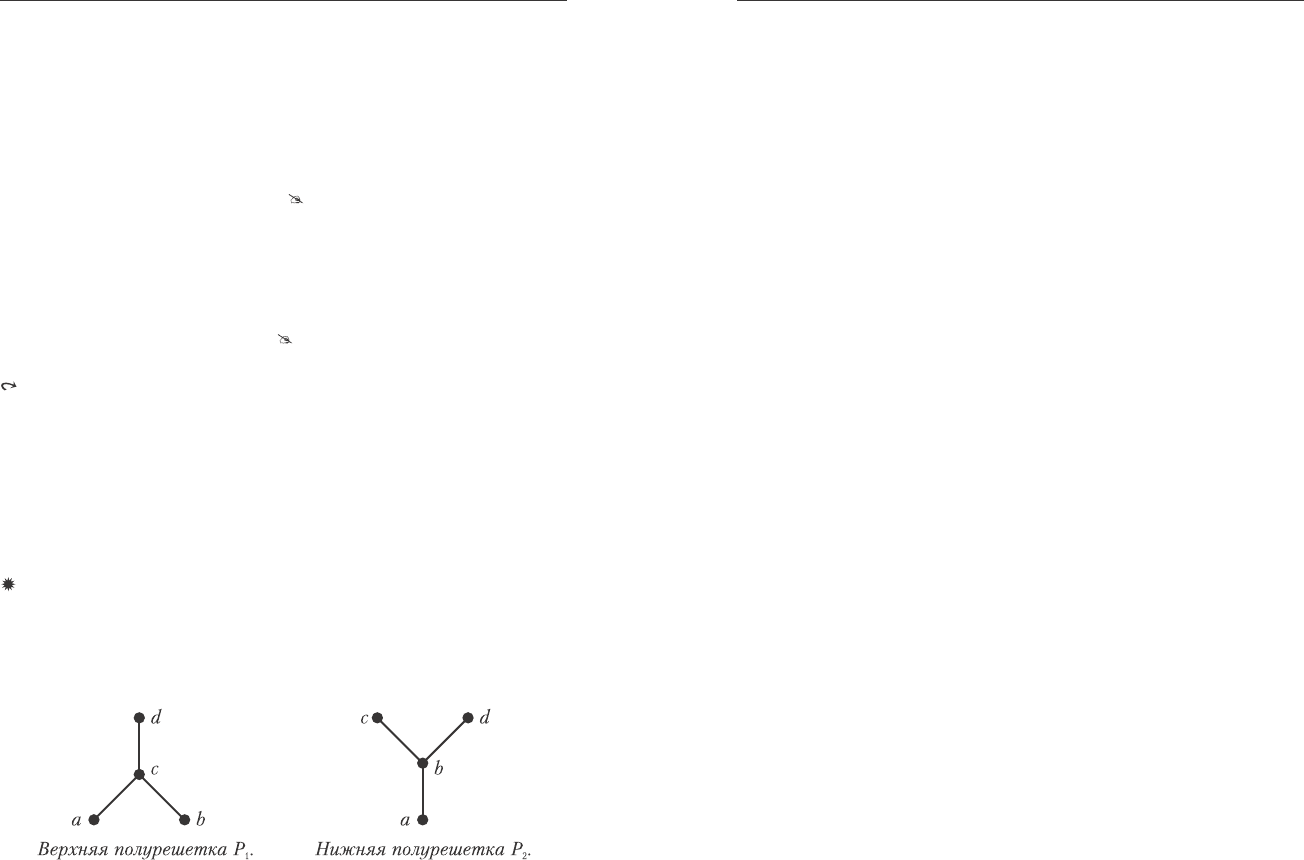
Ïðèìåð. Íà ðèñ. 6.2 ïðèâåäåíû äèàãðàììû âåðõíåé è íèæíåé

ïîëóðåøåòîê. Â ó-ìíîæåñòâå P

ëþáûå äâà ýëåìåíòà èìåþò

îáúåäèíåíèå, îäíàêî ýëåìåíòû a è b íå èìåþò ïåðåñå÷åíèÿ, ïîýòîìó

ÿâëÿåòñÿ âåðõíåé ïîëóðåøåòêîé; â ó-ìíîæåñòâå P

ëþáûå äâà

ýëåìåíòà èìåþò ïåðåñå÷åíèå, îäíàêî ýëåìåíòû c è d íå èìåþò îáúå-

äèíåíèÿ, ïîýòîìó ýòî íèæíÿÿ ïîëóðåøåòêà.

Ðèñ. 6.2. Ïîëóðåøåòêè.

Òåïåðü äîêàæåì âàæíóþ ëåììó, êîòîðàÿ ñâÿçûâàåò ïîëóðåøåòêó

êàê àëãåáðó ñ ïîíÿòèåì ó-ìíîæåñòâà. Ýòà ëåììà óòâåðæäàåò, ÷òî

åñëè çàäàíà àëãåáðà íà ìíîæåñòâå P ñ îäíîé áèíàðíîé îïåðàöèåé,

óäîâëåòâîðÿþùåé ñâîéñòâàì èäåìïîòåíòíîñòè, êîììóòàòèâíîñòè

è àññîöèàòèâíîñòè, òî ýòà îïåðàöèÿ çàäàåò îòíîøåíèå ïîðÿäêà íà

P, ò.å. ìíîæåñòâî, íà êîòîðîì çàäàíà ýòà îïåðàöèÿ, ÿâëÿåòñÿ ó-

ìíîæåñòâîì. Òàêèì îáðàçîì, ìû ìîæåì íè÷åãî íå çíàòü î ñóùåñòâî-

âàíèè êàêèõ-ëèáî îòíîøåíèé íà ìíîæåñòâå P, íî çàäàíèå îïåðàöèè

ñî ñâîéñòâàìè L1, L2, L3 îïðåäåëÿåò îòíîøåíèå ïîðÿäêà íà íåì.

Ëåììà 6.6. Åñëè â ïîëóðåøåòêå ñ áèíàðíîé îïåðàöèåé o

ïîëîæèòü

x ≤ y òîãäà è òîëüêî òîãäà, êîãäà xoó=x,

òî îíà ñòàíîâèòñÿ ó-ìíîæåñòâîì, â êîòîðîì inf{x, y}=xoy.

Ïîÿñíèì ñìûñë ëåììû. Â ëåììå çàäàíî íåêîòîðîå ìíîæåñòâî ñ

íåêîòîðîé áèíàðíîé îïåðàöèåé o, è, ïîñêîëüêó óêàçàíî, ÷òî

ìíîæåñòâî îáðàçóåò ïîëóðåøåòêó, òî ýòî îçíà÷àåò, ÷òî îïåðàöèÿ o

ÿâëÿåòñÿ èäåìïîòåíòíîé, êîììóòàòèâíîé è àññîöèàòèâíîé. Äàëåå

ìû ââîäèì íåêîòîðîå (ïîêà àáñòðàêòíîå) îòíîøåíèå ≤ íà ìíîæåñòâå

òàêèì îáðàçîì, ÷òî åñëè xoó=x, òî x≤y, è íàîáîðîò, åñëè x ≤ y, òî

xoó=x, ò.å. ýòè äâà óñëîâèÿ ðàâíîçíà÷íû. Íóæíî äîêàçàòü, ÷òî

îòíîøåíèå ≤ ÿâëÿåòñÿ îòíîøåíèåì ïîðÿäêà, è îïåðàöèÿ o èìååò

ñìûñë íàõîæäåíèÿ òî÷íîé íèæíåé ãðàíè x è y.

Äîêàçàòåëüñòâî.

1. Ñíà÷àëà äîêàæåì, ÷òî îòíîøåíèå ≤ ÿâëÿåòñÿ îòíîøåíèåì

ïîðÿäêà, ò.å. óäîâëåòâîðÿåò ñâîéñòâàì ðåôëåêñèâíîñòè,

àíòèñèììåòðè÷íîñòè è òðàíçèòèâíîñòè: Ð1, Ð2, Ð3.

Ïî ïðåäïîëîæåíèþ ëåììû, x ≤ y òîãäà è òîëüêî òîãäà, êîãäà

xoó=x. Èç çàêîíà èäåìïîòåíòíîñòè xox =x ñëåäóåò ðåôëåêñèâíîñòü

îòíîøåíèÿ: x ≤ x. Â ñèëó êîììóòàòèâíîñòè xoó=yox ïîëó÷àåì

àíòèñèììåòðè÷íîñòü: åñëè x≤ y, òî ïî óñëîâèþ xoó=x, è åñëè y≤x,

òî yox=y. Òîãäà, åñëè âûïîëíÿþòñÿ îäíîâðåìåííî x≤ y è x≤ y, òî

x= xoó=yox=y, ò.å. îòíîøåíèå ≤ àíòèñèììåòðè÷íî. Ïðèìåíÿÿ

àññîöèàòèâíûé çàêîí, èç x≤ y è y≤ z ïîëó÷èì x ≤ z. Äåéñòâèòåëüíî,

åñëè x≤ y è y≤ z, òî x = xoyè y= yoz, ò.å. x=xoó=xo(yoz)=

=(xoy)oz= xoz, îòêóäà x ≤ z, ò.å. äîêàçàíà òðàíçèòèâíîñòü ≤. Îòñþäà

ñëåäóåò, ÷òî ≤ ÿâëÿåòñÿ îòíîøåíèåì ïîðÿäêà.

2. Òåïåðü äîêàæåì, ÷òîxoy = inf{x, y} äëÿ ëþáûõ x, y. Äîêàæåì

ñíà÷àëà, ÷òî xoy ≤ x è xoy≤ y. Åñëè x≤ y, òî xoó = x ïî îïðåäåëåíèþ,

è, ñëåäîâàòåëüíî, xoó≤ y, à â ñèëó ðåôëåêñèâíîñòè x ≤ x ñïðàâåäëèâî

è xoó≤ x. Íàêîíåö, åñëè x è y íåñðàâíèìû, òî, â ñèëó òîãî, ÷òî

îïåðàöèÿ o âñþäó îïðåäåëåíà, íàéäåòñÿ z ≤ x è z ≤ y. Òîãäà zo(xoy)=

= (zox)oy = zoy = z, îòêóäà z ≤xoy, è, ñëåäîâàòåëüíî, xoy = inf{x,y}.

Ãëàâà 6 Ðåøåòêè