Таран Т.А. Основы дискретной математики

Подождите немного. Документ загружается.

20 21

Ïðèìåðû.

• Íà ìíîæåñòâå N îïðåäåëåíî îòíîøåíèå α: x<y. Òîãäà òðàíçè-

òèâíûì çàìûêàíèåì ýòîãî îòíîøåíèÿ äëÿ çíà÷åíèé 1<2<...<6

áóäåò îòíîøåíèå 1<6 (ñì. ðèñ. 2.7).

• Òðàíçèòèâíûì çàìûêàíèåì îòíîøåíèÿ «áûòü ñûíîì» ÿâëÿåòñÿ

îòíîøåíèå «áûòü ïðÿìûì ïîòîìêîì».

• Òðàíçèòèâíûì çàìûêàíèåì îòíîøåíèÿ «èìåòü îáùóþ ñòåíó» äëÿ

æèëüöîâ îäíîãî äîìà ÿâëÿåòñÿ îòíîøåíèå «æèòü íà îäíîì ýòàæå».

2.3.2. Îñíîâíûå ñâîéñòâà îòíîøåíèé

Áóäåì ðàññìàòðèâàòü îòíîøåíèÿ, çàäàííûå íà ìíîæåñòâå X, ò.å.

y, x,y ∈X.

Îïðåäåëåíèå 2.12. Îòíîøåíèå ρ íà ìíîæåñòâå X íàçûâàåòñÿ

ðåôëåêñèâíûì, åñëè äëÿ ëþáûõ x∈X âûïîëíÿåòñÿ xρx. Åñëè

äëÿ âñåõ x∈X íå âûïîëíÿåòñÿ xρx, òî îòíîøåíèå íàçûâàåòñÿ

àíòèðåôëåêñèâíûì.

Ïðèìåðû. Îòíîøåíèå ðàâåíñòâà ðåôëåêñèâíî. Îòíîøåíèå x≥y,

x, y∈R ðåôëåêñèâíî, òàê êàê x ≥ x. Îòíîøåíèå x > y, x, y∈R

àíòèðåôëåêñèâíî, òàê êàê íè äëÿ îäíîãî ÷èñëà íå âûïîëíèìî x>x.

Îïðåäåëåíèå 2.13. Îòíîøåíèå ρ íà ìíîæåñòâå X íàçûâàåòñÿ ñèì-

ìåòðè÷íûì, åñëè äëÿ ëþáûõ x∈X, y∈X, èç xρy ñëåäóåò yρx.

Èíûìè ñëîâàìè, îòíîøåíèå ñèììåòðè÷íî, åñëè âñÿêèé ðàç, êàê

âûïîëíÿåòñÿ xρy, âûïîëíÿåòñÿ è yρx.

Ïðèìåðû. Èç òîãî, ÷òî «x ðîäñòâåííèê y», ñëåäóåò, ÷òî «y

ðîäñòâåííèê x», îòíîøåíèå ñèììåòðè÷íî. Îòíîøåíèå «x  ñåñòðà

y», îïðåäåëåííîå íà ìíîæåñòâå âñåõ ëþäåé, íåñèììåòðè÷íî: âîçìîæ-

íî, ÷òî y ÿâëÿåòñÿ áðàòîì x. Îäíàêî òî æå îòíîøåíèå, îïðåäåëåííîå

íà ìíîæåñòâå æåíùèí, ÿâëÿåòñÿ ñèììåòðè÷íûì.

Îïðåäåëåíèå 2.14. Îòíîøåíèå ρ íà ìíîæåñòâå X íàçûâàåòñÿ

àíòèñèììåòðè÷íûì, åñëè äëÿ ëþáûõ x,y∈X, èç òîãî, ÷òî xρy

è yρx, ñëåäóåò x=y.

Ïðèìåðû. Îòíîøåíèå x ≤ y àíòèñèììåòðè÷íî: èç òîãî, ÷òî x≤y

è y ≤ x, ñëåäóåò, ÷òî x=y, ò.å. ýòî îäèí è òîò æå ýëåìåíò.

Åñëè äëÿ ëþáûõ x,y∈Õ èç òîãî, ÷òî xρy, ñëåäóåò, ÷òî íå

âûïîëíÿåòñÿ yρx, òî îòíîøåíèå íàçûâàåòñÿ àñèììåòðè÷íûì.

Îòíîøåíèÿ «x ïðåäîê ó» è «ó ïîòîìîê x» àñèììåòðè÷íû, ïðè÷åì

âòîðîå ÿâëÿåòñÿ îáðàòíûì ê ïåðâîìó. Îòíîøåíèå ñòðîãîãî ïîðÿäêà

x < y ÿâëÿåòñÿ àñèììåòðè÷íûì: åñëè âûïîëíÿåòñÿ x < y, òî íå

âûïîëíÿåòñÿ y < x.

Îïðåäåëåíèå 2.15. Îòíîøåíèå ρ íàçûâàåòñÿ òðàíçèòèâíûì,

åñëè èç òîãî, ÷òî xρy è yρz, ñëåäóåò xρz.

Ïðèìåð. Îòíîøåíèå «x ïðåäîê y» òðàíçèòèâíî: åñëè «x ïðåäîê

y» è «y ïðåäîê z», òî «x ïðåäîê z». Îòíîøåíèå x < y, ãäå x, y ∈ R,

òðàíçèòèâíî: åñëè x < y è y < z, òî x < z. Îòíîøåíèå «x ëþáèò y»,

â îáùåì ñëó÷àå íåòðàíçèòèâíî: åñëè «x ëþáèò y», à «y ëþáèò z», òî

èç ýòîãî íå ñëåäóåò, ÷òî «x ëþáèò z».

2.4. Îòíîøåíèå ýêâèâàëåíòíîñòè

Îïðåäåëåíèå 2.16. Îòíîøåíèå, êîòîðîå îáëàäàåò ñâîéñòâàìè

ðåôëåêñèâíîñòè, ñèììåòðè÷íîñòè è òðàíçèòèâíîñòè, íàçûâàåòñÿ

îòíîøåíèåì ýêâèâàëåíòíîñòè.

Ïðèìåðû îòíîøåíèé ýêâèâàëåíòíîñòè.

1. Îòíîøåíèå ðàâåíñòâà íà ëþáîì ìíîæåñòâå ÿâëÿåòñÿ îòíîøåíèåì ýê-

âèâàëåíòíîñòè, ïðè÷åì îòíîøåíèå ðàâåíñòâà ÿâëÿåòñÿ â íåêîòîðîì ñìûñëå

ìèíèìàëüíûì (ïðåäåëüíûì) ñëó÷àåì îòíîøåíèÿ ýêâèâàëåíòíîñòè.

2. Ãåîìåòðè÷åñêîå îòíîøåíèå ïîäîáèÿ òðåóãîëüíèêîâ íà ïëîñêîñòè

ÿâëÿåòñÿ îòíîøåíèåì ýêâèâàëåíòíîñòè.

3. Îòíîøåíèÿ ñðàâíèìîñòè ïî ìîäóëþ n â Z: x ñðàâíèìî ñ ó ïî

ìîäóëþ n, åñëè ðàçíîñòü xó äåëèòñÿ íà n (áåç îñòàòêà).

Îáîçíà÷àåòñÿ: x ≡ ó (mod n). Íàïðèìåð: 3 ≡ 6(mod 3), 7≡13(mod3).

4. Îòíîøåíèå ïàðàëëåëüíîñòè ïðÿìûõ â åâêëèäîâîì ïðîñòðàíñòâå

åñòü îòíîøåíèå ýêâèâàëåíòíîñòè.

5. Óòâåðæäåíèÿ âèäà sin

x+cos

x=1, (a+b)(ab)=a

b

ñîñòîÿùèå èõ ôîðìóë, ñîåäèíåííûõ çíàêîì ðàâåíñòâà, çàäàþò áè-

íàðíîå îòíîøåíèå íà ìíîæåñòâå ôîðìóë, îïèñûâàþùèõ ñóïåðïîçè-

öèè ýëåìåíòàðíûõ ôóíêöèé. Ýòî îòíîøåíèå ðàâíîñèëüíîñòè òàêæå

ÿâëÿåòñÿ îòíîøåíèåì ýêâèâàëåíòíîñòè: ôîðìóëû ðàâíîñèëüíû,

åñëè îíè çàäàþò îäíó è òó æå ôóíêöèþ.

6. Îòíîøåíèå «ñòóäåíòû x è y ó÷àòñÿ â îäíîé ãðóïïå», ãäå

x,y∈{«ñòóäåíòû ïåðâîãî êóðñà»}, åñòü îòíîøåíèå ýêâèâàëåíòíîñòè.

7. Îòíîøåíèå «æèòü â îäíîì ðàéîíå», îïðåäåëåííîå íà ìíîæåñòâå

ëþäåé, æèâóùèõ â ã. Êèåâå, ÿâëÿåòñÿ îòíîøåíèåì ýêâèâàëåíòíîñòè.

Ìíîæåñòâî âñåõ æèòåëåé Êèåâà ðàçáèâàåòñÿ ïîñëåäíèì îòíîøå-

íèåì ýêâèâàëåíòíîñòè íà ðÿä íåïåðåñåêàþùèõñÿ ïîäìíîæåñòâ, â

äàííîì ñëó÷àå íà ìíîæåñòâà ëþäåé, æèâóùèõ â îäíîì è òîì æå

ðàéîíå. Äâà æèòåëÿ ñ÷èòàþòñÿ ýêâèâàëåíòíûìè ïî äàííîìó îòíîøå-

íèþ, åñëè îíè æèâóò â îäíîì è òîì æå ðàéîíå, è â ýòîì ñìûñëå

îíè íåðàçëè÷èìû, ò.å. îíè îáëàäàþò îäíèì è òåì æå ñâîéñòâîì:

«æèòü â ðàéîíå «ÕÕÕ». Ýòî ñâîéñòâî ÿâëÿåòñÿ îïðåäåëÿþùèì

ñâîéñòâîì (ïðåäèêàòîì) ìíîæåñòâà âñåõ æèòåëåé ðàéîíà «ÕÕÕ».

Ñ äðóãîé ñòîðîíû, íåëüçÿ æèòü â äâóõ (è áîëåå) ðàéîíàõ ñðàçó (âî

âñÿêîì ñëó÷àå, ñîãëàñíî ïðîïèñêå), ïîýòîìó ìíîæåñòâà æèòåëåé

ðàçëè÷íûõ ðàéîíîâ íå ïåðåñåêàþòñÿ. Òàêèì îáðàçîì, îòíîøåíèå

Òåîðèÿ îòíîøåíèéÃëàâà 2

22 23

«æèòü â îäíîì ðàéîíå» ðàçáèâàåò âñå ìíîæåñòâî æèòåëåé ãîðîäà

íà ðÿä íåïåðåñåêàþùèõñÿ ïîäìíîæåñòâ, òàêèõ, ÷òî âíóòðè êàæäîãî

ïîäìíîæåñòâà âñå æèòåëè ýêâèâàëåíòíû ïî äàííîìó îòíîøåíèþ,

è íèêàêèå äâà æèòåëÿ ðàçíûõ ïîäìíîæåñòâ íå íàõîäÿòñÿ â îòíîøå-

íèè ýêâèâàëåíòíîñòè äðóã ñ äðóãîì. Òàêèå ïîäìíîæåñòâà íàçûâà-

þòñÿ êëàññàìè ýêâèâàëåíòíîñòè.

Äàäèì áîëåå ñòðîãîå îïðåäåëåíèå.

Îïðåäåëåíèå 2.17. Ïóñòü íà ìíîæåñòâå X çàäàíî îòíîøåíèå

ýêâèâàëåíòíîñòè ρ. Òîãäà ïîäìíîæåñòâî A⊆X íàçûâàåòñÿ

êëàññîì ýêâèâàëåíòíîñòè ïî îòíîøåíèþ ρ, åñëè A ñîñòîèò èç

âñåõ òåõ ýëåìåíòîâ x∈X, ÷òî äëÿ íåêîòîðîãî a∈X, a∈A è xρa.

Ìîæíî ïîñòðîèòü êëàññû ýêâèâàëåíòíîñòè ñëåäóþùèì îáðàçîì.

Âûáåðåì ýëåìåíò a

, ïðèíàäëåæàùèé X, è îáðàçóåì ïîäìíîæåñòâî

⊆X èç a

è âñåõ ýëåìåíòîâ, ýêâèâàëåíòíûõ a

. Ýòî áóäåò êëàññ

ýêâèâàëåíòíîñòè A

. Äàëåå âûáåðåì ýëåìåíò a

∈X, a

∉A

, è îáðàçó-

åì êëàññ A

, ñîñòîÿùèé èç âñåõ ýëåìåíòîâ, ýêâèâàëåíòíûõ a

, èò.ä.

Ïîëó÷èì ñèñòåìó êëàññîâ A

, A

, ..., òàêóþ, ÷òî ëþáîé ýëåìåíò a

∈X

âõîäèò òîëüêî â îäèí êëàññ, îáúåäèíåíèå âñåõ êëàññîâ A

∪A

∪...

îáðàçóåò ìíîæåñòâî X, è äëÿ ëþáûõ i, j A

∩ A

=∅, ò.å. ìíîæåñòâî

êëàññîâ ýêâèâàëåíòíîñòè îáðàçóåò ðàçáèåíèå ìíîæåñòâà X.

Ïîëó÷åííàÿ ñèñòåìà êëàññîâ ýêâèâàëåíòíîñòè îáëàäàåò ñëåäóþ-

ùèìè ñâîéñòâàìè.

Òåîðåìà 2.1.

1. Ïóñòü

åñòü îòíîøåíèå ýêâèâàëåíòíîñòè íà X. Òîãäà ìíîæå-

ñòâî êëàññîâ ýêâèâàëåíòíîñòè ïî îòíîøåíèþ ρ åñòü ðàçáèåíèå

ìíîæåñòâà X. Îáðàòíî, åñëè åñòü íåêîòîðîå ðàçáèåíèå ℜ ìíîæå-

ñòâà X, à îòíîøåíèå ρ òàêîâî, ÷òî aρb òîãäà è òîëüêî òîãäà,

êîãäà a∈A, b∈A, A⊆ℜ, òî ρ åñòü îòíîøåíèå ýêâèâàëåíòíîñòè

íà X.

2. Åñëè îòíîøåíèå ýêâèâàëåíòíîñòè ρ îïðåäåëÿåò ðàçáèåíèå ℜ

ìíîæåñòâà X, òî îòíîøåíèå ýêâèâàëåíòíîñòè, îïðåäåëÿåìîå ýòèì

ðàçáèåíèåì ℜ, ñîâïàäàåò ñ ρ. Îáðàòíî, åñëè íåêîòîðîå ðàçáèåíèå

Â ìíîæåñòâà X îïðåäåëÿåò íåêîòîðîå îòíîøåíèå ýêâèâàëåíò-

íîñòè ρ, òî ðàçáèåíèå ℜ ìíîæåñòâà X, îïðåäåëÿåìîå ýòèì îòíî-

øåíèåì ρ, ñîâïàäàåò ñ Â.

Äîêàçàòåëüñòâî. Äîêàçàòåëüñòâî ïåðâîé ÷àñòè òåîðåìû ñëåäóåò

èç ñâîéñòâ îòíîøåíèÿ ýêâèâàëåíòíîñòè. Êàæäûé ýëåìåíò X âîéäåò

õîòÿ áû â îäèí êëàññ ýêâèâàëåíòíîñòè. Ïðåäïîëîæèì, ÷òî íåêîòî-

ðûé ýëåìåíò b âõîäèò îäíîâðåìåííî â äâà êëàññà ýêâèâàëåíòíîñòè

è A

. Òîãäà ñóùåñòâóåò a

∈A

òàêîå, ÷òî a

ρb, è ñóùåñòâóåò a

∈A

òàêîå, ÷òî bρa

. Íî òîãäà, â ñèëó ñâîéñòâà òðàíçèòèâíîñòè, a

ρa

è,

ñëåäîâàòåëüíî, êëàññû A

è A

åñòü îäèí è òîò æå êëàññ.

Ïóñòü òåïåðü ℜ åñòü ðàçáèåíèå ìíîæåñòâà X. Îòíîøåíèå ρ

ñèììåòðè÷íî ïî îïðåäåëåíèþ. Åñëè a∈X, òî â ℜ íàéäåòñÿ òàêîå

ìíîæåñòâî A, ÷òî a∈A, òàê ÷òî ρ ðåôëåêñèâíî. Ïîêàæåì, ÷òî îíî

òðàíçèòèâíî. Ïóñòü aρb è bρc. Òîãäà â ℜ íàéäåòñÿ òàêîå A, ÷òî a,

b∈A, è òàêîå B, ÷òî b, c∈B. Ïîñêîëüêó b∈B è b∈A, òî A=B.

Ñëåäîâàòåëüíî aρc.

Íà îñíîâàíèè ýòîé òåîðåìû ìîæíî äàòü êîíñòðóêòèâíîå îïðåäå-

ëåíèå îòíîøåíèÿ ýêâèâàëåíòíîñòè: îòíîøåíèå ρ íà ìíîæåñòâå Õ

íàçûâàåòñÿ ýêâèâàëåíòíîñòüþ, åñëè ñóùåñòâóåò ðàçáèåíèå Õ íà

ïîäìíîæåñòâà {A

, A

,..., A

} òàêîå, ÷òî îòíîøåíèå xρó âûïîëíÿåòñÿ

òîãäà è òîëüêî òîãäà, åñëè x è ó ïðèíàäëåæàò îäíîìó è òîìó æå

ïîäìíîæåñòâó.

Áóäåì îáîçíà÷àòü êëàññ ýêâèâàëåíòíîñòè, ïîðîæäåííûé ýëåìåí-

òîì a∈X ÷åðåç [a]. Òîãäà, åñëè aρb, òî [a]=[b].

Îïðåäåëåíèå 2.18. Ìíîæåñòâî êëàññîâ ýêâèâàëåíòíîñòè ìíîæå-

ñòâà X ïî îòíîøåíèþ ρ íàçûâàåòñÿ ôàêòîð-ìíîæåñòâîì ìíîæå-

ñòâà X ïî îòíîøåíèþ ρ è îáîçíà÷àåòñÿ [X/ρ].

Ïðèìåðû.

1.Âñå êëàññû ýêâèâàëåíòíîñòè ïî îòíîøåíèþ ðàâåíñòâà ñîñòîÿò

èç îäíîãî ýëåìåíòà. Ôàêòîð-ìíîæåñòâî ïî îòíîøåíèþ ðàâåíñòâà

ñîñòîèò èç ýëåìåíòîâ ñàìîãî ìíîæåñòâà.

2.Ñâîéñòâî ïàðàëëåëüíîñòè ïðÿìûõ íà ïëîñêîñòè îïðåäåëÿåò

îòíîøåíèå ýêâèâàëåíòíîñòè. Ôàêòîð-ìíîæåñòâî ýòîãî îòíîøåíèÿ

ìíîæåñòâî âñåõ íàïðàâëåíèé íà ïëîñêîñòè. Îíî ìîæåò áûòü

îïèñàíî, êàê ìíîæåñòâî âñåõ óãëîâ íàêëîíà ïðÿìîé ê îñè àáñöèññ,

ò.å. èíòåðâàë [0°, 180°).

3. Ïóñòü õ, ó ∈ Z. Ðàññìîòðèì îòíîøåíèå ñðàâíèìîñòè ïî ìîäóëþ3:

xρy åñòü x≡y(mod3). Çàïèñü x≡y(mod 3) îçíà÷àåò,

÷òî ðàçíîñòüõó

äåëèòñÿ íà 3 áåç îñòàòêà. Áóäåì îáîçíà÷àòü ýòî òàê: xρyåñòü (õó)/3=

=k∈Z. Äîêàæåì, ÷òî x≡y(mod 3)  îòíîøåíèå ýêâèâàëåíòíîñòè.

3.1. Ïðîâåðèì âûïîëíåíèå ñâîéñòâà ðåôëåêñèâíîñòè: äëÿ âñÿêîãî

xxρx. Äåéñòâèòåëüíî, (xx)/3 = 0/3 = 0; 0∈Z, ñëåäîâàòåëüíî,

îòíîøåíèå ðåôëåêñèâíî.

3.2. Ïðîâåðèì âûïîëíåíèå ñâîéñòâà ñèììåòðè÷íîñòè: åñëè xρy, òî

óρõ. Ïóñòü (õó)/3 = k ∈Z. Òîãäà (óõ)/3 = (õó)/3 = k∈Z.

Ñëåäîâàòåëüíî, óñëîâèå ñèììåòðè÷íîñòè âûïîëíÿåòñÿ.

3.3. Ïðîâåðèì âûïîëíåíèå ñâîéñòâà òðàíçèòèâíîñòè: èç xρy è óρz

ñëåäóåò xρz. Ïóñòü (õó)/3 = k

∈Z, ò.å. õó = 3k

, è (yz)/3 =

∈Z, ò.å. yz = 3k

. Ðåøèì ýòó ñèñòåìó óðàâíåíèé, ñëîæèâ èõ:

õó+yz= 3(k

+k

), ò.å. xz = 3(k

+k

)= k

∈Z. Óñëîâèå

òðàíçèòèâíîñòè âûïîëíÿåòñÿ.

Òåîðèÿ îòíîøåíèéÃëàâà 2

24 Ãëàâà 2

Ñëåäîâàòåëüíî, îòíîøåíèå õ≡ó(mod 3) ÿâëÿåòñÿ îòíîøåíèåì

ýêâèâàëåíòíîñòè. Íàéäåì åãî ôàêòîð-ìíîæåñòâî [Z/ρ].

Ïðîèçâîëüíîå ÷èñëî õ∈Z ìîæíî çàïèñàòü â âèäå 3q+r, ãäå q,

r∈Z, 0≤r<3. Â îäèí è òîò æå êëàññ ýêâèâàëåíòíîñòè ïîïàäóò

âñå ÷èñëà, äàþùèå ïðè äåëåíèè íà 3 îäèíàêîâîå ÷èñëî r â îñòàòêå.

Ìû ïîëó÷èì òðè êëàññà ýêâèâàëåíòíîñòè: [0] = {0, 3, 6, 9, 12, };

[1] = {1, 4, 7, 10, 13, }; [2] = {2, 5, 8, 11, 14, }. Â êëàññ [0] ïîïàäàþò

âñå ÷èñëà, êîòîðûå äåëÿòñÿ íà 3 áåç îñòàòêà, â êëàññ [1]  âñå ÷èñëà,

ïðè äåëåíèè íà 3 äàþùèå â îñòàòêå 1, è â êëàññ [2]  âñå ÷èñëà,

äàþùèå â îñòàòêå 2. Êàæäûé êëàññ ìîæíî îõàðàêòåðèçîâàòü îäíèì

ïðåäñòàâèòåëåì ýòîãî êëàññà, è â äàííîì ñëó÷àå òàêèì

ïðåäñòàâèòåëåì óäîáíåå âñåãî âûáðàòü îñòàòîê r. Ñëåäîâàòåëüíî,

ôàêòîð-ìíîæåñòâîì Z ïî îòíîøåíèþ õ≡ó(mod 3) áóäåò

[Z/õ≡ó(mod 3)]={[0], [1], [2]}.

Ãëàâà 3. ÎÒÎÁÐÀÆÅÍÈß. ÔÓÍÊÖÈÈ

3.1. Îñíîâíûå ïîíÿòèÿ

Â ïðåäûäóùåé ãëàâå ìû ðàññìîòðåëè áèíàðíûå îòíîøåíèÿ,

êîòîðûå ÿâëÿþòñÿ ïîäìíîæåñòâàìè äåêàðòîâà ïðîèçâåäåíèÿ äâóõ

ìíîæåñòâ. Áèíàðíûå îòíîøåíèÿ, îïðåäåëåííûå íà äåêàðòîâîì

êâàäðàòå ìíîæåñòâà, ïðåäñòàâëÿþò íàèáîëüøèé èíòåðåñ, òàê êàê

îíè îáëàäàþò ðÿäîì ñâîéñòâ, êîòîðûå ïîçâîëÿþò âûäåëÿòü òàêèå

ïîëåçíûå îòíîøåíèÿ, êàê îòíîøåíèÿ ðàâåíñòâà, ýêâèâàëåíòíîñòè,

ïîðÿäêà. Äëÿ îòíîøåíèé, îáðàçîâàííûõ ðàçëè÷íûìè ìíîæåñòâàìè,

êîãäà

⊆E×F, ãîâîðèòü î ðåôëåêñèâíîñòè, ñèììåòðè÷íîñòè è

òðàíçèòèâíîñòè óæå íå èìååò ñìûñëà, òàê êàê ïåðâàÿ è âòîðàÿ

êîîðäèíàòà

ìîãóò èìåòü ðàçëè÷íóþ ïðèðîäó. Íàïðèìåð,

îòíîøåíèå «x ðîäèëñÿ â ãîäó y» ÿâëÿåòñÿ ïîäìíîæåñòâîì äåêàðòîâà

ïðîèçâåäåíèÿ ìíîæåñòâà ëþäåé è ìíîæåñòâà ëåò (ïîäìíîæåñòâà

öåëûõ ïîëîæèòåëüíûõ ÷èñåë) è ñòàâèò â ñîîòâåòñòâèå êàæäîìó

÷åëîâåêó ãîä åãî ðîæäåíèÿ. Äëÿ èññëåäîâàíèÿ ïîäîáíûõ îòíîøåíèé

ââîäÿòñÿ ïîíÿòèÿ ñîîòâåòñòâèÿ, îòîáðàæåíèÿ, ôóíêöèè.

Îïðåäåëåíèå 3.1. Ãîâîðÿò, ÷òî ìåæäó ìíîæåñòâàìè E è F îïðå-

äåëåíî ñîîòâåòñòâèå Ã, åñëè çàäàíî íåêîòîðîå ïðîèçâîëüíîå

ïîäìíîæåñòâî äåêàðòîâîãî ïðîèçâåäåíèÿ E×F. Ìíîæåñòâî E

íàçûâàåòñÿ îáëàñòüþ îïðåäåëåíèÿ, F  îáëàñòüþ çíà÷åíèé

ñîîòâåòñòâèÿ Ã.

Ñîîòâåòñòâèå, îáðàòíîå Ã, îáîçíà÷èì Ã

1

, ãäå F  îáëàñòü

îïðåäåëåíèÿ, E  îáëàñòü çíà÷åíèé Ã

1

Îïðåäåëåíèå 3.2. Îòîáðàæåíèåì ìíîæåñòâà E íà ìíîæåñòâî F

íàçûâàåòñÿ òàêîå ñîîòâåòñòâèå, êîòîðîå êàæäîìó ýëåìåíòó x∈E

ñîïîñòàâëÿåò ïî êðàéíåé ìåðå îäèí ýëåìåíò y∈F. Òîãäà ýëåìåíò

y íàçûâàåòñÿ îáðàçîì ýëåìåíòà x, à x  ïðîîáðàçîì ýëåìåíòà y,

èëè ïåðåìåííîé, èëè àðãóìåíòîì. Îòîáðàæåíèå E â F áóäåì

îáîçíà÷àòü f: E → F, ãäå f  èìÿ îòîáðàæåíèÿ.

Ïðèìåð. Íà ðèñ. 3.1 ïîêàçàíî ñîîòâåòñòâèå ìåæäó ìíîæåñòâàìè

E è F, íà ðèñ. 3.2  îòîáðàæåíèå ìíîæåñòâà E â ìíîæåñòâî F.

Ðèñ. 3.1. Ñîîòâåòñòâèå. Ðèñ. 3.2. Îòîáðàæåíèå.

26 27Ãëàâà 3 Îòîáðàæåíèÿ. Ôóíêöèè

3.1.1. Ñþðúåêöèÿ

Îïðåäåëåíèå 3.3. Îòîáðàæåíèå E íà F íàçûâàåòñÿ ñþðúåêòèâ-

íûì, èëè ñþðúåêöèåé, èëè íàëîæåíèåì, åñëè êàæäûé ýëåìåíò

y∈F åñòü îáðàç ïî êðàéíåé ìåðå îäíîãî ýëåìåíòà x∈E, ò.å.

∀y∈F∃x∈E (y=Ã(x)).

Óñëîâèå ∀ó∈F |Ã

1

(y)| ≥ 1 õàðàêòåðèçóåò ñþðúåêöèþ. Ýòî

îçíà÷àåò, ÷òî êàæäûé ýëåìåíò èç F èìååò íå ìåíåå îäíîãî ïðîîáðàçà

â E. Íà ãðàôå ñîîòâåòñòâèÿ â êàæäûé ýëåìåíò y âõîäèò ïî êðàéíåé

ìåðå îäíà äóãà (ðèñ. 3.3) è îáðàòíîå îòîáðàæåíèå Ã

1

(y) íå ïóñòî.

Ðèñ. 3.3. Ñþðúåêöèÿ.

3.1.2. Èíúåêöèÿ

Îïðåäåëåíèå 3.4. Îòîáðàæåíèå E â F íàçûâàåòñÿ èíúåêòèâíûì, èëè

èíúåêöèåé, èëè âëîæåíèåì, åñëè êàæäûé ýëåìåíò ó∈F åñòü îáðàç òîëüêî

îäíîãî ýëåìåíòà x∈E, ëèáî âîîáùå íå èìååò ïðîîáðàçà.

Â ýòîì ñëó÷àå E èíúåêòèâíî îòîáðàæàåòñÿ â F. Íà ãðàôå ñîîòâåò-

ñòâèÿ â êàæäûé ýëåìåíò y âõîäèò ñàìîå áîëüøåå îäíà äóãà, ò.å.

óñëîâèå ∀ó∈F |Ã

1

(y)| ≤ 1 õàðàêòåðèçóåò èíúåêöèþ. Íà ðèñ. 3.4.

ïîêàçàíà èíúåêöèÿ: â êàæäûé ýëåìåíò y âõîäèò ñàìîå áîëüøåå îäíà

äóãà; íåêîòîðûå ýëåìåíòû y íå èìåþò ïðîîáðàçîâ â E.

Ðèñ. 3.4. Èíúåêöèÿ.

3.1.3. Áèåêöèÿ

Îïðåäåëåíèå 3.5. Åñëè îòîáðàæåíèå ÿâëÿåòñÿ îäíîâðåìåííî è

ñþðúåêöèåé, è èíúåêöèåé, òî îíî íàçûâàåòñÿ áèåêòèâíûì îòî-

áðàæåíèåì, èëè áèåêöèåé.

Â ýòîì ñëó÷àå êàæäûé ýëåìåíò F ÿâëÿåòñÿ îáðàçîì íåêîòîðîãî,

è ïðèòîì åäèíñòâåííîãî, ýëåìåíòà èç E. Íà ãðàôå ñîîòâåòñòâèÿ íà

ðèñ. 3.5 ïîêàçàíà áèåêöèÿ: â êàæäûé ýëåìåíò y âõîäèò îäíà è òîëüêî

îäíà äóãà, ò.å. ïðè áèåêöèè êàæäûé îáðàç èìååò òîëüêî îäèí ïðî-

îáðàç: ∀ó∈F|Ã

1

(y)|=1.

Ðèñ. 3.5. Áèåêöèÿ.

3.1.4. Ôóíêöèîíàëüíûå îòîáðàæåíèÿ

Îïðåäåëåíèå 3.6. Ñîîòâåòñòâèå, ïðè êîòîðîì êàæäîìó x∈E

ñîïîñòàâëÿåòñÿ îäèí è òîëüêî îäèí ýëåìåíò ó∈F, íàçûâàåòñÿ

ôóíêöèîíàëüíûì ñîîòâåòñòâèåì, èëè ôóíêöèåé.

Äëÿ ôóíêöèîíàëüíîãî îòîáðàæåíèÿ âûïîëíÿåòñÿ óñëîâèå:

∀x∈E|Ã(x)|=1. Èíûìè ñëîâàìè, ôóíêöèÿ  ýòî ñîîòâåòñòâèå èëè

îòîáðàæåíèå, ïðè êîòîðîì äâà ðàçëè÷íûõ ýëåìåíòà íå èìåþò

îäèíàêîâûõ ïåðâûõ êîîðäèíàò, ò.å. åñëè <x,y>,<x,z>∈Ã, òî y=z.

Åñëè ôóíêöèîíàëüíîå ñîîòâåòñòâèå íå ÿâëÿåòñÿ îòîáðàæåíèåì, ò.å.

â E ñóùåñòâóþò ýëåìåíòû, íå èìåþùèå îáðàçà â F, òî îíî íàçûâàåòñÿ

÷àñòè÷íî îïðåäåëåííîé ôóíêöèåé. Ôóíêöèîíàëüíîå îòîáðàæåíèå

ÿâëÿåòñÿ ïîëíîñòüþ îïðåäåëåííîé ôóíêöèåé, èëè ïðîñòî ôóíêöèåé.

Â äàëüíåéøåì ìû áóäåì ðàññìàòðèâàòü òîëüêî ôóíêöèîíàëüíûå

îòîáðàæåíèÿ è îáîçíà÷àòü èõ ôóíêöèîíàëüíûìè ñèìâîëàìè ƒ, ϕ

èò.ï. Ôóíêöèÿ ìîæåò áûòü áèåêòèâíîé, ñþðúåêòèâíîé è èíúåêòèâ-

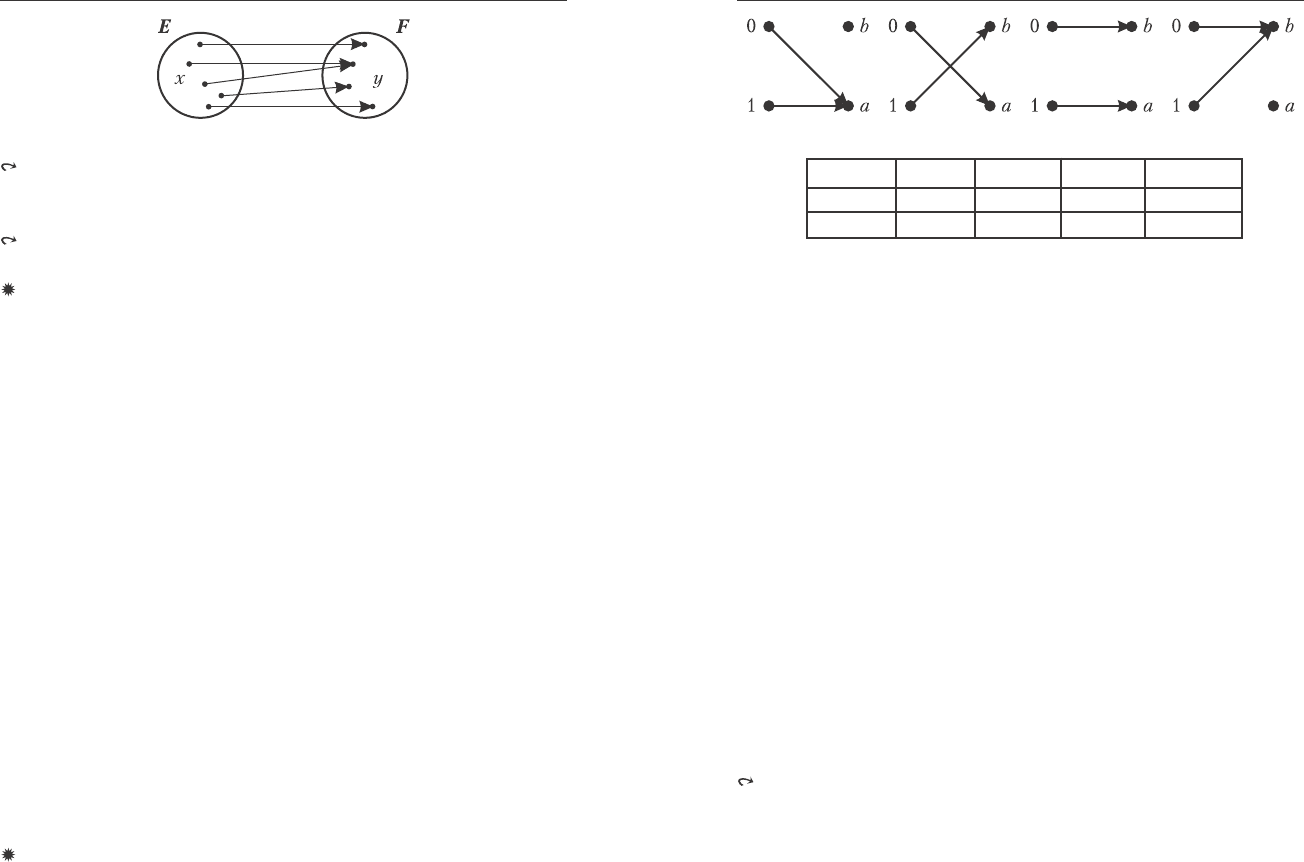
íîé, êàê ïîêàçàíî íà ðèñ. 3.6, 3.7, 3.8.

Ôóíêöèîíàëüíàÿ áèåêöèÿ E→F óñòàíàâëèâàåò òàêîå îòîáðà-

æåíèå, ïðè êîòîðîì êàæäûé ýëåìåíò èç E èìååò åäèíñòâåííûé îáðàç

â F, à êàæäûé ýëåìåíò èç F èìååò åäèíñòâåííûé ïðîîáðàç â E,

ïîýòîìó ôóíêöèîíàëüíàÿ áèåêöèÿ íàçûâàåòñÿ âçàèìíî îäíîçíà÷-

íûì ñîîòâåòñòâèåì. Ôóíêöèîíàëüíîå îòîáðàæåíèå E→F, êîòîðîå

ÿâëÿåòñÿ ñþðúåêöèåé, âîçìîæíî òîëüêî â òîì ñëó÷àå, åñëè êîëè÷å-

ñòâî ýëåìåíòîâ â E íå ìåíüøå êîëè÷åñòâà ýëåìåíòîâ â F, ò.å. |E|≥|F|.

Äëÿ ôóíêöèîíàëüíîé èíúåêöèè, íàîáîðîò, äîëæíî âûïîëíÿòüñÿ

ñîîòíîøåíèå |E|≤|F|.

Ðèñ. 3.6. Ôóíêöèîíàëüíàÿ

áèåêöèÿ.

Ðèñ. 3.7. Ôóíêöèîíàëüíàÿ

èíúåêöèÿ.

28 29Ãëàâà 3 Îòîáðàæåíèÿ. Ôóíêöèè

Îïðåäåëåíèå 3.7. Îòîáðàæåíèå ìíîæåñòâà E â E, îïðåäåëåííîå

ðàâåíñòâîì ƒ(x)=x, íàçûâàåòñÿ òîæäåñòâåííûì îòîáðàæåíèåì

(îïåðàòîðîì).

Îïðåäåëåíèå 3.8. Îòîáðàæåíèå ìíîæåñòâà â åãî ôàêòîð-ìíîæå-

ñòâî íàçûâàåòñÿ êàíîíè÷åñêîé ñþðúåêöèåé.

Ïðèìåðû îòîáðàæåíèé.

1. Ïóñòü çàäàíî ñîîòâåòñòâèå ƒ: R → R, òàêîå, ÷òî ƒ(x)=x

. Ýòî

ñîîòâåòñòâèå ÿâëÿåòñÿ îòîáðàæåíèåì, òàê êàê äëÿ êàæäîãî x∈R

ñóùåñòâóåò îáðàç ƒ(x)=x

. Îáëàñòü îïðåäåëåíèÿ ýòîãî îòîáðàæå-

íèÿ ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë R; îáëàñòü çíà÷åíèé

Im(R)=[0,∞). Îòîáðàæåíèå ƒ ôóíêöèîíàëüíî, òàê êàê êàæäîå

çíà÷åíèå x∈R èìååò òîëüêî îäèí îáðàç â R. Îòîáðàæåíèå

ƒ:R→[0,∞) ÿâëÿåòñÿ ôóíêöèîíàëüíîé ñþðúåêöèåé, òàê êàê äëÿ

êàæäîãî ƒ(x)∈[0,∞) ñóùåñòâóåò ïî êðàéíåé ìåðå îäèí ïðîîáðàç

x∈R.

2. Åñëè E  ìíîæåñòâî îãðàíè÷åííûõ êðèâûõ íà ïëîñêîñòè, òî

ôóíêöèÿ âû÷èñëåíèÿ äëèíû êðèâîé åñòü ñþðúåêöèÿ ƒ:E→R

3. Îòîáðàæåíèå ƒ:R→R, òàêîå, ÷òî ƒ(x)=2x+3, ò.å. ïðÿìàÿ, åñòü

áèåêöèÿ.

4. Îòîáðàæåíèå g:N→R, òàêîå, ÷òî g(x)=±√x, ÿâëÿåòñÿ áèåêöèåé,

íî íå ÿâëÿåòñÿ ôóíêöèîíàëüíûì îòîáðàæåíèåì.

5. Ñîîòâåòñòâèå ƒ:R→R, òàêîå, ÷òî ƒ(x)=x/sinx, ÿâëÿåòñÿ ÷àñòè÷-

íî îïðåäåëåííîé ôóíêöèåé: äëÿ sinx=0 çíà÷åíèå ôóíêöèè íå

îïðåäåëåíî.

6. Èíäåêñèðîâàíèå ýëåìåíòîâ íåêîòîðîãî ìíîæåñòâà åñòü

îäíîçíà÷íîå îòîáðàæåíèå ýòîãî ìíîæåñòâà â ïîäìíîæåñòâî

íàòóðàëüíûõ ÷èñåë N.

3.2. Êàðäèíàëüíàÿ ñòåïåíü ìíîæåñòâ

Åñëè E è F  äâà ìíîæåñòâà, òî ìîæíî ãîâîðèòü î íåêîòîðîì íîâîì

ìíîæåñòâå  ìíîæåñòâå ôóíêöèîíàëüíûõ îòîáðàæåíèé E â F.

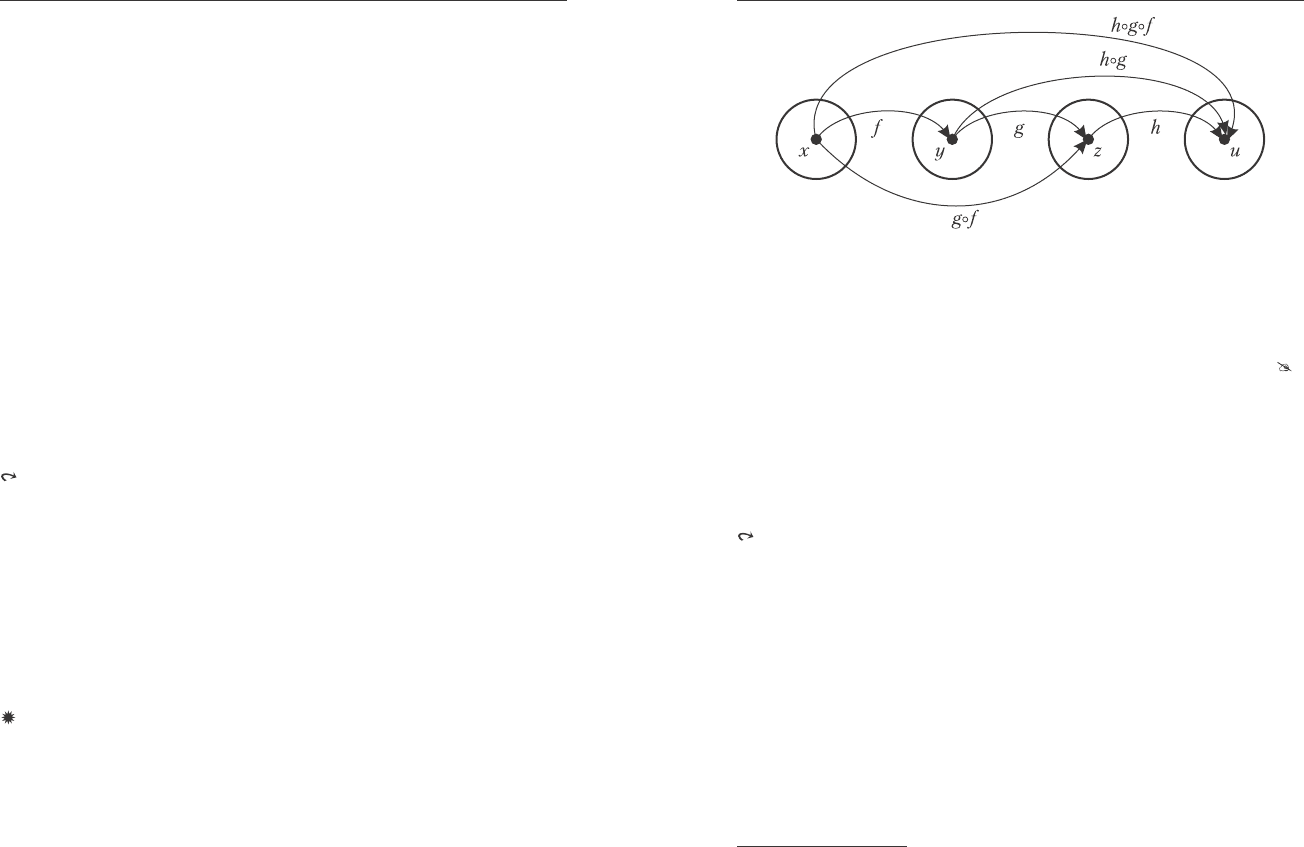
Ïðèìåð. Íà ðèñ. 3.9 ïîêàçàíî ìíîæåñòâî âñåõ ôóíêöèîíàëüíûõ

îòîáðàæåíèé èç E={0,1} â F={a,b}. Ýòî æå ìíîæåñòâî çàäàíî â

òàáëèöå  ýòî ìíîæåñòâî âñåõ îäíîìåñòíûõ ôóíêöèé, îïðåäåëåííûõ

íà E ñî çíà÷åíèÿìè â F.

Ðèñ. 3.9. Ìíîæåñòâî îòîáðàæåíèé E={0,1} â F={a,b}.

Èç òàáëèöû âèäíî, ÷òî ìíîæåñòâî âñåõ ôóíêöèé èç E={0,1} â

F={a,b} ìîæíî áèåêòèâíî îòîáðàçèòü íà äåêàðòîâî ïðîèçâåäåíèå

F×F, òàê êàê êàæäîé ôóíêöèè ìîæíî ïîñòàâèòü â ñîîòâåòñòâèå

óïîðÿäî÷åííóþ ïàðó èç F×F. Â äàííîì ïðèìåðå òàêîé áèåêöèåé

áóäåò: f

ó <a,a>, f

ó <a,b>, f

ó <b,a>, f

ó <b,b>.

Åñëè E ñîñòîèò èç n ýëåìåíòîâ x

, x

, ..., x

, òî ìíîæåñòâî

(îäíîìåñòíûõ) ôóíêöèé èç E â F ìîæíî áèåêòèâíî îòîáðàçèòü íà

, òàê êàê êàæäîå òàêîå îòîáðàæåíèå ýêâèâàëåíòíî çàäàíèþ êîðòå-

æà <y

, y

, ... , y

>∈F

îáðàçîâ ýëåìåíòîâ x

, x

, ..., x

ïðè ýòîì

îòîáðàæåíèè. Ïîýòîìó êîëè÷åñòâî ôóíêöèîíàëüíûõ îòîáðàæåíèé

îïðåäåëÿåòñÿ êîëè÷åñòâîì ýëåìåíòîâ â äåêàðòîâîì ïðîèçâåäåíèè

, ãäå n  êîëè÷åñòâî ýëåìåíòîâ ìíîæåñòâà E. Â íàøåì ïðèìåðå

äëÿ f:{0,1}→{a,b} êîëè÷åñòâî ôóíêöèé |f|=2

=4. Åñëè |E| = 3,

|F| = 2, òî |f| =2

. Â îáùåì ñëó÷àå |f| =|F|

|E|

Ýòî äàåò îñíîâàíèå îáîçíà÷àòü ìíîæåñòâî âñåõ ôóíêöèîíàëüíûõ

îòîáðàæåíèé {ƒ:E→F} â âèäå ñòåïåíè F

. Òàêèì îáðàçîì, ìû îïðå-

äåëèëè åùå îäíó îïåðàöèþ íàä ìíîæåñòâàìè  ýòî âîçâåäåíèå

ìíîæåñòâà â ñòåïåíü äðóãîãî ìíîæåñòâà: F

. Ðåçóëüòàòîì åå ÿâëÿåòñÿ

ìíîæåñòâî âñåõ ôóíêöèîíàëüíûõ îòîáðàæåíèé E→F, ò.å. ìíîæå-

ñòâî âñåõ îäíîìåñòíûõ ôóíêöèé, îïðåäåëåííûõ íà E ñî çíà÷åíèÿìè

â F. Â îòëè÷èå îò äåêàðòîâîé ñòåïåíè ìíîæåñòâà, ñòåïåíü ìíîæåñòâà

êàê ìíîæåñòâî âñåõ ôóíêöèîíàëüíûõ îòîáðàæåíèé E→F íàçû-

âàþò êàðäèíàëüíîé ñòåïåíüþ.

Îïðåäåëåíèå 3.9. Ìíîæåñòâî âñåõ ôóíêöèîíàëüíûõ îòîáðàæå-

íèé {ƒ:E→F} íàçûâàåòñÿ (êàðäèíàëüíîé) ñòåïåíüþ ìíîæåñòâ

è îáîçíà÷àåòñÿ F

Îòîáðàæåíèå ìíîæåñòâà E

â F, ãäå n∈N, E

 äåêàðòîâà ñòåïåíü

ìíîæåñòâà E, îáðàçóåò ôóíêöèþ îò n ïåðåìåííûõ. Ìíîæåñòâî âñåõ

n-ìåñòíûõ ôóíêöèé åñòü ìíîæåñòâî âñåõ (ôóíêöèîíàëüíûõ)

Ðèñ. 3.8. Ôóíêöèîíàëüíàÿ ñþðúåêöèÿ.

0 aabb

1 abab

30 31Ãëàâà 3 Îòîáðàæåíèÿ. Ôóíêöèè

îòîáðàæåíèé ƒ:E

→F, ò.å. ñòåïåíü ìíîæåñòâà

. Êîëè÷åñòâî

òàêèõ ôóíêöèé îïðåäåëÿåòñÿ êàê |f| =



Â ÷àñòíîñòè, îòîáðàæåíèå f:E×E→F  äâóìåñòíàÿ ôóíêöèÿ,

à ìíîæåñòâî F

E×E

åñòü ìíîæåñòâî âñåõ äâóìåñòíûõ ôóíêöèé,

îïðåäåëåííûõ íà E

E ñî çíà÷åíèÿìè â F. Êîëè÷åñòâî òàêèõ

ôóíêöèé îïðåäåëÿåòñÿ êàê |f| =|F|

|E×E|



Åñëè ïðè âîçâåäåíèè â ñòåïåíü E=∅, òî ƒ(∅)=∅, ñëåäîâà-

òåëüíî, F

∅

=∅.

Ïðèìåð. Îïðåäåëèì âñå âîçìîæíûå ôóíêöèè ƒ:E×E→F, ãäå

E= {0,1}, F={a,b}. Òàêèõ ôóíêöèé áóäåò 2

= 16.

Êàê âèäíî èç òàáëèöû, êàæäàÿ ôóíêöèÿ åñòü ìíîæåñòâî ïàð

{<<x

, x

>,y>}, íàïðèìåð, f

= {{<<0,0>,a>, <<0,1>,a>,

<<1,0>,b>, <<1,1>,b>}.

3.3. Ñâîéñòâà ôóíêöèîíàëüíûõ îòîáðàæåíèé

Ïóñòü ƒ  ôóíêöèîíàëüíîå îòîáðàæåíèå E â F è A  ïîäìíî-

æåñòâî E. Îáîçíà÷èì ÷åðåç ƒ(A) ïîäìíîæåñòâî F, îáðàçîâàííîå èç

âñåõ ýëåìåíòîâ ƒ(x), ãäå x∈A. Ïîäìíîæåñòâî ƒ(A) íàçûâàåòñÿ

îáðàçîì ïîäìíîæåñòâà A ïðè îòîáðàæåíèè f: A→ƒ(A), èëè

ñóæåíèåì ôóíêöèè Å→ƒ(Å). Î÷åâèäíî, ÷òî ƒ(∅)=∅. Èñõîäÿ èç

îòîáðàæåíèÿ ƒ, îïðåäåëèì íåêîòîðîå îòîáðàæåíèå A→ƒ(A). Ýòî

îòîáðàæåíèå ñîõðàíÿåò îïåðàöèè ⊂, ∩, ∪, \ â ñëåäóþùåì ñìûñëå.

(Â äîêàçàòåëüñòâàõ ñèìâîë ⇒ îçíà÷àåò «âëå÷åò», «ñëåäîâàòåëüíî»,

ñèìâîë ⇔ «ðàâíîñèëüíî», «ðàâíîçíà÷íî».)

Óòâåðæäåíèå 3.1. ÅñëèA⊂B,òîƒ(A)⊂ƒ(B).

Äîêàçàòü ñàìîñòîÿòåëüíî.

Óòâåðæäåíèå 3.2. ƒ(A∪B)=ƒ(A)∪ƒ(B).

Äîêàçàòåëüñòâî.

f(x)∈f(A∪B) ⇒ x∈A∪B ⇔ x∈A èëè x∈B ⇒ f(x)∈f(A)

èëè f(x)∈f(B) ⇔ f(x)∈f(A)∪f(B)⇒

⇒f(A∪B)⊆f(A)∪f(B). (1)

f(x)∈f(A)∪f(B) ⇔ f(x)∈f(A) èëè f(x)∈f(B) ⇒ x∈A

èëè x∈B ⇔ x∈A∪B⇒f(x)∈f(A∪B)⇒

⇒ f(A)∪f(B) ⊆ f(Α∪B). (2)

Èç (1) è (2) ⇒ ƒ(A ∪ B)=ƒ(A) ∪ ƒ(B).

Óòâåðæäåíèå 3.3. f(A\B)=f(A)\f(B).

Äîêàçàòåëüñòâî.

f(x)∈f(A\B) ⇒ x∈A\B ⇔ x∈A è x∉B ⇒ f(x)∈f(A) è

f(x)∉f(B) ⇔ f(x)∈f(A)\f(B) ⇒ f(A\B)⊆f(A)\f(B). (1)

f(x)∈ f(A)\f(B) ⇔ f(x)∈f(A) è f(x)∉f(B) ⇒ x∈A è x∉B⇔

⇔x∈A\B ⇒ f(x)∈f(A\B) ⇒ f(A)\f(B) ⊆ f(A\B). (2)

Èç (1) è (2) ⇒ ƒ(A\B)=ƒ(A)\ƒ(B).

Îäíàêî, îïåðàöèè ∩, ⊂ ïðè ýòîì îòîáðàæåíèè íå ñîõðàíÿþòñÿ,

èìååò ìåñòî ëèøü âêëþ÷åíèå.

Óòâåðæäåíèå 3.4. ƒ(A ∩ B) ⊂ ƒ(A) ∩ ƒ(B).

Äîêàçàòåëüñòâî.

f(x)∈f(A∩B) ⇒ x∈A∩B ⇔ x∈A è x∈B ⇒ f(x)∈f(A)

è f(x)∈f(B) ⇔ f(x)∈f(A)∩f(B) ⇒

⇒f(A∩B)⊆f(A)∩f(B). (1)

f(x)∈f(A)∩f(B) ⇔ f(x)∈f(A) è f(x)∈f(B) ⇒ x∈A è x∈B.

Îäíàêî âîçìîæíî, ÷òî A∩B=∅, è òîãäà f(A∩B)=f(∅)=∅,

íî ïðè ýòîì âîçìîæíî, ÷òî f(A)∩f(B)≠ ∅, è òîãäà

ƒ(A)∩ƒ(B) ⊄ ƒ(A∩B), ïîòîìó ìû îãðàíè÷èìñÿ ðåçóëüòàòîì (1).

Ïóñòü òåïåðü B ÿâëÿåòñÿ íåêîòîðûì ïîäìíîæåñòâîì ìíîæåñòâà

F. Áóäåì îáîçíà÷àòü ÷åðåç ƒ

1

(B) ïîäìíîæåñòâî E, îáðàçîâàííîå èç

âñåõ òàêèõ ýëåìåíòîâ x, ÷òî ƒ(x)∈B. Ïîäìíîæåñòâî ƒ

1

(B) íàçûâà-

åòñÿ ïðîîáðàçîì ìíîæåñòâà B ïðè îòîáðàæåíèè ƒ. Ýòî îïðåäåëåíèå

âîâñå íå ïðåäïîëàãàåò áèåêòèâíîñòè ƒ. Åñëè y∈F, òî ìîæíî

ãîâîðèòü î ƒ

1

({y}), íî ýòî  íåêîòîðîå ïîäìíîæåñòâî E, à íå ýëåìåíò

E. Îíî ìîæåò ñîäåðæàòü áîëåå îäíîãî ýëåìåíòà, åñëè ƒ íå ÿâëÿåòñÿ

èíúåêòèâíûì, è ìîæåò îêàçàòüñÿ ïóñòûì, åñëè ƒ íå ñþðúåêòèâíî.

Åñëè ƒ áèåêòèâíî, òî ƒ

1

({y})={ƒ

1

(y)}. Î÷åâèäíî, ÷òî ƒ

1

(∅)=∅.

Ìû ñâÿçàëè ñ îòîáðàæåíèåì ƒ îòîáðàæåíèå B→ƒ

1

(B)

ìíîæåñòâà ℘(F) âî ìíîæåñòâî ℘(E). Ýòî îòîáðàæåíèå ñîõðàíÿåò

îïåðàöèè ⊂, ∪, ∩, \, ′ â ñëåäóþùåì ñìûñëå.

Óòâåðæäåíèå 3.5. Åñëè A ⊂ B , òî ƒ

1

(A) ⊂ ƒ

1

(B).

Äîêàçàòü ñàìîñòîÿòåëüíî.

Óòâåðæäåíèå 3.6. ƒ

1

(A∪B)=ƒ

1

(A)∪ƒ

1

(B).

Äîêàçàòåëüñòâî.

x∈ƒ

1

(A∪B) ⇒ ƒ(x)∈A∪B ⇔ ƒ(x)∈A èëè ƒ(x)∈B ⇒

⇒x∈ƒ

1

(A) èëè x∈ƒ

1

(B) ⇔ x∈ƒ

1

(A)∪ ƒ

1

(B) ⇒

⇒ƒ

1

(A∪B)⊆ ƒ

1

(A)∪ƒ

1

(B). (1)

00aaaaaaaabbbbbbbb

01aaaabbbbaaaabbbb

10aabbaabbaabbaabb

11abababababababab

32 33Ãëàâà 3 Îòîáðàæåíèÿ. Ôóíêöèè

x∈ ƒ

1

(A)∪ ƒ

1

(B) ⇔ x∈ƒ

1

(A) èëè x∈ƒ

1

(B) ⇒ ƒ(x)∈A

èëè ƒ(x)∈B ⇔ ƒ(x)∈A∪B ⇒ x∈ƒ

1

(A∪B) ⇒

⇒ ƒ

1

(A)∪ƒ

1

(B) ⊆ ƒ

1

(A∪B). (2)

Èç (1) è (2) ⇒ ƒ

1

(A∪B)= ƒ

1

(A) ∪ƒ

1

(B).

Óòâåðæäåíèå 3.7. ƒ

1

(A∩B)=ƒ

1

(A)∩ƒ

1

(B).

Äîêàçàòåëüñòâî.

x∈ƒ

1

(A∩B) ⇒ ƒ(x)∈A∩B ⇔ ƒ(x)∈A è ƒ(x)∈B ⇒

⇒x∈ƒ

1

(A) è x∈ƒ

1

(B) ⇔ x∈ƒ

1

(A)∩ ƒ

1

(B) ⇒

⇒ƒ

1

(A∩B)⊆ ƒ

1

(A)∩ ƒ

1

(B). (1)

x∈ ƒ

1

(A)∩ ƒ

1

(B) ⇔ x∈ƒ

1

(A) è x∈ƒ

1

(B) ⇒ ƒ(x)∈A è

ƒ(x)∈B ⇔ ƒ(x)∈A∩B ⇒ x∈ƒ

1

(A∩B) ⇒

⇒ƒ

1

(A)∩ ƒ

1

(B) ⊆ ƒ

1

(A∩B). (2)

Èç (1) è (2) ⇒ ƒ

1

(A∩B)=ƒ

1

(A) ∩ƒ

1

(B).

Óòâåðæäåíèå 3.8. ƒ

1

(A′)=(ƒ

1

)′(A).

Äîêàçàòü ñàìîñòîÿòåëüíî.

Óòâåðæäåíèå 3.9. ƒ

1

(A\B)=ƒ

1

(A)\f

1

(B).

Äîêàçàòü ñàìîñòîÿòåëüíî.

3.4. Êîìïîçèöèÿ îòîáðàæåíèé

Îïðåäåëåíèå 3.10. Ïóñòü äàíû òðè ìíîæåñòâà E, F è G, è çàäàíû

îòîáðàæåíèÿ ƒ: E→F, g: F→G. Òîãäà êîìïîçèöèåé îòîáðàæå-

íèé goƒ: E→G íàçûâàåòñÿ îòîáðàæåíèå E â G, êîòîðîå

îïðåäåëÿåòñÿ ôîðìóëîé goƒ=g(ƒ(x)).

Èíûìè ñëîâàìè, åñëè ñóùåñòâóåò ìíîæåñòâî ïàð <x,y>∈ƒ è

<y,z>∈g, òî ìíîæåñòâî ïàð <x,z>∈go ƒ îáðàçóåò êîìïîçèöèþ

îòîáðàæåíèé goƒ. Çàïèñü goƒ ïðîèçâîäèòñÿ â ïîðÿäêå, îáðàòíîì

òîìó, â êîòîðîì ïðîèçâîäÿòñÿ îïåðàöèè ƒ: E→F, g: F→G. Òàêèì

îáðàçîì, â ìàòåìàòèêå ïðèíÿòî ïðàâèëî, ñîãëàñíî êîòîðîìó

êîìïîçèöèþ îòîáðàæåíèé goƒ íàäî íà÷èíàòü ñ âûïîëíåíèÿ

îïåðàöèè ƒ, êîòîðàÿ ðàñïîëîæåíà ñïðàâà.

Ïðèìåðû.

1. Ïóñòü f: R → R ⇔ y = x  1; g: R→R ⇔ y = e

. Êîìïîçèöèÿ

ôóíêöèé goƒ: R→R ⇔ y = e

 1, fog : y = e

x  1

2. Ïóñòü f: R → Z ⇔ y = [x] (öåëàÿ ÷àñòü ÷èñëà x); g:

Z →

{0, 1}

⇔

(y)mod2. Òîãäà gof: R→{0, 1}åñòü ([x])mod2  îñòàòîê îò äåëåíèÿ

öåëîé ÷àñòè ÷èñëà x íà 2.

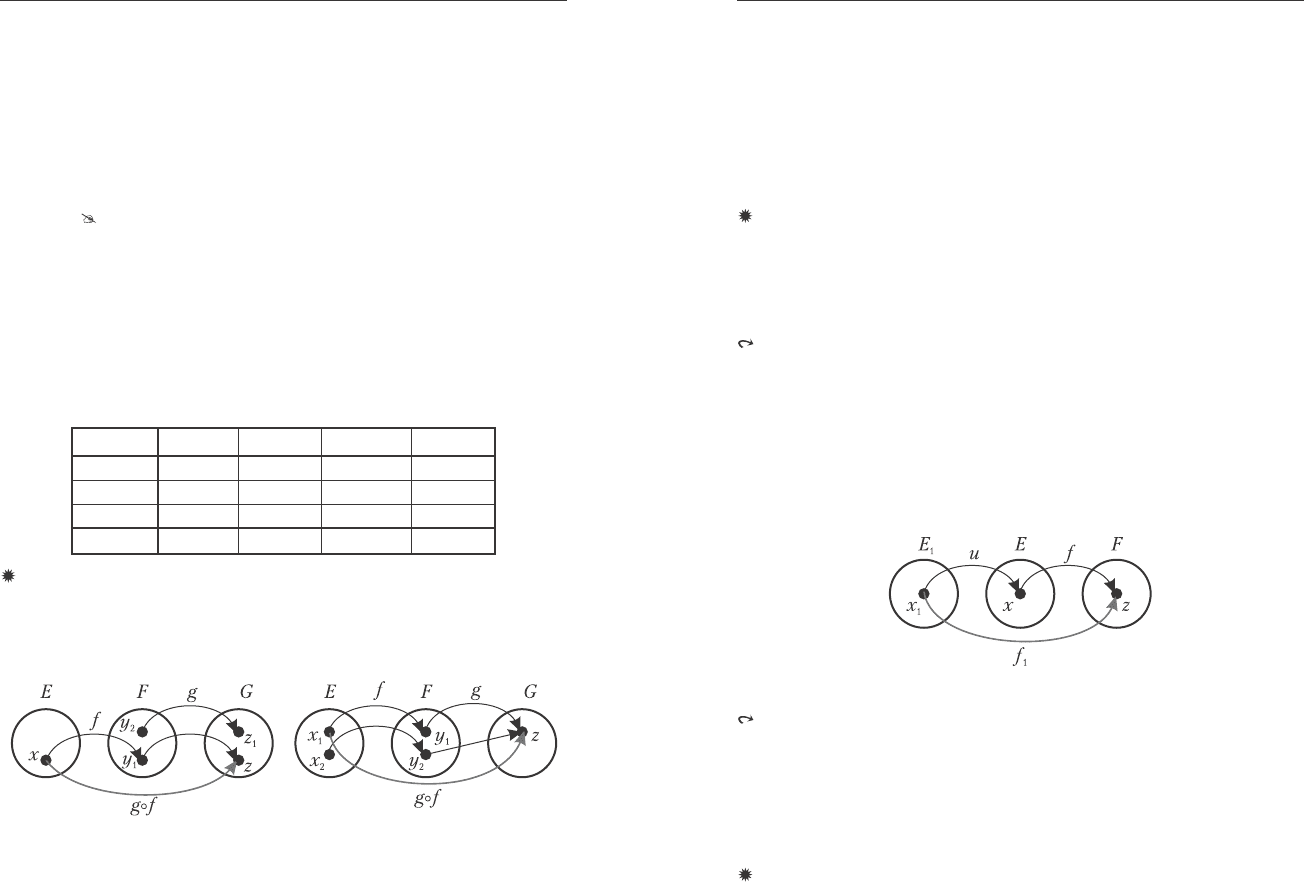
Òåîðåìà 3.1. Êîìïîçèöèÿ îòîáðàæåíèé àññîöèàòèâíà, ò.å., åñëè

ƒ, g, h  îòîáðàæåíèÿ E â F, F â G è G â H ñîîòâåòñòâåííî, òî

(hog)oƒ=ho (goƒ), ÷òî çàïèñûâàåòñÿ â âèäå: hogoƒ.

Ðèñ. 3.10. Êîìïîçèöèÿ îòîáðàæåíèé.

Äîêàçàòåëüñòâî. Ïóñòü <x,u>∈ho(goƒ), <x,z>∈goƒ,

<z,u>∈h. Ïîñêîëüêó <x,z>∈go ƒ, òî ñóùåñòâóåò òàêîå y, ÷òî

<x,y>∈ƒ, è <y,z>∈g, à ïîñêîëüêó ñóùåñòâóåò <z,u>∈h, òî

ñóùåñòâóåò è <y,u>∈hog. Ñëåäîâàòåëüíî, åñëè <x,y>∈ƒ è

<y,u>∈hog, òî ñóùåñòâóåò è <x,u>∈(hog)of (ñì. ðèñ.3.10).

Òåîðåìà 3.2. Êîìïîçèöèÿ îòîáðàæåíèé íå êîììóòàòèâíà.

Äîêàçàòåëüñòâî ýòîé òåîðåìû î÷åâèäíî, îíî îñíîâàíî íà ñàìîì

îïðåäåëåíèè êîìïîçèöèè.

Äëÿ ïðèìåðà ðàññìîòðèì äâà îòîáðàæåíèÿ ƒ: y=sinx è g: y=x

ãäå x, y∈R. Êîìïîçèöèÿ goƒ:y=sin

x, à êîìïîçèöèÿ ƒog: y=sinx

Î÷åâèäíî, ýòî ðàçëè÷íûå ôóíêöèè.

Îïðåäåëåíèå 3.11. Îòîáðàæåíèå ìíîæåñòâà E â E, ïðè êîòîðîì

êàæäûé ýëåìåíò ïåðåõîäèò â ñåáÿ, íàçûâàåòñÿ òîæäåñòâåííûì

îòîáðàæåíèåì è îáîçíà÷àåòñÿ I

. Äëÿ òîæäåñòâåííûõ îòîáðàæå-

íèé ñïðàâåäëèâû ðàâåíñòâà

foI

= I

of=f.

Òåîðåìà 3.3. Îòîáðàæåíèå f: E→F èìååò îáðàòíîå òîãäà è

òîëüêî òîãäà, êîãäà f  áèåêöèÿ.

Äîêàçàòåëüñòâî.

Äîñòàòî÷íîñòü. Åñëè f  èíúåêöèÿ è ñþðúåêöèÿ, òî íåîáõîäèìî

äîêàçàòü, ÷òî ñóùåñòâóåò ƒ

1

: F→E.

Òàê êàê ƒ(x)  ñþðúåêöèÿ, òî êàæäûé ýëåìåíò èç F èìååò õîòÿ

áû îäèí ïðîîáðàç â E: ∃x∈E (ƒ(x)=y), ò.å. ñîîòâåòñòâèå ƒ

1

: F→E

âñþäó îïðåäåëåíî íà F è, ñëåäîâàòåëüíî, ÿâëÿåòñÿ îòîáðàæåíèåì.

Åñëè âñå ðàññìàòðèâàåìûå îòîáðàæåíèÿ åñòü áèåêöèè, òî äëÿ êàæäîãî îòîáðà-

æåíèÿ ñóùåñòâóåò îáðàòíîå, è ìíîæåñòâî âñåõ îòîáðàæåíèé èç E â F îáðàçóåò

ãðóïïó, â êîòîðîé òîæäåñòâåííûå îòîáðàæåíèÿ I

, I

ÿâëÿþòñÿ ëåâîé è ïðàâîé

åäèíèöåé.

34 35Ãëàâà 3 Îòîáðàæåíèÿ. Ôóíêöèè

A òàê êàê ƒ(x)  èíúåêöèÿ, ò.å. äëÿ x

≠x

ƒ(x

)≠ƒ(x

), òî êàæäûé

ýëåìåíò y èìååò òîëüêî îäèí ïðîîáðàç, ñëåäîâàòåëüíî, îòîáðàæåíèå

1

: F→E ôóíêöèîíàëüíî.

Íåîáõîäèìîñòü. Ïóñòü f

1

: F→E  ôóíêöèîíàëüíîå îòîáðàæå-

íèå. Äîêàæåì, ÷òî ƒ  áèåêöèÿ.

Ïîñêîëüêó ƒ

1

 îòîáðàæåíèå, òî êàæäûé ýëåìåíò y èç F èìååò

ïðîîáðàç â E, ò.å. îòîáðàæåíèå ƒ ñþðúåêòèâíî. Ïîñêîëüêó îòîáðàæå-

íèå ƒ

1

ôóíêöèîíàëüíî, òî êàæäîìó îáðàçó ƒ(x) ñîîòâåòñòâóåò

åäèíñòâåííûé ïðîîáðàç x, ò.å. ƒ  èíúåêöèÿ. Ñëåäîâàòåëüíî, ƒ 

áèåêöèÿ.

Òåîðåìà 3.4. Åñëè ƒ è g  ôóíêöèîíàëüíûå îòîáðàæåíèÿ, ëèáî

ñþðúåêöèè, ëèáî èíúåêöèè, ëèáî áèåêöèè, òî ìîæíî äîêàçàòü

ðÿä óòâåðæäåíèé î ñâîéñòâàõ êîìïîçèöèè ýòèõ îòîáðàæåíèé.

Ýòè ñâîéñòâà îòîáðàæåíû â òàáë. 3.1, ãäå ñèìâîëàìè îáîçíà÷åíû:

Î  îòîáðàæåíèå, Ñ  ñþðúåêöèÿ, È  èíúåêöèÿ, Á  áèåêöèÿ.

Äîêàçàòåëüñòâî ýòèõ 16 óòâåðæäåíèé ïðåäîñòàâëÿåòñÿ ÷èòàòåëþ.

Òàáëèöà 3.1.

Ïðèìåð. Äîêàæåì óòâåðæäåíèå: êîìïîçèöèÿ èíúåêöèè è

ñþðúåêöèè åñòü îòîáðàæåíèå.

Äîêàçàòåëüñòâî. Ïóñòü g  ñþðúåêöèÿ, f  èíúåêöèÿ, goƒ  èõ

êîìïîçèöèÿ, è ïóñòü <x,y>∈f, <y,z>∈g, <x,z>∈goƒ (ñì.

ðèñ.3.11).

Ðèñ. 3.11. Êîìïîçèöèÿ èíúåêöèè è ñþðúåêöèè.

Ïîñêîëüêó g  ñþðúåêöèÿ, òî äëÿ âñÿêîãî z∈G ñóùåñòâóåò ïî

ìåíüøåé ìåðå îäèí ïðîîáðàç y∈F, è, âîçìîæíî, ñóùåñòâóþò ïàðû

,z

>∈g, <y

,z

>∈g, ãäå y

,y

∈F, z

,z

∈G. Òàê êàê f  èíúåê-

öèÿ, òî äëÿ âñÿêîãî x∈E ñóùåñòâóåò íå áîëåå îäíîãî îáðàçà y∈F.

Åëè y

åñòü îáðàç ýëåìåíòà x∈E, òî z

åñòü îáðàç ýëåìåíòàx â G,

ò.å. ñóùåñòâóåò ïàðà, <x,z

> ∈ goƒ. Ýëåìåíò y

ìîæåò íå èìåòü

ïðîîáðàçà â E, è, ñëåäîâàòåëüíî, íå êàæäûé ýëåìåíò z èìååò ïðîîáðàç

â E, îòêóäà ñëåäóåò, ÷òî goƒ íå ñþðúåêöèÿ.

Ïîñêîëüêó f  èíúåêöèÿ, òî ñóùåñòâóþò ïàðû <x

,y

>∈f,

,y

>∈f, è y

≠y

, à òàê êàê g  ñþðúåêöèÿ, òî âîçìîæíî, ÷òî

ñóùåñòâóþò ïàðû <y

,z>∈g, <y

,z>∈g, è, ñëåäîâàòåëüíî, ñóùå-

ñòâóþò ïàðû <x

,z>∈goƒ, <x

,z>∈goƒ, îòêóäà ñëåäóåò, ÷òî goƒ

íå èíúåêöèÿ. Ñëåäîâàòåëüíî, goƒ  ïðîñòî îòîáðàæåíèå.

Ïðèìåð. Ïóñòü f: R → R ⇔ y = x  1  áèåêöèÿ; g: R→R⇔y=e



èíúåêöèÿ (òàê êàê íåò íè îäíîãî ýëåìåíòà õ∈R, äëÿ êîòîðîãî

ó=0 åñòü îáðàç). Êîìïîçèöèÿ ôóíêöèé goƒ: R→R ⇔ y=e

2(x 1)



èíúåêöèÿ, ñîãëàñíî òåîðåìå 3.4.

3.5. Çàìåíà ïåðåìåííîé è çàìåíà ôóíêöèè

Îïðåäåëåíèå 3.12. Ïóñòü ƒ  ôóíêöèÿ, îïðåäåëåííàÿ íà E ñî

çíà÷åíèÿìè â F. Åñëè u ÿâëÿåòñÿ îòîáðàæåíèåì íåêîòîðîãî

ìíîæåñòâà E

âî ìíîæåñòâî E, òî ìîæíî ïîñòðîèòü íîâóþ ôóíê-

öèþ ƒ

=ƒou, îïðåäåëåííóþ íà E

ñî çíà÷åíèÿìè â F (ðèñ.3.12).

Ãîâîðÿò, ÷òî â ýòîì ñëó÷àå ïðîèçâåäåíà çàìåíà ïåðåìåííîé, èëè

çàìåíà èñõîäíîãî ìíîæåñòâà E íà E

, è ÷òî ƒ

ÿâëÿåòñÿ ïðîîáðà-

çîì ƒ ïðè ýòîé çàìåíå ïåðåìåííûõ. Ïðîèçâåäÿ â âûðàæåíèè

ƒ(x) ïîäñòàíîâêó x=u(x

), ïîëó÷àþò âûðàæåíèå ƒ

). Èíîãäà

ýòî îáîçíà÷àþò êàê ƒ*(x

)=ƒ(u(x

)).

Ðèñ. 3.12. Çàìåíà ïåðåìåííîé.

Îïðåäåëåíèå 3.13. Ïóñòü v ÿâëÿåòñÿ íåêîòîðûì îòîáðàæåíèåì

F â ìíîæåñòâî F

. Òîãäà ìîæíî îïðåäåëèòü íîâóþ ôóíêöèþ

ƒ*=voƒ, îïðåäåëåííóþ íà E ñî çíà÷åíèÿìè â F

(ðèñ. 3.13). Â

ýòîì ñëó÷àå ãîâîðÿò, ÷òî ïðîèçâåäåíà çàìåíà ôóíêöèè èëè çàìåíà

ìíîæåñòâà çíà÷åíèé F íà ìíîæåñòâî F

è ÷òî ƒ* ÿâëÿåòñÿ îáðàçîì

ƒ ïðè ýòîé çàìåíå. Çàìåíó ôóíêöèè íàçûâàþò åùå àïïëèêàöèåé

ôóíêöèé. Èíîãäà ýòî îáîçíà÷àþò êàê ƒ*(x)=v(ƒ(x)).

Ïðèìåð. Ïóñòü èñõîäíàÿ ôóíêöèÿ E→F: ƒ(x) = x

. Çàäàíû

ôóíêöèè: E

→E: u(x

) = x

+1; F→F

:v(x)= 2x. Âûïîëíèì çàìåíó

ïåðåìåííîé â ôóíêöèè ƒ(x): ƒ(u(x

)) = (x

+1)

. Âûïîëíèì çàìåíó

goƒ ÎÑÈÁ

ÎÎÎÎÎ

ÑÎÑÎÑ

ÈÎÎÈÈ

ÁÎÑÈÁ

ôóíêöèè â ôóíêöèè ƒ(x): v(ƒ(x)) = 2x

. Òàêèì îáðàçîì, ïðè çàìåíå

ïåðåìåííîé ìû ïîëó÷àåì íîâóþ ôóíêöèþ, çàâèñÿùóþ îò íîâîé

ïåðåìåííîé, à ïðè çàìåíå ôóíêöèè  íîâóþ ôóíêöèþ, çàâèñÿùóþ

îò òîé æå ñàìîé ïåðåìåííîé.

Ìîæíî ïðîèçâåñòè îäíîâðåìåííî è çàìåíó ïåðåìåííîé è çàìåíó

ôóíêöèè: ƒ

=voƒou. Çäåñü ƒ

ÿâëÿåòñÿ îáðàçîì ƒ ïðè çàìåíå ïåðå-

ìåííîé u è çàìåíå ôóíêöèè v. Íàïðèìåð, äëÿ îïðåäåëåííûõ âûøå

ôóíêöèé: ƒ

=voƒo u = v(ƒ(u(x

))) = 2(x

+1)

Ãëàâà 3

Ãëàâà 4. ÌÎÙÍÎÑÒÜ ÌÍÎÆÅÑÒÂ

4.1. Îïðåäåëåíèå ìîùíîñòè

Ïîíÿòèå ìîùíîñòè ìíîæåñòâ ñâÿçàíî ñ îöåíêîé ÷èñëà ýëåìåíòîâ â

íåì. Â êîíå÷íîì ìíîæåñòâå êîëè÷åñòâî ýëåìåíòîâ ìîæíî ïåðåñ÷èòàòü.

×èñëî ýëåìåíòîâ â ìíîæåñòâå Õ îáîçíà÷àåòñÿ îáû÷íî êàê |Õ|. Íàïðèìåð,

åñëè X = {a, b, c}, òî |X|=3. Åñëè äâà ìíîæåñòâà èìåþò îäèíàêîâîå ÷èñëî

ýëåìåíòîâ, òî ìåæäó íèìè ìîæíî óñòàíîâèòü âçàèìíî îäíîçíà÷íîå

ñîîòâåòñòâèå. Òîãäà âñå êîíå÷íûå ìíîæåñòâà, èìåþùèå îäèíàêîâîå

êîëè÷åñòâî ýëåìåíòîâ, áóäóò ýêâèâàëåíòíû ïî ÷èñëó ýëåìåíòîâ â íèõ è

îáðàçóþò îäèí êëàññ ýêâèâàëåíòíîñòè. Ýòîò êëàññ ýêâèâàëåíòíîñòè ìîæåò

áûòü îáîçíà÷åí öåëûì íàòóðàëüíûì ÷èñëîì, îïðåäåëÿþùèì êîëè÷åñòâî

ýëåìåíòîâ â ìíîæåñòâàõ. Âñå îäíîýëåìåíòíûå ìíîæåñòâà îáðàçóþò îäèí

êëàññ ýêâèâàëåíòíîñòè, äâóõýëåìåíòíûå äðóãîé, è òàê äàëåå. Êàæäîìó

íàòóðàëüíîìó ÷èñëó ñîîòâåòñòâóåò êëàññ ýêâèâàëåíòíîñòè, îáúåäèíÿþ-

ùèé âñå êîíå÷íûå ìíîæåñòâà ñ ÷èñëîì ýëåìåíòîâ, ðàâíûì äàííîìó ÷èñëó.

Ìîùíîñòü îáúåäèíåíèÿ íåñêîëüêèõ êîíå÷íûõ ìíîæåñòâ ìîæíî

íàéòè ïî ôîðìóëàì:

|X∪Y| = |X| +|Y|  |X∩Y|;

|X∪Y ∪ Z| = |X| +|Y| + |Z|  |X∩Y|  |X ∩Z|  |Y ∩ Z| + |X∩Y ∩Z|.

(×èòàòåëþ ïðåäëàãàåòñÿ äîêàçàòü ýòè ðàâåíñòâà ñàìîñòîÿòåëüíî

è íàéòè îáùåå âûðàæåíèå.)

Ðàññìîòðèì òåïåðü áåñêîíå÷íûå ìíîæåñòâà. Äëÿ íåêîòîðûõ áåñêî-

íå÷íûõ ìíîæåñòâ òîæå ìîæíî óñòàíîâèòü âçàèìíî îäíîçíà÷íîå ñîîòâåò-

ñòâèå ýëåìåíòîâ. Íàïðèìåð, äëÿ ìíîæåñòâà ÷åòíûõ íàòóðàëüíûõ ÷èñåë,

êîòîðîå ìîæíî ïðåäñòàâèòü â âèäå ñïèñêà: {2,4,6,}, ïîñëåäîâàòåëüíîñòü

(1, 2, 3, ) áóäåò íóìåðàöèåé ýòîãî ñïèñêà, ò.å. ñóùåñòâóåò îòîáðàæåíèå

ƒ(n)=2n, äëÿ êàæäîãî n∈N ìíîæåñòâà íàòóðàëüíûõ ÷èñåë N â ìíîæåñòâî

âñåõ ÷åòíûõ ïîëîæèòåëüíûõ öåëûõ ÷èñåë, êîòîðîå ÿâëÿåòñÿ áèåêöèåé.

Ñëåäîâàòåëüíî, ìíîæåñòâî âñåõ ÷åòíûõ íàòóðàëüíûõ ÷èñåë ýêâèâàëåíòíî

ìíîæåñòâó âñåõ íàòóðàëüíûõ ÷èñåë, ò.å. ÷åòíûõ ÷èñåë ðîâíî ñòîëüêî æå,

ñêîëüêî âñåõ íàòóðàëüíûõ ÷èñåë. Íî, ñ äðóãîé ñòîðîíû, ìíîæåñòâî íàòóðàëü-

íûõ ÷èñåë ìîæíî ðàçáèòü íà äâà ïîäìíîæåñòâà ÷åòíûõ è íå÷åòíûõ ÷èñåë,

ò.å. ÷åòíûõ ÷èñåë ðîâíî ïîëîâèíà èç âñåõ íàòóðàëüíûõ ÷èñåë! Ïîëó÷àåì,

÷òî â íåêîòîðîì ñìûñëå ÷àñòü ðàâíà öåëîìó

. È ýòî äåéñòâèòåëüíî òàê.

Ðèñ. 3.13. Çàìåíà ôóíêöèè.

Ýòîò ôàêò, çàêëþ÷àþùèéñÿ â òîì, ÷òî ìåæäó áåñêîíå÷íîé ñîâîêóïíîñòüþ è åå

ñîáñòâåííîé ÷àñòüþ ìîæíî óñòàíîâèòü âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå, îòìå÷àë-

ñÿ åùå Ïëóòàðõîì è äðóãèìè äðåâíèìè ó÷åíûìè. Â 1638 ãîäó Ãàëèëåé îòìåòèë,

÷òî ìåæäó öåëûìè ïîëîæèòåëüíûìè ÷èñëàìè è èõ êâàäðàòàìè ñóùåñòâóåò âçàèìíî

îäíîçíà÷íîå ñîîòâåòñòâèå, è íàçâàë «ïàðàäîêñîì» ñâîå íàáëþäåíèå, ïîñêîëüêó

ýòîò ôàêò âñòóïàåò â ïðîòèâîðå÷èå ñ åâêëèäîâîé àêñèîìîé, ñîãëàñíî êîòîðîé

öåëîå áîëüøå ëþáîé èç ñâîèõ ñîáñòâåííûõ ÷àñòåé, ò.å. ÷àñòåé, íå ñîâïàäàþùèõ ñî

âñåì öåëûì.

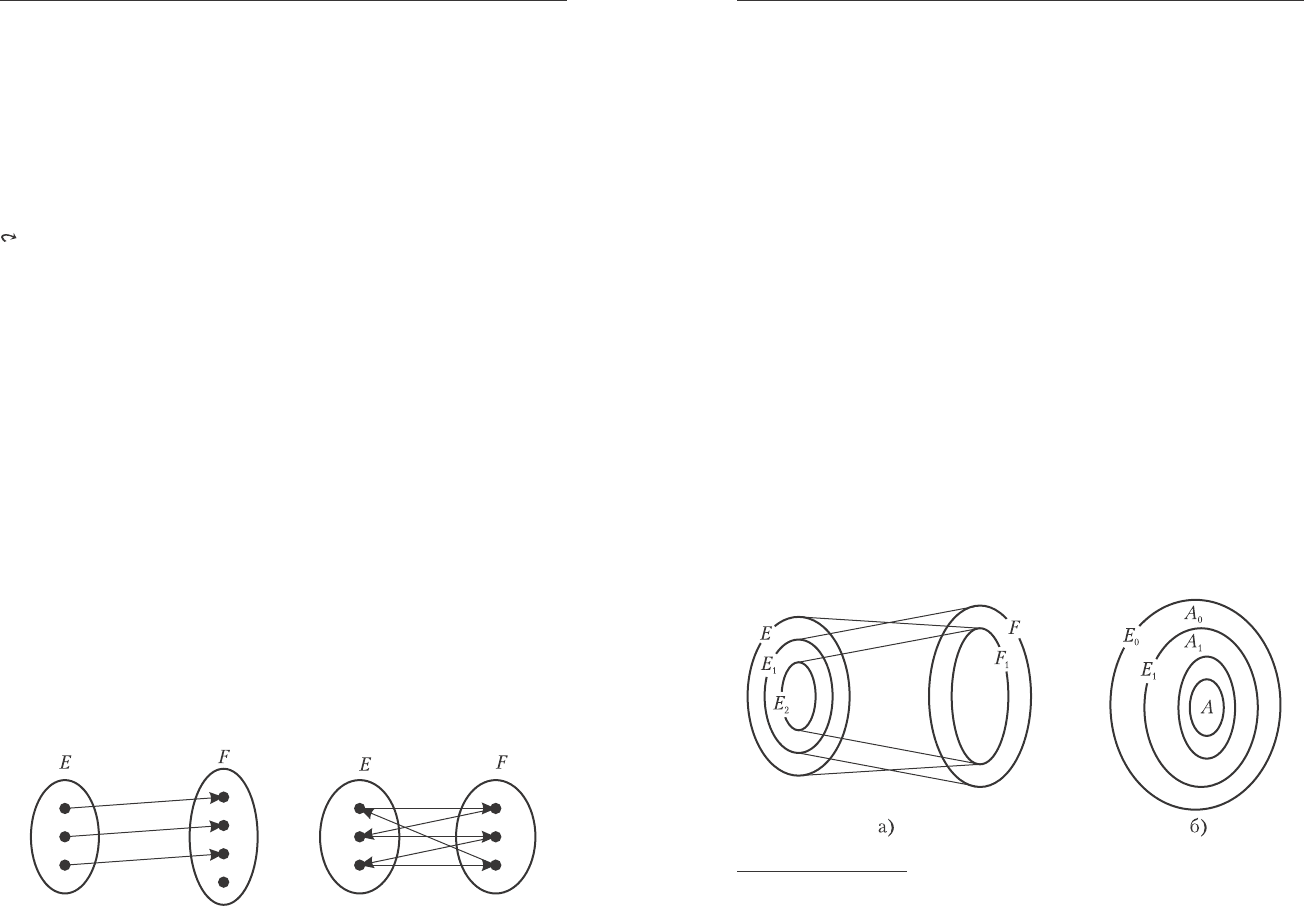
38 39

Ìîæíî ïîêàçàòü, ÷òî ñóùåñòâóåò áèåêöèÿ èç ìíîæåñòâà íàòóðàëüíûõ ÷èñåë

íà ëþáîå åãî áåñêîíå÷íîå ïîäìíîæåñòâî. Äåéñòâèòåëüíî, ïóñòü P⊂N.

Âûáåðåì â P íàèìåíüøèé ýëåìåíò è îáîçíà÷èì åãî x

; âû÷òåì ýòîò ýëåìåíò

èç P è íàèìåíüøèé ýëåìåíò èç âñåõ îñòàâøèõñÿ îáîçíà÷èì x

. Ïðîäîëæàÿ

ýòîò ïðîöåññ, ìû ïðèñâîèì íîìåð êàæäîìó ýëåìåíòó èç P. Ýòà íóìåðàöèÿ

åñòü áèåêöèÿ N→P: n→ x

, ãäå x

åñòü (n+1)-é â ïîðÿäêå âîçðàñòàíèÿ

ýëåìåíò P. Òàêèì îáðàçîì, ìíîæåñòâî íå÷åòíûõ ÷èñåë, ìíîæåñòâî

êâàäðàòîâ íàòóðàëüíûõ ÷èñåë è ìíîæåñòâî ëþáûõ ëèíåéíûõ êîìáèíàöèé,

íàïðèìåð, ax+b, ãäå a, b∈N, áóäóò ýêâèâàëåíòíû ìåæäó ñîáîé è âîéäóò

â îäèí êëàññ ýêâèâàëåíòíîñòè.

Îïðåäåëåíèå 4.1. Îòíîøåíèå ýêâèâàëåíòíîñòè, êîòîðîå îïðå-

äåëÿåòñÿ âçàèìíî îäíîçíà÷íûì ñîîòâåòñòâèåì äâóõ ìíîæåñòâ,

íàçûâàåòñÿ ðàâíîìîùíîñòüþ, à êëàññ ýêâèâàëåíòíîñòè

ðàâíîìîùíûõ ìíîæåñòâ íàçûâàåòñÿ ìîùíîñòüþ ýòèõ ìíîæåñòâ.

Ìîùíîñòü ìíîæåñòâà X îáîçíà÷àåòñÿ cardX. ×èñëî ýëåìåíòîâ

êîíå÷íîãî ìíîæåñòâà òàêæå íàçûâàåòñÿ ìîùíîñòüþ, òîãäà cardX=|X|.

Äëÿ ðàâíîìîùíûõ ìíîæåñòâ ÷àñòî èñïîëüçóåòñÿ îáîçíà÷åíèå E ∼ F.

4.2. Êàðäèíàëüíûå ÷èñëà

Ñðàâíåíèå áåñêîíå÷íûõ ìíîæåñòâ âîçìîæíî áëàãîäàðÿ

ñâîéñòâàì ôóíêöèîíàëüíûõ îòîáðàæåíèé. Èç îïðåäåëåíèÿ

èíúåêöèè ñëåäóåò, ÷òî èíúåêöèÿ èç ìíîæåñòâà E â ìíîæåñòâî F

âîçìîæíà òîëüêî â òîì ñëó÷àå, åñëè êîëè÷åñòâî ýëåìåíòîâ â E íå

áîëüøå, ÷åì êîëè÷åñòâî ýëåìåíòîâ â F: |E|≤|F| (äëÿ êîíå÷íûõ

ìíîæåñòâ), ïðè÷åì, åñëè íå ñóùåñòâóåò èíúåêöèè èç F â E, òî ýòî

íåðàâåíñòâî ïðåâðàùàåòñÿ â ñòðîãîå íåðàâåíñòâî |E|<|F| (ñì.

ðèñ.4.1). Åñëè æå ñóùåñòâóåò èíúåêöèÿ èç F â E, ïðè÷åì íå

îáÿçàòåëüíî ñîâïàäàþùàÿ ñ îáðàòíûì îòîáðàæåíèåì äëÿ èíúåêöèè

E→F, òî ýòî âîçìîæíî ëèøü òîãäà, êîãäà êîëè÷åñòâî ýëåìåíòîâ â

íèõ ñîâïàäàåò, ò.å. |E|=|F|, à â ýòîì ñëó÷àå ìîæíî íàéòè è âçàèìíî

îäíîçíà÷íîå ñîîòâåòñòâèå ìåæäó E è F, ò.å. áèåêöèþ.

Àíàëîãè÷íî, åñëè ñóùåñòâóåò ñþðúåêöèÿ èç E íà F, òàêàÿ, ÷òî

îäèí îáðàç â F èìååò íåñêîëüêî ïðîîáðàçîâ â E, òî êîëè÷åñòâî

ýëåìåíòîâ â E ñòðîãî áîëüøå êîëè÷åñòâà ýëåìåíòîâ â F, ò.å. |E|>|F|.

Ðèñ. 4.1. Èíúåêöèÿ E→F.

Ýòè ñâîéñòâà îáîáùàþòñÿ äëÿ ñëó÷àÿ áåñêîíå÷íûõ ìíîæåñòâ

ñëåäóþùåé òåîðåìîé.

Òåîðåìà 4.1 (Êàíòîðà  Áåðíøòåéíà

Ïóñòü Å è F  äâà ïðîèçâîëüíûõ áåñêîíå÷íûõ ìíîæåñòâà. Òîãäà:

à) ëèáî ñóùåñòâóåò èíúåêöèÿ èç E â F, ëèáî ñóùåñòâóåò èíúåêöèÿ

èç F â E (îäíî íå èñêëþ÷àåò äðóãîãî);

á) åñëè ñóùåñòâóþò èíúåêöèè E→F è F→E, òî ñóùåñòâóåò

áèåêöèÿ èç E â F.

Èíûìè ñëîâàìè, åñëè ìíîæåñòâî E ðàâíîìîùíî íåêîòîðîìó

ïîäìíîæåñòâó ìíîæåñòâà F, à ìíîæåñòâî F ðàâíîìîùíî íåêîòî-

ðîìó ïîäìíîæåñòâó ìíîæåñòâà E, òî E è F ðàâíîìîùíû.

Äîêàçàòåëüñòâî. Ïóñòü E ðàâíîìîùíî íåêîòîðîìó ïîäìíîæå-

ñòâó F

ìíîæåñòâà F, à F ðàâíîìîùíî íåêîòîðîìó ïîäìíîæåñòâó E

ìíîæåñòâà E (ñì. ðèñ. 4.2, a). Ïðè âçàèìíî îäíîçíà÷íîì ñîîòâåò-

ñòâèè ìåæäó E

è F ïîäìíîæåñòâî F

⊂F ïåðåõîäèò â íåêîòîðîå

ïîäìíîæåñòâî E

⊂E

. Ïðè ýòîì âñå òðè ìíîæåñòâà E, E

è E

ðàâíî-

ìîùíû, è íóæíî äîêàçàòü, ÷òî îíè ðàâíîìîùíû ìíîæåñòâó F, èëè,

÷òî òî æå ñàìîå, ìíîæåñòâó E

. Òåïåðü ìû ìîæåì çàáûòü ïðî ìíîæå-

ñòâî F è åãî ïîäìíîæåñòâà è äîêàçûâàòü òàêîé ôàêò:

åñëè E

⊂E

⊂E

, (ãäå E

 îáîçíà÷åíèå äëÿ E) è E

ðàâíîìîùíî E

òî âñå òðè ìíîæåñòâà ðàâíîìîùíû.

Ïóñòü f  ôóíêöèÿ, êîòîðàÿ îñóùåñòâëÿåò âçàèìíî îäíîçíà÷íîå

ñîîòâåòñòâèå E

→E

, òàê, ÷òî ýëåìåíò x∈ E

ñîîòâåòñòâóåò ýëåìåíòó

f(x)∈ E

. Êîãäà E

ïåðåõîäèò â E

, ìåíüøåå ìíîæåñòâî E

ïåðåõîäèò

â êàêîå-òî ìíîæåñòâî E

⊂E

(ñì. ðèñ. 4.2, á). Àíàëîãè÷íî, ñàìî E

ïåðåõîäèò â êàêîå-òî ìíîæåñòâî E

⊂E

. Ïðè ýòîì E

⊂E

, òàê êàê E

⊂E

Ðèñ. 4. 2. Ê äîêàçàòåëüñòâó òåîðåìû Êàíòîðà  Áåðíøòåéíà.

Ìîùíîñòü ìíîæåñòâÃëàâà 4

Êàíòîð ñôîðìóëèðîâàë ýòó òåîðåìó áåç äîêàçàòåëüñòâà â 1883 ãîäó, ïîîáåùàâ

âåðíóòüñÿ ê íåé ïîçæå, îäíàêî, íå âûïîëíèë ýòîãî îáåùàíèÿ. Ïåðâûå äîêàçà-

òåëüñòâà òåîðåìû áûëè äàíû Øð¸äåðîì (1896) è Áåðíøòåéíîì (1897).