Таран Т.А. Основы дискретной математики
Подождите немного. Документ загружается.


220 221Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
12.7.3. Äîêàçàòåëüñòâî ëîãè÷åñêèõ ñëåäîâàíèé
 äàííîì ðàçäåëå ìû ðàññìîòðèì äâà ñïîñîáà äîêàçàòåëüñòâà
ëîãè÷åñêèõ ñëåäîâàíèé: íåôîðìàëüíûé ñïîñîá, îñíîâàííûé íà äîêà-
çàòåëüñòâå îò ïðîòèâíîãî, è ôîðìàëüíûé âûâîä â èñ÷èñëåíèè ïðåäè-
êàòîâ. Â ñëåäóþùèé ãëàâå áóäåò ðàññìîòðåí áîëåå ýôôåêòèâíûé
ìåòîä, ïîçâîëÿþùèé àâòîìàòèçèðîâàòü ïðîöåññ äîêàçàòåëüñòâà
ëîãè÷åñêîãî ñëåäîâàíèÿ (ëîãè÷åñêîé îáùåçíà÷èìîñòè).
Ïðèìåð 12.1. Íà îáëàñòè îïðåäåëåíèÿ «ëþäè» çàäàíû âûñêàçûâàíèÿ:
1.Íåêîòîðûå ñòóäåíòû ëþáÿò ñâîèõ ïðåïîäàâàòåëåé.
2.Íèêòî íå ëþáèò íåâåæåñòâåííûõ ëþäåé.
Ñëåäîâàòåëüíî, íè îäèí ïðåïîäàâàòåëü íå ÿâëÿåòñÿ íåâåæåñòâåííûì.
Ïóñòü P(x): x ñòóäåíò, D(x): x ïðåïîäàâàòåëü, Q(x): x
íåâåæåñòâåííûé, L(x, y): x ëþáèò y. Ôîðìàëèçóåì ïîñûëêè:
F1: ∃x(P(x)&∀y(D(y) → L(x, y))),
F2: ∀x(P(x) → ∀y(Q(y) → ¬L(x, y))).
Çàêëþ÷åíèå G: ∀y(D(y) → ¬Q(y)).
Ïî îïðåäåëåíèþ, |F1|=T, |F2|=T. Ïðåäïîëîæèì, ÷òî |G|=F.
Èç ïðåäïîëîæåíèÿ |∀y(D(y)→¬Q(y))|=F ñëåäóåò, ÷òî ñóùåñòâóåò
ïî êðàéíåé ìåðå îäíî çíà÷åíèå y=a, òàêîå ÷òî |D(a)→¬Q(a)|=F,
îòêóäà ïîëó÷àåì, ÷òî |D(a)|=T, |¬Q(a)|=F, ò.å.|Q(a)|=T.
Èç ïîñûëêè F1: |∃x(P(x)&∀y(D(y) → L(x,y)))|=Tñëåäóåò, ÷òî
ñóùåñòâóåò ïî êðàéíåé ìåðå îäíî çíà÷åíèå x = b, òàêîå, ÷òî
|P(b)&∀y(D(y) → L(x,y))|=T, îòêóäà ïîëó÷àåì:|P(b)|=T è
|∀y(D(y) → L(b,y))|=T. Ïîñêîëüêó ïîñëåäíåå èñòèííî äëÿ âñÿêîãî
y, â òîì ÷èñëå, äëÿ y=a, ïîëó÷àåì |(D(a) → L(b,a))|=T, ò.å.
|(T→L(b,a))|=T, îòêóäà |L(b,a))|=T.
Ïîñêîëüêó ïîñûëêà F2: |∀x(P(x)→∀y(Q(a)→¬L(x,a)))|=Täëÿ
âñåõ çíà÷åíèé x è y, òî îíà èñòèííà è äëÿ x=b, y=a:
|P(b)→(Q(a)→¬L(b,a))|=T. À ïîñêîëüêó |P(b)|=T, òî
|Q(a)→¬L(b,a)|=T. Òàê êàê |Q(a)|=T, òî |¬L(b,a)|=T. Ïîëó÷àåì,
÷òî èñòèííû îáà óòâåðæäåíèÿ: |L(b,a)|=T è |¬L(b,a)|=T. Ïîëó-
÷åííîå ïðîòèâîðå÷èå äîêàçûâàåò ëîãè÷åñêîå ñëåäîâàíèå.
 ôîðìàëüíîì âûâîäå ïðèìåíÿþòñÿ ïðàâèëà: óíèâåðñàëüíîé êîí-
êðåòèçàöèè (ÓÊ), ýêçèñòåíöèàëüíîé êîíêðåòèçàöèè (ÝÊ), óäàëåíèÿ
& (óä. &), ââåäåíèÿ & (ââ. &), ïðàâèëî MP.
Ôîðìàëüíûé âûâîä.
1.∃x(P(x)&∀y(D(y) → L(x, y))) Ã1
2.∀x(P(x) → ∀y(Q(y) → ¬L(x, y))) Ã2
3.P(b)&∀y(D(y) → L(b, y))) ÝÊ(1)
4.P(b) óä. &(3)
5.∀y(D(y) → L(b, y)) óä. &(3)
6.P(b) → ∀y(Q(y) → ¬L(b,y))) ÓÊ(2)
7.∀y(Q(y) → ¬L(b, y))) MP(4, 6)
8.Q(z) → ¬L(b, z)) ÓÊ(7)
9.D(z) → L(b, z) ÓÊ(5)
10.L(b, z)) → ¬Q(z) ïðàâèëî êîíòðàïîçèöèè (8)
11.D(z) → ¬Q(z) ïðàâèëî ñèëëîãèçìà (9, 10)
12.∀y(D(y) → ¬Q(y)) Gen (11)
Ïðèìåð 12.2. Íà îáëàñòè îïðåäåëåíèÿ «ëþäè» çàäàíû âûñêàçûâàíèÿ:
1. Âñå ñòàðûå ÷ëåíû êîíãðåññà þðèñòû.
2. Âñå æåíùèíû-þðèñòû âîñõèùàþòñÿ êàêèì-íèáóäü ñóäüåé.
3. Òîëüêî ñóäüè âîñõèùàþòñÿ ñóäüÿìè.
4. Âñå ñóäüè âîñõèùàþòñÿ âñåìè ñóäüÿìè.
×òî äóìàåò ñóäüÿ Äæîíñ ïî ïîâîäó ñâîåé ñòàðîé òåùè, êîòîðàÿ
ÿâëÿåòñÿ ÷ëåíîì êîíãðåññà? Îòâåò: Äæîíñ âîñõèùàåòñÿ ñâîåé òåùåé.
Ïðîâåðèòü, ÷òî ýòî çàêëþ÷åíèå ëîãè÷åñêè ñëåäóåò èç çàäàííûõ
ïîñûëîê.
Ïóñòü õ ïðåäìåòíàÿ ïåðåìåííàÿ, êîòîðàÿ ïðèíèìàåò çíà÷åíèÿ
èç îáëàñòè îïðåäåëåíèÿ «ëþäè». Ââåäåì ïðåäèêàòû: J(x): x ñóäüÿ;
L(x): x þðèñò; C(x): x ÷ëåí êîíãðåññà; W(x): x æåíùèíà;
À(õ,ó): õ âîñõèùàåòñÿ ó, D Äæîíñ, T òåùà. Ôîðìàëèçóåì
ïîñûëêè.
1.∀õ(Î(õ)&C(x) → L(x))
Âñå ñòàðûå ÷ëåíû êîíãðåññà þðèñòû.
2.∀x(W(x)&L(x) → ∃y(J(y)&A(x,y)))
Âñå æåíùèíû-þðèñòû âîñõèùàþòñÿ êàêèì-íèáóäü ñóäüåé.
3.∀x∀y(J(y)&A(x,y) → J(x))
Òîëüêî ñóäüè âîñõèùàþòñÿ ñóäüÿìè.
4.∀x(J(x) → ∀y(J(y) → A(x,y)))
Âñå ñóäüè âîñõèùàþòñÿ âñåìè ñóäüÿìè.
5.J(D)
Äæîíñ ñóäüÿ,
6.W(T)&O(T)&C(T)
ñòàðàÿ òåùà, ÷ëåí êîíãðåññà.
Äîêàçàòü: A(D,T) ñóäüÿ Äæîíñ âîñõèùàåòñÿ òåùåé.
Ôîðìàëüíûé âûâîä.
1.∀õ(Î(õ)&C(x)→L(x)) Ã1
2.∀x(W(x)&L(x)→∀y(J(y)&A(x,y))) Ã2
3.∀x∀y(J(y)&A(x,y)→J(x)) Ã3

222 Ãëàâà 12
4.∀x(J(x)→∀y(J(y)→A(x,y))) Ã4
5.W(T)&O(T)&C(T)Ã5
6.J(D)Ã6
7.J(D)→∀y(J(y)→A(D,y)) ÓÊ (4)
8.∀y(J(y)→A(D,y)) MP (6,7)
9.J(T)→A(D,T) ÓÊ (8)
10.O(T)&C(T)→L(T) ÓÊ (1)
11.O(T)&C(T) óä. & (5)
12.L(T) MP (11,10)
13.L(T)→∃y(J(y)&A(T,y)) ÓÊ (2)
14.W(T) óä. & (5)
15.W(T)&L(T) ââ. & (12,14)
16.∃y(J(y)&A(T,y)) MP(13,15)
17.J(a)&A(T, a) ÝÊ (16)
18.J(a)&A(T,a)→J(T) ÓÊ (3)
19.J(T) MP(18, 17)
20.A(D,T) MP(9, 19)
Ãëàâà 13. ÀÂÒÎÌÀÒÈ×ÅÑÊÎÅ
ÄÎÊÀÇÀÒÅËÜÑÒÂÎ ÒÅÎÐÅÌ
13.1. Ââåäåíèå
Ïîèñê îáùåé ðàçðåøàþùåé ïðîöåäóðû äëÿ ïðîâåðêè îáùåçíà-
÷èìîñòè ôîðìóë áûë íà÷àò äàâíî. Ïåðâûì ïûòàëñÿ íàéòè òàêóþ
ïðîöåäóðó Ëåéáíèö (16461716), â äàëüíåéøåì íàä ýòèì ðàáîòàëà
øêîëà Ãèëüáåðòà. Ýòè ïîïûòêè ïðîäîëæàëèñü äî òåõ ïîð, ïîêà
׸ð÷ è Òüþðèíã íåçàâèñèìî äðóã îò äðóãà íå äîêàçàëè, ÷òî íå ñóùå-
ñòâóåò íèêàêîé îáùåé ðàçðåøàþùåé ïðîöåäóðû, íèêàêîãî àëãîðèò-
ìà, ïðîâåðÿþùåãî îáùåçíà÷èìîñòü ôîðìóë â ëîãèêå ïðåäèêàòîâ
ïåðâîãî ïîðÿäêà. Òåì íå ìåíåå, ñóùåñòâóþò àëãîðèòìû ïîèñêà äîêà-
çàòåëüñòâà, êîòîðûå ìîãóò ïîäòâåðäèòü, ÷òî ôîðìóëà îáùåçíà÷èìà.
Äëÿ íåîáùåçíà÷èìûõ ôîðìóë ýòè àëãîðèòìû, âîîáùå ãîâîðÿ, íå
çàêàí÷èâàþò ñâîþ ðàáîòó. Ïðèíèìàÿ âî âíèìàíèå ðåçóëüòàò ׸ð÷à
è Òüþðèíãà, ýòî ëó÷øåå, ÷òî ìîæíî îæèäàòü îò àëãîðèòìà ïîèñêà
äîêàçàòåëüñòâà.
 1930 ã. âàæíûé ïîäõîä ê àâòîìàòè÷åñêîìó äîêàçàòåëüñòâó
òåîðåì áûë äàí Ýðáðàíîì. Ïî îïðåäåëåíèþ îáùåçíà÷èìàÿ ôîðìóëà
åñòü ôîðìóëà, êîòîðàÿ èñòèííà ïðè âñåõ èíòåðïðåòàöèÿõ. Ýðáðàí
ðàçðàáîòàë àëãîðèòì íàõîæäåíèÿ èíòåðïðåòàöèè, êîòîðàÿ îïðîâåð-
ãàåò äàííóþ ôîðìóëó. Îäíàêî, åñëè äàííàÿ ôîðìóëà íà ñàìîì äåëå
îáùåçíà÷èìà, òî òàêîé èíòåðïðåòàöèè íå ñóùåñòâóåò è àëãîðèòì
îêàí÷èâàåò ðàáîòó çà êîíå÷íîå ÷èñëî øàãîâ. Ìåòîä Ýðáðàíà ñëóæèò
îñíîâîé äëÿ áîëüøèíñòâà ñîâðåìåííûõ ìåòîäîâ àâòîìàòè÷åñêîãî
ïîèñêà äîêàçàòåëüñòâà. Ãëàâíûé ðåçóëüòàò áûë ïîëó÷åí Ðîáèíñîíîì,
êîòîðûé ââåë òàê íàçûâàåìûé ìåòîä ðåçîëþöèé.
 îñíîâå ìåòîäà ðåçîëþöèé ëåæèò ïðîöåäóðà ïîèñêà îïðîâåð-
æåíèÿ, ò.å. âìåñòî äîêàçàòåëüñòâà îáùåçíà÷èìîñòè ôîðìóëû äîêà-
çûâàåòñÿ, ÷òî îòðèöàíèå ôîðìóëû ïðîòèâîðå÷èâî. Ìåòîä îïðîâåð-
æåíèÿ äëÿ äîêàçàòåëüñòâà ëîãè÷åñêîãî ñëåäîâàíèÿ çàêëþ÷àåòñÿ â
ñëåäóþùåì. Ïóñòü âûïîëíÿåòñÿ ëîãè÷åñêîå ñëåäîâàíèå: F1, F2 |=G.
Òîãäà |= F1&F2→G ëîãè÷åñêè îáùåçíà÷èìà, è, ñëåäîâàòåëüíî,
|¬(F1&F2→G)| = |F1&F2&¬G|≡F. Ïîñêîëüêó ïî îïðåäåëåíèþ
ïîñûëêè F1, F2 èñòèííû, ôîðìóëà F1&F2&¬G ìîæåò îáðàòèòüñÿ
â ëîæü òîëüêî, åñëè |¬G| = F, ò.å. åñëè |G| = T. Òîãäà ëîãè÷åñêîå
ñëåäñòâèå âûïîëíåíî. Â ïðèíöèïå ïðîöåäóðà îïðîâåðæåíèÿ ôîðìà-
ëèçóåò ìåòîä ðåäóêöèè. Ïðîáëåìà ïîèñêà àâòîìàòè÷åñêîãî äîêàçà-
òåëüñòâà ïðè èñïîëüçîâàíèè ïðîöåäóðû îïðîâåðæåíèÿ çíà÷èòåëüíî
îáëåã÷àåòñÿ áëàãîäàðÿ èñïîëüçîâàíèþ òàê íàçûâàåìûõ «ñòàíäàðò-
íûõ» ôîðì ôîðìóë. Ëþáóþ ôîðìóëó ëîãèêè ïðåäèêàòîâ ìîæíî
ïðèâåñòè ê ýêâèâàëåíòíîé åé ïðåäâàðåííîé íîðìàëüíîé ôîðìå,

224 225
êîãäà âñå êâàíòîðû âûíåñåíû âïåðåä, à â îáëàñòè äåéñòâèÿ êâàíòî-
ðîâ ôîðìóëà íàõîäèòñÿ â êîíúþíêòèâíîé íîðìàëüíîé ôîðìå. Åñëè
òàêàÿ ôîðìóëà èìååò òîëüêî êâàíòîðû âñåîáùíîñòè, òî îíà áóäåò
ëîæíà, åñëè íàéäåòñÿ õîòÿ áû îäíà èíòåðïðåòàöèÿ, êîòîðàÿ îáðà-
ùàåò åå â ëîæü. Òîãäà ýêâèâàëåíòíàÿ åé èñõîäíàÿ ôîðìóëà òàêæå
áóäåò ëîæíà, à åå îòðèöàíèå, ñîîòâåòñòâåííî, èñòèííî. Åñëè æå ñðåäè
êâàíòîðîâ èìåþòñÿ êâàíòîðû ñóùåñòâîâàíèÿ, òî ïðîáëåìà óñëîæ-
íÿåòñÿ. Îäíàêî, êâàíòîðû ñóùåñòâîâàíèÿ ìîæíî ñíÿòü (íà îñíîâà-
íèè ïðàâèëà ýêçèñòåíöèàëüíîé êîíêðåòèçàöèè), â ðåçóëüòàòå áóäåò
ïîëó÷åíà òàê íàçûâàåìàÿ «ñêóëåìîâñêàÿ ñòàíäàðòíàÿ ôîðìà». Òîãäà
ïîèñê îïðîâåðãàþùåé èíòåðïðåòàöèè ïðèìåíÿåòñÿ ê ýòîé ôîðìå.
13.2. Ïðåäâàðåííûå íîðìàëüíûå ôîðìû
Îïðåäåëåíèå 13.1. Ôîðìóëà À íàõîäèòñÿ â ïðåäâàðåííîé
íîðìàëüíîé ôîðìå (ÏÍÔ), åñëè îíà èìååò âèä: (Q
1
x
1
)...(Q
n
x
n
)Ì,
ãäå êàæäîå Q
i
x
i
åñòü ∃õ
i
èëè ∀õ
i
, à Ì ôîðìóëà â êîíúþíêòèâíîé
íîðìàëüíîé ôîðìå, íå ñîäåðæàùàÿ êâàíòîðîâ. (Q
1
x
1
)...(Q
n
x
n
)
íàçûâàåòñÿ ïðåôèêñîì, à Ì ìàòðèöåé ôîðìóëû À.
Òåîðåìà 13.1. Ñóùåñòâóåò ýôôåêòèâíàÿ ïðîöåäóðà ïðèâåäåíèÿ
ëþáîé ôîðìóëû ëîãèêè ïðåäèêàòîâ ê ýêâèâàëåíòíîé åé ïðåä-
âàðåííîé íîðìàëüíîé ôîðìå.
Äîêàçàòåëüñòâî òåîðåìû êîíñòðóêòèâíî, ò.å. äàåò àëãîðèòì ïðå-
îáðàçîâàíèÿ ëþáîé ôîðìóëû ê ïðåäâàðåííîé íîðìàëüíîé ôîðìå.
Òåîðåìà äîêàçûâàåòñÿ èíäóêöèåé ïî ÷èñëó ñâÿçîê m.
1. Ïóñòü m=0. Òîãäà ôîðìóëà À íå ñîäåðæèò ñâÿçîê è íàõîäèòñÿ
â ÏÍÔ.
2. Ïðåäïîëîæèì, ÷òî ñóùåñòâóåò ÏÍÔ äëÿ ôîðìóëû  ñ ÷èñëîì
ñâÿçîê n. Äîêàæåì, ÷òî ñóùåñòâóåò ÏÍÔ äëÿ ôîðìóëû À ñ ÷èñëîì
ñâÿçîê m=n+1.
1 ñëó÷àé. Ïóñòü ñóùåñòâóåò ÏÍÔ äëÿ Â=(Q
1
x
1
)...(Q
n
x
n
)Ì.
Ôîðìóëà À îáðàçîâàíà èç Â ñ ïîìîùüþ îïåðàöèè îòðèöàíèÿ:
À=¬(Q
1
x
1
)...(Q
n
x
n
)Ì. Ïî çàêîíàì äå Ìîðãàíà ñâÿçêà ¬ ïðîíîñèòñÿ
÷åðåç êâàíòîðû: ¬∀xÌ≡∃x¬Ì, ¬∃xÌ≡∀x¬Ì. Ïîëó÷åííàÿ ôîð-
ìóëà áóäåò íàõîäèòüñÿ â ÏÍÔ.
2 ñëó÷àé. Ôîðìóëà À îáðàçîâàíà èç äâóõ ôîðìóë Â1 è Â2 ñ
÷èñëîì ñâÿçîê n<m ñ ïîìîùüþ ñâÿçîê êîíúþíêöèè & èëè
äèçúþíêöèè ∨: (Q
1
x
1
)...(Q
n
x
n
)Ì1&(Q
1
y
1
)...(Q
n
y
n
)M2 èëè
(Q
1
x
1
)...(Q
n
x
n
)M1∨(Q
1
y
1
)...(Q
n
y
n
)M2. Òîãäà, åñëè ôîðìóëû Â1
è Â2 èìåþò êâàíòîðû ïî îäíîé è òîé æå ïåðåìåííîé, èñïîëüçóåì
çàêîíû çàìåíû ñâÿçàííûõ ïåðåìåííûõ:
∀xP(x)≡∀yP(y), ∃xP(x)≡∃yP(y),
òàê, ÷òîáû íè îäíà ñâîáîäíàÿ ïåðåìåííàÿ íå ñòàëà ñâÿçàííîé â
ðåçóëüòàòå ýòîé çàìåíû. Ïîñëå ýòîãî âîñïîëüçóåìñÿ çàêîíàìè êîì-
ìóòàòèâíîñòè äëÿ & è ∨ è çàêîíàìè ïðîíåñåíèÿ êâàíòîðîâ:
∀x(P(x)&B)≡∀xP(x)&B, ∀x(P(x)∨B)≡∀xP(x)∨B,
∃x(P(x)&B)≡∃xP(x)&B, ∃x(P(x)∨B)≡∃xP(x)∨B,
(B íå ñîäåðæèò âõîæäåíèé õ).
3 ñëó÷àé. Ôîðìóëà À îáðàçîâàíà èç  íàâåøèâàíèåì êâàíòîðà
∀ èëè ∃. Òîãäà, ïîñêîëüêó  íàõîäèòñÿ â ÏÍÔ, âíîâü ïîëó÷åííàÿ
ôîðìóëà áóäåò â ÏÍÔ.
Ïðèìåðû.
1. Ïðèâåäåì ê ÏÍÔ ñëåäóþùóþ ôîðìóëó:
∃xP(x) → ∀x(∃yD(y)&L(x, y)) = ¬∃xP(x) ∨ ∀x(∃yD(y)&L(x, y)) =
= ∀x¬P(x) ∨ ∀x(∃yD(y)&L(x, y)) = ∀x¬P(x) ∨ ∀z(∃yD(y)&L(z, y)) =
= ∀x(¬P(x) ∨ ∀z(∃yD(y)&L(z, y))) =
= ∀x(∀z(∃yD(y)&L(z, y)) ∨¬P(x)) =
= ∀x∀z(∃vD(v)&L(z, y)) ∨¬P(x))) =
= ∀x∀z∃v((D(v)&L(z, y)) ∨¬P(x))) =
= ∀x∀z∃v((D(v) ∨¬P(x))&(L(z, y)) ∨¬P(x))).
2. Ðàññìîòðèì ïîñûëêè ïðèìåðà 12.1.
∃x(P(x)&∀y(D(y) → L(x, y)))=∃x(P(x)&∀y(¬D(y) ∨ L(x, y)))=
=∃x(∀y(¬D(y) ∨ L(x, y))&P(x))=
=∃x∀y((¬D(y) ∨ L(x, y))&P(x)).
∀x(P(x) → ∀y(Q(y) → ¬L(x, y)))=∀x(¬P(x) ∨ ∀y(¬Q(y) ∨ ¬L(x, y)))=
=∀x(∀y(¬Q(y) ∨ ¬L(x, y)) ∨ ¬P(x))=
=∀x∀y(¬Q(y) ∨ ¬L(x, y) ∨ ¬P(x)).
13.3. Ñêóëåìîâñêèå ñòàíäàðòíûå ôîðìû
Îïðåäåëåíèå 13.2. Ïðåäâàðåííàÿ íîðìàëüíàÿ ôîðìà, ñîäåðæà-
ùàÿ òîëüêî êâàíòîðû âñåîáùíîñòè, íàçûâàåòñÿ ñêóëåìîâñêîé
ñòàíäàðòíîé ôîðìîé (ÑÑÔ).
Ïðîöåäóðà ïðèâåäåíèÿ ÏÍÔ ê ñêóëåìîâñêîé ôîðìå çàêëþ÷à-
åòñÿ â ýëèìèíàöèè (óäàëåíèè) êâàíòîðîâ ñóùåñòâîâàíèÿ.
Ïóñòü ôîðìóëà A íàõîäèòñÿ â ïðåäâàðåííîé íîðìàëüíîé ôîðìå
(Q
1
x
1
)...(Q
n
x
n
)M, ãäå M åñòü êîíúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà. Åñëè
êâàíòîð ñóùåñòâîâàíèÿ ïåðâûé ñëåâà êâàíòîð â ïðåôèêñå:
(∃x
1
)(Q
2
x
2
)...(...(Q
n
x
n
)M, òî åãî ìîæíî ýëèìèíèðîâàòü íà îñíîâàíèè
ïðàâèëà ýêçèñòåíöèàëüíîé êîíêðåòèçàöèè. Âûáåðåì êîíñòàíòó c,
îòëè÷íóþ îò äðóãèõ êîíñòàíò, âõîäÿùèõ â M, çàìåíèì âñå âõîæäåíèÿ
x
1
, âñòðå÷àþùèåñÿ â M, íà ñ, è âû÷åðêíåì êâàíòîð ∃x
1
èç ïðåôèêñà.
Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
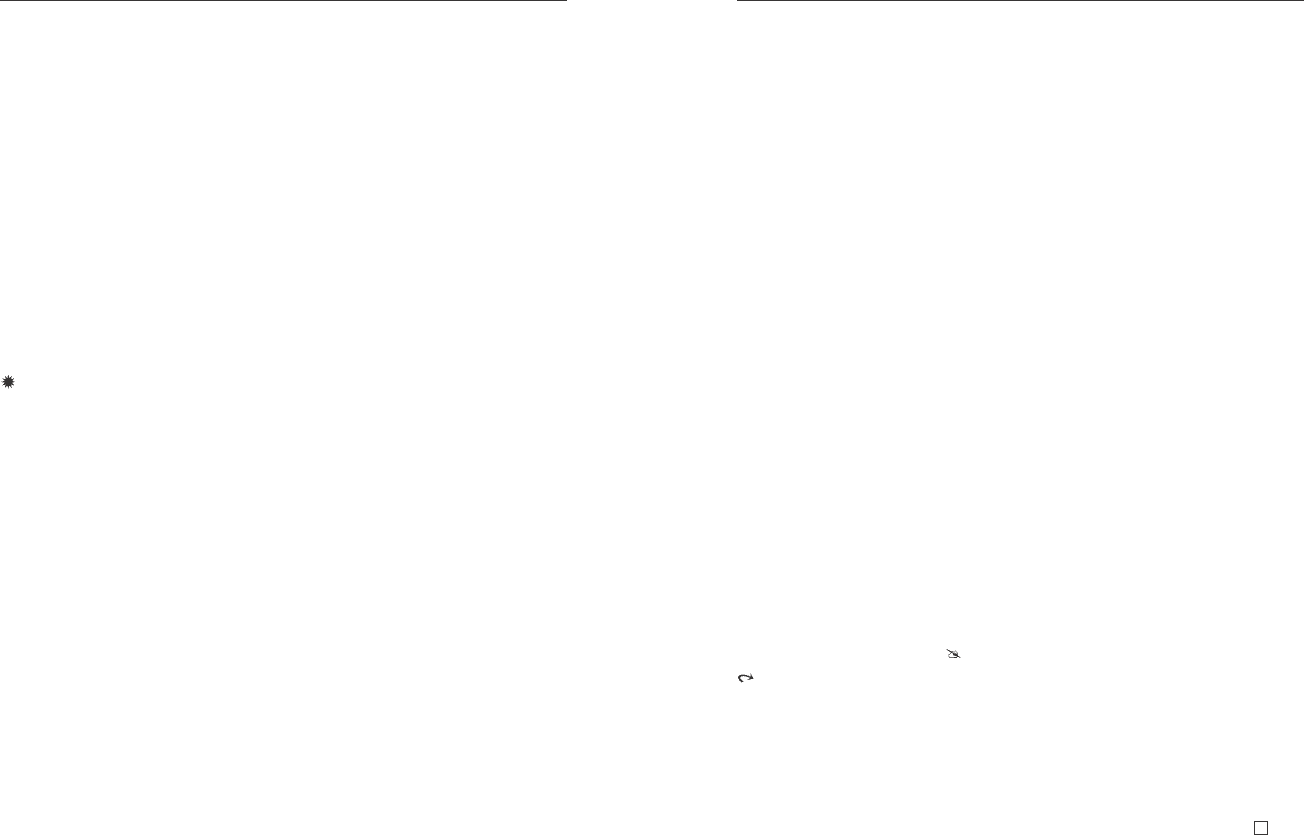
226 227
Åñëè æå ïåðåä êâàíòîðîì ñóùåñòâîâàíèÿ ñòîèò êâàíòîð âñåîáù-
íîñòè, íàïðèìåð, ∀x∃yM, òî ïåðåìåííàÿ y ïîïàäàåò â îáëàñòü äåé-
ñòâèÿ êâàíòîðà âñåîáùíîñòè, è âûðàæåíèå ∀x∃y (äëÿ êàæäîãî x
ñóùåñòâóåò y) îçíà÷àåò íàëè÷èå íåêîòîðîé ôóíêöèîíàëüíîé
çàâèñèìîñòè y = f(x). Åñëè êâàíòîðó ñóùåñòâîâàíèÿ ïðåäøåñòâóåò
íåñêîëüêî êâàíòîðîâ âñåîáùíîñòè, òî ôóíêöèÿ çàâèñèò îò âñåõ
ïåðåìåííûõ, ïî êîòîðûì íàâåøåíû ýòè êâàíòîðû.  îáùåì ñëó÷àå,
åñëè Qs
1
,,Qs
m
ñïèñîê âñåõ êâàíòîðîâ âñåîáùíîñòè, âñòðå÷àþ-
ùèõñÿ ëåâåå ∃x
r
, 1≤s
1
<s
2
<...<s
m
<r, ìû âûáåðåì m-ìåñòíûé
ôóíêöèîíàëüíûé ñèìâîë f, îòëè÷íûé îò äðóãèõ ôóíêöèîíàëüíûõ
ñèìâîëîâ, çàìåíèì âñå x
r
â M íà f(õ
s1
,,õ
sm
) è âû÷åðêíåì ∃x
r
èç
ïðåôèêñà. Çàòåì âåñü ýòîò ïðîöåññ ïðèìåíèì äëÿ âñåõ êâàíòîðîâ
ñóùåñòâîâàíèÿ â ïðåôèêñå; ïîñëåäíÿÿ èç ïîëó÷åííûõ ôîðìóë åñòü
ñêóëåìîâñêàÿ ñòàíäàðòíàÿ ôîðìà äëÿ êðàòêîñòè, ñòàíäàðòíàÿ
ôîðìà (ÑÑÔ) ôîðìóëû A. Ôóíêöèè, èñïîëüçóåìûå äëÿ çàìåíû
ïåðåìåííûõ êâàíòîðà ñóùåñòâîâàíèÿ, íàçûâàþòñÿ ñêóëåìîâñêèìè
ôóíêöèÿìè (êîíñòàíòû åñòü íóëüìåñòíûå ôóíêöèè).
Ïðèìåð. Ïîëó÷èì ñòàíäàðòíóþ ôîðìó ôîðìóëû A =
=∃x∀y∀z∃u∀v∃wP(x, y, z, u, v, w). Â ýòîé ôîðìóëå ëåâåå ∃x íåò
íèêàêèõ êâàíòîðîâ âñåîáùíîñòè, ëåâåå ∃u ñòîÿò ∀y è ∀z, à ëåâåå
∃w ñòîÿò ∀y, ∀z è ∀v. Ñëåäîâàòåëüíî, ìû çàìåíèì ïåðåìåííóþ x íà
êîíñòàíòó a, ïåðåìåííóþ u íà äâóìåñòíóþ ôóíêöèþ f(y, z),
ïåðåìåííóþ w íà òðåõìåñòíóþ ôóíêöèþ g(y, z, v). Òàêèì îáðàçîì,
ìû ïîëó÷àåì ñëåäóþùóþ ñòàíäàðòíóþ ôîðìó ôîðìóëû A: S=
=∀y∀z∀v P(a, y, z, f(y, z), v, g(y,z,v)).
Äëÿ ðàññìîòðåííûõ âûøå ïîñûëîê èç ïðèìåðà 12.1 ÑÑÔ èìååò âèä:
∃x∀y((¬D(y) ∨ L(x, y))&P(x)) ⇒ ∀y((¬D(y) ∨ L(à, y))&P(à)),
∀x∀y(¬Q(y) ∨ ¬L(x, y) ∨ ¬P(x)).
Åñëè ïðåäâàðåííàÿ íîðìàëüíàÿ ôîðìà ýêâèâàëåíòíà èñõîäíîé
ôîðìóëå, òî ñêóëåìîâñêàÿ ñòàíäàðòíàÿ ôîðìà ôîðìóëû A, âîîáùå
ãîâîðÿ, íå ýêâèâàëåíòíà åé. Íàïðèìåð, ïóñòü A=∃xP(x) è S=P(a)
åñòü ñòàíäàðòíàÿ ôîðìà ôîðìóëû A. Ïóñòü I åñòü ñëåäóþùàÿ
èíòåðïðåòàöèÿ: îáëàñòü D={a,b}, P(a)=F, P(b)=T. Òîãäà A
èñòèííà â I, íî S ëîæíà â I. Òàêèì îáðàçîì, Aíå ýêâèâàëåíòíàS.
Îäíàêî, åñëè P(a)=F, P(b)=F, òî |A| =F, è S=P(a) òàêæå
ïðèíèìàåò çíà÷åíèå F äëÿ ëþáîãî a. Òàêèì îáðàçîì, A≡S â òîì è
òîëüêî òîì ñëó÷àå, åñëè A ïðîòèâîðå÷èâà. Äîêàæåì, ÷òî ýòî äåéñòâè-
òåëüíî òàê.
Òåîðåìà 13.2. Ïóñòü S ñòàíäàðòíàÿ ôîðìà ôîðìóëû A. Òîãäà
A ïðîòèâîðå÷èâà â òîì è òîëüêî òîì ñëó÷àå, êîãäà S ïðîòè-
âîðå÷èâà.
Äîêàçàòåëüñòâî. Ïóñòü ôîðìóëà A íàõîäèòñÿ â ÏÍÔ, ò.å.
A=(Q
1
x
1
)... ...(Q
n
x
n
)M[x
1
,...,x
n
]. (Çàïèñü M[x
1
,...,x
n
] îçíà÷àåò, ÷òî
ìàòðèöà M ñîäåðæèò ïåðåìåííûå x
1
,...,x
n
). Ïóñòü Q
r
ïåðâûé ñëåâà
êâàíòîð ñóùåñòâîâàíèÿ. Ïóñòü A
1
=(∀x
1
)...(∀x
r1
)(Q
r+1
x
r+1
)
...(Q
n
x
n
)M[x
1
,...,x
r1
, f(x
1
,...,x
r1
),x
r+1
,,x
n
], ãäå f ñêóëåìîâñêàÿ
ôóíêöèÿ, ñîîòâåòñòâóþùàÿ x
r
, 1≤r≤n. Ìû õîòèì ïîêàçàòü, ÷òî A
ïðîòèâîðå÷èâà òîãäà è òîëüêî òîãäà, êîãäà A
1
ïðîòèâîðå÷èâà.
Ïðåäïîëîæèì, ÷òî A ïðîòèâîðå÷èâà. Åñëè A
1
íåïðîòèâîðå÷èâà, òî
ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ I, ÷òî A
1
èñòèííà â I, ò.å. äëÿ âñåõ
x
1
,...,x
r1
ñóùåñòâóåò ïî êðàéíåé ìåðå îäèí ýëåìåíò f(x
1
,...,x
r1
), äëÿ
êîòîðîãî (Q
r+1
x
r+1
)...(Q
n
x
n
)M[x
1
,...,x
r1
,f(x
1
,...,x
r1
),x
r+1
,...,x
n
]
èñòèííà â I. Òàêèì îáðàçîì, A èñòèííà â I, ÷òî ïðîòèâîðå÷èò ïðåäïî-
ëîæåíèþ, ÷òî A ïðîòèâîðå÷èâà. Ñëåäîâàòåëüíî, A
1
äîëæíà áûòü
ïðîòèâîðå÷èâà. Ñ äðóãîé ñòîðîíû, ïðåäïîëîæèì, ÷òî A
1
ïðîòèâîðå-
÷èâà. Åñëè A íåïðîòèâîðå÷èâà, òî ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ
I íà îáëàñòè D, ÷òî A èñòèííà â I, ò.å. äëÿ âñåõ x
1
,, x
r1
ñóùåñòâóåò
òàêîé ýëåìåíò x
r
, ÷òî (Q
r+1
x
r+1
)...(Q
n
x
n
)M[x
1
,...,x
r1
,f(x
1
,...,x
r1
),
x
r+1
,...,x
n
] èñòèííà â I. Ðàñøèðèì èíòåðïðåòàöèþ I, âêëþ÷èâ â íåå
ôóíêöèþ f(x
1
,...,x
r1
)=x
r
, êîòîðàÿ îòîáðàæàåò (x
1
,...,x
r1
)íà x
r
äëÿ
âñåõ x
1
,...,x
r1
â D, Îáîçíà÷èì ýòî ðàñøèðåíèå I′. Òîãäà äëÿ âñåõ
x
1
,...,x
r1
(Q
r+1
x
r+1
)...(Q
n
x
n
)Ì[x
1
,...,x
r1
,f(x
1
,...,x
r1
),x
r+1
,...,x
n
] èñòèííà
â I′, ò.å. A
1
èñòèííà â I', ÷òî ïðîòèâîðå÷èò ïðåäïîëîæåíèþ, ÷òî A
1
ïðîòèâîðå÷èâà. Ñëåäîâàòåëüíî, A äîëæíà áûòü ïðîòèâîðå÷èâîé.
Ïðåäïîëîæèì òåïåðü, ÷òî â A èìååòñÿ m êâàíòîðîâ ñóùåñòâîâàíèÿ.
Ïóñòü A
0
=A. Ïóñòü A
k
ïîëó÷àåòñÿ èç A
k1
çàìåíîé ïåðâîãî êâàíòîðà
ñóùåñòâîâàíèÿ â A
k1
ñêóëåìîâñêîé ôóíêöèåé, k=1, ..., m. Òîãäà
ñòàíäàðòíàÿ ôîðìà S=A
m
. Èñïîëüçóÿ òå æå ðàññóæäåíèÿ, ÷òî áûëè
äàíû âûøå, ìû ìîæåì ïîêàçàòü, ÷òî A
k1
ïðîòèâîðå÷èâà òîãäà è
òîëüêî òîãäà, êîãäà A
k
ïðîòèâîðå÷èâà ïðè k=1,...,m. Ñëåäîâàòåëüíî,
A ïðîòèâîðå÷èâà òîãäà è òîëüêî òîãäà, êîãäà S ïðîòèâîðå÷èâà, ÷òî
è òðåáîâàëîñü äîêàçàòü.
Îïðåäåëåíèå 13.3. Ïðåäèêàòíûå áóêâû áóäåì íàçûâàòü
ëèòåðàìè. Äèçúþíêöèÿ ëèòåð íàçûâàåòñÿ äèçúþíêòîì, èëè
êëàóçîé (clause) (èíîãäà êëîçîì). Îäíîëèòåðíûé äèçúþíêò
íàçûâàåòñÿ åäèíè÷íûì äèçúþíêòîì. Êîãäà äèçúþíêò íå ñîäåðæèò
íèêàêèõ ëèòåð, åãî íàçûâàþò ïóñòûì äèçúþíêòîì. Òàê êàê
ïóñòîé äèçúþíêò íå ñîäåðæèò ëèòåð, êîòîðûå ìîãëè áû áûòü
èñòèííûìè ïðè ëþáûõ èíòåðïðåòàöèÿõ, òî ïóñòîé äèçúþíêò
âñåãäà ëîæåí. Ïóñòîé äèçúþíêò îáîçíà÷àåòñÿ ñèìâîëîì
.
Ïóñòü S ñòàíäàðòíàÿ ôîðìà ôîðìóëû A. Ìàòðèöà ôîðìóëû,
ïðåäñòàâëåííîé â ÑÑÔ, íàõîäèòñÿ â êîíúþíêòèâíîé íîðìàëüíîé
ôîðìå, ò.å. â âèäå êîíúþíêöèè äèçúþíêòîâ. Áóäåì ïðåäñòàâëÿòü
ÑÑÔ ôîðìóëû A ìíîæåñòâîì äèçúþíêòîâ, ãäå êàæäàÿ ïåðåìåííàÿ
Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì

228 229
ñ÷èòàåòñÿ óïðàâëÿåìîé êâàíòîðîì âñåîáùíîñòè. Ìíîæåñòâî äèçú-
þíêòîâ ýòî ïðîñòî äðóãàÿ ôîðìà ïðåäñòàâëåíèÿ ñòàíäàðòíîé
ôîðìû ôîðìóëû A, ïîýòîìó â äàëüíåéøåì áóäåì îáîçíà÷àòü åãî
òàê æå, êàê è ÑÑÔ ñèìâîëîì S. Ñ÷èòàåì, ÷òî ìíîæåñòâî äèçúþíê-
òîâ S åñòü êîíúþíêöèÿ âñåõ äèçúþíêòîâ èç S. Íàïðèìåð, ÑÑÔ
ïîñûëêè èç ïðèìåðà 12.1: ∀y((¬D(y)∨ L(à,y))&P(à)) ìîæåò áûòü
ïðåäñòàâëåíà ìíîæåñòâîì äèçúþíêòîâ: S = {¬D(y) ∨ L(à, y), P(à)}.
Äàëåå, åñëè ìû èìååì A=A
1
&...&A
n
, ìû ìîæåì îòäåëüíî
ïîëó÷èòü ìíîæåñòâà äèçúþíêòîâ S
i
, i=1, , n, ãäå êàæäîå S
i
ïðåäñòàâëÿåò ñòàíäàðòíóþ ôîðìó A
i
. Çàòåì ïóñòü S=S
1
∪...∪S
n.
Òîãäà A ïðîòèâîðå÷èâà òîãäà è òîëüêî òîãäà, êîãäà S ïðîòèâîðå÷èâî.
Ãîâîðÿò, ÷òî ìíîæåñòâî äèçúþíêòîâ íåâûïîëíèìî, åñëè ñîîòâåòñòâó-
þùàÿ ñòàíäàðòíàÿ ôîðìà ïðîòèâîðå÷èâà, è âûïîëíèìî â ïðîòèâíîì
ñëó÷àå.
13.4. Ýðáðàíîâñêèé óíèâåðñóì
ìíîæåñòâà äèçúþíêòîâ
Ïî îïðåäåëåíèþ, ìíîæåñòâî äèçúþíêòîâ íåâûïîëíèìî òîãäà è
òîëüêî òîãäà, êîãäà îíî ëîæíî ïðè âñåõ èíòåðïðåòàöèÿõ íà âñåõ îáëàñ-
òÿõ. Òàê êàê íåâîçìîæíî ðàññìàòðèâàòü âñå èíòåðïðåòàöèè íà âñåõ
îáëàñòÿõ, áûëî áû óäîáíî, åñëè áû ìû ìîãëè ôèêñèðîâàòü îäíó òàêóþ
ñïåöèàëüíóþ îáëàñòü H, ÷òî S íåâûïîëíèìî òîãäà è òîëüêî òîãäà,
êîãäà S ëîæíî ïðè âñåõ èíòåðïðåòàöèÿõ íà ýòîé îáëàñòè. Ýðáðàí
ïîêàçàë, ÷òî òàêàÿ îáëàñòü ñóùåñòâóåò. Åå íàçûâàþò ýðáðàíîâñêèì
óíèâåðñóìîì ìíîæåñòâà äèçúþíêòîâ S è îïðåäåëÿþò ñëåäóþùèì
îáðàçîì.
Îïðåäåëåíèå 13.4. Ïóñòü H
0
ìíîæåñòâî êîíñòàíò, âñòðå÷à-
þùèõñÿ â S. Åñëè íèêàêàÿ êîíñòàíòà íå âñòðå÷àåòñÿ â S, òî H
0
ñîñòîèò èç îäíîé ïðîèçâîëüíîé êîíñòàíòû, íàïðèìåð, H
0
={a}.
Äëÿ i=1,2,... ïóñòü H
i+1
åñòü îáúåäèíåíèå H
i
è ìíîæåñòâà âñåõ
òåðìîâ âèäà f
n
(t
1
,...,t
n
) (ïðè âñåõ n) äëÿ âñåõ ôóíêöèé f
n
,
âñòðå÷àþùèõñÿ â S, ãäå t
j
(j=1,...,n) ïðèíàäëåæèò H
i
. Òîãäà
êàæäîå H
i
íàçûâàåòñÿ ìíîæåñòâîì êîíñòàíò i-ãî óðîâíÿ äëÿ S
è H
∞
íàçûâàåòñÿ ýðáðàíîâñêèì óíèâåðñóìîì äëÿ S.
Ïðèìåðû.
1. Ïóñòü S
1
={P(a), ¬P(x) ∨ P(f(x))}. Òîãäà
H
0
={a};
H
1
={a, f(a)};
H
2
={a, f(a), f(f(a))};
..................
H
∞
={a, f(a), f(f(a)), f(f(f(a))),...}.
Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
2. Ïóñòü S
2
={P(x) ∨ Q(x), ¬R(z), R(y) ∨ ¬Q(y)}. Òàê êàê íå ñóùå-
ñòâóåò íèêàêèõ êîíñòàíò â S, ïîëîæèì H
0
={a}. Ïîñêîëüêó íå
ñóùåñòâóåò íèêàêèõ ôóíêöèîíàëüíûõ ñèìâîëîâ â S, òî H=H
0
=
=H
1
=...={a}.
Îïðåäåëåíèå 13.5. Ïóñòü S åñòü ìíîæåñòâî äèçúþíêòîâ. Òîãäà
ìíîæåñòâî àòîìîâ âèäà P
n
(t
1
,...,t
n
) äëÿ âñåõ n-ìåñòíûõ
ïðåäèêàòîâ P
n
, âñòðå÷àþùèõñÿ â
S, ãäå t
1
,...,t
n
ýëåìåíòû ýðáðà-
íîâñêîãî óíèâåðñóìà S, íàçûâàåòñÿ ìíîæåñòâîì àòîìîâ ìíîæå-
ñòâà S, èëè ýðáðàíîâñêèì áàçèñîì S.
Ïðèìåð. Ýðáðàíîâñêèé áàçèñ ìíîæåñòâà äèçúþíêòîâ S
1
={P(a),
¬P(x) ∨ P(f(x))}:
À = {P(a), P(f(a)), P(f(f(a)), P(f(f(f(a))), }.
Ýðáðàíîâñêèé áàçèñ ìíîæåñòâà äèçúþíêòîâ S
2
={P(x) ∨ Q(x),R(z)∨
∨ ¬Q(x)}:
À = {P(a), Q(a), R(a)}.
Îïðåäåëåíèå 13.6. Îñíîâíîé ïðèìåð äèçúþíêòà C ìíîæåñòâà
äèçúþíêòîâ S åñòü äèçúþíêò, ïîëó÷åííûé çàìåíîé ïåðåìåííûõ
â C íà ýëåìåíòû ýðáðàíîâñêîãî óíèâåðñóìà S.
Ïðèìåð. Ïóñòü S={P(x), Q(f(y)) ∨ R(y)}, C=P(x) äèçúþíêò
â S è H={a, f(a), f(f(a)), ...} ýðáðàíîâñêèé óíèâåðñóì S. Òîãäà
P(a), P(f(a)), P(f(f(a))) åñòü îñíîâíûå ïðèìåðû C.
Îïðåäåëåíèå 13.7. Ïóñòü S ìíîæåñòâî äèçúþíêòîâ, H
ýðáðàíîâñêèé óíèâåðñóì S è I èíòåðïðåòàöèÿ S íàä H. Ãîâîðÿò,
÷òî I åñòü H-èíòåðïðåòàöèÿ ìíîæåñòâà S, åñëè îíà óäîâëåòâî-
ðÿåò ñëåäóþùèì óñëîâèÿì:
1. I îòîáðàæàåò âñå êîíñòàíòû èç S â ñàìèõ ñåáÿ;
2. ïóñòü f åñòü n-ìåñòíûé ôóíêöèîíàëüíûé ñèìâîë è h
1
,..., h
n
ýëåìåíòû H.  I ÷åðåç f îáîçíà÷àåòñÿ ôóíêöèÿ, êîòîðàÿ îòîáðà-
æàåò (h
1
,..., h
n
) (ýëåìåíò èç H
n
) â f(h
1
,..., h
n
) ( ýëåìåíò èç H).
Ïðè ýòîì íå âîçíèêàåò íèêàêèõ îãðàíè÷åíèé ïðè ïðèäàíèè
çíà÷åíèÿ ëþáîìó n-ìåñòíîìó ïðåäèêàòíîìó ñèìâîëó â S. Ïóñòü
A={A
1
, A
2
,..., A
n
,...} ýðáðàíîâñêèé áàçèñ ìíîæåñòâà S.
H-èíòåðïðåòàöèþ I óäîáíî ïðåäñòàâëÿòü â âèäå: I={m
1
, m
2
,..., m
n
,...},
ãäå m
j
åñòü A
j
èëè ¬A
j
äëÿ j=1, 2, ... Ñìûñë ýòîãî ìíîæåñòâà â òîì,
÷òî åñëè m
j
åñòü A
j
, òî àòîìó A
j
ïðèñâîåíî çíà÷åíèå «èñòèííî», â
ïðîòèâíîì ñëó÷àå çíà÷åíèå «ëîæíî».
Ïðèìåð. Ðàññìîòðèì ìíîæåñòâî S={P(x) ∨ Q(x), R(f(y))}. Ýð-
áðàíîâñêèé óíèâåðñóì H äëÿ S åñòü H={a, f(a), f(f(a)), ...}. Â S
âõîäÿò òðè ïðåäèêàòíûõ ñèìâîëà: P, Q è R. Ñëåäîâàòåëüíî, ýðáðà-
íîâñêèé áàçèñ S åñòü
A={P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)),...}.

230 231Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
Íåêîòîðûå H èíòåðïðåòàöèè ìíîæåñòâà S:
I
1
={P(a), Q(a), R(a), P(f(a)), Q(f(a)), R(f(a)),...},
I
2
={¬P(a), ¬Q(a), ¬R(a), ¬P(f(a)), ¬Q(f(a)), ¬R(f(a)), ...},
I
3
={P(a), Q(a), ¬R(a), P(f(a)), Q(f(a)), ¬R(f(a)),...}, è ò.ä.
Ìîæíî ïîêàçàòü, ÷òî äëÿ ëþáîé èíòåðïðåòàöèè íàéäåòñÿ ñîîò-
âåòñòâóþùàÿ åé H-èíòåðïðåòàöèÿ.
Òåîðåìà 13.3. Ìíîæåñòâî äèçúþíêòîâ S íåâûïîëíèìî òîãäà è
òîëüêî òîãäà, êîãäà S ëîæíî ïðè âñåõ H-èíòåðïðåòàöèÿõ â S.
Äîêàçàòåëüñòâî. Ïåðâàÿ ïîëîâèíà òåîðåìû î÷åâèäíà, òàê êàê
ïî îïðåäåëåíèþ S íåâûïîëíèìî òîãäà è òîëüêî òîãäà, êîãäà S ëîæíî
ïðè âñåõ èíòåðïðåòàöèÿõ íà ýòîé îáëàñòè. ×òîáû äîêàçàòü âòîðóþ
ïîëîâèíó òåîðåìû, ïðåäïîëîæèì, ÷òî S ëîæíî ïðè âñåõ H-èíòåðïðå-
òàöèÿõ â S. Ïîëîæèì, ÷òî S âûïîëíèìî. Òîãäà ñóùåñòâóåò òàêàÿ
èíòåðïðåòàöèÿ I íà íåêîòîðîé îáëàñòè D, ÷òî S èñòèííî ïðè I.
Ïóñòü I* åñòü H-èíòåðïðåòàöèÿ, ñîîòâåòñòâóþùàÿ I. Òîãäà S èñòèííî
ïðè I*. Ýòî ïðîòèâîðå÷èò ïðåäïîëîæåíèþ, ÷òî S ëîæíî ïðè âñåõ
H-èíòåðïðåòàöèÿõ â S. Ñëåäîâàòåëüíî, S äîëæíî áûòü íåâûïîëíèìî,
÷òî è òðåáîâàëîñü äîêàçàòü.
Òàêèì îáðàçîì, ìû äîñòèãëè öåëè, óñòàíîâëåííîé â íà÷àëå ýòîãî
ïàðàãðàôà, ò.å. íàì íåîáõîäèìî ðàññìàòðèâàòü òîëüêî èíòåðïðåòà-
öèè íàä ýðáðàíîâñêèì óíèâåðñóìîì, òî÷íåå, H-èíòåðïðåòàöèè, äëÿ
ïðîâåðêè òîãî, âûïîëíèìî ìíîæåñòâî äèçúþíêòîâ èëè íåò. Ïîýòîìó
âïðåäü, óïîìèíàÿ èíòåðïðåòàöèþ, ìû áóäåì èìåòü â âèäó H-èí-
òåðïðåòàöèþ.
H-èíòåðïðåòàöèè ìîæíî ïðåäñòàâëÿòü â âèäå ñåìàíòè÷åñêèõ
äåðåâüåâ. Êàê áóäåò âèäíî âïîñëåäñòâèè, íàõîæäåíèå äîêàçàòåëüñòâà
íåâûïîëíèìîñòè ìíîæåñòâà äèçúþíêòîâ ýêâèâàëåíòíî ïîñòðîåíèþ
ñåìàíòè÷åñêîãî äåðåâà. Áåç ïîòåðè îáùíîñòè ìîæíî ðàññìàòðèâàòü
òîëüêî áèíàðíûå ñåìàíòè÷åñêèå äåðåâüÿ.
Îïðåäåëåíèå 13.8. Åñëè A àòîì, òî ãîâîðÿò, ÷òî äâå ëèòåðû A
è ¬A êîíòðàðíû äðóã äðóãó, è ìíîæåñòâî {A, ¬A} íàçûâàþò
êîíòðàðíîé ïàðîé.
Îòìåòèì, ÷òî äèçúþíêò åñòü òàâòîëîãèÿ, åñëè îí ñîäåðæèò
êîíòðàðíóþ ïàðó, òàê êàê A∨¬A ≡ T, è ìíîæåñòâî äèçúþíêòîâ
íåâûïîëíèìî, åñëè îíî ñîäåðæèò äâà åäèíè÷íûõ êîíòðàðíûõ
äèçúþíêòà, òàê êàê A&¬A ≡ F.
Îïðåäåëåíèå 13.9. Ïóñòü S ìíîæåñòâî äèçúþíêòîâ è A åãî
ýðáðàíîâñêèé áàçèñ. Ñåìàíòè÷åñêîå (áèíàðíîå) äåðåâî äëÿ S åñòü
ðàñòóùåå âíèç äåðåâî T, â êîòîðîì êàæäîìó ðåáðó ïðèïèñàí
àòîì èç A èëè åãî îòðèöàíèå òàêèì îáðàçîì, ÷òî èç êàæäîãî
óçëà N âûõîäèò äâà ðåáðà, ïîìå÷åííûå êîíòðàðíûìè ëèòåðàìè,
è êàæäàÿ âåòâü äåðåâà íå ñîäåðæèò êîíòðàðíûõ ëèòåð.
Îáîçíà÷èì ÷åðåç I(N) îáúåäèíåíèå âñåõ ëèòåð, ïðèïèñàííûõ
ðåáðàì âåòâè, âåäóùåé ê óçëó N. Òîãäà äëÿ êàæäîãî óçëà N I(N) íå
ñîäåðæèò êîíòðàðíûõ ïàð.
Îïðåäåëåíèå 13.10. Ïóñòü A={A
1
, A
2
, ..., A
n
, ...} ýðáðàíîâñêèé
áàçèñ ìíîæåñòâà S. Ãîâîðÿò, ÷òî ñåìàíòè÷åñêîå äåðåâî äëÿ S
áóäåò ïîëíûì òîãäà è òîëüêî òîãäà, êîãäà äëÿ êàæäîãî i (i=1,
2,...) è êàæäîãî êîíå÷íîãî óçëà N ñåìàíòè÷åñêîãî äåðåâà (ò.å.äëÿ
óçëà, èç êîòîðîãî íå âûõîäèò íèêàêèõ ðåáåð) I(N) ñîäåðæèò
ëèáî A
i
ëèáî ¬A
i
. Òàêèì îáðàçîì, â ïîëíîì
ñåìàíòè÷åñêîì äåðåâå
êàæäàÿ âåòâü ñîîòâåòñòâóåò îäíîé H-èíòåðïðåòàöèè.
Êîãäà ýðáðàíîâñêèé áàçèñ ìíîæåñòâà S áåñêîíå÷åí, âñÿêîå ïîë-
íîå ñåìàíòè÷åñêîå äåðåâî äëÿ S áóäåò òîæå áåñêîíå÷íî. Ïîëíîå
ñåìàíòè÷åñêîå äåðåâî äëÿ S ñîîòâåòñòâóåò èñ÷åðïûâàþùåìó ïåðå-
áîðó âñåõ âîçìîæíûõ èíòåðïðåòàöèé äëÿ S. Åñëè S íåâûïîëíèìî,
òî S íå ñìîæåò áûòü èñòèííûì â êàæäîé èç ýòèõ èíòåðïðåòàöèé.
Òàêèì îáðàçîì, ìû ìîæåì îñòàíîâèòü ðîñò äåðåâà èç óçëà N, åñëè
I(N) îïðîâåðãàåò S. Ýòî ïîðîæäàåò ñëåäóþùèå îïðåäåëåíèÿ.
Îïðåäåëåíèå 13.11. Óçåë N íàçûâàåòñÿ îïðîâåðãàþùèì, åñëè
I(N) îïðîâåðãàåò íåêîòîðûé îñíîâíîé ïðèìåð äèçúþíêòà â S,
íî äëÿ ëþáîãî ïðåäøåñòâóþùåãî óçëà N′ I(N′) íå îïðîâåðãàåò
íèêàêîãî îñíîâíîãî ïðèìåðà äèçúþíêòà â S.
Îïðåäåëåíèå 13.12. Ãîâîðÿò, ÷òî ñåìàíòè÷åñêîå äåðåâî T çàìê-
íóòî òîãäà è òîëüêî òîãäà, êîãäà êàæäàÿ âåòâü T îêàí÷èâàåòñÿ
îïðîâåðãàþùèì óçëîì.
Ïðèìåðû.
1. Ïóñòü S={P, Q ∨ R, ¬P ∨ ¬Q, ¬P ∨ ¬R}.
Ýðáðàíîâñêèé áàçèñ ìíîæå-
ñòâà S åñòü A ={P, Q, R},
íåâûïîëíèìîå ìíîæåñòâî
îñíîâíûõ ïðèìåðîâ: {¬P,
¬Q∨¬R, P ∨ Q, P ∨ R}.
Ñåìàíòè÷åñêîå äåðåâî äëÿ S
ïîêàçàíî íà ðèñ.13.1,
çàìêíóòîå ïîääåðåâî âûäåëå-
íî áîëåå æèðíûìè ëèíèÿìè.
2. Ïóñòü S={P(x), ¬P(x)∨
∨Q(f(x)), ¬Q(f(a))}. Ýðáðà-
íîâñêèé áàçèñ A={P(a), Q(a), P(f(a)), Q(f(a)),}. Íåâûïîëíèìîå
ìíîæåñòâî îñíîâíûõ ïðèìåðîâ: {¬P(a), P(a)∨ ¬Q(f(a)), Q(f(a))}.
Ðèñ. 13.1. Êîíå÷íîå
ñåìàíòè÷åñêîå äåðåâî.
232 233Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
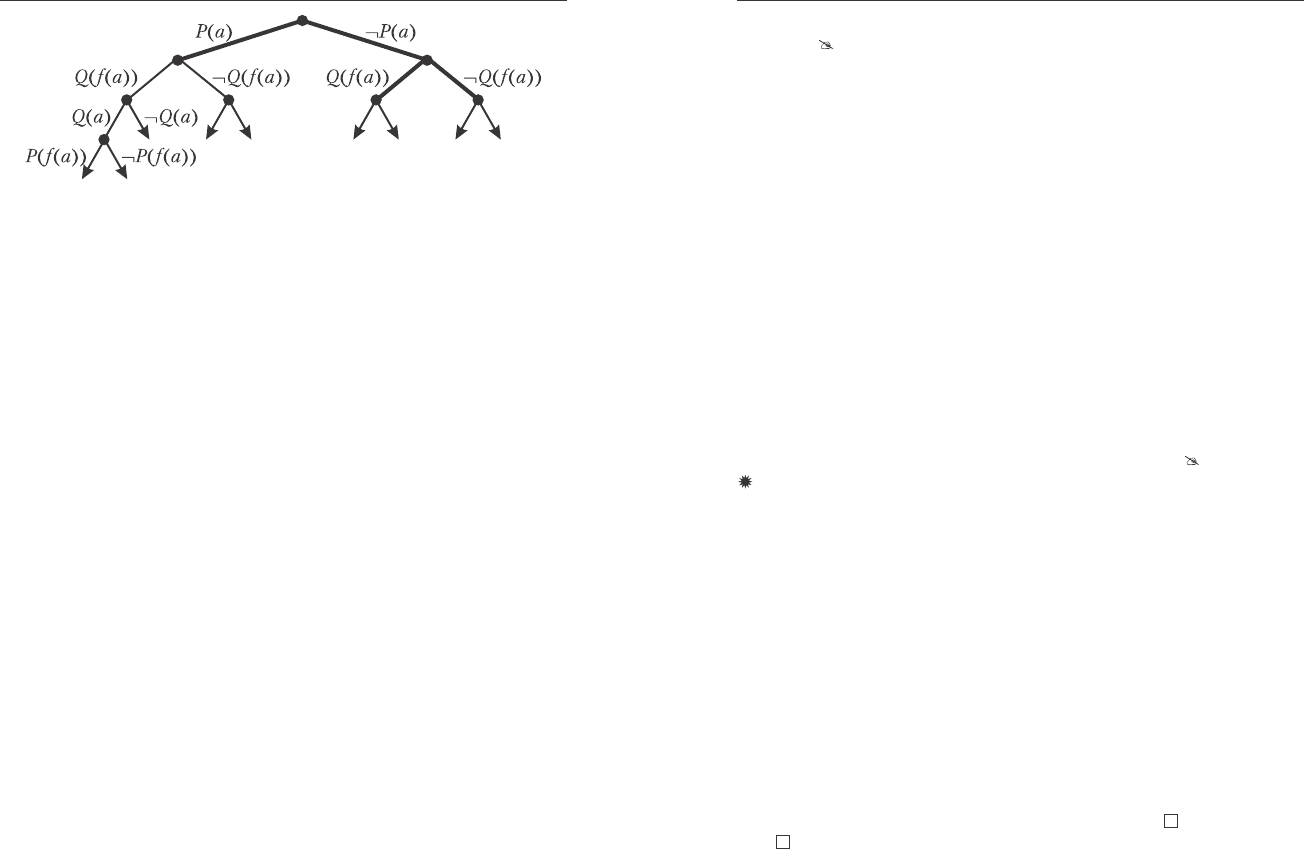
Ñåìàíòè÷åñêîå äåðåâî äëÿ S áóäåò áåñêîíå÷íûì (ñì. ðèñ.13.2);
çàìêíóòîå ïîääåðåâî âûäåëåíî áîëåå æèðíûìè ëèíèÿìè.
13.5. Òåîðåìà Ýðáðàíà
Ïðîöåäóðà Ýðáðàíà îñíîâûâàåòñÿ íà òåîðåìå 13.3, ïîýòîìó äëÿ
ïðîâåðêè íåâûïîëíèìîñòè ìíîæåñòâà äèçúþíêòîâ S ðàññìàòðèâà-
þòñÿ òîëüêî èíòåðïðåòàöèè íàä ýðáðàíîâñêèì óíèâåðñóìîì. Åñëè
S ëîæíî ïðè âñåõ èíòåðïðåòàöèÿõ íàä ýðáðàíîâñêèì óíèâåðñóìîì
S, òî ìîæíî çàêëþ÷èòü, ÷òî S íåâûïîëíèìî. Òàê êàê îáû÷íî ñóùå-
ñòâóåò ìíîãî, âîçìîæíî, áåñêîíå÷íîå ÷èñëî òàêèõ èíòåðïðåòàöèé,
îíè âûáèðàþòñÿ íåêîòîðûì ñèñòåìàòè÷åñêèì ñïîñîáîì ñ èñïîëüçî-
âàíèåì ñåìàíòè÷åñêèõ äåðåâüåâ.
Òåîðåìà 13.4 (òåîðåìà Ýðáðàíà, âàðèàíò 1). Ìíîæåñòâî äèçú-
þíêòîâ S íåâûïîëíèìî òîãäà è òîëüêî òîãäà, êîãäà ëþáîìó ïîë-
íîìó ñåìàíòè÷åñêîìó äåðåâó S ñîîòâåòñòâóåò êîíå÷íîå çàìêíó-
òîå ñåìàíòè÷åñêîå äåðåâî.
Äîêàçàòåëüñòâî. Äîïóñòèì, ÷òî S íåâûïîëíèìî. Ïóñòü Ò
ïîëíîå ñåìàíòè÷åñêîå äåðåâî äëÿ S. Ïóñòü äëÿ êàæäîé âåòâè B
äåðåâà Ò I
B
ìíîæåñòâî âñåõ ëèòåð, ïðèïèñàííûõ âñåì ðåáðàì
âåòâè B. Òîãäà I
B
åñòü èíòåðïðåòàöèÿ äëÿ S. Òàê êàê S íåâûïîëíèìî,
òî I
B
äîëæíà îïðîâåðãàòü îñíîâíîé ïðèìåð Ñ′ äèçúþíêòà Ñ â S.
Îäíàêî, òàê êàê Ñ′ êîíå÷íî, òî íà  äîëæåí ñóùåñòâîâàòü îïðîâåðãà-
þùèé óçåë N
B
(ëåæàùèé íà êîíå÷íîì ðàññòîÿíèè îò êîðíÿ). Ïî-
ñêîëüêó êàæäàÿ âåòâü Ò èìååò îïðîâåðãàþùèé óçåë, òî ñóùåñòâóåò
çàìêíóòîå ñåìàíòè÷åñêîå äåðåâî Ò′ äëÿ S. Äàëåå, òàê êàê èç êàæäîãî
óçëà â Ò′ âûõîäèò òîëüêî êîíå÷íîå ÷èñëî ðåáåð, òî Ò′ äîëæíî áûòü
êîíå÷íûì (ò.å. ÷èñëî óçëîâ â Ò′ êîíå÷íî), èíà÷å ìû ìîãëè áû íàéòè
áåñêîíå÷íóþ âåòâü, íå ñîäåðæàùóþ îïðîâåðãàþùèõ óçëîâ. Òàêèì
îáðàçîì, äîêàçàòåëüñòâî ïåðâîé ïîëîâèíû òåîðåìû çàâåðøåíî.
Ñ äðóãîé ñòîðîíû, åñëè äëÿ êàæäîãî ïîëíîãî ñåìàíòè÷åñêîãî
äåðåâà Ò äëÿ S ñóùåñòâóåò êîíå÷íîå çàìêíóòîå ñåìàíòè÷åñêîå
äåðåâî, òî êàæäàÿ âåòâü Ò ñîäåðæèò îïðîâåðãàþùèé óçåë. Ýòî
îçíà÷àåò, ÷òî êàæäàÿ èíòåðïðåòàöèÿ îïðîâåðãàåò S. Ñëåäîâàòåëüíî,
Ðèñ. 13.2. Áåñêîíå÷íîå ñåìàíòè÷åñêîå äåðåâî.
S íåâûïîëíèìî. Ýòî çàâåðøàåò äîêàçàòåëüñòâî âòîðîé ïîëîâèíû
òåîðåìû.
Òåîðåìà 13.5 (òåîðåìà Ýðáðàíà, âàðèàíò 2). Ìíîæåñòâî
äèçúþíêòîâ S íåâûïîëíèìî òîãäà è òîëüêî òîãäà, êîãäà ñóùå-
ñòâóåò êîíå÷íîå íåâûïîëíèìîå ìíîæåñòâî S′ îñíîâíûõ ïðèìåðîâ
äèçúþíêòîâ S.
Äîêàçàòåëüñòâî. Ïðåäïîëîæèì, ÷òî S íåâûïîëíèìî. Ïóñòü Ò
ïîëíîå ñåìàíòè÷åñêîå äåðåâî äëÿ S. Òîãäà ïî òåîðåìå Ýðáðàíà
(âàðèàíò 1) ñóùåñòâóåò êîíå÷íîå çàìêíóòîå ñåìàíòè÷åñêîå äåðåâî
Ò′, ñîîòâåòñòâóþùåå Ò. Ïóñòü S′ ìíîæåñòâî âñåõ îñíîâíûõ ïðèìå-
ðîâ äèçúþíêòîâ, êîòîðûå îïðîâåðãàþòñÿ âî âñåõ îïðîâåðãàþùèõ
óçëàõ Ò′. S′ êîíå÷íî, òàê êàê â Ò′ ñîäåðæèòñÿ êîíå÷íîå ÷èñëî îïðî-
âåðãàþùèõ óçëîâ. Òàê êàê S′ ëîæíî â êàæäîé èíòåðïðåòàöèè S′, òî
S′ íåâûïîëíèìî.
Ïðåäïîëîæèì, ÷òî ñóùåñòâóåò êîíå÷íîå íåâûïîëíèìîå ìíîæå-
ñòâî S′ îñíîâíûõ ïðèìåðîâ äèçúþíêòîâ â S. Òàê êàê êàæäàÿ èíòåð-
ïðåòàöèÿ I äëÿ S ñîäåðæèò èíòåðïðåòàöèþ I′ ìíîæåñòâà S′ è I′ îïðî-
âåðãàåò S′, òî I äîëæíà òàêæå îïðîâåðãàòü S′. Îäíàêî S′ îïðîâåðãàåòñÿ
â êàæäîé èíòåðïðåòàöèè I′. Ñëåäîâàòåëüíî, S′ îïðîâåðãàåòñÿ â êàæäîé
èíòåðïðåòàöèè I ìíîæåñòâà S. Ïîýòîìó S îïðîâåðãàåòñÿ â êàæäîé
èíòåðïðåòàöèè ìíîæåñòâà S′, çíà÷èò, S íåâûïîëíèìî.
Ïðèìåð. Ïóñòü S={¬P(x) ∨ Q(f(x), x), P(g(b)), ¬Q(y, z)}. Ýòî
ìíîæåñòâî íåâûïîëíèìî. Îäíî èç íåâûïîëíèìûõ ìíîæåñòâ
îñíîâíûõ ïðèìåðîâ äèçúþíêòîâ ìíîæåñòâà S åñòü S′=
={¬P(g(b))∨Q(f(g(b)),g(b)), P(g(b)), ¬Q(f(g(b)), g(b))}.
13.6. Ìåòîä ðåçîëþöèé
Äàëåêî íå âñåãäà ìîæíî ëåãêî íàéòè íåâûïîëíèìîå ìíîæåñòâî
îñíîâíûõ ïðèìåðîâ äèçúþíêòîâ. Òðóäíîñòè çàêëþ÷àþòñÿ â ïîðîæäåíèè
îñíîâíûõ ïðèìåðîâ äèçúþíêòîâ è ïîèñêå îïðîâåðãàþùèõ èíòåðïðåòàöèé.
Ïîñêîëüêó ìíîæåñòâî äèçúþíêòîâ ïðåäñòàâëÿåò ñîáîé êîíúþíêòèâíóþ
íîðìàëüíóþ ôîðìó, òî çàäà÷à ïðîâåðêè íåâûïîëíèìîñòè ýòîãî ìíîæåñòâà
ýêâèâàëåíòíà çàäà÷å ïðîâåðêè ëîæíîñòè êîíúþíêòèâíîé íîðìàëüíîé
ôîðìû, à ýòî çàäà÷à ýêñïîíåíöèàëüíîé ñëîæíîñòè. Ïîñëå ìíîãî÷èñëåííûõ
ïîèñêîâ áîëåå ýôôåêòèâíûõ ïðîöåäóð, Äæ. Ðîáèíñîíîì áûë ïðåäëîæåí
ìåòîä, íàçâàííûé ìåòîäîì ðåçîëþöèé.
Îñíîâíàÿ èäåÿ ìåòîäà ðåçîëþöèé ñîñòîèò â òîì, ÷òîáû ïðîâå-
ðèòü, ñîäåðæèò ëè ìíîæåñòâî S ïóñòîé äèçúþíêò
. Åñëè S ñîäåð-
æèò
, òî ìíîæåñòâî S íåâûïîëíèìî, åñëè íåò, òî íàäî ïðîâåðèòü,
ìîæåò ëè îí áûòü ïîëó÷åí èç äàííîãî ìíîæåñòâà äèçúþíêòîâ. Èíû-
ìè ñëîâàìè, íåîáõîäèìî íàéòè ìíîæåñòâî îñíîâíûõ ïðèìåðîâ,
îïðîâåðãàþùèõ èñõîäíîå ìíîæåñòâî äèçúþíêòîâ. Ýòà ïðîöåäóðà
îñíîâàíà íà ïðàâèëå ðåçîëþöèé.

234 235Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
Ïðàâèëî ðåçîëþöèé Ðîáèíñîíà. Åñëè äëÿ ëþáûõ äâóõ äèçúþí-
êòîâ Ñ
1
è Ñ
2
ñóùåñòâóåò ëèòåðà L
1
∈C
1
è êîíòðàðíàÿ åé ëèòåðà
L
2
∈C
2
(L
2
=¬L
1
), òî âû÷åðêíóâ L
1
èç Ñ
1
è L
2
èç Ñ
2
è ïîñòðîèâ
äèçúþíêò èç îñòàâøèõñÿ ëèòåð, ïîëó÷èì ðåçîëüâåíòó Ñ
1
è Ñ
2
:
C'
1
∨C'
2
, ãäå C'
1
= C
1
\L
1
, C'
2
= C
2
\L
2
.
Òåîðåìà 13.6. Ðåçîëüâåíòà Ñ åñòü ëîãè÷åñêîå ñëåäîâàíèå äèçú-
þíêòîâ Ñ
1
è Ñ
2
, ñîäåðæàùèõ êîíòðàðíûå ëèòåðû L è ¬L:
L
∨Ñ′
1
, ¬L
1
∨Ñ′
2
|= C'
1
∨C'
2
.
Äîêàçàòåëüñòâî. Ïðåäïîëîæèì, ÷òî |L
∨Ñ′
1
| = T, |¬L
∨Ñ′
2
| = T,
|C'
1
∨C'
2
| = F. Òîãäà |C'
1
|= F, |C'
2
| = F. Åñëè |L
∨Ñ′
1
| = T, òî |L
| = T, íî
|¬L
∨Ñ′
2
| = T, ñëåäîâàòåëüíî, |L
| = F. Ïîëó÷åííîå ïðîòèâîðå÷èå
äîêàçûâàåò òåîðåìó.
Ïðàâèëî ðåçîëþöèé ÿâëÿåòñÿ îáîáùåíèåì ìíîãèõ èçâåñòíûõ
íàì ïðàâèë âûâîäà. Íàïðèìåð, ïðàâèëî ñèëëîãèçìà: A → B, B → C
|= A → C ìîæåò áûòü ïåðåïèñàíî â âèäå: ¬A ∨ B, ¬B ∨ C |= ¬A ∨C,
÷òî ñîîòâåòñòâóåò ïðàâèëó ðåçîëþöèé. Ïðàâèëî ÌÐ: A, A → B |= B
ìîæåò áûòü ïåðåïèñàíî â âèäå: A ¬A ∨ B |= B, ÷òî òàêæå ñîîòâåòñòâó-
åò ïðàâèëó ðåçîëþöèé. Íàêîíåö, çàêîí ïðîòèâîðå÷èÿ A&¬A ≡ F
ðàâíîçíà÷åí ïðàâèëó: A, ¬A |=
, ñîãëàñíî êîòîðîìó ðåçîëüâåíòà
äâóõ êîíòðàðíûõ îäíîëèòåðíûõ äèçúþíêòîâ åñòü ïóñòîé äèçúþíêò.
Îïðåäåëåíèå 13.13. Ðåçîëþòèâíûé âûâîä èç ìíîæåñòâà äèçú-
þíêòîâ S åñòü ïîñëåäîâàòåëüíîñòü C
1
,C
2
,...,C
k
, òàêàÿ, ÷òî êàæäîå
C
i
ëèáî ïðèíàäëåæèò S, ëèáî ÿâëÿåòñÿ ðåçîëüâåíòîé ïðåäøåñòâó-
þùèõ C
i
. Åñëè ïîñëåäíèé äèçúþíêò C
k
=
, òî ìíîæåñòâî
äèçúþíêòîâ S ÿâëÿåòñÿ íåâûïîëíèìûì, à âåñü âûâîä íàçûâàåòñÿ
îïðîâåðæåíèåì S. Åñëè C
k
íå ÿâëÿåòñÿ ïóñòûì äèçúþíêòîì è
äàëüíåéøåå ïðèìåíåíèå ïðàâèëà ðåçîëþöèé íåâîçìîæíî, òî
ìíîæåñòâî S ÿâëÿåòñÿ âûïîëíèìûì.
Ïðèìåð. Ðàññìîòðèì ïðèìåð 10.1. (ñì. ãëàâó 10). Íåîáõîäèìî
ïðîâåðèòü ëîãè÷åñêîå ñëåäîâàíèå â ëîãèêå âûñêàçûâàíèé: P→S,
S→R, P|=R. Ñîñòàâèì ìíîæåñòâî äèçúþíêòîâ S, äëÿ ÷åãî êàæäóþ
ôîðìóëó ïðèâåäåì ê ÊÍÔ, à îò çàêëþ÷åíèÿ R âîçüìåì îòðèöàíèå.
Ïîëó÷èì:
1. ¬P ∨ S
2. ¬S ∨ R
3. P
4. ¬R
5. ¬S ðåçîëüâåíòà 4, 2
6. ¬P ðåçîëüâåíòà 5, 1
7.
ðåçîëüâåíòà 3, 6
Ïðàâèëî ðåçîëþöèé î÷åíü ìîùíîå ñðåäñòâî ëîãè÷åñêîãî äîêàçà-
òåëüñòâà. Ìîæíî ïîêàçàòü [×åíü,Ëè,1983] ïîëíîòó ìåòîäà ðåçîëþöèé,
ò.å. äîêàçàòü, ÷òî ìíîæåñòâî äèçúþíêòîâ S íåâûïîëíèìî òîãäà è òîãäà,
êîãäà ñóùåñòâóåò ðåçîëþòèâíûé âûâîä ïóñòîãî äèçúþíêòà èç S.
13.7. Ïîäñòàíîâêà è óíèôèêàöèÿ
Ïðèìåíåíèå ìåòîäà ðåçîëþöèé â ëîãèêå ïðåäèêàòîâ óñëîæíÿ-
åòñÿ òåì, ÷òî äèçúþíêòû ñîäåðæàò òåðìû, êîòîðûå ìîãóò íå
ñîâïàäàòü â äâóõ îäèíàêîâûõ ëèòåðàõ. Íàïðèìåð, Ñ
1
=P(x)∨Q(x),
C
2
=¬P(f(a))∨V(a). Â ýòèõ äèçúþíêòàõ íåò êîíòðàðíûõ ëèòåð,
îäíàêî, åñëè ìû ïîäñòàâèì f(a) âìåñòî õ â Ñ
1
, òî ïîëó÷èì
Ñ
1
′=P(f(a))∨Q(f(a)); òåïåðü ëèòåðû P(f(a)) è ¬P(f(a)) áóäóò
óæå êîíòðàðíû. Ïîëó÷èì ðåçîëüâåíòó Q(f(a))∨V(a).
Òàêàÿ ïðîöåäóðà ïîäñòàíîâêè îäíèõ òåðìîâ âìåñòî äðóãèõ ñ
öåëüþ ïîëó÷åíèÿ êîíòðàðíûõ ëèòåð íàçûâàåòñÿ óíèôèêàöèåé.
Îïðåäåëåíèå 13.14. Ïîäñòàíîâêà ýòî êîíå÷íîå ìíîæåñòâî
âèäà {t
1
/v
1
,, t
n
/v
n
}, ãäå v
i
ïåðåìåííàÿ, t
i
òåðì, îòëè÷íûé îò
v
i
, è âñå v
i
ðàçëè÷íû.
Îïðåäåëåíèå 13.15. Ïóñòü θ = {t
1
/v
1
,, t
n
/v
n
} è E âûðàæåíèå.
Òîãäà Eθ âûðàæåíèå, ïîëó÷åííîå èç E çàìåíîé âñåõ âõîæäåíèé
ïåðåìåííûõ v
i
(1≤ i ≤ n) íà òåðìû t
i
.
Îïðåäåëåíèå 13.16. Ïóñòü θ = {t
1
/v
1
,, t
n
/v
n
}, λ = {u
1
/y
1
,, u
k
/y
k
}
ïîäñòàíîâêè. Êîìïîçèöèÿ ïîäñòàíîâîê θ°λ ïîëó÷àåòñÿ èç ìíî-
æåñòâà {t
1
λ/v
1
,, t
n
λ/v
n
, u
1
/y
1
,, u
k
/y
k
} âû÷åðêèâàíèåì âñåõ
ýëåìåíòîâ t
j
λ/v
j
, äëÿ êîòîðûõ t
j
λ = v
j
(òîæäåñòâåííàÿ ïîäñòàíîâ-
êà), è âñåõ ýëåìåíòîâ u
i
/y
i
, òàêèõ, ÷òî y
i
∈{v
1
,, v
n
}.
Ïðèìåð. Ïóñòü θ = {t
1
/v
1
, t
2
/v
2
} = {f(y)/x, z/y}, λ = {u
1
/y
1
, u
2
/y
2
,
u
3
/y
3
} = {a/x, b/y, y/z}. Òîãäà θ°λ = {t
1
λ/v
1
, t
2
λ/v
2
, u
1
/y
1
, u
2
/y
2
, u
3
/y
3
}=
={f(b)/x, y/y, a/x, b/y, y/z}. Òàê êàê t
2
λ/x
2
= y/y, òî y/y äîëæíî
áûòü âû÷åðêíóòî èç ìíîæåñòâà θ°λ. Ýëåìåíòû a/x, b/y òàêæå äîëæ-
íû áûòü âû÷åðêíóòû, òàê êàê ïîäñòàíîâêè äëÿ x è y óæå îïðåäåëåíû.
 ðåçóëüòàòå ïîëó÷àåì: θ°λ = {f(b)/x, y/z}.
 ïðîöåäóðå äîêàçàòåëüñòâà ìåòîäîì ðåçîëþöèé íåîáõîäèìî
íàõîäèòü òàêèå ïîäñòàíîâêè, êîòîðûå ïîçâîëÿþò ñäåëàòü äâà è áîëåå
âûðàæåíèÿ òîæäåñòâåííûìè.
Îïðåäåëåíèå 13.17. Ïîäñòàíîâêà θ íàçûâàåòñÿ óíèôèêàòîðîì
ìíîæåñòâà {E
1
,, E
m
} òîãäà è òîëüêî òîãäà, êîãäà E
1
θ = = E
m
θ.
Ìíîæåñòâî {E
1
,, E
m
} íàçûâàåòñÿ óíèôèöèðóåìûì, åñëè äëÿ íåãî
ñóùåñòâóåò óíèôèêàòîð. Óíèôèêàòîð σ äëÿ ìíîæåñòâà âûðàæå-
íèé {E
1
,, E
m
} íàçûâàåòñÿ íàèáîëåå îáùèì óíèôèêàòîðîì, åñëè
äëÿ êàæäîãî óíèôèêàòîðà θ ýòîãî ìíîæåñòâà ñóùåñòâóåò òàêàÿ
ïîäñòàíîâêà λ, ÷òî θ = σ°λ.

236 237Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
Íàïðèìåð, äëÿ äâóõ äèçúþíêòîâ {P(a, y), P(x, f(b)} ïîäñòàíîâêà
{a/x, f(b)/y} ÿâëÿåòñÿ íàèáîëåå îáùèì óíèôèêàòîðîì.
Ââåäÿ ïîíÿòèå óíèôèêàöèè, ìû ìîæåì ðàññìîòðåòü ìåòîä ðåçî-
ëþöèé äëÿ ëîãèêè ïåðâîãî ïîðÿäêà.
Îïðåäåëåíèå 13.18. Åñëè äâå èëè áîëåå ëèòåð (ñ îäèíàêîâûì
çíàêîì) äèçúþíêòà Ñ èìåþò íàèáîëåå îáùèé óíèôèêàòîð σ, òî
Cσ íàçûâàåòñÿ ñêëåéêîé Ñ. Åñëè Cσ åäèíè÷íûé äèçúþíêò, òî
ñêëåéêà íàçûâàåòñÿ åäèíè÷íîé ñêëåéêîé.
Ïðèìåð. Ïóñòü Ñ=P(x)∨P(f(y))∨¬Q(x). Òîãäà ïåðâàÿ è âòî-
ðàÿ ëèòåðû èìåþò íàèáîëåå îáùèé óíèôèêàòîð σ={f(y)/x}. Ñëåäî-
âàòåëüíî, Cσ=P(f(y))∨¬Q(f(y)) åñòü ñêëåéêà Ñ.
Îïðåäåëåíèå 13.19. Ïóñòü C
1
è C
2
äâà äèçúþíêòà (íàçûâàåìûå
äèçúþíêòàìè-ïîñûëêàìè), êîòîðûå íå èìåþò íèêàêèõ îáùèõ
ïåðåìåííûõ. Ïóñòü L
1
è ¬L
2
äâå ëèòåðû â C
1
è C
2
ñîîòâåòñòâåí-
íî. Åñëè L
1
è L
2
èìåþò íàèáîëåå îáùèé óíèôèêàòîð σ, òî
äèçúþíêò (C
1
σ\L
1
σ)∨(C
2
σ\L
2
σ) íàçûâàåòñÿ (áèíàðíîé)
ðåçîëüâåíòîé C
1
è C
2
. Ëèòåðû L
1
è L
2
íàçûâàþòñÿ îòðåçàåìûìè
ëèòåðàìè.
Îïðåäåëåíèå 13.20. Ðåçîëüâåíòîé äèçúþíêòîâ-ïîñûëîê C
1
è C
2
ÿâëÿåòñÿ îäíà èç ñëåäóþùèõ ðåçîëüâåíò:
1) áèíàðíàÿ ðåçîëüâåíòà C
1
è C
2
;
2) áèíàðíàÿ ðåçîëüâåíòà C
1
è ñêëåéêè C
2
;
3) áèíàðíàÿ ðåçîëüâåíòà C
2
è ñêëåéêè C
1
;
4) áèíàðíàÿ ðåçîëüâåíòà ñêëåéêè C
1
è ñêëåéêè C
2
.
Ïðèìåð. Ïóñòü C
1
=P(x)∨P(f(y))∨R(g(y)) è C
2
=¬P(f(g(a)))∨
∨Q(b). Ñêëåéêà C
1
åñòü Ñ
1
'=P(f(y))∨R(g(y)). Âûïîëíèì ïîäñòà-
íîâêó g(a)/y. Áèíàðíàÿ ðåçîëüâåíòà Ñ
1
' è C
2
åñòü R(g(g(a)))∨Q(b).
Ñëåäîâàòåëüíî, R(g(g(a)))∨Q(b) åñòü ðåçîëüâåíòà C
1
è C
2
.
13.8. Ïðèìåðû èñïîëüçîâàíèÿ ìåòîäà ðåçîëþöèé
Ïðèìåð 13.1. Çàâåðøèì ðàññìîòðåíèå ïðèìåðà 12.1 ãëàâû 12.
ÑÑÔ ïîñûëîê ìû ïîëó÷èëè â 13.3:
∀y((¬D(y) ∨ L(à, y))&P(à)), ∀x∀y(¬Q(y) ∨ ¬L(x, y) ∨ ¬P(x)).
Íàéäåì îòðèöàíèå îò çàêëþ÷åíèÿ G è ïðèâåäåì åãî ê ÏÍÔ;
ïîëó÷èì:
¬∀y(D(y) → ¬Q(y)) = ∃y¬(¬D(y) ∨ ¬Q(y)) = ∃y(D(y)&Q(y)).
Ýëèìèíèðóåì êâàíòîð ∃ è ïîëó÷èì ÑÑÔ: D(b)&Q(b).
Ïîñòðîèì ðåçîëþòèâíûé âûâîä:
1. ¬D(y) ∨ L(à, y)
2. P(à)
3. ¬Q(y) ∨ ¬L(x, y) ∨ ¬P(x)
4.D(b)
5.Q(b)
6.¬L(x, b) ∨ ¬P(x){b/y}, ðåçîëüâåíòà 5, 3
7.¬L(a, b){a/x}, ðåçîëüâåíòà 2, 6
8.¬D(b){b/y}, ðåçîëüâåíòà 1, 7
9.
ðåçîëüâåíòà 4, 8
Ïðèìåð 13.2. Ïîñûëêà: «Êàæäûé, êòî õðàíèò äåíüãè, ïîëó÷àåò
ïðîöåíòû». Çàêëþ÷åíèå: «Åñëè íå ñóùåñòâóåò ïðîöåíòîâ, òî íèêòî
íå õðàíèò äåíåã». Ïóñòü S(x, y): «x õðàíèò y», M(x): «x åñòü äåíüãè»,
I(x): «x åñòü ïðîöåíòû» è E(x, y): «x ïîëó÷àåò y». Òîãäà ïîñûëêà
çàïèñûâàåòñÿ â âèäå: ∀x(∃y(S(x, y)&M(y)) → ∃y(I(y)&E(x,y))), à
çàêëþ÷åíèå: ¬∃xI(x) → ∀x∀y(S(x, y) → ¬M(y)).
Ïðèâåäåì ïîñûëêó ê ÑÑÔ:
∀x(∃y(S(x, y)&M(y)) → ∃y(I(y)&E(x, y))) =
= ∀x(¬∃y(S(x, y)&M(y)) ∨ ∃y(I(y)&E(x, y))) =
= ∀x(∀y(¬S(x, y) ∨ ¬M(y)) ∨ ∃y(I(y)&E(x, y))) =
= ∀x(∃z(I(z)&E(x, z))) ∨ ∀y(¬S(x, y) ∨ ¬M(y)) =
= ∀x∃z((I(z)&E(x, z)) ∨ ∀y(¬S(x, y) ∨ ¬M(y))) =
= ∀x∃z∀y ((I(z)&E(x, z)) ∨ (¬S(x, y) ∨ ¬M(y))) =
= ∀x∃z∀y ((¬S(x, y) ∨ ¬M(y) ∨ I(z))&(¬S(x, y) ∨ ¬M(y) ∨ E(x,z))).
ÑÑÔ ïîñûëêè:
∀x∀y ((¬S(x, y) ∨ ¬M(y) ∨ I(f(x))&(¬S(x, y) ∨ ¬M(y) ∨ E(x, f(x))).
 ðåçóëüòàòå ïîëó÷èì äèçúþíêòû:
1. ¬S(x, y) ∨ ¬M(y) ∨ I(f(x)),
2. ¬S(x, y) ∨ ¬M(y) ∨ E(x, f(x)).
Âîçüìåì îòðèöàíèå îò çàêëþ÷åíèÿ è ïðèâåäåì ê ÏÍÔ:
¬(¬∃xI(x) → ∀x∀y(S(x, y) → ¬M(y))) =
= ¬(¬¬∃xI(x) ∨ ∀x∀y(¬S(x, y) ∨ ¬M(y))) =
= ∀x¬I(x)&¬∀x∀y(¬S(x, y) ∨ ¬M(y))) =
= ∀z¬I(z)&∃x∃y(S(x, y)&M(y)).
Ïîñêîëüêó ïîëó÷åííàÿ ôîðìóëà ïðåäñòàâëÿåò ñîáîé êîíúþíê-
öèþ äâóõ ôîðìóë â ÏÍÔ, ìîæíî êàæäóþ èç íèõ ïðèâîäèòü ê
ÑÑÔ îòäåëüíî: ∀z¬I(z)&(S(a, b)&M(b)).
Èç îòðèöàíèÿ çàêëþ÷åíèÿ ïîëó÷èëè äèçúþíêòû:
3. ¬I(z),
4. S(a, b),
5. M(b).

238 239
Äàëüíåéøåå äîêàçàòåëüñòâî î÷åíü ïðîñòî:
6. ¬S(x, y) ∨ ¬M(y){f(x)/z} â 3, ðåçîëüâåíòà 3, 1
7. ¬M(b){a/x, b/y} â 6, ðåçîëüâåíòà 6, 4
8.
ðåçîëüâåíòà 7, 5
Ëîãè÷åñêîå ñëåäîâàíèå äîêàçàíî.
Ïðèìåð 13.3. Ïîñûëêà: «Ñòóäåíòû åñòü ãðàæäàíå». Çàêëþ÷å-
íèå: «Ãîëîñà ñòóäåíòîâ åñòü ãîëîñà ãðàæäàí.» Ïóñòü S(x): «x
ñòóäåíò», C(x): «x ãðàæäàíèí» è V(x, y): «x åñòü ãîëîñ y». Òîãäà
ïîñûëêà è çàêëþ÷åíèå çàïèøóòñÿ ñëåäóþùèì îáðàçîì:
∀y(S(y) → C(y)) (ïîñûëêà),
∀x(∃y(S(y)&V(x, y)) → ∃z(C(z)&V(x, z)) (çàêëþ÷åíèå).
Ñòàíäàðòíàÿ ôîðìà ïîñûëêè åñòü ∀y(¬S(y) ∨ C(y)).
Îòðèöàíèå çàêëþ÷åíèÿ ïðèâåäåì ê ÑÑÔ:
¬(∀x(∃y(S(y)&V(x, y)) → ∃z(C(z)&V(x, z))))=
=¬(∀x(∀y(¬S(y)∨¬V(x,y))∨∃z(C(z)&V(x,z))))=
=¬(∀x∀y∃z(¬S(y) ∨ ¬V(x, y) ∨ (C(z)&V(x, z))))=
=∃x∃y∀z((S(y)&V(x,y))&(¬C(z)∨¬V(x,z)));
ÑÑÔ: ∀z((S(b)&V(a,b))&(¬C(z)∨¬V(a,z))),
Çàïèøåì ìíîæåñòâî äèçúþíêòîâ è ïîñòðîèì ðåçîëþòèâíûé
âûâîä:
1. ¬S(y) ∨ C(y).
2. S(b),
3. V(a, b),
4. ¬C(z) ∨ ¬V(a, z).
5. C(b){b/y} â 1, ðåçîëüâåíòà 1, 2
6. ¬V(a, b){b/z} â 4, ðåçîëüâåíòà 5, 4
7.
ðåçîëüâåíòà 6, 3.
Ïðèìåð 13.4. Ïðîâåðèì ëîãè÷íîñòü óòâåðæäåíèÿ ËîñåâàÀ.Ô.
1
:
«Âåðà â ñóùíîñòè ñâîåé è åñòü ïîäëèííîå çíàíèå, è ýòè äâå ñôåðû
íå òîëüêî íå ðàçúåäèíèìû, íî äàæå íåðàçëè÷èìû».
Äîêàçàòåëüñòâî Ëîñåâà çàêëþ÷àåòñÿ â ñëåäóþùåì.
«Âåðóþùèé âåðèò â íå÷òî. Âåðà ñâîé ïðåäìåò ÿñíî îòëè÷àåò
îò âñÿêîãî äðóãîãî ïðåäìåòà. Òîãäà ýòîò ïðåäìåò îïðåäåëåí. Íî
åñëè îí îïðåäåëåí, îí îáëàäàåò ïðèçíàêàìè, îòëè÷àþùèìè åãî îò
âñÿêîãî äðóãîãî. Ýòî çíà÷èò, ÷òî ìû çíàåì ýòîò ïðåäìåò. Ìû çíàåì
âåùü, åñëè ïî ïðèçíàêàì ìîæåì îòëè÷èòü åå îò âñÿêîãî äðóãîãî.
Ñëåäîâàòåëüíî, âåðà è åñòü çíàíèå.»
1
À. Ô. Ëîñåâ. Äèàëåêòèêà ìèôà. Â êí. «Èç ðàííèõ ïðîèçâåäåíèé». Ì.: Ïðàâäà,
1990. (ñòð. 497).
Ïóñòü V(x, y): «x âåðèò â y», C(x, y): «x îòëè÷åí îò y», N(x, y):
«x çíàåò y». Ôîðìàëèçóåì ïîñûëêè.
1. Âåðóþùèé âåðèò â íå÷òî.
∀õ∃yV(x, y).
2. Âåðóþùèé ñâîé ïðåäìåò îòëè÷àåò îò âñÿêîãî äðóãîãî ïðåäìåòà.
∀x∃y(V(x, y) → ∀zC(y, z)).
3. Ìû çíàåì âåùü òîãäà, êîãäà ìû îòëè÷àåì åå îò âñÿêîé äðóãîé âåùè.
∀x∃y∀z(C(y, z) → N(x, y)).
4. Ñëåäîâàòåëüíî, âåðà åñòü çíàíèå.
∀x∃y(V(x, y) → N(x, y)).
Ïîñëå ïðèâåäåíèÿ ïîñûëîê è îòðèöàíèÿ çàêëþ÷åíèÿ ê ÑÑÔ,
ïîëó÷èì ìíîæåñòâî äèçúþíêòîâ è ðåçîëþòèâíûé âûâîä:
1. V(x, f(x)) x âåðèò â ïðåäìåò ñâîåé âåðû.
2. C(f(x), z) ∨ ¬V(x, f(x)) åñëè x âåðèò â f(x),
òî f(x) îòëè÷åí îò z.
3. N(x, f(x)) ∨ ¬C(f(x), z)x çíàåò f(x), åñëè ìîæåò
îòëè÷èòü åãî îò z.
4. V(b, y)ñóùåñòâóåò b, êîòîðûé âåðèò â y.
5. ¬N(b, y)b íå çíàåò y.
6. ¬Ñ(f(b), z){b/x, f(b)/y} â 2 è 4,
ðåçîëüâåíòà 5,3.
7. ¬V(b, f(b)) ðåçîëüâåíòà 6, 2.
8.
ðåçîëüâåíòà 1, 7.
Ïîëó÷àåì, ÷òî âåðà è çíàíèå îäíî è òî æå. Ýòî çàêëþ÷åíèå
âûçûâàåò ñîìíåíèÿ, íåñìîòðÿ íà òî, ÷òî ëîãè÷åñêîå ñëåäîâàíèå âû-
ïîëíåíî. Äåëî â òîì, ÷òî ïîñûëêè ýòîãî óòâåðæäåíèÿ ïðèíèìàþòñÿ
àâòîðîì çà èñòèííûå, îäíàêî ñ èõ èñòèííîñòüþ ìîæíî íå ñîãëàñèòü-
ñÿ. Íàïðèìåð, óòâåðæäåíèå «Ìû çíàåì âåùü òîãäà, êîãäà ìû îòëè÷àåì
åå îò âñÿêîé äðóãîé âåùè» âûçûâàåò ñîìíåíèå, îñîçíàíèå îòëè÷èÿ
îäíîé âåùè îò äðóãîé åùå íå åñòü çíàíèå. Ñîìíåíèå â èñòèííîñòè
îäíîé ïîñûëêè ïðèâîäèò ê òîìó, ÷òî è çàêëþ÷åíèå âûçûâàåò ñîìíå-
íèå, âåäü èç ïðîòèâîðå÷èâîé ñèñòåìû ïîñûëîê ìîæíî âûâåñòè
÷òî óãîäíî.
Ïðèìåð 13.5. Ñîãëàñíî ïðèíöèïó Ïèòåðà, ñëóæàùèé ïðîäâèãà-
åòñÿ ïî ñëóæåáíîé ëåñòíèöå äî òåõ ïîð, ïîêà îí íå äîñòèãíåò ñâîåãî
óðîâíÿ íåêîìïåòåíòíîñòè. Ñëåäóåò ëè èç ýòîãî, ÷òî íå ñóùåñòâóåò
êîìïåòåíòíûõ íà÷àëüíèêîâ?
Ïðîâåðèì ýòîò âûâîä, èñïîëüçóÿ ìåòîä ðåçîëþöèé. Âûáåðåì
ïðåäèêàòû: C(x): x ñëóæàùèé, K(x): x êîìïåòåíòíûé, N(x): x
íà÷àëüíèê, P(x): x ïðîäâèãàåòñÿ ïî ñëóæåáíîé ëåñòíèöå. Ôîðìàëèçó-
Ãëàâà 13 Àâòîìàòè÷åñêîå äîêàçàòåëüñòâî òåîðåì
