Таран Т.А. Основы дискретной математики

Подождите немного. Документ загружается.

180

ïðàâèëà ÌÐ. Â îäíîì èç ðàññêàçîâ î Øåðëîêå Õîëìñå ñëîæèëàñü

òàêàÿ ñèòóàöèÿ: «Íàì èçâåñòíî, ÷òî ïðåñòóïíèê íå ìîã ïîïàñòü â

êîìíàòó íè ÷åðåç äâåðü (A), íè ÷åðåç äûìîâîé õîä (B). Ìû çíàåì

òàêæå, ÷òî îí íå ìîã ñïðÿòàòüñÿ â êîìíàòå (C), ïîñêîëüêó â íåé

ïðÿòàòüñÿ íåãäå. Êàê æå òîãäà îí ïðîíèê ñþäà?  ×åðåç êðûøó(D)!

Áåç ñîìíåíèÿ. Îí ìîã ïðîíèêíóòü â ýòó êîìíàòó òîëüêî ÷åðåç

êðûøó.» Ýòî ðàññóæäåíèå ìîæíî ôîðìàëèçîâàòü òàê: À∨Â ∨Ñ∨D,

¬À, ¬Â,¬Ñ |=D, ÷òî ðàâíîñèëüíî: ¬À→(¬Â →(¬Ñ → D)), ¬À,

¬Â,¬Ñ |=D. Òðåõêðàòíîå ïðèìåíåíèå ïðàâèëà ÌÐ äîêàçûâàåò ýòî

ëîãè÷åñêîå ñëåäîâàíèå.

Íå ñëåäóåò çàáûâàòü, ÷òî ëîãè÷åñêîå ñëåäîâàíèå âûïîëíåíî òîëü-

êî òîãäà, êîãäà èç èñòèííûõ ïîñûëîê ñëåäóåò èñòèííîå çàêëþ÷åíèå.

Ïîýòîìó äîëæíà ñóùåñòâîâàòü õîòÿ áû îäíà èíòåðïðåòàöèÿ (ò.å.

èñòèííîñòíîå ðàñïðåäåëåíèå áóêâ, âõîäÿùèõ â êàæäóþ ïîñûëêó), íà

êîòîðîé âñå ïîñûëêè èñòèííû îäíîâðåìåííî. Åñëè òàêîé èíòåð-

ïðåòàöèè íå ñóùåñòâóåò, òî ñèñòåìà ïîñûëîê ïðîòèâîðå÷èâà è èç íåå

âûâîäèìî ëþáîå çàêëþ÷åíèå, ò.å. âìåñòå ñ íåêîòîðîé ôîðìóëîé A

âûâîäèìî è åå îòðèöàíèå ¬A. Ñ äðóãîé ñòîðîíû, ëîãè÷åñêîå ñëåäîâàíèå

ìîæåò îêàçàòüñÿ íå âûïîëíåííûì, åñëè ïîñûëîê íåäîñòàòî÷íî äëÿ

âûâîäà íóæíûõ çàêëþ÷åíèé. Â òàêèõ ñëó÷àÿõ, â çàâèñèìîñòè îò

ñîäåðæàíèÿ çàäà÷è, ìíîæåñòâî ïîñûëîê ìîæåò áûòü ïîïîëíåíî.

Ïðèìåð 10.5. Ïðîâåðèòü íåïðîòèâîðå÷èâîñòü ìíîæåñòâà ïîñûëîê:

A → ¬B&C, D ∨ E → G, G → ¬(H∨K), ¬C&E&H.

Ïðåäïîëîæèì, ÷òî ñóùåñòâóåò èíòåðïðåòàöèÿ, íà êîòîðîé âñå ïî-

ñûëêè ïðèíèìàþò èñòèííîå çíà÷åíèå:

1. |A → ¬B&C| = T,

2. |D ∨ E→ G| =T,

3. |G → ¬(H ∨ K)| = T,

4. |¬C&E&H| = T.

Èç 4 ñëåäóåò: |¬C| = T, |C| = F, |E| = T, |H| = T. Ïîäñòàâëÿÿ |C| = F â 1,

íàõîäèì: |A→¬B&F|=T, îòêóäà |A| = F. Ïîäñòàâëÿÿ |E| = T â 2,

ïîëó÷èì: |D∨T→G| =T, îòêóäà |G| =T. Ïîäñòàâèì ýòî çíà÷åíèå

â3, ïîëó÷èì |T→¬(H∨K)| = T, îòêóäà |¬(H∨K)| = T, ò.å. |H∨K|=F,

ñëåäîâàòåëüíî, |H| = F, |K| = F. Ïîëó÷èëè ïðîòèâîðå÷èå: |H| = T, |H|=F,

îòêóäà ñëåäóåò, ÷òî äàííàÿ ñèñòåìà ïîñûëîê ïðîòèâîðå÷èâà.

Ãëàâà 10

Ãëàâà 11. ÔÎÐÌÀËÜÍÛÅ ÒÅÎÐÈÈ.

ÈÑ×ÈÑËÅÍÈÅ ÂÛÑÊÀÇÛÂÀÍÈÉ

11.1. Îïðåäåëåíèå ôîðìàëüíîé òåîðèè

Òåîðèÿ íàçûâàåòñÿ ñîäåðæàòåëüíîé, åñëè ñóùåñòâóåò êàêàÿ-ëèáî

èíòåðïðåòàöèÿ îáúåêòîâ, îïåðàöèé, ñèìâîëîâ òåîðèè. Ëîãèêà

âûñêàçûâàíèé ÿâëÿåòñÿ ñîäåðæàòåëüíîé òåîðèåé, òàê êàê êàæäûé

ñèìâîë â íåé èíòåðïðåòèðóåòñÿ êàê ïðîñòîå âûñêàçûâàíèå, èñòèííîå

èëè ëîæíîå, ôîðìóëû òàêæå ìîãóò áûòü èñòèííûìè èëè ëîæíûìè,

è, íåñìîòðÿ íà òî, ÷òî ìû îòâëåêàåìñÿ îò ñîäåðæàòåëüíîãî ñìûñëà

âûñêàçûâàíèé, âñå ðàññóæäåíèÿ âåäóòñÿ â òåðìèíàõ èñòèííîñòè è

ëîæíîñòè. Â îòëè÷èå îò ñîäåðæàòåëüíûõ òåîðèé, ôîðìàëüíàÿ òåî-

ðèÿ (èñ÷èñëåíèå) ïðåäñòàâëÿåò ñîáîé ìíîæåñòâî ñèìâîëîâ è îòíî-

øåíèé ìåæäó íèìè, êîòîðûì íå ïðèïèñûâàåòñÿ íèêàêîãî ñîäåðæà-

òåëüíîãî ñìûñëà. Âñïîìèíàÿ î çàäà÷àõ ëîãèêè, ìîæíî ñêàçàòü, ÷òî

âûðàæåíèÿ è ôîðìóëû ôîðìàëüíîé òåîðèè ïðåäñòàâëÿþò «÷èñòûå»

ñõåìû ðàññóæäåíèé, êîòîðûì ìîæíî ïðèäàâàòü ñàìûé ðàçíîîá-

ðàçíûé ñìûñë, ò.å. ñòðîèòü ðàçëè÷íûå ìîäåëè òåîðèè.

Ôîðìàëüíûå òåîðèè ñòðîÿòñÿ ïî ñëåäóþùèì ïðàâèëàì.

Çàäàåòñÿ ñ÷åòíîå ìíîæåñòâî ñèìâîëîâ, êîòîðîå íàçûâàåòñÿ

àëôàâèòîì òåîðèè. Èç ýòîãî ìíîæåñòâà ñèìâîëîâ ñòðîÿòñÿ

êîíå÷íûå ïîñëåäîâàòåëüíîñòè, êîòîðûå íàçûâàþòñÿ ñëîâàìè èëè

âûðàæåíèÿìè äàííîé òåîðèè. Èç ìíîæåñòâà âûðàæåíèé âûäåëÿþò

ïðàâèëüíî ïîñòðîåííûå âûðàæåíèÿ  ôîðìóëû. Èç ìíîæåñòâà

ôîðìóë âûäåëÿþò ïîäìíîæåñòâî àêñèîì. Ìåæäó ôîðìóëàìè òåîðèè

îïðåäåëÿþò îòíîøåíèÿ  ïðàâèëà âûâîäà òåîðèè. Ïðàâèëà âûâîäà

ïîçâîëÿþò èç ìíîæåñòâà àêñèîì âûâîäèòü òåîðåìû. Òàêèì îáðàçîì,

ôîðìàëüíàÿ òåîðèÿ ÿâëÿåòñÿ àêñèîìàòè÷åñêîé òåîðèåé.

Îïðåäåëåíèå 11.1. Äîêàçàòåëüñòâîì òåîðåìû íàçûâàþò

ïîñëåäîâàòåëüíîñòü ôîðìóë À

,,A

, êàæäàÿ èç êîòîðûõ ëèáî

ÿâëÿåòñÿ àêñèîìîé, ëèáî ïîëó÷åíà èç ïðåäûäóùèõ ïî ïðàâèëàì

âûâîäà äàííîé òåîðèè. Êàæäàÿ ôîðìóëà â ñïèñêå ÿâëÿåòñÿ

òåîðåìîé äàííîé òåîðèè. Èíûìè ñëîâàìè, òåîðåìà ýòî

ôîðìóëà, âûâîäèìàÿ èç ìíîæåñòâà àêñèîì ïî ïðàâèëàì âûâîäà,

îïðåäåëåííûì â äàííîé òåîðèè. Çàïèñü |

J

îçíà÷àåò, ÷òî

ôîðìóëà A

âûâîäèìà â òåîðèè J, ò.å. ÿâëÿåòñÿ òåîðåìîé òåîðèèJ.

Îïðåäåëåíèå 11.2. Âûâîäîì ôîðìóëû À

èç ìíîæåñòâà ãèïîòåç

Γ íàçûâàåòñÿ ïîñëåäîâàòåëüíîñòü ôîðìóë À

,,A

, êàæäàÿ èç

êîòîðûõ ÿâëÿåòñÿ ëèáî àêñèîìîé, ëèáî ãèïîòåçîé èç ìíîæåñòâà

Γ, ëèáî ïîëó÷åíà èç ïðåäûäóùèõ ïî ïðàâèëàì âûâîäà. Ôîðìóëà

íàçûâàåòñÿ âûâîäèìîé èç ìíîæåñòâà ãèïîòåç Γ. Îáîçíà÷åíèå

182 183

Γ |

J

îçíà÷àåò, ÷òî ôîðìóëà À

âûâîäèìà èç ìíîæåñòâà ãèïîòåç

Γ â òåîðèè J.

Äîêàçàòåëüñòâî îòëè÷àåòñÿ îò âûâîäà òåì, ÷òî â íåì íå èñïîëü-

çóþòñÿ ãèïîòåçû, ïîýòîìó òåîðåìó ìîæíî îïðåäåëèòü êàê ôîðìóëó,

âûâîäèìóþ èç ïóñòîãî ìíîæåñòâà ãèïîòåç.

Ñâîéñòâà âûâîäèìîñòè.

1. Åñëè Γ| Â è Γ⊂∆, òî ∆| Â (∆  ìíîæåñòâî ôîðìóë).

Ýòî ñâîéñòâî íàçûâàåòñÿ ñâîéñòâîì ìîíîòîííîñòè âûâîäà. Îíî

îçíà÷àåò, ÷òî ôîðìóëà Â áóäåò ïî-ïðåæíåìó âûâîäèìà, åñëè ê

ìíîæåñòâó ãèïîòåç Γ, èç êîòîðûõ âûâîäèìà ôîðìóëà Â, äîáàâèòü

äðóãèå ãèïîòåçû, ò.å. ðàñøèðèòü ìíîæåñòâî ãèïîòåç Γ äî∆.

2. Γ |Â òîãäà è òîëüêî òîãäà, êîãäà ñóùåñòâóåò ∆⊆Γ, òàêîå

÷òî ∆ |Â. Ýòî ñâîéñòâî ïîëíîòû ìíîæåñòâà ãèïîòåç: äëÿ òîãî,

÷òîáû ôîðìóëà Â áûëà âûâîäèìà èç ìíîæåñòâà ãèïîòåç Γ, íåîáõî-

äèìî è äîñòàòî÷íî, ÷òîáû â Γ ñóùåñòâîâàëî ïîäìíîæåñòâî ∆⊆Γ,

èç êîòîðîãî âûâîäèìà ôîðìóëà Â. Èíûìè ñëîâàìè, íå âñå ãèïîòåçû

èç çàäàííîãî ìíîæåñòâà ãèïîòåç G îáÿçàòåëüíî äîëæíû èñïîëüçî-

âàòüñÿ â ïðîöåññå âûâîäà,  íåêîòîðûå ìîãóò îêàçàòüñÿ ëèøíèìè,

îäíàêî, çàäàííûõ ãèïîòåç äîëæíî áûòü äîñòàòî÷íî äëÿ âûâîäà Â.

3. Åñëè ∆|À, è äëÿ êàæäîãî Â

∈ ∆, Γ|Â

òî Γ|À. Ýòî

ñâîéñòâî òðàíçèòèâíîñòè îòíîøåíèÿ âûâîäèìîñòè. Îíî ïîçâîëÿåò

èñïîëüçîâàòü ðàíåå äîêàçàííûå òåîðåìû (âûâîäû), íå ïîâòîðÿÿ

âñåãî ñïèñêà ôîðìóë, ñîñòàâëÿþùèõ äîêàçàòåëüñòâî (âûâîä). Ïîýòî-

ìó ðàíåå äîêàçàííûå òåîðåìû è âûâîäû ìîãóò èñïîëüçîâàòüñÿ â

äðóãèõ äîêàçàòåëüñòâàõ êàê ñõåìû, â êîòîðûõ êàæäîå âõîæäåíèå

ïåðåìåííîé ìîæåò çàìåùàòüñÿ ïðîèçâîëüíîé ôîðìóëîé.

11.2. Èñ÷èñëåíèå âûñêàçûâàíèé.

Ôîðìàëüíàÿ òåîðèÿ L

Îïðåäåëåíèå 11.3.

1. Ñèìâîëàìè àëôàâèòà òåîðèè L ÿâëÿþòñÿ ïðîïîçèöèîíàëüíûå

áóêâû A, B, C,... ñ èíäåêñàìè èëè áåç èíäåêñîâ, ïðîïîçèöèîíàëü-

íûå ñâÿçêè ¬, →, è âñïîìîãàòåëüíûå ñèìâîëû ñêîáêè: ( è ).

2. Îïðåäåëåíèå ôîðìóëû.

•Âñÿêàÿ ïðîïîçèöèîíàëüíàÿ áóêâà åñòü ôîðìóëà.

•Åñëè À è Â åñòü ôîðìóëû, òî ôîðìóëàìè ÿâëÿþòñÿ (¬A),

(A→B).

•Äðóãèõ ôîðìóë íåò.

3. Â ôîðìàëüíîé òåîðèè L îïðåäåëåíî áåñêîíå÷íîå ìíîæåñòâî

àêñèîì, êîòîðûå çàäàþòñÿ òðåìÿ ñõåìàìè àêñèîì:

A1: A → (B → A);

A2: (A → (B → C)) → ((A → B) → (A → C));

A3: (¬B → ¬A) → ((¬B → A) → B).

Êîíêðåòíûå àêñèîìû ïîëó÷àþòñÿ ïîäñòàíîâêîé ôîðìóëû âìåñòî

êàæäîãî âõîæäåíèÿ îäíîé è òîé æå ïðîïîçèöèîíàëüíîé áóêâû.

4. Â òåîðèè L îïðåäåëåíî åäèíñòâåííîå ïðàâèëî âûâîäà MP:

A, A → B| B.

Äëÿ ñîêðàùåíèÿ çàïèñè ôîðìóë ââîäÿòñÿ ìåòàîïðåäåëåíèÿ:

ÌÎ1: ¬(À → ¬Â) = À & Â.

ÌÎ2: ¬À → Â = À ∨ Â.

ÌÎ3: (À → Â) & (Â → À) = À ≡ B.

11.3. Äîêàçàòåëüñòâî è âûâîä

â ôîðìàëüíîé òåîðèè L

Ðàññìîòðèì äîêàçàòåëüñòâî è âûâîä â òåîðèè L. Äîêàæåì òåîðå-

ìó A → A. Ïîñêîëüêó åäèíñòâåííûì ïðàâèëîì âûâîäà ÿâëÿåòñÿ

ÌÐ, íàì íóæíî âçÿòü òàêóþ àêñèîìó, ÷òîáû âûâîäèìàÿ ôîðìóëà

A→A îêàçàëàñü â êîíöå ôîðìóëû. Âîçüìåì ñõåìó àêñèîìû À2,

ñäåëàâ çàìåíó B íà A → A è C íà A. Ïîëó÷èì

(A → ((A → A) → A)) → ((A → (A → A)) → (A→A)).

Â ñõåìå àêñèîìû À1 òàêæå çàìåíèì B íà A → A, ïîëó÷èì

A → ((A → A) → A).

Òåïåðü ê ýòèì äâóì ôîðìóëàì ïðèìåíèì ïðàâèëî ÌÐ, â

ðåçóëüòàòå ÷åãî ïîëó÷èì

(A → (A → A)) → (A → A).

Â ñõåìå àêñèîìû À1 çàìåíèì B íà A, ïîëó÷èì

A → (A → A).

Ïðèìåíÿÿ ê äâóì ïîñëåäíèì ôîðìóëàì ïðàâèëî ÌÐ, ïîëó÷èì

A → A.

Äîêàçàòåëüñòâî è âûâîä ïðèíÿòî çàïèñûâàòü â ñòîëáèê, íóìåðóÿ

êàæäóþ ôîðìóëó è óêàçûâàÿ ñïðàâà â êà÷åñòâå êîììåíòàðèÿ, íà

êàêîì îñíîâàíèè ôîðìóëà âêëþ÷åíà â ýòó ïîñëåäîâàòåëüíîñòü.

Íèæå ïðèâîäÿòñÿ äîêàçàòåëüñòâà òåîðåì 1, 2.

Òåîðåìà 1. | A → A

1. (A → ((A → A) → A)) →

→ ((A → (A → A)) → (A→A)) A2

2. A → ((A → A) → A)A1

3. (A → (A → A)) → (A → A) MP(1, 2)

4. A → (A → A)A1

5. A → A MP(3, 4)

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

184 185

Òåîðåìà 2.|(¬A → A) → A

1. (¬A → ¬A) → ((¬A → A) → A)A3

2. ¬A → ¬A T1

3. (¬A → A) → A MP(1, 2)

Ïðè äîêàçàòåëüñòâå òåîðåìû 2 â ïóíêòå 2 ìû ññûëàëèñü íà äîêà-

çàííóþ ðàíåå òåîðåìó 1, ÷òî ôàêòè÷åñêè ñîîòâåòñòâóåò âêëþ÷åíèþ

â äîêàçàòåëüñòâî âñåõ ïóíêòîâ äîêàçàòåëüñòâà òåîðåìû 1.

Ïîñòðîèì âûâîäû.

Â1. Ïðàâèëî ñèëëîãèçìà.

A → B, B → C | A → C

1. A → B Ã1

2. B → C Ã2

3. (A → (B → C)) → ((A → B) → (A → C)) À2

4. (B → C) → (A → (B → C)) À1

5. A → (B → C) MP(2, 4)

6. (A → B) → (A → C) MP(3, 5)

7. A → C MP(1, 6)

Â2. Ïðàâèëî óäàëåíèÿ ñðåäíåé ïîñûëêè.

A → (B → C), B | A → C

1. A → (B → C)Ã1

2. B Ã2

3. (A → (B → C)) → ((A → B) → (A → C)) A2

4. (A → B) → (A → C) MP(1, 3)

5. B → (A → B)A1

6. A → B MP(2, 5)

7. A → C MP(4, 6)

Òàêèå ïðàâèëà âûâîäà, äîêàçàííûå ñðåäñòâàìè ôîðìàëüíîé

òåîðèè, íàçûâàþòñÿ ïðîèçâîäíûìè ïðàâèëàìè âûâîäà.

11.4. Ìåòàòåîðåìà î äåäóêöèè

Â ôîðìàëüíûõ òåîðèÿõ èñïîëüçóåòñÿ ñèìâîëè÷åñêèé ÿçûê äëÿ

îïèñàíèÿ íåêîòîðîé ñîäåðæàòåëüíîé òåîðèè. Ýòîò ÿçûê èìååò òî÷-

íî îïðåäåëåííûé ñèíòàêñèñ è ôîðìàëüíûå ñðåäñòâà ëîãè÷åñêîãî

âûâîäà (ïðàâèëà âûâîäà). Ñ ïîìîùüþ ýòèõ ñðåäñòâ èç âûáðàííûõ

àêñèîì ìîæíî âûâîäèòü òåîðåìû ôîðìàëüíîé òåîðèè. Îäíàêî,

îáñóæäåíèå ñâîéñòâ ôîðìàëüíîé òåîðèè è ïîëó÷àåìûõ ðåçóëüòàòîâ

îáû÷íî ïðîèçâîäèòñÿ â íåêîòîðîé äðóãîé òåîðèè, êîòîðóþ íàçûâà-

þò ìåòàòåîðèåé. ßçûê ýòîé ìåòàòåîðèè íàçûâàþò ìåòàÿçûêîì.

Ñàìó æå ôîðìàëüíóþ òåîðèþ íàçûâàþò òîãäà ïðåäìåòíîé, èëè

îáúåêòíîé òåîðèåé, à åå ÿçûê  ïðåäìåòíûì ÿçûêîì, èëè ÿçûêîì-

îáúåêòîì. Èçó÷åíèå ñâîéñòâ ôîðìàëüíîé òåîðèè, ïðîèçâîäèìîå ñî-

äåðæàòåëüíûìè ìàòåìàòè÷åñêèìè ìåòîäàìè ñðåäñòâàìè ìåòàÿçûêà,

íàçûâàþò òåîðèåé äîêàçàòåëüñòâ, èëè ìåòàìàòåìàòèêîé.

Ðàññìîòðèì íåêîòîðûå îñîáåííîñòè ôîðìàëüíîãî äîêàçàòåëü-

ñòâà è âûâîäà â òåîðèè L. Â êà÷åñòâå ìåòàÿçûêà ìû áóäåì ïîëüçî-

âàòüñÿ îáû÷íûì ðóññêèì ÿçûêîì. Òåîðåìû î ñâîéñòâàõ ôîðìàëüíîé

òåîðèè, äîêàçàííûå ñ ïîìîùüþ ñîäåðæàòåëüíîãî ìåòàÿçûêà, áóäåì

íàçûâàòü ìåòàòåîðåìàìè.

Ìåòàòåîðåìà î äåäóêöèè (ÌÒÄ).

Åñëè èç ìíîæåñòâà ôîðìóë Γ è ôîðìóëû À âûâîäèìà ôîðìóëà

Â, òî èç ìíîæåñòâà Γ âûâîäèìà ôîðìóëà À→Â, ò.å. åñëè

Γ, À|Â, òî Γ| À → Â.

Äîêàçàòåëüñòâî ýòîé ìåòàòåîðåìû ìîæåò áûòü ïðîâåäåíî ïî

ìåòîäó ìàòåìàòè÷åñêîé èíäóêöèè. Ïóñòü âûâîä ôîðìóëû Â  ýòî

ïîñëåäîâàòåëüíîñòü Â

, B

,, B

= B. Äîêàæåì ñëåäóþùóþ ìåòàëåììó.

Ìåòàëåììà. Èç Γ, À|Â

ñëåäóåò, ÷òî Γ|À → Â

(i=1,, n).

Äîêàçàòåëüñòâî ìåòàëåììû.

Áàçèñ èíäóêöèè. Ïóñòü i=1. Ðàññìîòðèì òðè ñëó÷àÿ.

à) Â

 àêñèîìà.

|Â

→ (À → Â

)À1

|À → Â

ïî ïðàâèëó MP

Γ|À → Â

ïî ñâîéñòâó âûâîäèìîñòè 1.

á) Â

=À, ò.å. Â

åñòü ñàìà ôîðìóëà À.

|À → À Ò1

Ïîñêîëüêó òåîðåìà âûâîäèìà èç ïóñòîãî ìíîæåñòâà ïîñûëîê,

îíà âûâîäèìà èç ëþáîãî ìíîæåñòâà ïîñûëîê, ñîãëàñíî ñâîéñòâó

âûâîäèìîñòè 1. Ïîýòîìó Γ|À → À, ÷òî ðàâíîñèëüíî Γ|À →Â

â) Â

∈ Ã, ò.å. Â

 ãèïîòåçà èç Γ.

Äîêàçàòåëüñòâî ïðîâîäèòñÿ òàê æå, êàê è â ñëó÷àå à).

Øàã èíäóêöèè. Ïóñòü ìåòàëåììà âûïîëíåíà äëÿ âñåõ k < i.

Äîêàæåì, ÷òî îíà âûïîëíÿåòñÿ ïðè k=i. Âîçìîæíû ÷åòûðå ñëó÷àÿ:

à) Â

 àêñèîìà; äîêàçàòåëüñòâî ïðîâîäèòñÿ

á) Â

=À; òàê æå, êàê è äëÿ áàçèñà

â) Â

∈ Γ; èíäóêöèè.

ã) Â

âûâîäèòñÿ ïî MP èç ïðåäûäóùèõ ôîðìóë, ò.å. â ïîñëåäîâà-

òåëüíîñòè Â

, , B

åñòü ôîðìóëû: Â

è Â

=Â

→ Â

, (m<l<i).

Òîãäà ïî ïðåäïîëîæåíèþ èíäóêöèè ñïðàâåäëèâû âûâîäû:

Γ | À → Â

Γ | À→Â

, ò.å. Γ|À → (Â

→ B

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

{

186 187

Ïî ñõåìå àêñèîìû À2

| (À → (Â

→ B

)) → ((À → Â

) → (À → B

)).

Ïðèìåíÿÿ äâàæäû ê ïîñëåäíèì òðåì âûðàæåíèÿì ïðàâèëî ÌÐ,

ïîëó÷èì Γ|À → B

Ïðè i=n ïîëó÷èì ôîðìóëèðîâêó ìåòàòåîðåìû î äåäóêöèè.

Ñïðàâåäëèâà ìåòàòåîðåìà, îáðàòíàÿ ìåòàòåîðåìå î äåäóêöèè.

Îáðàòíàÿ ìåòàòåîðåìà î äåäóêöèè.

Åñëè ñóùåñòâóåò âûâîä Γ |À → Â, òî ôîðìóëà Â âûâîäèìà èç

Γ è À, ò.å. åñëè Γ|À → Â, òî Γ, À|Â

Äîêàçàòåëüñòâî. Ïóñòü âûâîä ôîðìóëû À → Â èìååò âèä: Â

,...,

n1

, À → Â, ãäå Â

,..., B

n-1

 ôîðìóëû èç ìíîæåñòâà Γ. Òîãäà âûâîä

ôîðìóëû Â èç Γ è À áóäåò èìåòü âèä: Â

, ..., B

n1

, À → Â, À, Â, òàê

êàê Â ñëåäóåò èç À → Â è À ïî ïðàâèëó ÌÐ.

Èç ìåòàòåîðåìû î äåäóêöèè âûâîäèìû ñëåäñòâèÿ:

Ñëåäñòâèå 1 (Â1). Ïðàâèëî ñèëëîãèçìà: A → B, B → C|A→C.

Ñëåäñòâèå 2 (Â2). Ïðàâèëî óäàëåíèÿ ñðåäíåé ïîñûëêè:

A→ →(B→C),Â |À → C.

Ñëåäñòâèå 3 (Â3) Ïðàâèëî óäàëåíèÿ êðàéíåé ïîñûëêè:

(A →B)→ →C|B → C.

Ïðàâèëà ñèëëîãèçìà è óäàëåíèÿ ñðåäíåé ïîñûëêè áûëè äîêàçàíû

ðàíåå, áåç èñïîëüçîâàíèÿ ìåòàòåîðåìû î äåäóêöèè. Äëÿ ñðàâíåíèÿ

ïðèâåäåì äîêàçàòåëüñòâî ïðàâèëà Â2 ñ åå èñïîëüçîâàíèåì. Ïîëüçóÿñü

îáðàòíîé ìåòàòåîðåìîé î äåäóêöèè, áóäåì ñòðîèòü âûâîä:

A → (B → C),Â, À | C.

1. A → (B → C)Ã1

2. Â Ã2

3. À Ã3

4. B → C ÌÐ(1,3)

5. Ñ ÌÐ(2,4)

Òåïåðü, ïî ìåòàòåîðåìå î äåäóêöèè, ïîëó÷àåì âûâîä:

A→(B→C), Â|À → C.

(Â3) Ïðàâèëî óäàëåíèÿ êðàéíåé ïîñûëêè: (A → B) → C |B→C.

Ïðèìåíÿÿ îáðàòíóþ ìåòàòåîðåìó î äåäóêöèè, ïîëó÷èì:

(A→B)→ → C, B | C.

1. (A → B) → C Ã1

2. B Ã2

3. B → (A → B)À1

4. A → B ÌÐ(2, 3)

5. C ÌÐ(1, 4)

Ïî ìåòàòåîðåìå î äåäóêöèè, ïîëó÷àåì âûâîä: (A → B) → C|B→C.

Ïðèìåíåíèå ìåòàòåîðåìû î äåäóêöèè (ÌÒÄ) ïîçâîëÿåò èç ëþáî-

ãî ïðàâèëà âûâîäà ïîëó÷èòü òåîðåìó. Íàïðèìåð, ïðèìåíÿÿ äâà ðàçà

ÌÒÄ ê ïðàâèëó ñèëëîãèçìà, ïîëó÷èì òåîðåìó ñèëëîãèçìà:

A → B, B → C|A → C ïðàâèëî ñèëëîãèçìà

A → B | (B → C) →(A → C)ÌÒÄ

| (A → B) → ((B → C) →(A → C)) ÌÒÄ

Îáðàòíàÿ ìåòàòåîðåìà î äåäóêöèè (ÎÌÒÄ) ïîçâîëÿåò ïîëó÷àòü

ïðàâèëà âûâîäà èç òåîðåì. Íàïðèìåð, ïðèìåíÿÿ äâà ðàçà ÎÌÒÄ ê

àêñèîìå À3, ïîëó÷èì ïðàâèëî âûâîäà:

| (¬B → ¬A) → ((¬B → A) → B)A3

¬B → ¬A | ((¬B → A) → B) ÎÌÒÄ

¬B → ¬A, ¬B → A | B ÎÌÒÄ

Ïðèìåíåíèå ìåòàòåîðåìû î äåäóêöèè è ñëåäñòâèé èç íåå ïîçâî-

ëÿåò óïðîùàòü ïîñòðîåíèå âûâîäîâ è äîêàçàòåëüñòâ. Ðàññìîòðèì

ïðèìåðû òàêîãî ïðèìåíåíèÿ. (Íåîáõîäèìî îòìåòèòü, ÷òî ïðèâîäè-

ìûå íèæå äîêàçàòåëüñòâà íå ÿâëÿþòñÿ åäèíñòâåííûìè, ìîãóò áûòü

íàéäåíû è äðóãèå äîêàçàòåëüñòâà ñîîòâåòñòâóþùèõ òåîðåì.)

Òåîðåìà 3 (ñíÿòèÿ äâîéíîãî îòðèöàíèÿ). |¬¬À → À

1. (¬A → ¬¬A) → ((¬A → ¬A) → A)A3

2. ¬A → ¬A T1

3. (¬A → ¬¬A) → A Â2(1,2)

4. ¬¬A → A Â3(3)

Òåîðåìà 4 (ââåäåíèÿ äâîéíîãî îòðèöàíèÿ). |A → ¬¬A

1. (¬¬¬A → ¬A) → ((¬¬¬A → A) → ¬¬A)A3

2. ¬¬¬A → ¬A T3

3. (¬¬¬A → A) → ¬¬A MP(1,2)

4. A → ¬¬A Â3(3)

Òåîðåìà 5 (ïðîòèâîðå÷èÿ). |¬A→(A→B)

Ïîñòðîèì âûâîä: ¬A, A|B.

1. ¬A Ã1

2. A Ã2

3. (¬B → ¬A) → ((¬B → A) → B) À3

4. ¬A → (¬B → ¬A)À1

5. A → (¬B → A)À1

6. ¬B → ¬A ÌÐ(1,4)

7. ¬B → A ÌÐ(2,5)

8. (¬B → A) → B ÌÐ(3,6)

9. B ÌÐ(7,8)

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

188 189

Òåîðåìà 6 (êîíòðàïîçèöèè). | (¬À → ¬B)→(B → A)

Ïîñòðîèì âûâîä: ¬A → ¬B | B → A

1. ¬A → ¬B Ã1

2. (¬A → ¬B) → ((¬A → B) → A)À3

3. (¬A → B) → A ÌÐ(1,2)

4. B → A Â3(3)

Òåîðåìà 7 (êîíòðàïîçèöèè). | (B → A) → (¬A → ¬B)

Ïîñòðîèì âûâîä: B → A | ¬A → ¬B

1. B → A Ã1

2. ¬¬B → B Ò3

3. A → ¬¬A Ò4

4. ¬¬B → A Â1(2,1)

5. ¬¬B → ¬¬A Â1(3,4)

6. (¬¬B → ¬¬A) → (¬A → ¬B)T6

7. ¬A → ¬B MP(5,6)

Tåîðåìà 8. | A → (¬B → ¬(A → B))

Ïîñòðîèì âûâîä: A | ¬B → ¬(A → B)

1. ((A → B) → B) → (¬B → ¬(A → B)) T7

2. A Ã1

3. À, A → B | B ÌÐ

4. A | (A → B) → B ÌÒÄ(3)

5. (A → B) → B èç (2,4)

6. ¬B → ¬(A → B) ÌÐ(1,5)

Â äîêàçàòåëüñòâå ýòîé òåîðåìû ôàêòè÷åñêè èñïîëüçîâàëèñü ñðåä-

ñòâà ìåòàÿçûêà  èç ïðàâèëà ÌÐ ïðèìåíåíèåì ÌÒÄ áûëî ïîëó÷åíî

íîâîå ïðàâèëî âûâîäà: A | (A → B) → B.

Òåîðåìà 9. | (A → B) → ((¬A → B) → B)

Ïîñòðîèì âûâîä: A → B, ¬A → B | B

1. A → B Ã1

2. ¬A → B Ã2

3. (A → B) → (¬B → ¬A)T7

4. (¬A → B) → (¬B → ¬¬A)T7

5. ¬B → ¬A MP(1,3)

6. ¬B → ¬¬A MP(2,4)

7. (¬B → ¬¬A) → ((¬B → ¬A) → B)A3

8. (¬B → ¬A) → B MP(6,7)

9. B MP(5,8)

11.5. Ïðàâèëà ââåäåíèÿ è óäàëåíèÿ ñâÿçîê

Ïðè äîêàçàòåëüñòâå òåîðåì è ïîñòðîåíèè âûâîäîâ ìîæíî èñ-

ïîëüçîâàòü ïðîèçâîäíûå ïðàâèëà âûâîäà, äîêàçàííûå ðàíåå, â òîì

÷èñëå ïðàâèëà ââåäåíèÿ è óäàëåíèÿ ñâÿçîê (ñì. òàáë. 11.1).

Òàáëèöà 11.1.

Äîêàæåì íåêîòîðûå èç ýòèõ ïðàâèë.

Â4.

¬¬

¬  ââåäåíèå. À → Â, À → ¬Â | ¬À

1. A → B Ã1

2. A → ¬B Ã2

3. (A → B) → (¬B → ¬A)T7

4. (A → ¬B) → (¬¬B → ¬A)T7

5. ¬B → ¬A MP(1,3)

6. ¬¬B → ¬A MP(2,4)

7. (¬B → ¬A) → ((¬¬B → ¬A) → ¬A)T9

8. (¬¬B → ¬A) → ¬A MP(5,7)

9. ¬A MP(6,8)

Â5. &  óäàëåíèå 1. A & B | A.

Ïîëüçóÿñü ìåòàîïðåäåëåíèåì ÌÎ1, ïîëó÷èì ¬(A → ¬B) |A, è

ïðèìåíèì ÌÒÄ:

| ¬(A → ¬B) → A

1. ¬A → (A → ¬B)T5

2. (A → ¬B) → ¬¬(A → ¬B)T4

3. ¬A → ¬¬(A → ¬B) Â1(1,2)

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

Ñâÿçêà Ââåäåíèå Óäàëåíèå

→ Ã, À |Â ⇒ À, À → Â|Â (ÌÐ)

⇒ Ã|À → Â (ÌÒÄ) Ã

|À, Ã

|À → Â ⇒

⇒ Ã

,Ã

|Â

¬ Ã, À|Â; À, ¬À|Â (ñëàáîå óäàëåíèå

Ã, À| ¬Â ⇒ Ã| ¬À îòðèöàíèÿ)

(äîêàçàòåëüñòâî ¬¬À|À (óäàëåíèå

îò ïðîòèâíîãî) äâîéíîãî îòðèöàíèÿ)

&Ã

1

|À, Ã

2

|Â ⇒ Ã|A & B ⇒Ã|A

, Ã

2

|À&Â Ã|A & B ⇒Ã|B

∨ Ã|À ⇒ Ã|A ∨ Â Ã

1

|À ∨ Â; Ã

, À|C;

Ã|Â ⇒ Ã|À ∨ Â Ã

, Â|C ⇒ Ã

, Ã

3

|C

≡ À → Â,Â → À|À ≡ ÂÀ ≡ Â |À → Â;

À ≡ Â|Â → À

190 191

4. (¬A → ¬¬(A → ¬B)) → (¬(A → ¬B) → A)T6

5. ¬(A → ¬B) → A MP(3,4)

Â6. &  óäàëåíèå 2. A & B | Â

¬(A → ¬B) | Â ÌÎ1

| ¬(A → ¬B) → Â ÌÒÄ

Äîêàçàòü ñàìîñòîÿòåëüíî.

Â7. &  ââåäåíèå. À, Â | A & B

À, Â | ¬(A → ¬B) ÌÎ1

1. A Ã1

2. B Ã2

3. A → (¬¬B → ¬(A → ¬B)) Ò8

4. ¬¬B → ¬(A → ¬B) MP(1,3)

5. B → ¬¬B Ò4

6. ¬¬B MP(2,5)

7. ¬(A → ¬B) MP(4,6)

11.6. Äðóãèå ôîðìàëèçàöèè ëîãèêè âûñêàçûâàíèé

Ïîìèìî ¬ è →, ìîæíî èñïîëüçîâàòü äðóãèå ôóíêöèîíàëüíî

ïîëíûå íàáîðû ñâÿçîê, íàïðèìåð, ∨ è ¬ èëè & è ¬, òîãäà áóäóò

ïîëó÷åíû äðóãèå ôîðìàëèçàöèè ëîãèêè âûñêàçûâàíèé. Ðàññìîòðèì

òàêèå òåîðèè.

Òåîðèÿ L

(Ãèëüáåðòà, Àêêåðìàíà). Îñíîâíûå ñâÿçêè: ∨, ¬.

Ìåòàîïðåäåëåíèå: À → Â = ¬À ∨ Â.

Ñõåìû àêñèîì:

À1: A ∨ A → A.

A2: A → A ∨ B.

A3: A ∨ B → B ∨ A.

A4: (B → C) → (A ∨ B → A ∨ C).

Ïðàâèëî âûâîäà: ÌP.

Òåîðèÿ L

(Ðîññåðà). Îñíîâíûå ñâÿçêè: &, ¬.

Ìåòàîïðåäåëåíèå: A → B = ¬(A & ¬B).

Ñõåìû àêñèîì:

A1: A → (A & A).

A2: (A & B) → A.

A3: (A → B) → (¬(B & C) → ¬(C & A)).

Ïðàâèëî âûâîäà: MP.

Ôîðìàëüíàÿ òåîðèÿ, ïðåäëîæåííàÿ Êëèíè, èñïîëüçóåò ÷åòûðå

ëîãè÷åñêèå ñâÿçêè: ¬, →, &, ∨.

Òåîðèÿ L

(Êëèíè). Ñõåìû àêñèîì:

A1: A → (B → A).

A2: (A → (B → C)) → ((A → B) → (A → C)).

A3: (A & B) → A.

A4: (A & B) → B.

A5: A → (B → (A & B)).

A6: A → A ∨ B.

A7: B → A ∨ B.

A8: (A → C) → ((B → C) → (A ∨ B → C)).

A9: (A → B) → ((A → ¬B) → ¬A).

A10: ¬¬A → A.

Ïðàâèëî âûâîäà: ÌP.

11.7. Ñâîéñòâà ôîðìàëüíîé òåîðèè L

Äëÿ èññëåäîâàíèÿ ñâîéñòâ ôîðìàëüíîé òåîðèè îáû÷íî ñòðîèòñÿ

åå ìîäåëü. Ïðèïèñûâàíèå çíà÷åíèé ïåðâè÷íûì òåðìèíàì ôîðìàëü-

íîé òåîðèè íàçûâàåòñÿ åå èíòåðïðåòàöèåé. Åñëè ìíîæåñòâî îáúåê-

òîâ, âûáðàííûõ â êà÷åñòâå çíà÷åíèé ïåðâè÷íûõ òåðìèíîâ òåîðèè,

óäîâëåòâîðÿåò àêñèîìàì ôîðìàëüíîé òåîðèè, òî òàêàÿ èíòåðïðåòà-

öèÿ íàçûâàåòñÿ ìîäåëüþ ôîðìàëüíîé òåîðèè.

Îñíîâíûìè ñâîéñòâàìè ôîðìàëüíûõ òåîðèé ÿâëÿþòñÿ èõ íåïðî-

òèâîðå÷èâîñòü è ïîëíîòà. Òåîðèÿ íàçûâàåòñÿ ïðîòèâîðå÷èâîé, åñëè

îíà ñîäåðæèò òàêóþ ôîðìóëó A, ÷òî êàê A, òàê è ¬A ÿâëÿþòñÿ

òåîðåìàìè òåîðèè. Òåîðèÿ íå ÿâëÿþùàÿñÿ ïðîòèâîðå÷èâîé, íàçûâà-

åòñÿ íåïðîòèâîðå÷èâîé. Èíûìè ñëîâàìè, â íåïðîòèâîðå÷èâîé òåîðèè

íå ñóùåñòâóåò òàêîé ôîðìóëû A, ÷òî A è ¬A ÿâëÿþòñÿ òåîðåìàìè.

Ïðîòèâîðå÷èâûå òåîðèè ñ÷èòàþòñÿ íå èìåþùèìè íèêàêîé

öåííîñòè, òàê êàê ëþáàÿ ôîðìóëà òàêîé òåîðèè åñòü òåîðåìà, è,

ñëåäîâàòåëüíî, â íåé ìîæíî âûâåñòè ÷òî óãîäíî. Âîïðîñ î íåïðîòè-

âîðå÷èâîñòè òåîðèè ìîæíî óñòàíîâèòü ñ ïîìîùüþ ìîäåëè. Åñëè

òåîðèÿ ïðîòèâîðå÷èâà, òî êàæäàÿ åå ìîäåëü áóäåò ñîäåðæàòü

ïðîòèâîðå÷èå, òàê êàê ëþáàÿ ïàðà ïðîòèâîðå÷èâûõ ôîðìóë A è

¬A, ÿâëÿþùèõñÿ òåîðåìàìè òåîðèè, áóäóò ïåðåâîäèòüñÿ â

ïðîòèâîðå÷èâûå âûñêàçûâàíèÿ ìîäåëè. Òåîðèÿ íåïðîòèâîðå÷èâà,

åñëè äëÿ íåå óäàåòñÿ íàéòè ñâîáîäíóþ îò ïðîòèâîðå÷èé ìîäåëü.

Åñëè íåïðîòèâîðå÷èâîñòü òåîðèè äîêàçàíà (èëè õîòÿ áû ïðèíÿòà

íà âåðó), òî ðàññìàòðèâàåòñÿ âîïðîñ î åå ïîëíîòå. Ïîëíîòà òåîðèè

îçíà÷àåò, ÷òî îíà ñîäåðæèò äîñòàòî÷íîå äëÿ êàêèõ-ëèáî öåëåé êîëè-

÷åñòâî òåîðåì. Íàïðèìåð, åñëè èç òåîðèè L èñêëþ÷èòü ñõåìó àêñèîì

À3, òî â íåé ñòàíóò íåâûâîäèìûìè ìíîãèå òåîðåìû, ñîäåðæàùèå

îòðèöàíèÿ (òàê êàê À1, À2 íå ñîäåðæàò îòðèöàíèé). Î÷åâèäíî,

òàêàÿ òåîðèÿ áóäåò íåïîëíîé, íî ïîïîëíèìîé. Ðàçëè÷àþò îïðåäåëå-

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

192 193Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

íèÿ ïîëíîòû â óçêîì è â øèðîêîì ñìûñëå. Òåîðèþ ñ÷èòàþò ïîëíîé

â øèðîêîì ñìûñëå, åñëè ëþáîé ôîðìóëå A òåîðèè ñîîòâåòñòâóåò

òàêîå ïðåäëîæåíèå ìîäåëè, êîòîðîå ëèáî èñòèííî, ëèáî ëîæíî.

Òîãäà ëèáî A, ëèáî ¬A îêàçûâàåòñÿ èñòèííûì è äîëæíî áûòü âûâî-

äèìî â ôîðìàëüíîé òåîðèè, ò.å. ëþáàÿ ôîðìóëà A òåîðèè, ëèáî åå

îòðèöàíèå ¬A ÿâëÿåòñÿ òåîðåìàìè ôîðìàëüíîé òåîðèè.

Òåîðèÿ, êîòîðàÿ îäíîâðåìåííî íåïðîòèâîðå÷èâà è ïîëíà, ÿâëÿ-

åòñÿ ìàêñèìàëüíîé â òîì ñìûñëå, ÷òî äîáàâëåíèå ê íåé â êà÷åñòâå

àêñèîìû êàêîé-ëèáî ôîðìóëû, íå ÿâëÿþùåéñÿ åå òåîðåìîé,

ïðèâîäèò ê ïðîòèâîðå÷èâîé òåîðèè. Ýòî ñâîéñòâî ôîðìàëüíûõ òåî-

ðèé íàçûâàþò ïîëíîòîé â óçêîì ñìûñëå. Äîáàâëåíèå ê ñèñòåìå àêñè-

îì êàêèõ-ëèáî òåîðåì òåîðèè íå èçìåíÿåò åå ñâîéñòâ, íî òîãäà ñèñòå-

ìà àêñèîì ñòàíåò èçáûòî÷íîé, òàê êàê íåêîòîðûå àêñèîìû ìîæíî

áóäåò âûâåñòè èç äðóãèõ àêñèîì. Íàïðèìåð, ñèñòåìà àêñèîì Êëèíè

(òåîðèÿ L

) ñîäåðæèò èçáûòî÷íûå àêñèîìû, âûâîäèìûå èç äðóãèõ

àêñèîì. Ñèñòåìà àêñèîì, ñîäåðæàùàÿ òàêèå àêñèîìû, ÷òî íè îäíà

èç íèõ íå âûâîäèìà èç äðóãèõ, íàçûâàåòñÿ íåçàâèñèìîé. Ñâîéñòâî

íåçàâèñèìîñòè ñèñòåìû àêñèîì íå ÿâëÿåòñÿ îáÿçàòåëüíûì äëÿ

ôîðìàëüíûõ òåîðèé,  ýòî âîïðîñ ëàêîíè÷íîñòè è êîìïàêòíîñòè

ñðåäñòâ ôîðìàëüíîé òåîðèè.

Ðàññìîòðèì ñâîéñòâà òåîðèè L. Â êà÷åñòâå èíòåðïðåòàöèè ôîð-

ìàëüíîé òåîðèè L âûáåðåì àëãåáðó âûñêàçûâàíèé. Ïîñòàâèì â

ñîîòâåòñòâèå êàæäîé áóêâå òåîðèè L ïðîïîçèöèîíàëüíóþ áóêâó,

êàæäîé ôîðìóëå L ôîðìóëó ëîãèêè âûñêàçûâàíèé, êàæäîé

òåîðåìå òàâòîëîãèþ ëîãèêè âûñêàçûâàíèé. Íåòðóäíî óáåäèòüñÿ,

÷òî ñõåìû àêñèîì òåîðèè L ÿâëÿþòñÿ òàâòîëîãèÿìè àëãåáðû âûñêà-

çûâàíèé. Ñëåäîâàòåëüíî, ëîãèêà âûñêàçûâàíèé ÿâëÿåòñÿ ìîäåëüþ

òåîðèè L.

Îïðåäåëåíèå 11.4. Ôîðìàëüíàÿ òåîðèÿ ïîëíà îòíîñèòåëüíî ìî-

äåëè, åñëè êàæäîé òåîðåìå òåîðèè ñîîòâåòñòâóåò òîæäåñòâåííàÿ

èñòèííàÿ ôîðìóëà ìîäåëè, à êàæäîé òîæäåñòâåííî èñòèííîé

ôîðìóëå ìîäåëè ñîîòâåòñòâóåò òåîðåìà ôîðìàëüíîé òåîðèè.

Ïîêàæåì, ÷òî ôîðìóëà òåîðèè L òîãäà è òîëüêî òîãäà ÿâëÿåòñÿ

òåîðåìîé, êîãäà îíà ÿâëÿåòñÿ òàâòîëîãèåé ëîãèêè âûñêàçûâàíèé.

Ìåòàòåîðåìà 11.1. Êàæäàÿ òåîðåìà òåîðèè L ÿâëÿåòñÿ òàâòîëî-

ãèåé ëîãèêè âûñêàçûâàíèé.

Äîêàçàòåëüñòâî. Ñõåìàì àêñèîì À1, À2, À3 ñîîòâåòñòâóþò òàâòî-

ëîãèè ëîãèêè âûñêàçûâàíèé. Äëÿ ïðîâåðêè ýòîãî ïîëîæåíèÿ äîñòà-

òî÷íî ïîñòðîèòü èõ òàáëèöû èñòèííîñòè. Ïðàâèëî ÌÐ ñîõðàíÿåò

ñâîéñòâî òàâòîëîãè÷íîñòè ñîãëàñíî òåîðåìå 10.3 î òàâòîëîãèÿõ. Ïî-

ñêîëüêó ëþáàÿ òåîðåìà âûâîäèìà èç àêñèîì ñ ïîìîùüþ ïðàâèëà ÌÐ,

åé òàêæå áóäåò ñîîòâåòñòâîâàòü òàâòîëîãèÿ ëîãèêè âûñêàçûâàíèé.

Ìåòàòåîðåìà 11.2 (òåîðåìà î ïîëíîòå). Êàæäàÿ òàâòîëîãèÿ ëîãèêè

âûñêàçûâàíèé ÿâëÿåòñÿ òåîðåìîé ôîðìàëüíîé òåîðèè L.

Äîêàçàòåëüñòâî îñíîâûâàåòñÿ íà ñëåäóþùåé ìåòàëåììå.

Ìåòàëåììà. Ïóñòü ôîðìóëà À ëîãèêè âûñêàçûâàíèé çàâèñèò

îò ïðîïîçèöèîíàëüíûõ áóêâ B

, B

,,B

. Òîãäà êàæäîé ñòðîêå

òàáëèöû èñòèííîñòè ýòîé ôîðìóëû ñîîòâåòñòâóåò âûâîä ôîðìàëü-

íîé òåîðèè L âèäà B

',,B

'| A', ãäå B'=B, åñëè |B|=T, è B'=¬B,

åñëè |B|=F, A' =A èëè ¬A, åñëè |A|=Ò èëè F ñîîòâåòñòâåííî.

Ñìûñë ëåììû çàêëþ÷àåòñÿ â ñëåäóþùåì. Åñëè äàíà ôîðìóëà,

íàïðèìåð, Å=A→((A→B)→A), òî, ïîñòðîèâ åå òàáëèöó èñòèí-

íîñòè (òàáë. 11.2), ìîæíî îïðåäåëèòü, èç êàêèõ ïîñûëîê îíà âûâîäèìà.

Òàáëèöà 11.2.

Ñîãëàñíî ìåòàëåììå, äëÿ äàííîé ôîðìóëû ìîæíî ïîñòðîèòü

÷åòûðå âûâîäà: ¬À, ¬Â | Å; ¬À, Â | ¬Å; À, ¬Â |Å; À, Â |Å.

Äîêàçàòåëüñòâî ìåòàëåììû.

Äîêàçàòåëüñòâî ïðîâîäèòñÿ èíäóêöèåé ïî ÷èñëó ñâÿçîê n â ôîð-

ìóëå À.

1. Áàçèñ èíäóêöèè. Ïóñòü n=0, òîãäà A=B, ò.å. A ïðåäñòàâëÿåò

ñîáîé ïðîñòî ïðîïîçèöèîíàëüíóþ áóêâó B. Òîãäà ôîðìóëà À ìîæåò

ïðèíèìàòü îäíî èç äâóõ çíà÷åíèé, T èëè F, êàæäîìó èç êîòîðûõ

ñîîòâåòñòâóåò âûâîä: B |B è ¬B|¬B.

2. Øàã èíäóêöèè. Äîïóñòèì, ÷èñëî ñâÿçîê â ôîðìóëå À ðàâíî m

è ïðè ýòîì âûïîëíÿåòñÿ ìåòàëåììà. Äîêàæåì, ÷òî ìåòàëåììà âû-

ïîëíÿåòñÿ, åñëè n=m+1.

1 ñëó÷àé. Ôîðìóëà À îáðàçîâàíà ñ ïîìîùüþ ñâÿçêè îòðèöàíèÿ:

À = ¬Â, ãäå Â ñîäåðæèò m ñâÿçîê. Âîçìîæíû ñëåäóþùèå ñëó÷àè.

à) |B|=T, òîãäà |¬B|=F, ò.å. |A|=F. Íåîáõîäèìî äîêàçàòü, ÷òî

ñóùåñòâóåò âûâîä:

, , B'

|¬A.

Ñîãëàñíî ïðåäïîëîæåíèþ èíäóêöèè, ñóùåñòâóåò âûâîä: B'

,,B'

|B. Ñîãëàñíî òåîðåìå 4, B|¬¬B, òîãäà ïî ïðàâèëó ñèëëîãèçìà

,,B'

|¬¬B. Íî ¬¬B = ¬A, ïîñêîëüêó À = ¬Â, ñëåäîâàòåëüíî,

,,B'

| ¬A.

AB(A → B) → AB → ((A → B) → A)

FF F T

FT F F

TF T T

TT T T

194 195

á) |B|=F, |¬B|=T, |A|=T. Íåîáõîäèìî äîêàçàòü, ÷òî ñóùåñòâóåò

âûâîä B'

,, B'

|A, èëè, ÷òî òî æå ñàìîå, B'

,,B'

|¬B.

Òàê êàê |B|=F, òî ¬B=Â'. Âûâîä B'

,,B'

|Â' ñóùåñòâóåò ïî

ïðåäïîëîæåíèþ èíäóêöèè, çíà÷èò, ñóùåñòâóåò è B'

,,B'

| ¬B.

2 ñëó÷àé. Ôîðìóëà À îáðàçîâàíà ñ ïîìîùüþ ëîãè÷åñêîé ñâÿçêè

èìïëèêàöèè: A=B→C, ãäå Â è Ñ ñîäåðæàò íå áîëåå m ñâÿçîê. Ïî

ïðåäïîëîæåíèþ èíäóêöèè ñóùåñòâóþò âûâîäû:

B′

,, B′

|B′,

B′

,, B′

|C'.

Ðàññìîòðèì èñòèííîñòíûå ðàñïðåäåëåíèÿ.

à) |C|=T, |A|=T.

Íóæíî äîêàçàòü, ÷òî ñóùåñòâóåò âûâîä B'

,,B'

|A, ò.å. B'

,,

|B→ C.

Ïî èíäóêòèâíîìó ïðåäïîëîæåíèþ ñóùåñòâóåò âûâîä B'

,, B'

| C. Òîãäà èç ýòîãî âûâîäà è àêñèîìû A1: C → (B → C) ïî ÌÐ

ïîëó÷àåì: B'

,, B'

| B → C.

á) |B|=F, |A|=T.

Âûâîä B'

, , B'

| ¬B ñóùåñòâóåò ïî èíäóêòèâíîìó ïðåäïîëîæå-

íèþ. Òîãäà èç ýòîãî âûâîäà è òåîðåìû T5: |¬B → (B → C) ïî

ïðàâèëó ÌÐ ïîëó÷àåì: B'

,, B'

|B → C.

â) |C|=F, |B|=T, |A|=F. Äîêàçàòü, ÷òî ñóùåñòâóåò âûâîä B'

,,

| ¬A, ò.å. B'

,, B'

| ¬(B → C). Ïîñòðîèì ýòîò âûâîä.

1. B'

,, B'

| ¬C (ïî èíäóêòèâíîìó ïðåäïîëîæåíèþ)

2. B'

,, B'

| B (ïî èíäóêòèâíîìó ïðåäïîëîæåíèþ)

3. | B → (¬C → ¬(B → C)) T8

4. B'

,, B'

| ¬C → ¬(B → C) MP(2,3)

5. B'

, À = ¬Â,, B'

| ¬(B → C) MP(1,4)

Ìåòàëåììà äîêàçàíà.

Äîêàçàòåëüñòâî ìåòàòåîðåìû î ïîëíîòå.

Ïóñòü À  òàâòîëîãèÿ, çàâèñÿùàÿ îò ïðîïîçèöèîíàëüíûõ áóêâ

,, B

. Ñîãëàñíî ìåòàëåììå, äëÿ êàæäîãî èñòèííîñòíîãî ðàñïðåäå-

ëåíèÿ ïðîïîçèöèîíàëüíûõ áóêâ ñóùåñòâóþò âûâîäû:B'

,, B′

| A

(A′ ñîâïàäàåò ñ A, òàê êàê A èñòèííî â êàæäîé ñòðîêå òàáëèöû

èñòèííîñòè). Â òàáëèöå èñòèííîñòè èìåþòñÿ äâå ñòðîêè, êîòîðûå

ðàçëè÷àþòñÿ òîëüêî çíà÷åíèåì èñòèííîñòè B

. Äëÿ ýòèõ ñòðîê ñóùå-

ñòâóþò âûâîäû:

,, B

| A, ãäå |B

|=T è

,, ¬B

| A, ãäå |B

|=F.

Ïðèìåíèì ê íèì ìåòàòåîðåìó î äåäóêöèè. Ïîëó÷èì:

,, B′

n -1

| B

→ A,

,, B′

n -1

| ¬B

→ A.

Âîçüìåì òåîðåìó T9: | (B

→ A) → ((¬B

→ A) → A).

Ïðèìåíÿÿ äâàæäû ïðàâèëî ÌÐ, ïîëó÷èì, âûâîä B'

, , B′

n-1

|A.

Àíàëîãè÷íûì îáðàçîì ìû ìîæåì èñêëþ÷èòü âñå ïåðåìåííûå, è

çà n øàãîâ ïîëó÷èì |À.

Îïðåäåëåíèå 11.5. Ôîðìàëüíàÿ òåîðèÿ íåïðîòèâîðå÷èâà, åñëè

íå ñóùåñòâóþò òàêîé ôîðìóëû À, ÷òîáû À è ¬À îäíîâðåìåííî

ÿâëÿëèñü òåîðåìàìè òåîðèè.

Ìåòàòåîðåìà 11.3. Òåîðèÿ L íåïðîòèâîðå÷èâà.

Äîêàçàòåëüñòâî. Êàæäàÿ òåîðåìà òåîðèè L ÿâëÿåòñÿ òàâòîëîãèåé

ëîãèêè âûñêàçûâàíèé. Îòðèöàíèå ôîðìóëû, ÿâëÿþùåéñÿ òàâòî-

ëîãèåé, òàâòîëîãèåé íå ÿâëÿåòñÿ. Ñëåäîâàòåëüíî, íè äëÿ êàêîé ôîð-

ìóëû À íåâîçìîæíî, ÷òîáû À è ¬À áûëè òåîðåìàìè òåîðèè L.

Èç íåïðîòèâîðå÷èâîñòè L ñëåäóåò ñóùåñòâîâàíèå ôîðìóëû, êî-

òîðàÿ íå ÿâëÿåòñÿ òåîðåìîé òåîðèè L. Ñ äðóãîé ñòîðîíû, íåïðîòèâî-

ðå÷èâîñòü òåîðèè L ìîæíî âûâåñòè èç ôàêòà ñóùåñòâîâàíèÿ ôîð-

ìóëû òåîðèè, íå ÿâëÿþùåéñÿ òåîðåìîé. Äåéñòâèòåëüíî, åñëè òåîðèÿ

L ïðîòèâîðå÷èâà, ò.å. â íåé ñóùåñòâóþò òåîðåìû |¬A è |A, òî

äâóêðàòíûì ïðèìåíåíèåì ïðàâèëà ÌÐ èç òåîðåìû | ¬A → (A →B)

ïîëó÷àåì |B, ò.å. òîãäà â L âûâîäèìà ëþáàÿ ôîðìóëà. (Òåîðèþ, â

êîòîðîé íå âñå ôîðìóëû ÿâëÿþòñÿ òåîðåìàìè, ÷àñòî íàçûâàþò àáñî-

ëþòíî íåïðîòèâîðå÷èâîé).

Ïîëíîòà òåîðèè ïîíèìàåòñÿ â óçêîì è øèðîêîì ñìûñëå.

Îïðåäåëåíèå 11.6. Òåîðèÿ íàçûâàåòñÿ ïîëíîé (â óçêîì ñìûñëå),

åñëè äîáàâëåíèå ê íåé â êà÷åñòâå àêñèîìû ëþáîé íåäîêàçóåìîé

â ýòîé òåîðèè ôîðìóëû äåëàåò åå ïðîòèâîðå÷èâîé. Ïîëíîòà â

øèðîêîì ñìûñëå îçíà÷àåò, ÷òî êàæäóþ ôîðìóëó ìîæíî äîêàçàòü

ëèáî îïðîâåðãíóòü, ò.å. ëèáî | A, ëèáî | ¬A.

Ìåòàòåîðåìà 11.4. Òåîðèÿ L íåïîëíà â øèðîêîì ñìûñëå.

Äîêàçàòåëüñòâî. Äåéñòâèòåëüíî, íå ëþáàÿ ôîðìóëà èëè åå

îòðèöàíèå ÿâëÿþòñÿ òåîðåìàìè òåîðèè L. Åñëè âçÿòü íåéòðàëüíóþ

ôîðìóëó ëîãèêè âûñêàçûâàíèé, òî åå îòðèöàíèå òàêæå ÿâëÿåòñÿ

íåéòðàëüíîé ôîðìóëîé, ò.å. íè ñàìà ôîðìóëà, íè åå îòðèöàíèå íå

ÿâëÿþòñÿ òàâòîëîãèÿìè àëãåáðû âûñêàçûâàíèé. Ïîýòîìó ýòè ôîð-

ìóëû íå ÿâëÿþòñÿ òåîðåìàìè èñ÷èñëåíèÿ L.

Ìåòàòåîðåìà 11.5. Òåîðèÿ L ïîëíà â óçêîì ñìûñëå.

Äëÿ äîêàçàòåëüñòâà òåîðåìû íóæíî ïîêàçàòü, ÷òî òåîðèÿ L ñòàíî-

âèòñÿ ïðîòèâîðå÷èâîé ïðè äîáàâëåíèè ê åå ñèñòåìå àêñèîì ëþáîé

íåäîêàçóåìîé â ýòîé òåîðèè ôîðìóëû.

Äîêàçàòåëüñòâî. Òåîðèÿ L èìååò òðè ñõåìû àêñèîì A1, A2, A3

è ïðàâèëî âûâîäà MP. Ïîñòðîèì íîâóþ òåîðèþ L' , äîáàâèâ ê ñèñòåìå

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

196 197

àêñèîì L ôîðìóëó À, êîòîðàÿ íå ÿâëÿåòñÿ òàâòîëîãèåé àëãåáðû

âûñêàçûâàíèé. Òîãäà ôîðìóëà À ïðèíèìàåò õîòÿ áû îäíî ëîæíîå

çíà÷åíèå íà íåêîòîðîé èíòåðïðåòàöèè. Çíà÷èò, åñëè À ïðåäñòàâëåíà

êîíúþíêòèâíîé íîðìàëüíîé ôîðìîé, òî ýòà ôîðìà äîëæíà ñîäåð-

æàòü õîòÿ áû îäíó ýëåìåíòàðíóþ äèçúþíêöèþ δ, íå ñîäåðæàùóþ

íè îäíó ïåðåìåííóþ âìåñòå ñ åå îòðèöàíèåì: δ=B'

∨B'

∨∨B'

ãäå B'

= ¬B

, åñëè |B

| = T, è B'

=B

, åñëè |B

|=F. Â ýëåìåíòàðíîé

äèçúþíêöèè δ çàìåíèì êàæäîå âõîæäåíèå ïðîïîçèöèîíàëüíîé

áóêâû B'

íà Â, åñëè |B

|=F, è íà ¬Â, åñëè |B

|=Ò. Ïîëó÷èì:

δ′=B∨¬¬B∨∨B∨¬¬B=Â. Ïðîèçâåäåì äðóãóþ çàìåíó:

çàìåíèì B'

íà ¬Â, åñëè |B

| =F, è íà Â, åñëè |B

|=Ò. Ïîëó÷èì:

δ′′=¬B∨¬B∨∨¬B=¬Â. Â íîâîé òåîðèè L' ôîðìóëà À àêñè-

îìà, ò.å. |A. Ïîñêîëüêó A ïðåäñòàâèìà à âèäå ÑÊÍÔ, òî ïî ïðàâèëó

óäàëåíèÿ & ëþáàÿ äèçúþíêöèÿ δ êîíúþíêòèâíîé íîðìàëüíîé

ôîðìû òàêæå äîêàçóåìà, à ïîñêîëüêó äèçúþíêöèÿ δ ïðåäñòàâèìà

êàê â âèäå δ′, òàê è â âèäå δ′′, òî â L' èìååò ìåñòî | δ' è | δ′′, à ýòî

îçíà÷àåò, ÷òî |

¬B è |

B , ò.å. òåîðèÿ L' ïðîòèâîðå÷èâà.

Îïðåäåëåíèå 11.7. Ôîðìàëüíàÿ òåîðèÿ íàçûâàåòñÿ ðàçðåøèìîé,

åñëè ñóùåñòâóåò ýôôåêòèâíàÿ ïðîöåäóðà, ïîçâîëÿþùàÿ çà

êîíå÷íîå ÷èñëî øàãîâ îïðåäåëèòü, ÿâëÿåòñÿ ïðîèçâîëüíàÿ ôîð-

ìóëà òåîðåìîé èëè íåò.

Òåîðèÿ L ðàçðåøèìà, òàê êàê êàæäîé òåîðåìå òåîðèè ñîîòâåò-

ñòâóåò òàâòîëîãèÿ, à äëÿ ëþáîé òàâòîëîãèè ìîæíî ïîñòðîèòü òàáëè-

öó èñòèííîñòè.

Îïðåäåëåíèå 11.8. Ñèñòåìà àêñèîì ÿâëÿåòñÿ íåçàâèñèìîé, åñëè

íè îäíà èç àêñèîì íå ìîæåò áûòü âûâåäåíà èç äðóãèõ.

Ìåòàòåîðåìà 11.6. Ñõåìû àêñèîì À1, À2, À3 â òåîðèè L

íåçàâèñèìû.

Äîêàçàòåëüñòâî. Äîêàæåì íåçàâèñèìîñòü À1. Äëÿ ýòîãî íåîáõî-

äèìî ïîñòðîèòü òàêóþ íåïðîòèâîðå÷èâóþ ìîäåëü, â êîòîðîé âûïîë-

íÿþòñÿ âñå àêñèîìû, êðîìå ïåðâîé. Ïîñòðîèì ìîäåëü â òðåõçíà÷íîé

ëîãèêå, ãäå èñòèííîñòíûå çíà÷åíèÿ îïåðàöèé ¬ è → îïðåäåëåíû â

òàáë. 11.3, 11.4.

Ôîðìóëó À áóäåì ñ÷èòàòü âûäåëåííîé, åñëè îíà âñåãäà ïðèíè-

ìàåò çíà÷åíèå 0. Íåòðóäíî ïîêàçàòü, ÷òî ïðàâèëî ÌÐ ñîõðàíÿåò

ñâîéñòâî âûäåëåííîñòè. Ìîæíî ïîêàçàòü (ïîñòðîåíèåì òàáëèö èñ-

òèííîñòè), ÷òî ñõåìû àêñèîì À2, À3 ÿâëÿþòñÿ âûäåëåííûìè â

äàííîé ìîäåëè. Ñëåäîâàòåëüíî, âûäåëåííîé ÿâëÿåòñÿ è âñÿêàÿ ôîð-

ìóëà, âûâîäèìàÿ èç À2, À3 ñ ïîìîùüþ ïðàâèëà ÌÐ. Îäíàêî

ôîðìóëà À1 íå âûäåëåííàÿ,  äëÿ äîêàçàòåëüñòâà ýòîãî äîñòàòî÷íî

íàéòè îäèí íàáîð, íà êîòîðîì çíà÷åíèå À1 îòëè÷íî îò 0, íàïðèìåð:

1→ (2 → 1)=1 → 0=2.

Àíàëîãè÷íî ìîæíî äîêàçàòü íåçàâèñèìîñòü À2, ïîñòðîèâ äðóãóþ

òðåõçíà÷íóþ ìîäåëü, ãäå âûäåëåííûìè áóäóò àêñèîìû À1 è À3

×òîáû ïîêàçàòü íåçàâèñèìîñòü À3, äîñòàòî÷íî ïåðåîïðåäåëèòü

îòðèöàíèå òàê, ÷òîáû ¬õ=õ (òîæäåñòâåííàÿ îïåðàöèÿ). Òîãäà À1

è À2 ïî-ïðåæíåìó áóäóò òàâòîëîãèÿìè, à À3 óæå íå áóäåò

òàâòîëîãèåé.

Ïîäðîáíîå äîêàçàòåëüñòâî ìîæíî íàéòè â [Ìåíäåëüñîí, 1976].

Òàáëèöà.11.3. Òàáëèöà.11.4.

A ¬ÀABÀ → Â

01 0 0 0

11 1 0 2

20 2 0 0

012

112

210

022

120

220

Ôîðìàëüíûå òåîðèè. Èñ÷èñëåíèå âûñêàçûâàíèéÃëàâà 11

199

Ãëàâà 12. ÒÅÎÐÈß ÏÐÅÄÈÊÀÒÎÂ

ÏÅÐÂÎÃÎ ÏÎÐßÄÊÀ

12.1. Ïîíÿòèå ïðåäèêàòà

Ñóùåñòâóþò òàêèå ëîãè÷åñêèå ñõåìû ðàññóæäåíèé, êîòîðûå íå

ìîãóò áûòü îáîñíîâàíû â ëîãèêå âûñêàçûâàíèé. Ðàññìîòðèì óìîçàêëþ-

÷åíèå: «Âñå ëþäè ñìåðòíû (À). Ñîêðàò  ÷åëîâåê (Â). Ñëåäîâàòåëüíî,

Ñîêðàò ñìåðòåí (Ñ)». Î÷åâèäíî, ÷òî Ñ ñëåäóåò èç À è Â, îäíàêî,

ëîãè÷åñêîå ñëåäîâàíèå À, Â |= Ñ íåäîêàçóåìî â ëîãèêå âûñêàçûâàíèé.

Ïðè÷èíà çàêëþ÷àåòñÿ âî âíóòðåííåé ñòðóêòóðå âûñêàçûâàíèé.

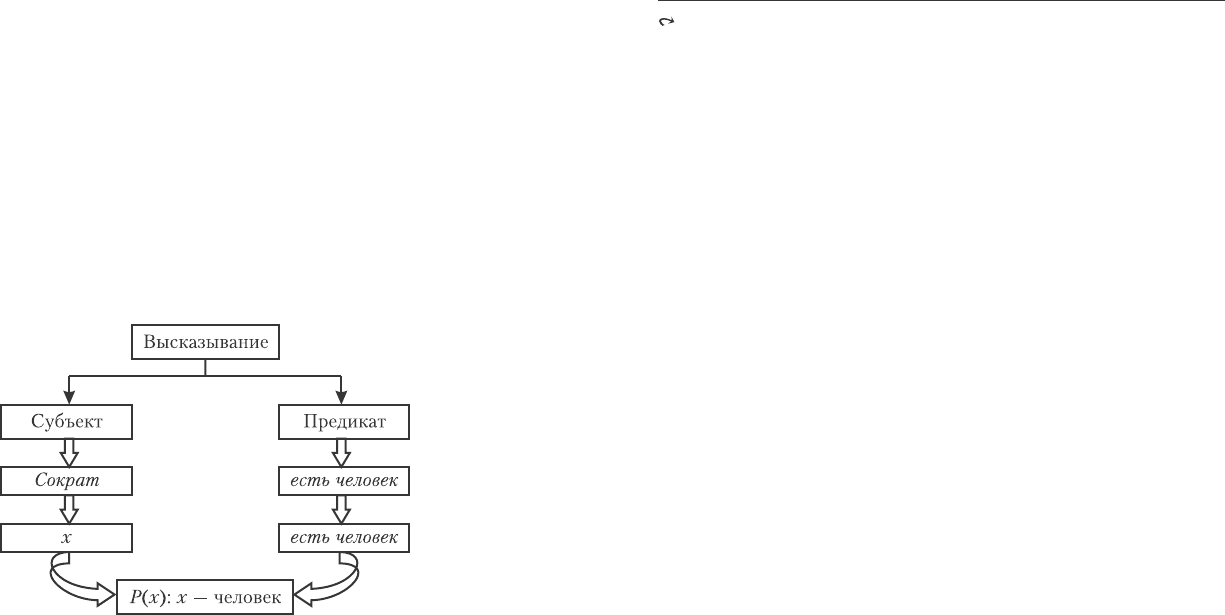
Âíóòðåííþþ ñòðóêòóðó âûñêàçûâàíèÿ ìîæíî ðàçäåëèòü íà ñóáú-

åêò è ïðåäèêàò, ãäå ñóáúåêò åñòü ïîäëåæàùåå, à ïðåäèêàò îïðåäåëÿåò

ñâîéñòâî ñóáúåêòà (ðèñ. 12.1).

Ðèñ.12.1. Ñòðóêòóðà âûñêàçûâàíèÿ.

Íàïðèìåð, Ñîêðàò  ýòî ñóáúåêò, êîòîðûé îáëàäàåò ñâîéñòâîì

áûòü ÷åëîâåêîì. Ýòî ñâîéñòâî ïðåäñòàâëÿåò ñîáîé îäíîìåñòíûé

ïðåäèêàò, îïðåäåëåííûé íà ìíîæåñòâå ëþäåé: «__ åñòü ÷åëîâåê».

Îáîçíà÷èì åãî P(x), ãäå x  ïåðåìåííàÿ, îáîçíà÷àþùàÿ òàê

íàçûâàåìîå «ñâîáîäíîå ìåñòî ïðåäèêàòà». Ïîäñòàâëÿÿ íà ìåñòî

ïåðåìåííîé õ îáúåêòû èç îáëàñòè îïðåäåëåíèÿ ïðåäèêàòà, ïîëó÷àåì

âûñêàçûâàíèÿ. Òàêèì îáðàçîì, îäíîìåñòíûé ïðåäèêàò, îïðåäåëåí-

íûé íà íåêîòîðîì ìíîæåñòâå îáúåêòîâ, çàäàåò ñâîéñòâî, êîòîðûì

ýòè îáúåêòû ìîãóò îáëàäàòü èëè íå îáëàäàòü. Ïðè ïîäñòàíîâêå íà

ñâîáîäíîå ìåñòî ïðåäèêàòà êàêîãî-ëèáî îáúåêòà èç åãî îáëàñòè îïðå-

äåëåíèÿ ïðåäèêàò îáðàùàåòñÿ â âûñêàçûâàíèå, èñòèííîå èëè ëîæ-

íîå. Òàêèì îáðàçîì, ïðåäèêàò ðàçáèâàåò ýòî ìíîæåñòâî íà äâå îáëàñ-

òè: îáëàñòè èñòèííîñòè è ëîæíîñòè.

Îïðåäåëåíèå 12.1. Îäíîìåñòíûì ïðåäèêàòîì P(x), îïðåäåëåí-

íûì íà ìíîæåñòâå Ì, íàçûâàåòñÿ âûðàæåíèå, êîòîðîå ïîñëå ïîä-

ñòàíîâêè â íåãî âìåñòî x ïðåäìåòà èç îáëàñòè îïðåäåëåíèÿ Ì

îáðàùàåòñÿ â âûñêàçûâàíèå. Îáëàñòü îïðåäåëåíèÿ ïðåäèêàòà

íàçûâàåòñÿ ïðåäìåòíîé îáëàñòüþ. Ýëåìåíòû èç îáëàñòè îïðåäå-

ëåíèÿ íàçûâàþòñÿ ïðåäìåòíûìè ïîñòîÿííûìè (ïðåäìåòàìè).

Ïåðåìåííàÿ, îò êîòîðîé çàâèñèò ïðåäèêàò, íàçûâàåòñÿ ïðåäìåò-

íîé ïåðåìåííîé.

Îäíîìåñòíûå ïðåäèêàòû òðàäèöèîííî ñëóæàò äëÿ ôîðìàëèçà-

öèè ïîíÿòèé. Ïîíÿòèå ïðåäñòàâëÿåò ñîáîé åäèíèöó ìûøëåíèÿ.

Àáñòðàêòíîå ìûøëåíèå îñíîâûâàåòñÿ íà ïîíÿòèÿõ, îòîáðàæàþùèõ

äåéñòâèòåëüíîñòü, ïîýòîìó àáñòðàêòíîå ìûøëåíèå íàçûâàþò ïîíÿ-

òèéíûì. Ïîíÿòèÿ âîçíèêàþò êàê ðåçóëüòàò îáîáùåíèÿ ìíîæåñòâà

ïðåäìåòîâ ïî ñèñòåìå ïðèçíàêîâ, îáùåé òîëüêî äëÿ ýòèõ âûäåëåí-

íûõ ïðåäìåòîâ. Ïðèçíàê  ýòî íàëè÷èå èëè îòñóòñòâèå ñâîéñòâà ó

ïðåäìåòà, à òàêæå íàëè÷èå èëè îòñóòñòâèå îòíîøåíèÿ ìåæäó ïðåä-

ìåòàìè. Ïîíÿòèå õàðàêòåðèçóåòñÿ ñâîèì ñîäåðæàíèåì è îáúåìîì.

Ñîäåðæàíèå ïîíÿòèÿ  ýòî ñèñòåìà ïðèçíàêîâ, íà îñíîâå êîòîðîé

ìíîæåñòâî ïðåäìåòîâ îáîáùàåòñÿ â ïîíÿòèè. Îáúåì ïîíÿòèÿ  ýòî

ìíîæåñòâî ïðåäìåòîâ, îáîáùàåìûõ è âûäåëÿåìûõ â ïîíÿòèè, ò.å.

ìíîæåñòâî ïðåäìåòîâ, êîòîðûå õàðàêòåðèçóþòñÿ ñèñòåìîé ïðèçíà-

êîâ, ñîñòàâëÿþùèõ ñîäåðæàíèå ïîíÿòèÿ. Íàïðèìåð, ïîíÿòèå «ðûáà»

ìîæíî îõàðàêòåðèçîâàòü êàê ìíîæåñòâî âñåõ æèâûõ ñóùåñòâ (îáúåì

ïîíÿòèÿ), êîòîðûå îáëàäàþò ïðèçíàêàìè: æèâóò â âîäå, ïëàâàþò,

èìåþò æàáðû, ïëàâíèêè è õâîñò (ñîäåðæàíèå ïîíÿòèÿ). Êàæäîå èç

ïåðå÷èñëåííûõ ñâîéñòâ ìîæíî çàäàòü îäíîìåñòíûì ïðåäèêàòîì,

îïðåäåëåííûì íà ìíîæåñòâå âñåõ æèâûõ ñóùåñòâ: V(x) x æèâåò â

âîäå, P(x)  x ïëàâàåò, G(x) x èìååò æàáðû, L(x)  x èìååò

ïëàâíèêè, R(x)  x èìååò õâîñò. Òàêèì îáðàçîì, ïîíÿòèå ðûáà ìîæåò

áûòü îïèñàíî âûðàæåíèåì: V(x)&P(x)&G(x)&L(x)&R(x).

Îáëàñòü èñòèííîñòè ýòîãî âûðàæåíèÿ ñîñòàâëÿåò îáúåì ïîíÿòèÿ 

ýòî âñå ñóùåñòâóþùèå ðûáû. Ìåæäó îáúåìîì è ñîäåðæàíèåì ïîíÿ-

òèÿ ñóùåñòâóåò îáðàòíàÿ çàâèñèìîñòü: ÷åì áîëüøå îáúåì, òåì

ìåíüøå ñîäåðæàíèå. Íàïðèìåð, ïîíÿòèå «îáèòàòåëè âîäíûõ ãëóáèí»

ìîæíî îïðåäåëèòü êàê «ìíîæåñòâî âñåõ ñóùåñòâ, æèâóùèõ â âîäå».

Ñîäåðæàíèå ýòîãî ïîíÿòèÿ îïèñûâàåòñÿ ïðåäèêàòîì V(x)  x æèâåò

â âîäå. Äîáàâèâ ñâîéñòâî P(x)  x ïëàâàåò, ìû óâåëè÷èì ñîäåðæàíèå

ïîíÿòèÿ, íî óìåíüøèì îáúåì: áóäóò èñêëþ÷åíû ìîëëþñêè, ðàêîîá-

ðàçíûå è ïðî÷èå îáèòàòåëè âîäíûõ ãëóáèí, êîòîðûå íå ïëàâàþò.

Äîáàâèâ íîâûå ñâîéñòâà, ìû åùå áîëåå óìåíüøèì îáúåì ïîíÿòèÿ.

Äâóìåñòíûé ïðåäèêàò çàäàåò îòíîøåíèå ìåæäó äâóìÿ îáúåê-

òàìè. Îáúåêòû ìîãóò ïðèíàäëåæàòü îäíîé è òîé æå, ëèáî ðàçíûì

îáëàñòÿì îïðåäåëåíèÿ. Íàïðèìåð, ïðåäèêàò P(x,y):x>y,ãäå

Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêà