СЗТУ Высшая математика

Подождите немного. Документ загружается.

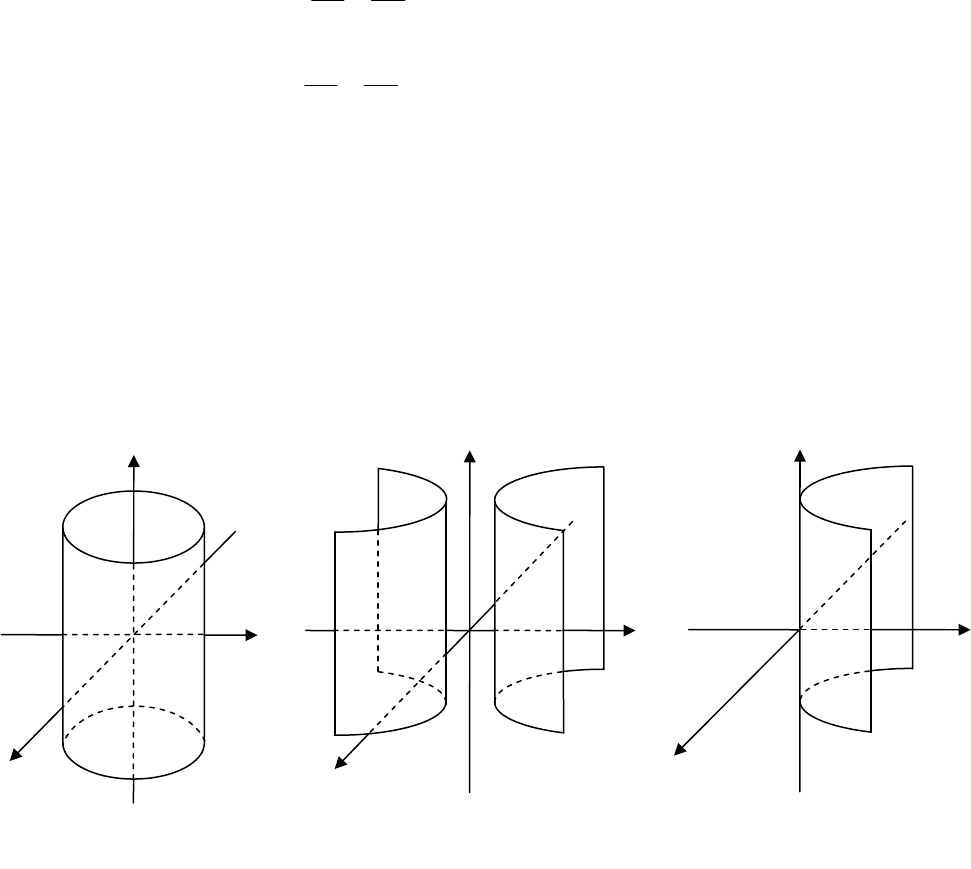
110

координат, ось совпадает с осью

, а ветви направлены вверх - в сторону по-

ложительных

Таким образом, рассматриваемая поверхность имеет форму седла с двумя

взаимно перпендикулярными плоскостями симметрии

Oxz

Oyz

(рис. 3.38).

Горизонтальные сечения гиперболического параболоида являются гипер-

болами, за исключением сечения плоскостью

0=z

, которое представляет со-

бой пару пересекающихся прямых.

Цилиндры второго порядка

Цилиндрической поверхностью или цилиндром называется поверх-

ность, образованная прямыми, проведенными через всевозможные точки за-

данной линии

параллельно заданной прямой

. При этом линия

называет-

ся

направляющей цилиндра, прямая

- осью цилиндра, а прямые, параллель-

ные оси и лежащие на цилиндре - его

образующими.

Уравнения второго порядка

=1,

(3.48)

=1,

−

(3.49)

=2ypx

(3.50)

задают в пространстве цилиндрические поверхности с осью

. Их направ-

ляющими являются, соответственно, эллипс, гипербола и парабола, заданные

на плоскости теми же уравнениями. Тип направляющей определяет название

цилиндра второго порядка:

эллиптический цилиндр (рис. 3.39), гиперболиче-

ский

цилиндр (рис. 3.40), параболический цилиндр (рис. 3. 41).

Рис. 3.41

Рис. 3.39

Рис. 3. 40

111

Решение примеров

Пример 1.

Привести уравнение

222

46220xyz xyz

+−++−=

к кано-

ническому виду, определить вид поверхности.

Решение. Дополним уравнение до полных квадратов всех трех перемен-

ных:

()()

(

)

222

44 69 212491xx yy zz− + + + + + + + −=++

После преобразований получим:

()()()

222

2314xyz−++++=

Полученное каноническое уравнение описывает сферу с центром в точке

В(2,-3,-1) и радиусом

4R =

Пример 2. Составить уравнение эллиптического параболоида с вершиной

в начале координат и осью симметрии Oz, если известно, что точки

(1,2,2)M −−

(1,1,1)N

лежат на этой поверхности.

Решение. Каноническое уравнение эллиптического параболоида с верши-

ной в начале координат и осью Oz имеет вид:

(3.51)

Точки M и N лежат на данной поверхности, поэтому их координаты долж-

ны удовлетворять уравнению эллиптического параболоида. Подставив коорди-

наты точек в уравнение (3.51), получим:

(1) (2)

=2,

=1.

⎧

−−

⎪

⎨

⎪

⎩

Преобразуем эту систему:

2222

42,

baab

⎧

⎪

⎨

⎪

⎩

Вычтем из первого уравнения второе и определим

и далее

Подставим найденные значения

в уравнение эллиптического пара-

болоида и упростим его:

Каноническое уравнение

эллиптического параболоида с указанными па-

раметрами имеет вид

()()

1, 5 3

z+=

Пример 3. Составить уравнения линий пересечения двуполостного гипер-

112

болоида

222

4xyz+−=−

и эллипсоида

22 2

211xy z

Решение.

Определим уравнения плоскостей, в которых лежат линии пере-

сечения поверхностей. Для этого найдем значения переменной z, удовлетво-

ряющие обоим уравнениям. Вычитая из второго уравнения первое, получим

315z

откуда

Подставляя найденные значения переменной z в уравнение любой из по-

верхностей, получим уравнения окружностей

1xy

, лежащих в плоско-

стях

5z =

5z =−

Таким образом двуполостный гиперболоид

222

4xyz

−=−

и эллипсоид

22 2

211xy z++ =

пересекаются по окружностям

1xy

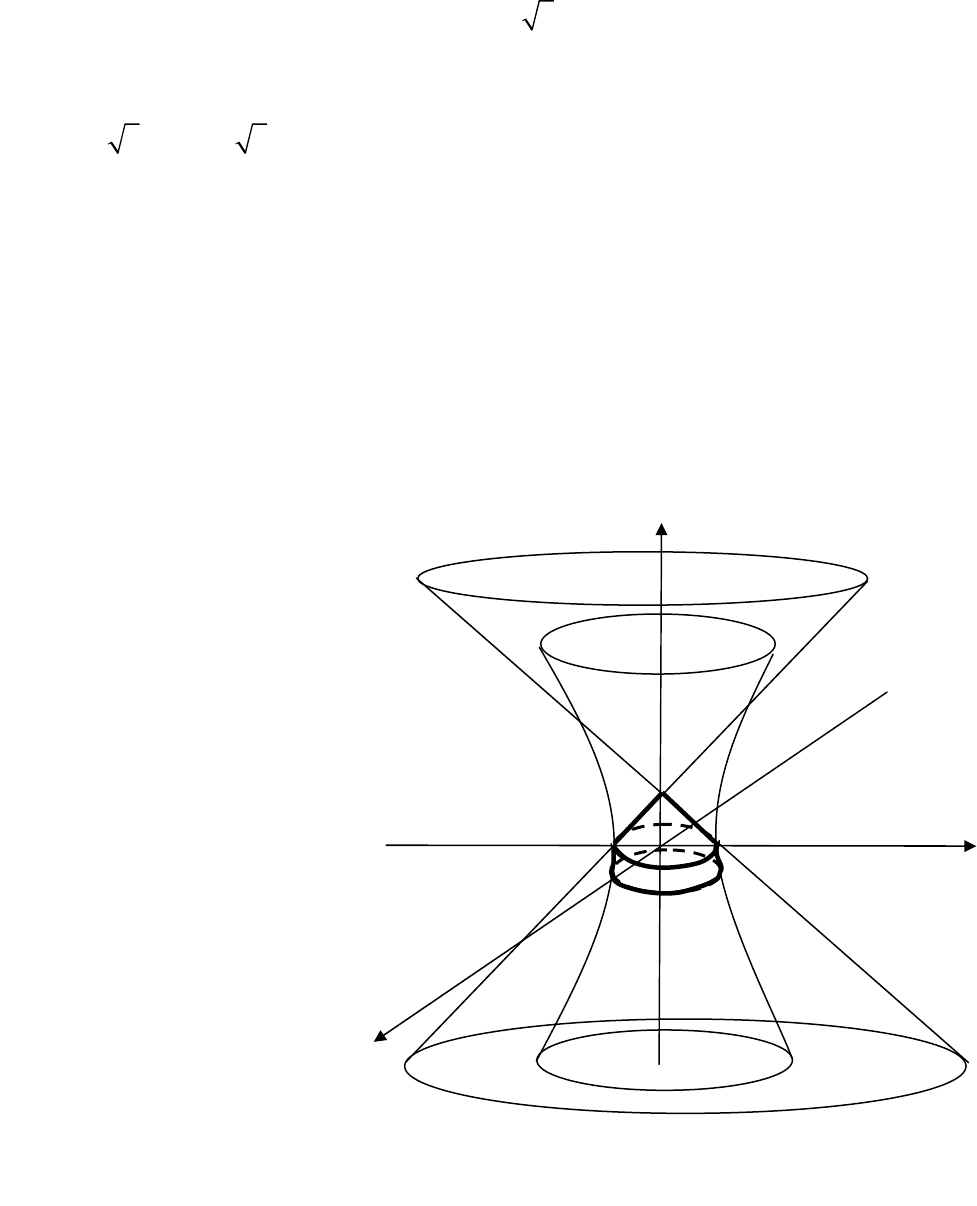
Пример 4. Определить вид поверхностей, ограничивающих тело, за-

данное в пространстве системой неравенств, и изобразить это тело:

22 2

222

(2)0,

12.

xy z

xyz

⎧

−− ≤

⎪

+−≤

⎨

⎪

−≤ ≤

⎪

⎩

Решение. Уравнение

()

20xy z+−− =

задает

в пространстве конус с

осью

, смещенный

вдоль оси

на две еди-

ницы. Эта поверхность

разбивает все пространство

на три части: точки самого

конуса, точки внутри и

снаружи конуса. Возьмем

произвольную точку внут-

ри конуса, например точку

О(0,0,0). Ее координаты

удовлетворяют первому

неравенству, поэтому нера-

венство описывает область

внутри конуса.

Уравнение

222

4xyz+−=

задает од-

нополостный гиперболоид

с осью вращения

. В сечении гиперболоида плоскостью z = 0 получаем

-1

Рис. 3.42

113

окружность с радиусом

2r =

. Координаты произвольной точки внутри ги-

перболоида (той же точки О(0,0,0)) удовлетворяют и второму неравенству,

поэтому данное неравенство также описывает область внутри гиперболоида.

Наконец, неравенство

1−≤

z ≤ 2 задает ту часть пространства, которая

лежит между плоскостями z=-1 и z = 2.

Из изложенного следует, что исследуемое тело имеет вид, указанный на

рис. 3.42.

Пример 5. Сделать схематический рисунок тела, заданного системой не-

равенств, указать вид поверхностей, ограничивающих тело:

44.

yx y

⎧

−≤

⎪

≤≤

⎨

⎪

−≤ ≤

⎪

⎩

Решение. Приведем уравнение

2yx y−=

к каноническому виду:

(1) 1yx

−

−=

В пространстве такое уравнение

описывает гиперболический цилиндр с

осью, смещенной вдоль оси Oy на одну

единицу. Первое неравенство описыва-

ет область внутри цилиндра (проверим

точку с координатами (0,5,0) на при-

надлежность этой части пространства).

Уравнения

yz =

опре-

деляют две пересекающиеся плоско-

сти, перпендикулярные координатной

плоскости Oyz. Вторые неравенства

описывают часть пространства между

ними.

Уравнения

4y =±

определяют

две параллельные плоскости, перпен-

дикулярные координатной плоскости

Oxy . Третьи неравенства описывают

часть пространства от плоскости

−

до плоскости

Ответ: исследуемое тело имеет вид, указанный на рис. 3.43.

Вопросы для самопроверки по теме 3.5

1. Дайте определение цилиндрической поверхности. Перечислите извест-

ные Вам цилиндры второго порядка. Какой вид они имеют?

2. Дайте определение эллипсоида. Какой вид имеет эта поверхность в ка-

нонической системе координат?

Рис. 3.43

2 4

4−

• • •

114

3. Какие линии представляют собой сечения эллипсоида плоскостями, па-

раллельными координатным?

4. Продолжите определение: “Однополостным гиперболоидом называет-

ся….. ”. Исследуйте форму этой поверхности форму методом сечений.

5. Дайте определение двуполостного гиперболоида.

6. В каком случае говорят о поверхностях вращения? Приведите примеры .

7. Запишите каноническое уравнение конуса второго порядка. Изобразите

эту поверхность.

8. Дайте определение эллиптического параболоида. Какой вид имеет эта

поверхность в канонической сист

еме координат?

9. Продолжите определение: “Гиперболический параболоид-это... ”.

3.6. Линейное векторное и евклидово пространства.

Квадратичные формы

При изучении данной темы Вам предстоит познакомиться со следующи-

ми понятиями:

• Линейное векторное пространство.

• Линейный оператор.

• Собственные числа и собственные векторы линейного оператора.

• Евклидово пространство.

• Квадратичная форма.

Множество V называется линейным векторным пространством, ес-

ли на нем определены две операции: сложение и умножение на число, при-

чем

1) abba+=+ для любых ,ab V

∈

(коммутативность сложения);

(

)

(

)

ab ca bc++=++ для любых

,,abc V

∈

(ассоциативность сложе-

ния);

(

)

(

)

aaλβ =λβ для любого aV

∈

и любых чисел

и λ (ассоциатив-

ность умноженная на число);

(

)

ab a bλ+=λ+λ для любых ,ab V

∈

и любого числа λ (дистрибутив-

ность умножения на число относительно сложения);

(

)

aaaλ+β =λ +β для любого aV

∈

и любых чисел

;

6) существует 0 – нейтральный элемент относительно сложения – такой,

что 0aa+= для всех aV∈ ;

7) 1aa= для всех aV∈ ;

8) для любого aV∈ существует противоположный ему элемент a

−

, так

что

(

)

0.aa+− =

Элементы линейного векторного пространства часто называют векто-

рами. Свойства линейных векторных пространств и примеры таких про-

странств можно найти в [2], гл.6, с.81-86.

115

Линейным оператором

, отображающим пространство V в про-

странство U , называется закон, ставящий в соответствие каждому вектору

V∈ единственный элемент ()

∈

, причем

(

)

() ()

xy Ax Ay

+β =λ +β для

всех ,

yV∈ и любых чисел

. Скобки в последней формуле обычно не

пишут. Действия над линейными операторами и примеры таких операторов

рассмотрены в [2], гл.6, с.92-95.

Ненулевой вектор

называется собственным вектором линейного

оператора

, если найдется такое число

, что

λ . В этом случае гово-

рят, что собственный вектор

отвечает собственному числу λ линейного

оператора

. Подробнее этот вопрос рассмотрен в [2], гл.6, с.98-101.

Вещественное линейное векторное пространство V называют евкли-

довым, если в нем определена операция, ставящая в соответствие любым

вектором

,ab V∈

вещественное число

(

)

,ab , называемое их скалярным про-

изведением, причем

1) ( , ) ( , )ab ba= для всех ,ab V

∈

;

(

)

(

)

,(,),abc ac bc+= + для всех ,,abc V

∈

;

(

)

,(,)ab abλ=λ для всех ,ab V

∈

и любого числа

;

(

)

,0,aa > если 0a ≠ .

Подробнее этот вопрос рассмотрен в [2], гл.6, с.87-92.

Квадратичной формой называют однородный многочлен второй сте-

пени от

, ,...,

xx:

12 111 1212 11

22 2 2 2

( , ,..., ) ...

...

nnn

Ôx x x c x c xx c xx

cx cxx

++++

++ +

"""""""""

nn n

cx+

Ее коэффициенты в этой записи образуют треугольную матрицу.

Удобнее каждый недиагональный коэффициент разделить на 2 и записать

дважды; тогда

12 111 1212 11

21 2 1 22 2 2 2

11 2 2

( , ,..., ) ...

...

... ,

nnn

nn n n nnn

Ôx x x ax a xx a xx

axx ax axx

axx axx ax

++++

+++ +

++ ++

"""""""""""""

где

ij ji

aa= . Введем матрицу квадратичной формы

11 12 1

21 22 2

nn nn

aa a

" """

116

Очевидно, она симметрична, т.е. .

Обозначим столбец

()

, ,...,

через X . Тогда

(, ,..., )

Ôx x x X AX= .

Можно доказать, что любая квадратичная форма с вещественными ко-

эффициентами с помощью линейного преобразования переменных, имеюще-

го невырожденную вещественную матрицу, приводится к диагональному

виду.

Подробнее о квадратичных формах рассказано в [2], гл.6, с.101-103.

4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Данный раздел включает шесть тем:

4.1. Функция.

4.2. Предел последовательности. Предел функции.

4.3. Способы вычисления пределов. Сравнение бесконечно малых

функций.

4.4. Непрерывность функции в точке и на промежутке. Точки разры-

ва функции, их классификация.

4.5. Понятие производной функции. Дифференцируемость функции.

Правила нахождения производной и дифференциала.

4.6. Производная сложной, обратной и параметрически заданной

функции. Производные и дифференциалы высших порядков.

В каждой теме излагается основной теоретический материал и приводятся

иллюстрирующие примеры. Завершает тему подробный разбор решения типо-

вых примеров.

После изучения раздела студентам очно-заочной и заочной форм обучения

надо решить пять задач из контрольной работы № 2 в соответствии со своим вари-

антом.

4.1. Функция

При изучении данной темы Вам предстоит ознакомиться со следующими во-

просами:

• Функция и способы ее задания;

• Основные характеристики функций;

• Обратная функция и сложная функция;

• Элементарные функции.

После изучения данных вопросов в опорном конспекте Вам следует от-

ветить на вопросы для самоконтроля.

Если Вы будете испытывать затруднения в ответах, обратитесь к [3], глава

1, с. 15-25 или к глоссарию – краткому словарю основных терминов и положений.

117

Определение функции, способы ее задания.

Основные характеристики функций

Понятие функции является не только основным понятием

математического анализа, но и в других разделах математики играет важную

роль. Понятие функции связано с установлением зависимости между двумя

переменными величинами.

Определение. Пусть даны два множества

, элементы

которых являются вещественными числами. Если в силу некоторого закона

каждому числу

X∈

ставится в соответствие одно и только одно число

∈

то говорят, что на множестве

задана функция

и пишут

(

)

, yfxxX

∈

Множество

называют областью (множеством) определения функции

()

и обозначается

()

;

называют аргументом функции. Множество

()

значений

Y∈

, которые поставлены в соответствие элементам

∈

называют множеством значений функции.

Если множество

()

содержит один-единственный элемент

(т.е.

всем

X∈

ставится в соответствие одно и то же число

), то функция

называется постоянной, и в этом случае пишут

(

)

constyfx C===

Графиком функции

()

в декартовой прямоугольной системе

координат

Oxy

называется множество точек плоскости

Oxy

с координатами

()

(

)

X∈

Способы задания функции:

1. Аналитический способ: функция задается в виде одной или нескольких

формул или уравнений. При этом если функция задается уравнением

(, ) 0,Fxy=

то говорят, что функция

()

задана неявно.

Если при аналитическом способе задания область определения не

указана, то предполагается, что она совпадает с множеством всех значений

аргумента, при которых соответствующая формула имеет смысл.

2. Графический способ: задается график функции.

3. Табличный способ: функция задается таблицей, в которой дан ряд

значений аргумента и соответствующих значений функции.

Примеры.

1. Найти область определения функции

−

Решение. Подкоренное выражение должно быть неотрицательным, а

знаменатель не должен равняться нулю. Таким образом, область определения

находится из неравенства:

40x −>

. Откуда получаем

(

)( )

;2 2;x

∈

−∞ − ∪ +∞

118

Ответ:

()

(

)

{

}

() ;2 2;Df =−∞−∪ +∞

2. Найти область определения функции

3log(1)

Решение. Первое слагаемое определено при всех вещественных

переменных, а логарифм определяется для положительных чисел. Значит,

область определения задается неравенством

10,x

или

(

)

1;x

∈

−+∞

Ответ:

()

() 1;Df =−+∞

Некоторые характеристики функций

1. Четные и нечетные функции

Определение. Функция

()

с областью определения

называется

чётной, если для любого

X∈ выполняется равенство

() ()

xfx

−

Функция

()

fx=

с областью определения

называется нечётной,

если для любого

X∈ выполняется равенство

() ()

xfx

−

=−

Функции, которые не являются ни четными, ни нечетными, называются

функциями общего вида. Из определения следует, что:

1. Область определения чётной и нечётной функций симметрична

относительно начала координат.

2. График чётной функции симметричен относительно оси ординат.

3. График нечётной функции симметричен относительно начала

координат.

Примеры.

1. Функция

() 2

xx x=−

является четной, т.к.

44 22

() ,()

xxx

−

=−=

и,

значит

() ()

xfx−=

2. Функция

()

−

является нечетной. Действительно,

333

222

() 2() 2 2

() ().

()

x x xxxx

xfx

xxx

−−− −+ −

−= = =− =−

−

3. Функция

() 5 3fx x=+

является функцией общего вида, так как при

замене

на

−

первое слагаемое, меняет знак, а второе остается без изменений

и, значит, меняется модуль значения функции.

2. Периодические функции

Определение. Функция

()

с областью определения

называется

периодической, если существует такое число

0T >

, что:

1) если

X∈

, то

TX−∈

∈

;

2) для любого

X∈

выполняется равенство

() ( )

xfxT

;

3) среди всех таких чисел

есть наименьшее. Это наименьшее

называется периодом функции

()

Пример.

Функция

() 3sin2 1

периодическая с периодом

,T =π

так как из

тригонометрии известно, что функция

sin

имеет период

соответственно

sin 2

имеет период

119

3. Ограниченные функции

Определение. Функция

()

с областью определения

называется

ограниченной сверху на множестве

, (

XX⊂

), если существует такое

число

, что для любого

X∈ выполнено неравенство

()

xM≤

. Функцию

()

fx=

называют ограниченной снизу на множестве

, если существует

такое

, что для любого

X∈ выполнено неравенство

()

xm≥

Функцию

()

fx=

называют ограниченной на множестве

, если

существует такое

0L >

, что для любого

∈

выполнено неравенство

()

xL||≤

Очевидно, что функция ограничена тогда и только тогда, когда она

ограничена сверху и ограничена снизу.

Отметим также, что сумма и произведение ограниченных функций также

есть ограниченная функция.

Пример.

Функция

()

ограничена на всей числовой прямой. Так как

0,x ≥

то

01,

≤≤

а это и означает ограниченность.

4. Монотонные функции

Определение. Функция

()

называется возрастающей на

некотором множестве

, если для любых

∈

из условия

следует,

что

() ( )

xfx<

, то есть большему значению аргумента отвечает большее

значение функции.

Функция

()

fx=

называется убывающей на

, если для любых

xX,∈

из условия

следует, что

() ( )

xfx>

, то есть большему

значению аргумента соответствует меньшее значение функции.

Если функция

()

fx=

возрастает на

или убывает на

, то она

называется

строго монотонной на

Функция называется

неубывающей на множестве

, если из условия

следует, что

() ()

xfx≤

, для любых

∈

, и

невозрастающей на

множестве

, если из условия

следует, что

() ()

xfx≥

, для любых

xX,∈

Возрастающие, убывающие, неубывающие и невозрастающие на

функции называются функциями,

монотонными на

Пример.

Функция

yx=

возрастает на всей числовой прямой. Действительно,

если

то