Сучкова Л.И. Абстрактный и структурный синтез автоматов

Подождите немного. Документ загружается.

Министерство образования и науки

Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический

университет им. И.И.Ползунова»

Л.И.Сучкова

Абстрактный и структурный синтез

автоматов

Барнаул – 2009

УДК 004.42

Сучкова, Л.И. Абстрактный и структурный синтез

автоматов: учебное пособие по дисциплине «Теория автома-

тов» / Л.И. Сучкова; АлтГТУ им. И.И. Ползунова. – Барнаул,

Изд-во АлтГТУ, 2009. – 162 c., ил.

В учебном пособии изложен теоретический материал

по разделам курса «Теория автоматов», приведены задания

для выполнения лабораторных работ по рассмотренным

пособии темам, дано описание обучающего программного

комплекса по курсу. Учебное пособие предназначено для

студентов, обучающихся на специальности «Вычислитель-

ные машины, комплексы, системы и сети».

Учебное пособие рассмотрено на заседании кафедры «Авто-

матика и вычислительные системы», протокол № 9 от

26.06.2009 г.

Рецензент: А.С. Шатохин, к.т.н

., профессор, прорек-

тор по информатизации АлтГУ

Содержание

1 Абстрактные автоматы-распознаватели………… 5

1.1 Общие понятия об абстрактных автоматах………… 5

1.2 Синтез и детерминизация конечных автоматов-

распознавателей………………………………………….

1.3 Алгоритм минимизации автоматов – распознавате-

лей………………………………………………………….

1.4 Связь между автоматами - распознавателями и ав-

томатными грамматиками…………………………….

2 Автоматы с магазинной памятью…………………. 29

3 Автоматы – преобразователи………………………. 34

3.1 Машина Тьюринга как универсальный тип абст-

рактного автомата – преобразователя……………………

3.2 Автоматы Мили и Мура……………………………. 39

3.2.1 Определение и способы задания автоматов Мили

и Мура……………………………………………………

3.2.2 Преобразования автоматов Мили и Мура………… 44

3.2.3 Минимизация преобразователей. Метод Ауфен-

кампа и Хона……………………………………………..

3.3 Тестирование абстрактных автоматов………………. 52

4 Сети Петри…………………………………………..… 58

4.1 Структура и функционирование сетей Петри………. 58

4.2 Моделирование систем и событий с помощью сетей

Петри………………………………………………………

4.3

Расширенные сети Петри…………………………… 65

5 Структурный синтез автоматов………………..….. 67

5.1 Понятие структурного синтеза. Теорема о струк-

турной полноте ……………………………………………

5.2 Типы элементарных автоматов памяти …………… 68

5.3 Канонический метод структурного синтеза автомата 74

5.4 Особенности синтеза структурных автоматов на

базе T, RS, JK – триггеров……………………………….

6 Асинхронные автоматы. Гонки в автоматах……. 95

6.1 Понятие асинхронного автомата…………………… 95

6.2 Устранение гонок …………………………………… 97

7. Микропрограммирование …………………………. 102

7.1 Операционный и управляющий автоматы………… 102

7.2 Синтез автомата Мили по ГСА…………………….. 106

7.3 Синтез автомата Мура по ГСА…………………….. 110

8 Упражнения для самостоятельной работы……… 114

8.1 Синтез автоматов распознавателей………………….. 114

8.2 Построение МП-автомата………………………….. 115

8.3 Построение машины Тьюринга……………………. 117

8.4 Синтез автоматов Мили и Мура……………………. 133

9 Программное обеспечение для интерпретации ра-

боты автоматов и их преобразований…………………

137

9.1 Общие

сведения о функциях программы…………. 137

9.2 Задание автоматов различных типов……………… 142

9.3 Детерминизация и минимизация автоматов-

распознавателей…………………………………………

145

9.4 Синтез и интерпретация МП-автоматов…………… 146

9.5 Структурный синтез автоматов……………………. 151

Список использованных источников…………………… 162

1 АБСТРАКТНЫЕ АВТОМАТЫ-РАСПОЗНАВАТЕЛИ

1.1 Общие понятия об абстрактных автоматах

Простейшей моделью вычислительного устройства, об-

рабатывающего входную информацию и формирующего вы-

ходную, является автомат.

Неформально автомат можно считать устройством,

имеющим блок управления и несколько лент для чтения

входной информации, записи выходной и промежуточной

информации. Блок управления в зависимости от читаемых и

записываемых на ленты данных может находиться в различ-

ных состояниях.

Определение. Автоматом называется дискретный пре-

образователь информации, способный принимать состояния

из некоторого множества А, переходить под воздействием

входных сигналов из одного состояния в другое и выдавать

выходные сигналы.

Определение. Если множество состояний автомата,

множества входных и выходных сигналов конечны, то

авто-

мат называется конечным автоматом.

Понятие состояния необходимо для обеспечения раз-

личной реакции автомата на входной сигнал в зависимости

от предыстории получения сигналов, в результате которой

автомат перешел в некоторое состояние. Состояния соответ-

ствуют памяти о прошлом, позволяя устранить время как яв-

ную переменную и выразить выходные сигналы как функцию

состояний и входов в данный момент времени.

Входную информацию принято кодировать символами

из входного алфавита Z. Выходная информация принято ко-

дируется символами из выходного алфавита W.

Математической моделью конечного автомата является

абстрактный автомат, который имеет один входной канал и

один выходной канал. Схема работы конечного автомата

приведена на рисунке 1.1. Автомат функционирует

в дис-

кретные моменты времени, интервал между которыми Т на-

зывается тактом. При этом в каждый дискретный момент

времени на вход автомата поступает одна буква входного

алфавита, автомат переходит из одного состояния в другое

или остается в прежнем состоянии и выдает одну букву

выходного алфавита.

Рисунок 1.1

В зависимости от того, как задается длительность такта

Т, различают автоматы синхронного действия (T = const)

и асинхронного действия (T ≠ const).

Для определения синхронных и асинхронных автоматов

вводится понятие устойчивого состояния.

Определение. Состояние a

автомата называется устой-

чивым, если, попав в это состояние под действием некоторо-

го сигнала z

, автомат выйдет из него только под действием

другого сигнала z

, отличного от z

Определение. Автомат, у которого все состояния устой-

чивы, называется асинхронным.

Автомат называется синхронным, если он не являет-

ся асинхронным. Мы будем рассматривать, в основном, син-

хронные автоматы, функционирующие в дискретные момен-

ты времени, которые можно обозначить целыми не отрица-

тельными натуральными числами, t=0,1,2,3,…., имеющими

смысл номера такта.

Определение. Дискретным преобразователем Глушко-

ва В.М. называется автомат, задаваемый совокупностью 6

объектов: (A,Z,W,а

,δ,λ), где A – произвольное множество

внутренних состояний автомата, Z = {z

, z

,…, z

} – множе-

ство входных сигналов (входной алфавит), W = {w

, w

,…,

} – множество выходных сигналов (выходной алфавит), а

– начальное состояние, δ

- функция переходов, определяю-

(

)

щая состояние автомата a(t+1), в котором автомат будет на-

ходиться в момент времени t+1, в зависимости от состояния

автомата a(t) и входного сигнала z(t) в момент времени t, т.е.

a(t+1) = δ [a(t),z(t)], λ - функция выходов, определяющая

значение выходного сигнала w(t) в зависимости от состояния

автомата a(t) и входного сигнала z(t) в момент времени t, т.е.

w(t) = λ[a(t), z(t)].

Если A = {a

,...,a

}, то есть оно конечно, то считает-

ся, что задан конечный автомат, причем наличие начального

состояния не является обязательным. Таким образом, конеч-

ный автомат в общем случае задается совокупностью из пяти

объектов:

(A,Z,W,δ,λ).

Автомат работает следующим образом: в каждый мо-

мент времени t он находится в определенном состоянии a(t)

из множества A возможных состояний, причем в начальный

момент времени t = 0 он всегда находится в состоянии a(t = 0)

= a

. В момент времени t автомат воспринимает входной сиг-

нал z(t), выдает выходной сигнал w(t) = λ[a(t), z(t)]

и перехо-

дит в следующее состояние

a(t+1) = δ[a(t), z(t)]. Другими

словами, абстрактный автомат каждой паре символов a(t) и

z(t) ставит в однозначное соответствие пару a(t+1) и w(t). Та-

кие автоматы называют детерминированными. Преобразо-

вание информации в детерминированных автоматах подчи-

няется следующим условиям:

1. Любое входное слово длиною L букв преобразуется в

выходное слово той же длины.

2. Если каждый раз перед подачей входных

сигналов ав-

томат находится в одном и том же состоянии, то при совпа-

дении в двух входных словах первых L1 букв, в выходных

словах первые L1 букв тоже совпадут.

Кроме детерминированных автоматов существуют веро-

ятностные или стохастические автоматы, в которых пере-

ход из одного состояния в другое под воздействием случай-

ных или детерминированных

входных сигналов происходит

случайно. Работа таких автоматов описывается уже матрицей

переходов

δ, элементами которой являются вероятности пе-

реходов из одного состояния в другое.

Мы будем изучать детерминированные автоматы.

Определение. Автомат называется инициальным, если в

нем выделено начальное состояние.

Определение. Полностью определенным называется аб-

страктный цифровой автомат, у которого функция переходов

и функция выходов определены для всех пар (a

, z

Определение. Частичным называется абстрактный ав-

томат, у которого

функция переходов или функция выходов,

или обе эти функции определены не для всех пар (a

, z

1.2 Синтез и детерминизация конечных автоматов-

распознавателей

Рассмотрим простейший тип конечного автомата – ав-

томат-распознаватель, который не формирует выходных сиг-

налов и характеризуется кортежем вида:

(A, Z, δ, a

, F), где Z

– входной алфавит; функция переходов δ: AxZ→A; a

– на-

чальное состояние автомата; F – множество заключительных

состояний автомата.

Автомат-распознаватель начинает работу с начального

состояния и в процессе чтения входных сигналов переходит в

другие состояния. Если автомат распознаватель завершает

работу в одном из заключительных состояний, то это служит

признаком принадлежности входной цепочки некоторому

входному языку. Иначе считается, что входная цепочка

языку

не принадлежит. Тем самым автомат-распознаватель являет-

ся распознающим средством задания языка.

Определение. Конечный автомат-распознаватель допус-

кает входную цепочку α, если α переводит его из начально-

го в одно из заключительных состояний.

Определение. Множество всех цепочек, допускаемых ав-

томатом, образует язык, допускаемый автоматом.

Определение. Язык, для которого

существует распо-

знающий его конечный автомат, называется автоматным или

регулярным языком.

Различают 4 способа задания конечных автоматов-

распознавателей – командами, графом, матрицей переходов и

таблицей переходов.

Пусть имеется регулярный язык L = ab

. Рассмотрим,

как задать распознающий его конечный автомат.

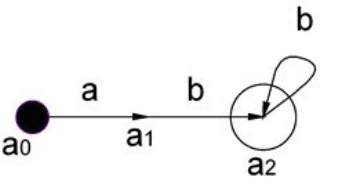
Пусть выбран способ задания - граф. В начальном со-

стоянии a

автомат читает одну букву “a” и переходит в со-

стояние a

. Далее, находясь в состоянии a

, автомат читает

букву “b” и переходит в состояние a

В состоянии a

автомат

в цикле, без перехода в другое состояние, читает букву “b”.

Состояние a

является заключительным, значит при нахож-

дении автомата в этом состоянии процесс распознавания це-

почки может завершиться. Автомат, заданный в виде графа,

приведен на рисунке 1.2.

Рисунок1.2

Цепочки языка имеют вид:

ab, abb, abbb, ....

Этот же автомат можно задать последовательностью команд:

, a → a

, b → a

F = {a

}

При задании автомата таблицей переходов в строках

таблицы указывают состояния автомата, а в столбцах – сим-

волы из входного алфавита Z. На пересечении строки, соот-

ветствующей состоянию a

, и столбца, соответствующего

символу z

, указывается состояние a

, в которое переходит

автомат при чтении z

, находясь в состоянии a

. Таблица пе-

реходов автомата, распознающего язык ab

, приведена на ри-

сунке 1.3.

В матрице переходов автомата строки и столбцы соот-

ветствуют состояниям, а на пересечении строки, соответст-

вующей состоянию a

и столбца, соответствующего состоя-

нию a

, записывается символ, читаемый при переходе из a

. Пример матрицы переходов приведен на рисунке 1.4.

Рассмотрим методы синтеза конечных автоматов-

распознавателей, являющиеся средством построения слож-

ных автоматов на основе более простых.

Рисунок1.3 – Таблица переходов

F = {a

}

Рисунок1.4 – Матрица переходов