Сучкова Л.И. Абстрактный и структурный синтез автоматов
Подождите немного. Документ загружается.

21
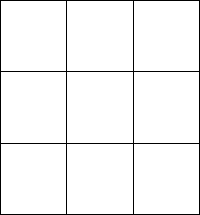
Построим таблицу переходов для данного автомата.
Таблица переходов автомата приведена на рисунке 1.21.
a b c
a
0
a
0
,
a
2
a
1
нач.
a
1
a
2
a
1
,
a
2
закл.
a
2
a
1
Рисунок 1.21
Затем начнем построение таблицы переходов детерми-
нированного автомата. Заносим в таблицу состояние а0, так
как оно является начальным. Затем формируем строку табли-
цы для а0. Так как при чтении символа “а” автомат переходит
в а0 и а2, то запишем вместо двух состояний одно с индексом
а02. Новое состояние также
занесем в таблицу, так как в него
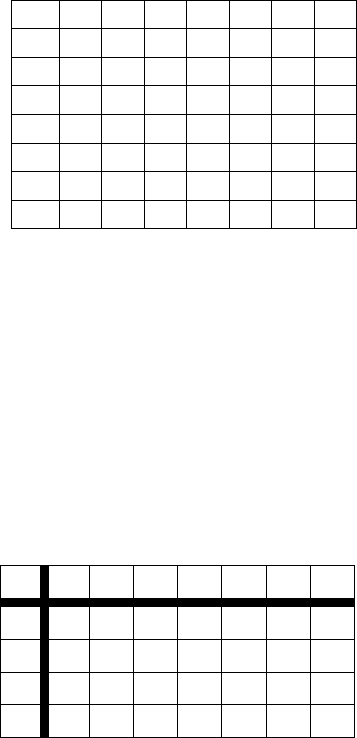
есть переход из начального. Процесс построения таблицы
переходов детерминированного автомата отражен на рисунке
1.22.
22
Рисунок 1.22
Алгоритм детерминизации автомата используется при
построении автомата, распознающего дополнение регулярно-
го языка. Сначала строится автомат, распознающий этот
язык, автомат детерминируется, все заключительные состоя-
ния делаются незаключительными, и незаключительные –
заключительными, затем вводится новая вершина, которая
будет заключительной, и в нее из каждой i-той вершины про-
водятся
дуги по тем символам, которые не распознаются в i-
той вершине. В новой вершине строим петли для всех симво-
лов входного алфавита конечного автомата-распознавателя.
1.3 Алгоритм минимизации автоматов-
распознавателей
При построении автомата возникает вопрос – нельзя ли
23
построить автомат, распознающий тот же язык, но имеющий
меньшее количество состояний. Рассмотрим процесс мини-
мизации уже построенного автомата.
Определение. Автоматы эквивалентны, если они распо-
знают один и тот же язык.
Определение. Два состояния p и q конечного автомата-
распознавателя называются m-эквивалентными, если при
распознавании любых цепочек длины m, начиная из этих со-
стояний
, автомат переходит в заключительное состояние,
либо не распознает эти цепочки.
Понятие m-эквивалентных состояний позволяет разбить
множество всех состояний на классы эквивалентных состоя-
ний и построить новый минимальный автомат, состояниями
которого будут классы эквивалентных состояний.
Рассмотрим алгоритм минимизации конечного автома-
та-распознавателя. Он заключается в построении на множе-
стве его состояний
таких разбиений p
0
,p
1
,…,p
t
, что в один
класс разбиения p
i
попадают m-эквивалентные состояния.
Если состояния не m-эквивалентны, то они называются m-
различимыми. При подаче пустой цепочки на вход автомата
он остается в том же состоянии, в котором находился. По-
этому разбиение p
0
состояний состоит из двух блоков – в
один блок попадают все заключительные, в другой – все не-
заключительные состояния. Удобно эти разбиения выполнять
с использованием матрицы перехода автомата-
распознавателя. В матрице переходов выделяем подматрицы,
в каждую из которых попадают эквивалентные состояния.
Далее анализируем каждую подматрицу. Если во всех стро-
ках подматрицы один
и тот же набор распознаваемых симво-
лов, то состояния не нуждаются в дополнительном разбие-
нии, они эквивалентны. Иначе разбиваем состояния подмат-
рицы на группы, в которых распознается один и тот же набор
символов. Процесс разбиений завершается, когда каждая
подматрица содержит в своих строках одинаковый набор
символов.
Этот алгоритм предполагает наличие конечного
числа
24
разбиений, минимальное число которых равно 2, а макси-
мальное – количеству состояний автомата.
Рассмотрим пример применения алгоритма. Пусть зада-
на матрица переходов автомата, представленная на рисунке
1.23, причем все состояния, кроме а0, являются заключитель-
ными.
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
1
a b
a
2
a c
a
3
a b
a
4
c a a
a
5
a b
a
6
a b
a
7
a b
a
8
a c
a1 – начальное состояние, F={a
2
,a
3
,a
4
,a
5
,a
6
,a
7
,a
8
}
Рисунок 1.23
Разбиваем состояния на 2 группы эквивалентности – в 1
группу включим состояние а
0
, во вторую – все остальные.
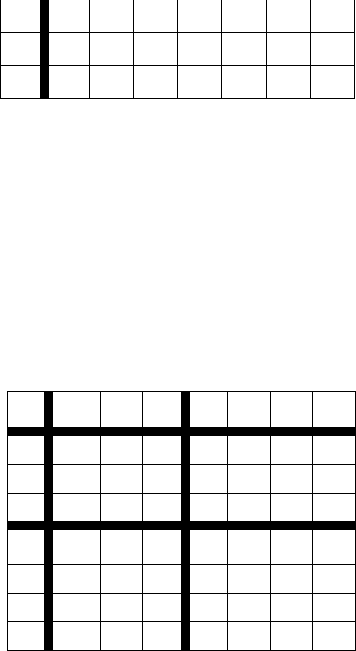
Разделим в матрице группы состояний жирными вертикаль-
ными и горизонтальными линиями (рисунок 1.24). Затем ана-
лизируем 4 получившиеся подматрицы. Если строки подмат-
рицы содержат разные наборы символов, то состояния, вхо-
дящие в подматрицу, не эквивалентны, и нуждаются в после-
дующем разбиении.
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
1
a b
a
2
a c
a
3
a b
a
4
c a a
a
5
a b
25
a
6
a b
a
7
a b
a
8
a c
Рисунок 1.24 - Матрица с 0-эквивалентным разбиением
Для нашего примера анализ 4 подматрицы показывает,
что в состояниях а2, а4, а8 автомат может прочитать символы
а и с, а в состояниях а3, а5, а6, а7 – символ b. Это означает,
что указанные группы состояний не эквивалентны друг дру-
гу, а состояния а2, а4, а8 можно выделить в
группу эквива-
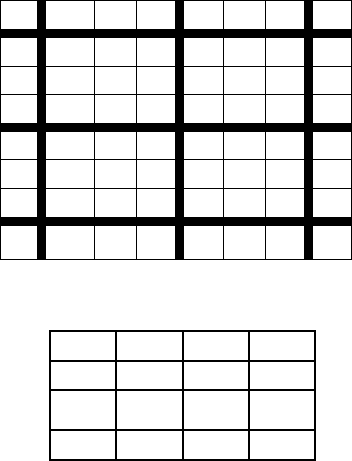
лентности. Затем нужно построить новую матрицу перехо-
дов, объединив эквивалентные состояния в группы (рисунок
1.25).
a
1
a
2
a
4
a
8
a
3
a
5
a
6
a
7
a
1
a b
a
2
c a
a
4
c a a
a
8
c a
a
3
a b
a
5
a b
a
6
a b
a
7
a b
Рисунок 1.25 - Матрица с 1-эквивалентным разбиением
В новой матрице отделим группы эквивалентных со-
стояний горизонтальными и вертикальными линиями. Полу-
чим 9 подматриц. Если минимальный автомат построен, то в
каждой подматрице в строках один и тот же набор символов,
либо они тсутствуют. Не удовлетворяют этому условию под-
матрицы 8 и 9, анализ которых показывает, что
состояние а5
не эквивалентно остальным состояниям своей группы, а зна-
чит, его нужно вынести в отдельную группу эквивалентно-
сти. Результат разбиения приведен на рисунке 1.26. Анализ
26
подматриц показывает, что получен минимальный автомат.
Он имеет 4 состояния, в каждом из которых читает набор
символов в строках соответствующей подматрицы (см. рису-
нок 1.26).
a
1
a
2
a
4
a
8
a
3
a
6
a
7
a
5
a
1
a b
a
2
с a
a
4
с a a
a
8
с a
a
3
a b
a
6
a b
a
7
a b
a
5
a b
a
1
a
248
a
367
a
5
a
1
a b
a
248
c a
a
367
a b
a
5
a b
Рисунок 1.26 - Матрица с 2-эквивалентным разбиением и
матрица минимального автомата
1.4 Связь между автоматами-распознавателями и ав-
томатными грамматиками
Покажем, что языки, порождаемые автоматными грам-
матиками, совпадают с языками, распознаваемыми конечны-
ми автоматами-распознавателями.
Пусть задана праволинейная грамматика. Рассмотрим
27
алгоритм построения конечного автомата-распознавателя для
порождаемого ею языка.
Каждому нетерминальному символу грамматики поста-
вим в соответствие состояние конечного автомата, добавим
еще одно состояние Q и сделаем его единственным заключи-
тельным состоянием. Состояние, соответствующее аксиоме,
сделаем начальным. Для правила вида а
i
→b а
j
в автомате по-
является команда a
i
b→a
j
, а для правила вида a
i
→b команда
а
i
b→Q.
Для того чтобы по конечному автомату-распознавателю
построить праволинейную грамматику, необходимо каждому
состоянию автомата поставить в соответствие нетерминал
грамматики, причем начальное состояние будет соответство-
вать аксиоме. Команде a
i
b→a
j
соответствует правило a
i
→b
a
j
, если a
j
заключительное состояние,
то добавляем в грамма-
тику правило a
i
→b.
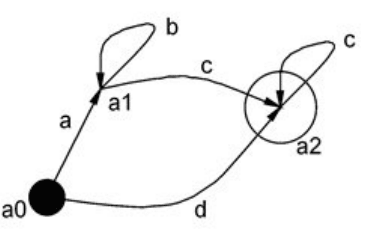
Например, пусть задан автомат-распознаватель, приве-
денный на рисунке 1.27.
Рисунок 1.27
Праволинейная грамматика, порождающая язык, распо-
знаваемый автоматом, строится по графу по выходящим из
каждой вершины дугам и имеет вид:
a
0
→ а a
1
| d a
2
| d
a
1
→ b a
1
| c a
2
| c
28
a
2
→ c a
2
| c
Рассмотрим алгоритм построения конечного автомата-
распознавателя для языка, порождаемого леволинейной
грамматикой. Каждому нетерминальному символу граммати-
ки поставим в соответствие состояние конечного автомата,
состояние, соответствующее аксиоме, сделаем заключитель-
ным, добавим еще одно состояние a
N
и сделаем его началь-
ным состоянием. Для правила a
i
→a
j
b в автомате появляется
команда a
j
b→a
i
, а для правила a
i
→b команда a
N
b →a
i
.
Для построения по автомату леволинейной грамматики
каждому состоянию автомата поставим в соответствие не-
терминал грамматики, добавим нетерминал a
N
, соответст-
вующий аксиоме. Команде a
i
b→a
j
соответствует правило
a
j
→a
i
b, если a
j
заключительное состояние, то добавляем в
грамматику правило a
N
→a
i
b, а если a
i
– начальное состояние,
то добавляем правило a
j
→b.
Рассмотрим пример построения леволинейной грамма-
тики. Пусть задан автомат-распознаватель, приведенный на
рисунке 1.28.
Построение леволинейной грамматики начнем с аксио-
мы, которой в графе не соответствует ни одна вершина. Пра-
вила грамматики для аксиомы записываются после перебора
всех входящих дуг
во все заключительные состояния автома-
та. Для вершин графа также необходимо рассматривать вхо-
дящие дуги. Правило с терминальной правой частью вклю-
чается в грамматику в случае, когда входящая дуга идет из
начальной вершины.
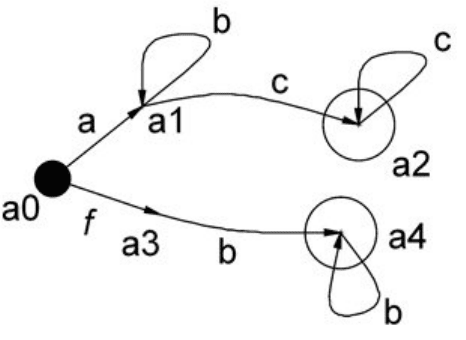
29
Рисунок 1.28
Леволинейная грамматика, порождающая язык, распо-
знаваемый автоматом на рис.1.28, имеет вид:
a
N
→ а
2
c | a
1
c | a
4
b | a
3
b
a
1
→ a
1
b | a
0
a | a
a
2
→ a
1
c | a
2
c
a
3
→ a
0
f | f
a
4
→ a
3
b | a
4
b
a
0
→
Так как для начальной вершины входящие дуги отсутст-
вуют, то символ a
0
грамматики является непродуктивным, а
значит, его можно удалить. Тогда преобразованная грамма-
тика после удаления а
0
будет иметь вид:
a
N
→ а
2
c | a
1
c | a
4
b | a
3
b
a
1
→ a
1
b | a
a
2
→ a
1
c | a
2
c
a
3
→ f
a
4
→ a
3
b | a
4
b
Наличие для конечных автоматов-распознавателей ле-
волинейных и праволинейных грамматик, порождающих
один и тот же регулярный язык, показывает их эквивалент-
30
ность.
2 АВТОМАТЫ С МАГАЗИННОЙ ПАМЯТЬЮ
Рассмотренные автоматы-распознаватели предназначе-
ны для распознавания не всех классов формальных языков, а
только для автоматных (класс 3 по Хомскому). Распознава-
ние более сложных языков осуществляется с помощью авто-
матов более сложных по логике работы, например, КС-языки
распознаются автоматами с магазинной памятью.
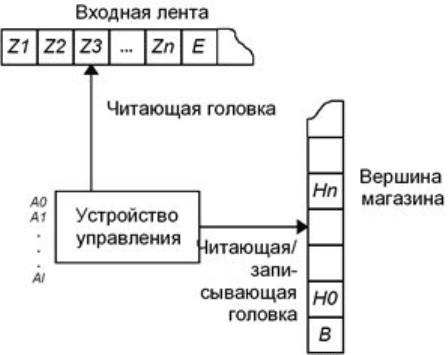
Рассмотрим неформальную
модель автомата с магазин-
ной памятью (МП-автомата). Будем считать, что автомат
имеет в своем составе входную ленту, устройство управления
и вспомогательную ленту, называемой магазином или стеком
(рисунок 2.1).
Рисунок 2.1
Входная лента разделяется на клетки (позиции), в каж-
дой из которых может быть записан символ входного алфа-
вита. При этом
предполагается, что в неиспользуемых клет-
ках входной ленты расположены пустые символы. Вспомога-
тельная лента также разделена на клетки, в которых могут
