Сучкова Л.И. Абстрактный и структурный синтез автоматов
Подождите немного. Документ загружается.

51
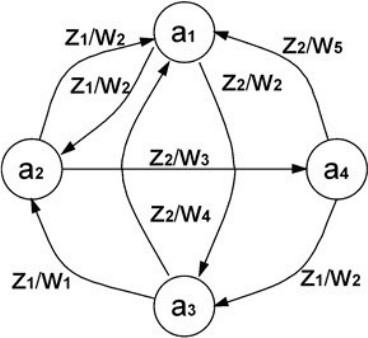
Рисунок 3.7 – Автомат А
Как следует из рис. 3.7, при попадании в состояние а
1
вырабатываются выходные сигналы w
2
, w
4
, w
5
, при попада-
нии в а
2
– w
1
, w
2
, a
3
– w
2
, a
4
– w
3
. Каждой паре «состояние a
i
- выходной сигнал w
j
», который вырабатывается при попа-
дании в это состояние, поставим в соответствие состояние b
k
эквивалентного автомата Мура с тем же выходным сигна-
лом w
j
: b
1
= (a
1
,w
2
), b
2
=(a
1
, w
4
), b
3
=(a
1
,w
5
), b
4
=(a
2
,w
1
),
b
5
=(a
2
,w
2
), b
6
=(a
3
, w
2
), b
7
=(a
4
,w
3
). Каждое состояние a
i
автома-
та Мили порождает некоторое множество A
i
состояний экви-
валентного автомата Мура: A
1
= {b
1
,b
2
,b
3
}, A
2
= {b
4
,b
5
}, A
3
=
{b
6
}, A
4
= {b
7
}, причем количество элементов в каждом A
i
определяется количеством различных выходных символов на
входящих дугах в a
i
. В эквивалентном автомате Мура для
нашего примера количество состояний равно 7. Для построе-
ния графа автомата Мура поступаем следующим образом.
Так как в автомате Мили есть переход из состояния а
1
в
состояние а
2
под действием сигнала z
1
с выдачей w
2
, то из
множества состояний A
1
= {b
1
, b
2
, b
3
}, порождаемых состоя-
нием а
1
автомата Мили в автомате Мура должен быть пере-
ход в состояния (a
2
,w
2
)=b
5
под действием z
1
.
Так как в автомате Мили есть переход из состояния а
1
в
52
состояние а
3
под действием сигнала z
2
с выдачей w
2
, то из
множества состояний A
1
= {b
1
, b
2
, b
3
} должен быть переход в
состояние (a
3
, w
2
) = b
6
под действием сигнала z
2
.
Иначе говоря, для каждого состояния a
i
графа автомата
Мили анализируем выходящие дуги и строим переходы из
состояний множества Аi в состояния, определяемые парой
«состояние после перехода-выходной сигнал». Выходные
сигналы для bk определяются по паре «состояние a
i
- выход-
ной сигнал w
j
». Так, для b
1
выходной сигнал w
2
, для b
2
– w
4
и
т.д.
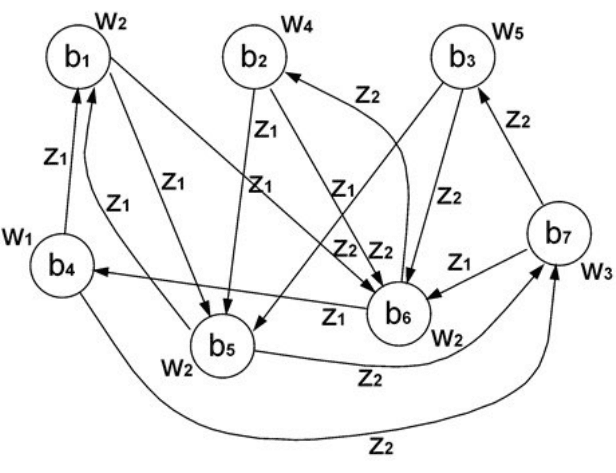
Граф эквивалентного автомата Мура представлен на ри-
сунке 3.8.
53
Рисунок 3.8 – Автомат Мура, эквивалентный автомату
А
3.2.3 Минимизация преобразователей. Метод Ауфен-
кампа и Хона
Рассмотрим метод минимизации полностью определен-
ных автоматов, предложенный Ауфенкампом и Хоном.
Основная идея этого метода, так же, как и для автома-
тов-распознавателей, заключается в разбиении всех состоя-
ний исходного абстрактного автомата на попарно непересе-
кающиеся классы
эквивалентных состояний и замене каждо-
го класса эквивалентности одним состоянием. Получающий-
ся в результате минимальный автомат имеет столько состоя-
ний, на сколько классов эквивалентности разбиваются со-
стояния исходного автомата.
Для автоматов Мили первоначально выделяются 1-
эквивалентные состояния, в которых реакции автомата в этих
состояниях на всевозможные входные слова совпадают. Объ-
единение
всех 1-эквивалентных состояний абстрактного ав-
томата образует 1-класс эквивалентности. Затем классы 1-
эквивалентных состояний разбиваются на классы 2-
эквивалентных состояний и т.д. Если для некоторого i раз-
биения состояний автомата на ( i +1) - классы совпадает с
разбиением на i-классы, то оно является требуемым разбие-
нием на классы эквивалентности, при этом такое разбиение
может быть получено
за конечное число шагов.
При минимизации полностью определенных автоматов
Мура вводится понятие 0-эквивалентности состояний и раз-
биение множества состояний на 0-эквивалентные классы: к
такому классу относятся одинаково отмеченные состояния
автомата Мура.Если два 0-эквивалентных состояния любым
входным сигналом переводятся в два 0-эквивалентных со-
стояния, то они называются 1-эквивалентными. Все даль-
нейшие классы эквивалентности состояний для автомата Му-
ра определяются аналогично приведенному для автоматов
54
Мили.
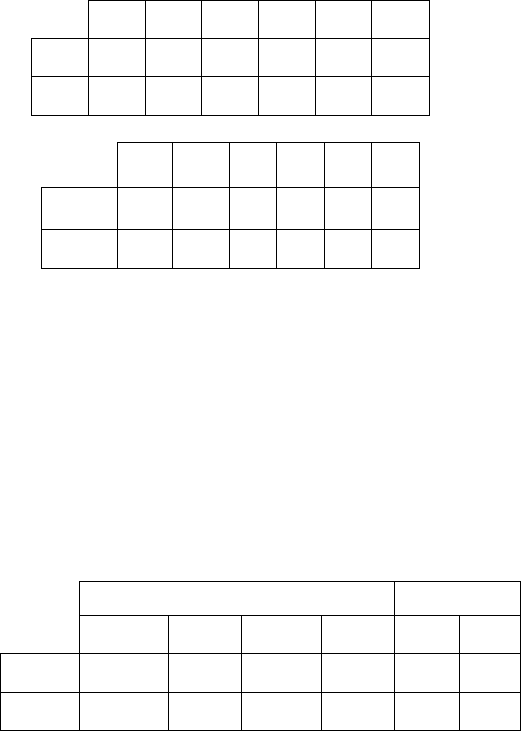
Рассмотрим пример минимизации автомата Мили Б, за-
данного таблицами переходов и выходов на рисунке 3.9.
a
1
a
2
a
3
a
4
a
5
a
6
z
1
a
3
a
4
a
3
a
4
a
5
a
6
z
2
a
5
a
6
a
5
a
6
a
1
a
2
a
1
a
2
a
3
a
4
a
5
a
6
z
1
w
1
w
1
w
1
w
1
w
1
w
1
z
2
w
1
w
1
w
2
w
2
w
1
w
1
Рисунок 3.9 – Таблицы переходов и выходов автомата
Мили Б
Из таблицы выходов получаем разбиение на 1-классы
эквивалентности π
1
, объединяя в эквивалентные классы B
i
состояния с одинаковыми столбцами:
π
1
= {B
1
, B
2
}; B
1
= {a
1
, a
2
, a
5
, a
6
}; B
2
= {a
3
, a
4
}
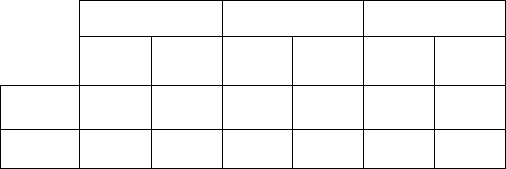
Для получения 2-эквивалентных состояний строим
таблицу 1-разбиения (рисунок 3.10), заменяя в таблице пе-
реходов состояние ai тем классом эквивалентности (B1 или
B2), которому принадлежит состояние.
B
1
B
2
a
1
a
2
a
5
a
6
a
3
a
4
z
1
B
2
B
2
B
1
B
1
B
2
B
2
z
2
B
1
B
1
B
1
B
1
B
1
B
1
Рисунок 3.10 – Таблица 1-разбиения
55
Из полученной таблицы 1-разбиения получаем 2-классы
эквивалентности C
i
и разбиение π
2
= {C
1
, C
2
, C
3
}, где
С
1
={a
1
,a
2
}, C
2
={a
5
,a
6
}, C
3
={a
3
,a
4
}. Сравнивая π
2
и π
1
, отмеча-
ем, что эти разбиения отличаются друг от друга. Поэтому
аналогично строим таблицу 2-разбиения (рисунок 3.11),
опять заменяя в таблице переходов состояния a
i
соответст-
вующими классами эквивалентности C
i
.
C
1
C
1
C
1
a
1
a
2
a
5
a
6
a
3
a
4
Z
1
C
3
C
3
C
2
C
2
C
3
C
3
Z
2
C
2
C
2
C
1
C
1
C
2
C
2
Рисунок 3.11 – Таблица 2-разбиения
Из полученной таблицы 2-разбиения получаем 3-классы
эквивалентности D
i
и разбиение π
3
={ D1, D2, D3}, где D1=
{a1, a2}, D2
= {a5, a6}, D3
= {a3, a4}.
Сравнивая π
3
и π
2
, замечаем, что D
1
= C
1
, D
2
= C
2
, D
3
=
C
3
, π
3
= π
2
. Следовательно, получили минимальный авто-
мат. Так как в результирующем разбиении всего три класса
эквивалентности, то минимальный автомат будет содержать
всего три состояния. Выбираем из каждого класса D
i
по од-
ному состоянию и получаем множество состояний A' мини-
мального автомата. Пусть, например, A'={a1, a4, a5}. Для по-
лучения минимального автомата из первоначальных таблиц
переходов и
выходов (рисунок 3.9) вычеркиваем столбцы,
соответствующие "лишним состояниям" a2, a3, a6. В резуль-
тате получается минимальный автомат Мили, эквивалентный
исходному автомату (рисунок 3.12).

56
а) б)
Рисунок 3.12 – Таблицы переходов (а) и выходов (б) ми-
нимального автомата
Минимизацией числа внутренних состояний автомата
заканчивается этап абстрактного синтеза.
3.3 Тестирование абстрактных автоматов
В основе тестирования (контроля и диагностики) конеч-
ных абстрактных автоматов лежит теория экспериментов с
автоматами. Эксперимент над автоматами заключается в
следующем:
• на
вход автомата подается последовательность вход-
ных символов,
• фиксируется реакция автомата (последовательность
выходных символов), и в результате анализа поведения авто-
мата делается заключение о том, в каком состоянии находит-
ся автомат и каков закон его функционирования.
При этом предполагается, что исследователю известна
таблица переходов/выходов исправного автомата и все вари-
анты
возможных таблиц, характеризующих неисправности
автомата.
Пусть автомат A при любой возможной неисправности
i=1,…,k превращается в один из автоматов {A
1
,A
2
,…,A
k
}={A
i
|
i=1,…,k}. Тогда задача контроля данного автомата X, кото-
рый должен работать как автомат A, заключается в выясне-
нии соотношения X=A. Если X≠A,то X∈{A
i
| i=1,…,k}. Задача
диагностики заключается в определении i, при котором X=A
i
.
Пример
. Автомат A задан таблицей:
a
1
a
4
a
5
Z
1
a
4
a
4
a
5
Z
2
a
5
a
5
a
1

57
Используем упрощенную запись, содержащую только
индексы состояний, входных и выходных символов:
Предположим, что возможны две неисправности, поро-
ждающие автоматы A
1
и A
2
соответственно:
Автомат А
1
Автомат А
2
Клетки таблиц для A
1
и A
2
, отличающиеся от A, под-
черкнуты. Рассмотрим объединение B автоматов A, A
1
и A
2
:
1 2 3 1
1
2
1
3
1
1
2
2
2
3
2

58
1
2
2/1 3/2 1/2 2
1
/1 3
1
/1 1
1
/2 2
2
/1 3
2
/2 1
2
/1
3/2 1/1 2/1 3
1
/2 1
1
/1 2
1
/1 3
2
/2 1
2
/1 2
2
/1
Проведем установочный эксперимент с автоматом B,
т.е. такой эксперимент, который позволит по выходной по-
следовательности однозначно определить состояние, в кото-
ром оказался автомат, причем неизвестное начальное состоя-
ние может быть любым из множества {1, 2, 3, 1
1
, 2
1
, 3
1
, 1
2
, 2
2
,
3
2
}. Для автомата B одной из возможных входных устано-
вочных последовательностей является z
1
z
1
z
1
z
2
z
2
, или 11122
(таблица 3.10).
Таблица 3.10 – Реакция B на установочную последователь-
ность
Начальное
состояние
Реакция автомата
Конечное со-
стояние
1
2
3
1
1
2
1
3
1
1
2
2
2
3
2
12221
22112
21211
11221
12112
21111
12121
21112
11211
2
3
1
2
1
3
1
1
1
2
2
3
2
1
2
В данном примере реакция автомата В на входную по-
следовательность 11122 позволяет однозначно установить
начальное и конечное состояния автомата, т.е. последова-
тельность 11122 является установочной.
Эта последовательность позволяет установить неис-
правность автомата A, т.е. осуществить диагностику авто-
мата, т.е. является ли испытуемый автомат X автоматом A,
A
1
или
A
2
.
Для контроля автомата, т.е. для определения истин-
ности утверждения, что X=A, можно использовать более ко-

59
роткую входную последовательность z
1
z
1
z
1
, или 111. Пред-
полагается, что множество возможных неисправностей то же,
что и в вышеприведенном примере (таблица 3.11).
Таблица 3.11 – Реакция B на контролирующую последова-
тельность
Начальное
состояние
Реакция автомата
Результат
1
2
3
1
1
2
1
3
1
1
2
2
2
3
2
122
22-
212
11-
121
211
121
211
11-
исправен
исправен
неисправен
неисправен
неисправен
неисправен
неисправен
неисправен
неисправен
Из таблицы 3.10 видно, что входные последовательно-
сти можно в отдельных случаях прерывать, т.к. в данном
примере не обязательно подавать 3 входных символа, в от-
дельных случаях достаточно двух.
Рассмотрим, каким образом строятся установочные по-
следовательности. Строим дерево, корнем которого будет
являться узел с индексами всех состояний автомата. Напри-
мер, для
автомата A в корне дерева будет множество {1,2,3}.
Затем строим вершины-потомки для корня. Их и ведущих к
ним от корня дуг будет столько, сколько различных пар
«входной сигнал / выходной сигнал» существует для задан-
ного автомата. Для автомата А возможно 4 пары
«вход/выход»: 1/1, 1/2, 2/1, 2/2, которыми пометим соответ-
ствующие дуги, ведущие к вершинам-потомкам
(рисунок
3.13).
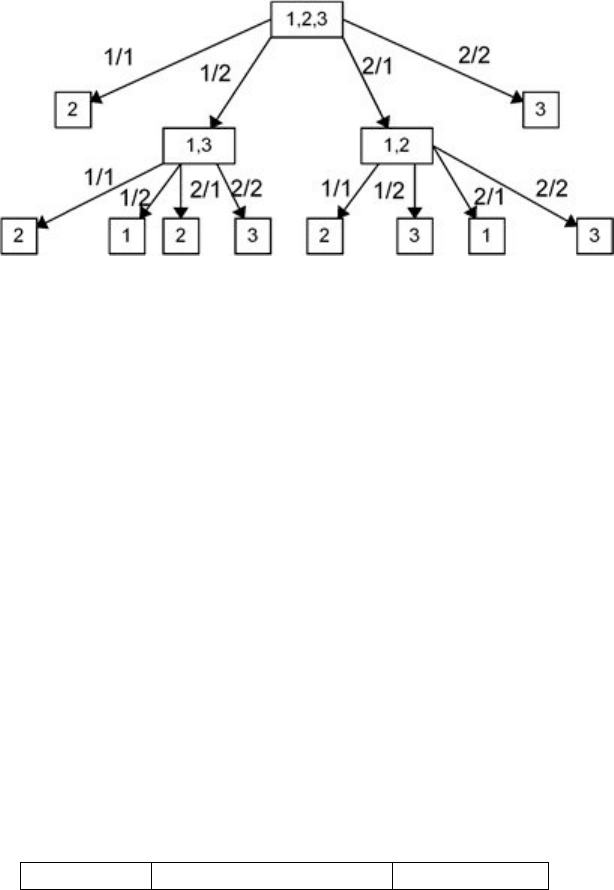
60
Рисунок 3.13 – Дерево для построения установочной по-
следовательности
Для формирования самих вершин-потомков использует-
ся совмещенная таблица переходов и выходов. Считаем, что
состояния в корне являются текущими. Тогда для дуги 1/1,
соответствующей входу 1 и выходу 1, из первой строки таб-
лицы (вход равен 1) видно, что для всех состояний 1, 2 и 3
(столбцы таблицы переходов
и выходов) существует переход
в единственное состояние 2, когда автомат выдает 1. Номер
состояния запишем в вершину-потомок для дуги 1/1. Для ду-
ги 1/2 из первой строки таблицы смотрим, в какие состояния
из 1,2 и 3 осуществляется переход при выдаче выхода 2. Это
состояния 1 и 3. Дальнейшие построения осуществляются
аналогично. Завершается построение дерева, когда в каждом
узле будет
записан индекс единственного состояния.
Тогда для автомата А входная цепочка, приводящая к
достижению вершины-листа дерева из корня, будет являться
установочной. Так, цепочка 11 является установочной, что
демонстрируется таблицей 3.12.
Таблица 3.12 – Реакция А на установочную последователь-
ность 11
Начальное Реакция автомата Конечное со-
