Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

191

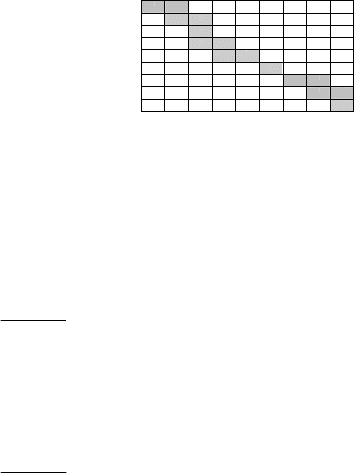
Рис. 1. Пример структуры матрицы Якоби системы

Вычисление вспомогательных векторов в методе Розенброка [3]

может эффективно производиться на параллельных вычислительных

комплексах с общей памятью. Степень параллелизма определяется

количеством стадий метода. Обращение матрицы

B, похожей по

структуре на приведенную на рис. 1, будем проводить итерационным

методом, записанным в канонической форме:

()

, ,..., ,

nm m m

ii i ii

−

=−

C δ Yk k Bk

где

diag

=CB

— блочно-диагональная часть матрицы B

, ς —

итерационный параметр.

Тогда итерационный метод может быть записан в виде

iijjijjii

−−

−

⎛⎞

−

=++−

⎜⎟

⎝⎠

∑∑

CfY k J k k

τβτμ

или

()

mmnmm

iiii ijjijj

−−

+−

⎛⎞

=− + + +

⎜⎟

⎝⎠

∑∑

kEDkCfY k Jk

ςςτ βτμ

Матрица

имеет блочно-трехдиагональный вид

22 22

000

−

−−

−

⎛⎞

⎜⎟

⎝⎠

ECB

CB E CB

CB E

KKKKK

с единичными диагональными блоками.

В случае, если в рассматриваемой задаче скорость течения не

меняет знак, то либо все блоки под диагональю, либо блоки над

диагональю нулевые. Тогда при выборе итерационного параметра

0 < ζ <1 все собственные числа матрицы

(

)

−ED

лежат внутри

единичного круга, таким образом выполнено достаточное условие

192

сходимости итерационного метода. Скорость сходимости в этом

случае максимальна при ζ = 1.

Если скорость переноса может менять знак или схема строится для

системы уравнений типа реакция–диффузия–конвекция, то

примыкающие к главной диагонали блоки в матрице будут

ненулевыми. В этом случае сходимость метода обеспечивается

совместным выбором шага интегрирования по времени τ

итерационного параметра ζ.

Действительно, при сколь угодно малых шагах интегрирования

системы (1) матрица

(

)

−ED

слабо отличается от единичной, так как

все блоки, расположенные вне главной диагонали, прямо

пропорциональны τ. Итерационный метод сходится при ζ = 1.

Увеличение шага интегрирования приводит к тому, что оценка

собственных чисел матрицы, отвечающей за изменение невязки на

итерациях, становится трудоемкой, а априорная оценка в зависимости

от шага — практически невозможной. Тем не

менее, при надлежащем

выборе итерационного параметра ζ возможно обеспечить сходимость

итерационного процесса.

Для тестирования итерационного метода была выбрана модельная

система из 11 связанных осцилляторов Ван-Дер-Поля. Результаты

расчетов по методу Розенброка с вычислением собственных векторов

путем прямого решения линейных систем и с использованием

описанного итерационного метода совпадают с точностью до

машинного

ε.

В многочисленных работах, например, [4, 5] было показано, что

вычисление вспомогательных векторов в методе Розенброка может

эффективно производиться на параллельных вычислительных

комплексах с общей памятью. При этом степень параллелизма

определяется количеством стадий метода.

Параллельная реализация метода Розенброка на машинах с

распределенной памятью неэффективна из-за значительного объема

информации, которой должны обмениваться

между собой процессоры.

Если не использовать схемы повышенного порядка аппроксимации

по пространству, матрица Якоби

J и соответствующие матрицы B

для

вычисления вспомогательных векторов получаются блочно-

диагональными, причем каждый блок соответствует одной

пространственной точке. При таком подходе эффективным становится

распараллеливание по пространству, которое может быть реализовано

как на машинах с общей памятью, так и на комплексах с

193

распределенной памятью, поскольку система кинетических уравнений

расщепляется на совокупность независимых систем ОДУ более

низкого порядка для каждой точки разностной сетки. Но такое

упрощение приводит к уменьшению порядка аппроксимации

разностных уравнений по пространственной переменной.

Распараллеливание предлагаемого подхода, естественно, зависит

от архитектуры вычислительного комплекса, на котором он будет

реализовываться. Для параллельных вычислительных

систем с общей

памятью пространственное распараллеливание ограниченно числом

имеющихся процессоров.

Наибольший практический интерес представляет

распараллеливание на системах с распределенной памятью, которое

осложняется структурой матрицы Якоби, так как большой объем

обменов информацией при точном вычислении вспомогательных

векторов сводит на нет весь эффект от ускорения вычислений.

Выходом из сложившейся ситуации является приближенное

вычисление

вспомогательных векторов на отдельных узлах комплекса.

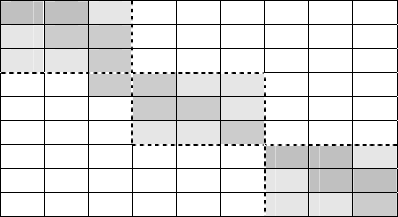
Рис. 2. Зоны ответственности узлов вычислительного комплекса для матрицы

в методе Розенброка (выделены светлым серым и пунктирными границами)

Разделим всю область интегрирования по пространству на зоны

ответственности по количеству узлов в параллельной машине.

Соответствующие зонам ответственности части матрицы в реализации

метода Розенброка изображены на рис. 2. Это области, в которых

процессоры будут вычислять значения соответствующих частей

вектора

Как показано на рисунке, расчет значений только по областям

ответственности ошибочен, так как он может не захватывать все

ненулевые блоки матрицы. Поэтому расчет следует вести в

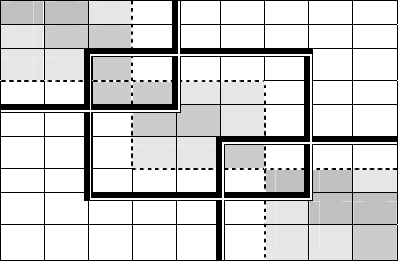
194

расширенных областях (работа с перекрытием), а полученные

значения брать только в зонах ответственности (см. рис. 3).

Очевидно, что точное решение системы ОДУ (1) можно получить

лишь в случае использования полной матрицы. Тем не менее, в рамках

используемого подхода расщепления по процессам такой метод

декомпозиции задачи представляется оправданным. При учете лишь

процессов переноса

область влияния дифференциального уравнения в

частных производных представляет собой одну точку — пересечение

характеристики, проведенной из рассчитываемого узла сетки, с

шаблоном разностной схемы. Учет правой части с весами является ее

линейной интерполяцией на предыдущем слое по времени. Принятая

схема разбиения по зонам ответственности позволяет проводить такую

интерполяцию, при этом при обмене насчитанными

значениями на

верхнем временном слое для передачи значений, которые

рассчитываются именно в областях перекрытия, необходимо

учитывать направление характеристик. Данный алгоритм расчета в

областях перекрытия позволит обеспечить порядок аппроксимации по

пространству не ниже первого, а внутри каждой зоны ответственности

– и более высокий.

Рис. 3. Зоны расчета узлов

На вычислительных комплексах с гибридной памятью (например,

кластер из SMP или multi-core узлов) возможно расширение зоны

ответственности каждого узла пропорционально числу процессоров.

При этом уменьшается число зон перекрытия, соответственно можно

ожидать уменьшения погрешности вычислений, связанных с

используемым способом декомпозиции матрицы.

195

Описанный подход очевидным образом обобщается на случаи

построения схем более высокого порядка аппроксимации для

уравнений «диффузия-конвекция», или на случай систем уравнений

«реакция-диффузия-конвекция» или «реакция-диффузия».

В настоящее время проводятся тестовые расчеты для оценки

погрешностей метода при решении модельных задач.

Литература

1. Толстых А.И. Компактные разностные схемы и их

применение в задачах аэрогидродинамики. — М.: Наука, 1990.

— 230 с.

Магомедов М.–К. М. , Холодов А. С. Сеточно-

характеристические численные методы. — М.: Наука, 1988. —

290 с.

Хайрер Э., Ваннер Г. Решение обыкновенных

дифференциальных уравнений. Жесткие и дифференциально–

алгебраические задачи. — М.: Мир, 1999. — 685 с.

Botchev M.A., Verwer J.G. A new approximate matrix

factorization for implicit time integration in air pollution modeling

// J. of Comput. and Appl. Math., Vol. 157, 2003. pp. 309–327.

Voss D.A., Khaliq A.Q.M. Parallel Rosenbrock methods for

chemical systems // Computers and Chemistry, 25, 2001. pp. 101–

107.

АНАЛИЗ ХАРАКТЕРИСТИК ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ

ПУТЕМ МОДЕЛИРОВАНИЯ

В.А. Кичкидов, Р.А. Бикташев

Пензенский государственный университет

В предыдущих выпусках данного сборника публиковались наши

статьи, посвященные разработке стохастических сетевых моделей

массового обслуживания, с помощью которых возможно проводить

анализ архитектур вычислительных систем. Данный метод был

проиллюстрирован анализом 4-процессорных систем на базе

архитектур IA32 и AA64, а именно была проанализирована работа

процессоров с подсистемой памяти. Данные архитектуры предлагают

принципиально

разные способы построения мультипроцессорной

системы, и наибольшая разница ощутима именно в работе с памятью.

196

Однако разработанные модели не учитывают особенности

функционирования современной памяти, работающей в пакетном

режиме. Такая память в разных фазах обслуживания процессорного

запроса ведет себя по-разному. В начальной, самой длительной фазе

происходит чтение строки памяти и передача первого слова в один из

регистров процессора и кэш. Другие фазы, связанные с пересылкой

кэш оставшейся части пакета, работают значительно быстрее:

происходит только передача, причем по одному слову в каждом

шинном цикле.

В данной статье приведен простой пример сравнения

одноканального и двухканального режима работы с оперативной

памятью современного процессора персональной ЭВМ с

использованием уточненных моделей.

В качестве аппаратной основы принята система с общей шиной

работающая по технологии Intel Quad Pumped Bus. Такая шина за 1

такт может передать до 4 готовых к передаче 64-разрядных слов.

Частоту работы шины возьмем равной 200МГц (800 МГц QPB). Такая

шина обработает за 5 нс от 1 до 4 64-битных порций данных. В

процессе работы процессор отправляет заявки в память с частотой,

положим, 0.1 заявка/нс. Такой поток возможен при активной

работе

современного процессора с памятью с учетом низкого процента кэш-

промахов.

Используем в расчетах небуферизированные модули памяти DDR

РС-3200 частотой 200 МГц и таймингами 3-3-3. Учитывая 3 различных

варианта доступа к памяти (случайный, псевдослучайный и

последовательный) и зная вероятности их возникновения, можно

высчитать, что первая порция данных будет предоставлена модулем

памяти в среднем через 25 нс

. Следующие 3 порции будут

предоставлены с промежутком в 5 нс – 1 такт модуля памяти. Работой

контроллера памяти в данном случае пренебрегли в целях разгрузки

модели. Также пренебрегаем сторонними нагрузками системной

шины.

197

ОШ

ОПф2

ОПф3

ОПф1

ОПф4

ЦП

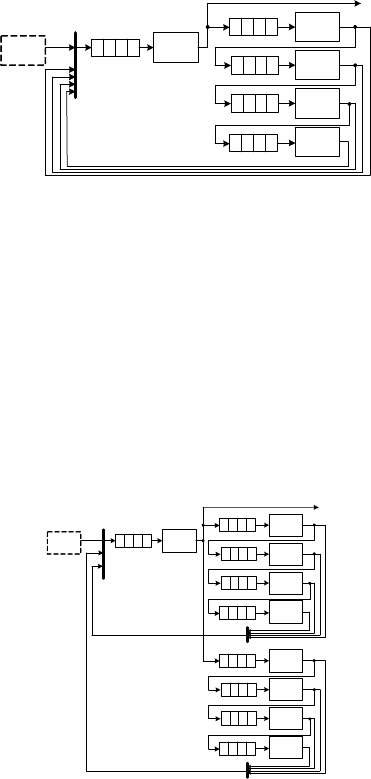
Рис. 1. Модель ВС с одноканальным режимом работы памяти. Модель А

В модели типа А фазы 1 - 4 (рис.1) представляют собой задержки

выдачи данных модулем оперативной памяти, описанные выше (25-5-

5-5 нс). Процессор (ЦП) генерирует заявки, которые проходят через

общую шину (ОШ), через все фазы ОП, снова через ОШ и

возвращаются в ЦП (в данном случае уничтожаются на терминаторе

Т). Заявки с каждой фазы ОП

перемещаются как на следующую по

порядку фазу обслуживания, так и на четырехканальную ОШ. Этим

моделируется работа технологии QPB.

Модель В (рис.2) отличается от А лишь количеством модулей и

каналов памяти. Заявка попадает в модуль памяти 1 или 2 с равной

вероятностью, соответствующие фазы модулей занимают одинаковое

количество времени.

ОШ

ОП1ф2

ОП1ф3

ОП1ф1

ОП1ф4

ЦП

ОП2ф2

ОП2ф3

ОП2ф1

ОП2ф4

Рис. 2. Модель ВС с двухканальным режимом работы памяти. Модель В

Результаты расчетов представлены в таблице 1.

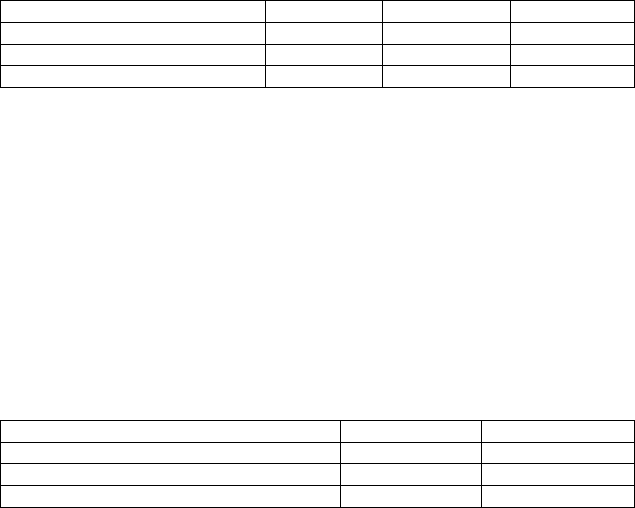
198

1 канал (нс) 2 канала (нс) Δ

Время обработки заявки 24 16.5 -31%

Пребывание заявки в очередях 10.5 2.9 -72%

Загрузка общей шины 0.16 0.2 +25%

Таблица 1. Результаты расчета моделей систем с одним процессором

Итак, введение второго канала памяти уменьшает время работы

процессора с памятью на треть в среднем, сводя время простоя заявок

к минимуму. Но при этом на четверть увеличивается загрузка общей

шины. Проведенное моделирование подкрепило количественно вполне

предсказуемый результат.

Данная модель пригодна и для моделирования памяти,

работающей в многопроцессорной системе. Причем при увеличении

количества процессоров изменение в модели затрагивает лишь

входной поток заявок. Так, в двухпроцессорной системе он

увеличивается в 2 раза, становясь равным 0.2 заявки/нс. Это еще раз

показывает высокую гибкость подобных моделей. Результаты

вычислений представлены в таблице 2.

1 канал (нс) 2 канала (нс)

Время обработки заявки 107.5 19.5

Пребывание заявки в очередях 93.9 5.6

Загрузка общей шины 0.23 0.23

Таблица 2. Результаты расчета моделей систем с двумя процессорами

Здесь наблюдается специфика систем массового обслуживания

открытого типа. При столь обильном входном потоке заявок в модели

А “ОПф1” оказывается близкой к перегрузке. Происходит

лавинообразный рост задержек, стремящийся к бесконечности.

Сравнивать в данном случае расчеты моделей А и В нельзя.

Но и эти результаты являются полезными. Столь высокие цифры

свидетельствуют о несоответствии

производительности системы

запрашивающей и обрабатывающей систем. В данном случае по

результатам расчетов можно сделать вывод, что одноканальный режим

работы с памятью с точки зрения соответствия производительностей

компонентов неприменим в двухпроцессорной системе, производящей

работу с активным использованием памяти (согласно условию задачи).

В нашем распоряжении в данный момент находятся несколько

сформированных моделей,

посвященных, в основном, подсистеме

памяти вычислительных систем. На основе данных моделей создается

методическое пособие для выполнения лабораторных работ по курсу

199

“Архитектура вычислительных систем”. Авторы работы с

благодарностью примут помощь и сотрудничество в дальнейшей

разработке данного вопроса.

Литература

1. Кичкидов В.А., Бикташев Р.А. Анализ работы с памятью

процессоров современных персональных ЭВМ и

мультипроцессоров на их основе. - "Технологии Microsoft в

теории и практике программирования" - материалы

конференции под ред. Р.Г. Стронгина. Нижний Новгород.

Изд-во Нижегородского университета. 2006 г. 338с.

Бикташев Р.А., Князьков В.С. Многопроцессорные системы:

архитектура, топология, анализ производительности: Учебное

пособие. - Пенза: Пенз. гос. ун-т. 2004 г.

ОСОБЕННОСТИ РАСПАРАЛЛЕЛИВАНИЯ АЛГОРИТМОВ

ОБУЧЕНИЯ МАШИН ОПОРНЫХ ВЕКТОРОВ

В.Ю. Колеватов, Е.В. Котельников

Вятский государственный гуманитарный университет

Машины опорных векторов в задачах классификации

Задача классификации заключается в распределении множества

объектов по нескольким заданным классам на основе общих

признаков. В литературе часто употребляются синонимы термина

«классификация», например, «распознавание образов» (Pattern

Recognition) или «категоризация текстов» (Text Categorization) в

зависимости от прикладной области.

Для формальной постановки задачи классификации будем считать,

что имеется всего два класса (задачу многоклассовой классификации

можно свести

к последовательности двухклассовых задач). Пусть

заданы:

множество Х обучающих объектов, заданных векторами

признаков: X={

, X

, ..., X

}, Х⊂R

(Х является подмножеством

евклидова пространства размерности d);

множество Y ответов для обучающих объектов: Y={y

, y

, ..., y

∈{–1, +1}.

200

Задача классификации состоит в построении алгоритма, который

каждому вектору

сопоставляет правильный ответ y

. В дальнейшем

построенный алгоритм должен применяться для классификации

произвольного вектора

Х, о классовой принадлежности которого

ничего не известно.

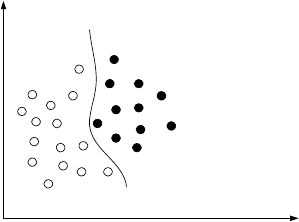
Приведем геометрическую интерпретацию задачи. На плоскости

заданы два множества объектов. Требуется найти уравнение линии

f(x

)=0, разделяющей оба множества (рис. 1). При этом для всех

заштрихованных кружков-объектов должно выполняться неравенство

f(x

)>0, а для всех пустых – неравенство f(x

)<0.

f(x

)=0

f(x

)>0f(x

)<0

Рис. 1. Геометрическая интерпретация задачи классификации

Суть метода опорных векторов (Support Vector Machine, SVM –

машина опорных векторов) удобно проиллюстрировать при помощи

геометрической интерпретации задачи классификации. Пусть два

множества точек можно разделить плоскостью (в двумерном

пространстве – прямой). Тогда таких плоскостей будет бесконечное

множество (рис. 2а).