Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

221

Обозначим через w(i), i ∈ V – весовую функцию, ставящую в

соответствие ветвям количество арифметических и логических

операций, выполняемых ими. На множестве ребер определим

функции, характеризующие объемы данных d(i, j) и средние размеры

сообщений m(i, j), передаваемых между ветвями за время выполнения

программы ([d(i, j)] = байт, [m(

i, j)] = байт, i, j ∈ V).

Пусть G

= (V

, E

) – граф распределенной ВС, V

= {1, 2, …, N} –

множество процессорных ядер, E

= V

× V

– множество логических

каналов связи (граф полный).

На множестве процессорных ядер задана весовая функция ω(c),

c ∈ V

, ставящая в соответствие процессорным ядрам их

производительности ([ω(c)] = FLOPS). На множестве ребер E

заданы

функции l(c

, c

, m) и b(c

, c

, m) – латентность и пропускная

способность канала связи между процессорными ядрами c

, c

∈ V

при

передаче сообщений размером m байт ([l(c

, c

, m)] = c.,

[b(c

, c

, m)] = бит/c.).

Требуется найти распределение параллельных ветвей (процессов)

по процессорным ядрам с целью минимизации ожидаемого времени

выполнения программы.

Иначе, необходимо построить инъективную функцию f: V → Vs,

ставящую в соответствие ветвям параллельной программы

процессорные ядра распределенной ВС. Требуется найти x

},:{

sij

VjVixX

∈

∈= ,

⎩

⎨

⎧

иначе.,0

;)( если,1 jif

Качество назначения ветвей параллельной программы на

процессорные ядра будем оценивать ожидаемым временем ее

выполнения.

Время выполнения

′

параллельной программы определяется

максимальным из времен выполнения ее ветвей. Время

′

выполнения

ветви

Vi ∈ параллельной программы складывается из времени

выполнения арифметических и логических операций процессорным

ядром и времени взаимодействия со смежными ветвями:

}{max}{max

comm

comp

tttt +=

′

∈∈

, где

∑

⋅=

comp

)(

- время

выполнения арифметических и логических операций процессорным

ядром, на которое назначена ветвь,

222

()

∑∑∑

===

⋅⋅=

jqip

comm

qpjitxxt

111

,,,

- время взаимодействия со

смежными ветвями.

Для оценки времени t(i, j, p, q) передачи сообщения между двумя

процессорными ядрам p, q

∈ V

, на которые назначены ветви i, j ∈ V ,

может быть использована модифицированная модель Хокни

(Hockney) [2]:

()

),(,,

),(

)),(,,(,,,

jimqpb

jid

jim

jid

jimqplqpjit +⋅=

Учитывая дополнительные ограничения, накладываемые

требованием инъективности функции f, получаем задачу (1) – (4)

оптимального назначения ветвей параллельной программы на

процессорные ядра распределенной ВС с целью минимизации времени

ее выполнения.

()

)(

1111

min,,,

)(

max)(

jqip

qpjitxx

xXT →

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⋅⋅+⋅=

∑∑∑∑

====

∈

при ограничениях:

(1)

∑

Mi ,...,2,1

(2)

∑

≤

Nj ,...,2,1

(3)

}1,0{∈

VjVi

∈

, .

(4)

Ограничения (2), (4) гарантируют назначение каждой ветви

параллельной программы на единственное процессорное ядро,

ограничения (3) обеспечивают назначение на ядро не более одной

ветви.

Для решения поставленной задачи разработана группа алгоритмов,

позволяющих за приемлемое время получать субоптимальные

распределения параллельных ветвей по процессорным ядрам. Первая

группа алгоритмов относится к классу вероятностных алгоритмов

локальной оптимизации [4], вторая основана

на алгоритмах обхода

графов и их разбиении.

223

Пакет оптимизации выполнения MPI-программ

В Центре параллельных вычислительных технологий Сибирского

государственного университета телекоммуникаций и информатики

(ЦПВТ СибГУТИ) ведется разработка программного пакета

MPITaskMap оптимизации выполнения MPI-программ на

(мульти)кластерых ВС.

В пакет входят средства анализа протоколов выполнения MPI-

программ и построения их информационных графов, средства оценки

производительности каналов связи коммуникационных сред, а также

модуль субоптимального распределения

ветвей параллельных

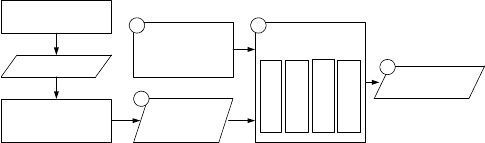
программ по процессорным ядрам системы. На рисунке приведена

структура пакета.

OTF Trace

MPI-Программа

VampirTrace

otfstat

Анализатор протоколов

выполнения MPI-программ

Информационны й

граф программы

commperf

Модуль оценки

производительности

каналов связи

Распределение

ветвей

(скрипт mpiexec)

taskmap

Модуль распределения

ветвей

PTA_PSA

(Simulated Annealing)

Chain Monte-Carlo

ME TI S

0 2

PTA_GT

Рис. 1. Функциональная структура программного пакета MPITaskMap

Основные этапы работа с системой:

пользователь осуществляет инструментацию MPI-программы

при помощи пакета VampirTrace и запускает ее на выполнение

(например, на входных данных меньшей размерности). В

результате выполнения инструментированной программы,

формируются протоколы выполнения (трасы) в формате OTF

(Open Trace Format);

сформированные протоколы поступают на вход модуля otfstat,

который осуществляет их анализ и построение

информационного графа MPI-программы;

на вход модуля taskmap подаются описание распределенной

ВС (производительности каналов связи, процессорных ядер и

т.д.), полученное средствами модуля commperf, а также

информационный граф программы, полученный от otfstat или

сформированный самим пользователем. Результат работы

модуля taskmap – сценарий запуска mpiexec с

субоптимальным распределением ветвей по процессорным

ядрам.

224

Результаты экспериментов

На вычислительном кластере ЦПВТ СибГУТИ проведено

исследование разработанных алгоритмов и программного пакета.

Кластер укомплектован четыремя двухпроцессорными узлами на базе

двухъядерных процессоров Intel Xeon 5150 и сетями связи стандартов

Gigabit/Fast Ethernet.

В качестве тестовых задач использовались MPI-программы из

пакетов NPB (NAS Parallel Benchmarks), HPL и SPEC MPI2007. В

таблице 1 приведены результаты запуска тестов на различных сетях

связи с распределением ветвей по ядрам алгоритмами Round Robin

(RR, стандартный алгоритм утилиты mpiexec) и PTA_PSA [3]. В

таблице 2 приведены результаты для алгоритма PTA_GT, основанном

на обходе информационного графа задачи.

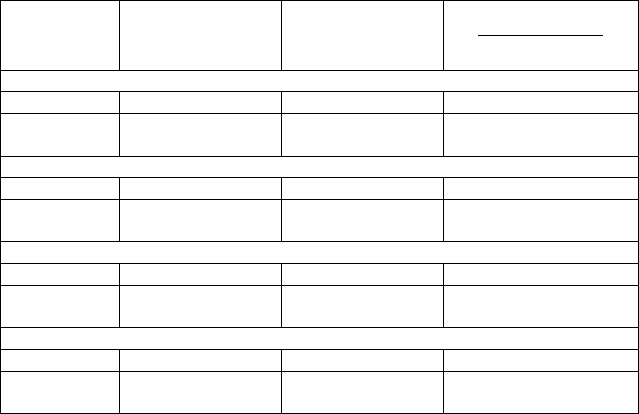
Сеть RR (mpiexec), с. PTA_PSA, с.

PSAPTARR

−

Тест NPB CG

Fast Ethernet 726.02 400.36 0.44

Gigabit

Ethernet

97.56 42.05 0.57

Тест HPL (PMAP=0, BCAST=5)

Fast Ethernet 1108.69 911.81 0.17

Gigabit

Ethernet

263.15 231.72 0.12

Таблица 1. Результаты экспериментов c алгоритмом PTA_SA

225

Сеть RR (mpiexec), с. PTA_TG, с.

TGPTARR

−

Тест HPL

Fast Ethernet 120.92 84.35 0.3

Gigabit

Ethernet

25.10 19.75 0.2

Тест NPB CG

Fast Ethernet 727.00 390.35 0.46

Gigabit

Ethernet

101.14 41.64 0.59

Тест NPB MG

Fast Ethernet 23.94 25.15 -0.04

Gigabit

Ethernet

4.06 4.18 -0.02

Тест NPB FT

Fast Ethernet 339.05 237.24 0.3

Gigabit

Ethernet

54.37 52.22 0.03

Таблица 2. Результаты экспериментов c алгоритмом PTA_TG

Как видно из результатов, качество назначения в значительной

степени зависит от структуры информационного графа задачи.

Например, информационный граф теста NPB MG полный с

однородными по объему данных связями, что существенно

ограничивает возможности по оптимизации размещения его ветвей.

Видно, что для программ с неоднородными информационными

графами сокращение времени выполнения, относительно запуска с

распределением ветвей алгоритмом RR может достигать 30 – 50

процентов.

Заключение

Результаты исследования разработанных алгоритмов и

программного пакета показывают, что при организации

функционирования распределенных ВС целесообразно учитывать

производительности каналов связи коммуникационных сред и

структуры параллельных программ.

Литература

1. Хорошевский В.Г. Архитектура вычислительных систем. – М.:

МГТУ им. Н.Э. Баумана, 2005.

226

Pjesivac-Grbovic J., Angskun T., Bosilca G., Fagg G.E., Gabriel

E., Dongarra J. Performance Analysis of MPI Collective

Operations:

[http://www.netlib.org/netlib/utk/people/JackDongarra/PAPERS/c

ollective-cc-2006.pdf], 2006.

Курносов М.Г. Назначение ветвей параллельной программы

на процессорные ядра распределенной вычислительной

системы // Материалы Международной научно-технической

конференции “Многопроцессорные вычислительные и

управляющие системы”, пос. Дивноморское, Геленджик,

Россия, 2007, с. 227 - 231.

РЕАЛИЗАЦИЯ РЕШЕНИЯ СЕТОЧНЫХ ЗАДАЧ

В РАСПРЕДЕЛЕННОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЕ

НА ОСНОВЕ ИНСТРУМЕНТАРИЯ ALCHEMI

Д. Ю. Лабутин, А. А. Алехин, Д. К. Боголепов

Нижегородский государственный университет

Введение

Решение сложных физических задач, описываемых уравнениями в

частных производных, с помощью построения сеточных функций при

большом количестве узлов приводит к решению систем линейных

уравнений большой размерности. Это приводит к целому ряду

трудностей, главная из которых — необходимость обработки

большого объема информации, что не всегда соответствует

быстродействию и объему оперативной памяти ЭВМ. Для

устранения

этих трудностей предложены различные модификации метода

конечных элементов, имеющие целью понизить порядок разрешающей

системы уравнений и увеличить вычислительные возможности

программ. Наиболее удачной модификацией оказалась идея

суперэлементов. Она основана на представлении сложной

конструкции в виде набора подструктур, каждая из которых

заменяется совокупностью базисных конечных элементов. Каждая из

подструктур рассчитывается отдельно

при закрепленных общих с

другими структурами границах. Результатом этого расчета является

получение матрицы жесткости подструктуры и матрицы нагрузок в ее

узлах. Подструктура, для которой такие матрицы определены,

называется суперэлементом [1].

227

Информация о суперэлементах используется для построения

системы уравнений расчета связей на границах суперэлементов. Эта

система уравнений содержит значительно меньше неизвестных, чем

исходная система уравнений. На этом завершается так называемый

прямой ход расчета.

На обратном ходе расчета каждую из подструктур рассчитывают

при заданной нагрузке и найденных на прямом ходе перемещениях ее

граничных узлов. Такой расчет также выполняется без особых

затруднений, так как подструктуры всегда описываются системой

уравнений невысокого порядка.

При расчете сложных и больших по объему конструкций

представление их в виде совокупности подконструкций одного уровня

может оказаться недостаточным из-за большого порядка уравнений,

описывающих расчетную схему каждой из подконструкций. Поэтому

расчетная схема

в этом случае строится в несколько этапов. Исходная

конструкция может быть представлена при этом в виде совокупности

иерархически построенных суперэлементов нескольких уровней.

Число этих уровней определяется как предполагаемой точностью

решения, так и возможностями используемых ЭВМ.

Рассмотрим некоторую расчетную область, в которой решается

некоторая задача (например, задача Дирихле или задача прогиба

пластины). Пусть в данной области задана сеточная функция и

построена задача определения амплитуд, которая представлена в виде

системы линейных алгебраических уравнений:

fAu =

где

– матрица жесткости задачи, u – вектор узловых значений

(амплитуд),

– некоторый вектор правой части.

Выделим в нашей области некоторые невзаимодействующие

между собой группы соседних узлов, занимающих подобласти

расчетной области и группу узлов, соответствующих оставшимся

узлам расчетной области

Для примера рассмотрим прямоугольную область, разбитую на

четыре непересекающиеся подобласти: получается четыре подобласти

и одна граница между областями. Тогда задача определения узловых

значений может быть записана в следующем виде:

228

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

0004030201

4044

3033

2022

1011

A000

0A00

00A0

000A

AAAA

где

– матрицы жесткости узлов подобластей

–

матрицы жесткости взаимодействия узлов подобласти

и узлов

подобласти

– векторы узловых значений подобластей

–

векторы правых частей, соответствующие подобластям

Полученная система уравнений совпадает с исходной системой с

точностью до перестановки строк. Нулевые блоки в матрице

появляются вследствие отсутствия прямого взаимодействия между

узлами выбранных подобластей.

Размер данной системы уравнений можно понизить. Распишем

первую строку полученной системы уравнений:

1010111

A fuAu =+

Считая, что матрица

невырожденная, выразим вектор

через

вектор граничных узлов

. Получим

)(A

0101

111

uAfu −=

−

Выражая аналогичным образом остальные три вектора

подставляя поочередно полученные выражения в систему, получим:

[

]

[

]

=−−−−

−−−−

040

440430

330320

220210

110100

* uAAAAAAAAAAAAA

[

]

)A()A()A()A(

44043

33032

22021

11010

fAfAfAfAf

−−−−

Эта система линейных уравнений имеет размер, равный

количеству узлов в подобласти граничных узлов

, что намного

меньше количества узлов в исходной области. Решением данной

системы уравнений будет вектор

, соответствующий значениям

амплитуд в узлах граничных элементов. Затем, зная вектор

восстанавливаются решения задачи

в остальных подобластях

В данном примере мы использовали такой подход, когда

неизвестные узлы в системе исключаются группами. В данном случае

указанные группы узлов рассматриваются как одно целое, что

соответствует концепции метода суперэлементов.

229

Существуют различные вариации данного метода, основанные на

выборе базисных функций для различных подобластей, построения

различных сеток для выбранных подобластей и границ. Не

исключается также повторная декомпозиция подобластей, что

приводит к использованию иерархически построенных

суперэлементов.

Различные варианты постановки задачи, способов выбора сеток,

как для подобластей

, так и для узлов границы

, приводят к

изменению структуры матрицы

. Данный факт вынуждает находить

значения матриц

iii

−

и векторов

iii

1−

при каждом решении

задачи. Для нахождения указанных матриц необходимо решать

матричное уравнение, что представляет собой достаточно трудоемкую

задачу. Количество правых частей данных матричных уравнений будет

равно числу узлов подобласти

, граничащих с текущей подобластью

. Процесс решения матричных уравнений может оказаться

достаточно трудоемким и превзойти по сложности выигрыш по

сведению исходной задачи к задаче для вектора

Необходимо отметить, что процесс решения матричных уравнений

для подобластей

является независимым. Поэтому основную

трудоемкую часть алгоритма решения задачи можно разбить на

полностью независимые части и использовать для этого технологии

параллельных или распределенных вычислений.

Для реализации указанного выше алгоритма создается

программный комплекс, основанный на использовании концепций

распределенных вычислений. В качестве платформы был выбран

инструментарий Alchemi, разрабатываемый в университете

Мельбурна. Данный инструментарий

распространяется с открытым

исходным кодом и доступен для свободного использования

(http://www.alchemi.net). Для оптимального решения рассматриваемой

задачи данный инструментарий был модифицирован с целью

обеспечения интерактивного взаимодействия с удаленными

вычислительными узлами.

При разработке программного комплекса закладывалось

требование о гибком использовании доступных вычислительных

ресурсов, объединенных в общую сеть на основе Ethernet.

Характерной особенностью такого использования

является

возможность объединения различных компьютерных ресурсов для

230

решения одной задачи, а также возможность гибкой адаптации

вычислительных мощностей в зависимости, например, от сложности

задачи.

Исходя из указанных требований, программный комплекс

поддерживает работу на множестве доступных машин, которое может

динамически изменяться в процессе работы. Для этого реализованы

механизмы повторных перерасчетов подзадач и динамической

балансировки нагрузки узлов.

Для эффективного использования

многопроцессорных SMP

систем, и в частности систем с многоядерными процессорами, в

расчетной части программного комплекса используется библиотека

Intel MKL, которая специально создавалась оптимизированной для

SMP (в т.ч. многоядерных) систем.

В процессе работы программный комплекс предоставляет

пользователю наглядную информацию о ходе выполнения расчетов.

Пользователь имеет возможность выбора задачи для решения, а также

настройки разбиения

исходной области. После завершения очередного

этапа расчетов программа визуализирует физическую модель упругой

пластины. Для этого применяется библиотека трехмерной графики

Open GL. Кроме того, пользователь может просматривать

информацию о задействованных вычислительных узлах: их

количество, информацию о решаемых в данный момент подзадачах и

количестве переданных данных.

Программный комплекс является демонстрацией новой модели

использования библиотеки

Intel MKL применительно к так

называемым “слабо–связанным” задачам.

Реализация расчетов в инструментарии Alchemi

Работа приложений, предназначенных для использования в рамках

инструментария Alchemi, основывается на следующей схеме:

 центральное приложение, работающее на машине клиента, в

функции которого входят:

 разбиение задачи на независимые потоки;

 соединение с Менеджером и отправка потоков на

исполнение;

 получение результатов исполнения потоков и склейка

их в решение;

 Менеджер: