Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

161

вычисления этого набора задач получим последовательность

. Тогда,

учитывая (1), получим:

() ( )

jjj

ijMjM

sn sn t

ttt

===

Общий вычислительный ресурс системы можно оценить как

00 0

1 1

00 0

00 0 000

0 0

N N

j j

M M jM jM

tt t

RRR R R RRt

tt t t

− −

= =

⎛⎞

==++ +…+ =

⎜⎟

⎝⎠

∑∑

Аналогично, получим:

()

jjMj

ntR=

() ()

jM m

jm j

nsn

где

()

– оценка сложности вычислительной задачи при различных

входных параметрах (

), полученная на j-ом вычислителе (

Оценим вычислительную сложность

()

задачи

-ого типа с

набором входных параметров

как

()

−

∑

. Для

получения непрерывной функции

()

необходимо

аппроксимировать дискретную функцию

()

. Выбор

зависит от

количества входных параметров, необходимых для построения

аппроксимирующей функции требуемой точности. Порядок

аппроксимации может задавать программист вычислительной задачи.

С помощью такого тестирования можно получить относительные

оценки вычислительной сложности одной задачи относительно другой

и относительные оценки вычислительного ресурса узлов. То есть если

ввести некоторую задачу в качестве эталонной, то можно оценивать

вычислительные ресурсы и сложности в абсолютных величинах.

Экспериментальное исследование

Предложенные выше идеи относительно структуры РВС и

алгоритм динамического планирования были реализованы в РВС,

основанной на использовании фреймворка OSGi. Для исследования

системы и работы алгоритма были взяты задачи вычисления интеграла

единичной окружности методом Монте-Карло и перемножения

квадратных матриц. Эти задачи зависят от одномерного набора

162

входных данных, не предполагают взаимодействия вычислителей и

хорошо распределяются по РВС. Объектами исследования были

относительные оценки сложности вычислительных задач, зависимости

сложностей вычислительных задач от набора входных параметров и

вычислительный ресурс вычислителей. В качестве эталонной задачи

использовалась задача вычисления интеграла единичной окружности,

т.к. она проста и ее сложность линейно зависит

от входного параметра

(количества точек).

Испытания проводились на компьютерах: (1) AMD Sempron

3000+(1.81 ГГц, 480 Мб ОЗУ), (2) Celeron (1.81 ГГц, 380Мб ОЗУ), (3)

Pentium (2.4 ГГц, 480 Мб ОЗУ), (4) AMD Sempron 3000+ (1.81 ГГц, 512

Мб ОЗУ).

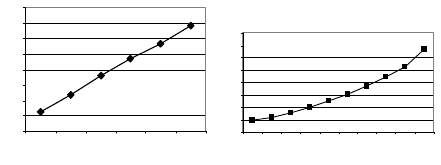
На рисунке 2 представлена зависимость вычислительной

сложности задачи вычисления интеграла методом Монте-Карло и

задачи перемножения квадратных матриц в зависимости от размера

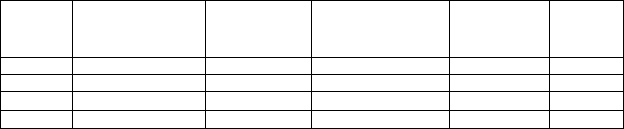
матрицы. В таблице 1 представлены примеры декомпозиции данных

при решении вычислительной задачи перемножения квадратных

матриц размером 2000х2000 элементов. Во времени вычисления

учитывается, в том числе, и время передачи результата по сети.

Теоретическое время вычисления

4074

t =

мс, среднее время

вычисления

4105

t =

Анализ приведенных экспериментальных данных показывает, что

задачу вычисления интеграла методом Монте-Карло действительно

можно использовать в качестве эталонной: ее график вычислительной

сложности близок к прямой, а график сложности перемножения

матриц явно имеет вид квадратичной зависимости.

2000

4000

6000

8000

10000

12000

14000

16000

8416670 16733336 25050002 33366668 41683334 50000000

0, 2

0, 4

0, 6

0, 8

1, 2

1, 4

1, 6

12345678910

размер матрицы

вычислительная слож ность

Рис. 2. Зависимость вычислительной сложности задачи вычисления интеграла

методом Монте-Карло и задачи перемножения квадратных матриц от размера

матрицы

163

Имя

узла

Характеристики

вычислителей

Выч. ресурс Декомпозиция

данных (строки)

Выч.

сложность

Время

выч.

(мс)

KTK2

(

)

453691184 496 0

8079400 4079

(

)

408243972 477 0

7183590 3886

KTK9 (3) 0,557553044 530 0,9841950 4389

KTK5

(

)

461904649 497 0

8128319 4068

Таблица 1. Время вычисления и декомпозиция данных задачи перемножения

матриц

Также нетрудно заметить, что практические результаты работы

алгоритма планирования хорошо согласуются с теоретическими

оценками. Это дает основания предполагать, что алгоритм будет также

работать и в более сложных системах.

Улучшение алгоритма планирования, совершенствование систем

РВС исследование их работы на более сложных вычислительных

системах рассматриваются авторами в качестве направлений

дальнейшей работы.

Заключение

В работе представлены требования к архитектуре РВС и алгоритму

динамического планирования, предложены математическая модель и

методы равномерной балансировки нагрузки на узлы вычислительной

системы, а также метод построения оценок вычислительного ресурса

узлов РВС, и вычислительной сложности задач. Предложенные

принципы реализованы в РВС, проведено исследование на тестовых

примерах.

Литература

1. Седельников М.С. Алгоритм распределения набора задач с

переменными параметрами по машинам вычислительной

системы // Автометрия.–2006.–№1.–С.68-75.

Хорошевский В.Г. Архитектура вычислительных систем.–

М.: МГТУ им. Н.Э. Баумана, 2005.

Голуб Дж., Ван Лоун Ч. Матричные вычисления.– М.: Мир,

1999.

Седельников М.С. Точный алгоритм распределения набора

задач по машинам вычислительной системы // Матер. Всерос.

науч. конф. молодых ученых «Наука. Техника. Инновации»/

Новосибирск: НГТУ – 2004. – С.65–78.

164

Сметанникова Е.Н. Численные методы: Конспект лекций /

Самарский государственный аэрокосмический университет,

Самара, 2002. – 98 с.

РЕАЛИЗАЦИЯ ЯВНОГО ЧЕБЫШЕВСКОГО МЕТОДА

РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ПУАССОНА

В МЕЛКОЗЕРНИСТОМ ЛОКАЛЬНО–ПАРАЛЛЕЛЬНОМ

СТИЛЕ ПРОГРАММИРОВАНИЯ

Г.В. Заручевская

Поморский государсвенный университет, Архангельск

Параллелизм супер-ЭВМ – магистральный путь развития

вычислительной техники. Господствующим способом

распараллеливания задач до сих пор является крупноблочное

распараллеливание [1]. Однако с ростом числа процессоров блоки

измельчаются, и вычисления в подавляющем большинстве случаев

будут идти медленнее: параллелизм вырождается. Избежать

вырождения можно при следующих условиях: обмены происходят и

одновременно, и

локально; задача должна быть разбита на множество

небольших однотипных подзадач, которые будут исполняться

параллельно на отдельных вычислительных машинах (ВМ); данные

максимально распределены по системе, а программы в каждой ВМ

используют минимально возможные наборы данных. Число обменов

данными между ВМ имеет тот же порядок, что и число

вычислительных операций. Такой подход

к распараллеливанию

алгоритмов носит название мелкозернистого локально-параллельного

программирования (МЛПП).

Рассмотрим два обязательных требования, при которых не

происходит снижения производительности МЛПП [2]:

Локальность взаимодействий, когда обмен данными

происходит только в пределах ограниченного физического и

структурного радиуса независимо от размеров задачи и

системы.

Параллелизм взаимодействий, когда все возможные в данный

момент обмены совершаются параллельно и одновременно с

процессом счета.

Количество глобальных операций не должно влиять на оценку

временной сложности задачи.

165

При описании алгоритма параллельных вычислений на ЭВМ

класса MIMD предполагается, что MIMD –машина состоит из p одина-

ковых процессоров, каждый из которых обладает определенным

объемом своей локальной памяти (одинаковым для всех параллельных

процессоров) и способен осуществлять численную обработку

информации в автономном и управляемом режимах.

Отметим существенные особенности архитектуры MIMD-машины,

при которых стиль МЛП

-программирования был наиболее

эффективен.

Попарное соединение процессоров осуществляется за очень

короткий промежуток времени и поэтому оно не учитывается.

Все возможные в данный момент обмены машинными

словами совершаются параллельно и одновременно с

процессом счёта за время, сравнимое со временем выполнения

одной арифметической операции (из-за близости связанных

процессоров в физическом пространстве).

Имеется возможность программировать структуру

межпроцессорных связей.

Обычно MIMD-машины имеют следующие структуры

межпроцессорных связей: линейка, кольцо, кольцо с хордами, сетка

(решетка), гиперкуб, дерево. Тем не менее, в теории однородных

вычислительных структур [3], помимо вышеперечисленных типов

структур межпроцессорных связей, рассматривается тор. Заметим, что

эта евклидова структура изоморфна сетке (решетке) процессоров, в

которой ВМ

на противоположных сторонах решетки связаны

регулярным каналом. При этом тор позволяет легко масштабировать

сетку другой, отличающейся от него, размерности. Действительно,

пусть сетка a×b вкладывается в тор C×D, a>C, b>D. Согласно [3],

такую тороидальную евклидову структуру будем обозначать E2{C,D}.

Каждому процессору тора (x,y) поставим в соответствие ячейку сетки

(x+Ck,y+Dn), k,n∈N. При таком распределении сеточных узлов в

тороидальной

структуре параллельный алгоритм соответствует МЛП–

стилю.

Введем для дальнейшего использования понятие процессорного

тороидально связанного куба C×D×E. Эту структуру можно

рассматривать как продолжение процессорного куба размерностью

C×D×E. Итак, пусть имеется процессорный куб C×D×E (рис.1).

166

Каждый процессор обозначается Pi,j,k, где i, j, k – координаты узла, в

котором располагается процессор. Дополним процессорный куб

следующими связями: каждый процессор P1,j,k соединим регулярным

каналом с процессором PС,j,k , j=1..D, k=1..E; Pi,1,k соединим

регулярным каналом с процессором Pi,D,k , i=1..C, k=1..E ; Pi,j,1

соединим регулярным каналом с процессором Pi,j,E , i=1..C, j=1..D.

Получим новую структуру – тороидально связанный куб C×D×E.

Заметим, что каждая плоскость, параллельная плоскостям COD, COE и

DOE и содержащая

процессорные узлы, представляет собой

тороидальную структуру. Очевидно, что структура, состоящая из

числа E вложенных друг в друга торов размерностью C×D,

соединенных специальным образом, изоморфна тороидально

связанному кубу C×D×E. Обе структуры вложимы в физическое

пространство, однако не являются планарными. Гипотетически можно

предположить, что конструкция вложенных торов позволит

обеспечить теплоотвод: их внутренняя

полость может быть

использована как расширитель для испарения хладоагента.

Конструкция вложенных торов содержит на порядок меньше

удаленных связей, чем тороидально связанный куб, а значит,

обеспечивает большую эффективность мелкозернистому локально-

параллельному стилю программирования.

Разработка и исследование МЛПП для задач математической

физики – одно из актуальных направлений современного

параллельного программирования. В [4] для этих целей

применяются

модели клеточных автоматов.

Целью настоящей работы является вложение данных МЛПП–

алгоритма решения некоторых задач математической физики для

массово-параллельных процессоров в соответствующие тороидальные

структуры с иллюстрацией межпроцессорных обменов.

В качестве модельной задачи рассмотрим задачу Дирихле для

самосопряженного уравнения второго порядка в прямоугольнике

= Ω∪Г={(x, y): 0≤x≤l

, 0≤y≤l

Lu=–

⎟

⎠

⎞

⎜

⎝

⎛

∂

))(

())(

(

= f(x,y), x∈Ω , u=g(x,y),

(x,y)∈Г. (1)

Предполагаем, что 0<c

≤k

≤c

, α=1,2.

В области

введем равномерную по обеим переменным

сетку

167

;,,...,1,0 , ,),{(

211

jhyNiihxyx

jiji

===Ω∈=

}.2,1,/,,...,1,0

ααα

hNNj l

Множество внутренних узлов обозначим ω, граничных – γ. Задаче

(1) на сетке ϖ=ω∪γ поставим в соответствие разностную задачу:

(

)

)(x,

(x,

)(x,

,x(

)v)

,x(a()v)

,x(a(v

∈

−=Λ

(2)

где a1(x, y)=k1(x-0,5h1, y); a2(x, y)=k2(x, y-0,5h2), а для разностных

отношений использованы стандартные обозначения [5].

Для решения задачи (2) явным чебышевским методом задают на ω

начальное приближение

(0)

и величину ε, определяющую окончание

итерационного процесса. Каждое последующее приближение

вычисляется по формуле

(k+1)

(k)

+τ

k+1

(f-Λ v

(k)

), v

(k)

=g, (3)

где {τ

}- оптимальный чебышевский набор параметров.

Рассмотрим выполнение алгоритма параллельных вычислений,

основанного на явном чебышевском методе в тороидальной структуре

процессоров E

{C,D}.

Распределим ячейки области ω таким образом, чтобы каждому

процессору тора E2{C,D} с координатами (x,y) поставить в

соответствие ячейки сетки (x+Ck,y+Dn), k,n∈N, т.е. сетка

произвольной размерности N1× N2 вкладывается в тор C×D, N1>C,

N2>D. Итак, область ϖ разбивается на ([N1/C]+1)⋅([N2/D]+1)

подобластей ωk,n, где k=1,…,([N1/C]+1), n=1, ..., ([N2/D]+1),

размерности C×D прямыми, параллельными обеим координатным

осям.

Шаг 1. Задаем начальное приближение

(0)

. Вводим в каждый

процессор счетчик итераций t, t=0 в начале выполнения программы.

Он определяет окончание итерационного процесса. Вычисляем и

храним во всех процессорах параметры{τ

Шаг 2. Рассмотрим вычисление приближения

(1)

в подобласти

1,1

Все процессоры по регулярному каналу совершают сдвиги

значений

i, j

данных: вправо – получают значение от левого соседа

i-1,j

и передают свое значение правому, влево – получают значение от

правого соседа

i+1,j

и передают свое значение левому, вниз – получают

168

значение от верхнего соседа

i,j+1

и передают свое значение нижнему, и

вверх – получают значение от нижнего соседа

i, j-1

и передают свое

значение верхнему. Граничные процессоры P(C,j) принимают данные

процессоров P(1,j), –они содержат значения

1 j,kC

; аналогично

процессоры P(i,D) принимают данные

1+nD,i

процессоров P(i,1).

Неиспользуемые данные будут теряться либо не учитываться.

Шаг 3. Каждый процессор вычисляет значение

j,i

в подобласти

1,1

Вычисление

значения

j,i

в остальных подобластях

k,n

, где k=1,…

([N

/C]+1), n=1, ..., ([N

/D]+1), осуществляется аналогично (см. п. 2 и

п.3.).

Шаг 4. ВМ увеличивает значение счетчика t на 1.

Если t=N+1, ВМ посылает флажок

i,j

=1 на магистральный канал.

Шаг 5. Как только все ВМ отправят на магистральный канал

флажки, вычислительный процесс прерывается во всех ВМ и хост —

машина через магистральный канал выводит вычисленные значения.

Операция прерывания является единственной глобальной операцией.

Пусть М – количество арифметических операций, необходимое

для вычисления (t+1)-го приближения к решению по формуле (3) в

одном узле сетки ω, Q=(N

-1)×(N

-1) количество узлов сетки ω, t –

среднее время выполнения одной арифметической операции ПП, t

время обмена одним машинным словом между двумя ПП.

Для определения коэффициентов, характеризующих явный

чебышевский метод с параллельной организацией вычислений, доста-

точно рассмотреть одну итерацию. Время для реализации одной

итерации по формуле (3) равно T

=MQt. Так как шаги 2), 3) являются

параллельными, то, предполагая время вычисления

(t+1)

в каждой ω

k,n

одинаковым, Q=N

⋅N

получим T

=M([N

/C]+1)⋅([N

/D]+1)(t+t

), и,

следовательно, коэффициент ускорения k

≈CD и коэффициент

эффективности k

≈1, т.е. параллелизм максимален.

По аналогии можно составить МЛП-алгоритм решения задачи

Дирихле для самосопряженного уравнения третьего порядка в

тороидальном кубе.

169

В заключение отметим, что существуют другие алгоритмы

распараллеливания итерационных методов решения разностных схем

эллиптических уравнений [5]. Однако эти алгоритмы крупноблочные и

к ним трудно применять технологию мелкозернистого локально-

параллельного программирования, они, как правило, реализуются либо

на кластерах, либо на планарных неразрезных процессорных матрицах.

Предложенную идею можно использовать для распараллеливания

других итерационных

методов решения разностных схем

эллиптических уравнений.

Литература

1. Воеводин В.В., Воеводин Вл. В. Параллельные вычисления.-

Спб.: БХВ-Петербург, 2002. –608 с.: ил.

Воробьев В.А. Об эффективности параллельных вычислений //

Автометрия.- 2000. - № 1. С. 50-58.

Воробьёв В.А. Теория однородных вычислительных систем:

однородные структуры. – Архангельск: Изд-во ПГУ им.

М.В. Ломоносова, 2001. – 95 с.

Бандман О.Л. Мелкозернистый параллелизм в математической

физике // Программирование.- 2001.- №4. С.12-25.

Молчанов И.Н., Галба Е.Ф. Параллельные вычисления в

методах сеток решения задач математической физики на

MIMD- машинах. –Киев, 1990.-41 с.

ИСПОЛЬЗОВАНИЕ КЛАСТЕРНЫХ ВЫЧИСЛЕНИЙ ДЛЯ

ОБУЧЕНИЯ СТУДЕНТОВ ХИМИЧЕСКОГО ФАКУЛЬТЕТА

МЕТОДАМ СОВРЕМЕННОЙ КВАНТОВОЙ ХИМИИ

С.В. Зеленцов

Нижегородский государственный университет

Современный этап развития химии и химической технологии

требует, чтобы студенты-химики овладевали квантово-химическими

методами. Указанные методы становятся в химии столь же

необходимы, как и инструментальные методы.

Методы современной квантовой химии предъявляют чрезвычайно

высокие требования к вычислительной системе для своей реализации.

В методе Хартри-Фока-Руутана вычислительная сложность возрастает

быстрее, чем

, где N – число электронов в молекуле. Использование

170

методов с учетом электронной корреляции приводит к более сильной

зависимости от числа электронов, часто вычислительная сложность

становится пропорциональной N

– N

. Кроме того, время квантово-

химического расчета сильно зависит от объема оперативной памяти,

доступной для задачи. Обмены с дисковой памятью для средних по

размеру молекул занимают основное время при решении задачи на

одноядерном персональном компьютере с объемом оперативной

памяти менее 1 GB. Задача усложняется еще более при расчетах

возбужденных состояний молекулы, расчет которых

становится все

более и более актуальным. Наиболее приемлемым вариантом

реализации таких расчетов является использование параллельных

(кластерных) вычислений.

Особенно сильно возрастает роль квантово-химических расчетов

на кластерах для обучения студентов. Благодаря высокой

производительности и практически отсутствующим ограничениям на

количество атомов в рассчитываемой молекуле, появляется

уникальная возможность обучать студентов на примерах расчетов

не

упрощенных моделей, но молекул, которые интересуют студента в его

учебно-научной деятельности. Кроме того, возможность

дистанционного расчета молекул на кластере позволяет оптимально

организовать учебный план обучающихся квантовой химии.

В рамках ФНП «Образование» Нижегородским государственным

университетом приобретены академические лицензии программного

комплекса Gaussian-03. Кроме того, на вычислительном кластере

ННГУ установлена программа NWChem фирмы PNNL (США

). Эти

ресурсы используются в режиме удаленного доступа по сети Интернет

для обучения студентов и аспирантов методам вычислительной

квантовой химии.

ОПТИМАЛЬНОЕ РЕЗЕРВИРОВАНИЕ РАСПРЕДЕЛЕННЫХ

ВЫЧИСЛИТЕЛЬНЫХ РЕСУРСОВ

М.Б. Ильяшенко

Запорожский национальный технический университет

Введение

Очередным этапом развития распределенных вычислений стало

появление технологии Grid, как инфраструктуры, состоящей из

находящихся в разных местах ресурсов, соединяющих эти ресурсы