Stewart J. Calculus

Подождите немного. Документ загружается.

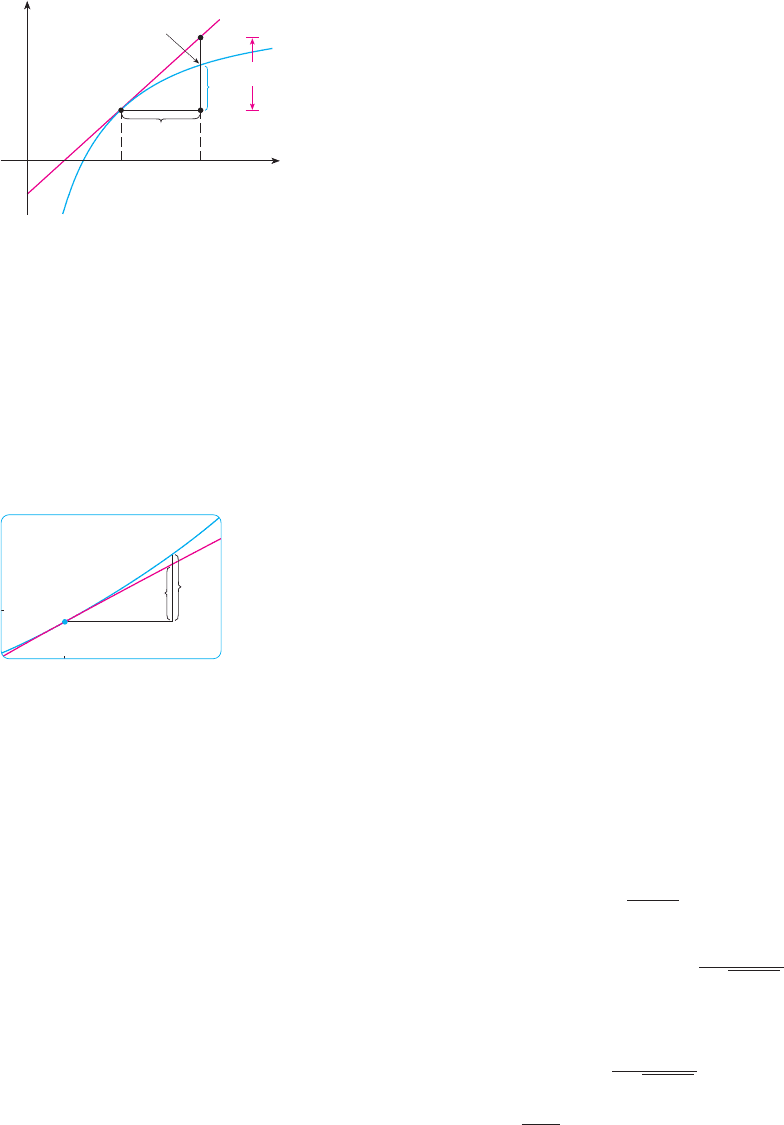
The geometric meaning of differentials is shown in Figure 5. Let and

be points on the graph of and let . The corresponding

change in is

The slope of the tangent line is the derivative . Thus the directed distance from S

to R is . Therefore represents the amount that the tangent line rises or falls

(the change in the linearization), whereas represents the amount that the curve

rises or falls when changes by an amount .

EXAMPLE 3 Compare the values of and if and

changes (a) from 2 to 2.05 and (b) from 2 to 2.01.

SOLUTION

(a) We have

In general,

When and , this becomes

(b)

When ,

Notice that the approximation becomes better as becomes smaller in

Example 3. Notice also that was easier to compute than . For more complicated func-

tions it may be impossible to compute exactly. In such cases the approximation by dif-

ferentials is especially useful.

In the notation of differentials, the linear approximation (1) can be written as

For instance, for the function in Example 1, we have

If a ! 1 and , then

and

just as we found in Example 1.

Our ﬁnal example illustrates the use of differentials in estimating the errors that occur

because of approximate measurements.

4.05

! f !1.05" # f !1" ! dy ! 2.0125

dy !

0.05

1 ! 3

! 0.0125

dx ! "x ! 0.05

dy ! f #!x" dx !

x ! 3

f !x" !

x ! 3

f !a ! dx" # f !a" ! dy

"ydy

"x"y # dy

dy ! $3!2"

! 2!2" $ 2%0.01 ! 0.14

dx ! "x ! 0.01

"y ! f !2.01" $ f !2" ! 0.140701

f !2.01" ! !2.01"

! !2.01"

$ 2!2.01" ! 1 ! 9.140701

dy ! $3!2"

! 2!2" $ 2%0.05 ! 0.7

dx ! "x ! 0.05x ! 2

dy ! f #!x" dx ! !3x

! 2x $ 2" dx

"y ! f !2.05" $ f !2" ! 0.717625

f !2.05" ! !2.05"

! !2.05"

$ 2!2.05" ! 1 ! 9.717625

f !2" ! 2

! 2

$ 2!2" ! 1 ! 9

y ! f !x" ! x

! x

$ 2x ! 1dy"y

dxx

y ! f !x""y

dyf #!x" dx ! dy

f #!x"PR

"y ! f !x ! "x" $ f !x"

dx ! "xfQ!x ! "x, f !x ! "x""

P!x, f !x""

192

|| ||

CHAPTER 3 DERIVATIVES

Îy

dx=Îx

x+Îx

y=ƒ

F I G U R E 5

F I G U R E 6

y=˛+≈-2x+1

(2,9)

Îy

N Figure 6 shows the function in Example 3 and

a comparison of and when . The

viewing rectangle is by .$6, 18%$1.8, 2.5%

a ! 2"ydy

EXAMPLE 4 The radius of a sphere was measured and found to be 21 cm with a pos-

sible error in measurement of at most 0.05 cm. What is the maximum error in using this

value of the radius to compute the volume of the sphere?

SOLUTION If the radius of the sphere is , then its volume is . If the error in the

measured value of is denoted by , then the corresponding error in the calcu-

lated value of is , which can be approximated by the differential

When and , this becomes

The maximum error in the calculated volume is about 277 cm .

Although the possible error in Example 4 may appear to be rather large, a bet-

ter picture of the error is given by the relative error, which is computed by dividing the

error by the total volume:

Thus the relative error in the volume is about three times the relative error in the radius.

In Example 4 the relative error in the radius is approximately

and it produces a relative error of about 0.007 in the volume. The errors could also be

expressed as percentage errors of in the radius and in the volume.0.7%0.24%

dr&r ! 0.05&21 # 0.0024

! 3

NOTE

dV ! 4

!21"

0.05 # 277

dr ! 0.05r ! 21

dV ! 4

"VV

dr ! "rr

V !

SECTION 3.9 LINEAR APPROXIMATIONS AND DIFFERENTIALS

|| ||

193

(a) (b)

14. (a) (b)

15–18 (a) Find the differential and (b) evaluate for the

given values of and .

15. , ,

16. , ,

17. , ,

18. , ,

19–22 Compute and for the given values of and

. Then sketch a diagram like Figure 5 showing the line

segments with lengths , , and .

19. , ,

20. , ,

21. , ,

22. , ,

"x ! 0.5x ! 1y ! x

"x ! 1x ! 4y ! 2&x

"x ! 1x ! 1y !

"x ! $0.4x ! 2y ! 2x $ x

"ydydx

dx ! "x

xdy"y

dx ! 0.05x !

&3y ! cos x

dx ! $0.1x !

&4y ! tan x

dx ! $0.01x ! 1y ! 1&!x ! 1"

dx ! 0.04x ! 0y !

4 ! 5x

dxx

dydy

y !

z ! 1&z

y ! !t ! tan t"

y ! !1 ! r

y !

u ! 1

u $ 1

13.

1– 4 Find the linearization of the function at .

1. , 2. ,

4. ,

;

Find the linear approximation of the function

at and use it to approximate the numbers and

. Illustrate by graphing and the tangent line.

;

6. Find the linear approximation of the function

at and use it to approximate the numbers and

. Illustrate by graphing and the tangent line.

;

7–10 Verify the given linear approximation at . Then deter-

mine the values of for which the linear approximation is accu-

rate to within 0.1.

7. 8.

10.

11–14 Find the differential of each function.

11. (a) (b)

12. (a) (b) y ! u cos uy ! s&!1 ! 2s"

y !

1 ! t

y ! x

sin 2x

4 $ x

x1&!1 ! 2x"

# 1 $ 8x

tan x # x

1 $ x

# 1 $

a ! 0

1.1

0.95

a ! 0

t!x" !

1 ! x

0.99

0.9

a ! 0

f !x" !

1 $ x

a ! 16f !x" ! x

3&4

a !

&2f !x" ! cos x

a ! 0f !x" ! 1&

2 ! x

a ! $1f !x" ! x

! 3x

aL!x"

E X E R C I S E S

3.9

(This is known as Poiseuille’s Law; we will show why it

is true in Section 9.4.) A partially clogged artery can be

expanded by an operation called angioplasty, in which a

balloon-tipped catheter is inﬂated inside the artery in order

to widen it and restore the normal blood ﬂow.

Show that the relative change in is about four times the

relative change in . How will a 5% increase in the radius

affect the ﬂow of blood?

39. Establish the following rules for working with differentials

(where denotes a constant and and are functions of ).

(a) (b)

(e) (f)

40. On page 431 of Physics: Calculus, 2d ed., by Eugene Hecht

(Paciﬁc Grove, CA: Brooks/Cole, 2000), in the course of

deriving the formula for the period of a

pendulum of length L, the author obtains the equation

for the tangential acceleration of the bob

of the pendulum. He then says, “for small angles, the value

of in radians is very nearly the value of ; they differ

by less than 2% out to about 20°.”

(a) Verify the linear approximation at 0 for the sine function:

;

(b) Use a graphing device to determine the values of for

which and differ by less than 2%. Then verify

Hecht’s statement by converting from radians to degrees.

Suppose that the only information we have about a function

is that and the graph of its derivative is as shown.

(a) Use a linear approximation to estimate and .

(b) Are your estimates in part (a) too large or too small?

Explain.

42. Suppose that we don’t have a formula for but we know

that

and

for all .

(a) Use a linear approximation to estimate

and .

(b) Are your estimates in part (a) too large or too small?

Explain.

t!2.05"

t!1.95"

t#!x" !

! 5

t!2" ! $4

t!x"

y=fª(x)

f !1.1"f !0.9"

f !1" ! 5

41.

xsin x

sin x # x

sin

! $t

sin

T ! 2

L&t

d!x

" ! nx

n$1

dxd

(

v du $ u dv

d!uv" ! u dv ! v dud!u ! v" ! du ! dv

d!cu" ! c dudc ! 0

vuc

23–28 Use a linear approximation (or differentials) to estimate the

given number.

23. 24. 25.

26. 27. 28.

29–30 Explain, in terms of linear approximations or differentials,

why the approximation is reasonable.

30.

The edge of a cube was found to be 30 cm with a possible

error in measurement of 0.1 cm. Use differentials to estimate

the maximum possible error, relative error, and percentage

error in computing (a) the volume of the cube and (b) the sur-

face area of the cube.

32. The radius of a circular disk is given as 24 cm with a maxi-

mum error in measurement of 0.2 cm.

(a) Use differentials to estimate the maximum error in the

calculated area of the disk.

(b) What is the relative error? What is the percentage error?

33. The circumference of a sphere was measured to be 84 cm

with a possible error of 0.5 cm.

(a) Use differentials to estimate the maximum error in the

calculated surface area. What is the relative error?

(b) Use differentials to estimate the maximum error in the

calculated volume. What is the relative error?

34. Use differentials to estimate the amount of paint needed to

apply a coat of paint 0.05 cm thick to a hemispherical dome

with diameter 50 m.

35. (a) Use differentials to ﬁnd a formula for the approximate

volume of a thin cylindrical shell with height , inner

radius , and thickness .

(b) What is the error involved in using the formula from

part (a)?

36. One side of a right triangle is known to be 20 cm long and

the opposite angle is measured as , with a possible error

of .

(a) Use differentials to estimate the error in computing the

length of the hypotenuse.

(b) What is the percentage error?

37. If a current passes through a resistor with resistance ,

Ohm’s Law states that the voltage drop is . If is

constant and is measured with a certain error, use differen-

tials to show that the relative error in calculating is approxi-

mately the same (in magnitude) as the relative error in .

When blood ﬂows along a blood vessel, the ﬂux (the

volume of blood per unit time that ﬂows past a given point)

is proportional to the fourth power of the radius of the blood

vessel:

F ! kR

38.

VV ! RI

'1(

30(

"rr

31.

!1.01"

# 1.06sec 0.08 # 1

29.

99.8

tan 44(1&1002

!8.06"

2&3

sin 1(!2.001"

194

|| ||

CHAPTER 3 DERIVATIVES

LABORATORY PROJECT TAYLOR POLYNOMIALS

|| ||

195

The tangent line approximation is the best ﬁrst-degree (linear) approximation to near

because and have the same rate of change (derivative) at . For a better approxi-

mation than a linear one, let’s try a second-degree (quadratic) approximation . In other

words, we approximate a curve by a parabola instead of by a straight line. To make sure that the

approximation is a good one, we stipulate the following:

(i) ( and should have the same value at .)

(ii) ( and should have the same rate of change at .)

(iii) (The slopes of and should change at the same rate at .)

1. Find the quadratic approximation to the function that

satisﬁes conditions (i), (ii), and (iii) with . Graph , , and the linear approximation

on a common screen. Comment on how well the functions and approximate .

2. Determine the values of for which the quadratic approximation in Problem 1

is accurate to within 0.1. [Hint: Graph , and on

a common screen.]

3. To approximate a function by a quadratic function near a number , it is best to write

in the form

Show that the quadratic function that satisﬁes conditions (i), (ii), and (iii) is

4. Find the quadratic approximation to near . Graph , the quadratic

approximation, and the linear approximation from Example 2 in Section 3.9 on a common

screen. What do you conclude?

5. Instead of being satisﬁed with a linear or quadratic approximation to near , let’s

try to ﬁnd better approximations with higher-degree polynomials. We look for an th-degree

polynomial

such that and its ﬁrst derivatives have the same values at as and its ﬁrst

derivatives. By differentiating repeatedly and setting , show that these conditions are

satisﬁed if , and in general

where . The resulting polynomial

is called the th-degree Taylor polynomial of centered at .

6. Find the 8th-degree Taylor polynomial centered at for the function .

Graph together with the Taylor polynomials in the viewing rectangle [$5, 5]

by [$1.4, 1.4] and comment on how well they approximate .

, T

f !x" ! cos xa ! 0

afn

!x" ! f !a" ! f #!a"!x $ a" !

f )!a"

!x $ a"

! * * * !

!n"

!a"

!x $ a"

k! ! 1 ! 2 ! 3 ! 4 ! * * * ! k

!k"

!a"

! f !a", c

! f #!a", c

f )!a"

x ! a

nfx ! anT

!x" ! c

! c

!x $ a" ! c

!x $ a"

! c

!x $ a"

! * * * ! c

!x $ a"

x ! af !x"

fa ! 1f !x" !

x ! 3

P!x" ! f !a" ! f #!a"!x $ a" !

f )!a"!x $ a"

P!x" ! A ! B!x $ a" ! C!x $ a"

PaPf

y ! cos x ! 0.1y ! cos x $ 0.1, y ! P!x"

f !x" ! P!x"x

fLPL!x" ! 1

fPa ! 0

f !x" ! cos xP!x" ! A ! Bx ! Cx

afPP)!a" ! f )!a"

afPP#!a" ! f #!a"

afPP!a" ! f !a"

P!x"

aL!x"f !x"x ! a

f !x"L!x"

;

TAYLOR POLYNOMIALS

L A B O R AT O R Y

P R O J E C T

196

|| ||

CHAPTER 3 DERIVATIVES

REVIEW

C O N C E P T C H E C K

Describe several ways in which a function can fail to be

differentiable. Illustrate with sketches.

What are the second and third derivatives of a function f ?

If f is the position function of an object, how can you inter-

pret and ?

State each differentiation rule both in symbols and in words.

(a) The Power Rule (b) The Constant Multiple Rule

(e) The Product Rule (f) The Quotient Rule

(g) The Chain Rule

State the derivative of each function.

(a) (b) (c)

(d) (e) (f)

(g)

10. Explain how implicit differentiation works.

11.

(a) Write an expression for the linearization of at .

(b) If , write an expression for the differential .

ings of and .dy"y

dx ! "x

dyy ! f !x"

y ! cot x

y ! sec xy ! csc xy ! tan x

y ! cos xy ! sin xy ! x

f +f )

Write an expression for the slope of the tangent line to the

curve at the point .

Suppose an object moves along a straight line with position

at time t. Write an expression for the instantaneous veloc-

ity of the object at time . How can you interpret this

velocity in terms of the graph of f ?

If and x changes from to , write expressions for

the following.

(a) The average rate of change of y with respect to x over the

interval .

(b) The instantaneous rate of change of y with respect to x

at .

Deﬁne the derivative . Discuss two ways of interpreting

this number.

(a) What does it mean for to be differentiable at a?

(b) What is the relation between the differentiability and conti-

nuity of a function?

differentiable at .a ! 2

f #!a"

x ! x

, x

y ! f !x"

t ! a

f !t"

!a, f !a""y ! f !x"

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

If is continuous at a, then is differentiable at a.

2. If and are differentiable, then

If and are differentiable, then

If is differentiable, then .

f !x"

f #!x"

f !x"

$ f !t!x""% ! f #!t!x"" t#!x"

$ f !x"t!x"% ! f #!x"t#!x"

$ f !x" ! t!x"% ! f #!x" ! t#!x"

If is differentiable, then .

If exists, then

If , then .

10.

11. An equation of the tangent line to the parabola

at is .

12.

!tan

x" !

!sec

y $ 4 ! 2x!x ! 2"!$2, 4"

y ! x

(

lim

t!x" $ t!2"

x $ 2

! 80t!x" ! x

lim

f !x" ! f !r".f #!r"

)

! x

)

2x ! 1

)

(

)

f #!x"

T R U E - FA L S E Q U I Z

Openmirrors.com

CHAPTER 3 REVIEW

|| ||

197

1. The displacement (in meters) of an object moving in a straight

line is given by , where is measured in

seconds.

(a) Find the average velocity over each time period.

(i) (ii)

(iii) (iv)

(b) Find the instantaneous velocity when .

2. The graph of is shown. State, with reasons, the numbers at

which is not differentiable.

3– 4 Trace or copy the graph of the function. Then sketch a graph

of its derivative directly beneath.

3. 4.

;

5. The ﬁgure shows the graphs of , , and . Identify each

curve, and explain your choices.

6. Find a function and a number a such that

7. The total cost of repaying a student loan at an interest rate of

r% per year is .

(a) What is the meaning of the derivative ? What are its

units?

(b) What does the statement mean?

f #!10" ! 1200

f #!r"

C ! f !r"

lim

!2 ! h"

$ 64

! f #!a"

f )f #f

4 6_1

t ! 1

$1, 1.1%$1, 1.5%

$1, 2%$1, 3%

ts ! 1 ! 2t !

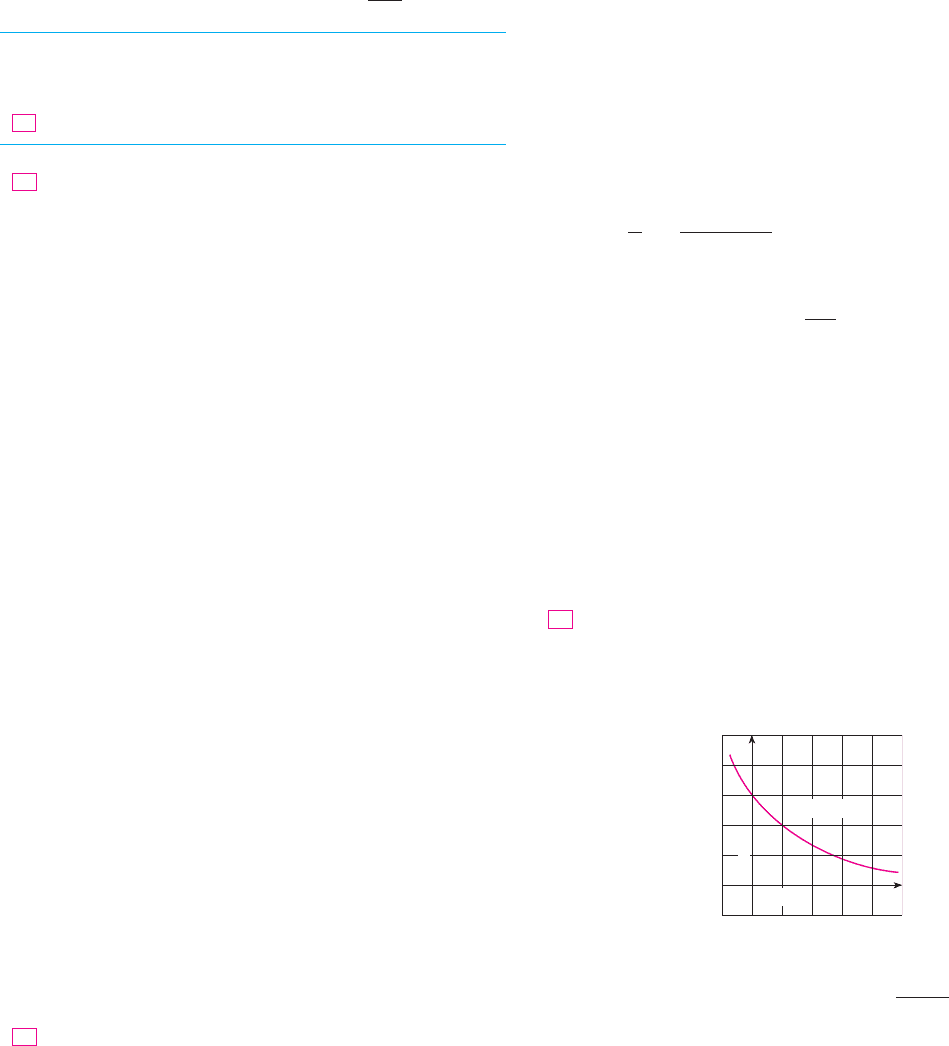
8. The total fertility rate at time t, denoted by , is an esti-

mate of the average number of children born to each woman

(assuming that current birth rates remain constant). The graph

of the total fertility rate in the United States shows the ﬂuctua-

tions from 1940 to 1990.

(a) Estimate the values of , , and .

(b) What are the meanings of these derivatives?

derivatives?

9. Let be the total value of US currency (coins and bank-

notes) in circulation at time . The table gives values of this

function from 1980 to 2000, as of September 30, in billions of

dollars. Interpret and estimate the value of .

10 –11 Find from ﬁrst principles, that is, directly from the

deﬁnition of a derivative.

10. 11.

12. (a) If , use the deﬁnition of a derivative to

ﬁnd .

(b) Find the domains of and .

;

to see whether your answer to part (a) is reasonable.

13– 40 Calculate .

13. 14.

15. 16.

17. 18.

19. 20.

y ! sin!cos x"y !

1 $ t

y !

x !

(

y ! 2x

! 1

y !

3x $ 2

2x ! 1

y !

y ! cos!tan x"y ! ! x

$ 3x

! 5"

f #f

f #!x"

f !x" !

3 $ 5x

f !x" ! x

! 5x ! 4f !x" !

4 $ x

3 ! x

f #!x"

C#!1990"

C!t"

1940 1960 1970 1980 19901950

1.5

2.0

2.5

3.0

3.5

y=F(t)

baby

boom

baby

bust

baby

boomlet

F#!1987"F#!1965"F#!1950"

F!t"

E X E R C I S E S

t 1980 1985 1990 1995 2000

129.9 187.3 271.9 409.3 568.6C!t"

53. At what points on the curve , ,

is the tangent line horizontal?

54. Find the points on the ellipse where the tangent

line has slope 1.

55. Find a parabola that passes through the

point and whose tangent lines at and

have slopes 6 and , respectively.

56. How many tangent lines to the curve ) pass

through the point ? At which points do these tangent

lines touch the curve?

57. If , show that

58. (a) By differentiating the double-angle formula

obtain the double-angle formula for the sine function.

(b) By differentiating the addition formula

obtain the addition formula for the cosine function.

59. Suppose that and , where

, , , , and .

Find (a) and (b) .

60. If and are the functions whose graphs are shown, let

, , and .

Find (a) , (b) , and (c) .

61–68 Find in terms of .

61. 62.

63. 64.

65. 66.

67. 68.

69–71 Find in terms of and .

69. 70.

71.

h!x" ! f ! t!sin 4x""

h!x" !

f !x"

t!x"

h!x" !

f !x" t!x"

f !x" ! t!x"

t#f #h#

f !x" ! t

(

tan

)

f !x" ! t!sin x"

f !x" ! sin! t!x""f !x" ! t!t!x""

f !x" ! x

t!x

"f !x" ! $ t!x"%

f !x" ! t!x

"f !x" ! x

t!x"

t#f #

C#!2"Q#!2"P#!2"

C!x" ! f ! t!x""Q!x" ! f !x"&t!x"P!x" ! f !x" t!x"

F#!2"h#!2"

f #!5" ! 11f #!2" ! $2t#!2" ! 4t!2" ! 5f !2" ! 3

F!x

" ! f !t!x""h!x" ! f !x" t!x"

sin!x ! a" ! sin x cos a ! cos x sin a

cos 2x ! cos

x $ sin

f #!x"

f !x"

x $ a

x $ b

x $ c

f !x" ! !x $ a"!x $ b"!x $ c"

!1, 2"

y ! x&!x ! 1

x ! 5x ! $1!1, 4"

y ! ax

! bx ! c

! 2y

! 1

0 , x , 2

y ! sin x ! cos x

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

31. 32.

33. 34.

35. 36.

37. 38.

39. 40.

41. If

, ﬁnd

42. If , ﬁnd .

43. Find if .

44. Find if .

45– 46 Find the limit.

45. 46.

47– 48 Find an equation of the tangent to the curve at the given

point.

47. , 48. ,

49–50 Find equations of the tangent line and normal line to the

curve at the given point.

49. ,

50. ,

51. (a) If , ﬁnd .

(b) Find equations of the tangent lines to the curve

at the points and .

;

on the same screen.

;

(d) Check to see that your answer to part (a) is reasonable by

comparing the graphs of and .

52. (a) If , , ﬁnd and .

;

(b) Check to see that your answers to part (a) are reasonable

by comparing the graphs of , , and .f )f #f

f )f #$

&2f !x" ! 4x $ tan x

f #f

!4, 4"!1, 2"y ! x

5 $ x

f #!x"f !x" ! x

5 $ x

!2, 1"x

! 4xy ! y

! 13

!0, 1"y !

1 ! 4 sin x

!0, $1"y !

$ 1

! 1

&6, 1"y ! 4 sin

lim

t l 0

tan

lim

x l 0

sec x

1 $ sin x

f !x" ! 1&!2 $ x"f

!n"

!x"

! y

! 1y )

t)!

&6"t!

" !

sin

f )!2"f !t" !

4t ! 1

y ! sin

(

cos

sin

)

y ! sin

(

tan

1 ! x

)

y !

!x $ 1"!x $ 4"

!x $ 2"!x $ 3"

y !

x tan x

x tan y ! y $ 1y ! tan

!sin

y !

sin mx

y !

cos

y !

!x !

y ! cot!3x

! 5"

y !

sin

sin!xy" ! x

$ y

y ! 1&

x !

y ! !1 $ x

cos y ! sin 2y ! xyy !

sec 2

1 ! tan 2

y ! sec!1 ! x

"xy

! x

y ! x ! 3y

y !

sin!x $ sin x"

y ! tan

1 $ x

198

|| ||

CHAPTER 3 DERIVATIVES

81. The angle of elevation of the sun is decreasing at a rate of

. How fast is the shadow cast by a 400-ft-tall

building increasing when the angle of elevation of the sun

is ?

;

82. (a) Find the linear approximation to

near 3.

(b) Illustrate part (a) by graphing and the linear

approximation.

to within 0.1?

83. (a) Find the linearization of at . State

the corresponding linear approximation and use it to give

an approximate value for .

;

(b) Determine the values of for which the linear approxima-

tion given in part (a) is accurate to within 0.1.

84. Evaluate if , , and .

85. A window has the shape of a square surmounted by a semi-

circle. The base of the window is measured as having width

60 cm with a possible error in measurement of 0.1 cm. Use

differentials to estimate the maximum error possible in com-

puting the area of the window.

86 – 88 Express the limit as a derivative and evaluate.

86. 87.

88.

89. Evaluate .

90. Suppose is a differentiable function such that

and . Show that .

91. Find if it is known that

92. Show that the length of the portion of any tangent line to the

astroid cut off by the coordinate axes is

constant.

2&3

! y

2&3

! a

2&3

$ f !2x"% ! x

f #!x"

t#!x" ! 1&!1 ! x

"f #!x" ! 1 ! $ f !x"%

f !t!x"" ! xf

lim

1 ! tan x

1 ! sin x

lim

cos

$ 0.5

lim

16 ! h

$ 2

lim

x l1

$ 1

x $ 1

dx ! 0.2x ! 2y ! x

$ 2x

! 1dy

1.03

a ! 0f !x" !

1 ! 3x

f !x" !

25 $ x

0.25 rad&h

4 ft

15 ft

72. A particle moves along a horizontal line so that its coordinate

at time is , , where and are

positive constants.

(a) Find the velocity and acceleration functions.

(b) Show that the particle always moves in the positive

direction.

73. A particle moves on a vertical line so that its coordinate at

time is , .

(a) Find the velocity and acceleration functions.

(b) When is the particle moving upward and when is it

moving downward?

interval .

;

(d) Graph the position, velocity, and acceleration functions

for .

(e) When is the particle speeding up? When is it slowing

down?

74. The volume of a right circular cone is , where

is the radius of the base and is the height.

(a) Find the rate of change of the volume with respect to the

height if the radius is constant.

(b) Find the rate of change of the volume with respect to the

radius if the height is constant.

75. The mass of part of a wire is kilograms, where

is measured in meters from one end of the wire. Find the

linear density of the wire when m.

76. The cost, in dollars, of producing units of a certain com-

modity is

(a) Find the marginal cost function.

(b) Find and explain its meaning.

item.

77. The volume of a cube is increasing at a rate of 10 .

How fast is the surface area increasing when the length of an

edge is 30 cm?

78. A paper cup has the shape of a cone with height 10 cm and

radius 3 cm (at the top). If water is poured into the cup at a

rate of , how fast is the water level rising when the

water is 5 cm deep?

79. A balloon is rising at a constant speed of . A boy is

cycling along a straight road at a speed of . When he

passes under the balloon, it is 45 ft above him. How fast is

the distance between the boy and the balloon increasing

3 s later?

80. A waterskier skis over the ramp shown in the ﬁgure at a

speed of . How fast is she rising as she leaves the

ramp?

30 ft&s

15 ft&s

5 ft&s

2 cm

&min

C#!100"

C!x" ! 920 ! 2x $ 0.02x

! 0.00007x

x ! 4

(

1 !

)

V !

h&3

0 , t , 3

t / 0y ! t

$ 12t ! 3t

cbt / 0x !

! c

CHAPTER 3 REVIEW

|| ||

199

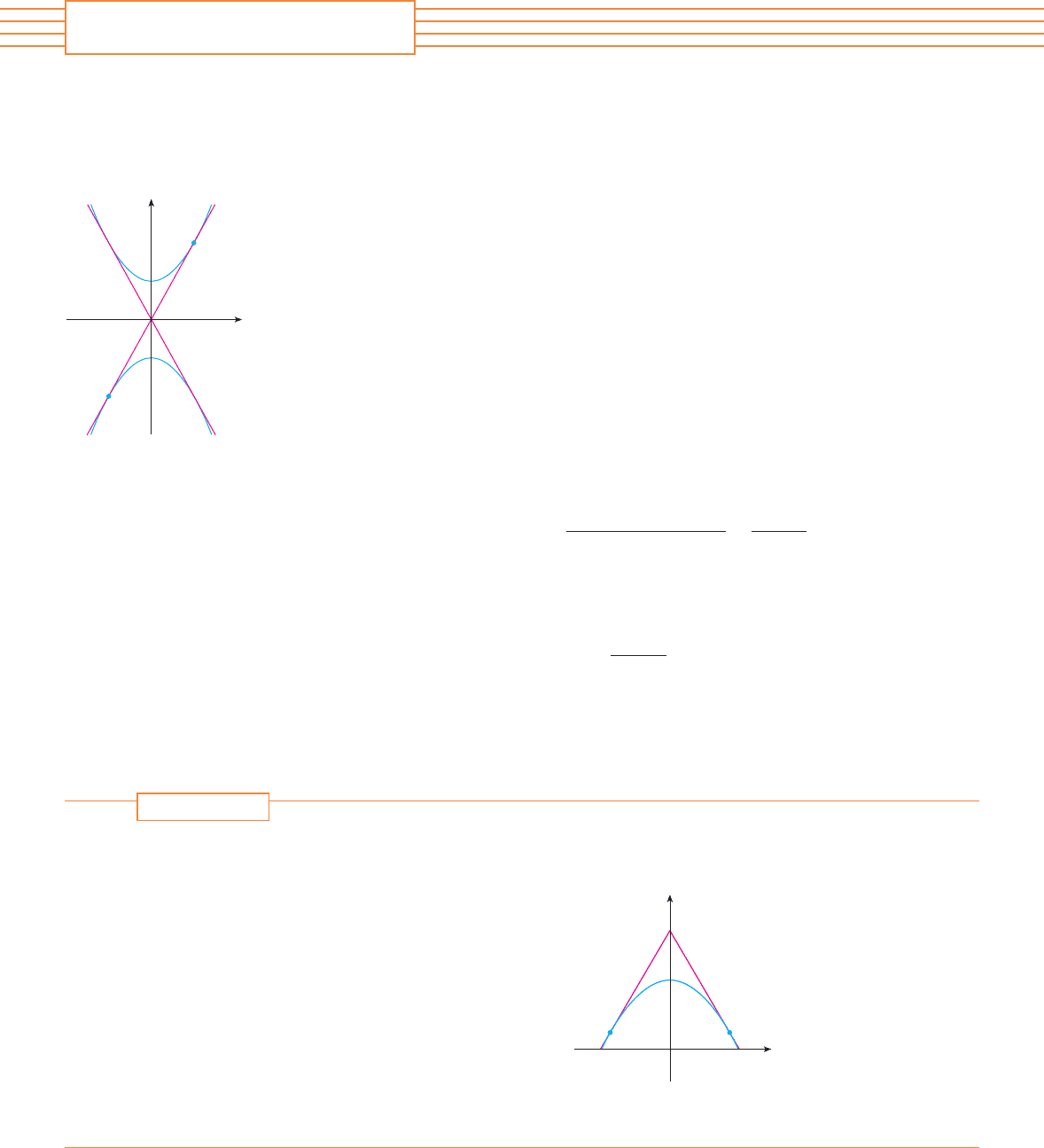
P R O B L E M S P L U S

200

Before you look at the example, cover up the solution and try it yourself ﬁrst.

EXAMPLE 1 How many lines are tangent to both of the parabolas and

? Find the coordinates of the points at which these tangents touch the

parabolas.

SOLUTION To gain insight into this problem, it is essential to draw a diagram. So we sketch

the parabolas (which is the standard parabola shifted 1 unit upward)

and (which is obtained by reﬂecting the ﬁrst parabola about the x-axis). If

we try to draw a line tangent to both parabolas, we soon discover that there are only two

possibilities, as illustrated in Figure 1.

Let P be a point at which one of these tangents touches the upper parabola and let a

be its x-coordinate. (The choice of notation for the unknown is important. Of course we

could have used b or c or or instead of a. However, it’s not advisable to use x in

place of a because that x could be confused with the variable x in the equation of the

parabola.) Then, since P lies on the parabola , its y-coordinate must be

Because of the symmetry shown in Figure 1, the coordinates of the point Q where the

tangent touches the lower parabola must be .

To use the given information that the line is a tangent, we equate the slope of the line

PQ to the slope of the tangent line at P. We have

If , then the slope of the tangent line at P is . Thus the condi-

tion that we need to use is that

Solving this equation, we get , so and . Therefore the

points are (1, 2) and ($1, $2). By symmetry, the two remaining points are ($1, 2)

and (1, $2).

1. Find points and on the parabola so that the triangle formed by the -axis

and the tangent lines at and is an equilateral triangle.

P Q

B C

xABCy ! 1 $ x

PROBLEM S

a ! '1a

! 11 ! a

! 2a

1 ! a

! 2a

f #!a" ! 2af !x" ! 1 ! x

1 ! a

$ !$1 $ a

a $ !$a"

1 ! a

!$a, $!1 ! a

1 ! a

.y ! 1 ! x

y ! $1 $ x

y ! x

y ! 1 ! x

y ! $1 $ x

F I G U R E 1

;

2. Find the point where the curves and are tangent to each

other, that is, have a common tangent line. Illustrate by sketching both curves and the

common tangent.

3. Show that the tangent lines to the parabola at any two points with

-coordinates and must intersect at a point whose -coordinate is halfway between

and .

4. Show that

5. Suppose is a function that satisﬁes the equation

for all real numbers x and y. Suppose also that

(a) Find . (b) Find . (c) Find .

6. A car is traveling at night along a highway shaped like a parabola with its vertex at the origin

(see the ﬁgure). The car starts at a point 100 m west and 100 m north of the origin and travels

in an easterly direction. There is a statue located 100 m east and 50 m north of the origin. At

what point on the highway will the car’s headlights illuminate the statue?

7. Prove that .

8. Find the th derivative of the function .

9. The ﬁgure shows a circle with radius 1 inscribed in the parabola . Find the center of the

circle.

10. If is differentiable at , where , evaluate the following limit in terms of :

lim

f !x" $ f !a"

f #!a"a 0 0af

y=≈

y ! x

f !x" ! x

&!1 $ x"n

!sin

x ! cos

x" ! 4

n$1

cos!4x ! n

&2"

f #!x"f #!0"f !0"

lim

f !x"

! 1

f !x ! y" ! f !x" ! f ! y" ! x

y ! xy

sin

1 ! cot x

cos

1 ! tan x

(

! $cos 2x

pxqpx

y ! ax

! bx ! c

y ! 3!x

$ x"y ! x

$ 3x ! 4

201

P R O B L E M S P L U S

F I G U R E F O R P RO B LE M 6