Stevenson J. Power system analysis
Подождите немного. Документ загружается.

316
CHAPTER 8 THE IMPEDANCE MODEL AN D
NETWORK
CALCULATIONS
We use these procedures, for example, when studying economic operation In
Chap. 13.
8.7 MUTULY COUPLED BNCHES
I
N
Zbus
So far we have not considered how to incorporatc mutually couplcd clcments of
the network into
Zh
u
s'
The proccdures for doing so are not dicult. But they
are somewhat unwieldy as we now demonstrate by extending the
Z
h
u
s
building
algorithm to provide for addition to thc network of one
p
air of mutually coupled
branches.l One of the branchcs may be aducd to
Z
u
rig
using thc
app
ro
p
riate
procedurc of Scc. K3, and thc qucstion rcmaining is how to add thc sccond
branch so that it mutually cou
p
lcs with thc branch already included in
Z
u
ri
g'
Wc
consider bus ® already established within Z
u
rig
in the fo llowing fo ur cases,
which continue the numbering system introduced in Sec. 8.3.
CASE 5. Adding mutually coupled
Zb fm existing bus ® to new bus ®
. Let us assume that the branch impedance Z
a
is already added to the energized
·network between nodes
and ® of Fig. 8.11. The bus impedance a trix
Z
orig then includes Z
a
and the existing buses , ®, a
d ® as shown.
Be.tween bus ® and the new bus ® of Fig. 8.11 it is required to add the
branch impedance Zb' which is mutually coupled to Za through mutual
impedance Z
M
' The voltage-drop equations for the two coupled branches are
given in Eq.
(7.9) and repeated here as
(8.78
)
(8
.79
)
where f
a
is the branch current ow in Z
a
from bus
to bus ® and the
current fb from bus ® to bus ® equals the negative of current injection f
q
.
Solving Eq. (8.78) for fa and substituting the result along with Ih
=
-Iq in Eq.
(8.79) give
(8.80)
In terms of bus voltages the voltage drops across the branches are given by
V = (V - V ) and Vb
=
(V - Vq ), and substituting these relationships in Eq.
a
m
n
p
IFor a more general treatment, see G. W. Stagg and A. H. EI-Abiad, Computer Methods in Power
,
System Analys, McGraw-Hill, Inc., New York, 1968.
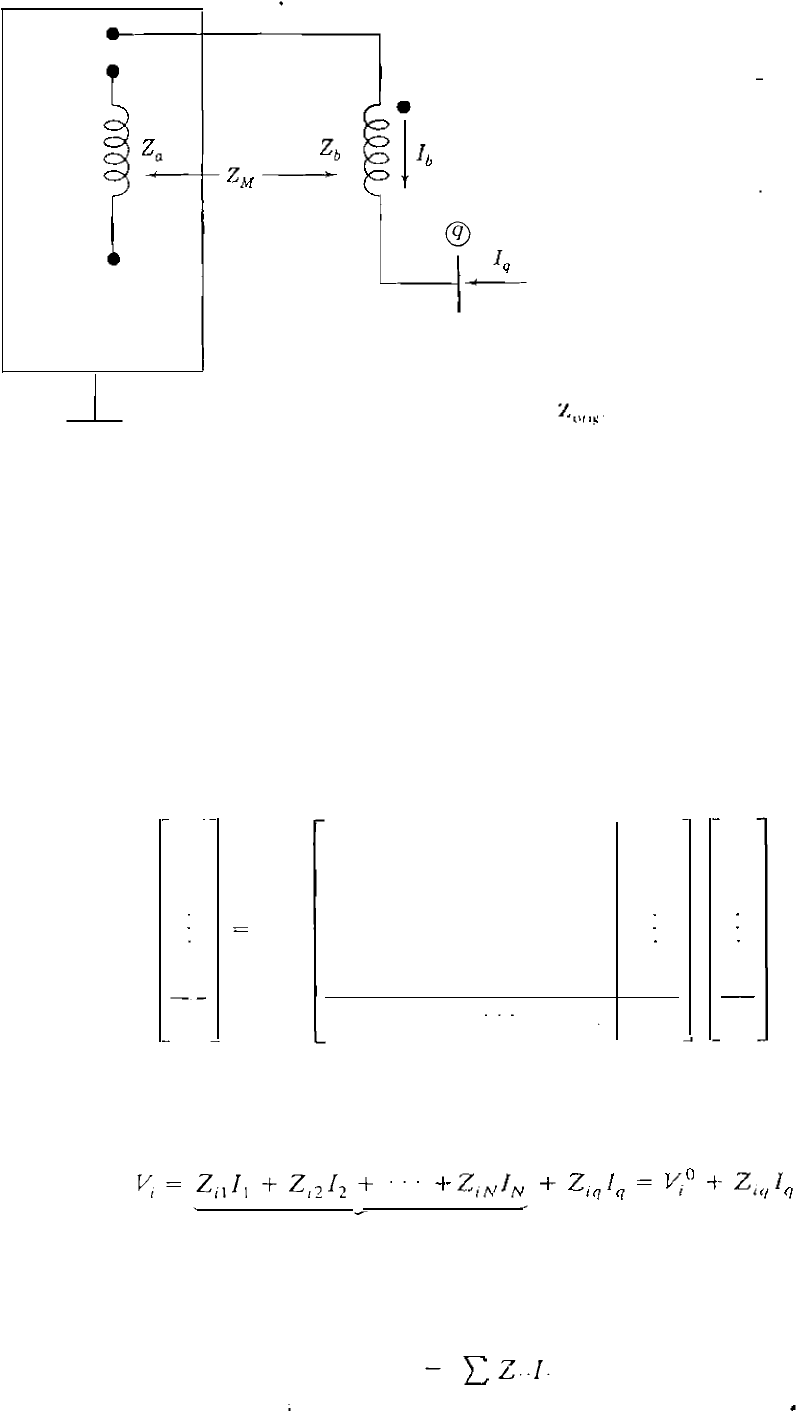
8.7
MUTUALLY COUPLED BRANCHES IN
Z
b
u
,
317
Zorig ®
•
I
,
I
®
FIG RE 8. 11
Adding m\
l
tually coupled branch Z" to
(8.80) yields
Reference
Z
M
[Z
�
1
V
=
V
·- -
(
V -
V)
- - -z 1
q
p
Z
m
n
Z
b
q
a
n
(
8.81
)
This equation gives the volta
g
e at new bus
®
with both mutually coupled
branches now included in the network. The bus impedance matrix for the
system augmented by new bus ® is given by
®
V
I
Z
l
q
1
1
V
2
Z
2
Q
1
2
Z
o
r
ig
(
8.8
2)
V
N
Z
N
q
I
N
V
q
®
Z
q
l
Z
q
2
Z
q
'
Z
q
q
I
q
and it is now required to nnd expressions ror the new clements with subscripts q
in row q and column q. A typical row i of Eq. (8.82) may be written in the form
V
O
/
where for convenience we have denoted
N
V
O
-
"Z.
I
.
r
L
I}}
j�)
(8
.
83)
(
8
.
8
4)
318
CHAPTER 8 THE IMPEDANCE MODEL AND NETWORK CALCULATIONS
Setting i equal to m, n, p, and q in Eq. (8.83) gives expressions for
V
m
,
V
n,
V
p
,
and Vq , which can be substituted in Eq. (8.81) to obtain
_
(
2
1�
_
2 ) I
2
b q
II
(
8.85)
Equation (8.85) is a general equation for the augmented network regardless of
the particular values of the current injections. Therefore, when 1
q
= 0, it must
follow from Eq. (8.85) that
2
V
a = Va -� (Va -
V
a
)
q
p
2
m
n
a
(8.86)
Substituting in Eq. (8.86) for v,�, Vn o, Vpo, and V
q
O from Eq. (8.84), collecting
terms, and equating coecients of lj on both sides of the resultant equation, we
nd tha t
(8.87)
for all values of j from 1 to N but not including q. Thus, except for 2qq, Eq.
(8.87) tells us how to calculate the entries in the new row q of the bus
impedance matrix using the known values of 2
M
, ZU, and certain elements of
Z
o
rig' Indeed, to obtain the entry in row q, each clement of row n is subtracted
from the corresponding element of row m and the dierence multiplied by
2
m
/Za is then subtracted from the corresponding element of row p. Thus, only '
rows m, n, and p of
Z
orig
enter into the calculations of new row q. Because of
symmetry, the new column q of Eq. (8.82) is the transpose of the new row q,
and so Zq
J
=
Zjq. The expression fo r the diagonal element Zqq is determined by
considering all currents except lq set equal to zero and then equating the
coecients of 1 q on both sides of Eq. (8.85), which gives
> (8.88)
This equation shows that there is a sequence to be followed in determining the
new elements of the bus impedance matrix. First, we calculate the elements 2qj
of the new row q (and thereby 2jq of column q) employing Eq. (8.87), and then
we use the newly calculated quantities 2mq, Znq' and 2pq to nd 2qq froI
?
Eq.
(8.88).
H.7 MUTUALLY COUPLED RANCHES IN Z
b
ul
319
There are three other cases of interest involving mutually coupled
branches.
CASE 6. Adding mutually coupled Zb from existing bus ® to reference
For this case the procedure is basically a special application of Case 5. First,
between bus ® and new bus ® we add impedance Zb coupled by mutual
impedance Z
M
to the impedance Za already included in
Z
orig'
Then, we
short-circuit bus ® to the reference node by setting
V
q equal to zero, which
yields the same matrix equation as Eq. (8.82) except that
V
q is zero. Thus, for
the modied bus impedance matrix we proceed to create a new row q and
column q exactly the same as in Case 5. Then, we eliminate the newly formed
row and column by the standard technique of Kron reduction since V is zero in
the column of vol tages 0 f Eq. (8.82).
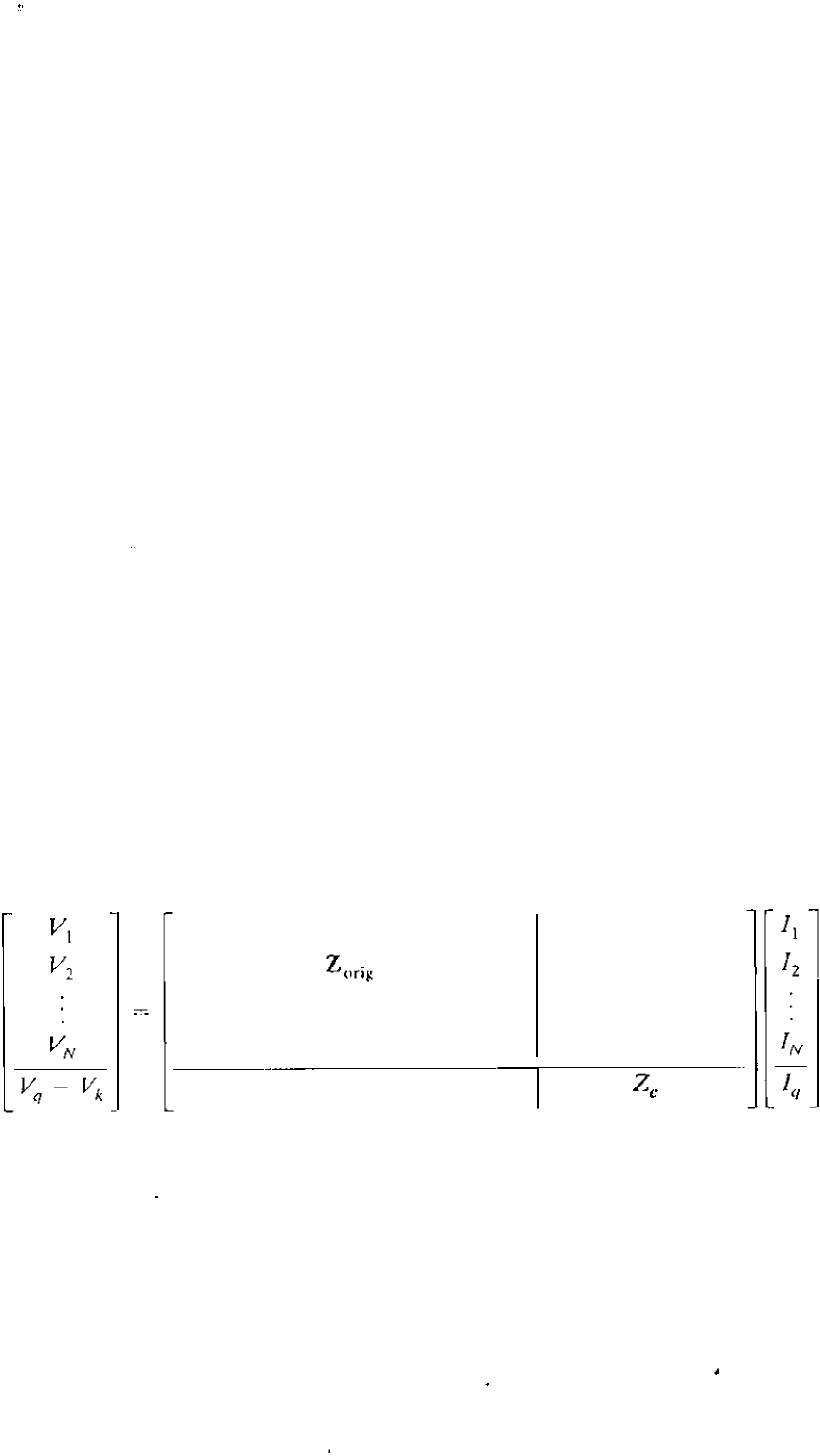
CASE 7. Adding mutually coupled Zh bctween cxisting buses ® and
The proce dure in this case essen tially combines Cases 5 and 4. To begin,
we follow the procedure of Case 5 to add the mutually coupled branch
impedance Zh from existing bus ® to a new temporary bus ®, recognizing
that Za is already part of
Z
orig'
The result is the augmented matrix of Eq. (8.82)
whose q-elements are given in Eqs. (8.87) and (8.88). Next, we short-circuit bus
® to bus ® by adding a branch of zero impedance between those buses. To
do so, we apply Case
4
to Eq. (8.82) as follows. Since (
V
q -
V
k) is required to be
zero, we nd an expression for that quantity by subtracting row k from row q in
Eq. (8.82) and then use the result to replace the existing row q of Eq. (8.82). By
symmetry as in Case 4, a new column follows directly from the transpose of the
new row, and we obtain
(row q -w k) of Eq . (8.82)
(col. q -col. k)
of
Eq. (8.82)
(
8.89
)
wh
ere Zc equals the sum CZ
q
q
+
Z -2Zqk) of elements drawn from Eq.
(8.82). Because (
V
q -
- 2008 — 2025 «СтудМед»
