Степанов А.Г. Динамика машин
Подождите немного. Документ загружается.


Для фундаментальных функций уравнения, характеризующие условие ортогональности,
имеют вид
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
j n X x X x dx X x X x dx X x X x dx
m
p
X x X x
m
p
X x X x
j n X x dx X x dx X x dx
m
p
X
m
p
X l
j n j n j n
l
l l
l
l
j n j n
j j j j j
l
l l
l
l
≠ + + +
+ + =
= + + + + ≠
+
−
+
−
∫∫∫
∫∫∫
;
;
; .
3 3 4 4
0
0
1
3 3
3
3
2 2
4
2
1
3
2
3
2
0
0
4
3
4
3
0
0 0
(8.63)
Квадрат нормы весовых и фундаментальных функций задачи
( ) ( ) ( ) ( ) ( )
.0
2
3
2
3
1
0
2
4
0
22
3
2
7
3
4
lX
p
m
X
p
m
dxxXdxxXdxxXX
jj
l
ll
l
j
l
jjj
++++=
∫ ∫∫
−
+
В заключение, еще раз отметим, что полученные выражения позволяют определить
постоянные интегрирования уравнения (8.16).
8.5. СВОБОДНЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
Если вязкоупругую механическую систему вывести из состояния равновесия, а затем
возмущающее воздействие убрать, то в системе возникнут колебания относительно
положения равновесия.
Процесс свободных колебаний описывается уравнением (8.9). Приняв в качестве решения
уравнения (8.15), запишем
( )
( ) ( )
( )
( ) ( )
u x t X x T t
u x t
t
X x T t
j j
j
j
j
, ;
,
.= =
=
∞
=
∞
∑ ∑
∂
∂
1 1
(8.64)
где X
j
(x) - фундаментальная функция вязкоупругого элемента;
T
j
(t) - функция времени.
Эти функции в общем виде определяются по уравнениям (8.14). Запишем функцию
T
j
(t) и ее производную
( )
( )
( ) ( )
[ ]
T t e C t D t
T t e D C t C D t
j
t
j j j j
t
j j j j j j j j j j
j
j
( ) ,
.
= +
= − − +
−
−
µ
µ
ω ω
ω µ ω ω µ ω
cos sin
cos sin
(8.65)
В разделе 8.3. для различных механических систем определены собственные числа
λ
j j
k l=
, коэффициенты A
j
и B
j
, следовательно, и фундаментальная функция
( )
X x A k x B k x
j j j j j
= +cos sin .
Ряды (8.64) будут решением задачи только в том случае, если коэффициенты C
j
и D
j
для каждой гармоники таковы, что эти ряды сходятся и сходятся ряды, получающиеся после
двукратного почленного дифференцирования первого соотношения по x и по t.
273
273

Решения (8.64) должны еще удовлетворять начальным условиям. Для этого
подбираются постоянные C
j
и D
j
. Подставим в равенство (8.65) t = 0, зависимости (8.64)
будут
( )
( )
( )
( )
( )
( )
( )
f x u x C X x
x
u x
t
D C X x
j j
j
j j j j j
j
= =
= = −
=
∞
=
∞
∑
∑
, ,
,
.
0
0
1
1
ϕ
∂
∂
ω µ
(8.66)
Умножим обе части равенства (8.66) на
( )
X x
n
и проинтегрируем в пределах от c до
d, получим
( ) ( ) ( ) ( )
( ) ( )
( )
( ) ( )
f x X x dx C X x X x dx
x X x dx D C X x X x dx
n j j n
j
c
d
c
d
n j j j j j n
j
c
d
c
d
=
= −
=
∞
=
∞
∑
∫∫
∑
∫∫
1
1
,
.ϕ ω µ
(8.67)
Из соотношений (8.67) определяются постоянные C
j
и D
j
.
Ранее было отмечено, что с целью уменьшения трудоемкости вычислительных
процессов по определению заданных функций даже при условии, что последние имеют
аналитические выражения, иногда целесообразно использовать численные методы.
При исследовании вынужденных колебаний правая часть волнового уравнения
может быть нелинейной. В этом случае частное решение неоднородного уравнения не
может быть выражено в квадратурах и необходимо перейти к численным методам решения
задачи, в которой в которых общее решение однородного уравнения определяется
коэффициентами C
j
и D
j
или начальными условиями функции T
j
(t). Поэтому, для того,
чтобы получить значения T
j
(t) и
( )T t
j
при численном интегрировании необходимо ввести
начальные условия для второго уравнения (8.13)
( )
( ) ( ) .T t T t b T t
j j j
+ + =2 0
2
µ
Так как это уравнение имеет решения (8.65) то, очевидно, при t = 0
T C T D C
j j j j j j j
( ) ;
( ) .0 0= = −ω µ
Для определения этих коэффициентов необходимо воспользоваться соотношениями
(8.41), (8.42), (8.48), (8.52), (8.56), (8.58), (8.61), (8.62), которые характеризуют
ортогональность фундаментальных функций исследуемых механических систем.
8.5.1. ВЕТВЬ УРАВНОВЕШИВАЮЩЕГО КАНАТА
Расчетная схема этой задачи приведена на рис. 8.2. Фундаментальная функция
определяется уравнением (8.17)
( ) ( )
X x j
x
l
j
= −sin
π
2
2 1 .
274
274

Коэффициент B
j
принят равным единице.
В разделе 8.4.1 показано, что для механической системы, представляющей ветвь
уравновешивающего каната и характеризующейся системой функций, ортогональной на
отрезке [0, l], справедливы приведенные ниже зависимости
( ) ( )
n j X x X x dx
j n
l
≠ =
∫
; ,0
0
( )
n j X x dx
j
l
= ≠
∫
; .
2
0
0
Поэтому из (8.67) получим
( ) ( ) ( )
C X x dx f x X x d x
j j
l
j
l
2
0 0
∫ ∫
=
,
( )
( ) ( ) ( )
D C X x dx x X x dx
j j j j j j
ll
ω µ ϕ− =
∫∫
2
00
.
Из этих выражений определяются C
j
и D
j
( ) ( ) ( ) ( )
C
f x X x dx
X
D C
x X x dx
X
j
j
l
j
j
j
j j
j
l
j
= = +
∫ ∫
0
1
2
0
1
2
1
;
ω
µ
ϕ
, (8.68)
где
X
j
1
2
- квадрат нормы функции
X x
j
( )
, определенной из уравнения (8.42).
Коэффициенты C
j
и D
j
, вычисленные по формулам (8.68) называются коэффициентами
Фурье функций f (x) и ϕ(x) по системе ортогональных функций [59].
Для определения начальных условий, т. е. функций
( )
f x
и
( )
ϕ x
, предположим, что к
нижнему сечению уравновешивающего каната (рис. 8.2) приложена сила S, а затем, при
начальной скорости v
0
, эта сила убирается. Начинаются свободные колебания. Под
действием силы S канат длиной l удлинится на величину
( )
u l
S
c
, ,0 =
где
c
EF
l
=
- жесткость каната, Н⋅м
-1
.
Так как деформация
( )
u l,0
распределится равномерно по всей длине каната, то,
очевидно, можно записать
275
275

( )
( )
f x
S
EF
x
x
v
l
x
=
=
,
.ϕ
0
(8.69)
Подставив значения
( ) ( )
X x f x
j
,
и
( )
ϕ x
в (8.68) получим
( )
( )
C
S
EF
x
l
j x dx
l
j x dx
j
l
l
=
−
−
∫
∫
sin
sin
2
2
π
π
2
2 1
2 1
0
0
.
( )
( )
( )
( )
( )
S
EF
x
l
j xdx
S
EF
j
l
j
l j
l
j
l
sin
sin cos
π
π
π
π
π
2
2 1
2
2 1
2
2 1
2
2 1
2
2 1
0
2
− =
−
−
−
−
−
∫
( )
sin
π
2
2 1 1j − = +
- для нечетного j = 1, 3, 5...;
( )
sin
π
2
2 1 1j − = −
- для четного j = 2, 4, 6...;
( )
cos
π
2
2 1 0j − =
- для всех j, поэтому
( )
( )
( )
x
l
j x dx
l
j
j
l
sin
π
π
2
2 1
4
2 1
1
2
2
2
1
0
− =
−
−
−
∫
.
Знаменатель равен
( )
( )
( )
sin - sin
2
π
π
π
2
2 1
1
2
2 2 1
2 1
1
2
0
l
j x dx l
l
j
j l
l
∫
= −
−
− =
.
Тогда
( )
( )
C
S
c j
j
j
=
−
−
−
8
2 1
1
2
2
1
π
.
(8.70)
Для определения коэффициента D
j
найдем значение интеграла, стоящего в числителе
второго выражения (8.68)
( )
( )
v
l
j x dx
v l
j
l
0
0
0
2
2 1 2
2 1
sin
π
π
− =
−
∫
.
Тогда
276
276

( )
D
v
j
C
j
j
j j
=
−
+
1
4
2 1
0
ω
π
µ .
(8.71)
Если усилие S было снято в момент, когда скорость v
0
= 0, коэффициент
D C
j
j
j
j
=
µ
ω
.
Если представить канат упругим элементом, то
µ
j
= 0
, и при v
0
= 0,
D
j
= 0
.
Таким образом, процесс свободных колебаний ветви уравновешивающего каната
описывается уравнениями
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
u x t T t X x
u x t
t
T t X x
u x t
t
T t X x
j j
j
j j
j
j j
, ;
,
;
,
;
=
=
=
=
∞
=
∞
∑
∑
1
1
2
2
∂
∂
∂
∂
( )
( )
( )
( )
( )
( )
T t e C t D t
T t e M t N t
T t e P t Q t
j
t
j j j j
j
t
j j j j
j
t
j j j j
j
j
j
= +
= +
= +
−
−
−
µ
µ
µ
ω ω
ω ω
ω ω
cos sin
cos sin
cos sin
;
;
,
где
( )
( )
M D C N C D
P N M Q M N
j j j j j j j j j j
j j j j j j j j j j
= − = − +
= − = − +
ω µ ω µ
ω µ ω µ
; ;
; .
Сила упругости каната определится из уравнения (8.3), которое можно представить
( )
( ) ( )
[ ]
( )
S x t EF T t T t X x
j j к j j j
,
.= +
′
µ
(8.72)
Полученные уравнения показывают, что ветвь уравновешивающего каната совершает
гармонические колебания.
Для того чтобы оценить влияние каждой гармоники на амплитуды колебаний
предположим, что канат - упругий элемент,
µ
к
и
µ
j
равны нулю, а усилие S убирается при
скорости
v
0
0=
, тогда из уравнения (8.71)
D
j
= 0
, а из уравнения (8.70)
( )
( )
C
S
c j
j
j
=
−
−
−
8 1
2 1
1
2
2
π
.
Если в качестве критерия выбрать амплитудное значение силы упругости, то
последняя при принятых допущениях определится как
277
277
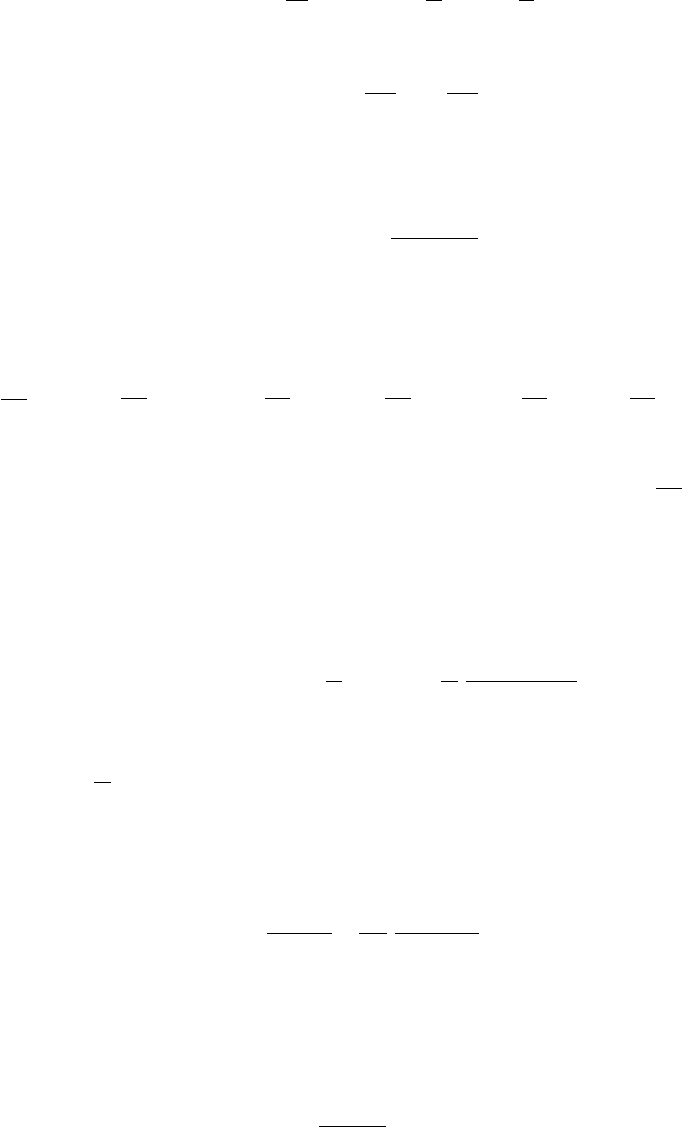
( )
( ) ( )
S x t EFC
l
j j
x
l
t
j j j
, .= − −
π π
ω
2
2 1
2
2 1cos cos
Амплитудные значения будут при
t
j j
= 0 2, , ...
π
ω
π
ω
.
Например, для верхнего сечения каната
( )
x = 0
амплитудные значения усилий будут
( )
( )
( )
S S
j
j
j
0 0 4
1
2 1
1
, .=
−
−
−
π
Таким образом, для 1 ÷ 6 гармоник
S
S
1
1 274= , ;
S
S
2
0 424= − , ;
S
S
S
S
S
S
S
S
3 4 5 6
0 255 0 182 0 14 0 115= = − = = −, ; , ; , ; , .
Отношение, суммы усилий шести гармоник к статической силе равно
S
S
j
j
=
=
∑
0 94991
1
6
,
.
Если проанализировать сходимость ряда для закономерности, характеризующей
координату, то максимальное значение деформации будет при
t = 0
и
x l= ,
поэтому при
v
0
0=
и
h
j
= 0
( )
( )
( )
u l C j
S
c
j
j j
, .0
2
2 1
8
2 1
2
2
= − =
−
sin
π
π
Величина
S
c
u
ст
=
- статическая деформация каната, имеющего жесткость c, под
действием силы S.
Тогда
( )
( )
( )
u l
u
j
j
ст
j
,
.
0
8 1
2 1
2
1
2
=
−
−
−
π
Эти величины соответственно для шести гармоник равны 0,811; 0,09; 0,032; 0,0165; 0,01;
0,0067. Сумма шести гармоник
( )
u l
u
j
ст
j
,
, .
0
0 966
1
6
=
=
∑
Таким образом, при исследовании динамических процессов ветви уравновешивающего
каната сумма шести гармоник характеризует искомый результат с точностью 4 - 5 %.
Пример 8.8. Исследовать закономерности формирования усилия в верхнем и среднем сечениях
уравновешивающего каната при свободных колебаниях.
Предположим, к нижнему сечению уравновешивающего каната приложена статическая сила S = 1
кН и при скорости v = 0 эта сила снимается. Начинается процесс свободных колебаний.
Исследования выполнены с помощью пакета Mathcad 7. Ниже приведена программа реализации
вычислительного процесса и построения графических зависимостей.
278
278

λ
j( )
π
2
2 j
⋅
1
−
( )
⋅:=
k j( )
λ
j( )
l
:=
b j( ) k j( ) a
⋅:= µ
j( )
δ
k
2
π⋅
b j( )
⋅:= µ
1( ) 0.156
=
µ
k
j( )
2
µ
j( )
⋅
b j( )( )
2
:=
ω
j( ) b j( )
2
µ
j( )
2
−:= ω
1( ) 6.553
=
f x( )
S
k
E F
k
⋅
x
⋅:= φ
x( ) v
0
:=
X j x
,
( ) sin k j( ) x
⋅
( )
:=
X1 j x
,
( ) k j( ) cos k j( ) x
⋅
( )
⋅:=
Ïðîâå ðèì, âûïîëíÿåòñÿ ëè óñëîâèå îðòîãîíàëüíîñòè?
0
l
xX 1 x
,
( ) X 2 x
,
( )
⋅
⌠
⌡
d
yields
0
Ñëåäîâàòåëüíî êîýôôèöèåíòû
C
k
j( )
è
D
k
j( )
ìîæíî îïðåäåëÿòü ïî ôîðìóëàì:
C
k
j( )
0
l
xf x( ) X j x
,
( )
⋅
⌠
⌡
d
0
l
xX j x
,
( )( )
2
⌠
⌡
d
:=
D
k
j( )
1
ω
j( )
0
l
x
φ
x( ) X j x
,
( )
⋅
⌠
⌡
d
0
l
xX j x
,
( )( )
2
⌠
⌡
d
µ
j( ) C
k
j( )
⋅+
⋅:=
C
k
1( ) 7.306
=
D
k
1( ) 0.174
=
T
k
j t
,
( ) exp
µ
j( )
−
t
⋅
( )
C
k
j( ) cos
ω
j( ) t
⋅
( )
⋅
D
k
j( ) sin
ω
j( ) t
⋅
( )
⋅+
( )
⋅:=
M
k
j( ) D
k
j( )
ω
j( )
⋅
C
k
j( )
µ
j( )
⋅−:=
N
k
j( ) C
k
j( )
ω
j( )
⋅
D
k
j( )
µ
j( )
⋅+
( )
−:=
T1
k
j t
,
( ) exp
µ
j( )
−
t
⋅
( )
M
k
j( ) cos
ω
j( ) t
⋅
( )
⋅
N
k
j( ) sin
ω
j( ) t
⋅
( )
⋅+
( )
⋅:=
S
dk
j t
,
( )
E F
k
⋅
T
k
j t
,
( )
µ
k
j( ) T1
k
j t
,
( )
⋅+
( )
⋅
X1 j 0
,
( )
⋅
S
cm
:=
t 0 .01
,
3
..:=
1
10
j
S
dk
j t
,
( )
¥
=
0 0.5 1 1.5 2 2.5 3
1.5
1
0.5
0.5
1
1.5
сумма 10 гармоник
1 гармоника
2 гармоника
3 гармоника
время. с
усилие, кН
1
10
j
S
dk
j t
,
( )
¥
=
S
dk
1 t
,
( )
S
dk
2 t
,
( )
S
dk
3 t
,
( )
t
ÓÐÀÂÍÎÂÅØÈÂÀÞÙÈÉ ÊÀÍÀÒ
Ïðîãðàììà 8.1
Èäåíòèôèêàòîðû:
n
-÷èñëî êàíàòîâ;
E
-ìîäóëü óïðóãîñòè êàíàòîâ;
F
k
-ïëîùàäü âñåõ ïðîâîëî÷åê â êàíàòå;
l
-äëèíà êàíàòà;
p
-ñóììàðíàÿ ëèíåéíàÿ ïëîòíîñòü êàíàòîâ;
S
k
-óñèëèå â êàíàòå;
δ
k
-ëîãàðèôìè÷åñêèé äåêðèìåíò êîëåáàíèé;
Îñòàëüíûå îáîçíà÷åíèÿ ñîîòâåòñòâóþò îáîçíà÷åíèÿì, ïðèíÿòûì â ðàçäåëå 8.3.8.
Íåêîòîðûå îòêëîíåíèÿ ñâÿçàíû ñî ñïåöèôèêîé ïðîãðàììèðîâàíèÿ â ïàêåòå Mathcad 7.
n 4
:=
F
k
7.16310
4
−
⋅:=
E 12.8 10
10
⋅:=
p 26
:=
l 900
:=
v
0
0
:= δ
k
.15
:=
a E
F
k
p
⋅
n
⋅:=
a 3.756 10
3
×=
S
cm
9.81 n
⋅
p
⋅
l
⋅:=
S
cm
9.182 10
5
×=
S
k
S
cm
:=
279
279
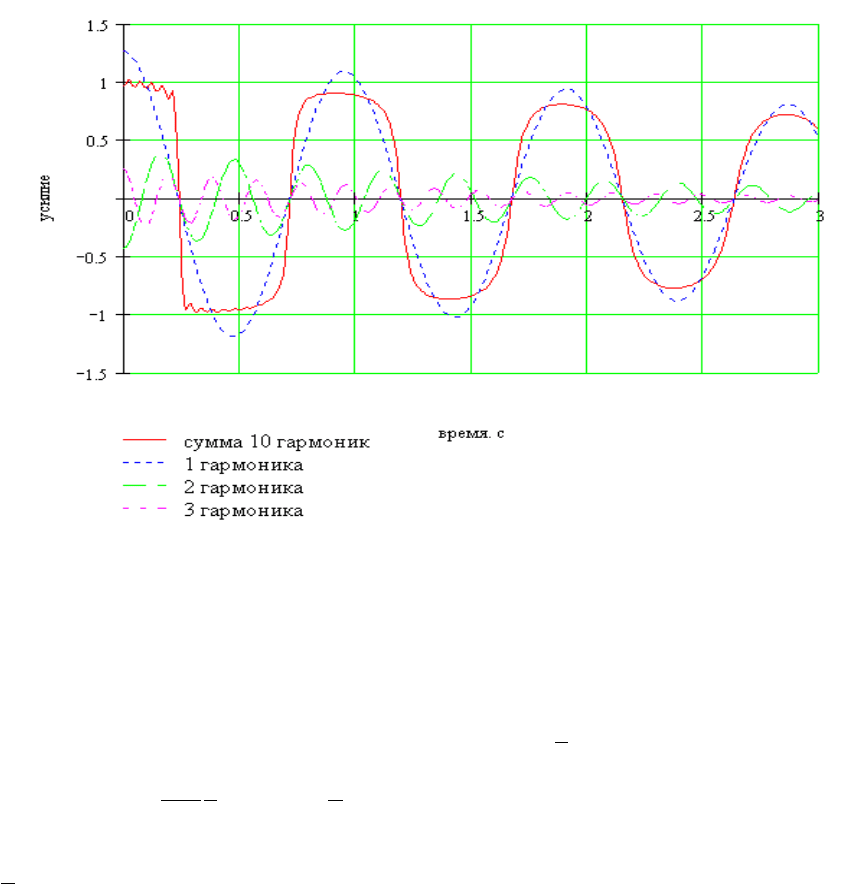
Рис. 8.14. Относительная величина усилия в верхнем сечении каната
Видно, что в начале процесса свободных колебаний в течение 1/4 периода динамическая
составляющая усилия остается постоянной, а затем резко уменьшается. Высокочастотные составляющие
суммарной кривой объясняются сложением 10 гармоник. Очевидно, если количество гармоник увеличить,
то суммарная характеристика усилий, на протяжении этого времени, будет постоянной, а ее величина равна
единице. Высшие гармоники быстро затухают и колебательный процесс становится гармоническим.
Для сечения каната, расположенного на середине (
x
l
= =
2
450
м), фундаментальная функция
( )
( )
( )
( ) ( )
X j к j
j
l
l
к j j1 450
2
2 1, =
= −
cos cos
4
λ
π
. Характеристика колебательного процесса будет
абсолютно аналогична характеристике, показанной на рис. 8.14. Амплитудная величина уменьшается в
cos
π
4
0 7≈ ,
раза.
8.5.2. МАССА, ПОДВЕШЕННАЯ НА КАНАТЕ.
Эквивалентная схема этой задачи показана на рис. 8.1. Если в качестве начальной
координаты принять точку крепления каната к верхнему основанию x = c = 0, а точка
крепления к массе имеет координату x = l = d, то выражения (8.67) имеют вид
( ) ( ) ( ) ( )
( ) ( )
( )
( ) ( )
f x X x dx C X x X x dx
x X x dx D C X x X x dx
n j j n
j
ll
n j j j j j n
j
ll
=
= −
=
∞
=
∞
∑
∫∫
∑
∫∫
,
.
1
00
1
00
ϕ ω µ
Используя выражение, характеризующее ортогональность фундаментальных
функций задачи (8.48), нетрудно заметить, что из этих выражений можно записать
280
280

( ) ( ) ( ) ( )
( ) ( )
[ ]
( ) ( )
( ) ( ) ( )
( ) ( )
( )
( )
при
при
j n
f x X x dx C
m
p
X l X l
x X x dx D C
m
p
X l X l
j=n;
f x X x dx C X x dx
x X x dx D C X x dx
n
l
j j n
j
n j j j j
j
j n
l
n n n
ll
n n n n n n
ll
≠
= −
= − −
=
= −
∫
∑
∑
∫
∫∫
∫∫
=
∞
=
∞
;
,
,
,
.
0
1
1
0
2
00
2
00
ϕ ω µ
ϕ ω µ
(8.73)
В первом выражении сумма распространяется на все значения j от 1 до ∞, кроме j = n.
Таким образом, выражения, в которых есть функции f (x) и
ϕ( )x
, можно записать
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
f x X x dx C
m
p
X l X l C X x dx
x X x dx D C
m
p
X l X l D C X x dx
n j j n n n
l
j
l
n j j j j j n n n n n n
l
j
l
= − +
= − − + −
∫
∑
∫
∫
∑
∫
=
∞
=
∞
2
0
1
0
2
0
1
0
,
( ) [ ][ ] ( ) .ϕ ω µ ω µ
(8.74)
В этих уравнениях неизвестны величины C
j
, C
n
и D
j
,
D
n
. Для того чтобы установить
взаимосвязь между ними, воспользуемся начальными условиями (8.69). Для координаты x
= l запишем
( ) ( )
( ) ( )
f l C X l l D C X l
f l C X l l D C X l
j j
j
j j j j j
j
n n
n
n n n n n
j
= = −
= = −
=
∞
=
∞
=
∞
=
∞
∑ ∑
∑ ∑
; ( ) ( ) ( );
; ( ) ( ) ( ).
1 1
1 1
ϕ ω µ
ϕ ω µ
Умножим обе части этих равенств на X
n
(l) и X
j
(l), а затем проинтегрируем в пределах
от 0 до l, получим
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
f l X l dx C X l X l dx
f l X l dx C X l X l dx
n
l
j
j
l
j n
j
l
n
j
l
n j
0
1
0
0
1
0
∫
∑
∫
∫
∑
∫
=
=
=
∞
=
∞
;
.
ϕ ω µ
ϕ ω µ
( ) ( ) ( ) ( ) ( ) ;
( ) ( ) ( ) ( ) ( ) .
l X l dx D C X l X l dx
l X l dx D C X l X l dx
n
l
j j j j j n
j
l
j
l
n n n n n j
n
l
= −
= −
∫
∑
∫
∫
∑
∫
=
∞
=
∞
0
1
0
0
1
0
281
281
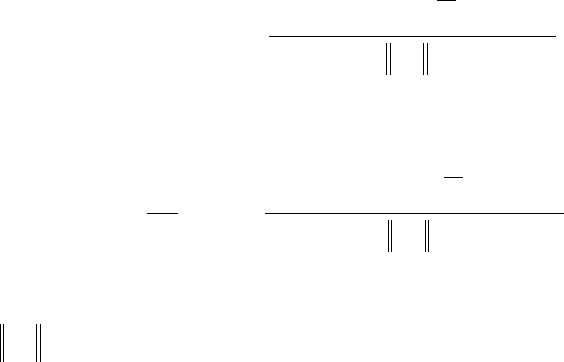
В этих выражениях в отличие от (8.67) все подынтегральные выражения - суть постоянные
величины, поэтому
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
j n f l X l l C X l X l l f l C X l
j n f l X l l C X l l f l C X l
n j j n
j
j j
j
j n j n n
≠ = =
= = =
=
∞
=
∞
∑ ∑
; ; ;
; ; .
1 1
2
j n l X l l D C X l X l l l D C X l
j n l X l l D C X l l l D C X l
n j j j j j n
j
j j j j j
j
j n n n n n n n n n n
≠ = − = −
= = − = −
=
∞
=
∞
∑ ∑
; ( ) ( ) ( ) ( ) ( ) ; ( ) ( ) ( );
; ( ) ( ) ( ) ( ) ; ( ) ( ) ( ).
ϕ ω µ ϕ ω µ
ϕ ω µ ϕ ω µ
1 1
2
Еще раз напомним, что сумма
С
j
j=
∞
∑
1
и
D
j
j=
∞
∑
1
распространяется на все значения j
от 0 до ∞, кроме j = n, поэтому можно записать
( ) ( ) ( )
( ) ( )
C X l f l C X l
D C X l l D C X l
j j n n
j
j j j j j n n n n n
j
= −
− = − −
=
∞
=
∞
∑
∑
1
1
,
( ) ( ) .ω µ ϕ ω µ
(8.75)
Подставив выражения (8.75) в (8.74), определим
( ) ( ) ( ) ( )
C
f x X x dx
m
p
f l X l
X
n
n n
l
n
=
+
∫
0
2
2
,
(8.76)
D C
x X x d x
m
p
l X l
X
n
n
n n
n n
l
n
= +
+
∫
1
0
2
2
ω
µ
ϕ ϕ( ) ( ) ( ) ( )
,
где
X
j
2
2
- квадрат нормы фундаментальной и весовой функций, определенной из
уравнения (8.50).
Значительно проще коэффициенты C
n
и D
n
определяются если использовать
свойства механической системы, которые говорят о том, что если к упругим связям
присоединены сосредоточенные массы, то тогда производные фундаментальных функций
ортогональны.
Для этого продифференцируем выражения (8.66) и умножим обе части на
′
X x
n
( )
, а
затем проинтегрировав, получим
′ ′
=
′ ′
∫
∑
∫
=
∞
f x X x dx C X x X x dx
n
l
j
j
l
j n
( ) ( ) ( ) ( ) .
0
1
0
282
282
