Спасский Б.А. Лекции по теории обработки геофизических данных
Подождите немного. Документ загружается.

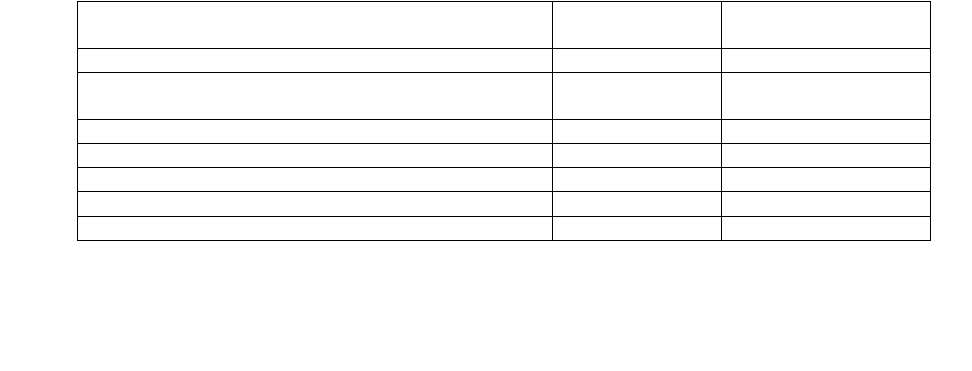
Характеристика основных классов сейсмических волн, регистрируемых
при работе в методе отраженных волн
Класс сигналов
Частотный
диапазон, Гц
Диапазон кажущихся
скоростей, м/с
Отраженные волны 10-80 1500 -
Преломленные, рефрагировнные и многократные
отраженно-преломленные волны 5-50 1000-20000
Поверхностные волны релеевского типа 3-30 100-1000
Многократно отраженные волны 10-60 1500 -
Случайные помехи, микросейсмы 10-100 -
Электрические наводки 48-52 -
Звуковые волны 60-125 300-350
Используя при производстве фильтрации различия в динамических (по частотному составу, энергии,
амплитудам и т.п.) и кинематических (по кажущимся скоростям или форме годографа) свойствах полезных волн
и волн-помех, можно на основе некоторых математических процедур добиться увеличения соотношения сигнал-
помеха.
В зависимости от характеристики входных сигналов и конкретной цели обработки различают несколько
видов фильтраций (рис. 7.1). Поскольку их разделение базируются на разных признаках, то один и тот же вид
фильтрации может быть одновременно отнесен к нескольким видам. Например, фильтрация может быть
инвариантной (постоянной) во времени, пространственно-временной, согласованной и выполняться в частотной
области. Т.е. в названии фильтра выносятся определения, отличающие его от других.
При цифровой обработке чаще используется линейные преобразования (линейная фильтрация), основные
свойства которых сводятся к следующему. Если функция на входе фильтра представляет собой сумму сигналов,
то получить результат фильтрации можно, применив фильтр к каждому входному сигналу и просуммировав
результат (принцип суперпозиции). Изменение последовательности проведения отдельных процедур
фильтрации не влияет на конечный результат. При этом выходной сигнал пропорционален входному сигналу
(принцип пропорциональности).
Если преобразования не обладают указанным свойством, то они относятся к классу нелинейных фильтров.
Чаще в геофизике используются линейные фильтры.
Важной характеристикой фильтрации является поведение оператора фильтра h(t) во времени. Если
коэффициенты оператора фильтра или частотная его характеристика не изменяются во времени (оператор
остается постоянным), то такие фильтры называются инвариантными во времени. В противном случае имеет
место переменная во времени фильтрация.
Обычно в сейсморазведке при регистрации полевых записей полоса пропускания аппаратурных устройств
остается неизменной во всем временном диапазоне, например, в полосе от 10 до 100 Гц. При этом с увеличением
времени записи частотный состав отраженных волн меняется вследствие явления частотно зависимого
поглощения, Вследствие этого высокочастотные составляющие регистрируемого сигнала поглощаются тем
больше, чем глубже залегает отражающий горизонт. Поэтому состав колебаний с увеличением времени
смещается в сторону нижних частот. С учетом этого в последние годы все шире используется переменная во
времени полосовая фильтрация (рис. 7.3), когда в каждый момент времени оператор фильтра настроен на
фактическую форму сигнала (на его амплитудно-частотный спектр).
Практически это сводится к применению нескольких инвариантных во времени фильтров. Каждый из них
работает в пределах некоторого интервала времени с перекрытием 0,2 - 0,3 с. В зонах перекрытия отсчеты
фильтруемых трасс суммируются с весами, линейно менявшимися от единицы до нуля и от нуля до единица
(рис. 7.3). Параметры переменной во времени фильтрации подбирают по результатам тестов.
7.4. Многомерная (пространственно-временная) фильтрация
Фильтры различаются также по числу каналов, принимающих участие в формировании одного выходного
(отфильтрованного) отсчета сигнала. Название фильтра в этом случае, зависит от того, по какой координате
измеряются отсчеты, служащие для формирования одного выходного значения фильтра. Фильтрация
называется временной, когда на вход фильтра подается одна функция, меняющаяся во времени. В том случае,
когда выходное значение фильтра формируется из ряда отсчетов, взятых на нескольких полевых записях,
записанных в разных точках пространства, но полученных в один и тот же момент времени, фильтрация
называется пространственной.
Наиболее общим видом многоканальной (многомерной) фильтрации является пространственно-временная
фильтрация, когда выходной сигнал формируется из записей нескольких каналов, расположенных в разных
точках пространства (профиля или площади), а в пределах каждого канала регистрации данных для проведения
фильтрации используются по одному или нескольким отсчетам, взятым в различные моменты времени.
Очевидно, что в сейсморазведке одноканальная фильтрация может быть только временной, а пространственная
и пространственно-временная фильтрация будут многоканальными. Например, к пространственной (двумерной
пространственно-пространственной) фильтрации можно отнести процедуру сглаживания карты какого-то
параметра р(Х, У). Да и сам процесс построения карты является, по сути, своеобразной пространственной
фильтрацией, поскольку при построении карты (проведении изолиний параметров) исключаются их мелкие
случайные погрешности.
31
В практике цифровой обработки известно множество различных пространственно-временных (двумерных)
фильтров. Рассмотрим для примера суть пространственно-временной (часто называемой f-k или F-K)
фильтрации, которая широко используется в сейсморазведке для подавления регулярных волн-помех
(поверхностных, кратно-отраженных и других, имеющих протяженные годографы). При этом необходимо
обратить внимание на следующее.
При преобразовании временных функций в частотную область вместо периода колебаний Т (временного
параметра) мы имеем спектральные параметры: частотны ω = 2πf = 2π/T (круговую частоту) или f = 1/Т
(циклическую частоту).
При переходе от координаты пространства в частотную область вместо пространственной координаты х мы
получаем параметр k
X
(пространственную частоту или волновое число). Они связаны между собой
соотношением
k
х
= 2π/λ = 2πf / V
каж
= ω / V
каж
, (7.8)
где λ = V
каж
·Т = V
каж
/f – это длина волны, а V
каж
- кажущаяся скорость (скорость движения фронта волны
вдоль поверхности наблюдения). Кажущаяся скорость определяется по наклону годографов регулярных
колебаний (по величине Δx/Δt). Чем ближе траектория волны регистрируемой на поверхности к вертикали, тем
ближе ее годограф к горизонтальной линии, и тем выше значение V
каж
. Соответственно, годографы регулярных
волн с высокой скоростью имеют небольшой наклон (близки к горизонтальной линии). Чем меньше скорость
регулярной волны, тем больший наклон имеет ее годограф (тем ближе он к вертикали).
В таблице 1 показаны пределы изменения величин частот f и кажущихся скоростей для разных классов волн,
которые чаще всего регистрируются на сейсмограммах в методе отраженных волн. На рис. 7.4 показаны (для
упрощения) лишь соответствующие этим волнам линии годографов.
Можно считать, что каждая сейсмограмма представляет собой пространственно-временную функцию s(t, x).
Хорошо видно (рис. 7.4 а), что в пространственно-временном представлении годографы различных классов
волн-помех накладываются на полезные однократно отраженные колебания (1), что усложняет их корреляцию и
дальнейшую обработку. Так годографы поверхностных волн (3) пересекают годографы однократных волн (1),
что ведет к плохой их корреляции в зонах интерференции.
Если перейти в частотную область, т.е. найти прямое двумерное преобразование Фурье, то получим (рис. 7.4
б) комплексный двумерный частотный спектр S(ω, k
x
) или S(f, k
x
). Иначе
S(f, k
x
) ↔ s(t, x).
В частотной области (рис. 7.4 б) по вертикали откладываются значения частоты f, а по горизонтали значения
пространственной частоты k
x
(числа волны). А линии, выходящие из начала координат (точки 0), соответствуют
различным значения V
каж
. Причем, в частотной области, наклон линейных годографов пропорционален величине
1/V
каж
, т.е. годографы соответствующие небольшим значениям V
каж
близки к горизонтали, а большим значениям
V
каж
– близки к вертикали.
Вследствие этого в плоскости (f, k
x
) точки, соответствующие отраженным волнам (1) располагаются в
верхней части рисунка 7.4 б вблизи оси частот (они имеют частоты близкие к 50 Гц и высокие кажущиеся
скорости в пределах от 1500 м/с и более). А поверхностные волны, характеризующиеся невысокими значениями
частот (3-30 Гц) и скоростей (100 – 1000 м/с) располагаются в юго-восточной части рисунка. Иначе говоря, в
плоскости (f, k
x
) происходит разделение местоположения зон регистрации этих волн. Поэтому, достаточно
применить фильтрацию, где в качестве граничного параметра будет выступать значение кажущейся скорости
V
каж, гран
, величина которой меньше скорости отраженных волн, но больше чем поверхностных. Для нашего
примера это может быть V
каж
= 1250 м/с.
Значения амплитудно-частотной характеристики такого фильтра H(f, k
x
)=H(V
каж
) будут (рис. 7.5 а ) равны 1
для значений скоростей выше V
каж, гран
= 1250 м/с, и будут равны 0 для тех, которые меньше V
каж, гран
. Обнуление
конусообразной зоны в пространстве (f, k) – это и есть одна из реализаций процесса, известного под названием
пространственной f-k-фильтрации. Поскольку линии соответствующие различным значениям V
каж
имеют разный
наклон, но сходятся в нулевой точке, и рисунок напоминает раскрытый веер (рис.7.5 б), то иногда некоторые
варианты f-k-фильтрации называют веерной или скоростной.
При создании f-k фильтров необходимо учитывать дискретность функций, которые подвергаются
фильтрации. Для этого необходимо правильно выбирать не только шаг квантования Δt во временной области, но
и соблюдать правильность выбора шага дискретизации сигналов по пространственной оси Δх. Именно поэтому
фильтрацию необходимо проводить в диапазоне частот ±ω
N
/2 и пространственных частот в диапазоне ±k
N
/2. В
противном случае будут возникать зеркальные (боковые) частоты.
Иногда фильтрацию по кажущимся скоростям проводят и по временным разрезам (на конечных стадиях
обработки). Ее называют в этом случае когерентной фильтрацией. Ее применение позволяет подчеркнуть
(усилить) оси синфазности в заданном диапазоне их наклонов.
7.5. Согласованные фильтры
Если известно, что и некотором полосе частот энергия полезного сигнала преобладает над энергией помех,
то, пропуская частотные составляющие спектра только в этом диапазоне, можно понизить уровень помех на
записях. Форма частотной характеристики фильтра в этом случае согласуется со спектром (формой) полезного
сигнала или спектра помех. Такие фильтры называются согласованными. Возможно использование нескольких
вариантов согласованных фильтров.
32
Например, фильтры нижних частот ФНЧ пропускают с большими амплитудами частотные составляющие в
области нижних частот (2.2 б), а высокочастотные компоненты сигнала пропускаемого через фильтр в
значительной степени ослабляются (не пропускаются через фильтр). Полоса пропускания отделяется от полосы
подавления так называемой граничной частотой f
гр
или ω
гр
= 2π f
гр
. Считается, что граничная частота
определяется в том случае, когда отношение амплитуды пропускаемой компоненты к максимальной амплитуде
становится менее величины 0,707 или менее - 3 дБ.
Поскольку процедуры фильтрации при обработке геофизических данных проводятся с дискретными
функциями, то в качестве верхней граничной частоты ФНЧ обычно используется частота Найквиста f
N
= f
дис
/2
или ω
N
, где f
дис
– частота квантования сигналов во времени или пространстве (частота дискретизации). Если
верхняя граничная частота будет больше частоты Найквиста, то в полосу пропускания будут попадать так
называемые боковые или зеркальные частоты, которые являются помехами. При использовании фильтров
нижних частот их f
гр
часто ограничиваются частотой f
гр
= f
макс
= f
N
/2. Поэтому фильтр в этом случае является
антиаляйсинговым, т.е. не позволяет усиливать величины амплитуд зеркальных или боковых частот (не
пропускает их). Частота f
макс
соответствует самой высокой частоте, которая попадает в полосу пропускания
используемого фильтра без искажений. Напомним, что при выборе шага дискретизации геофизических функций
во времени обычно используется формула
Δt = 1/(4 f
макс
).
Фильтры верхних частот (рис.2.2 в) или ФВЧ, наоборот, пропускают без ослабления высокочастотные
компоненты регистрируемых сигналов (выше f
гр
или ω
гр
), но не пропускаю нижние частоты (меньшие, чем f
гр
или ω
гр
).
Полосовые фильтры (рис. 2.2 г) пропускают без ослабления частотные компоненты в некоторой полосе,
ограниченной верхней и нижней граничными частотами. Некоторые них являются режекторными, т.е. они не
пропускают (ослабляют) частотные компоненты, попадающие в полосу гашения. Классическим не
пропускающим является режекторный фильтр (рис. 2.2 д), который вырезает составляющие сигнала близкие к
промышленной частоте (в диапазоне 46-54 Гц).
При создании операторов реальных фильтров необходимо учитывать возможность образования помех,
относящихся к явлениям Гиббса. Они возникают в связи с использованием в практике обработки ограниченных
во времени функций (в отличие от бесконечных функций, с которыми оперируют в теории) и использованием
для этого так называемых прямоугольных «функций-окон». Из теории следует, что чем длиннее оператор
фильтра использующегося при проведении фильтрации (в соответствие с формулой (1)), тем больше крутизна
боковых срезов его амплитудно-частотной характеристики. В этом случае вблизи краевых частей АЧХ, в зоне
резкого изменения крутизны бокового среза, возникают резкие высокочастотные изменения кривой АЧХ,
которые и называются эффектом Гиббса. За счет этого явления часть компонент из области гашения
пропускается. Чтобы избежать явлений Гиббса широко используют рекурсивную фильтрацию или используют
фильтры с плавными, нерезкими изменениями боковых срезов частотных характеристик.
В связи с этим говорят, что оператор фильтра должен иметь форму динозавра: маленькую головку на тонкой
шее, большое туловище и тонкий хвостик. Другими словами, импульсные реакции (операторы фильтров во
временной области), которые используются при производстве фильтрации, в начальной и конечной частях
должны характеризоваться плавными (небольшими) изменениями амплитуд.
7.6. Обратная фильтрация
Наиболее просто смысл обратной фильтрации можно рассмотреть на примере сейсмических записей.
Начальный сейсмический сигнал s
0
(t) (рис. 7.6 а), возникающий при возбуждений упругих колебаний с помощью
взрывчатых веществ, вначале имеет форму, близкую к единичному импульсу δ(t). Ему соответствует
широкополосный амплитудно-частотный спектр |S
0
(f)|. При распространении в среде и регистрации начальный
сигнал преобразуется в сигнал s(t), соответствующий на сейсмической трассе однократно отраженным волнам.
При прохождении в среде сигнал s(t) становится более растянутым во времени, его частота понижается
(рис.7.6 б). Его спектр |S(f)| - становится более узким и обедняется высокочастотными составляющими. Вместе с
тем, чтобы провести наиболее детальное расчленение сейсмического разреза на отдельные пласты, желательно
убрать из каждой трассы волны помехи и преобразовать каждый однократно отраженный сигнал s(t) к
первоначальному виду s
0
(t). Иными словами, необходимо сжать сигнал s(t) во временной области до единичного
импульса (или близкого к нему). Сейсмическая трасса в этом случае преобразуется в импульсную трассу,
близкую по виду к распределению значений коэффициентов отражения во времени.
Если считать, что реальная геологическая среда является некоторой системой L, характеризующейся своей
импульсной реакцией h(t) и амплитудно-частотной характеристикой |H(f)|, то можно процесс распространения
начального импульса в реальной среде можно записать в виде уравнений
s(t) = s
0
(t) * h(t) (7.8)
или
|S(f)| = |S
0
(f)| · |H(f)|. (7.9)
Из формулы (7.9) следует, что спектр начального сигнала может быть получен, если спектр отраженного
сигнала умножить на частотную характеристику |H´(f)| = 1/|H(f)|, то есть обратную |H(f)|:
|S
0
(f)| = |S(f)| · |H´(f)| = |S
0
(f)| · 1/|H(f)|. (7.10)
33

С учетом этого, фильтрация, проводимая с использованием формулы (7.10), и получала название обратной.
Во временной области в соответствии с уравнением (7.8), чтобы получить функцию s
0
(t), нужно провести
процедуру обратную свертке (которую в теории называют конволюцией). Иначе говоря, необходимо провести
деконволюцию. Отсюда и пошло второе название обратной фильтрации. Применение обратной фильтрации или
деконволюции к сейсмической трассе предполагает (в теории) ее преобразование в распределение единичных
импульсов s
0
(t) ≈ δt, амплитуда которых пропорциональна коэффициентам отражения (различию акустических
жесткостей на границах пластов).
Однако на практике решение такой задачи является недостижимым, поскольку помимо однократно
отраженных волн на сейсмических трассах присутствуют многочисленные помехи, интенсивность которых
часто превышает интенсивность полезных волн. Поэтому цель обработки в каждом конкретном случае зависит
от степени превышения энергии полезных сигналов над уровнем помех или величины отношения
сигнал/помеха. В этом случае для решения оптимальным образом поставленной перед фильтрацией задачи
применяются некоторые специальные критерии, а сами фильтры, с точки зрения выбранного критерия,
называются оптимальными (Сильвия, Робинсон, 1983).
Так при небольших значениях отношения сигнал/помеха (полезный сигнал по интенсивности значительно
слабее помехи) основной задачей обработки становится задача обнаружения сигнала на фоне помех за счет
увеличения отношения сигнал/помеха. В такой неблагоприятной ситуации следует добиваться максимально
возможной амплитудной разрешенности записи с тем, чтобы удалось хотя бы обнаружить присутствие в ней
полезных волн. При этом придется смириться с тем, что, возможно произойдет искажение формы записи и
уменьшение временной ее разрешенности. Обнаружение сигнала достигается путем подавления тех
составляющих частотного спектра, в которых мала доля энергии полезных волн относительно помех. Критерием
оптимальности фильтрации в этом случае служит получение на выходе фильтра максимума отношения
пикового (максимального) значения сигнала к среднеквадратическому уровню помех. Такой фильтр
называется фильтром обнаружения, он относится чаще всего к классу согласованных фильтров.
При проведении такой фильтрации происходит повышение амплитудной разрешенности записей, что ведет
к уменьшению ширины спектра отфильтрованного сигнала и к увеличению его длительности во времени. А это
явление сопровождается снижением временной разрешенности записи (возможности раздельного выделения
быстро следующих друг за другом во времени сигналов).
Таким образом, для повышения временной разрешенности сигналов необходимо сокращать их
длительность, и, следовательно, расширять спектр. А это - снижает их амплитудную разрешенность. Повышение
же амплитудной разрешенности - снижает их временную разрешенность. Поэтому на практике добиваются
компромиссного решения: достижение наибольшей временной разрешенности записи при обеспеченности
достаточной амплитудной разрешенности. Фильтрация должна способствовать обнаружению на сейсмической
трассе максимального числа полезных волн при удовлетворительной точности оценок их кинематических и
динамических параметров.
Другой критерий, широко используемый для создания оптимальных фильтров, предложил Н. Винер. Он
заключается в применении такого фильтра c оператором h(t) к сигналу s(t), когда среднеквадратическое от-
клонение отфильтрованного сигнала y(t) от желаемого результата g(t) по множеству случаев минимально, т.е.
{[s(t)*h(t) – g(t)]
cред
}
2
= min, (7.11)
где s(t)*h(t) = y(t) – подвергшийся фильтрации сигнал (на выходе фильтра).
Так, если полезный сигнал по амплитуде сравним с помехой, то в этом случае можно ставить задачу не
только обнаружения полезных волн, но и оценки их некоторых динамических параметров. С этой целью
необходимо с помощью фильтрации воспроизвести сигнал с наименьшими потерями, но максимально сильно
ослабить помехи. В качестве критерия оптимальности фильтрации принимают требование минимума величины
среднего квадратического отклонения профильтрованных колебаний от известной формы сигнала полезных
волн. Фильтр, реализующий подобное преобразование сейсмических колебаний, называется оптимальным
фильтром воспроизведения.
Если полезный сигнал значительно сильнее помехи, то в таких благоприятных условиях обнаружение
полезных волн не вызывает затруднений, поскольку высока амплитудная разрешенность записи. В этом случае
перед частотной фильтрацией можно ставить задачу сокращения длительности импульсов регистрируемых волн
– задачу повышения временной разрешенности сейсмической записи за счет некоторого снижения избыточной
амплитудной разрешенности. Критерием оптимальной фильтрации становится условие минимального среднего
квадратического отклонения амплитуд выходного сигнала от амплитуд заданного импульса короткой
длительности. Фильтр, осуществляющий такое преобразование, называют оптимальным обратным фильтром
или собственно деконволюцией.
Как было сказано ранее, сжать все сигналы до единичного импульса невозможно, поэтому задача обратного
оптимального фильтра - сделать спектр сигнала равномерным в области, где сигнал преобладает над помехой, и
ослабить спектр помехи в области, где она преобладает над сигналом. Применение такого фильтра позволяет в
среднем по множеству случаев его применения "сжать" полезные импульсы наилучшим способом в той степени,
которая возможна при данном соотношении спектров сигнала и помехи.
34

При построении таких фильтров нужно учитывать, что невозможно в принципе восстановить в сигнале
частоты, которые полностью подавлены. А при восстановлении частотных составляющих, ослабленных до
уровня шумов, одновременно происходит значительное усиление шума.
В практике сейсморазведки широко используется еще один оптимальный фильтр – оптимальный
корректирующий фильтр. Он строится на основе требования минимальности среднего квадратичного
отклонения профильтрованной записи от импульса любой заданной формы. Так корректирующий
(формирующий) фильтр общего вида позволяет преобразовать неизвестный входной сигнал в сигнал заданной
формы. Он реализуется в виде последовательной комбинации двух фильтров: обратного фильтра сжатия,
преобразующего входные сигналы в единичные импульсы, и фильтра, форма оператора которого соответствует
желаемой форме выходного сигнала.
Это позволяет выравнивать форму записи полезных волн по всем трассам, зарегистрированным в различных
условиях и тем самым устранять влияние нестабильности условий возбуждения и приема. Корректирующая
фильтрация проводится обычно перед суммированием трасс для повышения его эффективности.
Применяются также предсказывающая (прогностическая) деконволюция. В этом случае, зная форму
полезного сигнала, можно построить фильтр, который спрогнозирует появление этого сигнала в будущем (в
последующие моменты времени). При этом можно применять, как минимум, две модификации такого фильтра.
Первая из модификаций основана на том, что если форма колебаний известна, то по начальной фазе
опознанного на записях импульса можно прогнозировать появление последующих фаз колебаний (хвостовых
его частей) и подавить (обнулить) их. Результатом фильтрации будет сокращение длительности полезного
сигнала.
Во второй модификации предполагается по обнаруженным на трассах однократным волнам проведение
прогнозирования времен появления кратных волн и соответствующие вычитание их из сейсмических записей. В
практике морских работ широко используются так называемые дереверберационные фильтры, которые
позволяют предсказывать появление многократно отраженных колебаний (ревербераций), возникающих в толще
водного слоя между поверхностью и дном моря.
В этом случае считается, что предсказуемая часть входного сигнала состоит из волн-спутников и
ревербераций (кратных волн), а непредсказуемая - из полезных однократных отраженных волн от более
глубоких горизонтов. Поэтому фильтром предсказания называют фильтр, свертка которого с входным сигналом
позволяет получить значение этого входного сигнала в последующие моменты времени.
Если затем из входного сигнала вычесть рассчитанную последовательность, получаемую
после применения фильтра предсказания, то получим ошибку предсказания, т.е. разность
между реальными и предсказанными значениями. Если ошибка выходит за пределы
погрешности прогноза, это означает, что на интервале прогнозирования появляется некоторая
новая полезная волна, которая не могла быть предсказана по значениям входного процесса.
8. Детерминированный и статистический подходы к обработке геофизических данных
8.1. Детерминированный подход к обработке. Задачи и методы трансформации и
продолжения геопотенциальных полей
В настоящее время при обработке и интерпретации геофизических данных реализуется два
основных методологических подхода: детерминированный и вероятностно-статистический. При
детерминированном (детерминистическом) подходе, используемом главным образом при интерпретации
данных геопотенциальных методов (гравии- магниторазведки, электроразведки), применяются
аналитические методы теории потенциала, уравнения Максвелла и теория упругости. Величины
детерминированных сигналов точно предсказуемы. Например, физические явления, будущее поведение
которых с вполне приемлемой точностью можно предсказать на основе физических соображений или по
данным прошлых наблюдений. Так, суточные вариации напряженности магнитного поля Земля
Решение обратных задач при этом находится в форме единственно возможного решения, т.е. либо
в виде определений функциональной зависимости, либо в виде числа как частного значения аргумента
этой функциональной зависимости. Применение детерминированного подхода, т.е. аналитических
приемов обработки и интерпретации данных, вполне оправдано при наличии интенсивных сигналов
(аномалий) от геологических объектов, характеризующихся заметной дифференциацией физических
свойств и благоприятными для решения поставленных задач размерами, формой и глубиной залежи. Здесь
слово аналитический значит простейший. Аналитическая функция может быть представлена степенным
рядом. Аналитическое выражение или формула – это совокупность действий, которые нужно проделать в
определенном порядке, чтобы получить значение функции.
Применение вероятностно-статистического подхода связано с характерной особенностью
геофизических наблюдений, заключающихся в том, что полученные в отдельных точках данные следует
рассматривать как случайные события или как случайные величины. Случайным является расположение
геологических объектов, точек наблюдений, площадей съемок. Из-за наложения помех, вызванных
погрешностями измерений, геологическими неоднородностями ВЧР, неучтенными вариациями
физических свойств пород и т.д., сами физические поля реализуются случайным образом. Случайные
сигналы можно описать лишь некоторыми усредненными статистическими характеристиками.
35

Выбор модели сигнала определяется решаемой задачей. При этом, между обеими типами моделей
сигналов нет резкой границы.
Наблюдаемые гравитационные и магнитные поля являются сложными суммарными полями,
поскольку отражают влияние различных геологических объектов, имеющих разную форму, разные
параметры, залегающих на разных глубинах. При интерпретации материалов желательно иметь дело с
влиянием отдельных аномальных тел, которые и являются объектом изучения. Поэтому выделение
(подчеркивание) влияния одного тела (полезного сигнала) в суммарном измеряемом поле (помех) является
одной из важнейших при обработке данных. Для этого проводят специальные преобразования
(трансформации) полей. В результате производства трансформаций получаем новое поле данных
(трансформант), где полезная (сигнальная) информация выделяется в виде аномалий, т.е. в более
«чистом» виде, очищенной (в большей или меньшей степени) от влияния других факторов. Это позволяет
с большей точностью определить основные параметры аномалии: ее форму, размеры и амплитуду.
Желательно при этом, чтобы интенсивность аномалии, обусловленной влиянием искомого объекта,
превосходила бы интенсивность помех (аномалий от соседних объектов).
Иначе говоря, путем производства трансформаций необходимо подчеркнуть (усилить, выделить)
аномалии от определенных объектов для определения координат его местоположения в разрезе.
Если имеем некоторую пространственную функцию s(x), полученную в результате измерений по
профилю, то для выделения сигнальных аномалий необходимо провести ее трансформацию в
пространственной или частотной областях.
В пространственной области (х – координата пространства по профилю) для выделения
аномальной составляющей s
ан
(x) необходимо провести трансформацию (фильтрацию) поля системой L, то
есть
s
ан
(x) = L {s(x)}.
В частотной области имеем
s
ан
(x) =
1
( ) ( )
2
j x
S H e d
,
где S(ω) комплексный спектр анализируемой функции s(х), H(ω) комплексная частотная
характеристика фильтрующей системы L. Понятно, что комплексный спектр S
ан
(ω) трансформанты s
ан
(x)
будет равен
S
ан
(ω) = S(ω) H(ω). (8.1)
При проведении пространственной фильтрации обычно вместо частоты используется
пространственная частота или волновое число k. В этом случае формула (8.1) будет иметь вид
S (k) = S(k) H(k).
При этом необходимо учитывать, что любая трансформация полей новой информации к той,
которая имеется в исходном наблюденном поле, не добавляется. Трансформация лишь более наглядно
представляет отдельные особенности полей, выделяет или подчеркивает детали суммарных аномалий,
связанные с особенностями распределения масс горных пород в объекте. В частотной области система L
фактически является некоторым фильтром, который подчеркивает частотные компоненты,
соответствующе искомому объекту и ослабляет компоненты помех (производит целенаправленное
изменение соотношения между различными компонентами).
Трансформация полей осуществляется часто их фильтрацией, аналитическим продолжением
полей в верхнее или нижнее полупространство, вычислением различных интегральных характеристик
полей.
Аналитическое продолжение полей в область верхнего или нижнего полупространства по
заданным ее значениям в некоторой другой области (для другого уровня) – это восстановление значений
аналитических функций в точках пространства, где они не измерены.
Применение аналитического продолжения значений поля в область верхнего полупространства
основано на том, что значения разных локальных аномальных составляющих суммарного поля убывают
по-разному: быстрее от неглубоко залегающих мелких объектов, и гораздо медленнее от больших
региональных неоднородностей разреза (рис. 8.1). Частотные характеристики таких трансформаций
являются по существу фильтрами нижних частот (экспонентой с отрицательной степенью). Поэтому
спектр трансформированной вверх аномалии мало изменится в области нижних частот, тогда как
уменьшение амплитуд частотных составляющих в области верхних частот (мелкие локальные
составляющие и случайные погрешности измерений) уменьшаются гораздо сильнее.
Следовательно, если до трансформации мы имели, например, карту значений поля на уровне z =
0, равную U(x, y, z = 0), то после трансформации вверх мы получаем сглаженную на другом уровне z = h
аномалию U(x, y, z=h) (региональный фон). Вычитая полученную карту регионального фона из начальной
функции U(x, y, z = 0), получаем карту локальных аномалий ΔU(x, y):
ΔU(x, y) = U(x, y, z = 0) - U(x, y, z=h).
Продолжение поля в нижнее полупространство, а также вычисление производных от измеренных
аномалий, наоборот, обладают повышенной чувствительностью к неглубоко залегающим аномальным
массам и подчеркивают локальные аномалии, поскольку их значения быстрее затухают с расстоянием.
36

Причем, степень затухания тем быстрее, чем выше производная. Поэтому при реализации таких
трансформаций на практике необходимо иметь в виду, что способы их производства (способы
аналитического продолжения полей в нижнее полупространство, вычисление производных)
характеризуются высокочастотными характеристиками H(ω) (фильтрами верхних частот). Поэтому они
чувствительны также и к ошибкам наблюдений и могут резко подчеркивать их. Поэтому такие
трансформации нужно реализовывать после соответствующего подавления высокочастотных помех.
К детерминистическим методам обработки, таким образом, относятся усреднение, сглаживание,
аналитическое продолжение полей. При решении системы линейных уравнений используется параметр
регуляризации, который позволяет уменьшить вариации величин дисперсии помех при вероятностно-
статистическом подходе. Суть регуляризации (по Тихонову) состоит в том, что при решении системы
линейных уравнений производится минимизация отклонений точного решения задачи от приближенного с
учетом специального функционала (стабилизатора).
||Р
точн
- Р
прибл
||
2
+ αΩ
(Р)
→min,
где Р
точн
и Р
прибл
– точное и приближенные решения, α – параметр регуляризации, Ω
(Р)
-
функционал, учитывающий априорные свойства искомого решения.
Сглаживание, интерполяция и аппроксимация аномалий
Для подавления высокочастотных помех особенно важна роль сглаживания аномалий
(фактически являющихся фильтрами нижних частот), при проведении которого случайные погрешности,
растущие при трансформациях быстрее значений полезных аномалий, могут их полностью затушевать.
Наиболее часто применяют следующие способы сглаживания: усреднение по равноотстоящим точкам,
интегральное усреднение по интервалу профиля, по окружности или по площади круга. Часто используют
сглаживание по 5 точкам (или другому их количеству), пересчеты (продолжение) поля вверх на
небольшие высоты.
Сглаживание по 5 точкам проводится по формуле
Uсгл (0) = 17/35 [U(0)] + 24/35 [U(ΔX)]
ср
- 6/35 [U(2ΔX)]
ср
.
Интерполяция – построение приближенного или точного аналитического выражения
функциональной зависимости, если известны значения функций в дискретном ряде точек, т.е. это процесс
нахождения значений функции s(х) во всех точках интервала (х
0
, …, х
n
) числовой оси, если известны
значения s
i
этой функции в конечном числе точек данного интервала. Наиболее проста линейная
интерполяция.
Аппроксимация – это приближенное выражение математических величин (чисел, функций и пр.)
через другие, более простые (алгебраические или тригонометрические). Например кривую линию можно
представить как ее аппроксимацию в виде предела длин ломаных линий, длина которых стремится к
нулю. Экстраполяция – это распространение результатов, полученных из наблюдений над одной из
частей некоторого пространства, на другую его часть.
8.2. Случайные функции, статистический подход к обработке.
Стационарность и эргодичность
Случайным процессом или случайной функцией Х(t) называется непрерывная или дискретно
заданная функция, которая в результате эксперимента может принимать тот или иной заранее
неизвестный вид. Значения Х могут изменяться либо во времени, либо по глубине (каротажная
диаграмма) либо по горизонтали (по профилю). Конкретный вид случайной функции (случайного
процесса), устанавливаемый в результате эксперимента (измерений), называется реализацией. Иначе,
случайный процесс описывается семейством реализаций. При этом, каждая серия измерений дает
различные реализации, которые вряд ли повторятся в будущем и которые нельзя предсказать с большой
точностью.
При обработке случайных процессов (функций), поэтому, желательно построить один
обрабатывающий алгоритм, который в среднем хорошо бы работал для всей совокупности получаемых
реализаций, которые отражают общие (статистические) свойства случайного процесса. При изучении
случайных функций, поэтому, используется аппарат теории вероятностей и статистики. Результатом
обработки являются распределения вероятностей определения значений искомого параметра.
Поэтому случайные функции описываются не точными значениями измеряемых величин в
различные моменты времени (различных точках пространства), а отображают их статистические
(вероятностные или стохастические) характеристики, которые дают нам информацию о том, как в среднем
будут изменяться многочисленные реализации, каковы в среднем их общие основные свойства.
Применение статистического подхода к геофизическим данным обусловлено также тем, что
приходится обрабатывать очень большие объемы информации. Любые же данные, когда их достаточно
много, приобретают статистических характер, если даже каждый из элементов информации сам по себе не
является случайным.
С учетом этого случайные функции изучаются с помощью статистических характеристик:
математического ожидания (среднего значения), дисперсии, функций авто- и взаимной корреляции и т.д.
Так оценка математического ожидания
X
определится по формуле
37
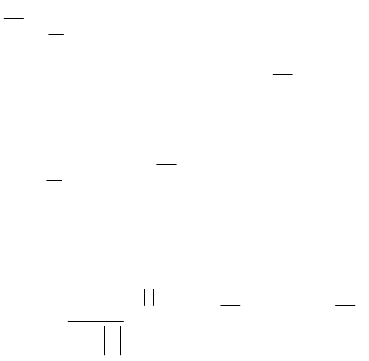
1
1
n
K
k
X X
n
.
Выражение «оценка величины
X
» употребляется в том смысле, что эту величину мы не знаем и
не можем измерить точно, а в результате измерений получаем лишь приближенное значение величины Х,
которое и называется ее оценкой. Величина
2
1
1
( )
n
K
k
D X X
n
называется дисперсией случайного процесса. Она характеризует степень разброса отсчетов
случайной функции относительно их математического ожидания (среднего значения).
Функция автокорреляции определится выражением
1
1
( ) ( ) ( )
n
K k
k
b X X X X
n
.
Здесь Х
К
– это наблюденные значения измеряемого поля, τ = t
2
– t
1
- это разность аргументов (в
данном случае времен) и τ = 0; ± Δτ; ± 2Δτ, …
Очень важным случаем случайных процессов являются случайные стационарные процессы. Их
статистические характеристики не меняются во времени: математическое ожидание остается постоянным
во времени, значения функции автокорреляции не зависят от положения начального момента отсчета
времени, а зависят только от промежутка во времени τ = t
2
– t
1
между первым и вторым моментами
отсчета.
Стационарность случайной функции значительно упрощает ее статистическое описание. Поэтому
при обработке материалов ряда геофизических методов на начальном этапе обработки проводят
специальные процедуры, после которых функции можно считать стационарными случайными
процессами.
Так сейсмические трассы нельзя считать стационарными, поскольку их мощность (квадрат
амплитуд) и спектральный состав значительно изменяются (уменьшаются) с течением времени. Чтобы
устранить эти причины нестационарности, проводят регулировку амплитуд и фильтрацию колебаний.
Сейсмическую трассу можно считать стационарной, если длина участка трассы с примерно одинаковой
формой сигнала в 15-20 раз превосходит длительность отдельных сейсмических импульсов.
При изучении стационарных процессов возникает очень важный вопрос: нельзя ли определить
статистические свойства процесса, используя лишь одну достаточно протяженную реализацию. Решение
этого вопроса зависит от природы случайного процесса. Так, если статистические свойства всех
реализации будут в общих чертах одинаковы, то, для получения их статистических характеристик,
достаточно использовать усреднение параметров одной реализации. Такие стационарные случайные
процессы, обладающие свойством подобия реализаций, называются эргодическими стационарными
случайными процессами. Для них можно заменит усреднение по ансамблю реализаций осреднением
одной достаточно протяженной реализации.
8.3. Корреляционно-регрессионный анализ. Эвристические алгоритмы
Важной задачей обработки геофизических данных является изучение зависимостей между
особенностями геофизических полей и физическими (петрофизическими) характеристиками горных
пород. Зависимость, когда одна величина вызывает изменение другой, называется статистической
(стохастической). При определении статистических зависимостей различают во-первых корреляцию,
когда устанавливается существование взаимосвязи между двумя (или более) случайными величинами и
оценивают тесноту (степень) этой связи,
Во-вторых, изучают регрессию, когда выявляют характер (форму) этой зависимости между
величинами У и Х, и возможности оценки У по Х (или Х по У). Причем Х, У или и Х, и У – являются
случайными величинами. Регрессионный анализ – это раздел математической статистики, объединяющий
практические методы исследования регрессионных зависимостей между величинами по статистическим
данным. Проблема регрессии характерна тем, что о распределении изучаемых величин нет достаточной
информации. Поэтому для установления связи между величинами в эксперименте используется модель,
основанная на упрощенных допущениях.
Наиболее простыми являются линейные регрессии. Находя уравнение линейной регрессии,
можно определить прогнозную оценку Ỷ исследуемого параметра:
Ỷ = a
0
+ aX,
где a
0
и a - это свободный член и некоторый множитель пропорциональности между Ỷ и Х,
значения X характеризуют величины геофизических параметров.
Наиболее распространенными методами оценки регрессии являются метод наименьших
квадратов и максимума правдоподобия.
Построение и исследование функций объединяются ныне общим термином тренд-анализ. Он
предполагает выделение из фактически наблюдаемых вдоль линии или на площади данных сис-
38

тематической составляющей, которая отражает направленные изменения изучаемого признака и служит
основой построения карты тренда. На языке формул это выражается уравнением
s(x
i
, y
i
) = F(x
i
, y
i
) - ΔF(x
i
, y
i
),
где s(x
i
, y
i
) – систематическая составляющая, F(x
i
, y
i
) – фактические значения функции, ΔF(x
i
, y
i
) –
случайные вариации значений функции. Именно по значениям систематической составляющей и строится
график (карта) тренда.
Простейшие варианты тренд-анализа давно осуществлялись «вручную», с помощью приемов так
называемого сглаживания скользящим окном из 3 или 5 точек. Результат приближения (аппроксимации)
поверхности тренда к фактическим данным может быть разным приемов в зависимости от свойств
применяемых математических приемов обработки (наименьших квадратов, полиномиального
приближения и т.п.).
Отыскание линейных корреляционных связей между, например, геофизическими данными и
свойствами осадочных отложений широко используются при интерпретации. Эта задача проще всего
решается построением графиков корреляции (кросс-плотов) между скважинными данными, например,
эффективными мощностями песчаных пластов и амплитудой отраженных волн на трассах, полученных
вблизи скважин. Основным инструментом практической интерпретации геофизических данных стало
построение кроссплотов. С помощью кроссплота можно пытаться установить наличие и силу связи одного
параметра с любым другим. Если связь есть, она проявится. Сильной связи будет соответствовать высокий
коэффициент корреляции. Таким образом, имеется возможность от любого геофизического параметра
(например, скорости) перейти к целевому параметру (например, пористости) с помощью уравнения линии,
аппроксимирующей кроссплот, и установить степень неопределенности получаемой оценки целевого
параметра с помощью коэффициента корреляции.
Главным достоинством интерпретации на основе кроссплотов является простота - не нужно
никакой модели, не нужны никакие предположения, не требуется причинный характер устанавливаемых
связей.
Недостатком кроссплота является разброс его точек, который всегда больше, чем хотелось бы.
Стремление снизить негативный эффект разброса вызвало к жизни специфические средства
статистической интерпретации: факторный анализ, аппарат множественной регрессии, а в дальнейшем -
геостатистику, нейронные сети и распознавание образов. По сравнению с простой "кроссплотной"
интерпретацией эти средства реализуют более глубокий и более строго обоснованный анализ связей
между одним или несколькими входными параметрами и целевым параметром. Но такой анализ во всех
перечисленных подходах остается чисто формальным, без каких-либо попыток выявления причинных
связей, которые игнорируются.
В обработке геофизических данных наряду с процедурами, имеющими строгое математическое
обоснование, используются так называемые эвристические алгоритмы, построенные на интуитивно-
эмпирических предпосылках. Это формализованные приемы, выработанные в практической деятельности.
В условиях недостатка априорной информации велико значение опыта (интуитивного характера подбора
некоторых факторов), который пока не поддается аналитическому описанию. Эвристические приемы
позволяют сокращать количество просматриваемых вариантов при поисках решения задачи, но не
гарантируют наилучшего решения, если нет достаточного опыта решения сходных задач.
Литература
Спасский Б.А. Цифровая обработка сейсмических данных / Перм. ун-т. Пермь, 1986. 96 с.
Стр.19 – 46 и 75 – 85.
39
