Спасский Б.А. Лекции по теории обработки геофизических данных
Подождите немного. Документ загружается.


номер. Так n-ое значение выборки
)( tnx
можно обозначить через
n
x
, а соответствующее этому значению
момент времени
tn
через
n
t
. Поэтому величина n выступает в роли номера отсчета дискретной функции
)(nx
в области времени.
В частотной области функции x(n) будет соответствовать дискретный комплексный спектр X(m), где
m – это номер отсчета значений данного спектра в точках, взятых по оси частот через некоторый интервал по
частоте
tN
2
, (4.4)
т.е. в точках
,
0
1
,
2
2
, …,
m
m
, …,
1N
.
С учетом этого, аргументы гармонических функций
t
заменим дискретными
N
nmtnmt
nm
2
. Формула прямого преобразования Фурье с учетом вышесказанного
запишется следующим образом
1
0
)()()(
N
n
tj
tj
nm
enxdtetxX
. (4.5)
Опуская масштабный множитель
t
, будем иметь
1
0
2
)()(
N
n
Nmnj
enxmX
(4.6)
или
1
0
/2exp)()(
N
n
NmnjnxmX
. (4.7)
Обратное дискретное преобразование Фурье запишется следующим образом
1
0
1
0
/2
/2exp)(
1
)(
1
)(
N
m
N
m
Nmnj
NmnjmX
N
emX
N
nx
. (4.8)
Таким образом, все операции при компьютерной обработке данных проводятся с
последовательностями чисел (дискретными функциями). Каждая дискретная функция состоит из N значений,
представленных во временной или частотной областях. Все интегральные формулы, соответствующие
непрерывным функциям, записываются в виде сумм.
Так, операция свертки дискретного сигнала x(n) с дискретной импульсной реакцией фильтра h(n)
запишется таким образом
k
k
knk
n
k
kn
xhhxny
0
)(
. (4.9)
Здесь k – это номер по порядку дискретных значений функций x(n) или h(n). Если k=0, то берется n-
ое (последнее) значение функции x(n) и нулевое (первое) значение функции h(n). Если n=1, то берем
предпоследнее значение функции x(n) и второе значение функции h(n) и т.д. Таким образом, при свертке одна
из функций оказывается обращенной во времени, что и должно происходить при расчете свертки.
4.4. Особенности спектров дискретных функций
Как указывалось выше, каждой дискретной функции в области времени x(n) с шагом квантования
t
соответствует в спектральной области комплексный спектр X(m), который также является дискретным.
Шаг квантования по оси частот равен
или
f
. Для того, что проще понять – какие изменения
происходят со спектром X(m) в сравнении со спектром X(f) непрерывной функции – вспомним следующее.
Из теории следует, что амплитудно-частотный спектр
)(
X
периодической аналоговой функции
x(t) с периодом T описывается рядом Фурье и, соответственно, является дискретным, с шагом
T/2
(рис.4.3 а). Спектр
)(
X
непериодической аналоговой функции x(t) описывается интегралом Фурье
(бесконечным множеством синусоидальных и косинусоидальных колебаний). То есть спектр становится
непрерывным в интервале частот от
до
, период T колебаний, поэтому, стремится к
бесконечности, а интервал дискретизации по частоте
стремится к нулю. При этом в практике обычно
считается, что основная энергия сигнала сосредоточена в некотором интервале частот – ω
гр
< ω < +ω
гр
.
Если непериодическую аналоговую функцию x(t) сделать дискретной x(n), то в соответствие со
вторым свойством спектров (подобия прямых и обратных преобразований Фурье) можно утверждать
следующее. Если периодической функции соответствует дискретный спектр, то у дискретной функции должен
быть периодический спектр. Именно это и наблюдается в практике. Дискретной функции x(n) соответствует
дискретный периодический (с периодом Ω = 2π/Δt) спектр X(m), где m – номер дискретный значений спектра
21

дискретной функции. Спектр X(m) существует в интервале частот от - ∞ до +∞ и связан со спектром
непрерывной функции X(ω) соотношением (рис. 4.2 в)
2
( ) ( )
k
k
X m a X
t
. (4.10)
Здесь k = 0, ±1, ±2, …, ±∞, a = 1/ Δt – коэффициент пропорциональности.
Главный (при k = 0) и побочные (|k| ≥ 0) экстремумы дискретного спектра (периодической функции
X(m)) совпадают с точностью до постоянного множителя a со спектром X(ω) непрерывной функции x(t) при
условии, что Δt ≤ 2π/Ω. Побочные периоды располагаются справа и слева от главного (рис. ).
При этом, каждый период Ω = 2π/Δt функции X(m) представлен N отсчетами, отстоящими друг от
друга по частоте на величину Δω = 2π/(NΔt).
Возникновение побочных периодов (зеркальных или боковых частот) можно объяснить следующим
образом (рис. 4.4). Соединяя точки x
1
, x
2
, …, x
N-1
дискретной функции x(n) плавной линией можно
восстановить аналоговую функцию x(t), которой соответствует при k = 0 главный период дискретного спектра
X(m). Однако, через те же отсчеты x
1
, x
2
, …, можно провести и другие кривые с гармоническим заполнением,
имеющим частоту ω = k·2π/Δt, когда k = 1, 2, и т.д. Этим частотам и будут соответствовать остальные
побочные периоды спектра X(m).
Из формулы (4.10) следует, что положение побочных периодов на оси частот спектра X(m) целиком
определяется шагом дискретизации во времени Δt. При уменьшении Δt побочные периоды отдаляются от
главного и друг от друга (рис.4.2 г-д). В предельном случае, когда Δt стремится к нулю, а дискретная функция
x(n) преобразуется в непрерывную функцию x(t), то побочные периоды дискретного спектра X(m)сдвигаются
по оси частот на бесконечно большое значение от главного максимума, т.е. X(m) → X(ω).
При увеличении Δt побочные периоды спектра X(m) сближаются с главным и друг с другом,
накладываясь друг на друга (рис.4.2 г). За счет этого и возникают искажения частотного состава спектров
дискретных сигналов, когда шаг квантования не соответствует условию (4.3), т.е. возникают явления
аляйсинга.
В предельном случае, когда величина шага квантования Δt стремится к бесконечность, то все
побочные максимумы спектра X(m), сближаясь бесконечно друг к другу, образуют широкополосный спектр.
4.5. Восстановление аналоговых функций по дискретным. БПФ
Чтобы правильно восстановить непрерывный сигнал x(t) по его дискретному аналогу, достаточно
пропустить дискретный сигнал x(nΔt) через фильтр нижних частот с прямоугольной характеристикой H
фнч
(f)↔
h
фнч
(t). Согласно свойству подобия прямых и обратных преобразований Фурье, прямоугольному импульсу во
временной области соответствует так называемая щелевая или интерполяционная функция в частотной
области (рис. 1.4). И наоборот, прямоугольной функции в области частот (с амплитудно-частотной
характеристикой H
фнч
(f) фильтра нижних частот) соответствует временная характеристика (импульсная
реакция) h
фнч
(t), определяемая в соответствие с формул (1.8) следующим образом
h
фнч
(t) = sin (πΔf t)/(πΔf t),
где Δf = 2f
0
, а ω
0
= 2π f
0
– определяет граничную частоту фильтра (рис. ).
С учетом этого, каждый дискретный сигнал на входе фильтра будет представлен на выходе
импульсной реакцией h
фнч
(t) (щелевой функцией), амплитуда основного максимума которой равна величине
дискретного отсчета x(nΔt) в момент nΔt, и которая характеризуется на выходе запаздыванием τ = nΔt
относительно начального времени t = 0. Выходной сигнал, соответствующий непрерывной (аналоговой)
функции x(t), таким образом, будет восстанавливаться суммой всех щелевых функций с соответствующими
дискретным значениям амплитудами и сдвигами, т.е. свертке
x(t) = x(nΔt) * h
фнч
(nΔt). (4.11)
Иначе, восстановление аналогового сигнала х(t) по его выборкам сводится к использованию интерполяционных
процедур. А выражение (4.11) можно записать и таким образом
0
0
sin ( )
( ) ( )
( )
n
t n t
x t x n t
t n t
,
где ω
0
максимальная частота в амплитудно-частотном спектре |Х(ω) | функции x(t).
Из формулы следует, что сигнал x(t) можно получить, если пропустить последовательность х(nΔt) через
идеальный аналоговый фильтр нижних частот с частотой среза ω
гр
= π/Δt.
Понятно, что точное воспроизведение аналогового сигнала x(t) будет только в случае, когда шаг
квантования Δt соответствует теореме Котельникова (4.3).
Для ускорения процесса расчетов спектральных характеристик (сокращения машинного времени)
широко используется специальный алгоритм, получивший название Быстрого Преобразования Фурье
(БПФ). Его эффективность возрастает с увеличением длительности используемых для расчетов
операторов.
5. Z-преобразования
5.1. Понятие Z-преобразований
Удобным методом решения разностных уравнений линейных систем является z-преобразование.
Если преобразовать непрерывную функцию x(t) в дискретную x(n), то дискретная функция представляет
22
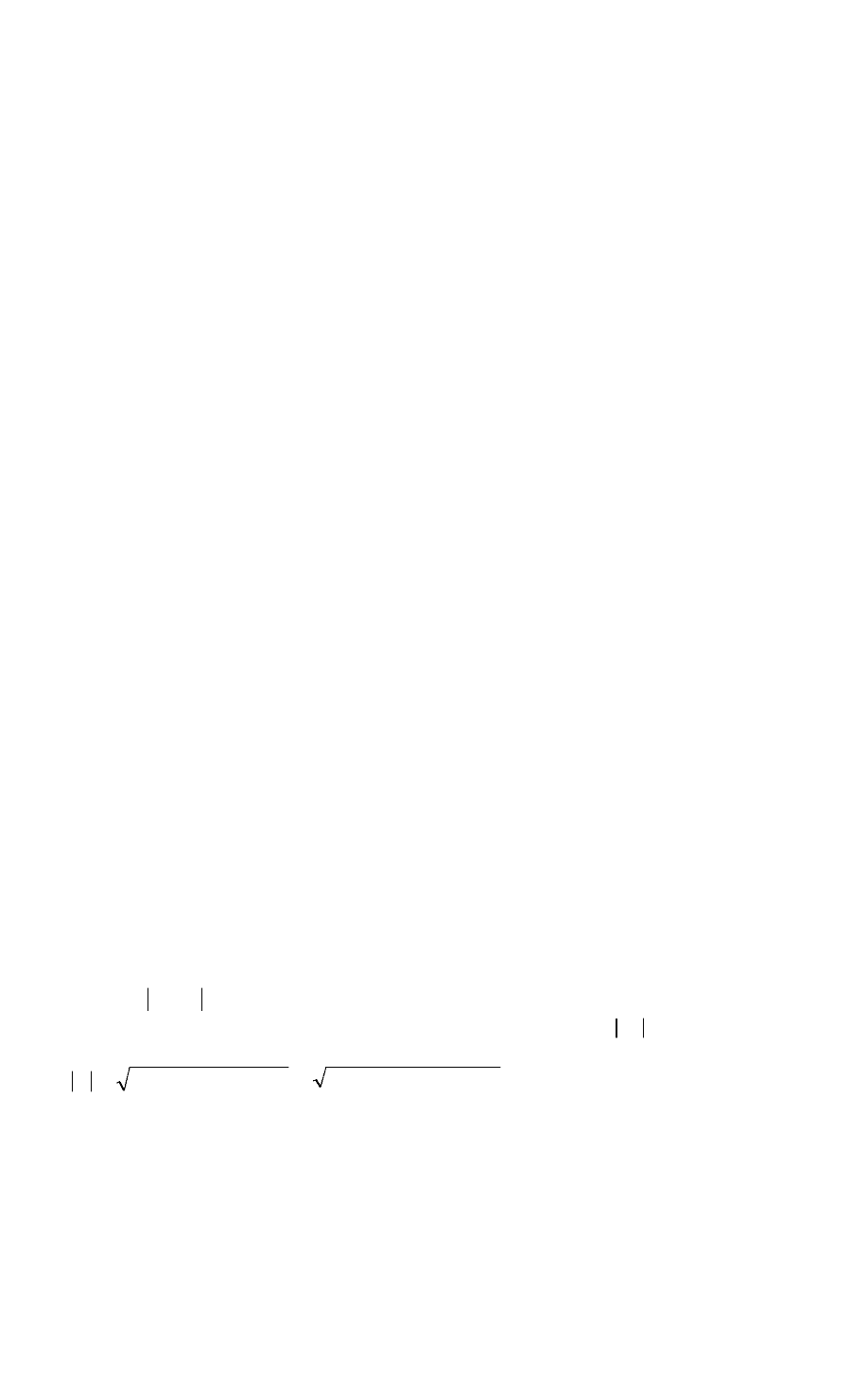
собой простую последовательность единичных импульсов
)(t
умноженных на значения функции в
точках дискретизации с шагом
t
:
...)(...)2()()()(
210
tntxttxttxtxnx
n
(5.1)
При t=0 преобразование Фурье единичного импульса
)(t
равно единице:
1)( dtt
.
Если
)( ttt
, то
.1)(
tj
edttt
(5.2)
Если
)( tntt
, то
tnj
edttnt
1)(
. (5.3)
С учетом этого, преобразование Фурье последовательности (1) дает ряд
......
2
210
tnj
n
tjtj
exexexx
. (5.4)
Вводя обозначение
Ze
tj
, получим Z-преобразование X(Z) от функции x(n):
0
2
210
......)(
n
n
n
n
n
ZxZxZxZxxZX
. (5.5)
Таким образом, дискретная функция x(n) может быть записана в виде многочлена по Z. Величина
n, в общем случае, может изменяться в пределах от
до
. Следует иметь в виду, что Z-
преобразование непрерывной функции x(t), как и любая дискретная функция x(n), зависит только от
значений функции в точках отсчета и не учитывает вариаций аналоговой функции x(t) между точками
отсчета.
Некоторые авторы (Кулханек, 1981 и др.) определяют Z-преобразование в форме
n
n
ZxZX )(
, (5.6)
где
tj
eZ
.
В геофизике более широко при применении Z-преобразований используется выражение (5.5).
Переход от одной формы Z-преобразования к другой осуществляется путем замены
Z
на
1
Z
. Это
следует иметь в виду при чтении различных литературных источников.
5.2. Отображение Z-преобразований на плоскости
Распространенным способом анализа дискретных цифровых последовательностей является z-
преобразование (z-transform). Оно играет для дискретных сигналов и систем такую же роль, как для
аналоговых – преобразование Лапласа. Большое значение z-преобразование имеет для расчетов
рекурсивных цифровых систем обработки сигналов.
Комплексный спектр X(m) дискретной функции x(n) – это функция вещественной угловой
частоты
. Функция X(Z), являющаяся Z-преобразованием функции x(n), зависит от комплексной
переменной Z. С учетом формулы Эйлера можно записать
tjteZ
tj
sincos
= Re(Z) – j Im(Z), (5.7)
где Re(Z) =
tCos
и Im(Z) =
tSin
- действительная и мнимая части комплексной
функции Z.
С другой стороны, комплексную функцию
)(
Z
можно записать в векторной форме
)(
)()(
j
eZZ
. (5.8)
Для любой вещественной частоты
абсолютная величина
Z
(модуль или амплитудно-
частотный спектр) равна единице, поскольку
tSintCosZZZ
2222
)(Im)(Re
=1.
Поэтому, все частотные компоненты
n
(бесконечные во времени синусоидальные и
косинусоидальные колебания с частотой
nn
f
2
) представлены отдельными точками в комплексной
плоскости, которые располагаются в этой плоскости на единичной окружности (рис. 5.1а). При изменении
от -
/
t
до
t/
(в течение одного периода
t /2
) комплексная переменная Z
последовательно пробегает все значения на единичной окружности, т.е. соответствующие точки Z делают
полный оборот на комплексной плоскости от точки со значением –1 через значения -j, 1, j и снова -1 по
направлению против часовой стрелки (рис.5.1б). При дальнейшем увеличении (уменьшении) частоты
значения Z будут образовывать новый период
(повторный оборот вектора Z ) и весь процесс
циклически будет повторяться.
Если действительный аргумент
заменить комплексной частотой
jvw
, то
tj
eZ
=
tvtjw
ee
, (9)
23

т.к. во втором сомножителе имеем:
tvtvjtjvj
2
.
С учетом структуры формулы (5.8):
)(
)()(
j
eZZ
, (5.10)
в выражение (5.9) модуль величины Z и ее фазовый спектр будут соответственно равны:
tv
eZ
,
twZ )(
.
Из данного выражения следует, что действительная часть v комплексной частоты
имеет смысл
угла вектора, а мнимая часть w определяет модуль (длину) вектора, соответствующего комплексного
числа Z. Если значения w меняется в пределах от
t /
до
t/
, а v изменяется от 0 до
, то
соответствующие этим значениям точки Z будут располагаться на всей комплексной плоскости вне
единичного круга. Если же значения v будет меняться от
до 0, то значения Z будут занимать
область внутри единичной окружности. С использованием значений Z, определяемых по формуле (5.8),
области расположения точек на плоскости будут обратными вышесказанным.
5.3. Свойства Z-преобразований
Свойство 1. Множитель
n
Z
означает задержку (сдвиг) соответствующего дискретного значения
функции (когда имеем
n
n
Zx
) или самой функции (когда имеем
)(nxZ
n
) на величину
tn
в
направлении возрастания времени относительно начального времени t = 0.
Так, если функция x(n) соответствует следующей последовательности чисел
x(n) = (1, 0, 0), то X(Z) =
1...001...
2102
2
1
1
0
0
ZZZZaZaZa
.
Если
x(n) = (0, 1, 0), то X(Z) = Z.
x(n) = (0, 0, 1), то X(Z) =
2
Z
.
x(n) = (6, -1, -1), то X(Z) =
2
6 ZZ
.
x(n) = (6, 5, 1), то
2
56)( ZZZX
.
Свойство 2. Z-преобразование любой временной последовательности есть своеобразное
представление комплексного спектра: оно наглядно отражает структуру последовательности x(n) во
временной области и в то же время обладает некоторым преимуществом спектральных
последовательностей. Одним из таких важных свойств является то, что числовые коэффициенты
n
aaaa ,...,,,
210
, полученные при перемножении Z-преобразований
)()(
21
ZXZX
двух дискретных
функций
)(
1
nx
и
)(
2
nx
равны коэффициентам, полученным при свертке этих функций
)()(
21
nxnx
.
Свойство 3. Как следует из алгебры, любой полином n-ой степени можно разложить на n
линейных (первой степени) сомножителей, коэффициенты которых определяются корнями полинома.
Поэтому многочлены Z-преобразований могут быть представлены в виде произведения сомножителей
(диполей). Например, имеем Z-преобразования
Y(Z) = 6 + 5Z +
2
Z
= (3 + Z)(2 + Z) и X(Z) = 6 – Z
2
Z
= (3+Z)(2-Z).
Отношение этих Z-преобразований соответствует частотной характеристике H(Z) некоторой
системы, равное дроби Z-преобразований спектра выходного сигнала Y(Z) и спектра входного сигнала
X(Z)
M
k
k
k
N
k
k
k
Zy
Zy
ZX
ZY
ZH
1
1
)(
)(
)(
, (5.11)
то корни числителя будут называться нулями, а корни знаменателя – полюсами. Для определения
корней необходимо сомножители числителя и знаменателя приравнять нулю. Т.е. для числителя имеем: 3
+ Z = 0,
3
1
Z
и 2 + Z = 0,
2
2
Z
. Следовательно, нулями будут кружки на рис. 5.2 с
координатами
1
Z
и
2
Z
.
Для расчета координат полюсов приравняем нулю сомножители знаменателя, т.е. 3 + Z =0,
3
3
Z
и 2 – Z = 0,
2
4
Z
. Поэтому полюсами будут точки с координатами
3
Z
и
4
Z
(кружочки на
рис.5.2).
5.4. Графическое изображение преобразований Фурье, Лапласа
и Z-преобразований
Прямые преобразования Фурье позволяют представить функцию x(t) как сумму гармонических
колебаний различных частот, параметры которых (амплитуды и фазы) составляют комплексный спектр
)(
X
.
24
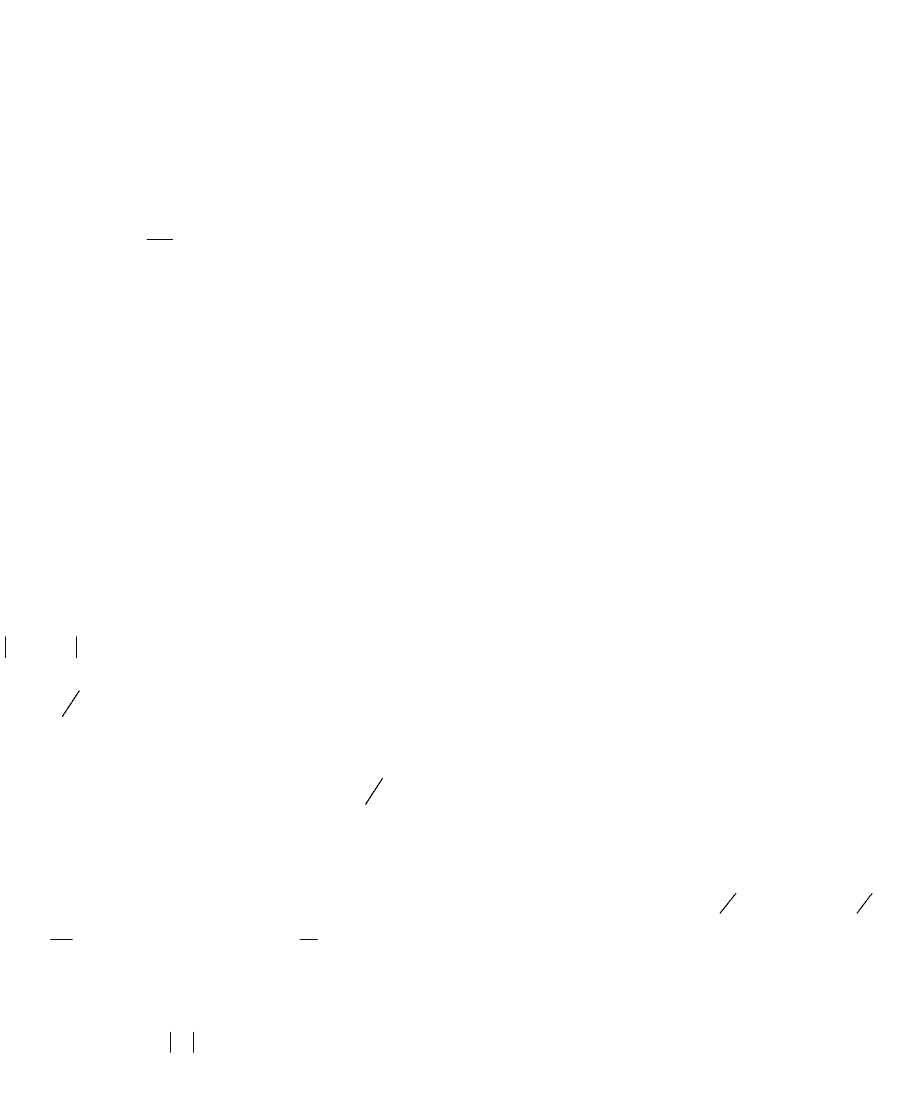
dtetxX
tj
)()(
.
При этом считается, что частота колебаний
является действительной и может меняться в
пределах
. При графическом изображении амплитудно-частотного и фазово-частотного спектров,
которые составляют комплексный спектр, ось частот обычно является горизонтальной (рис.5.3 а).
В технике часто используются преобразования Лапласа, имеющие вид
dtetxpX
pt
L
)()(
, (5.12)
j
j
pt
L
j
dpepXtx )()(
2
1
, при t>0,
где
jp
это некоторый комплексный параметр частоты, связанный с непрерывным
временем t.
Преобразование (5.12) превращает действительную функцию x(t) действительного аргумента t в
некоторую, в общем случае комплексную функцию
)( pX
L
, определенную в некоторых точках
комплексной плоскости p. В случаях, когда действительная часть p равна нулю (т.е.
0
), то
преобразование Лапласа (являясь преобразованием общего вида) сводятся к преобразованиям Фурье,
являющихся частным случает от преобразований Лапласа.
При графическом изображении преобразований Лапласа (рис.5.3 б) ось частот
j
в плоскости p
располагается вертикально, а ось
горизонтально. Переход от частоты
к параметру p =
j
означает изменение пути интегрирования. В преобразовании Фурье оно ведется по вещественной
переменной
, а в преобразовании Лапласа интегрирование производится по прямой лежащей на
плоскости комплексного переменного
jp
и проходящей параллельно мнимой оси
j
на
расстоянии
от нее.
Если непрерывная функция x(t) становится дискретной x(n), то ее амплитудно-частотный спектр
)(mX
- становится периодическим. При правильно выбранном шаге квантования
t
, основной и
побочные (зеркальные) экстремумы будут следовать друг за другом по оси частот с периодом повторения
t
2
(рис. 5.3 а).
Аналогично, при получении графических изображений дискретных преобразований Лапласа, вся
плоскость параметра p разбивается на отдельные полосы по мнимой оси
j
. Каждая полоса
соответствует периоду повторения
t
2
(рис. 5.3 б).
При использовании Z-преобразований, различные частоты
отсчитываются вдоль единичной
окружности (рис. 5.3 в). Иначе, единичная окружность в Z-плоскости имеет тот же смысл, что и ось
j
в
p-плоскости. При этом, взаимно-однозначное отображение p-плоскости на Z-плоскость единичного круга
осуществляется только для определенной полосы в p-плоскости от
2
j
N
до
2
j
N
, где
t
2
=
N
2
. Здесь
t
N
- это частота Найквиста.
Графическое представление Z-преобразований и преобразований Лапласа часто используется для
определения степени устойчивости цифровых систем. С учетом вышесказанного, левая полуплоскость
преобразований Лапласа отображается вне единичной окружности Z-преобразований, а правая - внутрь
единичного круга (
1Z
), а сама окружность соответствует оси
j
(рис.5.3) . Чтобы провести расчет
преобразований Лапласа для некоторого параметра
jp
1
, для этого (рис.9а) необходимо провести
интегрирование от точки а, где
0
, по часовой стрелке по контуру abcdef, т.е.
1
= bc = de. На рис. 6б
показано отображение этого контура в Z-плоскости, где обход контура проводится против часовой
стрелки. При этом левая половина p-плоскости Лапласа- преобразований и пространство вне единичной
окружности Z-плоскости (заштрихованные зоны на рис. 5.3 б, в) соответствуют зонам устойчивости
анализируемых цифровых систем.
5.5. Геометрическое истолкование корней Z-преобразований
Очень часто при проектировании систем обработки (например, при конструировании фильтров)
не всегда удобно применять их дифференциальные уравнения, поскольку разделение этих уравнений на
действительную и мнимую части обычно трудоемко даже для простейших систем. Для этого гораздо
проще использовать их Z-преобразования, которые чаще всего представляются дробями по степеням Z
согласно выражению (11). Раскладывая числитель и знаменатель H(Z) на сомножители, функция H(Z)
может быть однозначно определена с точностью до постоянного множителя своими нулями и полюсами
для любого значения Z (Кулханек, 1981).
25

M
k
k
k
N
k
k
k
Zx
Zy
ZH
0
0
)(
=
M
M
N
N
ZxZxZxx
ZyZyZyy
...
...
2
210
2
210
=
))...()((
))...()((
2211
2211
ZdcZdcZdc
ZbaZbaZba
pp
ll
=
=
p
k
k
k
l
k
k
k
Z
b
c
Z
b
a
C
1
1
)(
)(
= С
p
k
k
l
k
k
ZP
ZL
1
1
)(
)(
. (5.13)
Здесь C – некоторый числовой коэффициент, зависящий от произведений величин
kkkk
dcba ,,,
; а
k
L
и
k
P
- описывают значения нулей и полюсов (корней), которые характеризуют свойства данной
системы с частотной характеристикой H(Z). Если установить положение полюсов и нулей на комплексной
плоскости, то, используя геометрическое истолкование нулей и полюсов, можно рассчитать амплитудно-
частотную
)( fH
и фазово-частотную
)( f
H
характеристики системы. Так
p
pk
k
l
k
k
P
L
fH
1
)(
,
l
k
p
k
kkH
f
1 1
)(
. (5.14)
Геометрически
k
L
и
k
P
- это расстояния от нулей и полюсов до произвольных точек
единичной окружности с определенными значениями частоты
n
f
. Аналогично фазово-частотная
характеристика определяется суммированием углов
k
и
k
, образованных векторами, соединяющих
нули и полюса с точками частот
n
f
, и положительным направлением действительной оси Z-плоскости.
Полный фазовый угол для произвольной частоты
n
f
равен сумме углов векторов нулей минус сумму
углов векторов полюсов.
5.6. Z-преобразования и форма сигналов
В сейсморазведке при интерпретации данных широко используется изучение формы импульсов
упругих колебаний, распространяющихся в реальных средах. Поскольку форма любого сигнала
определяется комплексным спектром, то при одинаковых амплитудно-частотных спектрах сигналы могут
отличаться по форме в зависимости от их фазово-частотных спектров. С использованием аппарата Z-
преобразований очень удобно изучать фазовые спектры.
Как показано выше, Z-преобразование можно представить в виде произведения простых
сомножителей (диполей) вида
)( Zba
nn
или
),(
nn
ba
.
Если у всех сомножителей некоторого Z-преобразования
)(
1
ZX
величина
n
a
больше, чем
n
b
, то сигналы называются минимально-фазовыми или минимально-запаздывающими. Такие сигналы
обладают небольшой длительностью во времени (по сравнению с другими сигналами, обладающими
такими же амплитудными спектрами, но отличающиеся по форме фазового спектра). Начальные фазы
минимально-фазовых импульсов обладают повышенными значениями энергий и характеризуются
высокочастотным составом. Нули Z-преобразований таких сигналов располагаются вне единичной
окружности.
Если сомножители
n
a
меньше, чем
n
b
, то такие сигналы называются максимально- фазовыми.
Нули таких сигналов располагаются внутри единичной окружности.
Для примера возьмем функцию
)(
1
nx
с ординатами
2/1,1
, Z-преобразование которой
будет иметь вид (соответствующий минимально-фазовой функции)
ZZX )2/1(1)(
1
.
Корнем (нулем) такого Z-преобразования будет значение
2Z
(рис. 5.4).
26

Если считать, что шаг квантования функции x(n) равен 0,002 с, а, следовательно, значение
частоты Найквиста
2502/
дискрN
ff
Гц, где частота дискретизации функции x(n) с шагом
квантования
t
будет равна
500/1 tf
дискр
Гц.
С учетом геометрического истолкования корней Z-преобразований, по формуле (12) можно
графически определить величины амплитудно-частотных
)(
1
fX
и фазово-частотных
)(
1
f
характеристик функции
)(
1
nx
для значений частот: 0,
,4/
N
f
,2/
N
f
4/3
n
f
,
.N
f
Эти
значения частот находятся на единичной окружности. Поскольку нулем Z-преобразования
)(
1
ZX
является значение 2, то величины
)(
1
fX
для заданных значений частот будут равны соответственно
длинам соответствующих отрезков.
Аналогично можно определить величины углов
фазового спектра для этих же значений
частот. Значение угла для частоты f=0, т.е.
0)0(
, поскольку направление отрезка Ос совпадает с
осью
)Re(Z
и угол сОс равен нулю. Для частоты
4/
N
f
величина
)4/(
N
f
равна углу Оса, для
частоты
2/
N
f
величина
определяется углом Осб и т.д Постепенно возрастая, затем, к значению
частоты
N
f
, углы
- снова убывают до нуля. Аналогично, но с другим знаком, меняются углы
и в
сторону отрицательных частот. Максимальные значения углов не превышают 40 градусов.
Если взять максимально-фазовую функцию типа
)(
2
nx
с ординатами
1,
2
1
, то ее Z-
преобразование
)(
2
ZX
= -1/2 + Z. Корнем (нулем) этого Z-преобразования будет величина Z = 1/2 .
Откладывая на графике точку нуля и делая такие же построения как и в предыдущем случае (рис.5.4),
находим значения амплитудно-частотного
)(
2
fX
и фазово-частотного
)(
2
f
спектров. Хорошо
видно, что амплитудно-частотные спектры совпадают, а фазово-частотные в значительной степени
отличаются.
В последние годы при обработке данных сейсморазведки широко используются так называемые
0-фазовые сигналы. Они характеризуются симметричной формой (относительно точки t = 0), наименьшей
длительностью в области времени (из всех сигналов, имеющих один амплитудно-частотный спектр) и
один экстремум повышенной амплитуды. Например, функция
)(
3
tx
с ординатами (0,4; + 0,18; -1,25;
+0,18; 0,4), которая имеет Z-преобразование
)(
3
ZX
=
212
4,018,025,118,04,0 ZZZZ
, -
является нуль-фазовой (рис.5.4).
6. Конечность сигналов и функции-окна
6.1 Влияние конечности функций на результаты спектрального анализа
Многие аналитические выражения, с которыми геофизикам приходится иметь дело в теории обработки
информации, записываются в виде интегральных выражений с бесконечными пределами интегрирования. Так,
комплексный спектр X
∞
(ω) и соответствующая ему бесконечная во времени функция x
∞
(t) связан соотношением
X
∞
(ω) =
( )expx t j t dt
. (6.1)
Бесконечные пределы интегрирования не создают трудностей при аналитических расчетах, но
совершенно неприемлемы при работе с эмпирическими данными, поскольку полученные в полевых условиях
наблюдения всегда ограничены (конечны). А ограничение функций во времени (или пространстве) ведет к
возникновению погрешностей в частотной области, т.е сглаживанию ее спектров. Поэтому влияние
длительности функций на конечные результаты вычислений спектральных характеристик этих функций всегда
нужно учитывать при проведении обработки.
Конечные (ограниченные во времени) функции x
огр
(t) обычно рассматривают как некоторую часть
бесконечной временной последовательности x
∞
(t), видимую через некоторое временное окно длительностью ΔT.
Иначе, реальная конечная функция x
огр
(t) есть неограниченная функция x
∞
(t), умноженная на функцию w(t)
временного окна (w – первая буква английского слова window - окно). Во временной области это запишется
таким образом
x
огр
(t) = x
∞
(t) · w(t). (6.2)
Соответственно в частотной области комплексный спектр X
огр
(ω) ограниченной во времени функции x
огр
(t)
будет определяться выражением
X
огр
(ω) = X
ω
(ω) * W(ω). (6.3)
Здесь W(ω) – спектр функции-окна.
Поэтому преобразование Фурье X
огр
(ω) наблюденной при эксперименте конечной последовательности
чисел является искаженной (сглаженной) версией комплексного спектра бесконечной последовательности,
поскольку в результате спектрального анализа реальной (ограниченной) функции x
огр
(t) получаем не истинный
X
∞
(ω) спектр, а интеграл свертки (6.3), искажающий спектр X
∞
(ω).
Достаточно часто в качестве функции-окна используется прямоугольная функция, т.е.
27

w(t) = { 1 при значениях 0 ≤ t ≤ ΔT и 0 при t < 0 и t > ΔT.
Для прямоугольной функции w(t) парой преобразования Фурье (амплитудно-частотной характеристикой |
W(f)|) является функция, называемая щелевой или интерполяционной (рис.6.1):
|W(f)| = sin p/p,
где p = 2πf
0
t, f
0
= это частота, связанная с граничной частотой, зависящей от длительности временного
окна. Амплитуда ее главного максимума пропорциональна ΔT, а расстояние (в данном случае величина Δf на
оси частот) от максимального значения до ближайшего нулевого значения пропорционально 1/ΔT. Иными
словами, ширина основного максимума интерполяционной функции sin p/p зависит от величины ΔT (рис.6.1).
Для примера предположим, что в качестве исходной функции x
∞
(t) имеется бесконечная по
протяженности косинусоида единичной амплитуды и частотой 50 Гц. Ее амплитудно-частотным спектром (при
использовании окна бесконечной протяженности) является короткий импульс (одиночная линия единичной
амплитуды) на частоте 50 Гц (рис. 6.2). Если длительность окна будет уменьшаться, то ширина основного
максимума амплитудного спектра |W(f)| функции окна будет становиться шире. Поэтому ширина спектра |
X
огр
(ω)|) также будет увеличиваться. Причем, чем короче становится сигнал во временной области (короче
длительность функции-окна w(t)), тем шире в частотной области становится интерполяционная функция и тем
сильнее происходит сглаживание (размывание) деталей первоначального спектра X
ω
(ω). В пределе, когда для
определения спектра берется одно значений исходной функции x
∞
(t), то основной максимум АЧХ спектра
X
огр
(ω) становится бесконечно широким и в нем присутствуют все частотные компоненты с одинаковыми
амплитудами (спектр становится равномерным).
Если анализируемый сигнал является более сложным и содержит несколько частотных
составляющих в составе спектра X
ω
(ω), то каждая из них будет размыта под воздействием
одной и той же функции |W(f)|, которая тем шире, чем уже анализируемый сигнал в области
времени. Если в спектре имеются две близкие частотные составляющие, которые нужно
разделить при анализе (например, одну подавить (помеха), а другую подчеркнуть (полезный
сигнал)), то для этого необходимо иметь наблюдение соответствующей длительности.
Аналогично, для более точной оценки знаний студента нужна достаточно продолжительная
беседа, причем, чем дольше беседа, тем точнее оценка знаний студента.
6.2. Роль функций-окон при обработке экспериментальных данных.
Явления Гиббса
Из вышесказанного становится понятным, что точность воспроизведения каждой частотной
составляющей ограниченной во времени функции (минимальная ширина спектральных пиков «взвешенных»
окном последовательностей временных отсчетов) определяется шириной главного лепестка (максимума)
функции |W(f)| и не зависит от исходных данных. Наличие вспомогательных максимумов интерполяционной
функции также приводит к искажениям спектров, которые часто в технике называются «просачиванием» или
«утечкой».
Явления «просачивания» часто возникают при процедурах обработки или фильтрации сигналов и могут
маскировать присутствие слабых сигналов. Так процесс прохождения сигнала
)()(
Xtx
через систему
обработки (с параметрами
)()(
Hth
) можно описать формулами (2.13) и (2.14):
)()()(
HXY
.
)()()( thtxty
.
Здесь y(t) ↔ Y(ω) – сигнал на выходе системы и его комплексный спектр.
Из свойств спектров следует, что чем больше длительность входного сигнала x(t) во времени или
импульсной реакции системы (оператора фильтра) h(t), - тем уже их частотные характеристики X(ω) или
H(ω), и тем круче их боковые срезы.
При возникновении явлений просачивания происходит утечка мощности сигнала на частотах далеких от
главного максимума спектрального окна, что искажает оцениваемые спектры, особенно в случае узкополосных
процессов, когда спектры имеют достаточно большую крутизну боковых срезов. Причем, эти искажения
проявляются тем сильнее, чем резче меняется характер (крутизна бокового среза) частотной характеристики, а
также чем больше начальная и конечная амплитуды (краевые значения) временной функции подвергающейся
анализу (или операторов их обработки).
Такого типа частотные искажения обрабатываемых спектров сигналов иногда относят к явлениям Гиббса.
Хотя более точно (с позиций математики) явления Гиббса объясняются неравномерной сходимостью ряда Фурье
(состоящего из конечного числа используемых при анализе членов ряда) в точках разрыва анализируемой
функции (в точках резкого изменения значений функции). Явления Гиббса приводят к появлению
высокочастотных дополнительных максимумов и минимумов (рис.6.2) в районе боковых срезов частотных
характеристик Н(ω) или их спектров мощности (энергетических спектров Е(ω)). Если умножить сигнал на
прямоугольную функцию во временной области, то разрывы на краях прямоугольного импульса создадут «звон»
в частотной области.
Для уменьшения явлений Гиббса и нахождения, оптимальных по точности характеристик спектров
используют различные по параметрам функции-окна (весовые функции). Применяя такие функции, постепенно
28

с обоих концов уменьшающие значения отсчетов временных характеристик x(t) или h(t), мы искажаем до
некоторой степени сам проходящий через систему (фильтр) сигнал, но препятствуем возникновению искажений
их спектральных характеристик. Сглаживание функций способствует «округлению» (заглаживанию) возможных
разрывностей на концевых участках исследуемых функций, что и уменьшает величину искажений Гиббса.
Задача «выбора формы окон» и состоит в ослаблении звона.
К весовым функциям обычно предъявляют следующие требования.
1. Функция W(f) должна иметь основной максимум в области центральной частоты. Максимум должен
быть узкополосным. Его ширина должна быть соизмерима с шириной самых мелких деталей интересующих нас
частотных составляющих спектра Х
∞
(ω). При этом, шириной главного максимума можно управлять с помощью
числа членов ряда x(t) или h(t), т.е. длительностью сигнала.
2. Амплитуда побочных максимумов функции W(ω) должны быть существенно меньше главного
максимума. А скорость спада их амплитуд должны быть по возможности большой (чтобы они вносили
небольшой вклад в формирование спектра X
огр
(ω)). На величину побочных максимумом влияет вид усечения
функции-окна w(t). Усечение в форме плавного сглаживания конечных участков w(t) обычно уменьшает их
амплитуду.
Прямоугольная весовая функция удовлетворяет первому требованию, т.к. имеет узкий главный максимум.
Но она не удовлетворяет второму требованию, т.к. амплитуда побочных максимумов достаточно велика.
Прямоугольная функция, поэтому не искажает временную функцию, но может вносить значительные искажения
в частотной области.
Некоторые виды функций-окон, широко используемые в практике цифровой обработки представлены на
рис. 6.3 .Здесь Т
е
и В
е
эквивалентная длительность окна во временной области и эквивалентная этой
длительности полоса пропускания основного максимума функции окна в частотной области W(ω). А
М
–
максимальный уровень боковых лепестков спектра W(ω).
В практике чаще умножают временную функцию х(t) на сглаживающую весовую функцию-окно. В
результате получают сглаженную к концам временную функцию, по которой и определяют конечный
(сглаженный) спектр.
Реже, по функции х(t) рассчитывают спектр X(ω), который затем сглаживается с помощью весовой
функции W(ω). При этом следует помнить, что в соответствие с формулами (6.2) и (6.3) применение весовой
функции сводится к умножению в области времени и свертке в частотной области.
Общий подход к выбору наилучшей формы весовой функции основан на компромиссе между обоими
требованиями, позволяющими при минимальных искажениях временных функций получить оптимальные
искажения их частотных характеристик.
7. Цифровая фильтрация
7.1. Основы цифровой фильтрации
Одно из центральных мест в комплексе процедур обработки геофизических данных занимает фильтрация.
Фильтрация – это обычно линейное преобразование информации, основной целью которого является подавление
той ее части, которая относится к шумам (помехам) и подчеркивание (пропускание) сигнальной информации,
характеризующей изучаемый объект. Иначе говоря, основная цель фильтрации – повышение соотношения
сигнал/помеха. В настоящее время под фильтрацией понимают любое преобразование информации,
сопровождающееся изменением ее начальных временных или частотных характеристик. Поэтому большинство
процедур обработки (даже суммирование, сглаживание и т.п.) являются по своей сути фильтрацией, поскольку
вносят изменения в форму или спектральные особенности обрабатываемых геофизических функций.
Многое в теории цифровых фильтров берет начало в области аналоговых фильтров, осуществляемых с
помощью аппаратурных устройств, состоящих из совокупности элементов электронных схем. Под
конструированием цифрового фильтра понимают обоснование и разработка алгоритма его расчета. Начальная
точка создания цифрового фильтра – это математическая формулировка задачи фильтрации, т.е. математическая
модель обрабатываемых данных, описание свойств искомого сигнала и подлежащих подавлению помех, а также
выбор целевого критерия производства фильтрации.
В качестве математической модели чаще всего используется аддитивная (суммарная) модель вида
y(t) = s(t) + n(t), (7.1)
где y(t) – это наблюденная геофизическая информация, состоящая из полезного сигнала s(t) об измеряемом
объекте и различного рода помех n(t). Иногда в основу производства фильтрации (например, в сейсморазведке)
кладется мультипликативная, полученная при умножении или свертке функций, или мультипликативно-
аддитивная модель типа
y(t) =
)()()( tntxts
, или
)()()()( tntxtsty
. (7.2)
Здесь x(t) – некоторый дополнительный параметр полезного сигнала или помех. В любой модели сигнал и
помеха описываются некоторым числом детерминистических (определяемых на основе некоторых формул) или
статистических (определенных на основе статистических характеристик) параметров (граничные частоты,
дисперсия нерегулярного шума и т.п.). При этом термин «фильтр» (система L, осуществляющая фильтрацию)
часто заменяется термином «оператор фильтра» L, т.е.
)()( tyLty
L
,
29

где
)(ty
L
- это отфильтрованная геофизическая информация, подвергшаяся фильтрации, а y(t) – входная
(начальная) функция.
Цифровая фильтрация в геофизике обычно осуществляется с использованием дискретных данных. Поэтому,
если в текстах, приведенных ниже, при написании формул используются обозначения характерные для
непрерывных функций y(t), s(t) и их комплексных спектров Y(f), S(f), то на самом деле подразумеваются их
дискретные (цифровые) аналоги:
ft
Yy
или
)()( mYny
,
ft
Ss
. Здесь n – это номер дискретного
значения временной функции, а m – это номер дискретного значения комплексного спектра в частотной области.
7.2. Пути производства (алгоритмы) фильтрации
1. Наиболее простой путь проведения цифровой фильтрации это свертка начальной информации y(t) и
оператора (импульсной реакции) фильтра h(t) во временной области:
)()()( thtyts
, (7.3)
где s(t) - это результат фильтрации (например, полезный сигнал).
В дискретном виде формула (7.3) запишется в виде
l
k
klk
hyns
0
)(
. (7.4)
2. Фильтрацию можно проводить в спектральной области. Для этого нужно путем быстрых преобразований
Фурье найти комплексный спектр начальной функции Y(f) и комплексную частотную характеристику фильтра
H(f). По формуле
)()()( fHfYfS
(7.5)
получить комплексный спектр отфильтрованной функции, а затем путем обратных преобразований Фурье
найти саму функцию после фильтрации
)()( fSts
.
3. Аналогично фильтрацию можно провести с использованием Z-преобразований этих функций, определив
Z-преобразование отфильтрованного сигнала по формуле
)()()( ZHZYZS
. (7.6)
Затем от функции S(Z) легко перейти к временной последовательности s(t).
4. Широко используют для производства фильтрации так называемые рекурсивные фильтры или
фильтрацию с обратной связью. Проведение рекурсивной фильтрации желательно в том случае, когда для
фильтрации используется фильтр с достаточно большой крутизной бокового среза амплитудно-частотной
характеристики. В этом случае будут возникать высокочастотные искажения Гиббса (см. раздел 6.2), которые
могут значительно исказить отфильтрованный сигнал (рис.7.2). Здесь блок с индексом Z характеризует
некоторую задержку сигнала в цепи обратной связи
Поэтому при производстве рекурсивной фильтрации (рис.7.2 a) сигнал пропускается несколько раз через
фильтр (или несколько подобных фильтров) с пологим боковым срезом, при использовании которого явлений
Гиббса не возникает (или они создают незначительные по величине погрешности). При пропускании уже
отфильтрованного сигнала через тот же самый фильтр (или ему подобные) несколько раз, эффективная
крутизна суммарного фильтра возрастает, а явления Гиббса практически не возникают (рис.7.2 в).
На практике при рекурсивной фильтрации входной сигнал фильтруется коротким во времени простым
оператором (с пологой частотной характеристикой), часть (рис. 7.2) отфильтрованного сигнала задерживается на
время одного шага квантования
t
или нескольких шагов квантования и после задержки повторно
пропускается через тот же фильтр. Сумму обоих фильтрованных сигналов частично после задержки во времени
снова пропускают через фильтр. Результат фильтрации снова складывается с первым и т.д. Процесс рекурсивной
фильтрации можно описать с помощью операции свертки следующим образом
l
k
klk
hyns
0
)(
+
m
k
kmk
sd
1
. (7.7)
7.3. Типы цифровых фильтров
Процедуры улучшения отношения амплитуд полезных сигналов к амплитудам помех, основанные на
использовании различных частотных или пространственно-временных характеристик полезных сигналов и
помех, занимают центральное место в комплексе обработки геофизических данных. Совокупность таких
процедур различной природы объединяется общим понятием фильтрации.
Рассмотрим основные типы фильтров на примере обработки сейсмических данных. В сейсморазведке было
давно замечено, что регистрируемые полезные сейсмические волны и волны-помехи в среднем достаточно
заметно различаются между собой, как это видно из приводимых в таблице данных, по частотному спектру и
диапазону изменения кажущихся скоростей (пространственно-временному параметру). Кажущаяся скорость
характеризует скорость распространения фронта той или иной волны вдоль линии наблюдения. В конкретных
сейсмогеологических условиях приведенные границы параметров являются еще более узкими, что делает
различие между волнами более контрастным.
Таблица 7.1
30
