Спасский Б.А. Лекции по теории обработки геофизических данных
Подождите немного. Документ загружается.


i
i
i
i
txLtxLtxLtxLty )(...)()()()(
21
.
Или
i
i
txLtxLtxLtxtxL )(...)()(...)()(
2121
.
Таким образом, реакция систему на сумму входных воздействий равна сумме реакций на каждое
воздействие.
Отсюда вытекает принцип суперпозиции: процесс прохождения сложного сигнала можно представить
как одновременное, независимое прохождение через систему каждой его компоненты (каждой синусоиды или
косинусоиды), а выходной сигнал составляет их сумму.
Свойство однородности сводится к следующему.
Если x(t) есть сумма одинаковых входных сигналов a(t), т.е.
X(t) = a(t) + a(t)+ … = na(t),
то
y(t) =
)()( tLantnaL
.
Иными словами, линейная комбинация входных сигналов преобразуется системой в линейную
комбинацию выходных сигналов. Отсюда выводится свойство прямой пропорциональности между
амплитудами входного и выходного сигналов, т.е. свойства линейной системы не зависят от величины
проходящего через систему сигнала, что выражается в линейности амплитудной характеристики данной
системы.
Оба условия линейности можно записать следующим образом
( )} ( )
i i
i i
L n x t n L x t
.
В нелинейных системах не выполняются принципы аддитивности и однородности. Поэтому форма
колебаний на выходе нелинейной системы начинает зависеть от величин амплитуд колебаний на входе, что
приводит к возникновению нелинейных искажений в процессе прохождения сигнала через нелинейную
систему. При этом необходимо представлять себе, что всякая система, рассматриваемая как линейная,
является таковой только в определенном диапазоне амплитуд сигналов, когда амплитуды не слишком велики.
А при увеличении значений амплитуд входных сигналов нелинейные искажения могут возникать в любых, в
том числе и в считающихся линейными, системах.
2.2. Частотные характеристики систем
Как и каждая функция, которые регистрируются и обрабатываются в геофизике, любая система
передачи сигналов имеет свою спектральную характеристику (комплексный спектр). Если для анализа систем
используется математический аппарат преобразований Лапласа (операционное исчисление), то комплексный
«спектр» H(p) системы называется функцией передачи (передаточная функция или коэффициент передачи).
Передаточная функция системы H(p) описывает зависимость чувствительности системы от комплексной
частоты входного сигнала
jp
. Иногда говорят не о чувствительности, а о коэффициенте усиления.
Если вместо параметра
jp
взять
jp
, когда σ = 0, то перейдем к преобразованиям Фурье
и получим комплексную частотную характеристику
)(
jH
либо просто
)(
H
или H(f).
Если через X(f) – обозначить комплексный спектр входного сигнала, а Y(f) – спектр выходного, то
частотная характеристика системы определится как
H(f) = Y(f)/X(f). (2.1)
Частотная характеристика имеет очевидную физическую интерпретацию: если на вход идеальной
системы поступает гармоническое колебание (например, косинусоида) с частотой f, то на выходе системы
тоже будет наблюдаться гармоническое колебание с этой же частотой f. Однако амплитуда выходного сигнала
(в зависимости от параметров системы) может быть отлична от амплитуды входного сигнала и, кроме того,
выходной сигнал может быть сдвинут по фазе относительно входного.
Другими словами, если x(t) и y(t) являются входным и выходным сигналами и если в качестве
входного сигнала использовать синусоиду
ftXtx
2sin)(
,
то выходным сигналом также будет синусоида y(t), но ее амплитуда Y и фаза φ могут измениться в
соответствие с параметрами H(f)
)2sin()(
ftYty
.
Отношение амплитуд выходного и входного сигналов (каждой частотной компоненты) дают
амплитудно-частотную характеристику системы
)( fH
, которая определяется выражением
)()()( fXfYfH
, (2.2)
а сдвиг по фазе между x(t) и y(t) – даст фазово-частотную характеристику
)( f
= φ
y
(f) – φ
x
(f) . (2.3)
11

Поэтому, комплексной частотной характеристикой H(f) называется комплексная функция частоты,
описывающая амплитудные и фазовые искажения, вносимые системой в комплексный спектр проходящего
через нее сигнала. Амплитудно-частотной характеристикой (АЧХ) называют модуль комплексной
характеристики
)( fH
, описывающий изменение чувствительности (коэффициента усиления) системы в
зависимости от частоты f сигнала. Фазово-частотной характеристикой системы (ФЧХ) называется фазовая
функция
)( f
H
, описывающая сдвиг системой во времени различных гармоник сигнала в зависимости от
частоты. Соответственно
( ) ( ) ( ) , ( ) ( ) ( )
y x H
Y f X f H f f f f
. (2.4)
Если графическое изображение АЧХ системы представляет собой в координатах амплитуда-частота
горизонтальную линию (рис. 2.2 а), а ФЧХ является нулевой, то такая система не искажает спектр
проходящего сигнала. Если форма АЧХ и ФЧХ системы (степень пропускания или непропускания разных
частотных компонент) меняется в зависимости от частоты, то такая система является частотным фильтром. В
зависимости от местоположения частотного диапазона повышенной чувствительности АЧХ (полосы
пропускания) характеристики фильтров делятся на фильтры нижних частот (ФНЧ), фильтры верхних
частот (ФВЧ) и полосовые (режекторные) фильтры. Теоретический вид этих частотных характеристик
представлен на рис.2.2 б, в, г, д.
Практические кривые АЧХ имеют более сглаженный вид (рис 2.3). Для качественной оценки свойств
фильтров пользуются параметрами, характеризующими основные черты формы АЧХ: граничная частота и
крутизна спада бокового среза АЧХ. Граничной частотой фильтра
),(
гргр
f
- называется значение частоты,
разграничивающей частотные диапазоны областей пропускания, где амплитуды прошедших через систему
сигналов составляют не менее 0,707 от максимального значения (уменьшаются от максимума на 3 дБ), и
область подавления, где амплитуда проходящего сигнала имеет амплитуду менее, чем 0,707 от максимального.
Для полосовых фильтров, которые обладают некоторой полосой пропускания частотных гармоник сигнала
(подавления в режекторных фильтрах), выделяют нижнюю и верхнюю граничные частоты.
Крутизной в заданной точке АЧХ называется величина наклона касательной, выраженная в единицах
системы координат АХЧ. Чаще всего крутизну определяют в точке, соответствующей граничной частоте, где
она является показателем скорости изменения чувствительности фильтра (АЧХ системы) в области перехода
от полосы пропускания к полосе подавления. В практике теории цепей используется понятие
логарифмической частотной характеристики, когда при графическом изображении АЧХ по осям координат
величину относительных амплитуд гармоник
)(lg fH
и частоту lgf откладывают в логарифмических
масштабах.
Для измерения логарифмической крутизны АЧХ применяются специальные единицы – децибелы на
октаву (дБ/октаву). Октавой называется интервал изменения частоты в 2 раза. В случае, когда величина
коэффициента усиления системы возрастает в 2 раза, то в децибелах это составит
20 log2
6 дБ.
В соответствии с этой формулой связь коэффициентов усиления с количеством децибел выглядит
таким образом
Числа десятичной системы: в 2 раза в 10 раз (10
1
) в 1000 (10
3
) в 100 000 (10
5
)
Числа в децибелах: 6 дБ 20 дБ (20 x 3) = 60 дБ (20 x 5) = 100 дБ.
С учетом формул (1.1), (1.3) и (1.7 – 1.9) для любой комплексной частотной характеристики H(f), ее
АЧХ
)( fH
и ФЧХ
)( f
можно записать
)(
)()(
fj
efHfH
,
),()()(
22
fbfafH
(2.4)
.
)(
)(
)(
fa
fb
arctgf
Здесь a(f) и b(f) действительная и мнимая части комплексной частотной характеристики H(f), т.е.
согласно выражению (1.7)
H(f) = a(f) - jb(f). (2.5)
2.3. Единичная функция
Чтобы описать свойства линейной системы в области времени, на ее вход можно подать некоторый
стандартный сигнал с известными характеристиками. Реакция или отклик системы на этот сигнал и будет
характеризовать свойства данной системы. В качестве таких стандартных сигналов обычно используются
единичная функция
)(t
или единичный импульс
)(t
.
Единичная функция
)(
t
(функция Хевисайда или функция включения тока) математически
определяется следующим образом (рис.2.4 а): она равна 0 при значениях времени t меньших
и равна 1 при
12
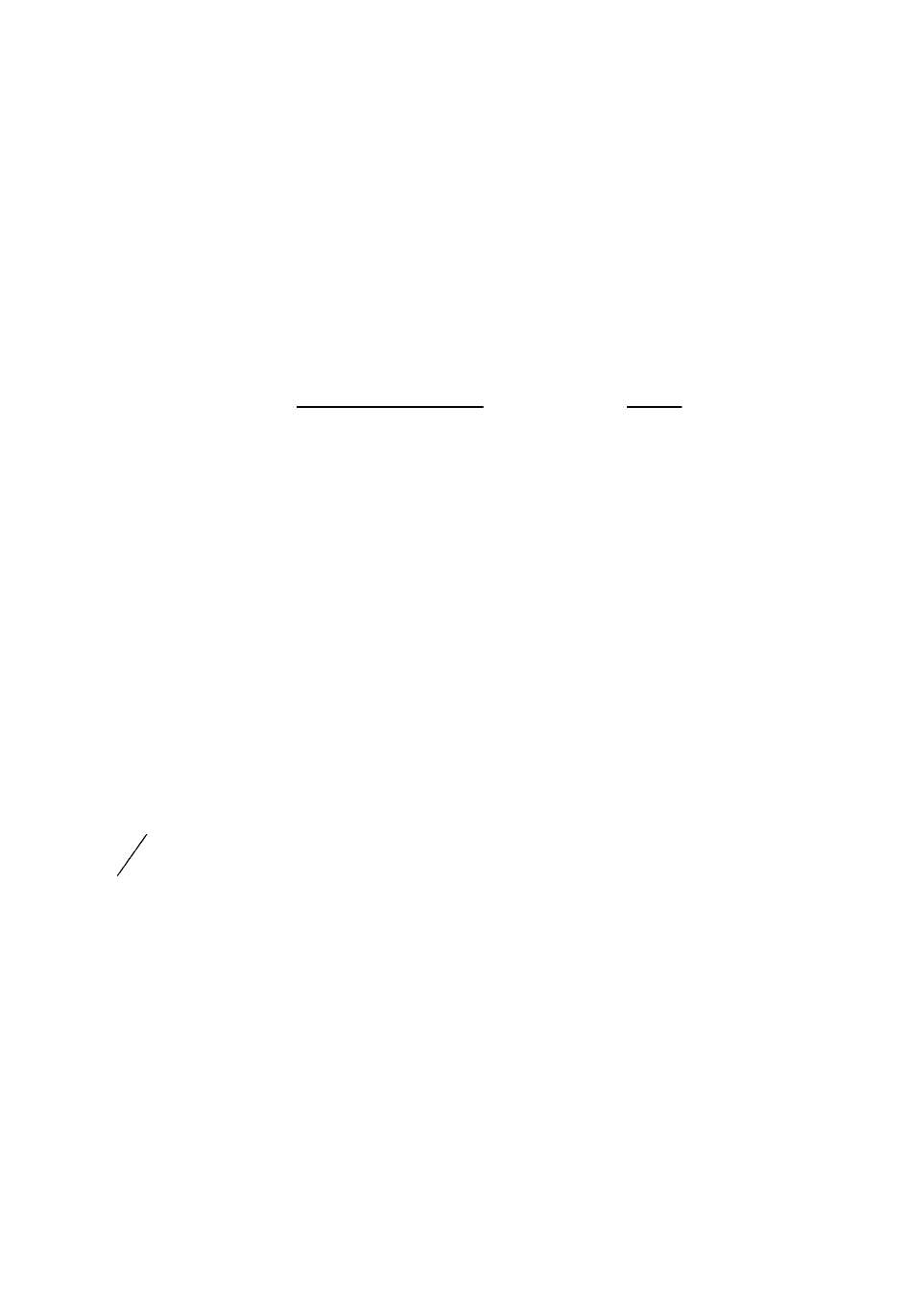
t
. С учетом этого, произвольную функцию x(t) можно представить в виде суммы последовательно
возникающих в моменты t
i
= t – iΔt = t – τ
i
прямоугольных «ступенек» с различными амплитудами
)(
ta
i
.
Здесь Δt интервал во времени, с которым происходит отсчет ступенек.
x(t)
)(
i
i
i
ta
. (2.6)
Амплитуда
i
a
каждой такой ступеньки (импульса) равна разности отсчетов функции
i
x
и
1i
x
в
моменты времени
i
и
1i
. Ее можно представить выражением
)()()()(
1
iiiii
xxtta
,
здесь
)(
i
t
это и есть единичная функция с амплитудой равной единице.
Отсюда с учетом выражения (2.6) получаем
i
ii
xxtittx )()()(
1
.
При уменьшении интервала
t
сумма стремится к интегралу, а сама величина
t
становится
бесконечно малым сдвигом
. Поэтому
i
t
dxtd
d
dx
tt
t
ttixtix
tittx
0 0
,
0
)()(
)(
)(
)()(
)(lim)(
.
В общем случае это выражение можно записать так
dtxdxttx )()()()()(
,,
. (2.7)
Отсюда следует, что любую функцию х(t) можно разложить на бесконечное множество ступенек,
амплитуды которых равны разности амплитуд в соседние моменты времени (рис.2.4 б).
Единичную функцию
)(t
часто называю ограничивающей или обрезывающей. Чтобы обрезать
функцию x(t) в момент
t
«слева», ее нужно помножить на
)(
t
, а чтобы ограничить x(t) в момент
t
«справа», нужно ее умножить на
)(1
t
, то есть вычислить значение
)(1
tx
.
2.4. Прямоугольный и единичный импульсы
С учетом вышесказанного, прямоугольный импульс длительностью
t
можно представить как
разность двух единичных функций, смещенных друг относительно друга на величину
t
. Иногда ее
называют вырезывающей функцией. Если из какой-либо функции x(t) нужно вырезать кусок длительностью
t
, то эту функцию умножают на прямоугольную функцию заданной длительности (рис. 2.4 в). Понятие
прямоугольной функции широко используется в теории и часто обозначается «rect» или box (t).
Часто полагают, что при изменении ее длительности площадь прямоугольной функции остается
постоянной и равна единице. В этом случае величина ее амплитуды будет пропорциональна ее длительности,
т.е. величине
t
1
.
Если единичный импульс сжимать по оси времен, т.е.
0t
, то величина амплитуды
прямоугольного импульса будет стремиться с бесконечности и прямоугольный импульс превратится в так
называемый единичный импульс (дельта-функция) или импульс Дирака
t
. Его величина равна нулю для всех
времен за исключением времени t=0. Единичный импульс может занимать произвольное положение на оси
времен, например, может быть сдвинут по оси времен относительно начала координат (t=0) на величину
,
то есть имеем импульс
)(
t
. В этом случае бесконечно большое значение будет наблюдаться на времени
t
.
Важным свойством единичного импульса является то, что его площадь равна единице, то есть
1)( dtt
или
i
i
t
t
AdttA )(
, (2.8)
где
- произвольная положительная величина, A – масштабирующий множитель.
Свертка единичного импульса
)(
i
tt
с произвольной функцией x(t) дает значение этой функции в
точке t = t
i
)()()(
ii
txdttttx
. (2.9)
Другими словами формулу (2.9) можно записать в таком виде
dtxdtx )()()()(
. (2.10)
13
Сравнение функций
)(t
и
)(t
показывает, что единичный импульс является производной от
единичной функции, т.е.
)()(
,
tt
.
Соответственно формулы (2.7) и (2.10) идентичны. Их физический смысл состоит в том, что любую
функцию x(t) можно разложить или на серию единичных функций или импульсов, запаздывающих друг по
отношению к другу на бесконечно малое время
и имеющих амплитуды равные отсчетам анализируемых
функций, соответствующих этим временам (запаздыванию относительно 0). При этом, если единичная
функция
)(t
легко может быть получена на практике (например, включая или выключая постоянный ток
на входе любого устройства), то единичный импульс
)(t
- это функция теоретическая, получить которую в
практике затруднительно. Обе они широко используются при анализе различных систем (цепей).
2.5. Временные характеристики систем
Так, если на вход системы L подать единичную функцию
)(t
(функцию включения тока), то на
выходе системы L появится некоторая функция g(t), называемая переходная характеристика или переходная
функция (рис.2.5 а). С учетом выражения (2.7), произвольный сигнал x(t), поступающий на вход системы L,
характеризующейся переходной характеристикой g(t), можно представить как интегральную сумму
запаздывающих на бесконечно малый промежуток времени
d
единичных функций с бесконечно-малой
амплитудой
dx
dt
dtxd
dx )(
)(
,
. При этом, появление каждой единичной функции на входе
системы приведет к возникновению переходной характеристики g(t) на выходе этой системы (рис.2.5.а).
Интегральная сумма всех этих переходных характеристик
)(
tg
, появляющихся на выходе с
соответствующими запаздываниями
, в соответствие с принципом суперпозиции, и будет формировать
отклик y(t) системы L на все
)(
t
(рис. 2.5.в). Математически это запишется таким образом
1 1
0 0
,,
)()()()()(
t t
dtgxdtgxty
или
)()()(
,
tgtxty
. (2.11)
Поскольку единичную функцию легко создать в реальных условиях, включая или выключая
постоянный ток на входе любого устройства, то переходные характеристики (переходные функции) широко
используются на практике для анализа различных видов аппаратурных устройств.
С другой стороны, если на вход системы L подать единичный импульс (дельта-функцию)
)(t
, то
на выходе системы L возникнет сигнал h(t), называемый импульсной реакцией (рис. 2.5 б) или импульсной
переходной характеристикой (функцией). В соответствии с выражением (2.10), произвольный сигнал x(t)
можно разложить на бесконечное множество единичных импульсов, запаздываюших на величину
относительно момента t = 0 подачи входного сигнала на вход системы L. Каждый из единичных импульсов
будет на выходе системы L (рис. 5.2 б) создавать соответствующую ему импульсную реакцию h(t). Сумма этих
импульсных реакций и будет формировать выходной сигнал y(t) или
1 1
0 0
)()()()()()()(
t t
thtxdhtxdthxty
. (2.12)
Таким образом, свойства любой системы при анализе сигналов в области времени можно описать с
использованием переходной характеристики g(t) или импульсной переходной характеристики h(t). Если g(t)
широко используется при анализе аппаратурных устройств, то вторую h(t) очень удобно использовать при
цифровой обработке данных. В этом случае h(t) часто называют оператором системы L или весовой функцией.
С учетом выражения (20) выходной сигнал y(t) на выходе системы L равен свертке входного сигнала x(t) и
импульсной переходной характеристики системы h(t).
2.6.Анализа воздействия систем на проходящие сигналы
Предположим, что имеется произвольная система L, на вход которой поступает входной сигнал x(t), а
выходным сигналом является функция y(t). И входной сигнал, и функция на выходе характеризуются своими
комплексными спектрами (рис.2.1)
)()(
Xtx
и
)()(
Yty
.
Перед тем, как рассмотреть принципы анализа произвольных линейных систем, остановимся на
связях отдельных параметров систем.
Как было показано выше, единичный импульс является производной от единичной функции, т.е.
dt
td
t
)(
)(
. Аналогично можно определить связь между импульсной переходной характеристикой
)(th
и переходной характеристикой g(t) системы L
h(t) =
dt
tgd )(
или
)()(
,
tgth
.
14
Понятно, что каждая временная характеристика произвольной системы L имеет свою частотную
характеристику, получаемую на основе преобразований Фурье:
)()( fHth
или
)()(
Hth
,
а
)()( fGtg
или
)()(
Gtg
.
На основе теорем о свойствах спектров и их производных можно записать, что
)()(
GjH
или
jHG /)()(
.
Функция H(f) или
)(
H
- это комплексная частотная характеристика системы L. Если
)(
X
-
комплексный спектр входного сигнала, а
)(
Y
- спектр выходного, то согласно формуле (2.1)
)()()(
XYH
.
Отсюда следует, что если известен комплексный спектр входного сигнала
)(
X
и комплексная
частотная характеристика
)(
H
системы L, то возможно определить комплексный спектр
)(
Y
выходного или
)()()(
HXY
. (2.13)
В учетом свойств спектров: произведению спектров в частотной области соответствует свертка
соответствующих функций в области времени. Поэтому
)()()( thtxty
. (2.14)
Именно формулы (2.13) и (2.14) используются для описания характера воздействия систем (во
временной или спектральной областях) на проходящие через них сигналы. На их основе можно записать
deHXdeYty
tjtj
)()()()(
.
При этом нужно помнить, что для определения амплитудно-частотного спектра
)(
Y
выходного
сигнала необходимо перемножить соответствующие характеристики входного сигнала и системы, а для
получения его фазового спектра
)(
y
- необходимо сложить соответствующие фазовые характеристики
)()()(
HXY
и
)()()(
hxy
. (2.15)
Если сложная система L состоит из нескольких более простых систем (например
21
, LL
),
включенных последовательно друг за другом, то для них имеем
)()()()()()(
21
HHXHXY
LL
,
)()()()()()(
21
HHXHXY
LL
,
)()()(
LxL
.
)()()()()()(
21
ththtxthtxty
L
.
Если системы L
1
и
2
L
соединены параллельно друг другу, то
)()()()()()()()()()(
2121
HXHXHHXHXY
LL
.
)()()()()()()(
21
thtxthtxthtxty
LL
.
3. Корреляционные и энергетические характеристики
3.1. Корреляционные функции. Функция взаимной корреляции
При обработке геофизической информации большое значение в практике имеют корреляционные
функции. На их использовании основаны многие способы выделения полезной информации на фоне шумов.
Обычно корреляционные функции позволяют определить степень подобия каких-то процессов. Так функция
взаимной корреляции
)(
2,1
r
или ФВК позволяет установить сходство (подобие) формы двух функций
)(
1
tx
и
)(
2
tx
при различных временных сдвигах
между ними. Процесс расчета ФВК можно
представить таким образом.
Анализируемые функции располагают рядом на графике, совмещая по оси времен их начало.
Проводят перемножение значений обеих функций друг на друга и выполняют интегрирование произведений.
Результатом такой процедуры является значение
2,1
r
для значения
0
, т.е. осредненное значение
произведений ординат функций для нулевого сдвига между функциями, полученными на заданном интервале
времени. Аналогично находят такие суммы произведений значений функций при разных сдвигах
обеих
функций как положительных (в сторону увеличения времен), так и отрицательных (в другую сторону).
График зависимости
)(
2,1
r
и есть ФВК. Очевидно, что максимальные значения функции взаимной
корреляции будут наблюдаться в том случае, когда форма сигналов
)(
1
tx
и
)(
2
tx
подобна при заданном
сдвиге. Значения ФВК близкие к нулю будут соответствовать случаю отсутствия подобия (наибольшего
различия). Математически этот процесс проводят с использованием выражения
15

dttxtxdttxtxr )()()()()(
21212,1
. (3.1)
Процесс нахождения ФВК подобен свертке двух функций, но при расчете ФВК не проводится обращения
(переворота) одной из функций во времени.
Чтобы максимальные значения ФВК не превышали бы единицу (в случае максимального подобия
функций), обычно ФВК нормируют, т.е. расчетные значения делят, например, на величину
)0(
2,1
r
при
0
:
5,0
2
2
2
1
21
2,1
)()(
)()(
)(
dttxdttx
dttxtx
r
.
Если в качестве функции
)(
1
tx
выступает синусоида с частотой f
1
, а функция
)(
2
tx
состоит из
колебаний многих частот, то расчет ФВК позволяет извлечь эту частоту
1
f
из второй функции, т.е. величины
функции взаимной корреляции будут пропорциональны значениям этой частоты
1
f
, имеющимся в функции
)(
2
tx
.
Если обе функции
)(
1
tx
и
)(
2
tx
являются сложными, состоящими из многих частотных компонент,
сигналами, то функция взаимной корреляции будет содержать те частоты, которые являются общими для
обоих сигналов. ФВК достигает максимума в том случае, когда большая часть частотных компонент (частот)
обоих сигналов будут иметь одинаковые фазы. Таким образом, ФВК позволяет обнаружить лучшее
соответствие (сходство) между двумя функциями, даже если эти функции засорены помехами (имеют в
составе разные (неодинаковые) компоненты). Фаза (фазово-частотный спектр) каждой частотной компоненты
функции взаимной корреляции соответствует разности фаз этих частотных компонент имеющихся в обеих
функциях
)(
1
tx
и
)(
2
tx
.
3.2. Функция автокорреляции
Результат корреляции любой функции со своей копией (самой функции с собой) называется функцией
автокорреляции
)(
b
или ФАК. Она является частным случаем функции взаимной корреляции, когда
)()(
21
txtx
, иначе
)()()()()()()()(
11111,11
xx
bbdttxtxdttxtxrb
. (3.2)
Это выражение показывает, что функция автокорреляции является симметричной относительно начальной
точки, где
0
, где она достигает максимума. Поскольку ФАК является результатом взаимной корреляции
сигнала с самим собой, то фазы всех частотных компонент (равные при расчете ФВК разности фаз обеих
функций) будут одинаковыми и разность фаз будет равна нулю. Поэтому функция автокорреляции не несет
информации о фазах частотных компонент, на которые она раскладывается.
В практике обычно используются нормированные ФАК
dttx
dttxtx
b
2
1
11
_
)(
)()(
)(
.
Основные особенности ФАК сводятся к следующему
- ФАК образуется как результат интегрирования по всей оси времен t произведения сигнала с его копией,
сдвинутой на интервал времени
. Каждому сигналу соответствует определенная ФАК, но не наоборот. По
ФАК нельзя восстановить форму сигнала так же, как по известной площади плоской фигуры, нельзя
определить ее форму.
- ФАК имеет размерность мощности или энергии сигнала и является четной функцией временного сдвига.
- Любое значение автокорреляционной функции не превосходит ее значение в точке, где
0
.
- ФАК периодического сигнала – сама является периодической функцией с тем же периодом, что и
анализируемый сигнал x(t). Причем периодичность по ФАК выявляется даже лучше, чем по функции x(t).
- У всех сигналов, кроме периодических, ФАК убывает по мере увеличения
. Степень спада значений
ФАК характеризуется интервалом корреляции.
Широко применяется понятие ФАК при анализе случайных функций. Так, если анализируемая функция
осложнена случайными помехами, то основной максимум ФАК (когда
0
) будет по амплитуде
значительно превышать все последующие экстремумы.
3.3. Энергия и мощность сигналов
Помимо амплитуд и фаз различных частотных компонент сигнала при обработке информации удобно
рассматривать энергетические характеристики функций. Основными энергетическими характеристиками
16
сигналов как функции времени являются мгновенная (текущая) мощность p(t), полная энергия E или средняя
мощность
ср
p
. В общем случае мгновенная мощность (энергия) находится как величина, пропорциональная
квадрату амплитуды
)()(
2
txtp
.
Мгновенная мощность не аддитивна, т.е.
)()()()(
2
2
2
1
2
21
txtxtxtx
.
Во временном представлении средняя мощность любой вещественной функции x(t) определяется
выражением (Бат, 1980)
ср
p
2
2
2
)(
1
lim
T
T
T
dttx
T
, (3.3 а)
когда этот предел существует. Здесь T период колебаний либо интервал времени. В практическом случае,
когда T ограничено, функция
2
)(tx
называется мгновенной энергией, а интеграл типа
x
Edttx
2
)(
или
1
2
1
2
)()(
2
t
t
t
t
x
dttxdttpE
(3.3 б)
- полной энергией функции x(t), если подинтегральное выражение сходится. При этом, временная функция
x(t) может обозначать изменение любой величины: напряженности геомагнитного поля, скорости смещения
частиц среды, силы тока и т.д.
С учетом (3.3а) и (3.3б)
xср
E
T
p
1
,
где
12
ttT
.
3.4. Теорема Парсеваля (Релея). Энергетические спектры
Чтобы найти связь между мощностью сигнала и его спектром воспользуемся теоремой Парсеваля или
теоремой Релея
0
222
)(
1
)(
2
1
)()(
2
1
)(
dXdXdXXdttx
. (3.3в)
Действительная величина
2
)(
X
известна как спектр мощности
)(
x
E
или энергетический спектр,
либо более точно как спектральная плотность мощности или спектральная плотность энергии, т.е.
мощность или энергия, приходящаяся на единичный интервал оси частот. Иначе
2
)()()()(
XXXE
x
. (3.3г)
Поскольку в выражение (3.3г) входит квадрат абсолютного значения амплитудного спектра
)(
X
,
информация о фазовом спектре отсутствует. Это означает, что если задана только мощность, то восстановить
первоначальный сигнал x(t) невозможно, в отличие от того случая, когда задана функция
)(
X
,т.е. и
амплитудно-, и фазово-частотный спектры. Поэтому сигналы с идентичными амплитудными, но разными
фазовыми спектрами, будут иметь одинаковые спектры мощности. При этом, сдвиг функции во времени не
повлияет на ее энергетический спектр. Но изменение масштаба времени
att
соответственно изменяет
энергию в a раз.
Из выражений (11в) и (11г) следует
)()(
xx
Eb
. (3.4)
Функции автокорреляции некоторых геофизических явлений часто уменьшаются по экспоненциальному
закону с увеличением временного сдвига
eb
x
)(
или
0
cos)(
eb
x
,
0a
.
Подобные процессы называются марковские. Энергетические спектры таких функций в технике называются
красным шумом. Чем шире полоса частот амплитудного спектра таких функций – тем быстрее затухает
функция автокорреляции (тем уже ее основной максимум). Если в амплитудном спектре присутствуют
бесконечно большое частотных компонент, то функция автокорреляции представлена единичным импульсом.
Функции такого типа называются белым шумом.
3.5. Взаимные энергетические спектры. Когерентность
Если имеется две функции
)()(
11
Xtx
и
)()(
22
Xtx
обладающие энергетическими спектрами
2
11
)()(
XE
и
2
22
)()(
XE
, то можно вычислить взаимный энергетический спектр
)(
2,1
E
этих функций
17
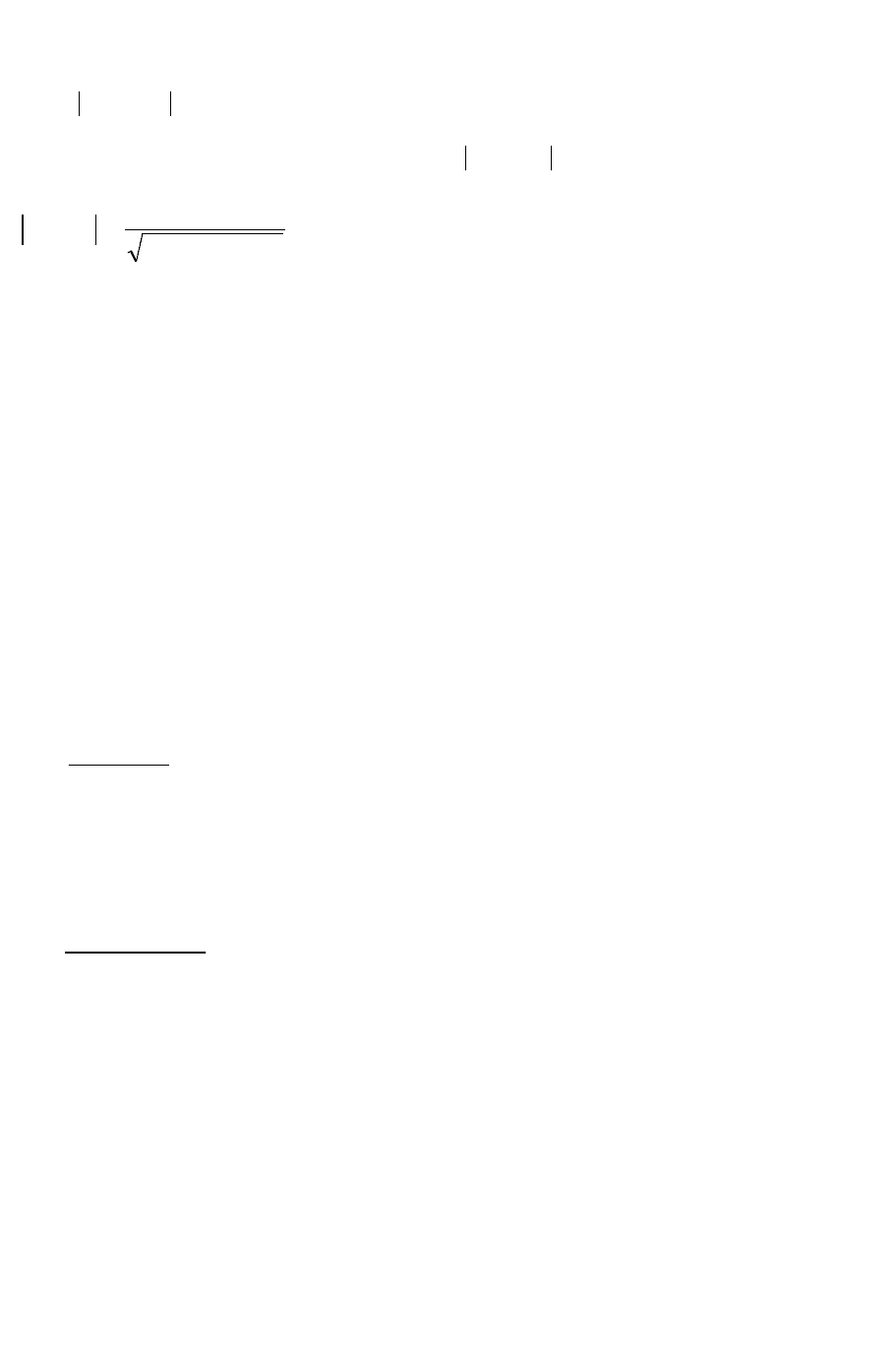
)()()(
212,1
XXE
. (3.5а)
В отличие от энергетических спектров
)(
1
E
или
)(
2
E
, которые всегда вещественные и
положительные, взаимный энергетический спектр в общем случае является комплексным. Поэтому только его
модуль
)(
2,1
E
может использоваться в качестве меры взаимной энергии. На основе взаимного
энергетического спектра часто используется понятие когерентности.
Когерентность или коэффициент когерентности
)(
2,1
сигналов
)(
1
tx
и
)(
2
tx
определяется
следующим образом (Бат, 1980):
)()(
)(
)(
21
2,1
2,1
EE
E
. (3.5б)
Когерентность, если не обращать внимания на ее нормирующий знаменатель, фактически является
спектром функции взаимной корреляции. Иначе можно записать
)()(
2,12,1
rE
. (3.6)
В физике когерентность характеризует согласованное по какому-либо признаку протекание во времени
нескольких колебательных или волновых процессов.
Если функция взаимной корреляции определяет подобие формы колебаний двух процессов, то при
определении понятия когерентности в основу понятия кладется подобие функций по энергии. Поэтому,
например, при суммировании сейсмических трасс, являющихся смесью записей полезного сигнала и помех,
соседние трассы считаются когерентными, если их суммарная амплитуда велика, поскольку сигналы
отдельных каналов подобны и, складываясь в фазе, дают большую суммарную амплитуду. Там же, где
суммарная амплитуда мала, то сигналы на соседних трассах отличаются друг от друга и не являются
когерентными. Если сдвиг во времени между энергетически выраженными колебательными процессами на
нескольких сейсмических трассах, остается постоянным во времени или меняется по строго определенному
закону, то такие процессы также являются когерентными. В практике сейсморазведки (Шерифф, Гелдарт и
др., 1982) для расчета когерентности функции
)( tnx
используют не нормированные значения взаимных
энергетических спектров, а отношение энергии (квадрата амплитуд) суммарной записи к сумме энергий
отдельных мгновенных значений амплитуд
kn
A
,
, где n – это номер мгновенного значения трассы во
времени, а величина k – номер трассы:
k
kn
k
kn
n
A
A
2
,
2
,
.
Здесь числитель – суммарная энергия нескольких трасс (выходной сигнал), а знаменатель – сумма энергий
входных трасс. Если такой параметр рассчитать в пределах некоторого окна
T
, то его называют подобием
S:
Tt
t k
kn
Tt
t k
kn
A
A
S
)(
)(
2
,
2
,
.
Связь всех вышеупомянутых временных и спектральных характеристик функций x
1
(t) и x
2
(t) показана на
рис. 3.1.
4. Особенности преобразования дискретных функций
4.1. Дискретные функции
В практике при цифровой обработке информации с использованием вычислительной техники обычно
используются не непрерывные функции, а дискретные (или, более точно, - цифровые). Процесс
преобразования непрерывных (аналоговых) функций в дискретные осуществляется путем квантования (отбора
мгновенных значений) их во времени (рис. 1.1). В процессе дискретизации непрерывный сигнал x(t) или его
комплексный спектр Х(ω) заменяются (как в частотной, так и во временной областях) последовательностью
мгновенных значений функций, взятых через определенные интервалы времени
t
или частоты
. Эти
значения являются шагом квантования функций х(t) или Х(ω) во временной или частотной областях. Иначе
говоря, квантование преобразует непрерывную (аналоговую) функцию x(t) или ее комплексный спектр
)(
X
в серию амплитудных выборок или отсчетов (числовых последовательностей или рядов чисел), т.е. в
дискретные функцию
t
x
или
X
.
Поэтому дискретные временные функции описываются так называемыми решетчатыми функциями,
т.е. последовательностями значений х(nΔt) или просто х(n), где Δt = const - это шаг квантования во времени, а
n = 0, 1, 2, …N-1, – целые числа, определяющие номер дискрета по оси времен. Комплексные дискретные
18

спектры в этом случае выражаются функциями X(mΔω) или X(m), где m – также целые числа, которые
определяют номер отсчета комплексного спектра по оси частот, а Δω шаг квантования комплексного спектра
по оси частот. N – это общее количество дискретных значений функций x(n) или X(m). Величины дискретных
функций (выборки или отсчеты) на интервале измерения точно соответствуют значениям аналоговой
функции x(t) в заданные моменты времени nΔt или частоты mΔω.
Иногда в теории обработки различают импульсные и дискретные функции. Дискретная функция
t
x
или х(n), состоит из последовательности N отсчетов во временном интервале
Nn 0
и может быть
представлена в таком виде (Кондратьев, 1977):
1
0
21
)(
ˆ
)(...)(
ˆ
...)2(
ˆ
)(
ˆ
)(
ˆ
N
n
not
tnttnxtntxttxttxtxx
,
(4.1) здесь
)(
ˆ
t
- дельта-функция Кронекера, длительность которой меньше
t
и которая отлична от
нуля лишь в точке отсчета, где она равна 1,
)( tnxx
n
- это значение функции в точке с номером отсчета
функции n и запаздыванием во времени
tn
относительно начала, n = 0, 1, 2, …, n, …, N-1.
В дискретных системах этот импульс играет такую же роль, как единичный импульс Дирака
)(t
в
импульсных системах. Можно сказать и так: импульс Кронекера
)(t
, являющийся практическим сигналом
равным 1, не может подвергаться интегральным преобразованиям, так как
0)(
dtt
. В отличие от
импульса
)(t
, единичный импульс Дирака
)(t
в точке отсчета равен бесконечности, а
( ) 1t dt
, (4.2)
т.е. имеет единичную площадь.
Поэтому с импульсными функциями можно осуществлять любые интегральные преобразования, в том
числе, и преобразования Фурье.
Поскольку импульсные функции, являющиеся теоретическими, отличаются от функций дискретных
(практических) в формуле (1) лишь формой импульса (Кронекера или Дирака), то при цифровой обработке
все дискретные функции мысленно заменяются импульсными. А так как цифровые значения обеих функций
зависят лишь от вида самой функции x(t) в точках отсчета, то такая замена не сказывается на результатах
расчетных числовых значений, но позволяет использовать интегральные преобразования с дискретными
функциями при расчетах.
На самом деле в практике цифровой обработки используются так называемые цифровые функции
(рис. 1.1 б). Они представляют собой квантованные по уровню, т.е. измеренные по величине амплитуд
дискретные значения, которые принимают в дискретные моменты времени nΔt или частоты mΔω величины,
определяемые набором из нескольких разрядов (уровней) квантования. Знак и величина цифровой функции в
каждой точке отсчета кодируется набором цифр (обычно чисел в двоичной системе счисления). Поэтому
каждое значение цифровой функции определяется с некоторой погрешностью, зависящей от числа разрядов
квантования по уровню.
4.2. Выбор шага квантования во времени. Частота Найквиста
При цифровой обработке непрерывные (аналоговые) функции x(t) заменяются дискретными
t
x
.
После обработки дискретных функций на компьютере, часто возникает необходимость снова восстановить
обработанную функцию в аналоговом (непрерывном) виде. Если величина шага квантования (шага
дискретизации)
t
выбрана неправильно, то при последующем восстановлении дискретного сигнала в
непрерывную форму могут возникать искажения, часто называемые термином аляйсинг (от английских слов
aliasing или folding).
Для определения оптимального шага квантования (при большом шаге квантования будут наблюдаться
искажения функций, а при малом – резко повышается стоимость компьютерной техники и время обработки) в
геофизике обычно используется теорема, сформулированная В.А.Котельниковым (Харкевич, 1962) для
передачи информации по каналам связи. В соответствие с этой теоремой – если требуется передать по каналу
связи непрерывную во времени функцию x(t) с ограниченным спектром, нет нужды при ее дискретизации
использовать бесконечно большое число отдельных мгновенных значений. Достаточно передать отдельные
значения, отсчитанные через время
t
. При обработке геофизической информации для выбора шага
квантования Δt используют следующую формулу
макс
f
t
4
1
= Т
мин
/4 (секунды), (4.3)
где
макс
f
- это максимальная частотная компонента (гармоника) спектра функции x(t), которая еще
не искажается при данном шаге квантования
t
. Т
мин
– минимальный период колебаний, соответствующий
этой частоте. Отсюда следует, что для правильного преобразования непрерывной функции в дискретную
функцию необходимо иметь, как минимум, четыре отсчета на период.
19

Так, при регистрации сейсмических данных часто используют шаг квантования
002,0t
секунды. Это связано с тем, чтобы пропускать без искажений частотные через систему обработки компоненты
вплоть до частоты 125 Гц. В соответствии с формулой (2) максимальная частота, равная 125 Герцам, еще не
искажается (также как и более низкочастотные компоненты 124, 123 Гц и т.д.) при преобразовании
непрерывных функций, поступающих от сейсмоприемников, к дискретному виду. Компонента сигнала 126 Гц
уже будет искажаться.
Рассмотрим более детально процесс возникновения искажений при дискретизации сигналов, который
фактически сводится к образованию ложных боковых или зеркальных частотных компонент. Введем понятие
частоты дискретизации или частоты квантования
t
f
кв
1
и понятие частоты Найквиста
2/
квN
ff
=
1/(2Δt). Так, если шаг квантования
002,0t
с, то
500002,0/1
кв
f
Гц, а
2502/500
N
f
Гц.
Предположим, что исходная непрерывная функция x(t) специальным устройством преобразуется в
дискретную функцию
t
x
, а затем, дискретная функция опять преобразуется в непрерывную
)(tx
(рис.4.1).
Сравнение начальной x(t) и конечной
)(tx
функций позволит оценить характер возникающих искажений.
При этом, на вход устройства преобразования в качестве непрерывного сигнала x(t) будем подавать
гармоническую функцию (например, косинусоиду) определенной частоты.
Если шаг квантования равен 0,002 с (
500
кв
f
Гц), то частота Найквиста равна 250 Гц. Пусть
вначале частота входного сигнала
вх
f
больше частоты Найквиста и равна 300 Гц. На выходе устройства
преобразования вследствие явлений наложения получим значение
200
вых
f
Гц, которое определяется из
соотношения
вхкввых
fff
. (4.4а)
Если частота входного сигнала 450 Гц, то частота на выходе, в соответствие с (4.4а), составит 50 Гц.
Эти искажения (при условии, что
Nвх
ff
) возникают вследствие того, что при заданных условиях
(шаге квантования 0,002 с) при преобразовании входного сигнала в дискретную форму возникает менее двух
отсчетов на один период функции x(t). При дальнейшем преобразовании полученные дискретные значения
заменяются (аппроксимируются) непрерывной кривой, частота которой не совпадает с частотой начальной
функции. Такое явление в практике часто наблюдается при просмотре кинофильмов, когда на экране
показывают колеса автомобиля (или телеги) движущегося с большой скоростью, не соответствующей частоте
движения кадров фотопленки. В этом случае скорость движения колес может замедляться или их вращение
начинается в противоположную сторону.
Если
Nвх
ff
, то на каждый период входного сигнала имеем ровно два дискретных отсчета входной
функции и частотных искажений не возникает. Однако фаза и амплитуда выходного сигнала в значительной
степени зависят от момента (фазы) отсчета мгновенного значения сигнала при его дискретизации (рис.4.2).
Если отсчеты происходят в моменты, когда амплитуда входной сигнал близка к нулю (рис.4.2 а), то и на
выходе системы эти значения будут небольшими (нулевыми). Если отсчеты будут совпадать с максимумами,
то амплитуда на выходе (рис.4.2 б) будет даже больше амплитуды на входе (вследствие замены ступенчатой
функции на косинусоидальную).
Поэтому, при заданном условии, величины амплитуд могут изменяться в пределах 0 - 1,27
(относительно начального значения равного 1), а погрешность восстановления амплитуд гармоник может
достигать 100%. При уменьшении частоты входного сигнала эти погрешности уменьшаются (рис.4.2.в) и на
частоте f = 125 Гц они не превышают 3 дБ или величины 0,707 от начального значения (как это принято в
теории фильтров). Именно эта частота 125 Гц соответствует значению
макс
f
, которая в соответствие с
формулой (2) еще не искажается при преобразованиях.
С учетом вышесказанного, перед производством преобразования непрерывных функций в дискретные
(в цифровой регистрирующей геофизической аппаратуре), необходимо применить фильтры нижних частот,
которые не пропустят в тракт регистрации компоненты, частота которых превышает
макс
f
. Именно частота
макс
f
и является граничной для данного фильтра.
4.3. Формулы дискретных преобразований Фурье
Прямое преобразование Фурье для непрерывных функций можно записать в виде
dtetxX
tj
)()(
.
При дискретных преобразованиях Фурье (ДПФ) непрерывная функция x(t) и ее комплексный спектр
)(
X
заменяются соответствующими дискретными аналогами
t
x
и
X
. При этом, обе функции будут
состоять из N дискретных значений каждая. Функция x(t) будет представлена выборками в моменты времени
0,
t
,
t2
, …,
tn
, …,
tN )1(
. Каждое из N значений дискретной временной функции имеет свой
20
