Смирнова Е.Ю. Техника финансовых вычислений на Excel

Подождите немного. Документ загружается.

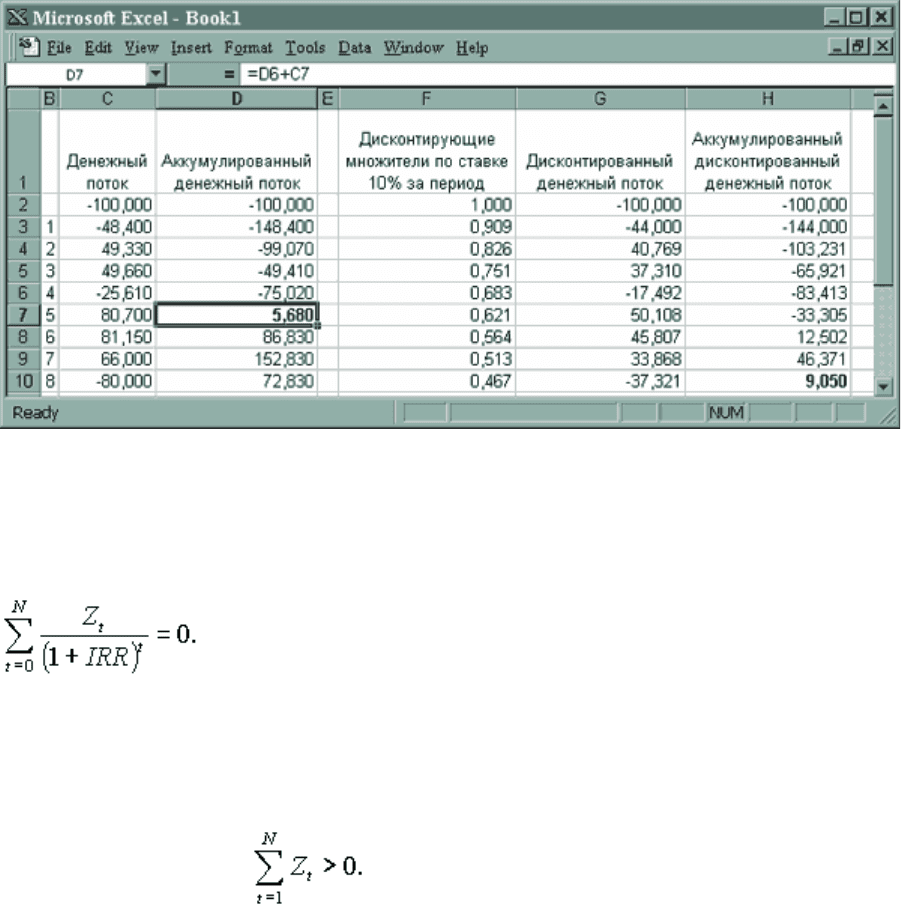
Рис. 46. Определение простого и дисконтированного сроков окупаемости проекта.

Важным критерием принятия инвестиционный решений на основе дисконтирования денежного потока является

внутренняя норма доходности (англ internal rate of return). Это такое значение нормы математического

дисконтирования, при котором текущая стоимость денежного потока абсолютно равна инвестициям. Внутренняя

норма доходности является корнем IRR неявного уравнения, в левой части которого стоит многочлен (полином)

степени N.

 Из основной теоремы алгебры следует правило знаков Декарта, в соответствии с которым число

положительных вещественных корней многочлена, включая кратные, равно k – числу перемен знака в ряду

коэффициентов многочлена, или k минус положительно чётное число. Если k = 1, то уравнение имеет

единственное положительно решение.



Следствием правила знаков Декарта является следующее утверждение: если Z

<0 и все Z

,…,Z



0, то

существует единственное решение (1+IRR) > 0, то есть IRR > –1.

 IRR > 0 при условии

 Справедливо также правило Норстрёма

, сформулированное через число перемен знака в ряду элементов

аккумулированного денежного потока (см. рис. 46): если последний член аккумулированного денежного

потока не равен нулю, и при этом в ряду значений элементов аккумулированного денежного потока знак

меняется только один раз, то для исходного денежного потока существует единственное положительное

значение внутренней нормы доходности IRR.

Денежный поток, имеющий единственное положительное значение внутренней нормы доходности IRR, называется

регулярным.

Найти значение внутренней нормы доходности в Excel можно подбором параметра (см. рис. 47), или встроенной

финансовой функцией IRR (см. рис. 48).

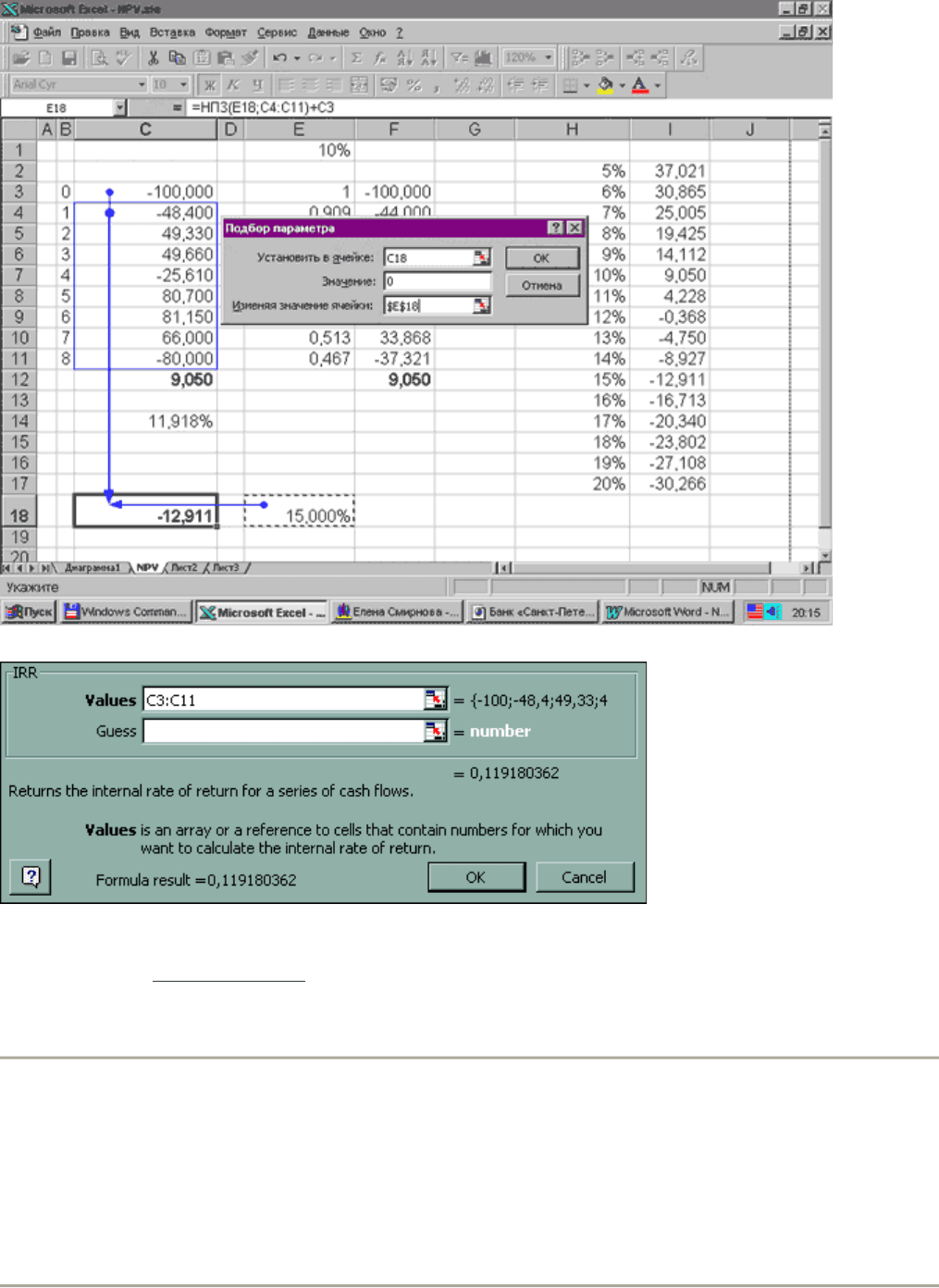
Рис. 47. Подбор значения внутренней нормы доходности.

Рис. 48. Вычисление внутренней нормы доходности встроенной функцией IRR .

Первый аргумент этой функции – табличный интервал ячеек, где в хронологическом порядке расположены элементы

денежного потока, начиная с нулевого. Именно к этому значению программа будет подгонять дисконтированный

доход, изменяя процентную ставку. Второй необязательный аргумент (значение 10% установлено по умолчанию)

задает предполагаемый ответ для начала итеративной процедуры приближенных вычислений. В исходной

русификации IRR называется ВНДОХ, а в новейшей - ВСД (внутренняя ставка доходности).

1 Коссов В.В., Лившиц В.Н., Шахназаров А.Г. Методические рекомендации по оценке эффективности

инвестиционных проектов: официальное издание. М., 1999.

2 Сюдсэтер К., Стрём А., Берк П. Справочник по математике для экономистов / Пер с норвежск. Под ред.

Е.Ю.Смирновой. СПб.: Экономическая школа, 2000.

БЛОК 6: Аннуитетные финансовые функции

из книги "Техника финансовых вычислений на Excel" Смирновой Е. Ю.

Аннуитетные финансовые функции

При изучении материала этого блока вы узнаете, что такое:

 потоки платежей постнумерандо и пренумерандо;

 вечная рента (бессрочный аннуитет) и срочный аннуитет;

 текущая и будущая стоимость аннуитета;

 процентная ставка за период между платежами;

 погашение долга равными платежами;

 равномерное погашение долга.

Аннуитетом называется поток платежей одинакового размера, поступающих через равные промежутки времени.

Период времени между двумя последовательными платежами является расчетным при начислении процентов.

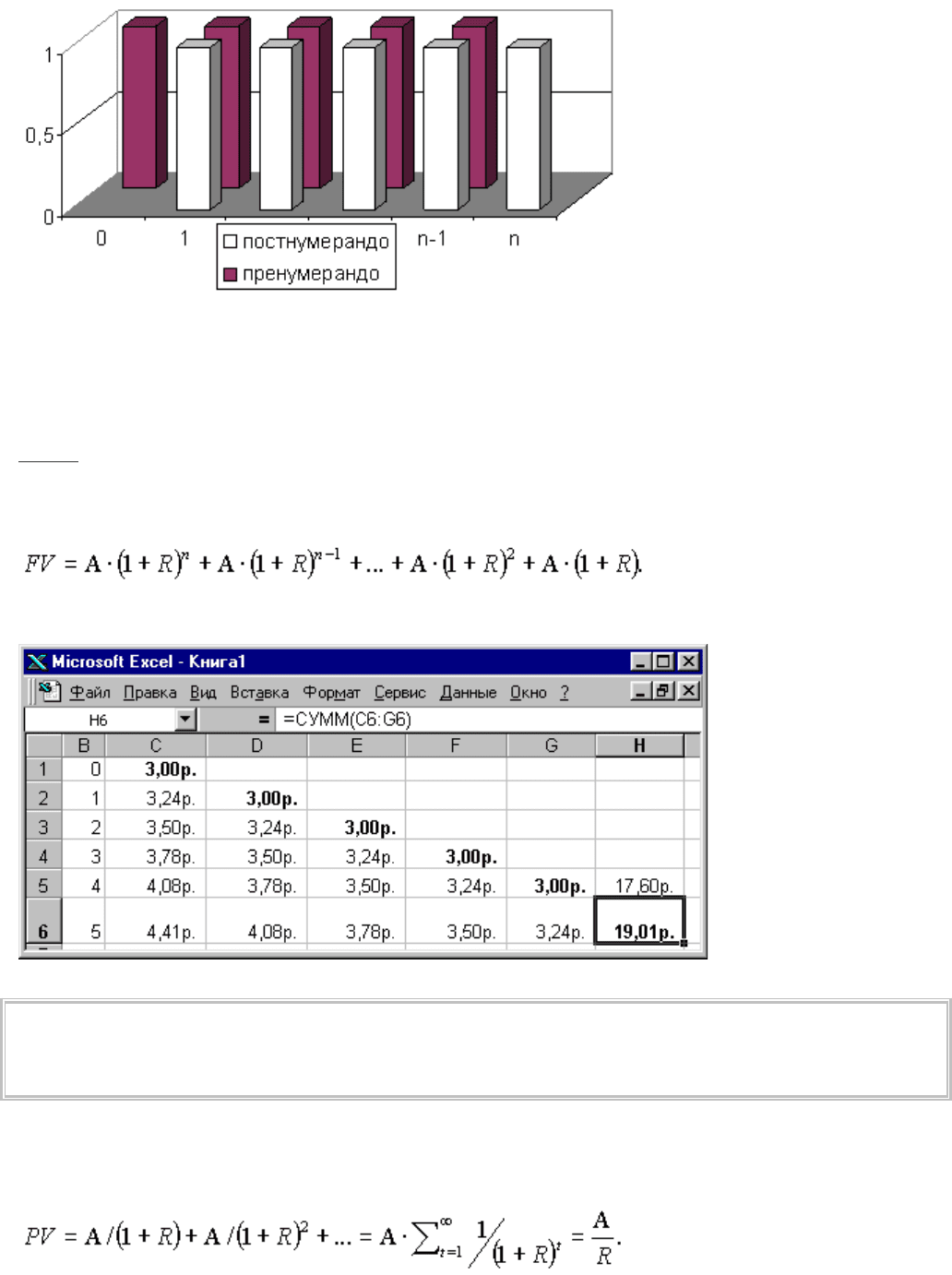
Рис. 49. Тип аннуитета задает распределение n платежей одинакового размера

по границам процентных периодов внутри срока аннуитета.

В зависимости от момента поступления первого платежа различают два типа потоков платежей – пренумерандо

(первый платеж в начале первого периода) и постнумерандо (в конце). За счет более раннего поступления денежных

средств и удлиненного на один период срока начисления процентов в случае пренумерандо можно достигнуть

больших финансовых результатов по сравнению с потоком платежей, вносимых в конце периода.

Пример. Пять платежей по три рубля каждый нужно внести по схеме пренумерандо. Получатель аннуитета использует эти

средства с доходностью R = 8% за период между платежами.

Какова будущая стоимость FV этого срочного аннуитета (срок n = 5) в конце пятого периода в результате начисления

процентов на все поступившие платежи? Обозначим размер одного платежа буквой A. Тогда

В условиях нашего примера поток платежей пренумерандо позволяет их получателю накопить сумму 19,01 руб., а в

случае аннуитета постумерандо она бы составила только 17,60 руб. (см. рис. 50) .

Рис. 50. Вычисление будущей стоимости каждого платежа и аннуитета пренумерандо в конце срока.

Задание

Какую сумму достаточно вложить на 5 периодов с начислением 8% сложных, чтобы в конце срока снять 19,01

руб.?

Текущая стоимость бессрочного аннуитета (вечной ренты при бесконечно большом сроке n) есть сумма всех

членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0

сходится.

Формула текущей стоимости срочного аннуитета постнумерандо для n <  выводится как разница текущей

стоимостей двух бессрочных аннуитетов. Из текущей стоимости на момент времени 0 вечной ренты постнумерандо

вычитается текущая стоимость такой же вечной ренты, начинающейся на n периодов позже. Вторая стоимость

численно равна первой, но относится к моменту времени n, поэтому перед вычитанием её необходимо

дисконтировать по той же ставке R на n периодов в прошлое.

Эквивалентная ей в конце срока будущая стоимость срочного аннуитета постумерандо есть

Процентный множитель будущей стоимости аннуитета FVIFA(R,n) – Future Value Interest Factor of Annuity

является основным финансовым коэффициентом, который показывает, какую сумму можно накопить, постоянно

получая выплаты единичного размера в течение срока n при начислении R % сложных за каждый период на уже

аккумулированные денежные средства.

Процентный множитель текущей стоимости аннуитета PVIFA(R,n) – Present Value Interest Factor of Annuity также

является финансовым коэффициентом, и показывает, какую сумму достаточно инвестировать в начальный момент

времени, чтобы потом регулярно в течении срока, состоящего из n процентных периодов получать платежи

единичного размера с учетом начисления на оставшиеся денежные средства R% сложных за период.

Знакомство с условностями автоматизации финансовых расчетов в среде процессора электронных таблиц начнем со

встроенной функции =FV(rate; nper; pmt; pv; type)

=БЗ(норма; число_периодов; выплата; нз; тип) в исходной русификации

=БС(ставка; кпер; плт; пс; тип) в новейшей русификации.

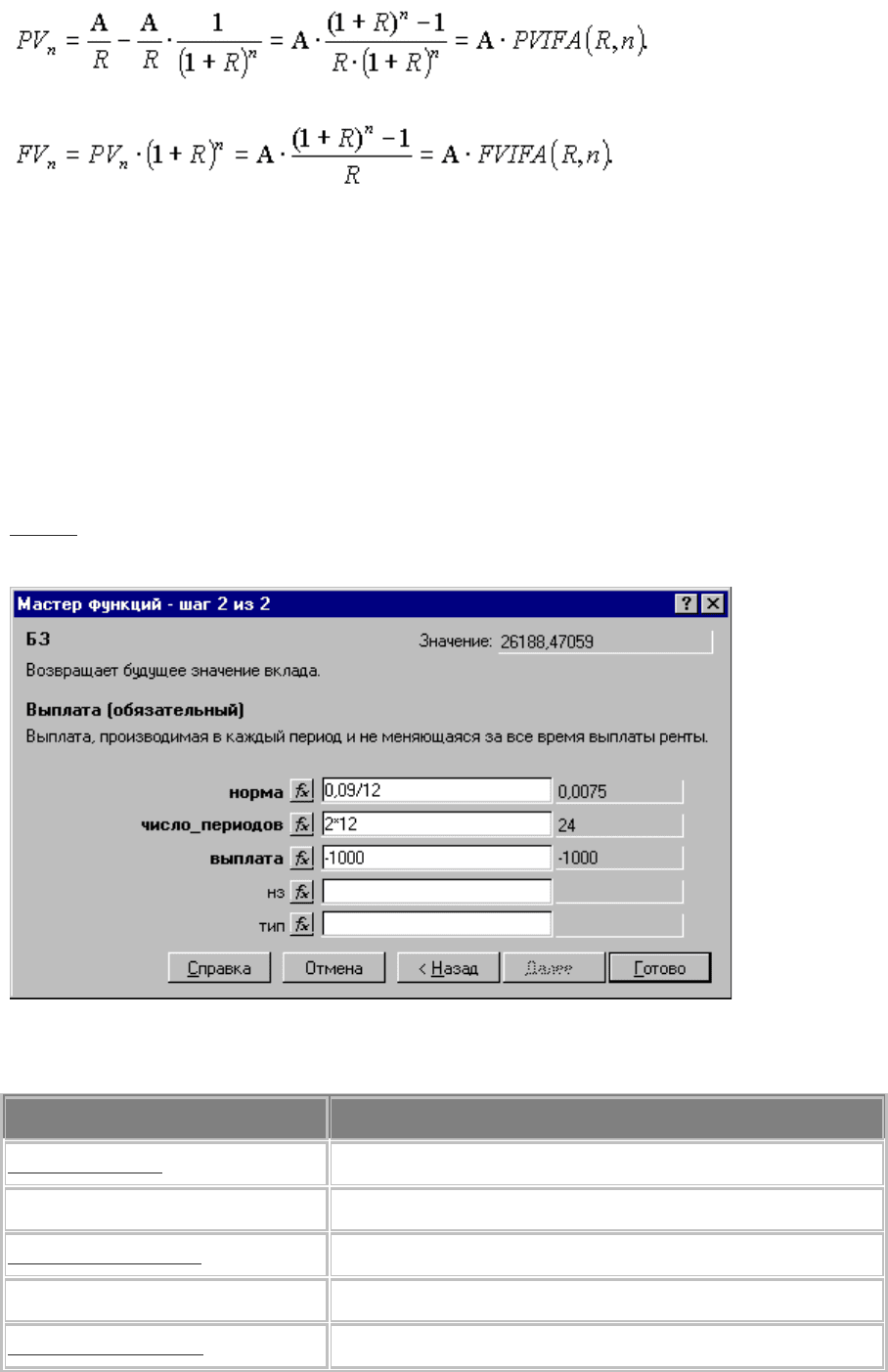
Пример. Господин Иванов в конце каждого месяца переводит 1000р. за счет в банк, начисляющий ежемесячно сложные проценты

по номинальной ставке 9% годовых. Какая сумма накопится на счете за два года, при сохранении на это время всех указанных

условий без изменения?

Рис. 51. Применение функции БЗ=FV для расчета будущей стоимости аннуитета.

Таблица 13

Аннуитетные финансовые функции в исходной русификации

Показатель Встроенная функция Excel

Будущая ценность БЗ(норма;число_периодов;выплата;нз;тип)

Future value FV(rate;nper;pmt;pv;type)

Сегодняшняя ценность ПЗ(норма;кпер;выплата;бс;тип)

Present value PV(rate;nper;pmt;fv;type)

Периодический платеж ППЛАТ(норма;кпер;нз;бс;тип)

Payment PMT(rate;nper;pv;fv;type)

Количество периодов КПЕР(норма;выплата;нз;бс;тип)

Number of periods NPER(rate;pmt;pv;fv;type)

Процентная ставка НОРМА(кпер;выплата;нз;бс;тип;предположение)

Interest rate RATE(nper;pmt;pv;fv;type;guess)

Таблица 14

Аннуитетные финансовые функции в новейшей русификации

Показатель Встроенная функция Excel 2002

Будущая ценность БС(ставка;кпер;плт;пс;тип)

Future value FV(rate;nper;pmt;pv;type)

Сегодняшняя ценность ПС(ставка;кпер;плт;бс;тип)

Present value PV(rate;nper;pmt;fv;type)

Периодический платеж ПЛТ(ставка;кпер;пс;бс;тип)

Payment PMT(rate;nper;pv;fv;type)

Количество периодов КПЕР(ставка;плт;пс;бс;тип)

Number of periods NPER(rate;pmt;pv;fv;type)

Процентная ставка СТАВКА(кпер;плт;пс;бс;тип;предположение)

Interest rate RATE(nper;pmt;pv;fv;type;guess)

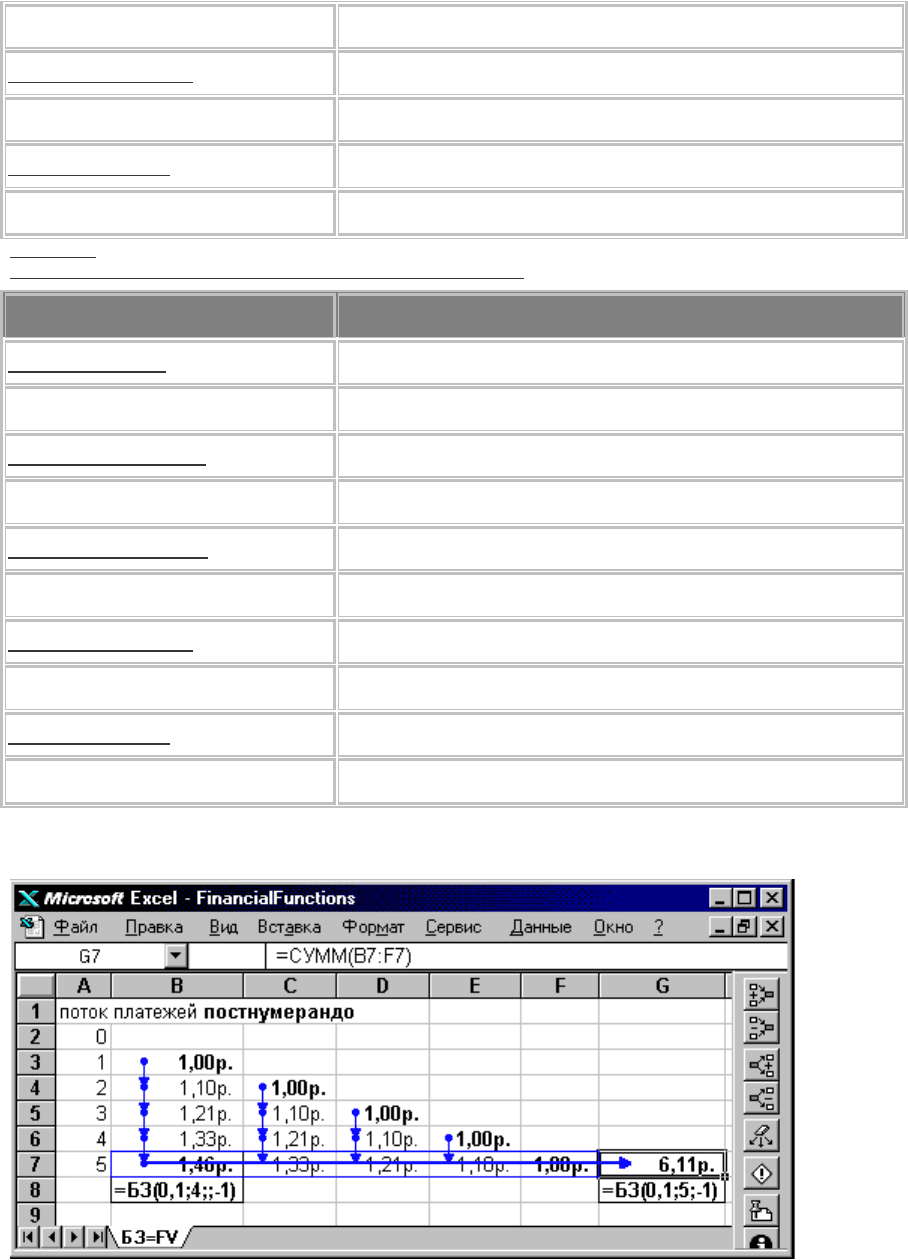
Выполним расчет будущей стоимости аннуитета поэтапно. Ниже, на рис. 52, в восьмой строке таблицы рабочего листа дан формат

вызова функции =БЗ, возвращающий то же самое числовое значение, которое в ячейке седьмой строки найдено по рекуррентным

формулам.

Рис. 52. "Аннуитетный треугольник" постнумерандо.

В зависимости от выбора пользователем из полного списка аргументов встроенной функции =БЗ(норма; число_периодов;

выплата; нз; тип) подмножества тех аргументов, значения которых известны в задаче, можно с помощью одной и той же

функции посчитать и наращенную сумму вклада, и будущую стоимость аннуитета, причем с переключением формул между

типами потоков платежей постнумерандо и пренумерандо.

Рассмотрим полностью возможные варианты.

1,46 р. = FV(0,1;4;0;-1;0) =FV(0,1;4;0;-1;0) =FV(0,1;4;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после четырех

раз (число_периодов=4) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов

10% (норма=0,1) без дополнительных поступлений и выплат. В связи с полным отсутствием в течение срока промежуточного

потока платежей нет смысла уточнять и момент их поступления в нулевом размере (тип=0, значение используется по умолчанию).

1,61 р. =FV(0,1;5;0;-1;0) =FV(0,1;5;0;-1;0) =FV(0,1;5;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после пяти раз

(число_периодов=5) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10%

(норма=0,1) без дополнительных поступлений и выплат (выплата=0, тип=0).

6,11 р. = FV(0,1;5;-1;0;0) = FV(0,1;5;-1;0;0) =FV(0,1;5;-1) – будущая стоимость потока пяти периодических платежей

(число_периодов=5) единичного размера, вносимых (выплата=-1) регулярно в конце периода (потоку постнумерандо

соответствует тип=0, значение используется по умолчанию) при начислении 10% сложных (норма=0,1) за период между

моментами внесения платежей на поступившие ранее средства.

6,72 р. = FV(0,1;5;-1;0;1) FV(0,1;5;-1;0;1) =FV(0,1;5;-1;;1) – будущая стоимость потока пяти периодических платежей

(число_периодов=5) единичного размера (выплата=-1), поступающих в начале периода (потоку пренумерандо соответствует

тип=1) при начислении за каждый период между платежами 10% сложных (норма=0,1).

Пример. Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15 долл. на сберегательный

счет в банк, начисляющий на всю растущую сумму сложные проценты по номинальной ставке 15% годовых. В каком возрасте

этот человек может стать миллионером?

Выразим срок (число периодических платежей) из формулы будущей стоимости аннуитета:

Задание

Используя определение и свойства логарифма, самостоятельно продолжите вывод формулы срока

накопления миллиона в условиях задачи и найдите ответ на поставленный вопрос.

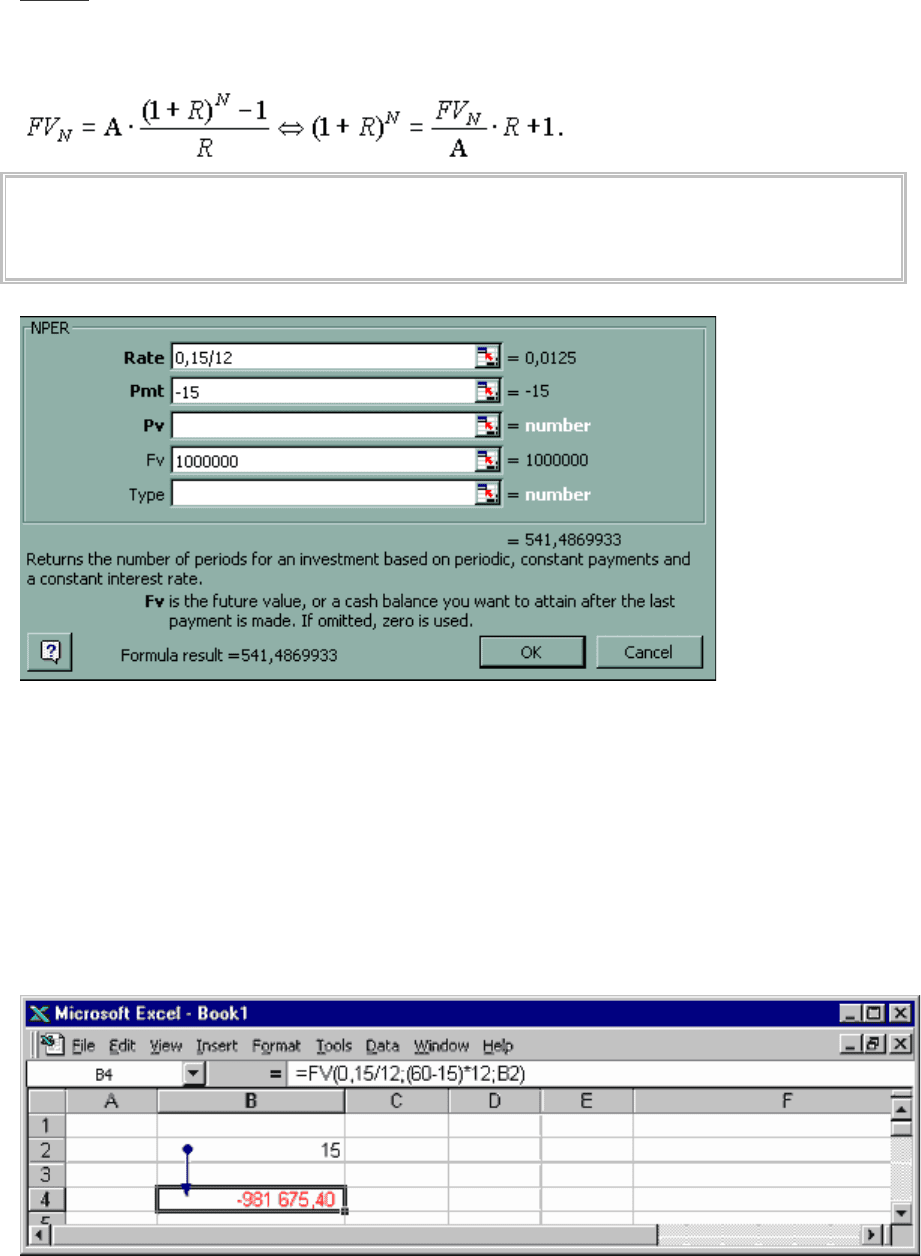
Рис. 53. Применение функции КПЕР=NPER для определения срока аннуитета.

Найденный срок выражен в месяцах. 542/12=45 полных лет, так что сумма 15+45 дает искомый в задаче возраст 60

лет.

Какую сумму достаточно вложить на такой же срок единовременно, чтобы при той же доходности при ежемесячном

начислении сложных процентов накопить 1 млн.долл.?

Ответ: -1190,948=PV(0,15/12;542;;1000000).

При какой годовой процентной ставке удастся накопить миллион к 55 годам?

Ответ: 17,3% =RATE((55-15)*12;-15;;1000000)*12.

При каком размере ежемесячного платежа удастся накопить миллион к 50 годам без изменения ставки 15%?

Ответ: -68,13 долл.= PMT(0,15/12;(50-15)*12;;1000000).

Варьировать параметры задачи можно и неявно, подгоняя влияющие исходные данные, например, размер

ежемесячного платежа, под искомую будущую стоимость 1 млн.долл. (см. рис. 54).

Рис. 54. Подбор значения будущей стоимости аннуитета изменением размера платежа.

Неявное уравнение, используемое всеми финансовыми калькуляторами и электронными таблицами для расчета

неизвестных показателей аннуитета по известным можно обнаружить в Справочной системе Excel в разделе,

посвященном функции =ПЗ. Для преодоления проблем с терминологией здесь оно приводится в обозначениях

оригинала:

Таблица 15

Реакция неявного уравнения на нулевые значения финансовых параметров

Наращение однократно вложенной

суммы

Накопление будущей суммы потоком вносимых через равные периоды

времени платежей одинакового размера

Если в условиях задачи отсутствует

поток выплат, то PMT=0, и за счет

нулевого первого сомножителя всё

второе слагаемое равно нулю

Если же решается аннуитетная задача, в которой известен размер платежа, а

дополнительные единовременные начальные вложения отсутствуют, то в

силу условия PV=0 элиминируется первое слагаемое, и остается зависящая от

размера платежа формула будущей стоимости аннуитета с начислением

процентов за период между платежами.

Получается балансовая модель роста

сложных процентов, учитывающая

направление движения средств: то,

что дали в долг – положительно, а то,

что будет потом возвращаться

кредитору с процентами обратно, с

точки зрения должника,

отрицательно

Второй сомножитель по умолчанию равен единице (случаю постнумерандо

соответствует тип=0), а если оценивается аннуитет пренумерандо (тип=1), то

получается процентный множитель (1+RATE), отражающий дополнительный

период начисления сложных процентов за счет более раннего начала

поступления потока платежей

Для существования ненулевых корней этого соотношения знаки величин

затрат и поступлений должны быть друг другу противоположны

Пример. Инвестор выдает должнику кредит в объеме 300 тыс. руб. Возврат долга планируется в виде квартального аннуитета с

выплатой 75 тыс. руб. постнумерандо (обыкновенной финансовой ренты) на протяжении 5 кварталов.

Оценим процентную ставку R за один квартал. Подставляя исходные данные в формулу текущей стоимости

аннуитета, получаем следующее уравнение относительно новой переменной x = (1 + R) – процентного множителя за

один квартал:

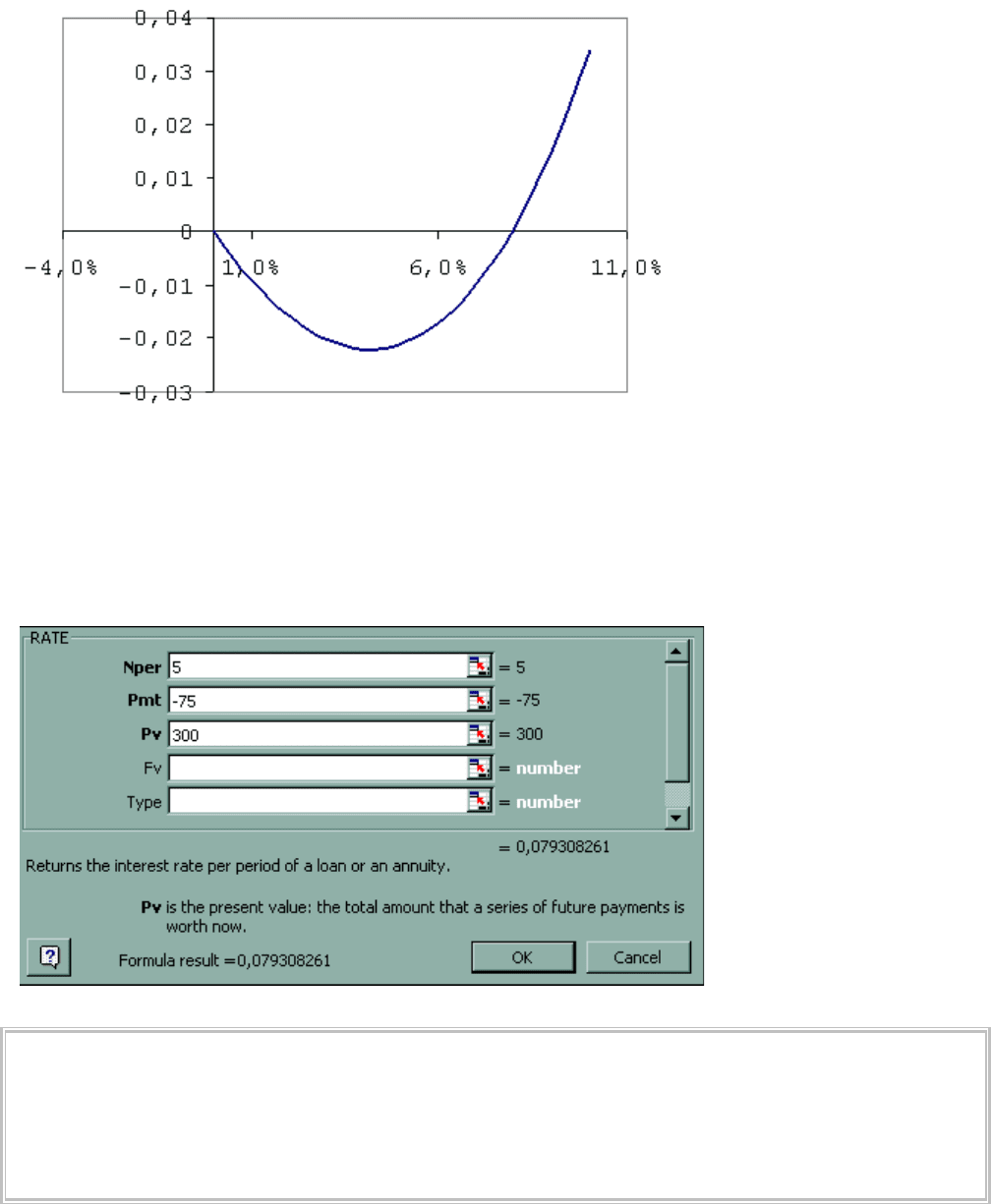
Рис. 55. Поведение заданного многочлена шестой степени от ставки R на интервале [0%; 10%].

Глядя на график этой функции, построенный на рис. 55 в зависимости от значений квартального процента R, можно

предположить, что искомый ответ находится в районе 7–8% и подобрать его итеративно. Выявив графически

интервал значений ставки, внутри которого находится ответ, например, [6%;11%], необходимо проверить

подстановкой в условия задачи какую-нибудь внутреннюю точку, и по результатам проверки сузить область поиска,

сдвинувшись левее или правее. Так постепенно с заданной точностью подбирается процент аннуитета. Встроенная

функция финансовая функция RATE работает не по аналитической формуле (в общем случае ее не существует!), а

обращается к процедуре итеративного подбора корней многочлена методом Ньютона

Рис.56 Применение функции НОРМА=RATE для нахождения доходности аннуитета.

Задание

Используя процедуру Excel Подбор параметра, подгоните к 300 тыс. руб. значение суммы строки нулевого

периода в "верхнем аннуитетном треугольнике" (см. рис. 57).

Какая процентная ставка R за период доставляет эту текущую стоимость?

Повторите подбор, используя в качестве зависимой от исходного значения ставки R формулы обращение ко

встроенной функции PV=ПЗ.

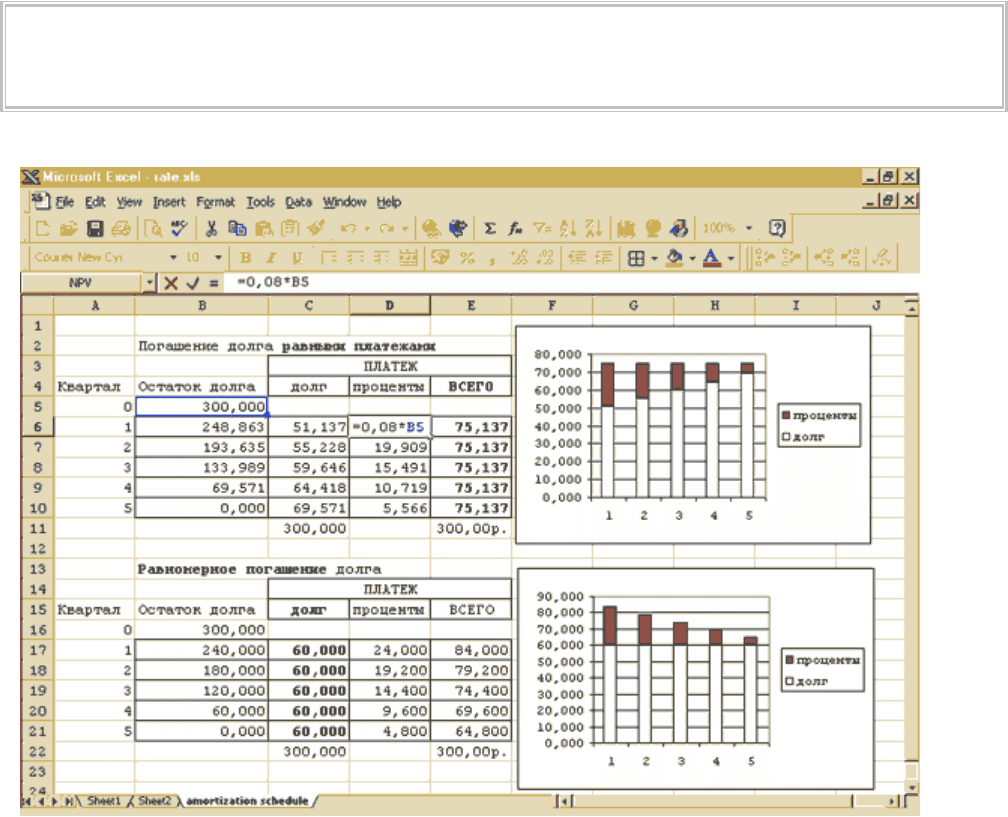
Рис. 57. "Верхний аннуитетный треугольник".

Задание

Каким должен быть размер периодического платежа, чтобы внесение пяти одинаковых платежей такого размера

по схеме постнумерандо позволило погасить долг 300 тыс. руб. по ставке 8% за период?

Проценты начисляются на невыплаченную часть долга ("правило США

"). При соблюдении равенства

периодических платежей друг другу изменяется пропорция между двумя составными частями платежа (см. рис. 58).

Рис.58. Сравнение графиков погашения долга.

Сначала по аннуитетной формуле (здесь это сделано при помощи функции PMT) определяется сумма платежа – 75

137 тыс. руб. Затем каждый платеж разбивается на части следующим образом: PMT = PPMT + IPMT.

Меньшая и постоянно уменьшающаяся часть платежа IPMT (от англ. interest payment): 24000, 19909, 15491, 10719 и

5566 соответствует процентам на остаток долга, который постепенно погашается. Долг уменьшается каждый раз не

на всю сумму платежа, а только на его растущую часть PPMT (от англ. principal payment), остающуюся после уплаты

процентов за непогашенный долг предыдущего периода:

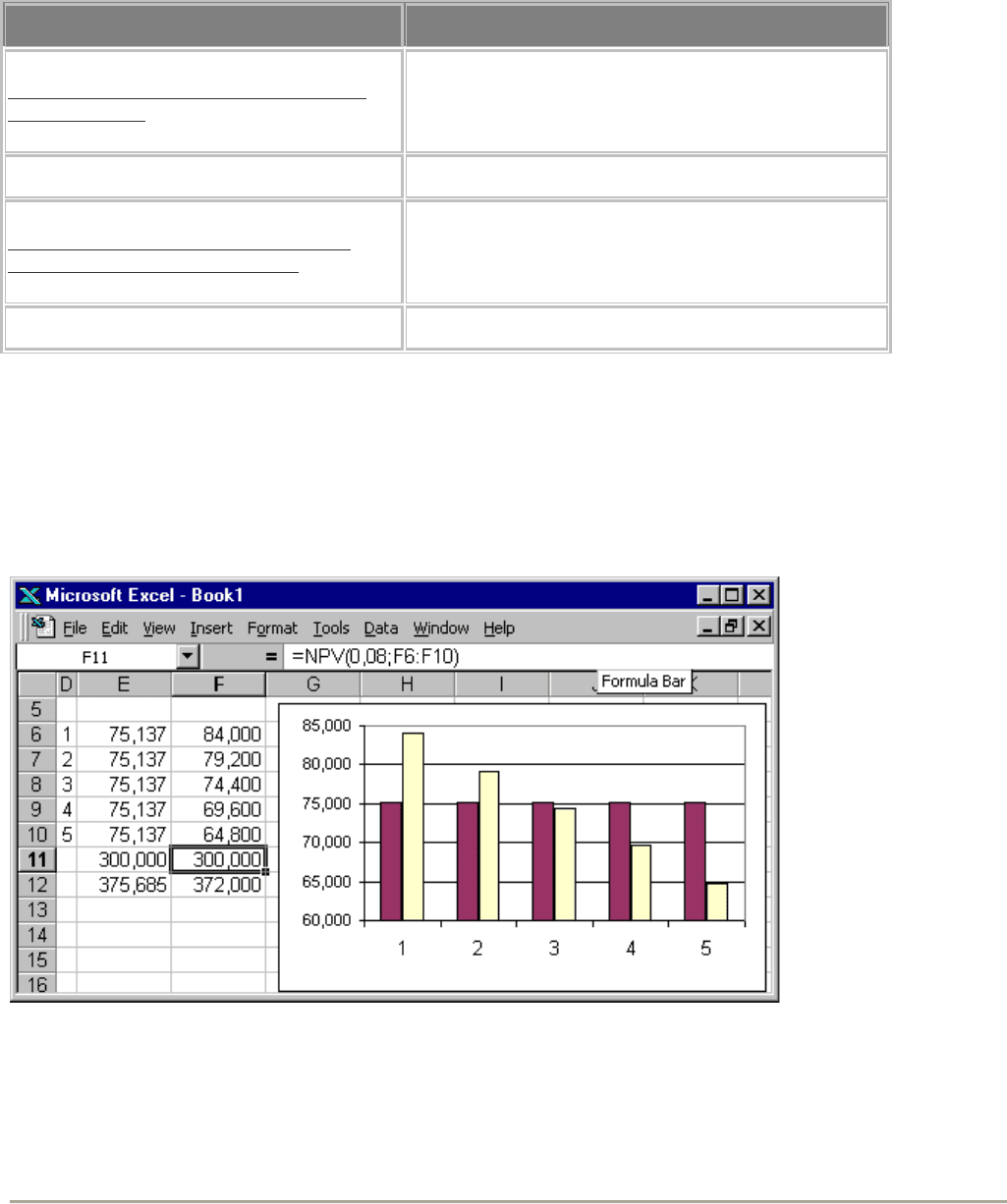
1 кв.: 8%*300000=24000, погашение 75137–24000=51137, остаток 300000–51137=248863

2 кв.: 8%*248863=19909, погашение 75137–19909=55228, остаток 248863–55228=193635

3 кв.: 8%*193635=15491, погашение 75137–15491=59646, остаток 193635–59646=133989

4 кв.: 8%*133989=10719, погашение 75137–10719=64418, остаток 133989–64418= 69571

5 кв.: 8%* 69571= 5566, погашение 75137– 5566=69571, остаток 69571–69571= 0.

Сумма всех частей платежа PPMT, погашающих долг, равна 300 тыс.руб. Дисконтированная же по ставке

кредитования (процентная ставка в данном примере R = 8%) сумма платежей PMT также равна исходной сумме

долга. Для расчета частей периодического платежа, размер которых зависит от текущего периода k, в Excel также

имеются встроенные функции PPMT и IPMT (см. табл. 16).

Таблица 16

Функции для расчета двух переменных составляющих частей постоянной суммы платежа)

Показатель Встроенная функция Excel

Часть платежа, идущая в зачет погашения

основного долга

ОСНПЛАТ(норма;период;кпер;тс;бс;тип) в исходной

русификации

ОСПЛТ(ставка;период;кпер;пс;бс;тип) в новейшей

русификации

Principal Payment PPMT(rate;k;nper;pv;fv;type) в оригинальной версии

Часть платежа,равная процентной плате

за остаток долга в данном периоде

ПЛПРОЦ(норма;период;кпер;тс;бс;тип) в исходной

русификации

ПЛПРОЦ(ставка;период;кпер;пс;бс;тип) в новейшей

русификации

Interest Payment IPMT(rate;k;nper;pv;fv;type) в оригинальной версии

Так, например, можно получить разбиение второго платежа на погашение основного долга –

55,228=PPMT(0,08;2;5;300) и процентную часть –19,909=IPMT(0,08;2;5;300).

Можно предложить бесконечно много других способов разбиения во времени выплаты основного долга и процентов

по нему на несколько частей. Одной из наиболее распространенных простых и стандартных схем, используемых в

российской практике является равномерное погашение, при котором одинаковы не общие суммы платежей, а их

только части, погашающие долг. Сумма нескольких равных частей, погашающих долг, равна исходной сумме долга.

Тогда процентная часть считается по ставке за период умножением на равномерно убывающий долг, а размер

каждого отдельного платежа выводится как сумма двух частей. Дисконтированная по ставке кредитования сумма

платежей по-прежнему равна исходной сумме долга.

Рис.59. Эквивалентность потоков платежей погашения долга по разным схемам.

Обе рассмотренные схемы погашения долга: и равными платежами, и неравными, эквивалентны друг другу по

начальной стоимости кредита. Это обстоятельство иногда используют в анализе инвестиционных проектов, вычисляя

аннуитет (размер годового платежа), эквивалентный исходному денежному потоку в смысле равенства чистого

дисконтированного дохода. При простом арифметическом суммировании всех платежей без дисконтирования эти

потоки друг от друга отличаются, но с точки зрения экономической теории процента, такое "измерение дохода" за

несколько периодов не имеет смысла, поскольку полагает цену денег во времени равной нулю, что на финансовом

рынке невозможно.

3 См., напр.: Уотшем Т. Дж., Паррамоу. Количественные методы в финансах. М., 1999.