Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

348

D.

C.

Theodoridis,

Y.

Boutalis, and M. A. Christodoulou

approximated

with

the

help

of

two

independent

fuzzy subsystems. We also

assume

the

existence

of

disturbance

expressed as modeling

error

terms

de-

pending

on

both

input

and

system

states.

Every

fuzzy

subsystem

is ap-

proximated

from a family

of

HONNF's,

each one being

a

group

of

fuzzy rules. Weight

updating

laws

are

given

and

we prove

that

when

the

structural

identification is

appropriate

and

the

modeling

error

terms

are

within

a

certain

region

depending

on

the

input

and

state

values,

then

the

er-

ror

reaches zero

very

fast. Also,

an

appropriate

state

feedback is

constructed

to

achieve

asymptotic

regulation

of

the

output,

while keeping

bounded

all

signals

in

the

closed loop.

The

chapter

is organized

as

follows. Section 2

presents

the

Fuzzy

systems

description using

indicator

functions

and

HONNF's.

The

direct

adaptive

Neuro-Fuzzy

regulation

of

systems

being in

Brunovsky

canonical form is given

in

section 3, where

the

problem

formulation

and

the

weight

updating

laws

are

derived. Section 4

presents

simulation

results

and

comparisons while section

5 concludes

the

work.

2 FUzzy

system

description

using

rule

firing

indicator

functions

and

HONNF

Consider a

nonlinear

function

f(x)

E

R,

x E X c R

n

approximately

de-

scribed

by

a

Mamdani-type

Fuzzy

System

(FS).

Let

.fl;"h,

...

,j"

be

defined as

the

subset

of

x E X belonging

to

the

(jl,j2,

...

,jn)th

input

fuzzy

patch

and

pointing

-

through

the

function

fe)

-

to

the

subset

which belong

to

the

[th

output

fuzzy

patch.

In

other

words, .fl;,,12,

...

,j"

contains

input

values x

that

are

associated

through

a fuzzy rule

with

output

values

f(x).

Furthermore,

the

FS

receiving as

input

the

n-tuple

of

x =

(Xl,

X2,

...

,x

n

)

gives

as

output

an

approximate

of

f (x) using fuzzy rules

and

well known fuzzy

inference procedure.

According

to

the

above

notation

the

Rule

Firing

Indicator

Function(RFIF)

or

simply

Indicator

Function

(IF)

connected

to.fl

l

.

. is defined as fol-

Jl

,J2,···

,In

lows:

[..

. x t =

)1,)2,···,)"

I (

())

{ a(x(t)) if (x(t))

E.fl

l

.

)1,)2,.·.,)n

0 otherwise

(1)

where a(x(t))

denotes

the

firing

strength

of

the

rule. According

to

standard

fuzzy

system

description,

this

strength

depends

on

the

membership

value

of

each

Xi

in

the

corresponding

input

membership

functions /-LFji

and

more

specifically

[26],

a(x(t)) =

min[/-LFj1

(Xl

(k)),

...

/-LFj"

(xn(k))].

Then,

assuming

a

standard

defuzzification

procedure

(e.g. weighted average),

the

functional

representation

of

the

fuzzy

system

can

be

written

as

f(x(t))

= L

!J"

...

,jn

X

(I1)~"

...

,jn

(x(t))

(2)

Nonlinear Systems

in

Brunovsky Canonical Form: A Neuro-Fuzzy Algorithm 349

where

the

sumation

is carried over all

the

available fuzzy rules.

l)"

...

,

j"

is

any

constant

vector consisting

of

the

centers

of

fuzzy

partitions

of f d

ete

rmined

by

l

and

(I1)~"

...

,j"

(x(t)) is

the

IF

defined in (1) divided by

the

sum

of

all

IF

participating

in

the

summation

of

2.

Based

on

the

fact

that

functions

of

high

ord

er neurons are capable

of

approximating

discontinuous functions

[4

]

and

[12]

use high

order

neural

net-

work functions

HONNF's

in

order

to

approximate

an

IF. A

HONNF

is defined

as:

L

N(x(t); w, L) = L

Whot

II

p~j(hot)

(3)

hot

=l jEhot

where

hot

=

{h,

h ,

...

,

h}

is a collection

of

L

not-ordered

subsets

of

{1,2,

..

.

,n},

dj(hot)

are

non-negative integers. Pj

are

the

eleme

nts

of

the

following vector,

where

S denotes

the

sigmoid function defined as:

1

s(x) - a -

rv

- 1 +

e-{3x

I

(4)

(5)

with

a,

/3,

'I

being positive real numbers

and

W

:=

[Wl"

'WL]T

are

the

HONNF

weights. Eq. (3)

can

also be

written

as

L

N(x(t); w, L) = L WhotShot(X(t))

(6)

hot=l

where Shot(X(t))

are

high

order

terms

of

sigmoid functions of x.

Following

the

above

notation

(II)~,

,

..

,j"

in (2)

can

be

approximated

by

N

1

. (x) = N(x(t);wJJ ,···,jn;I,LJI,···,j

n;l

)

J1,···,]n

So, Eq. (2)

can

be

rewritten

as

~-l

I

f(x(t))

= L h ,

...

,jn

x N

j"

..

,jJx(t))

(7)

From

the

above definitions

and

Eq. (7)

it

is obvious

that

the

accuracy

of

the

approximation

of

f(x)

depends

on

the

approximation

abilities

of

HONNFs

and

on

an

initial

estimate

of

the

centers

of

the

output

membership

functions.

These

centers

can

be

obtained

by

experts

or

by off-line techniques

based

on

gathered

data.

Any

other

information

the

input

membership

functions is

not

necessary because it is replaced by

the

HONNFs.

3

Direct

adaptive

neuro-fuzzy

regulation

3.1

Problem

formulation

and

neuro-fuzzy

representation

Problem

formulation

We consider nonlinear

dynamical

syst

ems

of

the

Brunovski canonical form

350

D.

C.

Theodoridis,

Y.

Boutalis, and M. A. Christodoulou

::i;

= Aex + bc[j(x) + g(x) .

u]

(8)

where

the

state

x E Rn is

assumed

to

be completely

measured,

th

e

control

input

u E R, j

and

9

are

scalar nonlinear

functionS[O~~f

..

the

tate

f

ein

:

onl~oo~'

lll]-

volved in

the

dynamic

equation

of

x

n

.

Also, Ae = 0

o 0

and

be

=

[0

The

state

regulation

problem

is known

as

our

attempt

to

force

the

state

to

zero from

an

arbitrary

initial value

by

applying

appropriate

feedback

control

to

the

plant

input.

However,

the

problem

as

it

is

stated

above for

the

system

(8), is

very

difficult

or

even impossible

to

be solved since

the

j,

9

are

assumed

to

be

completely unknown. To overcome

this

problem

we assume

that

the

unknown

plant

can

be

describ

ed

by

the

following model arriving from a neuro-

fuzzy

repres

e

ntation

described below,

plus

a modeling

erro

r

term

w(x, u)

(9)

where x j ,

Xg

are

vectors

containing

the

centers

of

the

partitions

of

every

fuzzy

output

variable

of

j(x)

and

g(x) respectively,

determin

ed by

the

designer

and

Wj,

W;

are

unknown

weight matrices. 8

j,

8

g

are

sigmoidal vectors

containing

high

order

sigmoidal

terms terms

with

parameters

which also

determined

by

the

designer.

Therefore,

the

state

regulation

problem

is

analyzed

for

the

system

(9)

instead

of

(8). Since,

Wj

and

W;

are

unknown,

our

solution

consists of

designing a control law

u(Wj,

W

g

, x)

and

appropriate

update

laws for

Wj

and

Wg

to

guarantee

convergence

of

the

state

to

zero

and

in

som

e cases,

which will be

analyzed

in

the

following sections,

boundedness

of

x

and

of

all

signals in

the

closed loop.

The

following mild

assumptions

are

also imposed

on

(8),

to

guarantee

the

existence

and

uniqueness

of

solution for

any

finite initial

condition

and

u E U

c

.

Assumption

1.

Given a class U

e

C R

of

admissible

inputs,

then

for

any

u E U

e

and

any

finite initial condition,

the

state

traj

ecto

ries

are

uniformly

bounded

for a

ny

finite T >

O.

Meaning

that

we

do

not

allow

systems

processing

trajectories

which escape

at

infinite, in finite

time

T,

T being

arbitrarily

small. Hence, Ix(T) I <

00.

Assumption

2.

The

j,

9

are

continuous

with

resp

ect

to

their

arguments

and

satisfy a local Lipschitz

condition

so

that

the

solution

x( t)

of

(8) is

unique

for

any

finite initial condition

and

u E U

c

.

Nonlinear Systems ill Brullovsky Canonical Form: A Neuro-Fuzzy Algorithm

351

Neuro-fuzzy

representation

We

are

using

a fuzzy

approximation

of

the

system

in

(8), which uses

two

fuzzy

subsystem

blocks for

the

description

of

f(

x)

and

g(

x)

as

follows

f(x)

=

~

Xfl.

.

xNfl.

. (x)

~

}1,}2"",)n

J1,)2,·

·,)n

(10)

(11)

where

the

summation

is

carried

out

over

the

number

of

all available fuzzy

rules, N

f

,

N

g

are

appropriate

HONNF's

and

the

meaning

of

indices.

l

.

)1

,J2,···

,)n

has

already

been

described

in

Section

2.

In

order

to

simplify

the

model

structure,

since

some

rules

result

to

the

same

output

partition,

we

could

replace

the

NNs

associated

to

the

rules

hav-

ing

the

same

output

with

one

NN

and

therefore

the

summations

in

(10),(11)

are

carried

out

over

the

number

of

the

corresponding

output

partitions.

Therefore,

the

system

of

(8) is

replaced

by

the

following

equivalent

Brunovsky

form

Fuzzy

-

High

Order

Neural

Network

(F-HONN),

which

depends

on

the

centers

of

the

fuzzy

output

partitions

x

fi

and

x

gi

(12)

where

Npf

and

Npg

are

the

number

of

fuzzy

partitions

of

f

and

g respec-

tively.

Or

in

a

more

compact

form

(13)

where,

similar

to

(9),

xf,

Xg

are

vectors

containing

the

centers

of

the

parti-

tions

of

every

fuzzy

output

variable

of

f (x)

and

g( x) respectively,

sf

(x),

Sg

(x)

are

vectors

containing

high

order

combinations

of

sigmoid

functions

of

the

state

x

and

Wf,

Wg

are

matrices

containing

respective

neural

weights ac-

cording

to

(6)

and

(12).

The

dimensions

and

the

contents

of

all

the

above

matrices

are

chosen so

that

both

xfWfsf(x)

and

XgWgSg(x)

are

scalar.

For

notational

simplicity

we also

assume

that

all

output

fuzzy

variables

are

par-

titioned

to

the

same

number,

m,

of

partitions.

Under

these

specifications x f

is a 1 x m

row

vector

of

the

form

where

xfp

denotes

the

center

or

the

fuzzy

p-th

partition

of

f.

These

cen-

ters

can

be

determined

manually

or

automatically

with

the

help

of

a fuzzy

c-means

clustering

algorithm

as a

part

of

the

off-line fuzzy

system

struc-

tural

identification

procedure

mentioned

in

the

introduction.

Also,

sf(x)

=

[sj,(x)

s!k(x)f,

where

each

Sfi(X)

with

i = {1,2,

...

,k},

is a

high

352

D.

C.

Theodoridis,

Y.

Boutalis, and

M.

A. Christodoulou

order

combination

of

sigmoid functions

of

the

state

variables

and

Wf

is a

m x k

matrix

with

neural

weights.

Wf

can

be also

written

as

a collection of

column vectors

Wi,

that

is

Wf

=

[W}

Wi

Wi]'

where l =

1,2,

... ,

k.

Similarly,

Xg

is a 1 x m row vector

of

the

form

where x

gk

denotes

the

center

or

the

k-th

partition

of

g.

W

g

,

Sg(x)

have

the

same

dimensions as

Wf,

sf

(x) respectively.

3.2

Adaptive

regulation

with

modeling

error

effects

In

this

subsection

we

present

a

solution

to

the

adaptive

regulation

problem

and

investigate

the

modeling

error

effects

when

the

dynamical

equations

have

the

Brunovsky

canonical form. Assuming

the

presence

of

modeling

error

the

unknown

system

can

be

written

as

(9).

The

regulation

of

the

system

can

be

achieved by selecting

the

control

input

to

be

(14)

with

v =

kx

(15)

where k is a

vector

of

the

form k =

[k

n

...

k2

klJ

E R

n

be such

that

all

roots

ofthe

polynomial

h(s)

=

sn

+ k1s

n

-

1

+ ... + k

n

are

in

the

open

left half-plane.

Define now,

the

regulation

error

as

~

=-x

(16)

After

substituting

Eq.

(14)

to

the

n -

th

state

equation

of

Eq.

(9)

and

straightforward

manipulations

we

have

that

where ilc =

Ac

- bck is a

matrix

with

its eigenvalues

on

the

left

half

plane.

W

f

=

Wf

-

Wj

and

Wg

=

Wg

-

W;.

W

f

and

Wg

are

estimates

of

Wj

and

W;

respectively

and

are

obtained

by

update

laws which

are

to

be

designed

in

the

sequel. After

substituting

Eq. (16), (17) becomes

~

=

ilc~

+

bc[x

f

Wfs

f(x)

+

Xg

WgSg(x)u

- w(x,

u)J

(18)

To continue, consider

the

Lyapunov

candidate

function

v =

~e

p~

+

2~1

tr

{

Wf

T W

f

} +

2~2

tr

{

WJW

g

}

Where

P > 0 is chosen

to

satisfy

the

Lyapunov

equation

Pile

+

il~

P = - I

(19)

Nonlinear Systems

in

Brunovsky Canonical Form: A Neuro-Fuzzy Algorithm 353

If

we

take

the

derivative

of

Eq. (19)

with

respect

to

time

we

obtain

. 1 2 T -

V =

-211~11

+

~

PbcXfWfSf(X)

+

T - T

~

PbcXgWgSg(X)u-~

Pbcw(x,u)+

~1

tr

{

WfTW

f

} +

~2

tr

{

Wg

TW

g

}

Hence, if we choose

(20)

(21 )

V becomes

v

~

-~

11~112

+

11~llllPllllw(x,

u)11

(22)

It

can

be

easily verified

that

Eqs. (20)

and

(21)

after

making

the

appropriate

operations,

result

in

the

following weight

updating

laws

(23)

(24)

where

~

is

the

vector

defined in (16), u is a

scalar

and

11, 12

are

positive

constants

expressing

the

learning

rates.

The

above

equations

can

be

also

element

wise

written

as:

a) for

the

elements

of

Wf

(25)

or

equivalently

wj

=

-11~nPn

(xf)T

sf,

(x)

for

alll

=

I,

2, ... ,

k,

j =

1,

2,

... ,

m,

~n

is

the

n -

th

element

of

the

vector

~

and

P

n

is

the

last

n -

th

row

of

P.

b) for

the

elements

of

Wg

(26)

or

equivalently

WJ

=

-12~nPn

(Xg)T

Sg,

(x)u,

for all l =

1,2,

... , k

and

j =

1,2,

...

,m.

Furthermore,

we

can

make

the

following

Assumption.

Assumption

3.

The modeling error

term

satisfies

I

w(x,

u)

I~

e~

Ixi

+

e~

lui

where

e~

and

e~

are known positive constants.

Also, we

can

find

an

a priori

known

constant

e

u

> 0,

such

that

354

D.

C.

Theodoridis,

Y.

Boutalis, and M. A. Christodoulou

and

Assumption

3 becomes equivalent

to

where

£1

=

£~

+

£~£u

is a positive

constant.

Employing

Assumption

3, Eq. (22) becomes

v

:::;

-~

11~112

+

£1

11~llllPllllxll

since

Ilxll

=

II~II

then

Eq. (29) becomes

v

:::;

-~

11~112

+

£1

IIPIIII~112

:::;

-

(~

-

£1

IIPII)

11~112

(27)

(28)

(29)

(30)

Hence, if we chose

IIPII

<

2t

then

the

Lapyunov

candidate

function becomes

negative.

We

are

now

ready

to

prove

the

following

theorem

Theorem

1.

The

control law (14)

and

(15)

together

with

the

update

laws

(23)

and

(24)

guarantee

the

following

properties

• limt-+oo

~(t)

=

0,

limt

-+oo

x(t) = 0

provided

that

IIPII

<

2}!

and

Assumption

3 is satisfied.

Proof.

From

Eq. (30)

we

have

that

V E

Loo

which implies

~,Wj,

Wg

E Loo.

Furthermore

Wj

=

Wj

+

Wi

E

Loo

and

Wg

=

Wg

+

Wg

* E Loo. Since

~

E

Loo

this

also implies x E Loo. Moreover, since V is a

monotone

decreasing

function of

time

and

bounded

from below,

the

limt-+

oo

V(t)

=

Voo

exists so

by

integrating

V from 0

to

00

we have

which implies

that

I~I

E L

2

.

We also have

that

~

=

Ac~

+

bc[xj

WjSj(x)

+

Xg

WgSg(x)u -

w(x,

u)]

Nonlinear Systems

in

Brunovsky Canonical

Form:

A Neuro-Fuzzy Algorithm 355

Hence

and

since U E L

oo

,

the

sigmoidals

and

center

matrices

are

bounded

by

definition, W

f

,

Wg

E

Loo

and

Assumption

3 hold, so since

~

E

L2

n

Loo

and

~

E L

oo

,

applying

Barbalat's

Lemma

we conclude

that

limt->oo

~(t)

=

O.

Now, using

the

bounded

ness

of

u,

sf(x),

Sg(x), x

and

the

convergence

of

~(t)

to

zero, we have

that

Wf,

Wg

also converge

to

zero. Hence we have

that

limt---+oo

x(t) =

-limt->oo

~(t)

= 0

Thus,

limt---+oo

x(t) =

O.

Remark

1.

We

can't

conclude

anything

about

the

convergence

of

the

synaptic

weights

Wf

and

Wg

to

their

optimum

values

Wi

and

W;

respectively from

the

above analysis.

The

existence

of

signal u is

associated

with

conditions

which

guarantee

that

XgWgSg(x) #

O.

It

can

be

shown

that

using

appropriate

projection

method

[9],

the

weight

updating

laws

can

be

modified so

that

the

existence

of

the

control

signal

can

be

assured.

However,

this

development

is

not

presented

in

this

chapter.

The

relevant

results

along

with

the

ones given

here

are

to

be

presented

shortly

in a

forthcoming

work.

4

Simulation

results

To

demonstrate

the

potency

of

the

proposed

scheme we

present

two simula-

tion

results.

One

of

them

is

the

well

known

benchmark

"Inverted

Pendulum"

and

the

other

one is

the

"Van

der

pol" oscillator.

Both

of

them

present

com-

parisons

of

the

proposed

method

with

the

well

established

approach

on

the

use

of

RHONN's

[21].

The

comparison

shows off

the

regulation

superiority

of

our

method

under

the

presence

of

modeling errors.

4.1

Inverted

pendulum

Let

the

well known

problem

of

the

control

of

an

inverted

pendulum.

Its

dynamical

equations

can

assume

the

following

Brunovsky

canonical

form

[22]

.

rnlx~

cos

Xl

sin

Xl

gSlnxl

'Tnc+

rn

X2

= -

1(1-

=C08

2

Xl)

3

rHC+rn

~

+

=C+

m

U + d

(

4

=c082

"")

I

'3-

rrtC+

m

with

d =

5X2

+ 10sin(lOx2) +

sin(2u)

(31)

where

Xl

= e

and

X2

=

iJ

are

the

angle from

the

vertical

position

and

the

angular

velocity respectively. Also, 9 = 9.8

m/

S2

is

the

acceleration

due

to

356

D.

C.

Theodoridis,

Y.

Boutalis, and

M.

A.

Christodoulou

gravity, me is

the

mass of

the

cart,

m is

the

mass of

the

pole,

and

I is

the

half-length

of

the

pole. We choose me = 1 kg, m = 0.1

kg,

and

I = 0.5

min

the

following simulation.

It

is

our

intention

to

compare

the

direct control abilities

of

the

proposed

Neuro-Fuzzy

approach

with

RHONN's

[21]

(page 62-71). We also, make

the

appropriate

changes

to

RHONN's

in

order

to

be

equivalent

with

F-HONNF

's

(brunovsky form) for comparison

purposes

.

For

the

proposed

F-HONNF

approach

we use

the

adaptive

laws which

are

described by Eqs. (23)

and

(24)

and

the

control law described by Eqs. (14)

and

(15). Numerical

training

data

were

obtained

by using Eqs. (31)

with

initial conditions

[Xl

(0)

X2(0)]

=

[-

;2

0]

and

sampling

time

10-

3

sec.

We

are

using

the

proposed

approach

with

Eq

. (13)

to

approximate

In-

verted

Pendulum

dynamics

and

send

data

to

sigmoidal terms.

Our

Neuro-

Fuzzy model was chosen

to

use 5

output

partitions

of

f

and

5

output

partitions

of

g.

The

number

of

high

order

sigmoidal

terms

(HOST) used in

HONNF's

(for

F-HONNF

and

RHONN) were chosen

to

be

5:

(s(xd,

S(X2),

s(xd

.

S(X2)'

s2(xI),

S2(X2)).

In

order

the

proposed

model

to

be

equivalent

with

RHONN's

regarding

to

other

parameters

except

the

initial weig

hts

(Wf(O) = 0

and

Wg(O)

= 1 for

F-HONNF

and

Wf(O) = 0

and

Wg(O)

= 0.016 for RHONN) we have chosen

the

updating

learning

rates

1'1

= 5

and

1'2

= 1

and

the

parameters

of

the

sigmoidal

terms

such as

al

= 0.1,

a2

= 3, b

l

= b

2

= 1

and

Cl

= C2 =

O.

Also,

after careful selection, kl

= 2

and

k2

= 80 . Fig. (1) shows

the

regulation

of

states

Xl

and

X2 (with blue line for

F-HONNF

and

red line for

RHONN's),

while

fig.

(2) gives

the

evolution

of

control

input

u,

the

errors

el,

e2

and

the

modeling

error

d(X2'

u)

respectively.

The

m

ean

squared

error

(MSE) for

RHONN

and

F-HONNF

approaches

were

measured

and

are

shown in Table

1,

demonstrating

a significant (order

of

magnitude)

increase in

the

regulation

performance

of

F-HONNF

against

RHONN's.

Example

RHONN

F-HONNF

Inverted

Pendulum

MSExj

0.0010

6.0794

. 10 - 4

MSEx2

0.9252 0.3368

Table

1.

Comparison

of

RHONN's

and

F-HONNF

approaches

for

the

Inverted

Pendulum.

4.2

Van

der

pol

Van

der

Pol

oscillator is usually used as a simple be

nchmark

probl

em

for

test

ing control schemes.

It's

dynamical e

quations

are

given by

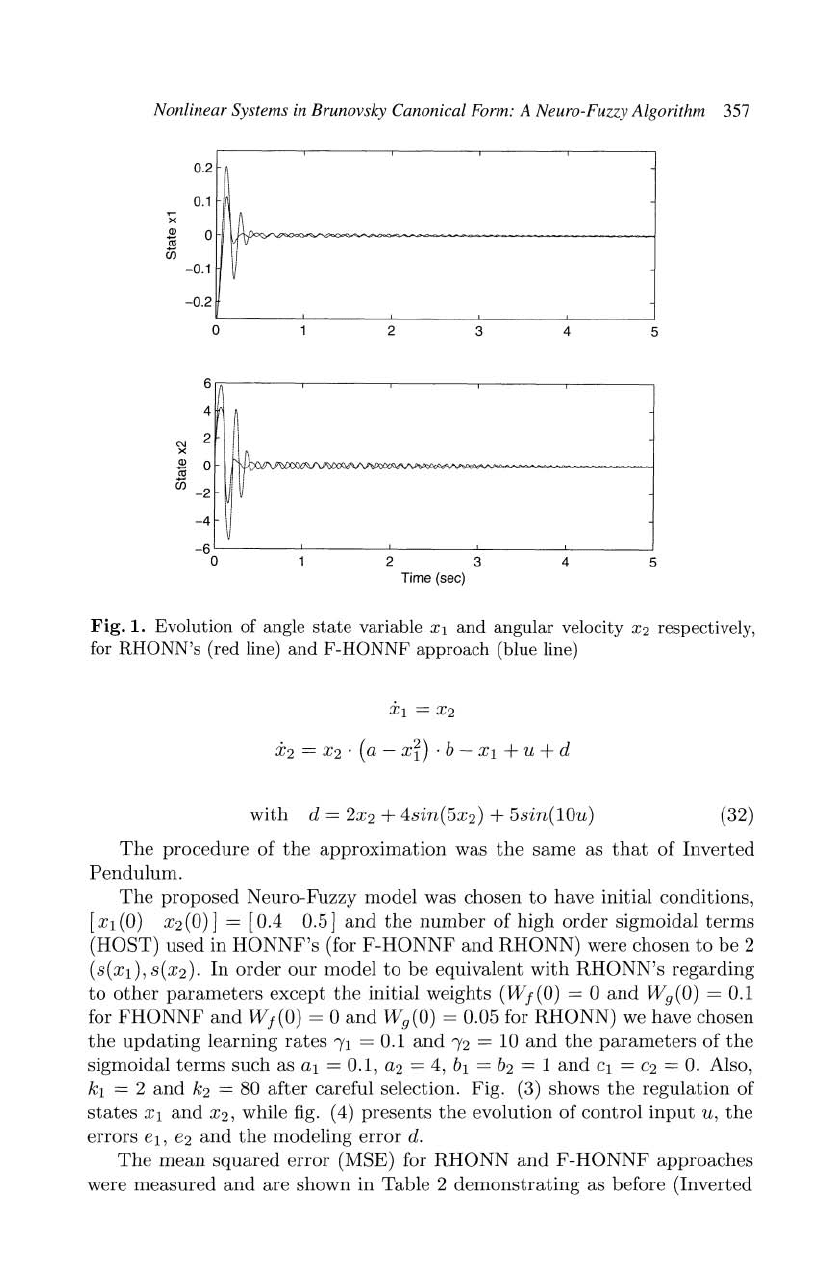
Nonlinear Systems in Brunovsky Canonical Form: A Neuro-Fuzzy Algorithm 357

0.2

,\

II

x

0.1

jll\A

* 0

~~~~~~~~-----------1

(J5

II

-0.1

~

-0.2

o

2

3 4

5

4

1

1\

.

il

';i 2

II,.

* 0

mly:0,\P\iXX'7VV'''XI''NV~v'''A-~~-

(J5

-2

,Ii

V

-4

\/

V

_6L---

__

L-

______

~

______

~

______

~

______

~

o

2

3 4

5

Time (sec)

Fig.

1.

Evolution

of angle

state

variable

Xl

and

angular

velocity

X2

respectively,

for

RHONN's

(red

line)

and

F-HONNF

approach

(blue

line)

X2

=

X2

.

(a

- xi) . b -

Xl

+ U + d

with

d =

2X2

+ 4sin(5x2) + 5sin(10u)

(32)

The

procedure

of

the

approximation

was

the

same

as

that

of

Inverted

Pendulum.

The

proposed

Neuro-Fuzzy model was chosen

to

have initial conditions,

[Xl

(0) X2(0)] = [0.4 0.5]

and

the

number

of

high

order

sigmoidal

terms

(HOST) used in

HONNF's

(for

F-HONNF

and

RHONN)

were chosen

to

be

2

(s(xd,

S(X2)' In

order

our

model

to

be

equivalent

with

RHONN's

regarding

to

other

parameters

except

the

initial weights (Wf(O) = 0

and

Wg(O)

= 0.1

for

FHONNF

and

Wf(O) = 0

and

Wg(O)

= 0.05 for

RHONN)

we have chosen

the

updating

learning

rates

{I

= 0.1

and

{2

= 10

and

the

parameters

of

the

sigmoidal

terms

such as

al

= 0.1,

a2

= 4, b

I

= b

2

= 1

and

CI

= C2 =

O.

Also,

kI = 2

and

k2

= 80

after

careful selection. Fig. (3) shows

the

regulation

of

states

Xl

and

X2,

while fig. (4)

presents

the

evolution

of

control

input

u,

the

errors

eI,

e2

and

the

modeling

error

d.

The

mean

squared

error

(MSE) for

RHONN

and

F-HONNF

approaches

were

measured

and

are

shown in Table 2

demonstrating

as

before (Inverted

Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

Подождите немного. Документ загружается.