Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications
Подождите немного. Документ загружается.


328
V.
D.
Sotiropoulos and
A.
D.
Sotiropoulos
Particular attention is focused in the present paper
in
the phenomena
of
bifurcation and chaos in music compositions. Many musical works, when
dealing with chaotic music, have been using the classical mathematical
recurrence models
of
the logistic equation or the Henon equation. A
comprehensive description
of
the use
of
logistic equation in composing music is
posted in the world wide web by Elaine Walker [7].
Our work departs from this
approach in that it proposes a new mathematical model to algorithmically
compose music. This model is based on geometry and, specifically, on a triangle
which is formed by its two sides and the angle between them; the two sides
representing the sound amplitude and frequency separated by an arbitrary angle
between them. The frequency
of
the next sound
is
represented by the square root
of
the third side
of
the triangle. Applied repeatedly, this model defines a
recurrence equation whose solutions result in a complete music composition.
2. The model
We propose a frequency-amplitude triangle whose cosine law is used
as
a
recurrence equation to algorithmically compose music. The triangle is defined by
two sides and the angle between them; one
of
the sides is the sound frequency,
x,
at a step (note), the other side is the sound amplitude,
y,
at the same step, while
the angle between them
is
a free parameter
to
be chosen by the composer. The
resulting third side
of
the triangle is defined as the square root
of
the sound
frequency,
x,
of
the next step (note). This frequency, using the cosine law,
is
given in terms
of
the frequency and amplitude
of
the preceding step (note) as:
xn+
1 =
Xn
2
+ Y n
2
-
2x
n
y
ncos
8
(I)
The sound amplitude,
y,
at each step depends, in general, on the amplitude and
frequency
of
the same or previous step(s) in any way the composer chooses, that
is,
in
any functional manner:
Yn
= f
(x
n
,
Xn-l
, ... ,
xn-m)
(2)
where
m=0,1,2,3,
... ,
n=m+l,m+2,
...
Once the composer chooses the initial frequency or frequencies, the recun-ence
equation
(I)
yields all the sound frequencies
Xn
and, thus, the complete music
composition since the sound amplitudes
Yn
are given by equation (2).
It
is
convenient from the computational point
of
view to use small
numbers for x that are used
in
the mathematical literature for recurrence
equations and do not correspond to actual sound frequencies. The mathematical
frequencies
Xn
are then converted to standard MIDI (Musical Instrument Digital
Interface) note numbers ranging from 0 to 127 by using the following equation
midikey
= floor (127(1 +x)/2 +0.5)
(3)
where midi key is the MIDI note number and floor(z) is the largest integer not
greater than
z.
We note that equation (3) is valid for x between
-1
to +1.
If
the
largest value
of
x that comes out
of
the recurrence equation (1)
is
greater than 1
then, in equation (3), x
is
adjusted accordingly to yield note numbers between 0

Music Composition from Cosine Law
of
Frequency-Amplitude Triangle 329
and 127. For example, for
0:Sx:S4,
l+x
in equation (3)
is
substituted by xl2. The
actual frequency,
f,
of
notes in an A440 equal temperament is given in terms
of
MIDI note numbers by the formula
f
I (440 Hz) =
imidik
ey - 69)1l2 (4)
3. Analysis
First, we refer to two special cases
of
our frequency - amplitude triangle
composition model given by the recurrence equation
(1):
i)
(Sa, b)
in which the amplitude
of
a note being linearly proportional to the frequency
results in frequencies that fall on a single curve. The resulting frequencies, only
after a few steps, either go to zero or infinity depending on the values
of
b, e,
and the initial frequency. For cose
0::
bl2 which is satisfied
if
b
:S
2, the resulting
frequencies, only after a few steps, go to zero
if
the initial frequency
is
smaller
than one.
ii)
Yn
= 1 , cose = 0.5,
(6a, b, c)
which, for initial frequency equal to
2,
is Sylvester's sequence with resulting
frequencies that are equal to
2,
3, 7, 43, 1807, 3263443,
...
To test our proposed composition model for bifurcation and chaos, we
consider in detail the case:
Yn
=
b,
(7a, b)
that is, the case where note loudness remains constant throughout the
composition. With the following change
of
parameters and variables
r =
I
±,j
g(b,
cose),
g(b, cose) = 4b
2
(cos
2
e -1) + 4bcose
+1
(8a, b)
a = -I Ir, c = 0.5+bcose/r
(9a, b)
z=ax+c
(10)
equation (7b) becomes
(11
)
which is the well known logistic recurrence equation whose resulting solutions
are
of
meaning for r
0::
1.
This, together with equations (8a, b), yields
g(b, cose) = 4b
2
( cos
2
e -1) + 4bcose + 1
0::
0
(12)
which is satisfied for all
e's
such that
cose
0::
1-
1/(2b) ,
bo::
0.5
(13a,
b)

330
V.
D.
Sotiropoulos and
A.
D.
Sotiropoulos
where
(l3b)
is
the requirement for acute angles. Therefore, our proposed
triangular recurrence model defined by equation (7b) yields a composition for
any angle
8 when the loudness b
is
smaller than 0.5 and for angles satisfying
(13a) for all other b's.
Having knowledge from the classical logistic equation (11)
of
the
values
of
r which yield no bifurcation or multiple bifurcations means that
we
can
know a priori the composition's features
as
the loudness b and the angle 8 are
related to r by the equation
(14)
If
we
choose an angle 8 having a value satisfying (13a) for a chosen b equal
to
or greater than 0.5 and arbitrary for all other
b'
s,
equation (14) will tell
us
which
r
we
are picking in the classical logistic map and, thus, what will be the features
of
our composition in terms
of
bifurcation and chaos. However, there are infinite
pairs
of
values (b, cos8) which
if
substituted in equation (14) yield the same r.
Therefore, it is important to examine equation (14) from the point
of
view
of
determining the characteristics
of
the values
of
band
cos8 for a given
rand,
thus, a given
roo
Solving equation (14) for cos8 yields
(15)
which is to be taken together with the conditions
b
2:
.y(l-
r02)/2,
ro:S
1
(16)
and
(17)
in
order to have acute and real angles respectively. Equation (15) readily yields
the angle
8
n
for which the nth period doubling (bifurcation) occurs
as
where
(I8b)
are known from the classical logistic map. It is understood that the loudness b
satisfies condition
(17). Another feature to point out
is
the existence
of
a
minimum cos8 for a given
ro>
1 which is obtained from the zero slope
of
cos8
of
equation (15)
as
(19)
which occurs
at
(20)
When the amplitude b
is
smaller than this value, cos8 approaches one and, in
fact, becomes one at the value
of
b given by the equation
in
(17). For b larger
than the value defined in
(20), cos8 approaches again one in a fashion described
by
(l3a).

Music Composition from Cosine Law
of
Frequency-Amplitude Triangle
331
Therefore, to compose music using the specific triangular recurrence
equation (7b) with a priori knowledge
of
its bifurcation and chaos features,
we
need to choose the value
of
r
o
, then select the sound amplitude b to satisfy (17)
for most cases
of
interest, next calculate the triangular model's angle 8 using
(15), and last compute all the frequencies
Xn
of
the composition from iterating
equation (7b).
The proposed general triangular composition model as expressed by the
recurrence equation (1) will result in frequencies
Xn
whose features in terms
of
its periodicity will depend on the chosen functional dependence
of
the amplitude
on frequency or frequencies expressed by equation (2). For example, for a
dependence on the frequency
of
the same step (note) to a power deviating
slightly from zero, there is a dramatic change on the periodicity
of
the resulting
frequencies.
Let's
take, as an example,
Yn=2x
n
1/8
to represent equation (2). Then,
on changing to a new mathematical frequency
z=x
7/8
12,
equation (1) for the case
when the angle
of
the triangular model is zero becomes simply
(21)
From the form
of
this recurrence equation it is expected, on comparison with the
classical logistic recurrence equation as was done for other recurrence equations
by Skiadas and Skiadas[8], that the resulting frequencies will be chaotic, as
indeed they are. This will be demonstrated numerically in the following section.
However, when the angle
of
the triangular model
is
non-zero, the frequencies do
need be chaotic
as
is the case when cos8=O.95 for which the frequencies exhibit
a one-period doubling. This will be demonstrated numerically in the section that
follows.
We examined other fractional power models for the functional
dependence
of
the amplitude on frequency as well. We found that the frequency
tends to a single value for a range
of
powers smaller or equal to one independent
of
the triangle's angle, in agreement with the result obtained analytically in case
i above where the power is equal to one.
4. Numerical Results and Chaotic Compositions
The parameter range affecting the presence
of
single or multiple periodicity
of
the composition's frequencies for the constant amplitude triangular model was
analytically examined in detail in the previous section. Here, this parameter
range is depicted graphically. In Figures
1,
2 the cosine
of
angle
8,
the angle
between the amplitude and frequency for each note defining the triangular
compositional model is plotted versus the amplitude's magnitude b for
ro
defined
by (14) smaller or equal to one, and greater than one respectively. Figures
1,2
represent graphically equation (15).
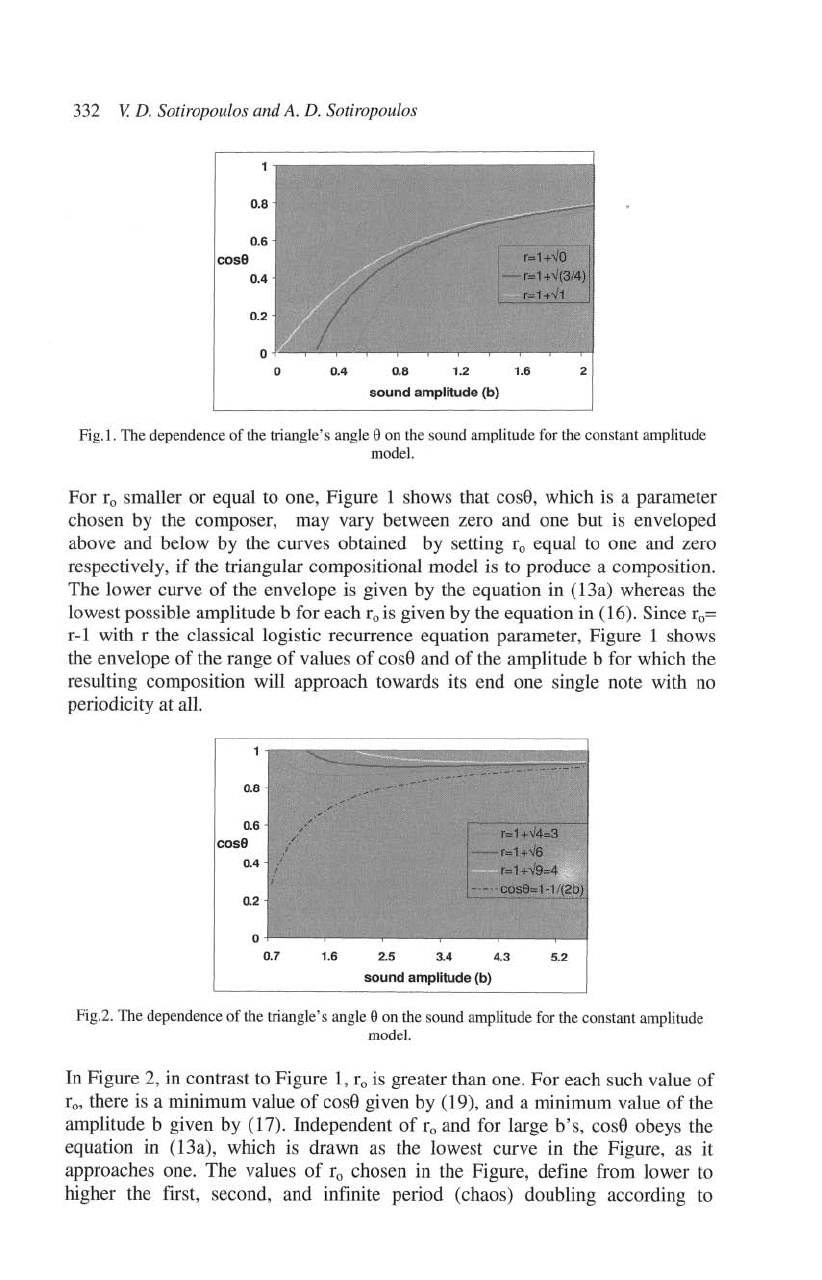
332
V.
D.
Sotiropou/os and A.
D.
Sotiropoulos
I
leose
0.8
0.4
0.2
o
Fig.I.
The
dependence
of
the triangle's angie 0 on the sound amplitude for the eOllstunt amplitude
model.
For
fo
smaller
or
equal to one, Figure 1 shows that
cosO,
which is a parameter
chosen
by
the composer, may vary between zero and one but is enveloped
above and
helow by the curves obtained by setting
1'0
equal to one and zero
respectively,
if
the triangular compositional model
is
to produce a composition.
The
lower curve
of
the envelope is given
by
the equation in (13a) whereas the
lowest possible amplitude b for each
1'0
is
given by the equation in (16). Since
1'0=
r-1
,"vith
r the classical logistic
reClU'fenCe
equation parameter, Figure 1 shows
the envelope
of
the range
of
values
of
cose
and
of
the amplitude b for which the
resulting composition
will approach towards its end one single note with no
periodicity at
aU.
2.5
sound
amplitude (b)
Fig.2. The dependence
of
the triangle' s angle (l on the
sound
amplitude for the constant amplitl!de
model.
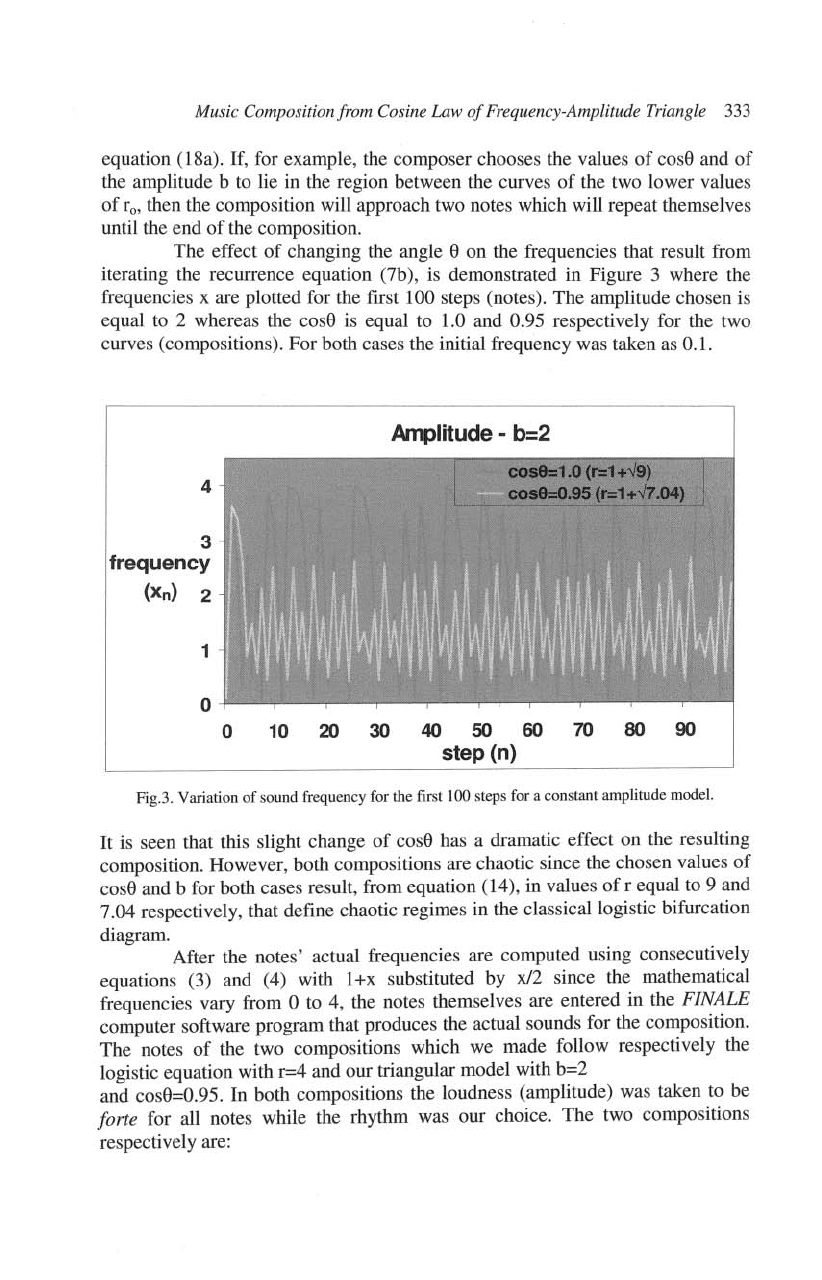
In Figure 2, in contrast to Figure
1,
fo
is greater than one.
For
each
such value
of
1'",
there is a minimum value
of
cose
given by (19), and a minimum value
of
the
amplitude b given by (17). Independent
of
1'0
and for large
b's,
cose
obeys the
equation in
(l3a),
which is drawn as the lowest curve in the Figure, as
it
approaches one,
The
values
of
r"
chosen
in
the Figure, define from lower to
higher the first, second, and infinite period (chaos) doubling according to
Music Compositionjinm Cosine Law
of
Frequency-Amplitude Triangle
333
equation (18a). If, for example, the composer chooses the values
of
cosO
and
of
the amplitude b
to
lie
in
the region between the curves
of
the two lower values
of
r",
then the composition will approach two notes which will repeat themselves
until the end
of
the composition.
The effect
of
changing the angle 6 on the frequencies that result from
iterating the recurrence equation (7b), is demonstrated in Figure 3 where the
frequencies x are plotted for the first 100 steps (notes). The amplitude chosen
is
equal
to
2 whereas the cosS is equal to 1.0 and 0.95 respectively for the two
curves (compositions). For both cases the initial frequency was taken as 0.1.
4
3
ifrequency
!
(Xn)
2
1
o
o
10
20
30
40 50
60
70
step (n)
Fig.3. Variation
of
souud frequency for the first 100 steps for a constant amplitude model.
It
is seen that tllis slight change
of
cosS has a dramatic effect on the resulting
composition. However. both compositions are chaotic since the chosen values
of
cose and b for both cases result.
from
equation (14), in values
of
r equal to 9 and
7.04 respectively, that define chaotic regimes
in
the classical logistic bifurcation
diagram.
After the notes' actual frequencies are computed using consecutively
equations (3) and (4) with
l+x
substituted by x/2 since the mathematical
frequencies vary from
()
to 4, the notes themselves are entered in the FINALE
computer software program that produces the actual sounds for the composition.
The notes
of
the two compositions which we made follow respectively the
logistic equation with r=4 and our tliangular model with
b::::2
and cose=O.95. In both compositions the loudness (ampHtude) was taken to be
forte for all notes while the rhythm was our choice. The two compositions
respectively are:

334
V.
D.
Sotiropoutos and A.
D.
Sotiropoulos
ScOTe
lr.
: .
~
I·
....
'\~t~"~~~~~~,
(~~~~-;
=:[~=:~~~~

Music Composition.timn Cosine La,!'
of
Frequency-Amplitude Triangle 335
,
j5~"
.\~:
"~i~
__
,
~i
. _
.:
!
l~:';:~I=.i"ijiiG~~
~~.'"
8""-"-'---'
,'?'-
,'1"'"
!i"-'--
'
'''
g'
IS\:'
.
15'r
!~--ffj6'-~'r~-
.~~~"".,.:;c-~
I~~~~,.~~
'1"''>1,:
_
it"
.
"~,,
8"'-
t
ISIIm-
-
.-;
8it~'-~-.'.
~~------.---,--.-
..
--.---
..
, .
.,.
..
--'--'
1':
~ilIt-
f!~.'
j'!;'
~~'
IS"':
IS"','
#t-.
-.'
J5~O
1'1"',:,
J.'
E "
l:c~
,
~.
c:
!::'f'
f
~~=3;=F~¥~i='-~
'~4tf1ff2~41E~~
(~~:,:
'f
-
..
~~~
l8"f~,
"
8'~------':-'-~---~"
,
,~.:-.:":----,
~,"
JI-,-
I~';""e
" '
~
__
:.
g
_~ril
I·
---~~--~~~--1~"=~
I
-.~~
(~=E~~~~%:-;:-~~
)~~cc=-."~~~~~:;+~:~~~~~
(~-=-~":C.~~<:3F~-=:.it--~4T-~~~
17"--'--
K,--,~J~)~,.
q'<i-
,
I"
!
~
i I q ,
[1'---'
1 •
,""""""'.
Ij..-t._
- - - _
-;
Tt
is remarked that
our
notation is non-conventional and is not intended
for anyone
else other than the computer to play it. Both compositions were
played on June 4,
2009 for the audience
of
the Chaos 2009 international
conference in Chania, Greece during
the presentation
of
our paper,
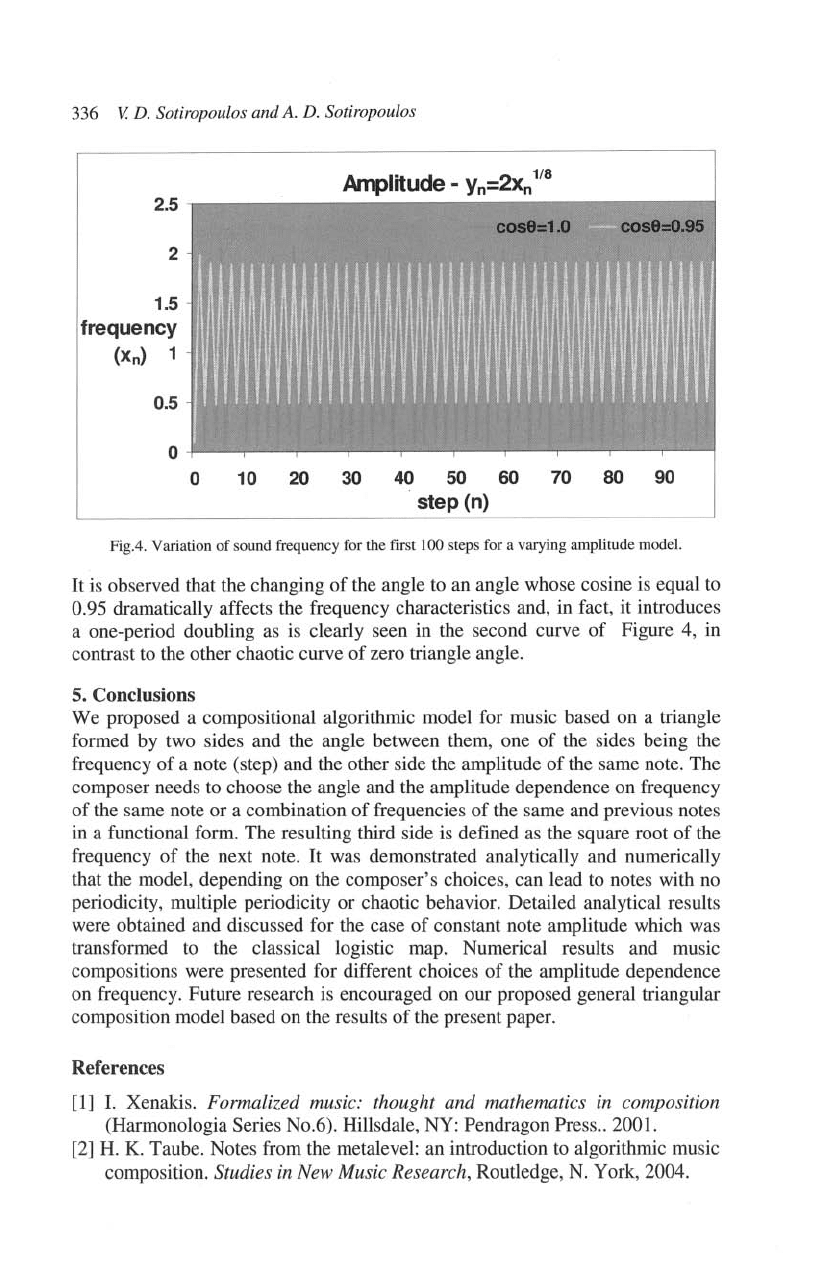
A different amplitude model and, thus, a different recurrence equation
is chosen next to demonstrate graphically its effect on the resulting frequencies
of
the composition. The amplitude
of
each note (step) is taken to depend
on
the
frequency
of
the same note raised 10 the power
of
118,
with its magnitude being
equal to 2 when the mathematical frequency is equal to
1.
Then, for a zero
triangular angle the recurrence equation
is given by equation (21), the iterations
of
which yield chaotic hequencics as may be seen in Figure 4 where the
frequencies x
axe
plotted for the first 100 notes (steps) having picked
an
initial
frequency value equal to
O.
J _
336
V.
D. Sotiropoulos and A.
D.
Sotiropoulos
o
10 20 30
40
50
60
70
80
90
step (n)
Fig.4. Variation
of
so
un
d frequency for the first 100 steps for a varying amplitude model.
It
is observed that the changing
of
the angle to an angle whose cosine is equal to
0.95 dramatically affects the frequency characteristics and, in fact, it introduces
a one-period doubling as is clearly seen in the second curve
of
Figure 4,
in
contrast to the other chaotic curve
of
zero triangle angle.
5. Conclusions
We proposed a compositional algorithmic model for music based on a triangle
fonn
ed by two sides and the angle between them, one
of
the sides being the
frequency
of
a note (step) and the other side the amplitude
of
the same note. The
composer needs to choose the angle and the amplitude dependence on frequency
of
the same note or a combination
of
frequencies
of
the same and previous notes
in a functional form. The resulting third side is defined as the square root
of
the
frequency
of
the next note.
It
was demonstrated analytically and numerically
that the model, depending on the composer's choices, can lead to notes with no
periodicity, mUltiple periodicity
or
chaotic behavior. Detailed analytical results
were obtained and discussed for the case
of
constant note amplitude which was
transformed to the classical logistic map. Numerical results and music
compositions were presented for different choices
of
the amplitude dependence
on frequency. Future research is encouraged on our proposed
gcneral triangular
composition model based on the results
of
the present paper.
References
[1]
1.
Xenakis. Formalized music: thought and mathematics
in
composltwll
(Harmonologia Series No.6). Hillsdale, NY: Pendragon Press
..
2001.
[2]
H.
K.
Taube. Notes from the metalevel: an introduction to algorithmic music
composition. Studies
in
New Music Research, Routledge, N. York, 2004.

Music Compositionjrom Cosine Law
oj
Frequency-Amplitude Triangle 337
[3]
Karlheinz Essl: Algorithmic composition.
in:
Cambridge Companion
to
Electronic Music, ed. by
N.
Collins and
J.
d'Escrivan, Cambridge University
Press 2007.
[4]
Z.
D.
Browning. Banjaxed. Capstone Records,
N.
York, 1999.
[5]
S.
Tepei. Manifold compositions: formal control, intuition, and the case for
comprehensive software. Proceedings
2005 International Computer Music
Conference, Copenhagen, Denmark, 2007.
[6]
G.
E. Garnett. The aesthetics
of
interactive computer music. Computer Music
Journal, 25:21-33,2001.
[7]
E.
Walker. Chaos melody theory.
www.ziaspace.com/eiaine!ChaosMelodyTheory.pdf
[8]
C.
H. Skiadas and
C.
Skiadas. Chaotic Modelling and Simulation. CRC
Press,
N.
York, 2009.
