Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

118

D.

Khots and

B.

Khots

8

Geodesic

equation

with

chaos

theory

interpretation

Consider

the

following:

··i+

'\""'

n,\"",

nr

i

(.j

·k) 0

X n

L...j

L...k

jk

Xn

X

Xn

X =

with

j,

kEG.

Then

we have

the

following

Th

8

If

· P - . P . P • P . P . P ·th

G·

P . P

eorem.

x -

XO.X1

...

Xl

X

I

+

1

...

Xn'

WZ

P E

,XO

=

Xl

=

...

=

xf

=

0,

0::;; I

::;;

n,

n <

21

::;;

q,

then

we have

Xi

=

0,

i.e., the geodesic curve

is a line.

P

1

·j

·k

.J.J

.j.j

.j

·k·k

·k

roo.

X

Xn

X - X

O

·X

1

···

Xl

X

I

+

1

...

Xn

Xo

.X1

...

Xl

X

I

+

1

...

Xn

(0.0

...

OxI+1

...

x~

Xn

0.0

...

0#+1

...

x~)

=

O.

QED.

9

Acknowledgments

The

authors

thank

Professor

Christos

H. Skiadas for his

invitation

to

par-

ticipate

at

the

Chaotic

Modeling

and

Simulation

International

Conference

(CHAOS2009).

References

l.B.Khots

and

D.Khots.

Mathematics

of

relativity

webbook,

urI:

www.mathrelativity.com.

2004.

2.B.Khots

and

D.Khots.

Extraction

of

dynamical

equations

from

chaotic

data.

Lecture Notes

in

Theoretical and Mathematical Physics, 7:269-306, 2006.

3.B.Khots

and

D.Khots.

Observer's

mathematics

-

mathematics

of

relativity.

Ap-

plied

Mathematics

and Computations, 187:228-238, 2007.

4.D.Khots

and

B.Khots.

Quantum

theory

and

observer's

mathematics.

American

Institute

of

Physics

(AlP),

965:261-264, 2007.

New Models

of

Nonlinear Oscillation Generators

Alexander A. Kolesnikov

Technological Institute

of

Southern Federal University,

Synergetics and Control

Processes Department

44, Nekrasovky str., Taganrog, 347928, Russia

(e-mail: anatoly.kolesnikov@gmail.com)

Introduction

119

One

of

the fundamental problems

of

the modern nonlinear

dynamics is a complex problem

of

oscillations control in various nature

systems. Numerous foreign and Russian scientific articles and studies

are published concerning regular and chaotic oscillations control. Also

wide international conferences and symposia are conducted concerning

the same problem which is one

of

causes

of

nonlinear dynamics and

synergetics (a science

of

self-organisation in complex systems)

evolution. That important control problem has not properly resolved

yet.

In

our opinion it requires to be further developed.

Hereof the synergetic approach for auto-oscillation system

synthesis is considered in this report. The approach is based on the

known

Analytic Design

of

Aggregated Regulators (ADAR). According

to ADAR, desired

invariant manifolds (energetic integrals

of

motion)

are added to state space

of

synthesized system [1-3]. Such approach

provides analytical calculation

of

feedbacks forming required behavior

of

the nonlinear oscillating processes.

Three basic models

of

oscillators (self-oscillating 2-order

systems) studied all over the world for many years are the following:

Van-der-Paul Equation

x(t)-,ul{1-alx

2

)x(t)+w

2

x=O

(1)

Rayleigh Equation

Poincare Equation

XI

(t)

=

-WX2

+ XI

(A

2

-

X? -

xi),

X2

(t)

=

+WXl

+

X2

(A

2

-

XI

2

-

xi).

(2)

(3)

Dozens

of

studies and scientific papers are indented to analysis and

application

of

these Equations showing behavior

of

wide group

of

engineering systems and devices. Now only estimated periodic

120

A.

A. Kolesnikov

solutions

of

Equations (1) and (2) are known. Amplitude and frequency

can be estimated depending on values

of

parameters

JLi

and a

i

from

these solutions. Here it's obviously that the lesser

JL

i' the closer

oscillations to harmonic and vice versa - the more

JLi'

the more rapid

relaxation oscillations. In regard to

Poincare Equation (3), one has the

exact analytical solutions

[23]. In fact,

if

polar coordinates

XI

= rcos¢

and x

2

=

-rsin¢

are input to (3) then:

r(t)=r(A

2

-r

2

)

and i>(t)=w. (4)

Equation (4) solutions are the following:

2

r(t)= A ro .

2 +

(A

2)

_2A

2

( '

ro

-ro e

¢(t)

={J)t

+¢o .

(5)

(4) and (5) imply that stable harmonic oscillations with amplitude A

and frequency (J) are formed in system (3) in time:

Xis

(t)

= Acos(wt + ¢o);

X2

s (t) = -Asin({J)t + ¢o). (6)

Note the following one feature

of

equations (3) rarely mentioned in

scientific literature. For that take

A

2 2 2

If/ = - XI -

X2

,

(7)

as some energetic macro variable, where A is analog

of

oscillations

energy.

If

allow If/e = 0 (7) then from system (3) we get the following

equations:

or

(7) implies that motion on manifold If/e = 0 is also shown

10

the

following folded differential I-order equation:

XJ/f/(t)=~2E-W

2

XJ2/f/

'

A

2

{J)2

Where E =

--

IS energy

of

steady oscillations. It means that

2

If

e = 0 system (3) behavior on manifold is shown in conservative

New Models

of

Nonlinear Oscillations Generators

121

model (8) which has harmonic solution

of

type (6). Meanwhile prior to

entry on

'fie = 0 the system (3) is dissipative one.

It's

easy to show with

its divergence:

. . ()

aX

I

aX

2

(2

2

2)

2 2

dlVX

t

=-+-=

2 A

-Xl

-X

2

-2XI

-2X2

<0.

aX

l

aX

2

In

fact on manifold 'fie = 0 (7) input energy and dissipation

energy is balanced. So all trajectories

of

system (3) are attracted to

energetic invariant manifold

'fie = 0 (7) (harmonic attractor, i.e. stable

boundary cycle on its phase plane). This fact is important for

development

of

new methods

of

oscillation generators synthesis on

base

of

synergetic approach [1-3]. Unfortunately such analytical

expressions

of

Van-der-Paul (1) and Rayleigh (2) Equations boundary

cycles are unknown yet. Now other forms

of

self-oscillating systems

significantly

of

lesser popUlarity than Van-der-Paul, Rayleigh, and

Poincare Equations are described in literature.

It

must be emphasized

that there are no regular methods

of

analytical synthesis

of

non-linear

oscillation generators in literature. Below we describe analytical

efficiency

of

ADAR

[1-3] method for non-linear problem

of

synthesis

of

various self-oscillating systems with specified amplitude and

frequency

of

harmonic oscillations.

1. Unified Van-der-PauVRayleighIDuffing Generator

Consider a system:

(9)

It's

required to synthesize a feedback law

u{xI'

xJ

providing

appropriate harmonic attractors (stable boundary cycles with desired

amplitude

A and frequency

OJ

of

self-oscillations) in phase space

of

closed system. According to

ADAR

[27-29] introduce basic energetic

macro variable:

(10)

and invariant expression

(11)

where function

I/fl

(t)

can be interpreted as power

of

synthesized

system. According to

(11) and equations (9) and (10) form feedback

law

122

A.

A_

Kolesnikov

aF

x

2

U]

=--+-'1/]-

ax]

~

(12)

Obviously that equation (11) is asymptotically stable in large relative

to

condition

'1/]

= 0 (10). It's shown with Lyapunov function V =

0,5'1/]2

.

Time derivative

of

that function

(13)

at

T]

> 0 is always negative.

It's

suggesting that (11) is stable. Subject

to

(10) and (12) closed system equation (9) is:

..

()

[2

()

05.

2

].

()

aF{xJ

0

x]

t - A - F

x]

- ,

x]

t +

=.

ax]

(14)

According

to

(13) the system (14) has energetic attractor

'1/1

= 0 (10).

Subject to potential function

F{x])

selected in (14), various

types

of

self-oscillating systems can be get. Motions

of

these systems

on manifold

'1/]

= 0 (10) are

of

the following types, for example:

(a) harmonic

(15)

(b) Duffing

(16)

Substituting potential functions (15) and (16) in (14) we get harmonic

oscillation generator or Duffing generator respectively. For instance,

using

Fd

(Xl)

we get unified Van-der -PaullRayleigh/Duffing oscillator

according to (14):

x

J

(t)-

~

[A2

- 0,501

x~

-

fJ

x~

-

0,5xJ

2

~]

(t)+ 0/ x

J

+

4fJx~

= O. (17)

~

On manifold

'l/J

= 0 (10) the system (17) is described with Duffing

equation:

(18)

This equation has different dynamic characteristics depending on

relation

of

OJ

and fJ. For example, at

fJ

= 0 from (18) we get

New Models

of

Nonlinear Oscillations Generators

123

conservative equation

of

type (S) with potential function F (15). Then

g

equation (17) become an unified Van-der-PaullRayleigh/Duffing

generator:

with asymptotically stable harmonic attractor (boundary cycle

If/l

= 0

(10)

to which all phase plane trajectories are attracted). In other words,

equation (19) is generator

of

harmonic oscillations:

x(t)=asin(mt+¢o) (20)

with specified amplitude a and frequency

(f).

Generator (19)

combines

Van-der-Paul (1) and Rayleigh (2) generators into unified

non-linear oscillator

of

new class. It is interesting to note that system

(19) has a property

of

self-similarity as after affix enters on attractor

If/]

= 0 (10) at

fJ

= 0 the system continues to be described with the

same equation

(IS). In other words, attractors are "embedded" one into

another [1-3]. Obviously that

if

oi

»1,

then member

0,5alx~

will

dominate in comparison with member

0,5x~.

In this case properties

of

equation (19) are closer to properties

of

Van-der-Paul Equation. On the

contrary

if

m

2

«

1,

then member

0,5x~

will dominate and equation

(19) will be similar to Rayleigh Equation (2). Results

of

generator (19)

simulation with parameters

A = 1; m =

1;

T =

0,5

and XlO = 1; x

20

= 0

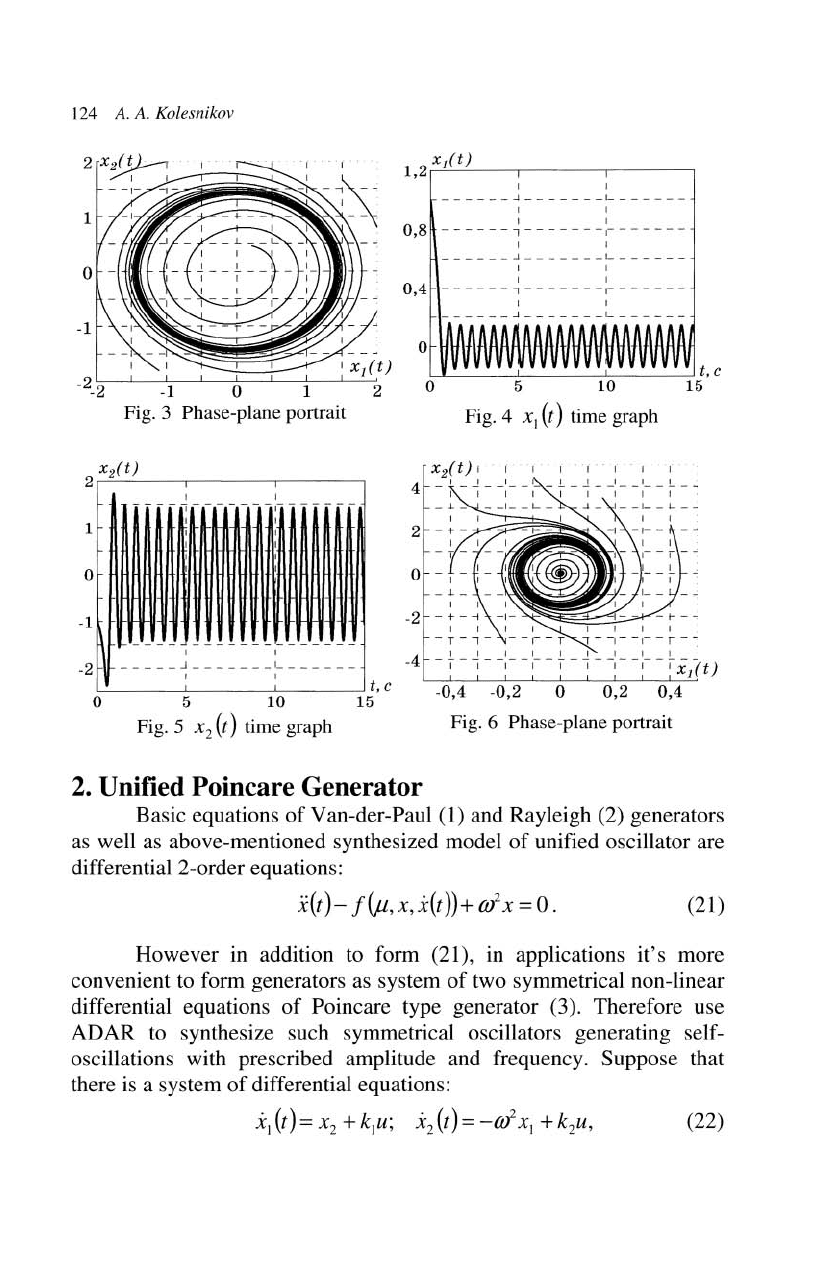
are shown in fig. 1-3. Results

of

generator (19) simulation with

parameters

A =

I;

m =

10;

T = 0,5 are shown in fig. 4-6. These results

fully verify theoretical statements

of

ADAR [1-3].

1

x<~

,

, ,

,II

,

/\

,

, , , ,

-

,

-

,

-;

,

-

- -

,

-

,

, ,

1

X

2

(t)

,

'

/\

,

~

,

,II

,

_L

,

'-

,

-

, ,

-

, ,

,- ,

- -

,

;-

, , , ,

,

, ,

, , , ,

,

, , ,

,

, , ,

-

- -

-

,

, ,

- -

-

, , ,-

-I-

,

,-

, , , ,

,

, ,

,

-

J

,

- -

~

- -

, ,

-

,

-

, ,

,

l _

,

-

,

'-

-

-'

,

- -

,

~

, , , ,

,

, , ,

o

, ,

,

, , , ,

,

, , , , ,

, ,

,

_ J _

,

-

,

~

,

-

,

_ 1- _

,

, ,

, , , ,

,

l

,

- - -

,

-

,

-'

,

-

,

_L_

, , ,

, , , ,

,

, , , ,

,

L_

- -

,

L

- - -

_L

V,

\I

, , ,

,

'V

,

v'

,

, ,

, , , , ,

1J

L

~-

- - '

-

~

,

- - -

,

v:

, , ,

, ,

y

'v

, ,

II:

Y

t,

c

10

20

30

40

50

-1

o

t, C

10

20

30

40

50

0

Fig. 1 Xl

(t)

time graph

Fig. 2

x

2

(t)

time graph

124

A. A. Kolesnikov

--

-

- -

~-

--

-

-~-

-

--

1

0,8

, ,

--

- - - -

,-

---

-

--

r - -

--

-

---

~-

--

- -

-

-~-

-

--

,

0,4

,

---

- -

-,

- - - - -

--

r-

- - -

--

-

---

~-

--

- - -

-~-

-

--

-1

0 1

Fig. 3 Phase-plane portrait

I I

---

-,-

- -

---

- r -

----

-

1

o

-1

--

- - -

--

- - - - - - - - - -

--

-2

I ,

_ _ _ _ _

~

__

_

__

L

__

_ _ _ _

, I

I I I I I I I I

-4 - T -

..,

- - - - ,- - T -

..,

- -, - - ,- -

,-

Xl-

(t)

L-

______

~

__

____

_L

______

~

t,c

5

10

15

o

-0,4

-0,2

0

0,2 0,4

Fig. 5 x

2

(t)

time graph

Fig. 6 Phase-plane portrait

2. Unified Poincare Generator

Basic equations

of

Van-der-Paul (1) and Rayleigh (2) generators

as

well

as

above-mentioned synthesized model

of

unified oscillator are

differential 2-order equations:

x(t)-

1(;1,

x,

x(t))+

oJ

x =

o.

(21)

However in addition

to

form (21), in applications it's more

convenient to form generators as system

of

two symmetrical non-linear

differential equations

of

Poincare type generator (3). Therefore use

ADAR to synthesize such symmetrical oscillators generating self-

oscillations with prescribed amplitude and frequency. Suppose that

there is a system

of

differential equations:

Xl

(t)

= x

2

+ klu; x

2

(t)

= -oJ

Xl

+ k

2

u,

(22)

New Models

of

Nonlinear Oscillations Generators

125

with some coordinate function

U(X

j

,

x

2

)

in the right part.

It

is required

to

synthesize

u(x

l

,

x

2

)

so

as

self-oscillations with desired amplitude

and frequency are always formed in

system (22). According to ADAR

introduce the following energetic macro variable:

If/ = A

2

-

o,Sui

x~

-

O,Sx~

. (23)

Then substituting

If/ (23) into invariant expression

Tvi(t)

+

F(x

p

x

2

)1f/

=

0;

T >

0,

subject to system (22) we get feedback law

(

)(k

2 )

F(x

j

,x

2

)

U X

I

,X

2

JOJ

Xl

+k2X2

=

If/.

T

Compose equations

of

closed system (22), (24):

(24)

. ( )

kl

(2

) ( 2 2 2 2 )

Xl

t

=X2

+-

klOJ

Xl

+k2X2

A -O,SOJ Xl

-0,SX2

;

T (2S)

. ( ) 2

k2

(2

) ( 2 2 2 2 )

X2

t =

-OJ

Xl + T

klOJ

Xl

+ k

2

X

2

A -

O,SOJ

Xl -

0,SX2

.

Given symmetrical system (2S) is unified Poincare type generator (3).

On manifold IjI = ° (23), function U = ° (24) and system (2S) is

formed with confluent equations

Xl

\If

(t)

= X

2

\1f;

X

2

\1f

(t)

= -

OJ2

Xl

\If

fully coinciding with (8).

It

means that stable harmonic oscillations

with prescribed amplitude and frequency are always appeared in the

system

(2S) by some time depending on parameter

T.

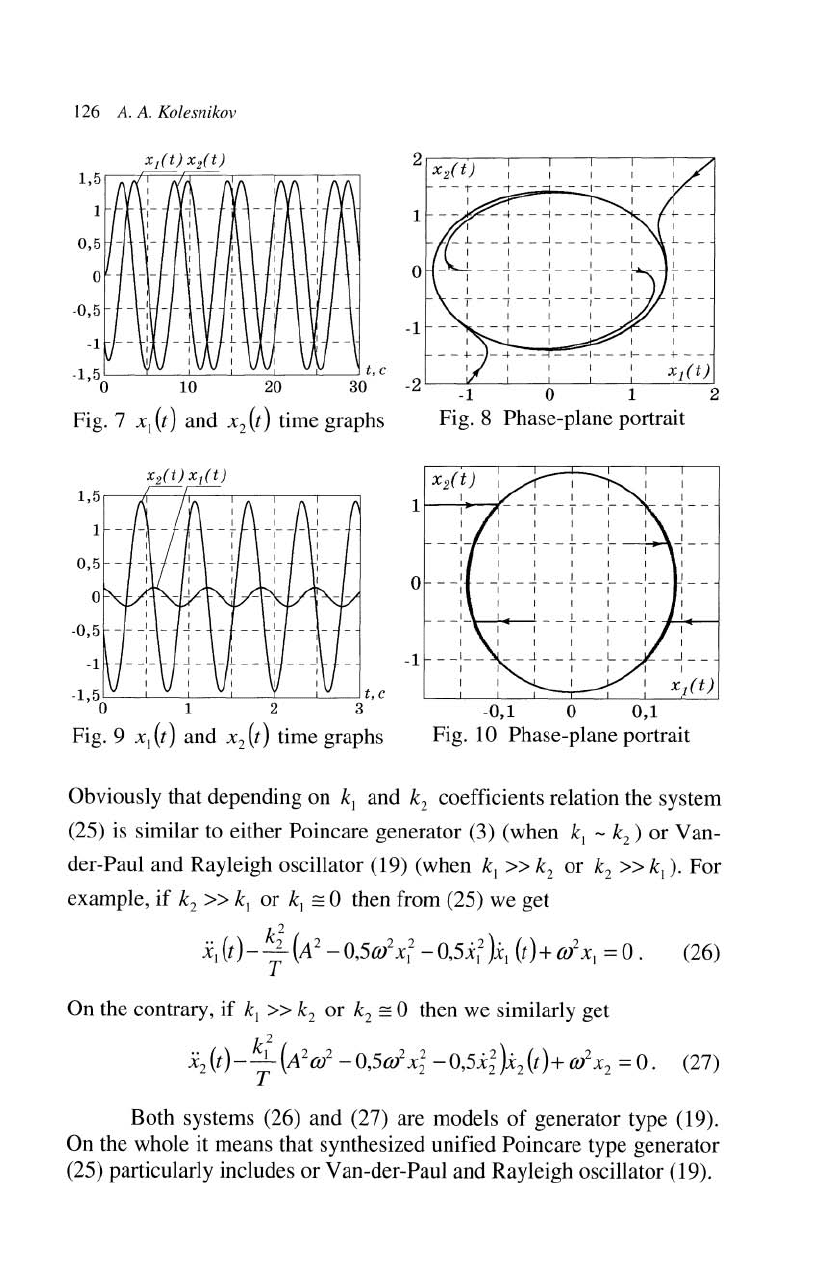
Results

of

system

(2S) simulation with parameters A = 1 ;

(j)

= 1; kl =

k2

= 1; T =

O,S

are

shown in figures 7 and

8.

Results

of

system (2S) simulation with

parameters

A =

I;

OJ

=

10;

k

j

=

10;

k2

=

I;

T =

0,5

are shown

III

figures 9 and 10. These results also verify theoretical statements

of

ADAR [1-3].

126 A. A. Kolesnikov

-1

5

L---'L""-_c-=--=---L-=----=--L----'-L------.J

t, C

, 0

10

20

30

Fig. 7 Xl

(t)

and X

2

(t)

time graphs

1,5~~~--!c.--~-~-~~

1

0,5

-

-1 5 t, C

, 0 1 2 3

Fig. 9 Xl

(t)

and x

2

(t)

time graphs

-1

x

1

(t)

_2L-~L-~---L---L--~--~~

-1

0 1 2

Fig. 8 Phase-plane portrait

11---':"-~

,

0--

--:--

,

-1

--,--

-0,1 0

0,1

Fig.

lO

Phase-plane portrait

Obviously that depending on

kl and

k2

coefficients relation the system

(25) is similar to either

Poincare generator (3) (when kl - k

2

)

or Van-

der-Paul and Rayleigh oscillator (19) (when kl

»k2

or

k2

»k

l

).

For

example,

if

k2

»kl

or kl

==

0 then from (25) we get

Xl

(t)-

ki

(A

2

-

O,5aixj2 -

O,5x~

)x

j

(t)+

alxl

= 0 .

T

(26)

On the contrary,

if

kl

»k2

or

k2

==

0 then we similarly get

..

()

k

l

2

(A2

2

05

2 2

05.

2

).

()

2 0

X

2

t - -

(j)

- ,

(j)

X

2

- , X

2

X

2

t + (J) X

2

= .

T

(27)

Both systems (26) and (27) are models

of

generator type (19).

On the whole it means that synthesized unified Poincare type generator

(25) particularly includes or

Van-der-Paul and Rayleigh oscillator (19).

New Models

of

Nonlinear Oscillations Generators

127

Conclusion

Note the following circumstances: Firstly, order

of

differential

equations

of

attractors (boundary cycles

of

self-oscillating systems) is

always first. That fact is not underlined in oscillations theory literature

for some reason.

Secondly, energetic invariants of kind

1fI;

= 0 (7), (10), and (23)

have been introduced

to

synthesize new types

of

nonlinear oscillation

generators. Such invariants present natural properties

of

these

generators. So on base

of

energetic invariants, using ADAR [1-3], new

types

of

nonlinear oscillation generators are synthesized. These types

include well-known generator equations as special cases.

References

[1]

Kolesnikov A.A. Synergetics control theory. Moscow: Energoatomizdat,

1994.

[2]

Kolesnikov

AA

Synergetics and Control Theory Problems. Moscow:

PHYSMATHLIT,2004.

[3]

Kolesnikov A Synergetics Methods

of

Complex Systems Control: System

Synthesis Theory. Moscow: URSS,

2006.

Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

Подождите немного. Документ загружается.