Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

108

N.

Jevtic

and

J.

S.

Schweitzer

d.

Histograms

of

these

PSRF

are

obtained

at

eaeh position.

c.

The

histograms

are

assembled according

to

position

along

the

seleeted

direction.

8

An

Example

of

Efficient

Nonlinear

Local

Projective

Noise

Reduction

0.002 0.004 0.008 0.000

0.0"10

0,012

(1.014

0.016

O.O'j8

Frequency (mHz)

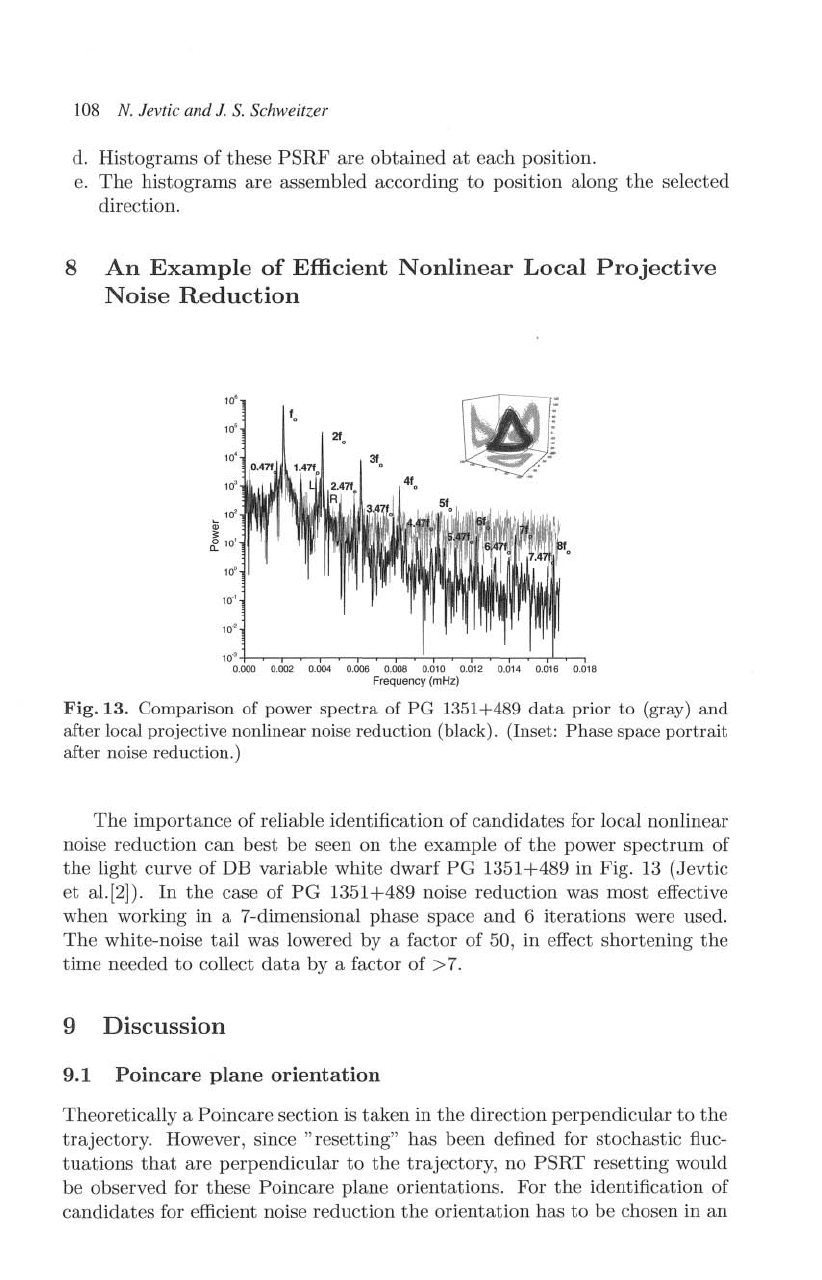
F i

g.

13.

Comparison

of

pmvor

spectra

of

PC

1351+489

data

prior

to

(gray)

and

after

loeal

projective

nonlinear

noise

reduction

(black). (Inset:

Phase

space

portrait

after

nOiSf)

n,duction.)

The

importance

of

reliable identification

of

candidates

for local nonlinear

noise

reduction

can

best

be

seen

on

the

example of

the

power

spectrum

of

the

light;

curve

of

DB

variable white

dwarf

PG

1i351

+489

in

Fig.

1:5

(Jevtic

et

a1.[2]).

In

the

case

of

PG

13C)1

+489

noise

reduction

was

most

effective

when working in a 7-dimensional

phase

space

and

6

iterations

were used.

The

'white-noise

tail

was lowered

by

a factor

of

50,

in

efIt~ct

shortening

the

time

needed

to

collect

data

by a factor

of

>7.

9

Discussion

9.1

Poincare

plane

orientation

Theoretically a

Poincare

section is

taken

in

the

direction

perpendicular

to

the

trajectory.

However, since

"resetting"

has

been

defined for

stochastic

fluc-

tuations

that

are

perpendicular

to

the

trajectory,

no

PSHT

resetting

would

be observed for

these

Poincare

plane

orientations.

For

the

identification

of

candidates

for efficient noise

reduction

the

orientation

has

to

be

chosen

in

a.n

Identifying Chaotic and Quasiperiodic Time-Series Candidates

109

arbitrary

direction in respect

to

the

trajectory.

This

'fuzziness' can, however,

work for us.

If

in

addition

to

the

position of

the

Poincare

surface,

its

orienta-

tion

is varied

through

27r,

then

for

resetting

which is

normal

to

the

trajectory,

the

'

theoretical'

direction

would yield a

minimum

in

th

e

the

number

of

frac-

tional

PSRT.

As a result,

this

orientation

can

be used

to

select a reference

level

that

has

minimal

resetting,

with

additive

noise being responsible for

the

observed noise.

This

has

th

e

potential

to

allow us

to

quantify

the

relative

contributions

of

resetting

and

additive

noise.

Further

work will

address

the

question

of

the

optimal

orientation

of

Poincare

surfaces for

th

e

purpose

of

noise

reduction

and

quantification

in

other

types

of

systems.

9.2

Noise

quantification

Many

questions

remain

to

be answered before a noise

quantification

me

asure

can

be defined.

The

first

that

come

to

mind

are:

If

a 'cl

ea

n'

traj

ec

tory

can

be

defined for comparison, a

measure

of

resetting

are

both

the

amplitude

of

the

displace

ment

off

th

e

trajectory

and

the

le

ngth

of

traj

ec

tory

missing before

reset. Would a

product

or

a

ratio

of

the

two

be

a

'good'

measure

of

the

effect

of

resetting

stochastic

fluctua

tions

?

This

in

turn

raises

the

question

of

the

definition

of

a 'clean'

trajectory.

In

an

iterative

process

what

is

the

standard

numb

er of

it

e

rations?

And

finally,

whether

we

decide

that

the

product

or

the

ratio

of

the

excursions off

the

trajectory

and

the

length

of

the

traj

ec

tory

involved in

the

excursion

are

a

'good'

measur

e,

should

an

average

of

this

measur

e

or

sum

along

the

trajectory

be

used?

Or

should

it

be

normalized on

the

whole

trajectory?

10

Closing

Comments

At

this

time,

many

issues

remain

open

as

can

be

seen in

the

previous s

ect

ion.

In

addition

to

the

procedural

issues

addressed

above also

of

importance

is

the

mor

e general

qu

es

tion

of

the

relationship

of

the

traditional

Fourier power

spectrum

and

the

3-D

PSRF

spectrum

proposed

here.

In

th

e Fourier spec-

trum

of

PC

1351+489

the

ratio

between

the

power

in

the

fundament

al

and

the

first

harmonic

is 10:1.

In

th

e 3-D

PSRF

spectrum

at

th

e average

of

the

data

this

ratio

is 1:1. Could

this

also

be

used as a

measure

of

noise?

Moreover,

digital

data

acquisition,

with

the

possibility

of

variabl

e

binning

as

in

the

e

xampl

e

of

PC

1351+489,

can

yield

an

estimate

of

th

e

time

sca

le

of

the

turbulence.

The

answer

to

this

question

can

only be given

after

th

e effect

of

th

e delay is identified

and

provision is

made

to

elimin

ate

this

dependence.

And

last

but

not

least, could

this

lead

to

an

e

stim

a

te

of

time-local

parameters

of

the

medium

such

as

thermal

response TC timescales

(Montgomery

[3])?

11

Acknowledgements

Dr.

Mausumi

Dikpati

of

HAO,

NCAR

for

th

e

dynamo

mod

el

dat

a.

110

N.

Jevtic

and

J.

S.

Schweitzer

The

WET

for

the

variable white dw

arf

data:

the

xCov12

campaign

tea

m,

particularly

Antonio K

anaa

n

and

Steve Kawaler.

The

University

of

Connecticut

Rese

arch

Foundation

and

the

Bloomsburg

University

Faculty

Travel

Fund

The

Max

Planck

Institut

e for Complex Systems for

the

TISEAN

software:

R.

Hegger, H.

Kantz,

and

T.

Schreiber,

Practical

impl

ementat

ion

of

nonlinear

time

series methods:

The

TISEAN

package, CHAOS,

9,413

(1999)

References

l.J.

Stark

et

al.

Embeddings

for forced

systems

ii:

Stochastic

forcing.

JNonlinSci

,

13:519, 2003.

2.N.

Jevtic

et

al. Nonlinear

time

series analysis of pg1351

+489

lig

ht

intensity

curve

s.

ApJ,

635:527- 539, 2005.

3.M.

Montgom

ery. A

renorm

a

li

za

tion

group

with

periodic behavior. CoAst, 154:38,

2008.

4.J.

Stark.

Embed

dings for forced

system

s

i:

Deterministic

forcing.

JNonlinSci

,

9:255- 332, 1999.

5.F. Takens.

Detecting

strange

attractors

in

turbulence.

In

D. A.

Rand

and

L.-

S.

Young,

editors,

Dynamical

Systems

and Turbulence,

page

366381, London,

1981. Springer-Verlag.

Chaos

from

Observer's

Mathematics

Point

of

View

Dmitriy

Khots

1

and

Boris

Khots

2

1 3710 S.

202nd

Avenue

Omaha,

Nebraska,

USA

(e-mail:

dkhots@cox.net

)

2

Compressor

Controls

Corp

4725 121st

Street

Des

Moines, Iowa,

USA

(e-mail:

bkhots@cccglobal.com)

I I I

Abstract:

This

work

considers

Chaos

aspects

in

a

setting

of

arithmetic

provided

by

Observer's

Mathematics

(see

www.mathrelativity.com).

We

prove

that

the

physi-

cal

speed

is a

random

variable,

cannot

exceed

some

constant,

and

this

constant

does

not

depend

on

an

inertial

coordinate

system.

Certain

results

and

communications

pertaining

to

these

theorems

are

provided.

Keywords:

observer,

chaos,

arithmetic,

derivative,

Lorentz.

1

Introduction

The

following discussion is

based

on

the

work

introduced

in

Khots

et al.[l].

Further

information

can

also

be

found in

Khots

et

al.

[2]

and

Khots

et

al.

[3].

We consider a finite well-ordered

system

of

observers,

where

each

observer

sees

the

real

numbers

as

the

set

of all infinite

decimal

fractions.

The

observers

are

ordered

by

their

level

of

"depth",

i.e. each observer

has

a

depth

number

(hence, we

have

the

regular

integer ordering),

such

that

an

observer

with

depth

k sees

that

an

observer

with

depth

n < k sees

and

deals

(to

be

defined

below)

not

with

an

infinite

set

of

infinite decimal fractions,

but,

actually,

with

a finite

set

of

finite decimal fractions. We call

this

set

W

n

,

i.e.

it

is

the

set

of

all decimal fractions,

such

that

there

are

at

most

than

n digits in

the

integer

part

and

n digits in

the

decimal

part

of

the

fraction. Visually,

an

element

in

Wn looks like _ ... _ . _ ...

_.

Moreover,

an

observer

with

a given

'-v-" '-v-"

n n

depth

is

unaware

(or

can

only

assume

the

existence)

of

observers

with

larger

depth

values

and

for his purposes, he deals

with

"infinity".

These

observers

are

called naive,

with

the

observer

with

the

lowest

depth

number

-

the

most

naive. However, if

there

is

an

observer

with

a

higher

depth

number,

he sees

that

a given observer

actually

deals

with

a finite

set

of finite

decimal

fractions,

and

so on. Therefore, if we fix

an

observer,

then

this

observer sees

the

sets

W

n1

,

...

, W

nk

with

nl

<

..

, <

nk

indicating

the

depth

level,

and

realizes

that

the

corresponding

observers see

and

deal

with

infinity.

When

we

talk

112

D.

Khots

and

B.

Khots

about

observers, we

shall

always

have

some

fixed

observer

(called

'us')

who

oversees all

others

and

realizes

that

they

are

naive.

The

"Wn-observer" is

the

abbreviation

for

somebody

who

deals

with

Wn while

thinking

that

he

deals

with

infinity.

The

following

sections

describe

application

of

the

idea

of

relativity

in

mathematics

to

various

mathematical

fields.

2

Arithmetic

We

begin

by

defining

sets

Wn which

consist

of

all finite

decimal

fractions

such

that

there

are

at

most

n

digits

in

the

integer

part

and

at

most

n

digits

in

the

decimal

part.

That

is,

the

set

Wn

contains

all

elements

of

the

form

a = aO.al ... a

n

where

the

integer

part

can

be

written

as

ao

= bn-1 ... b

o

,

where

b

n

-

l

,

...

, b

o

,

aI,

....

,

an

E

{O,

1, ... , 9}.

If

n <

m,

then

Wn

naturally

embeds

into

Wm

by

placing

O's

in

the

n +

pt

through

mth

decimal

places. We call

the

embedding

ipn,m :

Wn

--> W

m

.

Here

are

some

examples: let 2.34 E W

2

and

then

ip2,4

(2.34) = 2.3400 E W

4

. Similarly,

Wm

projects

onto

Wn

by

cutting

off

the

superfluous

digits

on

the

right

of

the

decimal

point.

Let

cPm.n

: Wm --> Wn

be

the

projection,

then,

for

example,

if 45.4301 E W

4

,

then

cP4,2

(45.4301) = 45.43 E W

2

.

If

the

integer

part

of

a

fraction

contains

more

than

n digits,

then

cPm,n

is

not

defined.

Now, given

C =

CO,Cl"'C

n

,

d = do.dl ... d

n

E Wn we

endow

Wn

with

the

following

arithmetic

(+n,

-n,

X

n

, -;-n):

Definition

1.

Addition

and

subtraction

C ±n d = { C ±

d,

if C ±

dE

Wn

not

defined, if C ± d

¢:.

Wn

N

and

we

write

(( ...

(Cl

+n

C2)

... )

+n

CN)

=

2.=

n

Ci

for

Cl,

...

,

CN

iff

the

contents

i=l

of

any

parenthesis

are

in

W

n

.

Definition

2.

Multiplication

n

n-k

cXnd=

2.=

n

2.=

nO.O

... Ock·O.O ... Od

m

k=O

m=O

'-v-" '-v-"

k-l

m-l

where

c,

d > 0,

Co'

do

E W

n

,

0.0

... 0

Ck'

0.0

... 0 d

m

is

the

standard

product,

and

-

'-v-"

k-l

m-l

k = m = 0

means

that

O.~Ck = Co

and

O.~dm

=

do.

If

either

C < 0

or

k-l

m-l

d <

0,

then

we

compute

iel

Xn

Idl

and

define C

Xn

d = ±

Ici

Xn

Idl,

where

the

sign ± is defined as usual.

Note,

if

the

content

of

at

least

one

parentheses

(in

not

in

W

n

,

then

C Xn d is

not

defined.

Chaos from the Observer's Mathematics Point

of

View

113

Definition

3. Division

-'--

d_{"if3!IEWn

Ixnd=c

C • n -

not

defined, if no such 1 exists

or

it

is

not

unique

Let

n =

2,

so we

are

in W

2

.

Here

are

som

e examples

of

elements

of

W

2

:

3.14,

-99,0.1

E W

2

and

0.115, 123.9, - 100000

1-

W

2

.

Now,

the

examples

of

arithmetic:

2.08

+2

11.9 = 13.98;

(-2.08)

+2

11.9 = 9.82; 80

+2

24 =

not

defined;

21.36-

2

0.87 = 20.49;

1.36-

2

16.95 =

-15.59;

1.36

-2(

-99

.9

5)

=

not

defined;

11

X2

8 = 88;

(-5)

X2

19 =

-95;

11

X2

12 =

not

defined;

3.41

X2

2.64 = 8.98; 3.41

X2

(-2.64)

=

-8.98;

3.41

X2

42.64 =

not

defined;

99.41

X2

1.64 =

not

defined; 0.85

X2

0.02 = 0;

80724

= 20; 1

7n

0.5 =

not

defi

ned

(since we

get

10 differe

nt

I'S); 1

7n

3 =

not

defined (since no 1

exists) .

3

Derivatives

From

the

point

of

view

of

Wn-obs

erv

er

(we will call such observers "naive",

since

they

"think"

that

they

"live" in

Wand

deal

with

W)

a real function Y

of

a r

ea

l variable

x,

y =

y(x),

is called differentiable

at

x =

Xo

(see

Khots

et

al.

[4])

if

there

is a derivative

'()

l'

y(x)

-

y(xo)

y

Xo

=

1m

x->xo.x#xo

x -

Xo

What

does

the

above

statement

mean

from

point

of view of lVm-observer

with

m > n?

It

means

that

I(y(x)

-n

y(xo))

- n (y'(xo)

Xn

(x

-n

xo))1

::;

0.0

...

01

wh

enever Iy(x)

-n

y(xo)1 =

0.0

.

..

OYI

YI

+1

...

Yn

and

I(x

_n

xo)1

=

'-v--'

~

n I

0.0

...

OXk

Xk+1

...

Xn

for 1

::;

k,

I

::;

n,

and

Xk

- non-zero

digit

.

'-.;---'

k

We now

state

the

main

theorems.

Theorem

1.

From the point

of

view

of

a W m -obse

rver

a derivative calculated

by a Wn -observer (m >

n)

is

not

defined uniquely.

Proof.

Put

y'(xo)

=

±ao

·

a1

...

a

p

a

p

+l .

,.

an

with

aO

·al

...

a

p

a

p

+l

...

an

;::::

o

and

p

::;

n.

Then

0.0

...

OYI

Yl+l

..

.

Yn

=

~

I

aO.a1

...

a

p

a

p

+1

...

an

Xn

0.0

...

OXk

Xk+1

...

Xn

=

'-.;---'

k

aO.a1

...

a

p

b

p

+

1

..

, b

n

Xn

0.0

...

OXk

Xk+1

...

Xn

'-.;---'

k

for

any

digits b

p

+

1

,

...

,b

n

and

p = n -

k.

Hence

y'(xo)

E V = {±ao.a1

.,

. a

p

a

p

+1

...

a

n

la

p

+1,""

an E

{O,

1,

...

, 9}}

and

IVI

=

10

k

.

QED.

114

D.

Khots and

B.

Khots

Theorem

2. From the point

of

view

of

a Wm -observer with m > n, ly'(xo)1

::;

C~k,

where

C~k

E W n is a constant defined only

by

n, I, k and

not

dependent

on

y(x).

Proof. We

hav

e

±

O.

0 .

..

OYI

Yl+1

.

..

Yn

= (±aO·a1

...

an)

Xn

(±O.O

...

OXk

Xk+1

.

..

xn)

'--v--'

'--v--"'

I k

with

Xk

- non-zero digit

and

aO.a1

...

a

p

a

p

+1

..

. an

2'

O.

Now, if I > k

then

ao

=

0;

if 1= k

then

ao::; 9

and

if 1< k

then

ao

< 9 x 10k-1. H

en

ce

QED.

{

I,

if

I > k

Cl,k

= 10

if

I = k

n ,

9 X 10k-

1,

if I < k

Theorem

3.

From the point

of

view

of

a W m -observer, when a Wn -observer

(with m > n

2'

3)

ca

lculat

es

the second derivative:

Y(X3)-Y(XJ)

Y(X2)-Y(XO)

Y"(Xo) = lim

Xl

-+XO

,X l¥=-

XO

,

X2---+XO

,

X2¥:XO,X3---+X

l

,X:3#

X l

(x3-xd

X2

-

X

O

we

get the following inequality:

n

provided that

y"

(xo) i-

O.

Proof.

For

the

Wm-observer e

xistenc

e of y"(xo)

means

that

1((y(X3)

-n

y(xd)

Xn

(X2

-n

xo)

-n

((Y(X2)

-n

y(:ro))

Xn

(X2

-n

xo))) - n y"(xo)

Xn

((I

X

2

-n

xol

Xn

I

X

3

-n

:];

11)

Xn

IX1

-n

xol)1

::;

O.~

,

whenever

I(X2

-n

n

~

xo)1

::;

0.0

...

Op

*

...

* a

nd

I(X3

-n

xdl

::;

0.0

. ..

Oq

* ... *

and

I(

X1

-n

xo)1

::;

'-v-"

k I

n

~

0.0

..

.

Or

* ... * where p,

q,

r

are

non-zero digits, asterisks

are

any

digits

and

'-v-"

s

3

::;

k + I + s

::;

n.

Then

given y"(xo) i- 0 we

hav

e

(IX2

- n xol

Xn

IX3

- n

Xli)

Xn

IX1-nxol2'

O.~.

QED.

n

Chaos from the Observer's Mathematics Point

of

View

lIS

4

Chaos

theory

interpretation

The

following

hypotheses

illustrate

possible

Chaos

theory

interpretation

of

•

Hypotheses

1.

Theorem

1

could

offer

an

explanation

of

why

physical

spe

ed

(or

acceleration)

is

not

uniquely

defined

and,

from

the

point

of

vi

ew

of

a

measurement

system

(observer),

it

is possible

to

consider

speed

(or

acceleration)

as a

random

variable

with

distribution

dependend

on

the

measurement

system.

Let

v

be

the

speed

with

v =

Vo.1il

...

Vn

- k +

~;;-,:k

where

~;;-,:k

E {a. 0 . . . ° V

n

-k+1

...

V

n

} -

random

variable, m > n,

and

the

'-v--"

n-k

distribution

function

is

F::.

,k(x) =

p(~;;-,:k

< x).

•

Hypothes

es

2.

Th

eorem 2

could

offer

an

explanation

of

why

the

speed

of

any

physical

body

cannot

exceed

some

constant,

(the

speed

of

light, for

example).

Independence

of

this

constant

on

explic

it

expression

of

space-

tim

e

function

could

offer

an

explanation

of

why

the

speed

of

light

does

not

d

epe

nd

on

an

in

ertia

l

coordinate

system.

•

Hypo

theses 3.

Th

eorem

3

could

offer

an

explantion

of

the

various

uncer-

tainty

principles,

when

a

product

of

a finite

number

of

physical

variables

has

to

be

not

less

than

a

certain

con

s

tant.

This

can

be

seen

not

just

from

consideration

of

second

derivatives,

but

of

any

derivative.

•

Hypoth

eses 4.

Theorems

1, 2,

and

3

combined

may

provid

e

an

insight

into

the

connection

between

classical

and

quantum

mechanics

.

5

Newton

equation

with

chaos

theory

interpretation

Let

F(x

, t) = m

Xn

X.

Then

we

have

the

following

Theorem

4.

If

the

body

with mass m = mO.m1

...

mkmk+1

...

m

n

, with

mE

W

n

,

mov

es

with acceleration

X,

Ixl

= X

O.X1

...

XI

X

I+1

..

,

Xn,

with X E W

n

,

and mo =

TTL1

=

...

=

mk

= 0,

mk

+1

01

0, k <

n,

Xo

=

Xl

=

...

=

Xl

= 0,

l <

n,

k + l + 2 E W

n,

n < k + I + 2

:::::

q,

then F (x, t) = 0.

Proof. In this case m

Xn

Ixi

= 0.

QED.

Corollary

1.

If

1=

n - 1 and k = 0, i.e., m < 1, then

F(x,

t).

Theorem

5.

If

1=

n - 1 and

xn

01

° then IF(x,

t)1

< 9.

Proof. IF(x,

t)1

= m

Xn

I

xl

< 9

...

9.9

.

..

9

xn

O. O

...

09

=

8.9

..

.

91

< 9.

-

'-v--" '-v--"

'-v--"

n

n n- 1

n-1

QED.

Theorem

6.

Ifmo

~~,

° < p

:::::

n,

xo

~~,

° <

r:::::

n,

n <

p+r:::::

p r

q,

then there is no force

F(x,

t), such that

F(x

, t) = m

Xn

X.

Proof. m

Xn

x>

mo

Xn

Xo

does

not

exist

in

W

n

.

QED.

116

D.

Khots and

B.

Khots

6

Schrodinger

equation

with

chaos

theory

interpretation

Consider

the

following:

~Ch

Xn

h)

Xn

wxx

+n

((2 Xn

m)

Xn

V)

Xn

W =

i((2

xn

m)

xn

h)Wt , where W =

w(x,

t), h is

the

Planck's

Constant,

h =

1.054571628(53) X

10-

34

m

2

kgjs.

Then

we have

the

following

Theorem

7.

Let

36 < n < 68, m = mO.m1

...

mkmk+1

...

m

n

, with m E

W

n

, mo = m1 =

...

=

mk

= 0, mk+1 # 0, k + 35 <

n,

V = 0,

then

,T,

_

,T,O

,T,l

,T,I,T,I+l

,hn d

,T,O

-

,T,l

- °

,T,I+l

,T,n

f d

'¥t

-

'¥t

·'¥t

...

'¥t'¥t

...

'¥t

an

'¥t

-

...

'¥t

-

,'¥t

,

...

,

'¥t

are

ree

an

in

{O,

1,

...

,

9},

where l = n

~

k

~

36, i.e.,

Wt

is a random variable, with

n

~

Wt

E

{(O.~*

...

*)}, where * E

{O,

1,

...

, 9}.

Proof. We have

~(hxnh)

= 0,

(2x

n

m)x

n

V = 0, i.e.,

i((2x

n

m)x

n

h)w

t

=

°

and

l = n

~

k

~

36.

QED.

Corollary

2.

Let

36 < n < 68, m = mO.m1

...

mkmk+l

...

m

n

, with m E

W

n

,

rno

=

rn1

=

...

=

mk

= 0, mk+1 # 0. Also, let V =

VO'V1

...

VsVs+1

...

V

n

,

with V E W

n

,

Vo

= 1JI =

...

=

Vs

= 0, V

s

+1

# 0, with

{kk

+ 35

2

< n , then

+s+

>n

Wt

=

wp

.wl

. . . wiw;+l

..

.

w;:

and

wp

=

..

.

wi

= 0, W;+l, .

..

,w;: are free

and

in

{O,

1,

...

, 9}, where l = n

~

k

~

36, i.e.,

Wt

is a random variable, with

n

~

Wt

E

{(O.~*

...

*)}, where * E

{O,

1,

...

,

9}.

I

7

Lorentz

transform

with

chaos

theory

interpretation

Let

K

and

K'

be

two

inertial

coordinate

systems

with

x~axis

and

x'

~axis

permanently

coinciding. We consider only

events

which

are

localized

on

the

x(x')~axes.

Any

such

event

is

represented

with

respect

to

the

coordinate

system

K

by

the

abscissa

x

and

the

time

t,

and

with

respect

to

the

system

k'

by

the

abscissa

x'

and

the

time

t'

when

x

and

t

are

given. A light signal,

which is

proceeding

along

the

positive

x~axis

is

transmitted

according

to

the

equation

x = C Xn t

or

x

~n

C

Xn

t = 0. Since

the

same

light-signal

has

to

be

transmitted

relative

to

k'

with

the

velocity

c,

the

propagation

relative

to

the

system

k'

will

be

represented

by

the

analogous

formula

x'

~n

C Xn t' = °

Those

space-time

points

(events) which satisfy

the

first

equation

must

also

satisfy

the

second

equation.

Obviously will

be

the

case

when

the

relation

Al

xn

(x'

~n

C

xn

t') =

ILl

Xn

(.1:

~n

C

Xn

t) is fulfilled in general,

where

A1,IL1

E W

n

,

IA11,

IIL11

?:

1

are

constants;

for,

according

to

the

last

equation

disappearance

of

(x

~n

C

Xn

t) involves

the

disappearance

of

(x'

~n

C

Xn

t').

Chaos from the Observer's Mathematics Point

of

View

117

Note,

that

classical

equation

x' - ct' =

).,(x

- ct) is

not

valid since if)., < 1,

x -

ct

=

0.0

...

01,

then).,

Xn

(x

-n

C x

t)

=

x'

-n

C

Xn

t'

=

O.

If

we

apply

'-v--'

n-l

quite

similar considerations

to

light

rays

which

are

being

transmitted

along

the

negative

x-axis,

we

obtain

the

condition

).,2

Xn

(x'

+n

c

Xn

t') =

IL2

Xn

(x

+n

c

Xn

t)

with

)"2,IL2

E W

n

,

1).,21,

IIL21

~

1.

For

the

origin

of

K'

we have

permanently

x'

= 0

and

x = v

Xn

t, where v is

the

velocity

with

which

the

origin of

K'

is

moving relative

to

K.

Then

we have

{

).,l

Xn

(v

Xn

t

-n

C

Xn

t')

=

ILl

Xn

(-C

Xn

t')

(Ad

).,2

Xn

(v

Xn

t

+n

C

Xn

t') =

IL2

Xn

(C

Xn

t')

(A

2

)

These

two

equations

(Ad

and

(A

2

)

have

to

be

identical, i.e., for each of

equation,

the

sets

(t', t) have

to

be

the

same,

or

there

is a dependence A,

t=f(t')

Furthermore,

the

principle

of

relativity

teaches us

that,

as

judged

from

K,

the

length

of a

unit

measuring-rod

which is

at

rest

with

reference

to

k'

must

be

exactly

the

same

as

the

length, as

judged

from

K',

of

a

unit

measuring-

rod

which is

at

rest

relative

to

K.

Let

x'

= 1

and

t =

O.

Then

we have

the

following

system

(Ed:

{

).,l

Xn

x =

ILl

Xn

(1

-n

C

Xn

t')

).,2

Xn

x =

IL2

Xn

(1

+n

C

Xn

t')

Also, let x = 1

and

t' =

O.

Then

we have

the

following

system

(E2):

And

now

we

have

the

equation

(E):

x =

x'

where x is

the

solution

of

(Ed

and

x'

is

the

solution

of

(E2)' Now

we

have

a

system

{

(A)

(E)

Solution of

this

system

is

the

set

S = {().,l,

ILl,

).,2,

IL2)},

where

).,1,

ILl,

).,2,

IL2

E

W

n

,

1).,11,

lILli,

1).,21,

IIL21

~

1.

We call

the

system

of

equations

{

).,l

Xn

(Xl

-n

C

Xn

tl) =

ILl

Xn

(x

-n

C

Xn

t)

).,2

Xn

(x'

+n

C

Xn

t') =

IL2

Xn

(x

+n

C

Xn

t)

with

().,l,

ILl,

).,2,

IL2)

E S

the

Lorentz

Transform

in

Observer's

Mathematics.

Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications

Подождите немного. Документ загружается.